On the Use of JMAK Theory to Describe Mechanical Amorphization: A Comparison between Experiments, Numerical Solutions and Simulations
Abstract
1. Introduction
- The initial parent phase is progressively and completely replaced by a product phase;
- The volume of any transformed region is tiny with respect to the whole volume of the system;
- Nucleation is random;
- The shape of the growing phase is convex;
- The linear growth rate can be expressed as a product of a time-dependent function and a direction-dependent function.
2. Materials and Methods
3. Results and Discussion
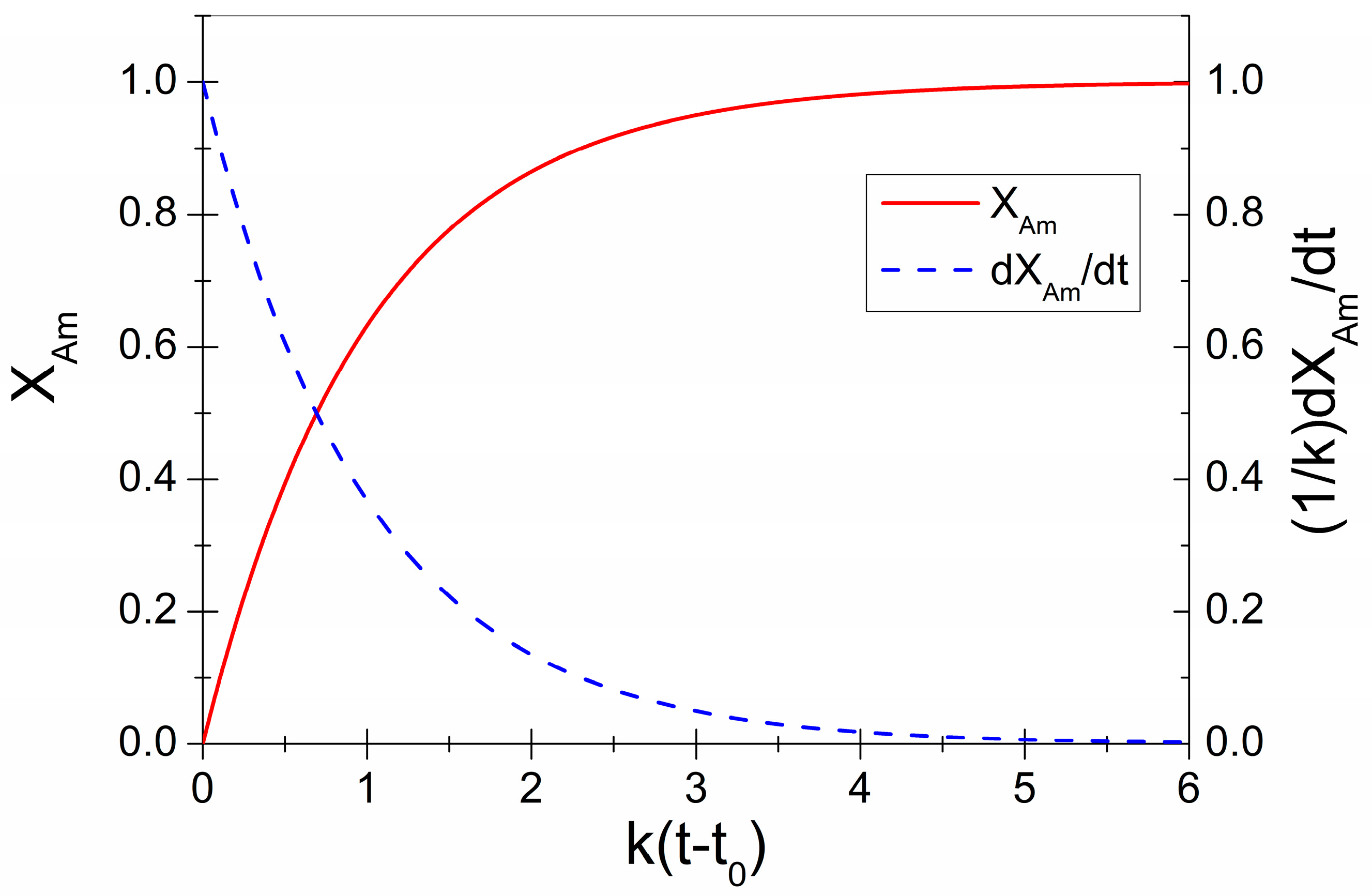
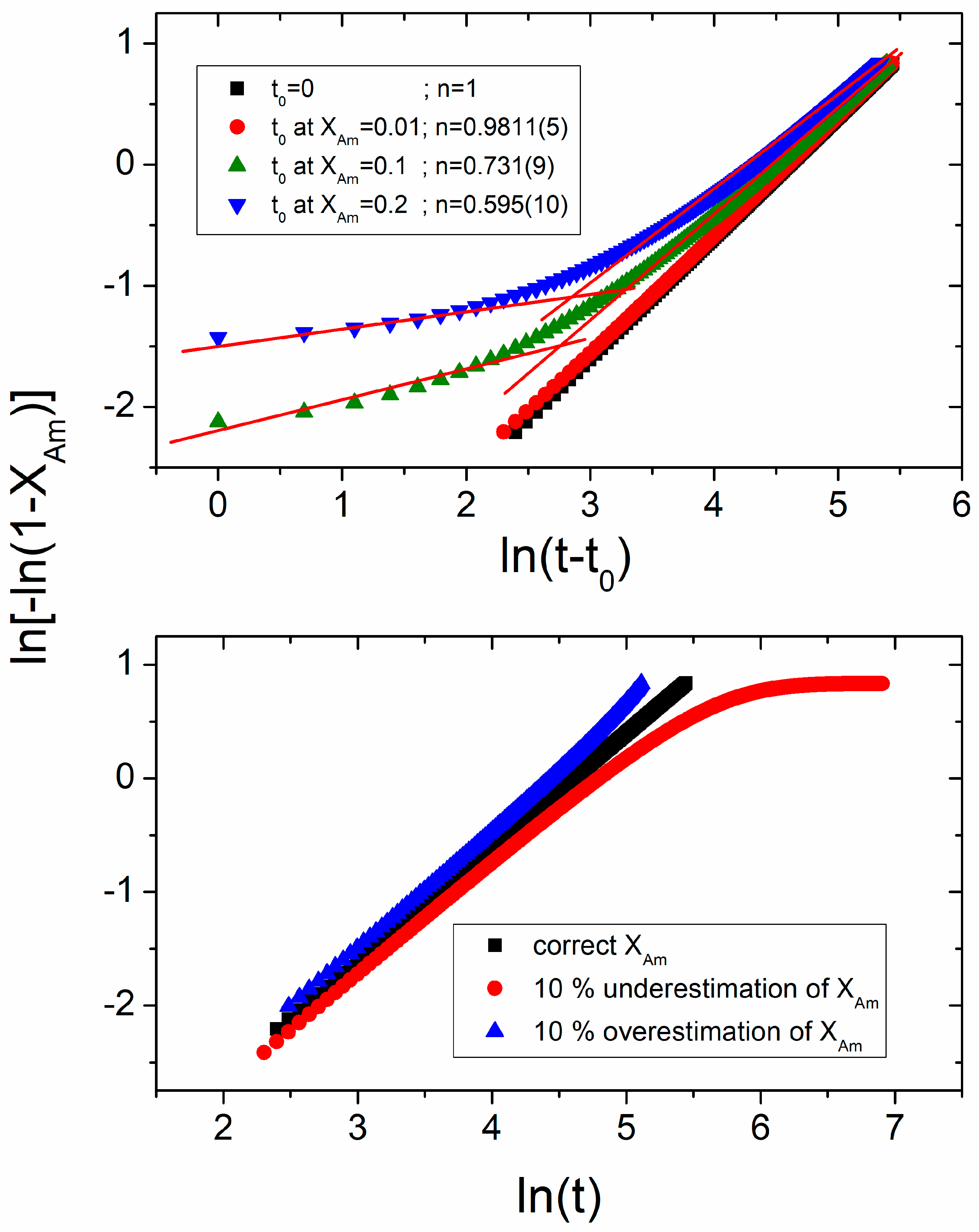
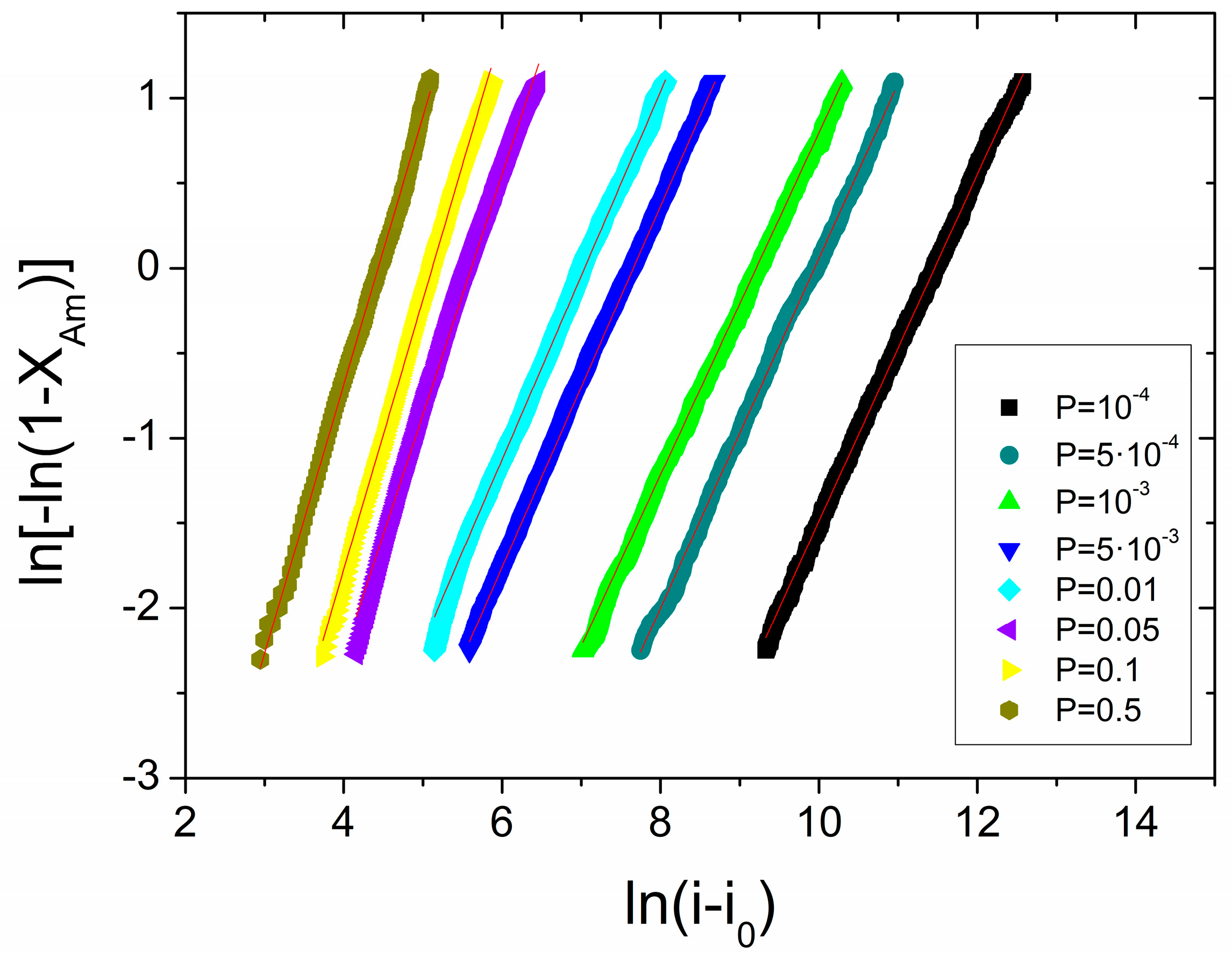
3.1. Mechanical Amorphization Described by JMAK Theory
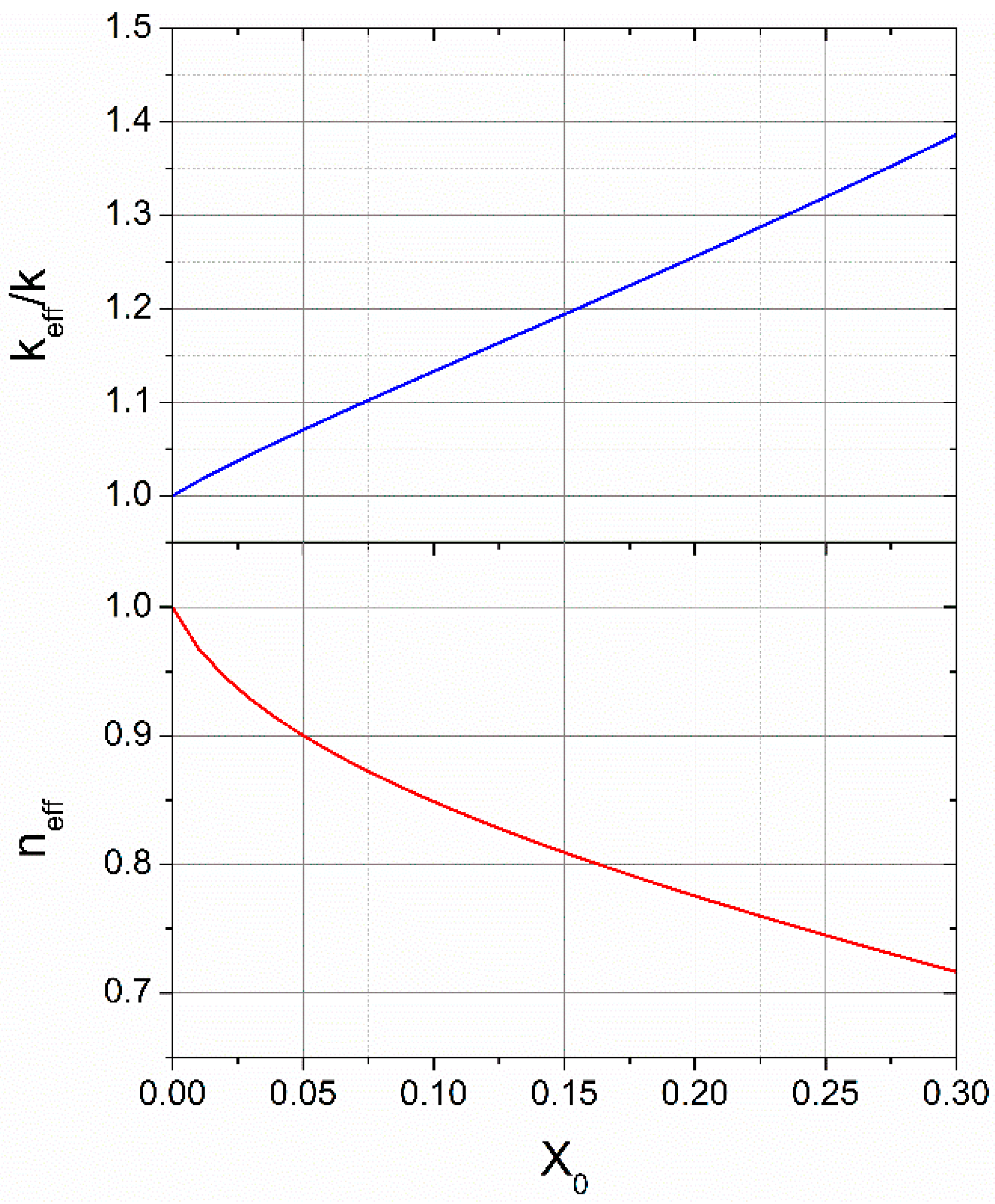
Explanation for Effective Avrami Exponents Below 1
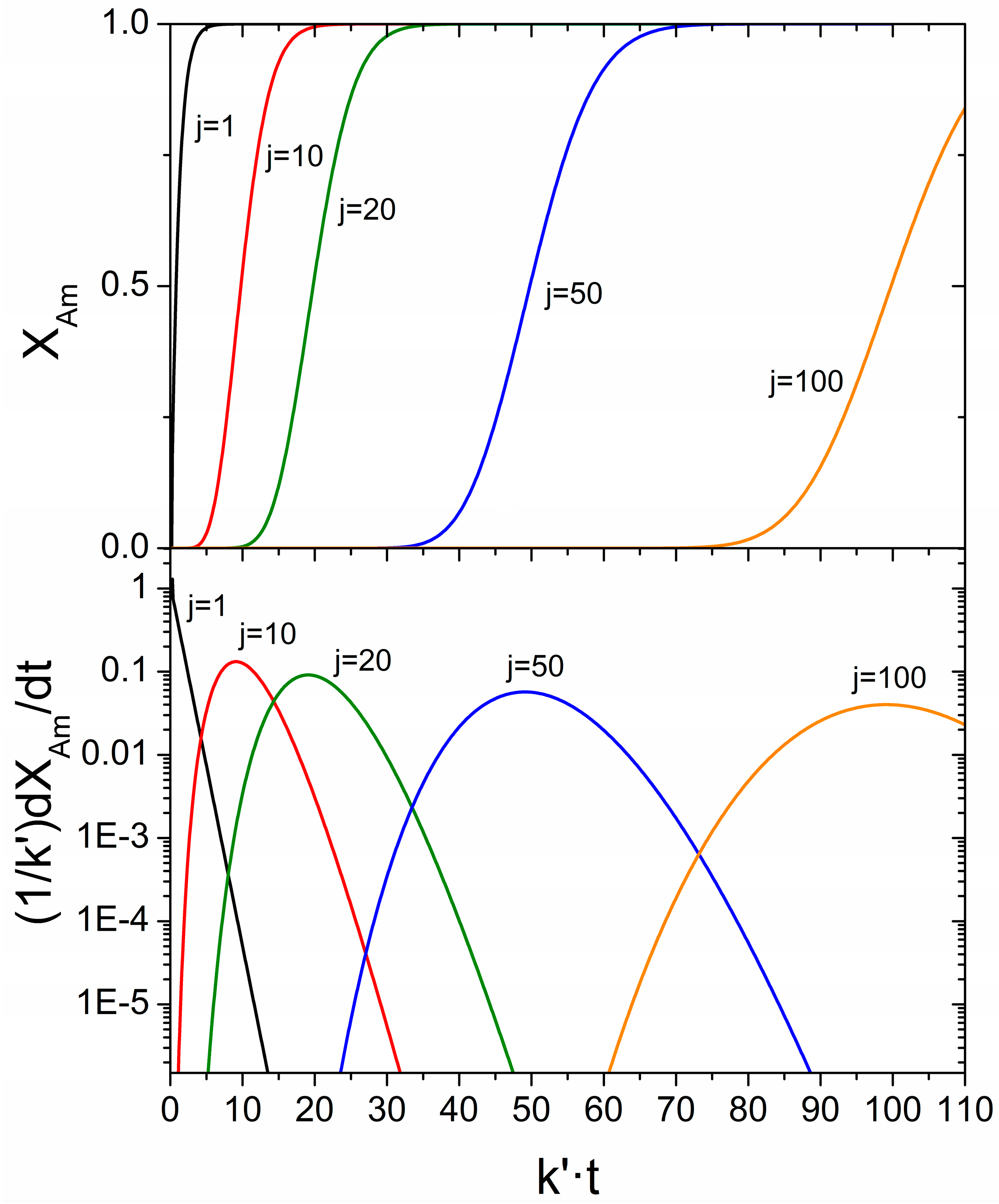
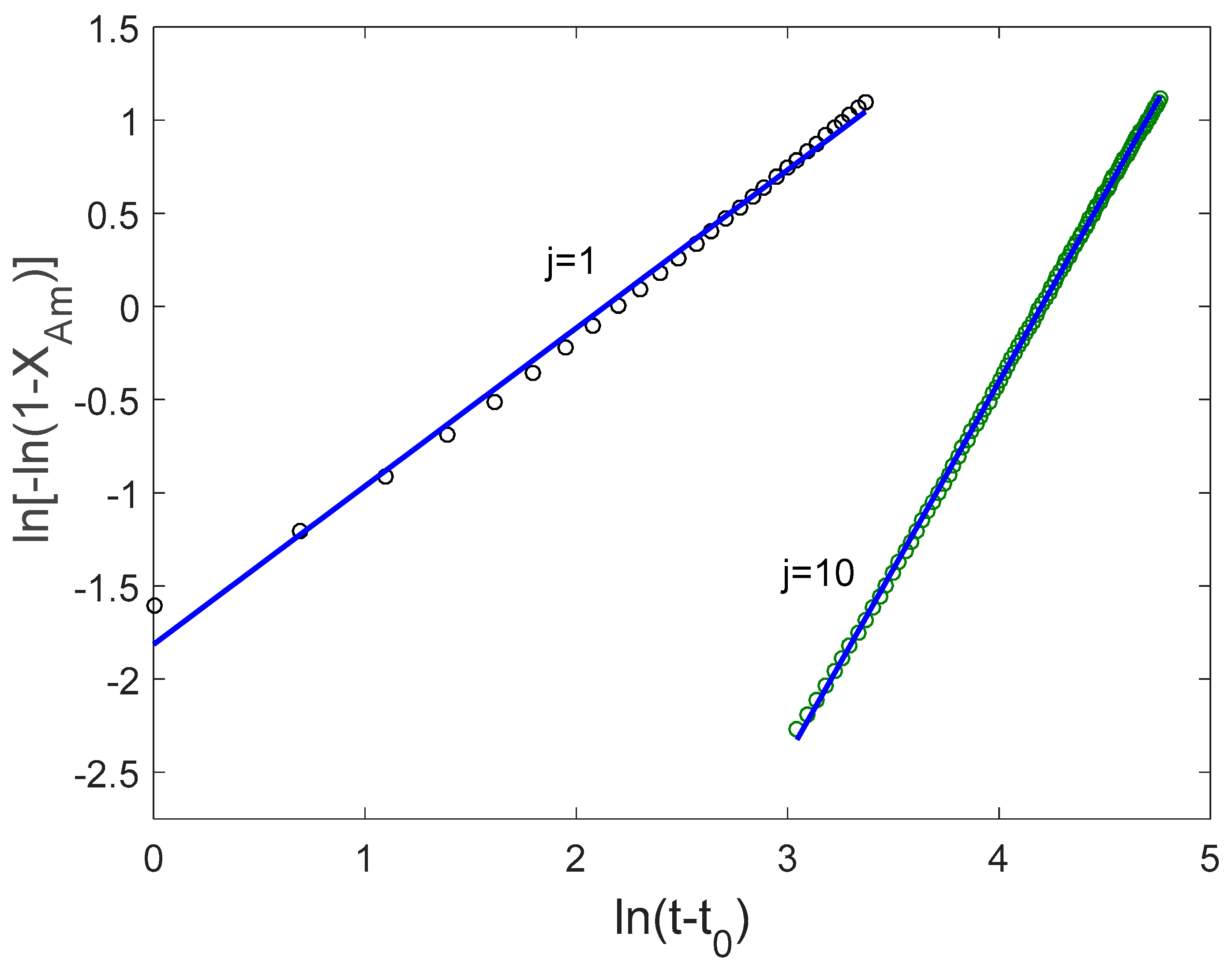
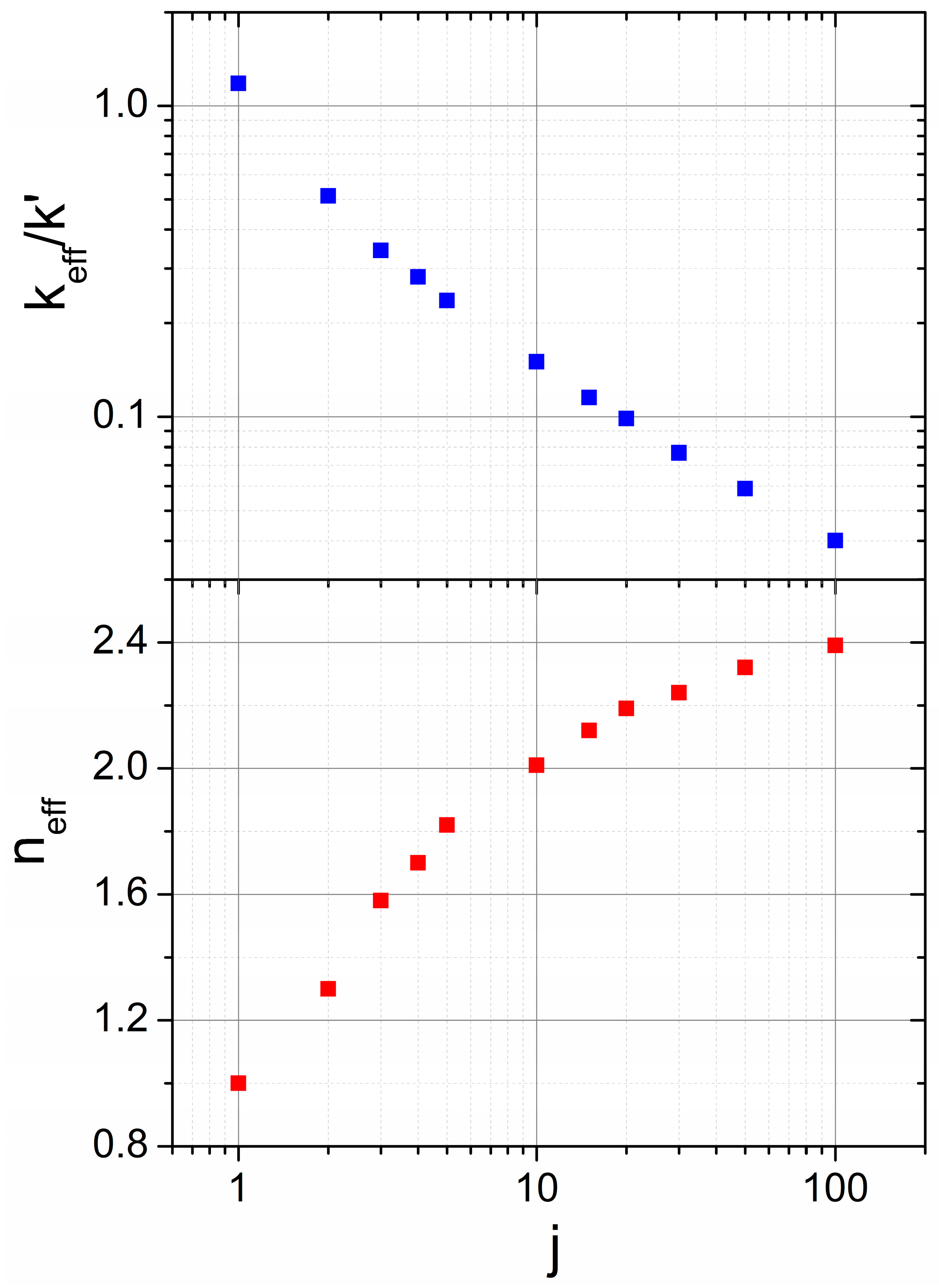
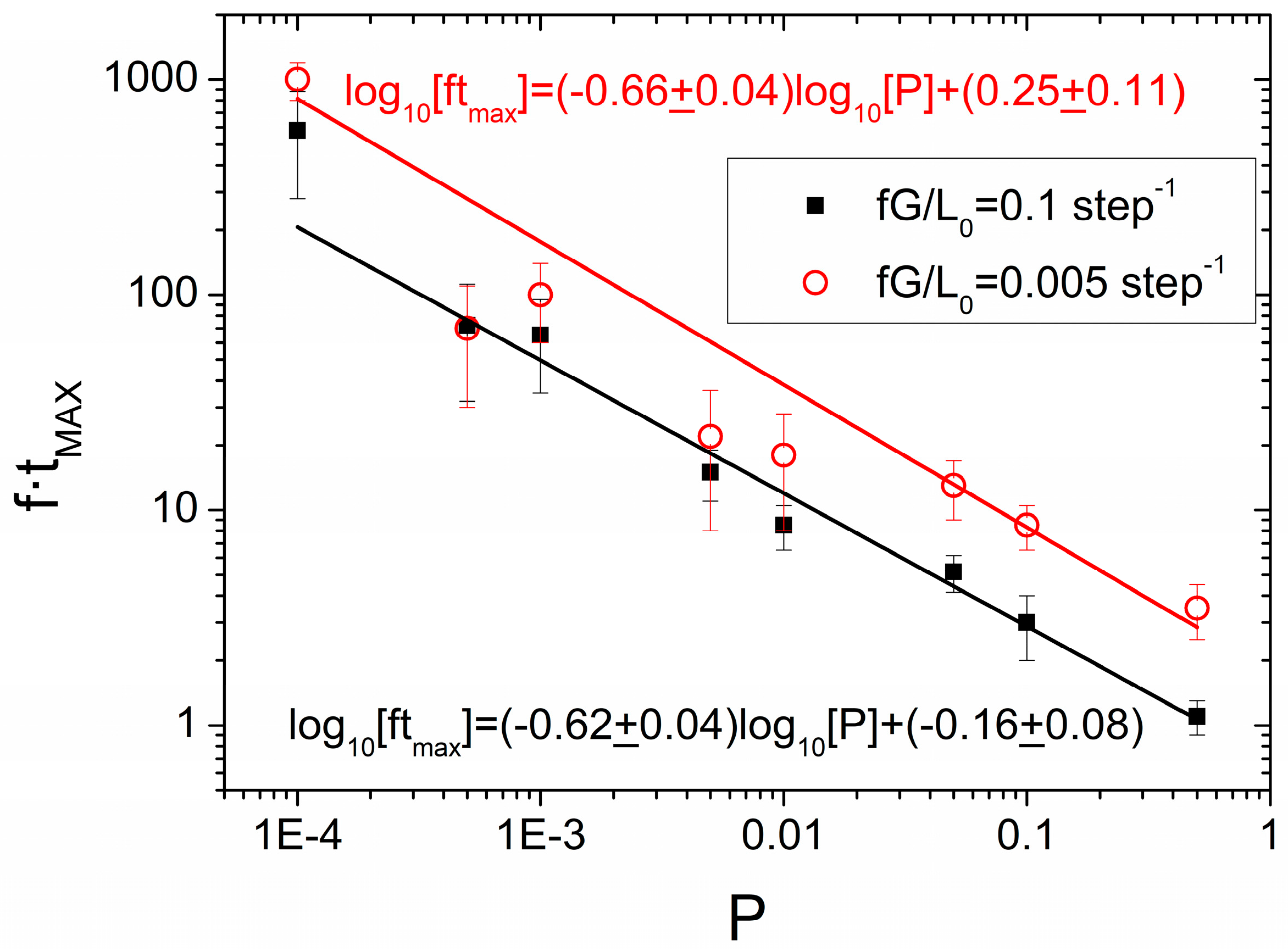
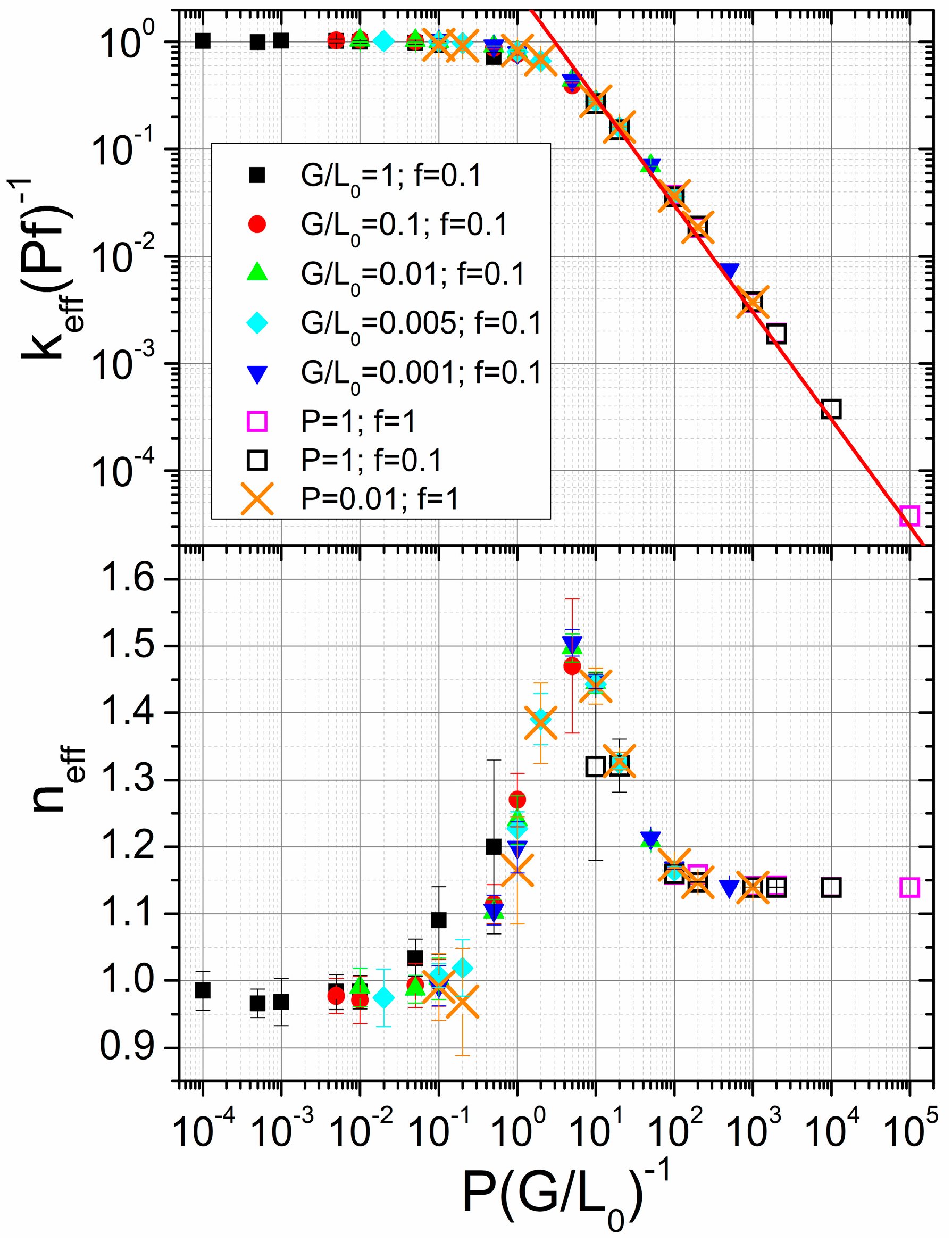
3.2. Mechanical Amorphization Described by the Number of Collisions
Application of the JMAK Analysis to Delogu and Cocco’s Model
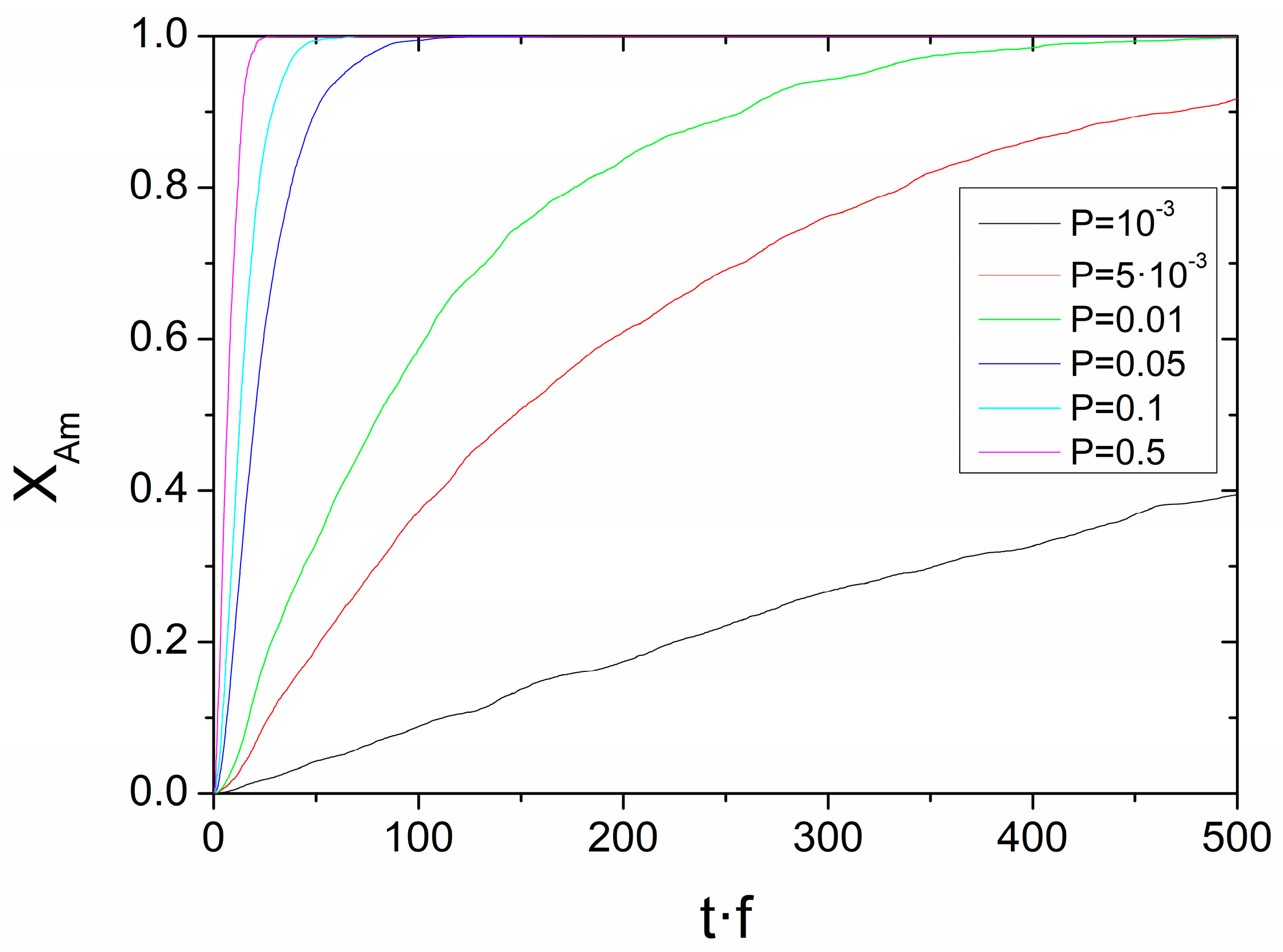
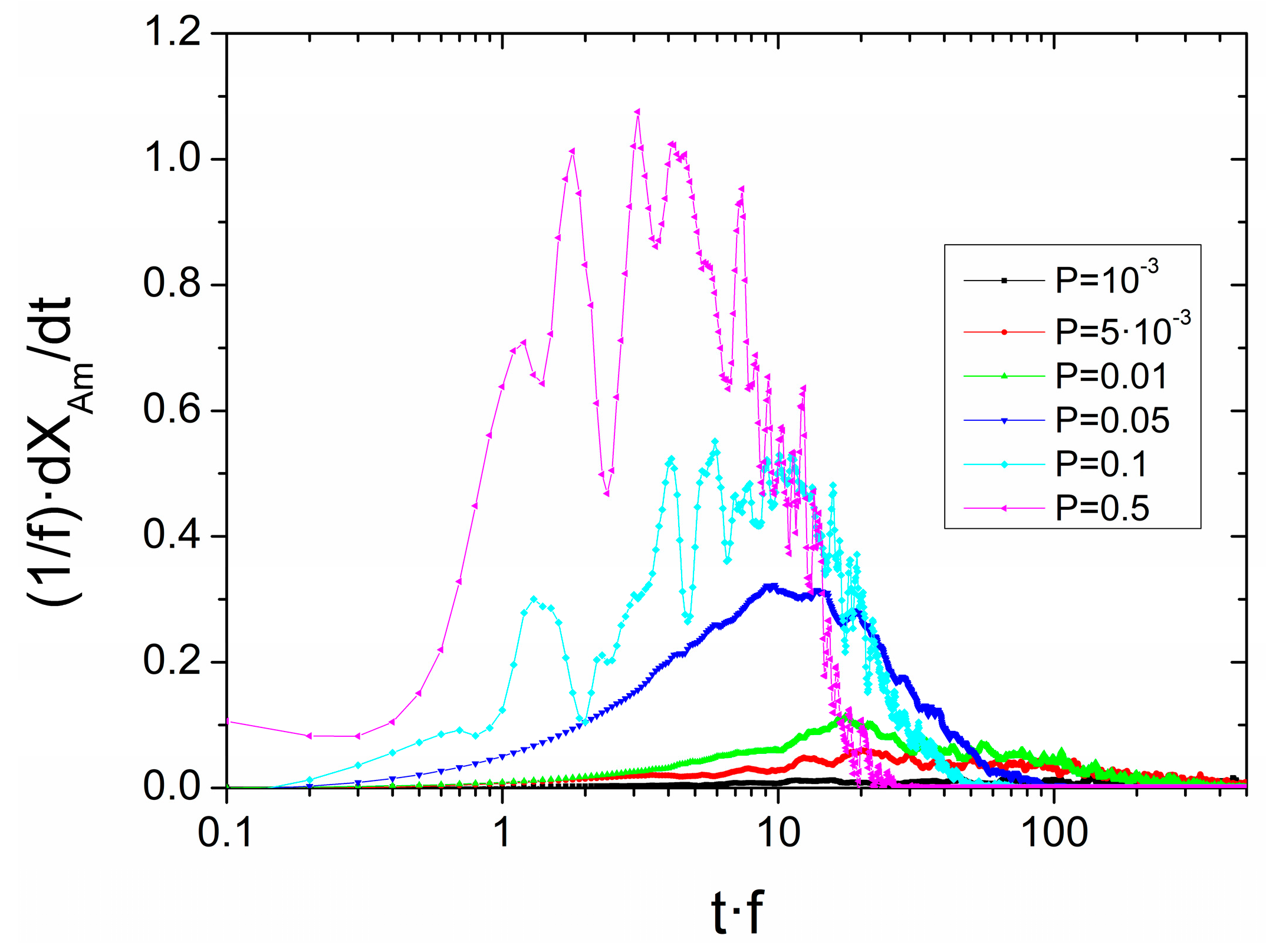
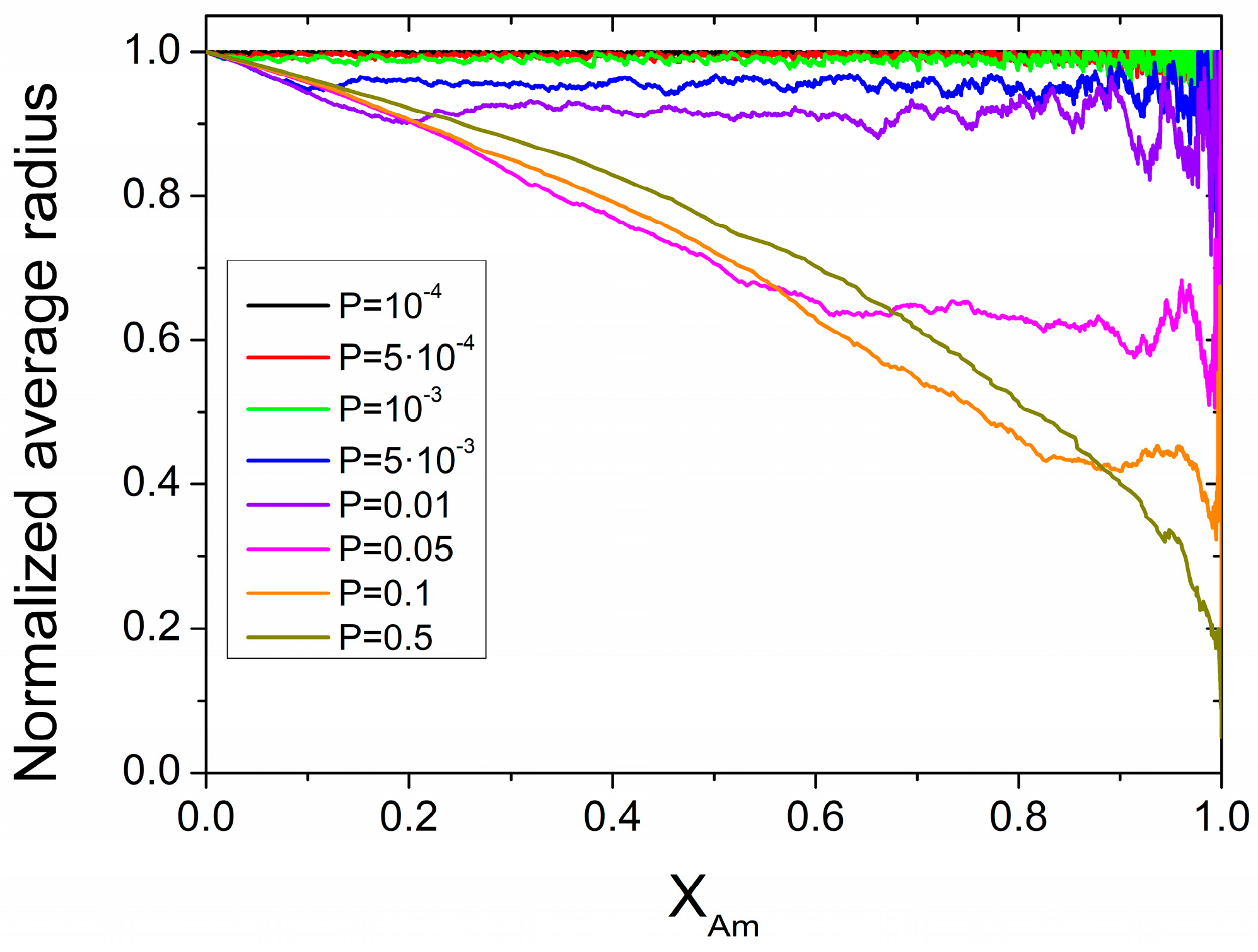
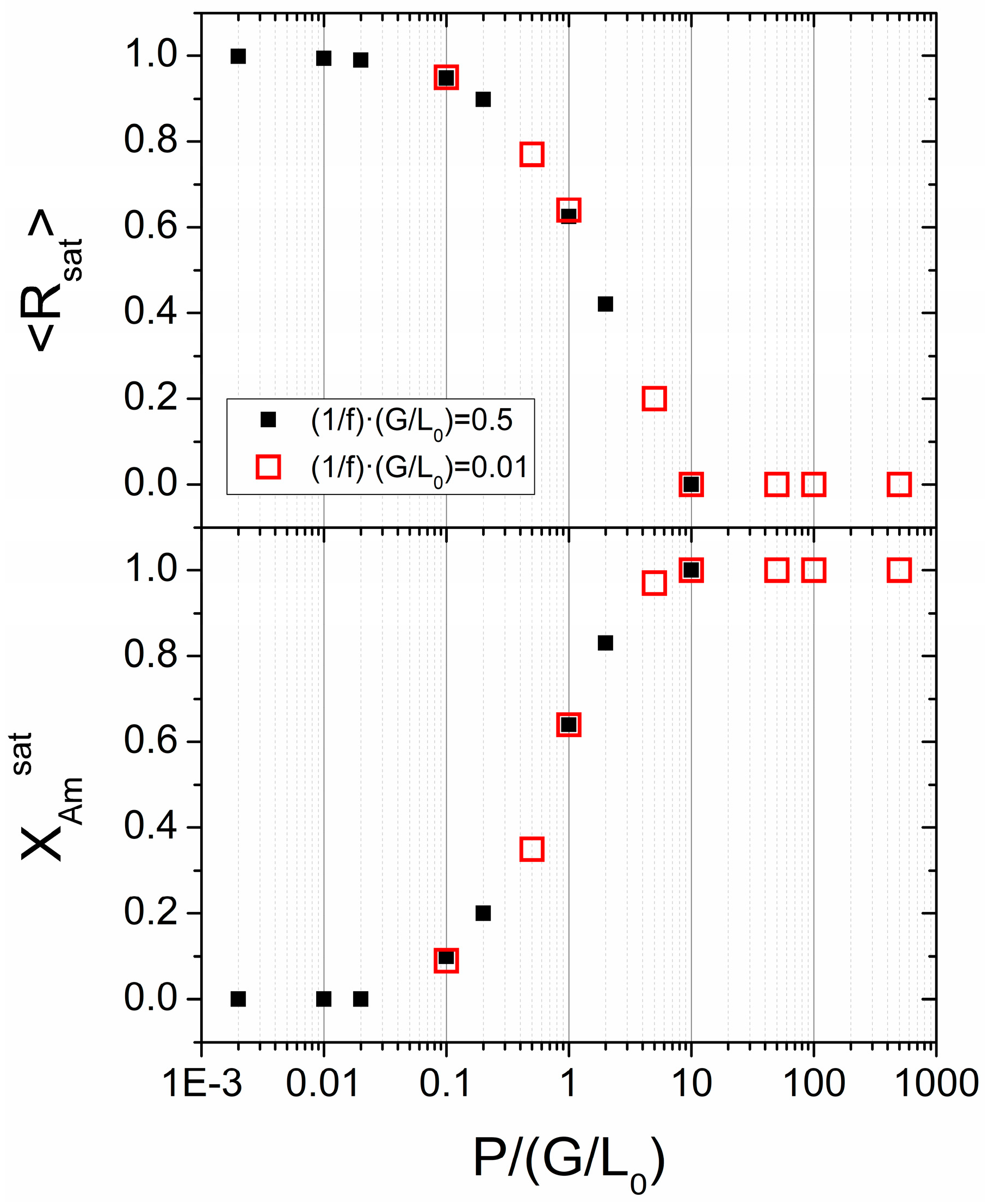
3.3. Simulations Based on a Probabilistic Activation of the Amorphization Process
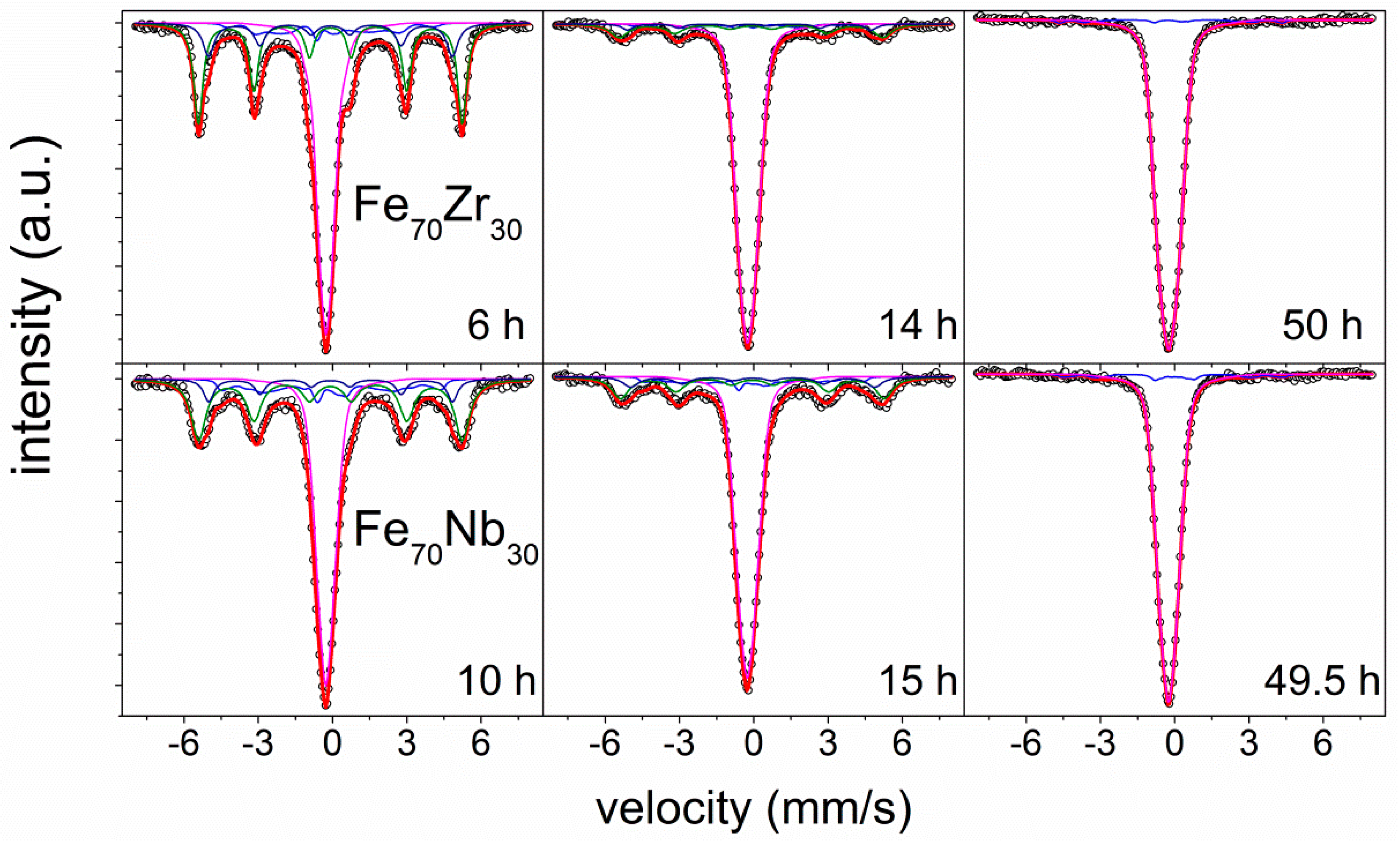
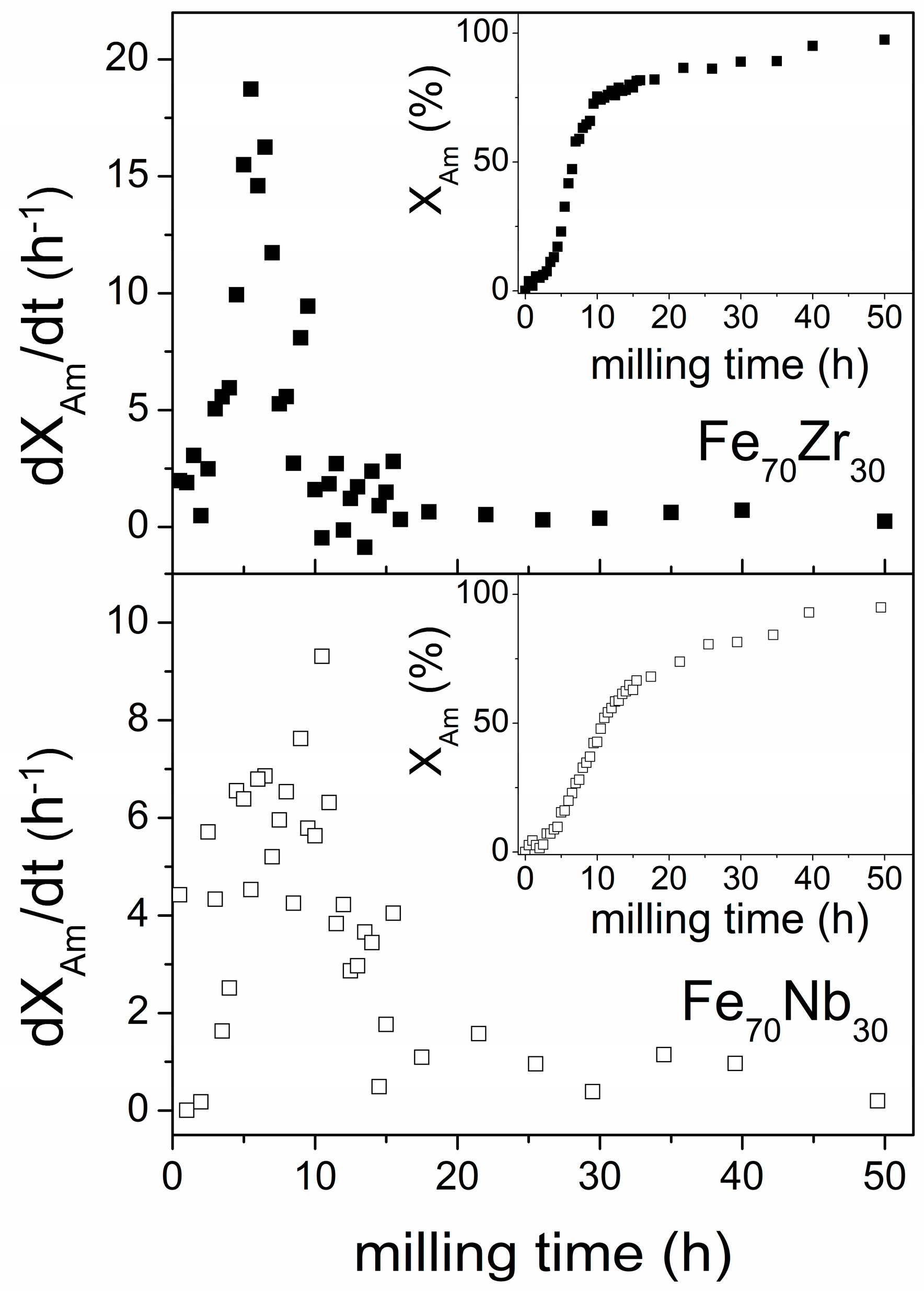
3.4. Experimental Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Klement, W.; Willens, R.H.; Duwez, P. Non-crystalline structure in solidified gold-silicon alloys. Nature 1960, 187, 869–870. [Google Scholar] [CrossRef]
- Suryanarayana, C. Mechanical alloying and milling. Prog. Mater. Sci. 2001, 46, 1–184. [Google Scholar] [CrossRef]
- Balaz, P.; Achimovicova, M.; Balaz, M.; Billik, P.; Cherkezova-Zheleva, Z.; Criado, J.M.; Delogu, F.; Dutková, E.; Gaffet, E.; Gotor, F.J.; et al. Hallmarks of mechanochemistry: From nanoparticles to technology. Chem. Soc. Rev. 2013, 42, 7571–7637. [Google Scholar] [CrossRef] [PubMed]
- Yermakov, A.Y.; Yurchikov, Y.Y.; Barinov, V.A. Magnetic-properties of amorphous powders prepared by the mechanical grinding of Y-Co alloys. Fiz. Met. Metallogr. 1981, 52, 1184–1193. [Google Scholar]
- Koch, C.C.; Cavin, O.B.; McKamey, C.G.; Scarbrough, J.O. Preparation of amorphous Ni60Nb40 by mechanical alloying. Appl. Phys. Lett. 1983, 43, 1017–1019. [Google Scholar] [CrossRef]
- Schultz, L. Formation of amorphous metals by mechanical alloying. Mater. Sci. Eng. 1988, 97, 15–23. [Google Scholar] [CrossRef]
- Moreno, L.M.; Blázquez, J.S.; Ipus, J.J.; Borrego, J.M.; Franco, V.; Conde, A. Magnetocaloric effect of Co62Nb6Zr2B30 amorphous alloys obtained by mechanical alloying or rapid quenching. J. Appl. Phys. 2014, 115. [Google Scholar] [CrossRef]
- Ipus, J.J.; Blázquez, J.S.; Conde, C.F.; Franco, V.; Borrego, J.M.; Lozano-Pérez, S.; Conde, A. Relationship between mechanical amorphization and boron integration during processing of FeNbB alloys. Intermetallics 2014, 49, 98–105. [Google Scholar] [CrossRef]
- Schwarz, R.B.; Johnson, W.L. Formation of an amorphous alloy by solid-state reaction of the pure polycrystalline metals. Phys. Rev. Lett. 1983, 51, 415. [Google Scholar] [CrossRef]
- Weeber, A.W.; Bakker, H. Amorphization by ball milling: A review. Phys. B Condens. Matter. 1988, 153, 93–135. [Google Scholar] [CrossRef]
- Bellon, P.; Averback, R.S. Non-equilibrium roughening of interfaces in crystals under shear: Application to ball milling. Phys. Rev. Lett. 1995, 74, 1819–1822. [Google Scholar] [CrossRef] [PubMed]
- Hammerberg, J.E.; Holian, B.L.; Röder, J.; Bishop, A.R.; Zhou, S.J. Nonlinear dynamics and the problem of slip at material interfaces. Phys. D Nonlinear Phenom. 1998, 123, 330–340. [Google Scholar] [CrossRef]
- Lund, A.C.; Schuh, C.A. Atomistic simulation of strain-induced amorphization. Appl. Phys. Lett. 2003, 82. [Google Scholar] [CrossRef]
- Delogu, F.; Cocco, G. Molecular dynamics investigation on the role of sliding interfaces and friction in the formation of amorphous phases. Phys. Rev. B 2005, 71. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. On the statistical theory of the crystallization of metals. Bull. Acad. Sci. USSR 1937, 1, 355–359. [Google Scholar]
- Johnson, W.A.; Mehl, R.F. Reaction kinetics in processes of nucleation and growth. Trans. Am. Inst. Min. Metall. Eng. 1939, 135, 416–442. [Google Scholar]
- Avrami, M. Granulation, phase change, and microstructure kinetics of phase change. III. J. Chem. Phys. 1941, 9, 177–184. [Google Scholar] [CrossRef]
- Siegrist, M.E.; Siegfried, M.; Löffler, J.F. High-purity amorphous Zr52.5Cu17.9Ni14.6Al10Ti5 powders via mechanical amorphization of crystalline pre-alloys. Mater. Sci. Eng. A 2006, 418, 236–240. [Google Scholar] [CrossRef]
- Delogu, F.; Takacs, L. Mechanochemistry of Ti–C powder mixtures. Acta Mater. 2014, 80, 435–444. [Google Scholar] [CrossRef]
- Burbelko, A.A.; Fras, E.; Kapturkiewicz, W. About Kolmogorov’s statistical theory of phase transformation. Mater. Sci. Eng. A 2005, 413, 429–434. [Google Scholar] [CrossRef]
- Ipus, J.J.; Blázquez, J.S.; Lozano-Pérez, S.; Conde, A. Microstructural evolution characterization of Fe-Nb-B ternary systems processed by ball milling. Philos. Mag. 2009, 89, 1415–1423. [Google Scholar] [CrossRef]
- Delogu, F.; Cocco, G. Kinetics of amorphization processes by mechanical alloying: A modeling approach. J. Alloy. Compd. 2007, 436, 233–240. [Google Scholar] [CrossRef]
- Manchón-Gordón, A.F.; Ipus, J.J.; Blázquez, J.S.; Conde, C.F.; Conde, A. Evolution of Fe environments and phase composition during mechanical amorphization of Fe70Zr30 and Fe70Nb30 alloys. J. Non-Cryst. Solids 2018, 494, 78–85. [Google Scholar] [CrossRef]
- Delogu, F. A combined experimental and numerical approach to the kinetics of mechanically induced phase transformations. Acta Mater. 2008, 56, 905–912. [Google Scholar] [CrossRef]
- Blázquez, J.S.; Ipus, J.J.; Moreno-Ramírez, L.M.; Álvarez-Gómez, J.M.; Sánchez-Jiménez, D.; Lozano-Pérez, S.; Franco, V.; Conde, A. Ball milling as a way to produce magnetic and magnetocaloric materials: A review. J. Mater. Sci. 2017, 52, 11834–11850. [Google Scholar] [CrossRef]
- Blázquez, J.S.; Ipus, J.J.; Conde, A. Time evolution of mechanical amorphization: A kinetic model. Scr. Mater. 2017, 130, 260–263. [Google Scholar] [CrossRef]
- Blázquez, J.S.; Ipus, J.J.; Franco, V.; Conde, C.F.; Conde, A. Extracting the composition of nanocrystals of mechanically alloyed systems using Mössbauer spectroscopy. J. Alloy. Compd. 2014, 610, 92–99. [Google Scholar] [CrossRef]
- Burke, J. The Kinetics of Phase Transformations in Metals; Pergamon: Oxford, UK, 1965. [Google Scholar]
- Chen, B.; Lutker, K.; Raju, S.V.; Yan, J.; Kanitpanyacharoen, W.; Lei, J.; Yang, S.; Wenk, H.R.; Mao, H.K.; Williams, Q. Texture of nanocrystalline nickel: Probing the lower size limit of dislocation activity. Science 2012, 338, 1448–1451. [Google Scholar] [CrossRef] [PubMed]
- Alleg, S.; Hamouda, A.; Azzaza, S.; Bensalem, R.; Sunol, J.J.; Greneche, J.M. Solid state amorphization transformation in the mechanically alloyed Fe27.9Nb2.2B69.9 powders. Mater. Chem. Phys. 2010, 122, 35–40. [Google Scholar] [CrossRef]
- Konishi, Y.; Kadota, K.; Tozuka, Y.; Shimosaka, A.; Shirakawa, Y. Amorphization and radical formation of cystine particles by a mechanochemical process analyzed using DEM simulation. Powder Technol. 2016, 301, 220–227. [Google Scholar] [CrossRef]
- Moumeni, H.; Alleg, S.; Greneche, J.M. Formation of ball-milled Fe-Mo nanostructured powders. J. Alloy. Compd. 2006, 419, 140–144. [Google Scholar] [CrossRef]
- Louidi, S.; Bentayeb, F.Z.; Sunol, J.J.; Escoda, L. Formation study of the ball-milled Cr20Co80 alloy. J. Alloy. Compd. 2010, 493, 110–115. [Google Scholar] [CrossRef]
- Loudjani, N.; Bensebaa, N.; Alleg, S.; Djebbari, C.; Greneche, J.M. Microstructure characterization of ball-milled Ni50Co50 alloy by Rietveld method. Phys. Stat. Sol. Appl. Mater. Sci. 2011, 208, 2124–2129. [Google Scholar] [CrossRef]
- Shen, Y.P.; Hng, H.H.; Oh, J.T. Formation kinetics of Ni-15% Fe-5% Mo during ball milling. Mater. Lett. 2004, 58, 2824–2828. [Google Scholar] [CrossRef]
- Lei, R.S.; Wang, M.P.; Wang, H.P.; Xu, S.Q. New insights on the formation of supersaturated Cu-Nb solid solution prepared by mechanical alloying. Mater. Character. 2016, 118, 324–331. [Google Scholar] [CrossRef]
- Abdellaoui, M.; Gaffet, E. The physics of mechanical alloying in a planetary ball mill—Mathematical treatment. Acta Metall. Mater. 1995, 43, 1087–1098. [Google Scholar] [CrossRef]
- Concas, A.; Lai, N.; Pisu, M.; Cao, G. Modelling of comminution processes in Spex Mixer/Mill. Chem. Eng. Sci. 2006, 61, 3746–3760. [Google Scholar] [CrossRef]
- Ipus, J.J.; Blázquez, J.S.; Franco, V.; Millán, M.; Conde, A.; Oleszak, D.; Kulik, T. An equivalent time approach for scaling the mechanical alloying processes. Intermetallics 2008, 16, 470–478. [Google Scholar] [CrossRef]
- Blázquez, J.S.; Franco, V.; Conde, A. Enhancement of the magnetic refrigerant capacity in partially amorphous Fe70Zr30 powders obtained by mechanical alloying. Intermetallics 2012, 26, 52–56. [Google Scholar] [CrossRef]
- Pizarro, R.; Barandiarán, J.M.; Plazaola, F.; Gutiérrez, J. Synthesis and characterization of amorphous Fe75Zr25 obtained by ball milling. J. Magn. Magn. Mater. 1999, 203, 143–145. [Google Scholar] [CrossRef]
- Vélez, G.Y.; Alcázar, G.A.P.; Zamora, L.E.; Tabares, J.A. Structural and magnetic study of the Fe2Nb alloy obtained by mechanical alloying and sintering. J. Supercond. Nov. Magn. 2014, 27, 1279–1283. [Google Scholar] [CrossRef]
- Concas, G.; Congiu, F.; Spano, G.; Bionducci, M. Investigation of the ferromagnetic order in crystalline and amorphous Fe2Zr alloys. J. Magn. Magn. Mater. 2004, 279, 421–428. [Google Scholar] [CrossRef]
- Povstugar, V.; Butyagin, P.Y.; Dorofeev, G.A.; Elsukov, E.P. Kinetics of the initial stage of mechanical alloying in the Fe(80)Zr(20) system. Colloid J. 2002, 64, 178–185. [Google Scholar] [CrossRef]
- Pizarro, R.; Garitaonandia, J.S.; Plazaola, F.; Barandiarán, J.M.; Grenèche, J.M. Magnetic and Mössbauer study of multiphase Fe-Zr amorphous powders obtained by high energy ball milling. J. Phys. Condens. Matter 2000, 12, 3101–3112. [Google Scholar] [CrossRef]


| Composition | Avrami Exponent | XAm Range (%) | Experimental Technique | Reference |
|---|---|---|---|---|
| Fe27.9Nb2.2B69.9 | 1 | 0–90 | Mössbauer | [30] |
| Cystine | 0.46 | 25–100 | XRD | [31] |
| Fe-6wt. %Mo | 0.83 ± 0.05 0.33 ± 0.04 | 30–60 60–80 | XRD | [32] |
| Cr20Co80 | 0.81 | 10–60 | XRD | [33] |
| Ni50Co50 | 0.34 | 60–75 | XRD | [34] |
| Ni15Fe5Mo80 | 1.049 | 10–70 | XRD | [35] |
| Cu-10wt. %Nb | 1.3 | 0–10 | XRD | [36] |
| Fe70Zr30 | 0.88 ± 0.05 | 20–80 | Mössbauer | This work |
| Fe70Nb30 | 0.89 ± 0.03 | 30–80 | Mössbauer | This work |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blázquez, J.S.; Manchón-Gordón, A.F.; Ipus, J.J.; Conde, C.F.; Conde, A. On the Use of JMAK Theory to Describe Mechanical Amorphization: A Comparison between Experiments, Numerical Solutions and Simulations. Metals 2018, 8, 450. https://doi.org/10.3390/met8060450
Blázquez JS, Manchón-Gordón AF, Ipus JJ, Conde CF, Conde A. On the Use of JMAK Theory to Describe Mechanical Amorphization: A Comparison between Experiments, Numerical Solutions and Simulations. Metals. 2018; 8(6):450. https://doi.org/10.3390/met8060450
Chicago/Turabian StyleBlázquez, Javier S., Alejandro F. Manchón-Gordón, Jhon J. Ipus, Clara F. Conde, and Alejandro Conde. 2018. "On the Use of JMAK Theory to Describe Mechanical Amorphization: A Comparison between Experiments, Numerical Solutions and Simulations" Metals 8, no. 6: 450. https://doi.org/10.3390/met8060450
APA StyleBlázquez, J. S., Manchón-Gordón, A. F., Ipus, J. J., Conde, C. F., & Conde, A. (2018). On the Use of JMAK Theory to Describe Mechanical Amorphization: A Comparison between Experiments, Numerical Solutions and Simulations. Metals, 8(6), 450. https://doi.org/10.3390/met8060450






