Strengthening versus Softening of Nanotwinned Copper Depending on Prestress and Twin Spacing
Abstract
:1. Introduction
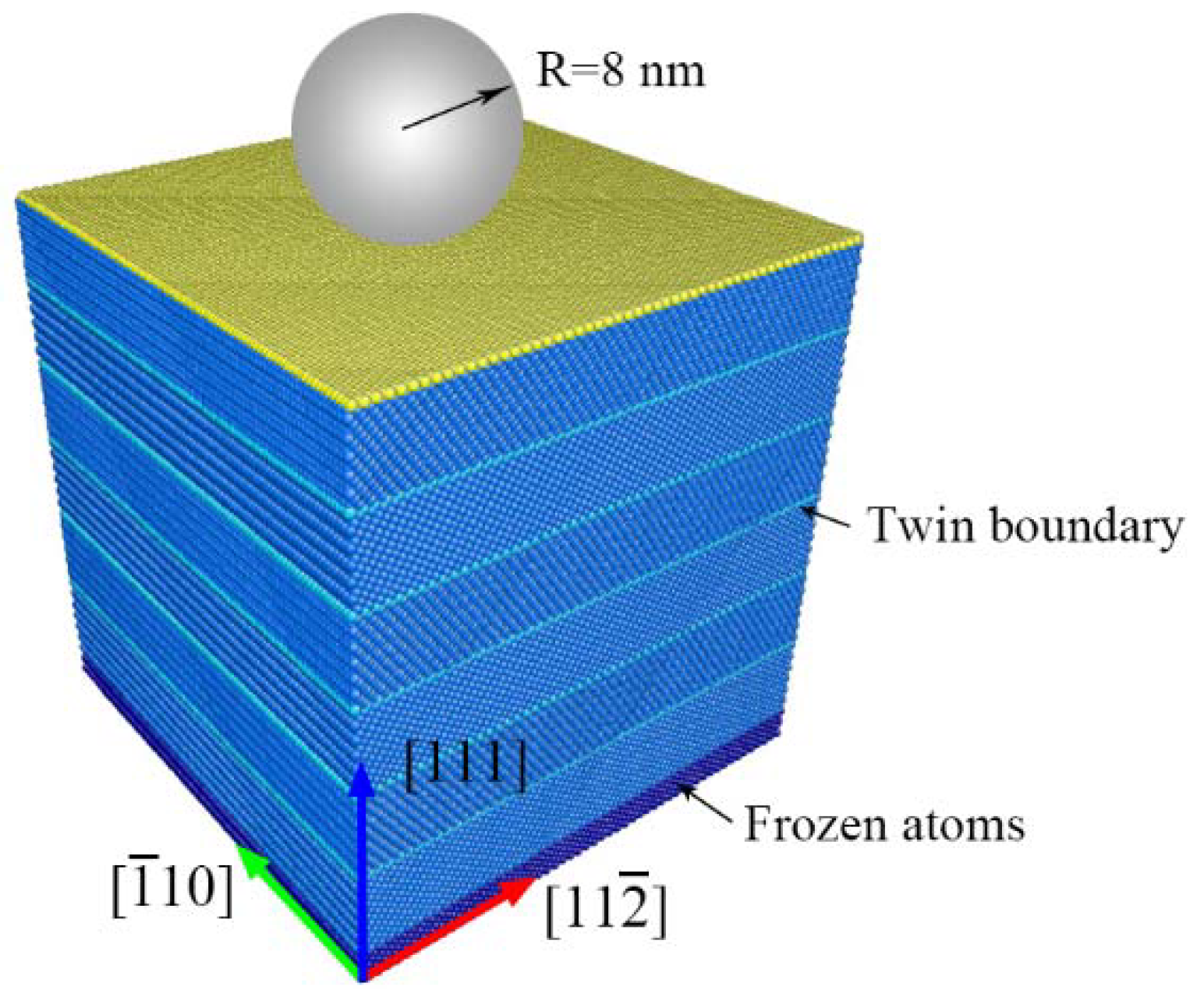
2. Methods
3. Results and Discussion
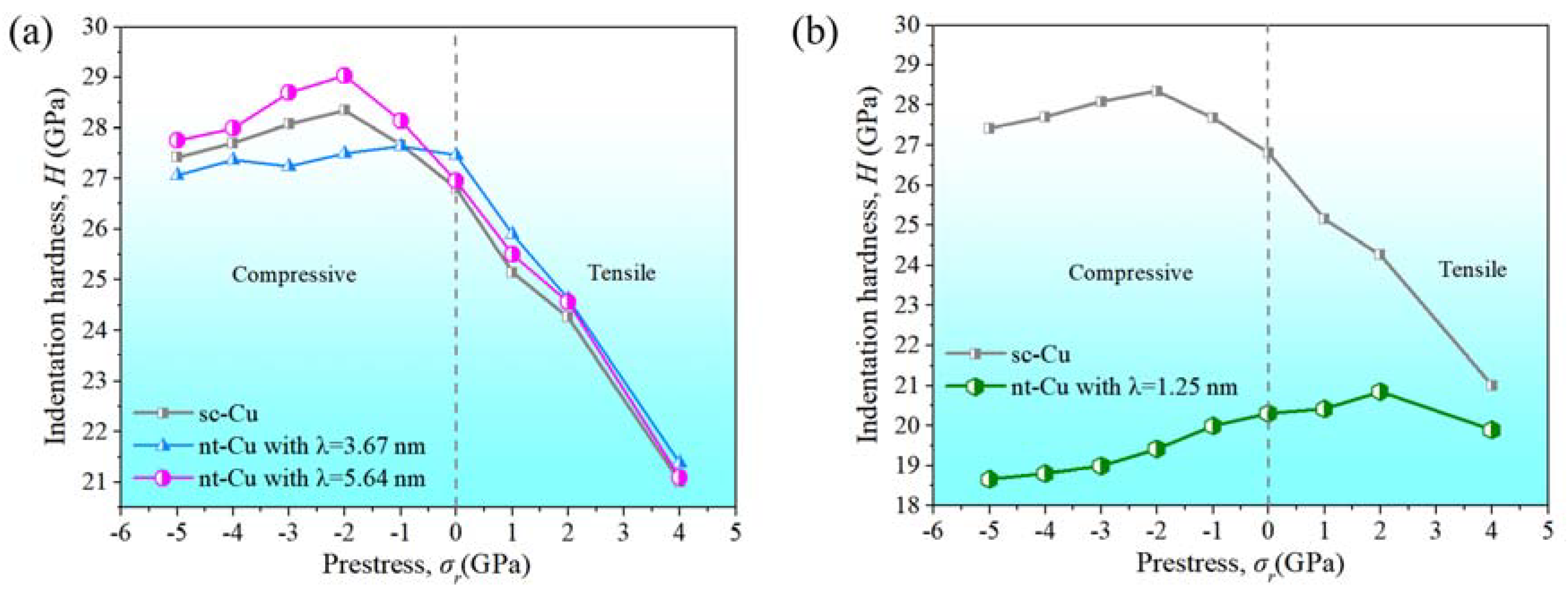
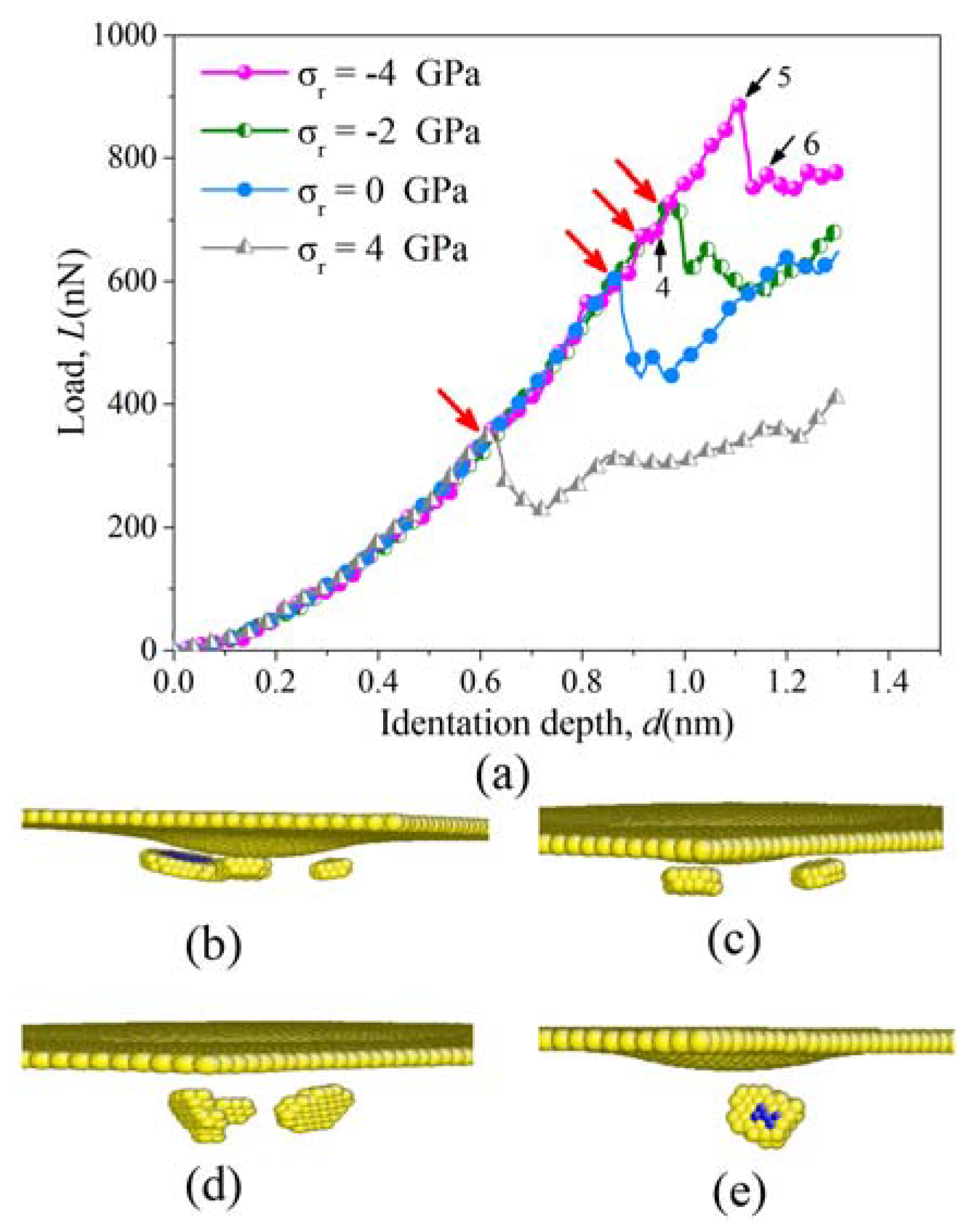
3.1. Mechanical Behavior
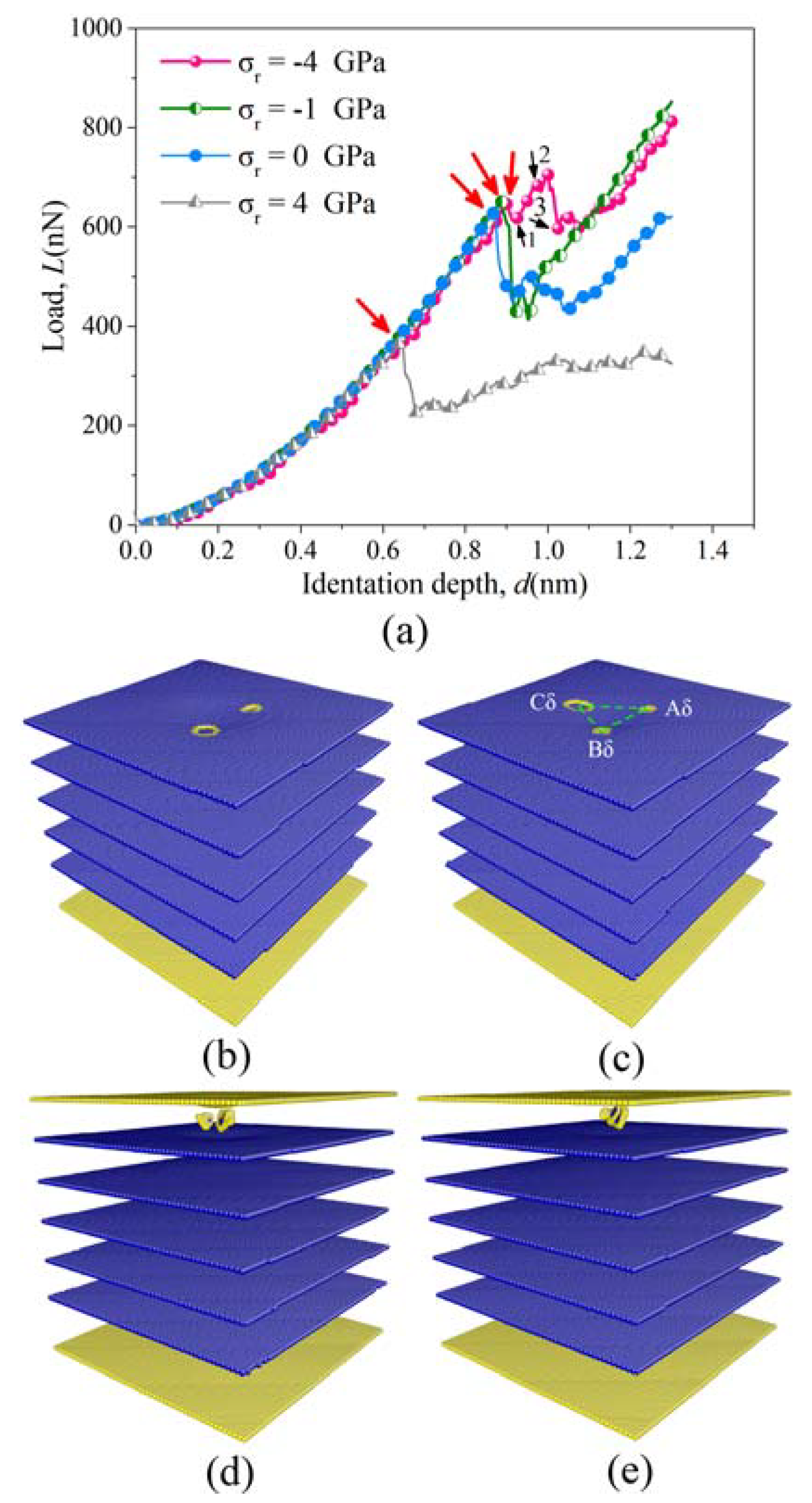
3.2. Deformation Mechanism at the Atomic Level
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Lu, K.; Lu, L.; Suresh, S. Strengthening materials by engineering coherent internal boundaries at the nanoscale. Science 2009, 324, 349–352. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Chen, X.; Huang, X.; Lu, K. Revealing the maximum strength in nanotwinned copper. Science 2009, 323, 607–610. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Shen, Y.F.; Chen, X.H.; Qian, L.H.; Lu, K. Ultrahigh strength and high electrical conductivity in copper. Science 2004, 304, 422–426. [Google Scholar] [CrossRef] [PubMed]
- Jang, D.C.; Li, X.Y.; Gao, H.J.; Greer, J.R. Deformation mechanisms in nanotwinned metal nanopillars. Nat. Nanotechnol. 2012, 7, 594–601. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Sansoz, F.; Huang, J.; Liu, Y.; Sun, S.; Zhang, Z.; Mao, S.X. Near-ideal theoretical strength in gold nanowires containing angstrom scale twins. Nat. Commun. 2013, 4, 1742. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.H.; Lu, L. Work hardening of ultrafine-grained copper with nanoscale twins. Scr. Mater. 2007, 57, 133–136. [Google Scholar] [CrossRef]
- Lu, L.; You, Z.S.; Lu, K. Work hardening of polycrystalline Cu with nanoscale twins. Scr. Mater. 2012, 66, 837–842. [Google Scholar] [CrossRef]
- Pan, Q.; Zhou, H.; Lu, Q.; Gao, H.; Lu, L. History-independent cyclic response of nanotwinned metals. Nature 2017, 551, 214–221. [Google Scholar] [CrossRef] [PubMed]
- Afanasyev, K.A.; Sansoz, F. Strengthening in gold nanopillars with nanoscale twins. Nano Lett. 2007, 7, 2056–2062. [Google Scholar] [CrossRef]
- Deng, C.; Sansoz, F. Fundamental differences in the plasticity of periodically twinned nanowires in Au, Ag, Al, Cu, Pb and Ni. Acta Mater. 2009, 57, 6090–6101. [Google Scholar] [CrossRef]
- Zhu, L.L.; Ruan, H.H.; Li, X.Y.; Dao, M.; Gao, H.J.; Lu, J. Modeling grain size dependent optimal twin spacing for achieving ultimate high strength and related high ductility in nanotwinned metals. Acta Mater. 2011, 59, 5544–5557. [Google Scholar] [CrossRef]
- Deng, C.; Sansoz, F. Size-dependent yield stress in twinned gold nanowires mediated by site-specific surface dislocation emission. Appl. Phys. Lett. 2009, 95, 091914. [Google Scholar] [CrossRef]
- Li, X.Y.; Wei, Y.J.; Lu, L.; Lu, K.; Gao, H.J. Dislocation nucleation governed softening and maximum strength in nano-twinned metals. Nature 2010, 464, 877–880. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Fang, L.; Sun, K.; Han, J. Direct observation of dislocations originating from perfect twin boundaries. Scr. Mater. 2011, 65, 501–504. [Google Scholar] [CrossRef]
- Guo, X.; Xia, Y.Z. Repulsive force vs. Source number: Competing mechanisms in the yield of twinned gold nanowires of finite length. Acta Mater. 2011, 59, 2350–2357. [Google Scholar] [CrossRef]
- Wei, Y. Anisotropic size effect in strength in coherent nanowires with tilted twins. Phys. Rev. B 2011, 84, 014107. [Google Scholar] [CrossRef]
- Sun, J.; Li, C.; Han, J.; Shao, X.; Yang, X. Size effect and deformation mechanism in twinned copper nanowires. Metals 2017, 7, 438. [Google Scholar] [CrossRef]
- Sun, J.; Fang, L.; Ma, A.; Jiang, J.; Han, Y.; Chen, H.; Han, J. The fracture behavior of twinned Cu nanowires: A molecular dynamics simulation. Mater. Sci. Eng. A 2015, 634, 86–90. [Google Scholar] [CrossRef]
- Sun, J.; Cheng, L.; Han, J.; Ma, A.; Fang, L. Nanoindentation induced deformation and pop-in events in a silicon crystal: Molecular dynamics simulation and experiment. Sci. Rep. 2017, 7, 10282. [Google Scholar] [CrossRef] [PubMed]
- Sebastiani, M.; Johanns, K.E.; Herbert, E.G.; Pharr, G.M. Measurement of fracture toughness by nanoindentation methods: Recent advances and future challenges. Curr. Opin. Solid State Mater. Sci. 2015, 19, 324–333. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 2004, 19, 3–20. [Google Scholar] [CrossRef]
- Liu, Y.; Hay, J.; Wang, H.; Zhang, X. A new method for reliable determination of strain-rate sensitivity of low-dimensional metallic materials by using nanoindentation. Scr. Mater. 2014, 77, 5–8. [Google Scholar] [CrossRef]
- Choi, I.; Kim, Y.; Wang, Y.M.; Ramamurty, U.; Jang, J. Nanoindentation behavior of nanotwinned Cu: Influence of indenter angle on hardness, strain rate sensitivity and activation volume. Acta Mater. 2013, 61, 7313–7323. [Google Scholar] [CrossRef]
- Pham, T.; Kim, S. Determination of equi-biaxial residual stress and plastic properties in structural steel using instrumented indentation. Mater. Sci. Eng. A 2017, 688, 352–363. [Google Scholar] [CrossRef]
- Suresh, S.; Giannakopoulos, A.E. A new method for estimating residual stresses by instrumented sharp indentation. Acta Mater. 1998, 46, 5755–5767. [Google Scholar] [CrossRef]
- Huber, N.; Heerens, J. On the effect of a general residual stress state on indentation and hardness testing. Acta Mater. 2008, 56, 6205–6213. [Google Scholar] [CrossRef]
- Lee, Y.H.; Kwon, D. Estimation of biaxial surface stress by instrumented indentation with sharp indenters. Acta Mater. 2004, 52, 1555–1563. [Google Scholar] [CrossRef]
- Zhu, L.; Xu, B.; Wang, H.; Wang, C. Measurement of residual stresses using nanoindentation method. Crit. Rev. Solid State 2015, 40, 77–89. [Google Scholar] [CrossRef]
- Schall, J.D.; Brenner, D.W. Atomistic simulation of the influence of pre-existing stress on the interpretation of nanoindentation data. J. Mater. Res. 2004, 19, 3172–3180. [Google Scholar] [CrossRef]
- Sun, K.; Shi, J.; Ma, L. Atomistic Insights into the Effects of Residual Stress during Nanoindentation. Crystals 2017, 7, 240. [Google Scholar] [CrossRef]
- Sun, K.; Shen, W.; Ma, L. The influence of residual stress on incipient plasticity in single-crystal copper thin film under nanoindentation. Comput. Mater. Sci. 2014, 81, 226–232. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular-dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Mishin, Y.; Mehl, M.J.; Papaconstantopoulos, D.A.; Voter, A.F.; Kress, J.D. Structural stability and lattice defects in copper: Ab initio, tight-binding, and embedded-atom calculations. Phys. Rev. B 2001, 63, 224106. [Google Scholar] [CrossRef]
- Ziegenhain, G.; Hartmaier, A.; Urbassek, H.M. Pair vs many-body potentials: Influence on elastic and plastic behavior in nanoindentation of fcc metals. J. Mech. Phys. Solids 2009, 57, 1514–1526. [Google Scholar] [CrossRef]
- Tsuzuki, H.; Branicio, P.S.; Rino, J.P. Structural characterization of deformed crystals by analysis of common atomic neighborhood. Comput. Phys. Commun. 2007, 177, 518–523. [Google Scholar] [CrossRef]
- Li, J. AtomEye: An efficient atomistic configuration viewer. Model. Simul. Mater. Sci. 2003, 11, 173–177. [Google Scholar] [CrossRef]
- Stukowski, A.; Albe, K.; Farkas, D. Nanotwinned fcc metals: Strengthening versus softening mechanisms. Phys. Rev. B 2010, 82, 224103. [Google Scholar] [CrossRef]
- Wang, Y.M.; Sansoz, F.; Lagrange, T.; Ott, R.T.; Marian, J.; Barbee, T.W., Jr.; Hamza, A.V. Defective twin boundaries in nanotwinned metals. Nat. Mater. 2013, 12, 697–702. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.M.; Jin, Z.H.; Gao, H.J. Repulsive force between screw dislocation and coherent twin boundary in aluminum and copper. Phys. Rev. B 2007, 75. [Google Scholar] [CrossRef]
- Tabor, D. The Hardness of Metals; Clarendon Press: Oxford, UK, 1952. [Google Scholar]
- Jin, Z.H.; Gumbsch, P.; Ma, E.; Albe, K.; Lu, K.; Hahn, H.; Gleiter, H. The interaction mechanism of screw dislocations with coherent twin boundaries in different face-centred cubic metals. Scr. Mater. 2006, 54, 1163–1168. [Google Scholar] [CrossRef]
- Frøseth, A.; Van Swygenhoven, H.; Derlet, P.M. The influence of twins on the mechanical properties of nc-Al. Acta Mater. 2004, 52, 2259–2268. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Sun, J.; Han, Y.; Zhu, H.; Fang, L. Strengthening versus Softening of Nanotwinned Copper Depending on Prestress and Twin Spacing. Metals 2018, 8, 344. https://doi.org/10.3390/met8050344
Han J, Sun J, Han Y, Zhu H, Fang L. Strengthening versus Softening of Nanotwinned Copper Depending on Prestress and Twin Spacing. Metals. 2018; 8(5):344. https://doi.org/10.3390/met8050344
Chicago/Turabian StyleHan, Jing, Jiapeng Sun, Ying Han, Hua Zhu, and Liang Fang. 2018. "Strengthening versus Softening of Nanotwinned Copper Depending on Prestress and Twin Spacing" Metals 8, no. 5: 344. https://doi.org/10.3390/met8050344
APA StyleHan, J., Sun, J., Han, Y., Zhu, H., & Fang, L. (2018). Strengthening versus Softening of Nanotwinned Copper Depending on Prestress and Twin Spacing. Metals, 8(5), 344. https://doi.org/10.3390/met8050344