Failure Analysis of PHILOS Plate Construct Used for Pantalar Arthrodesis Paper II—Screws and FEM Simulations
Abstract
:1. Introduction
1.1. Bone Screw Aspects of Design
- The screw heads can be crossed, hexagonal, or star. The crossed screw head driver has a good advantage in torque transmission [8]. However, a hexagonal driver provides a strong and insensitive alignment connection with the screw.
- The screw shaft represents a smooth link with no threads and might be (1) fully threaded with the cross-sectional diameter decreasing from the head to the bottom tip of the screw; (2) has a similar diameter for both the shaft and the thread root and provides strength and alignment inside the holes, however, it may require over drilling during surgery; and (3) have a similar diameter for both the shaft and the thread major diameter, however, with a weaker shaft [9].
- Screw threads with a constant angle increase the depth and pitch of the screw, while decreasing the pitch of the screw decreases the depth but keeps the angle constant. The surface of the thread should be perpendicular to the pullout load direction [9].
- The screw tip can be cork, blunt, self-tapping, or self-cutting. A self-tapping tip has a sharp flue that needs a lower amount of force. However, it needs 30–40% more torque to be placed [9].
1.2. Biomechanics of Bone Screws
2. Background
3. Visual Examination
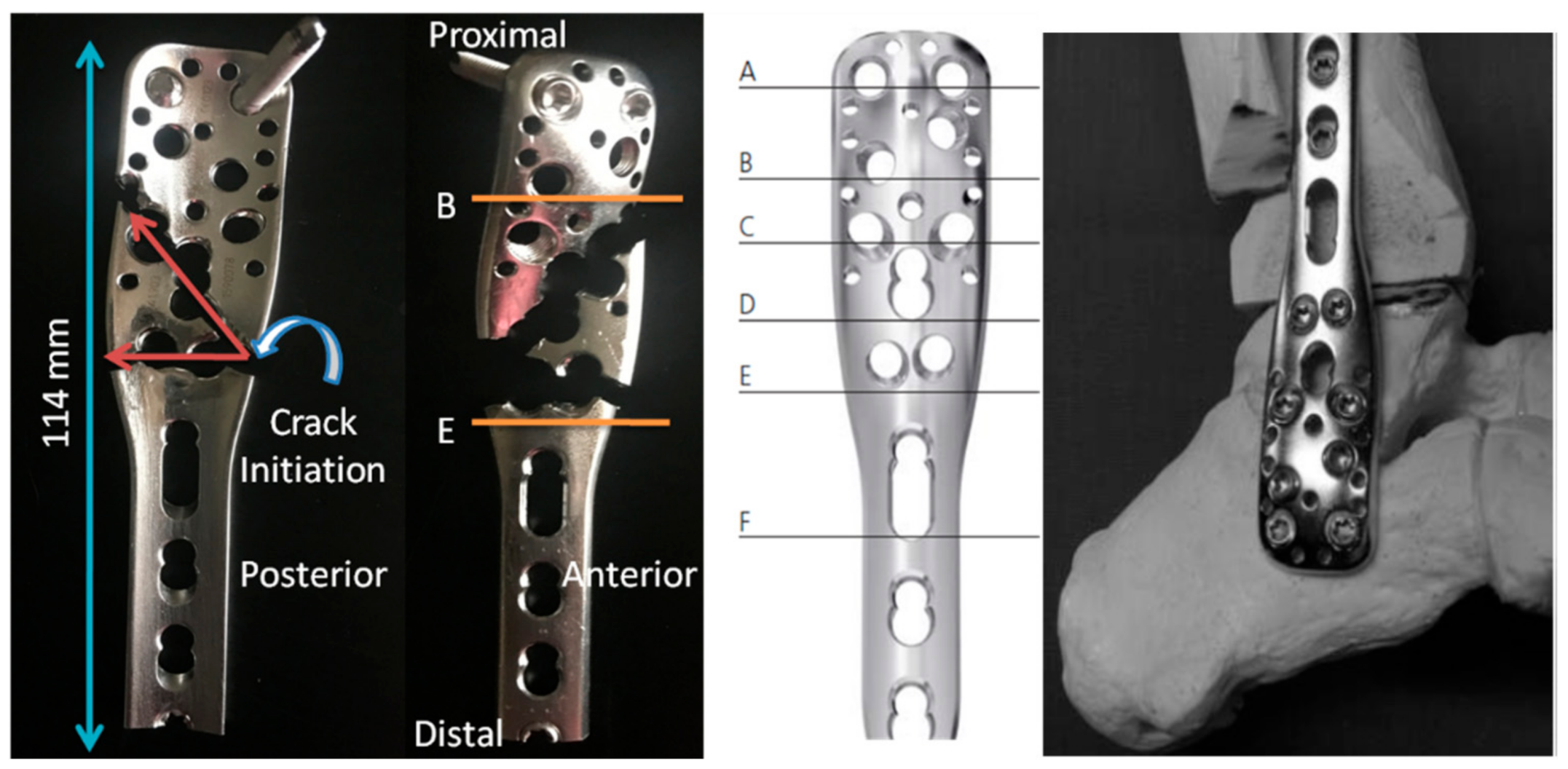
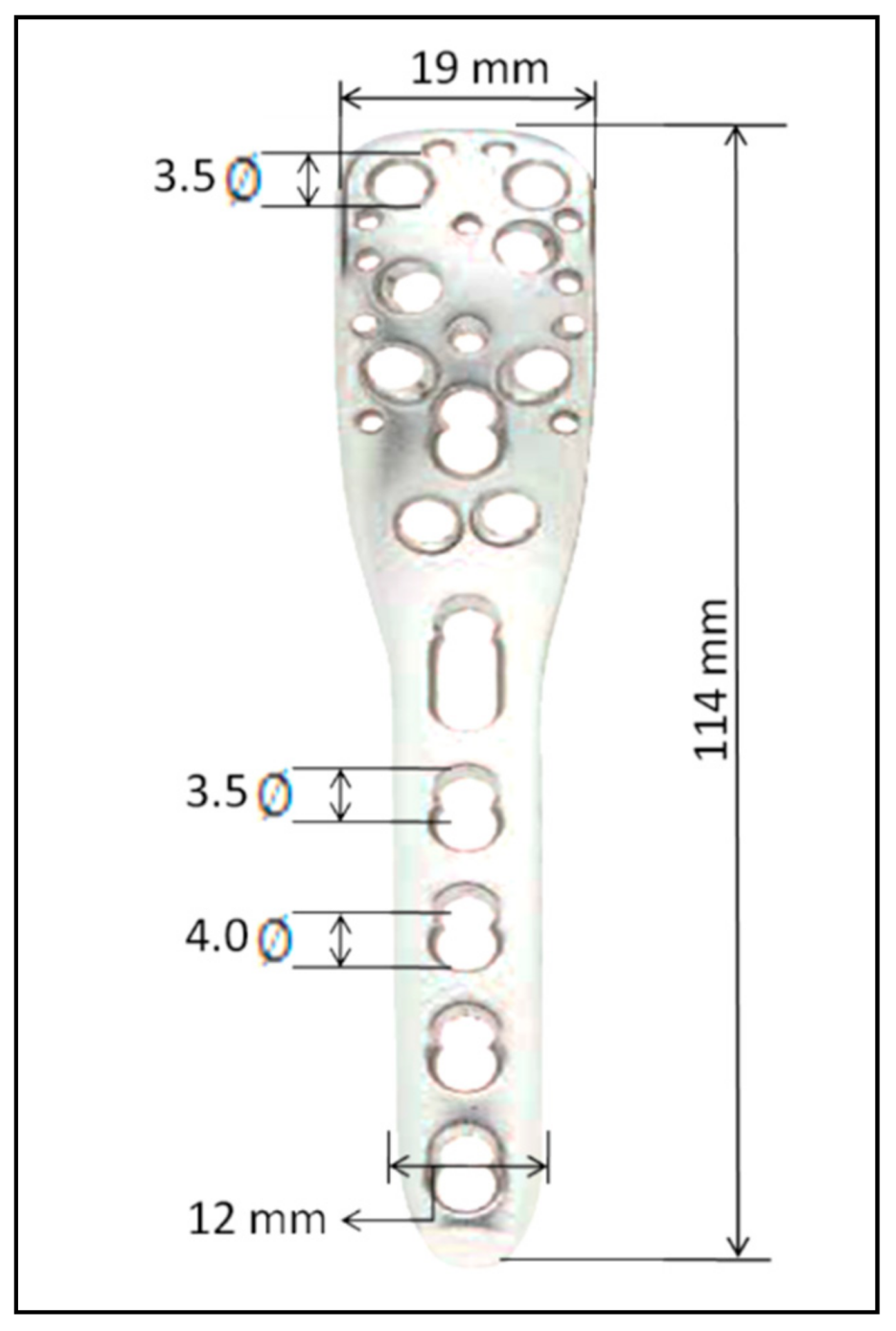
3.1. The Plate
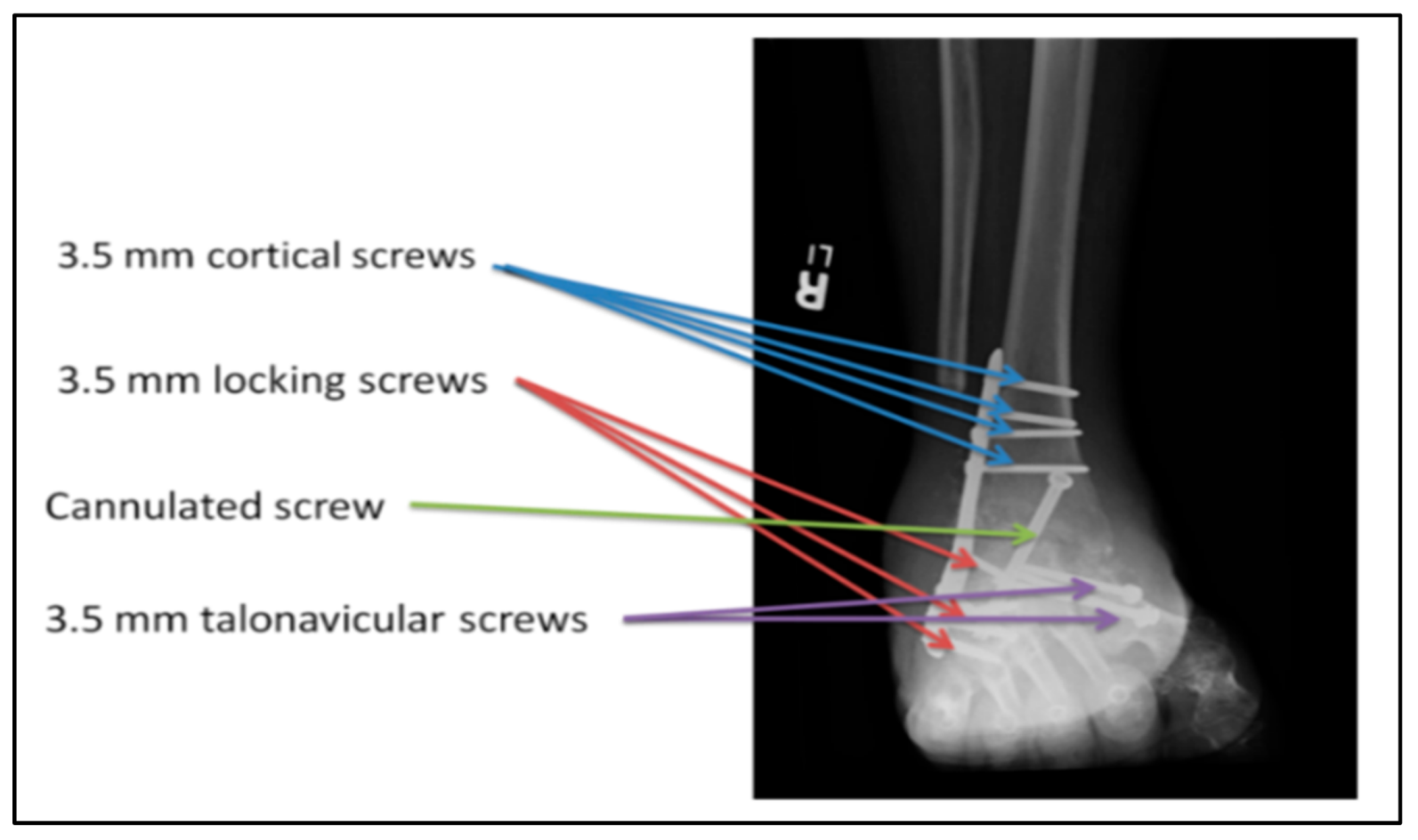
3.2. The Screws
4. Fractographic Examination
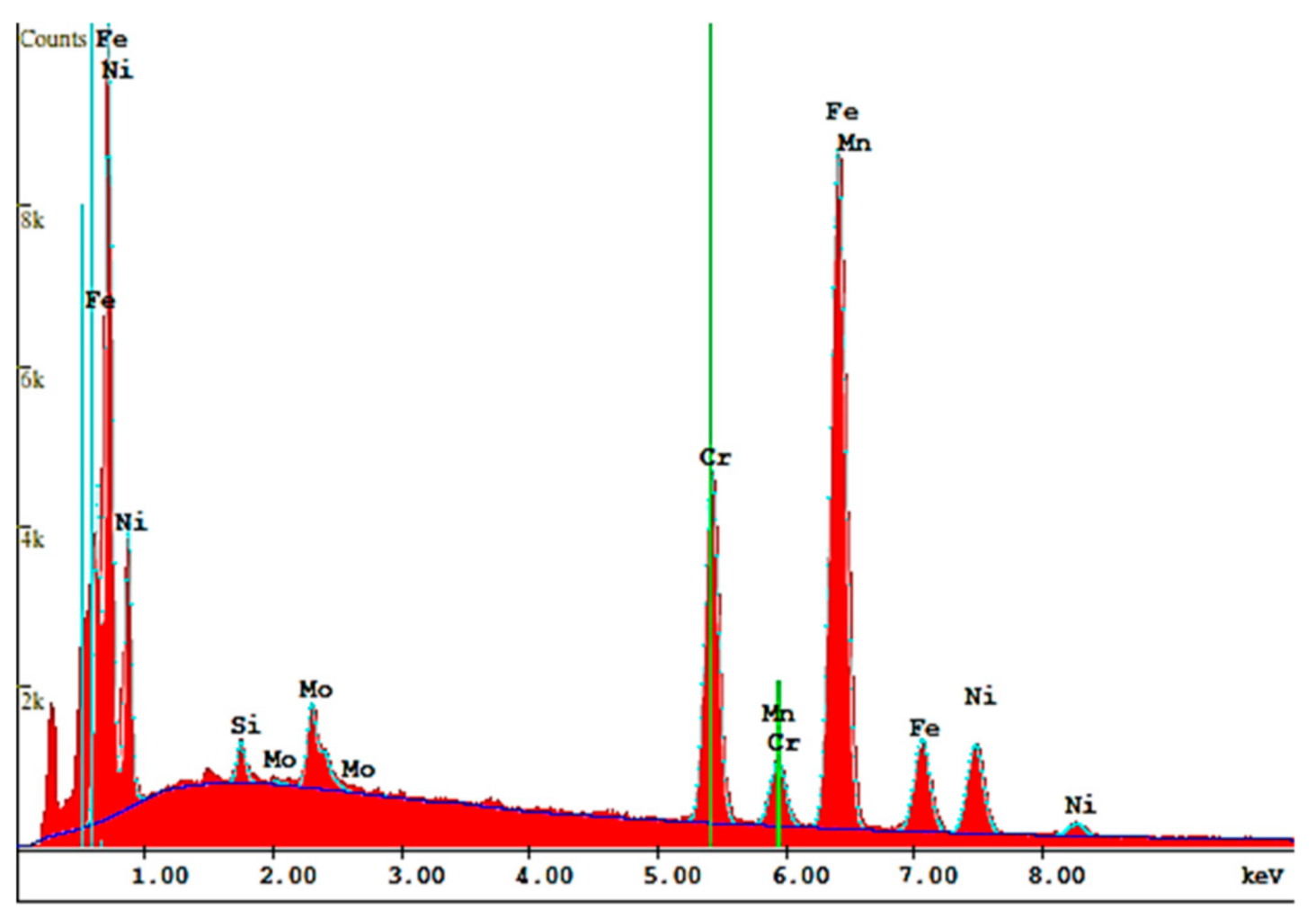
5. Material Conformity
6. Computational Simulations of Failures
6.1. Finite Element Analysis
6.2. The Results
7. Discussion
8. Conclusions
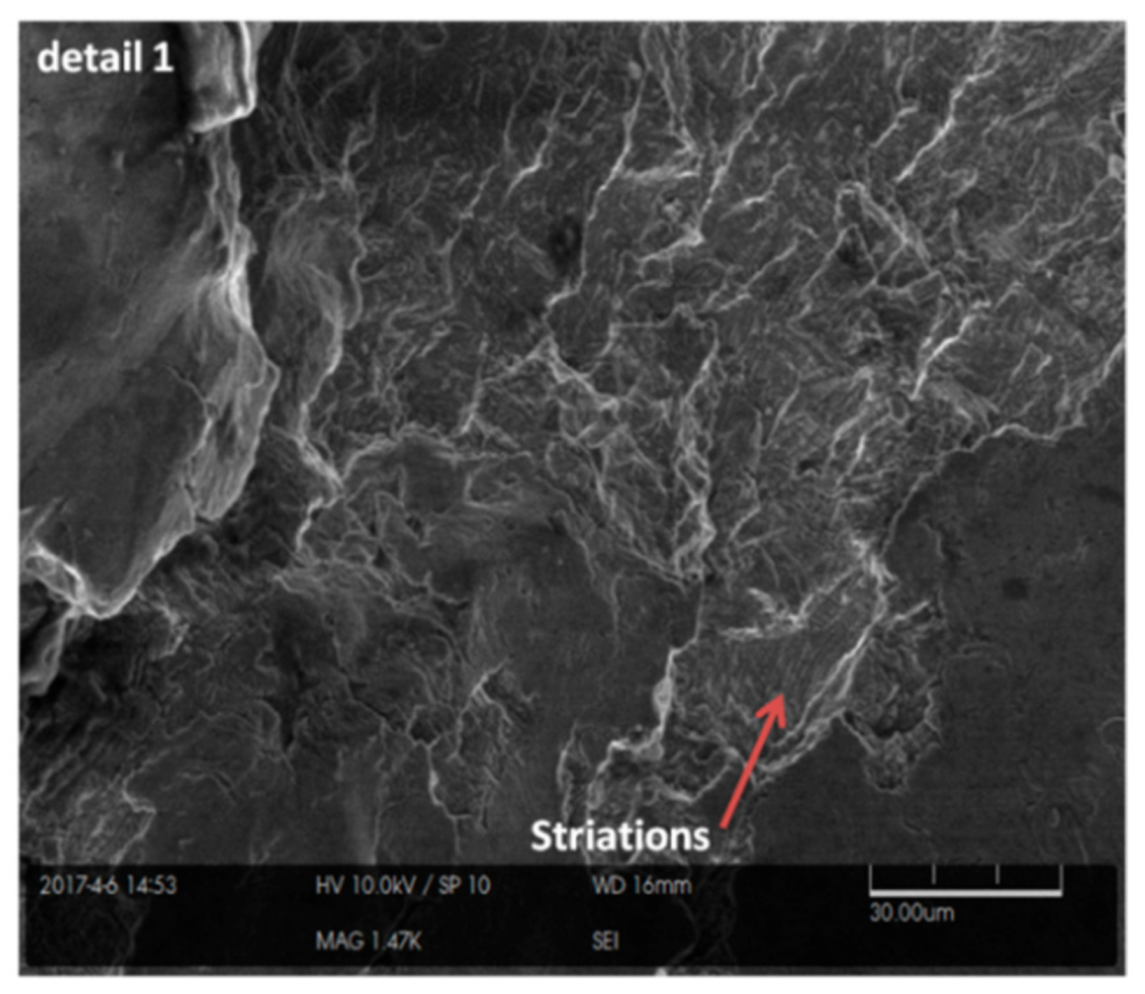
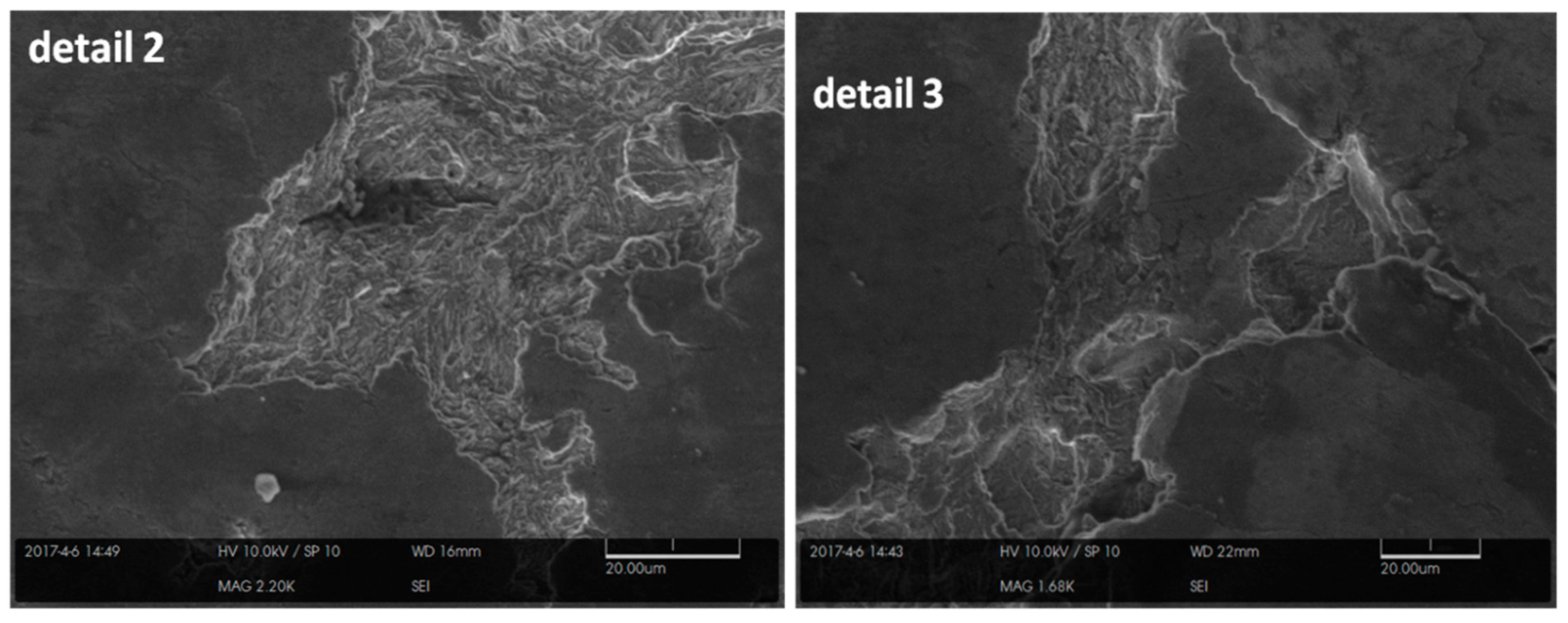
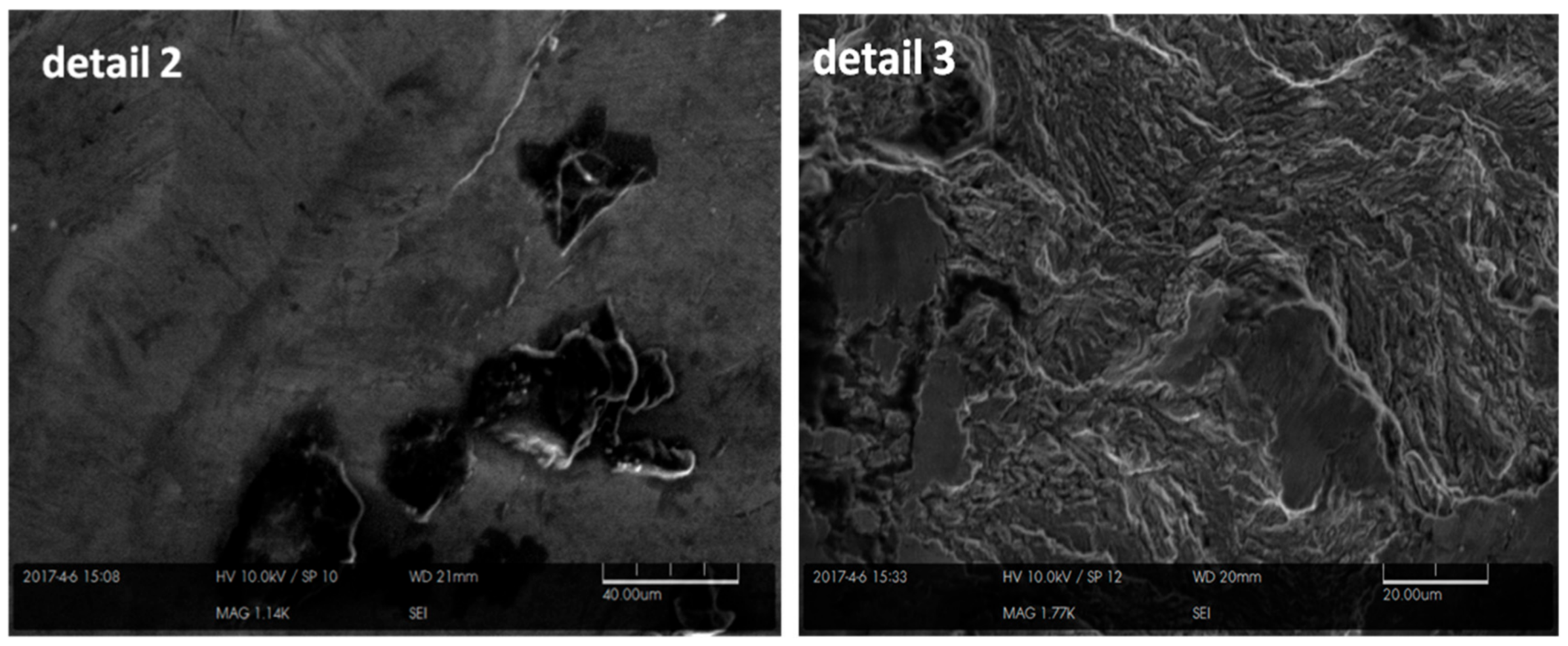
- Fractographic examination of the cortical and locking screws supports the mechanism of corrosion-fatigue fracture from crack initiation sites due to the presence of inclusion bodies and pits and regions of high plastic strains due to load bear. The regular features, such as beach marks and striations, were present indicating fatigue and/or corrosion fatigue controlled the failure process.
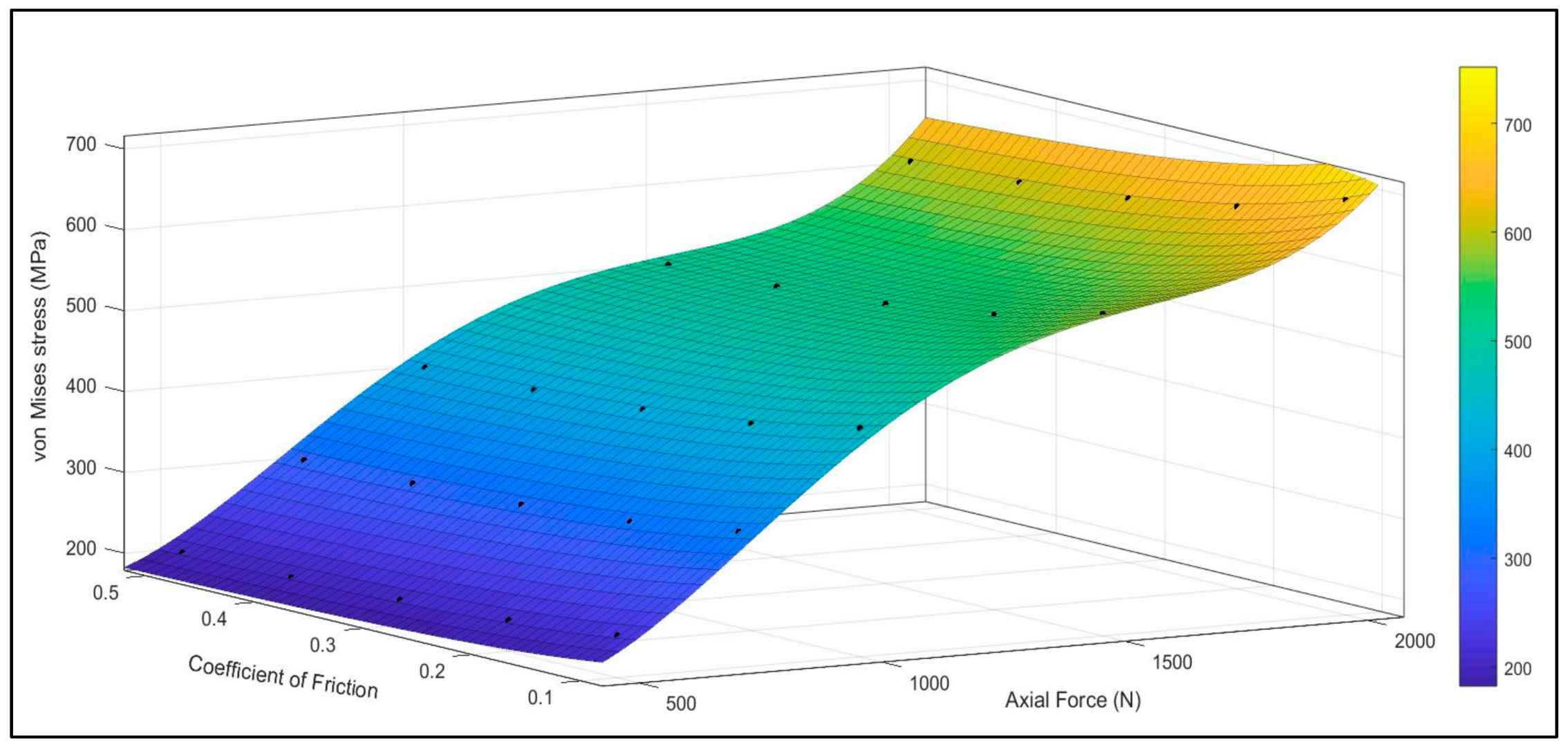
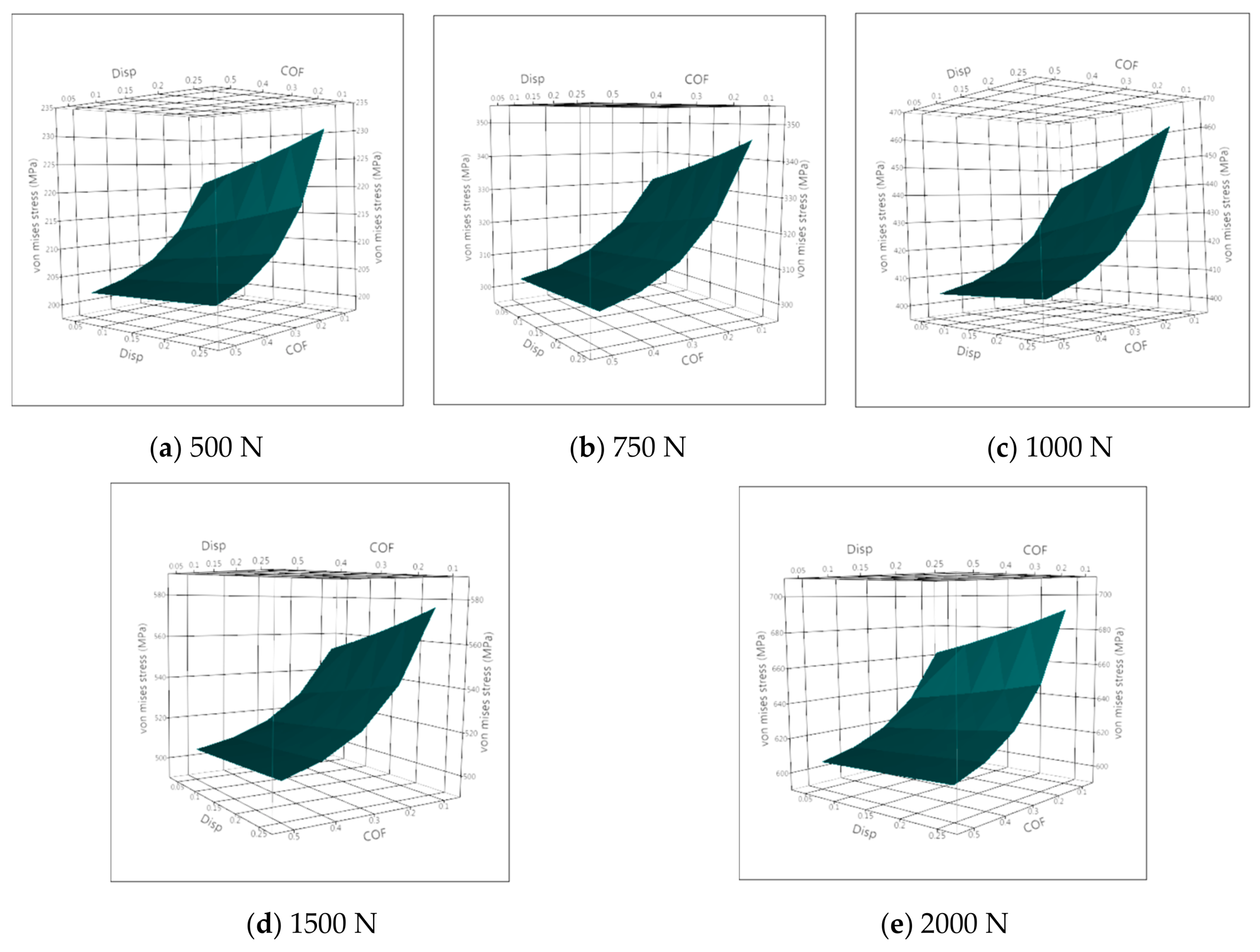
- The simulations showed that the maximum von Mises stresses of the PHILOS plate increased by 2.2% with the increase in cortical screw displacement as expected as the screws began to fail, giving rise to higher macro-motion of the construct at the same time lowering the coefficient of friction between the contacts.
- The analysis of cortical screws showed that the stresses increased by 7.4% as the angle between the screw and the plate increased.
- The stresses in the locking screws were lower than the cortical screws by 25.5%, and this may be a result of the locking screws’ fixed angles with less range of motion.The finite element simulation of the plate validated the loading conditions and regions of stress development that supported the visual and fractographic examinations causing the physical failure of the PHILOS system.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A








References
- Ahmad, J.; Pour, A.E.; Raikin, S.M. The modified use of a proximal humeral locking plate for tibiotalocalcaneal arthrodesis. Foot Ankle Int. 2007, 28, 977–983. [Google Scholar] [CrossRef] [PubMed]
- Mendicino, R.W.; Catanzariti, A.R.; Saltrick, K.R.; Dombek, M.F.; Tullis, B.L.; Statler, T.K.; Johnson, B.M. Tibiotalocalcaneal arthrodesis with retrograde intramedullary nailing. J. Foot Ankle Surg. 2004, 43, 82–86. [Google Scholar] [CrossRef] [PubMed]
- Fox, I.M.; Shapero, C.; Kennedy, A. Tibiotalocalcaneal arthrodesis with intramedullary interlocking nail fixation. Clin. Podiatr. Med. Surg. 2000, 17, 19–31. [Google Scholar] [PubMed]
- Shearman, A.D.; Eleftheriou, K.I.; Patel, A.; Pradhan, R.; Rosenfeld, P.F. Use of a proximal humeral locking plate for complex ankle and Hindfoot fusion. J. Foot Ankle Surg. 2016, 55, 612–618. [Google Scholar] [CrossRef] [PubMed]
- Berend, M.E.; Glisson, R.R.; Nunley, J.A. A biomechanical comparison of intramedullary nail and crossed lag screw fixation for tibiotalocalcaneal arthrodesis. Foot Ankle Int. 1997, 18, 639–643. [Google Scholar] [CrossRef] [PubMed]
- Chiodo, C.P.; Acevedo, J.I.; Sammarco, V.J.; Parks, B.G.; Boucher, H.R.; Myerson, M.S.; Schon, L.C. Intramedullary rod fixation compared with blade-plate-and-screw fixation for tibiotalocalcaneal arthrodesis: A biomechanical investigation. J. Bone Joint Surg. Am. 2003, 85, 2425–2428. [Google Scholar] [CrossRef] [PubMed]
- Goswami, T.; Patel, V.; Dalstrom, D.J.; Prayson, M.J. Mechanical evaluation of fourth-generation composite femur hybrid locking plate constructs. J. Mater. Sci. Mater. Med. 2011, 22, 2139. [Google Scholar] [CrossRef] [PubMed]
- Perren, S.M. Technical and biomechanical aspects of screws used in bone surgery. Int. J. Orthop. Trauma 1992, 2, 31–48. [Google Scholar]
- Asnis, S.E.; Kyle, R.F. (Eds.) Cannulated Screw Fixation: Principles and Operative Techniques; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Patel, V. Biomechanical Evaluation of Locked and Non-Locked Constructs under Axial and Torsion Loading. (Electronic Thesis or Dissertation). 2008. Available online: https://etd.ohiolink.edu/ (accessed on 14 April 2018).
- Gautier, E.; Sommer, C. Guidelines for the clinical application of the LCP. Injury 2003, 34, B63–B76. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.C.; Wang, J.L.; Hou, S.M.; Chao, C.K.; Lin, J. Pushout strength of tibial locking screws: Development of finite element models. J. Chin. Inst. Eng. 2003, 26, 817–823. [Google Scholar] [CrossRef]
- Hughes, A.N.; Jordan, B.A. The mechanical properties of surgical bone screws and some aspects of insertion practice. Injury 1972, 4, 25–38. [Google Scholar] [CrossRef]
- Chapman, J.R.; Harrington, R.M.; Lee, K.M.; Anderson, P.A.; Tencer, A.F.; Kowalski, D. Factors affecting the pullout strength of cancellous bone screws. J. Biomech. Eng. 1996, 118, 391–398. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.; Zhang, C.; Gu, W.; Zeng, B. Ankle arthrodesis by lateral malleolus osteotomy and internal fixation with locking proximal humeral plate. Zhongguo Xiu Fu Chong Jian Wai Ke Za Zhi (Chin. J. Repar. Reconstr. Surg.) 2011, 25, 781–784. [Google Scholar]
- Ina, J.; Vallentyne, M.; Hamandi, F.; Shugart, K.; Boin, M.; Laughlin, R.; Goswami, T. Failure Analysis of PHILOS Plate Construct Used for Pantalar Arthrodesis Paper I—Analysis of the Plate. Metals 2018, 8, 180. [Google Scholar] [CrossRef]
- SYNTHES. 3.5 mm LCP Proximal Humerus Plate—Stainless Steel and Titanium Technique Guide. 2002. Available online: http://synthes.vo.llnwd.net/o16/LLNWMB8/US%20Mobile/Synthes%20North%20America/Product%20Support%20Materials/Technique%20Guides/DSUSTRM10161133_ProxHumPl_STG_150dpi.pdf (accessed on 7 February 2017).
- Atlas Specialty Metals. Stainless Steel—Grade 316 L—Properties, Fabrication and Applications (UNS S31603). 2004. Available online: http://www.azom.com/article.aspx?ArticleID=2382# (accessed on 7 February 2017).
- Azevedo, C.R.F. Failure analysis of a commercially pure titanium plate for osteosynthesis. Eng. Fail. Anal. 2002, 10, 153–164. [Google Scholar] [CrossRef]
- Kanchanomai, C.; Phiphobmongkol, V.; Muanjan, P. Fatigue failure of an orthopedic implant–A locking compression plate. Eng. Fail. Anal. 2008, 15, 521–530. [Google Scholar] [CrossRef]
- Amalraju, D.; Dawood, A.S. Mechanical strength evaluation analysis of stainless steel and titanium locking plate for femur bone fracture. IRACST Eng. Sci. Technol. Int. J. 2012, 2, 2250–3498. [Google Scholar]
- ASTM. Annual Book of ASTM Standards; Construction; Soil and Rock (I); ASTM: West Conshohocken, PA, USA, 2005; Volume 13.01. [Google Scholar]
- Allen, R.F. Standard specification for wrought 18 chromium-14 nickle-2.5 molybdenum stainless steel bar and wire for surgical implants (F138). In Annual Book of ASTM Standards, Medical Devices and Services; ASTM: West Conshohocken, PA, USA, 1998. [Google Scholar]
- SYNTHES. Screws, Drill Bits, Taps and Guide Wires. 2002. Available online: http://www.cambridgeorthopaedics.com/easytrauma/classification/commonfiles/Synthes%20screws.pdf (accessed on 7 February 2017).
- Hamandi, F.; Goswami, T. Macrodamage Accumulation Model for a Human Femur. Appl. Bionics Biomech. 2017, 2017, 4539178. [Google Scholar] [CrossRef] [PubMed]
- Michael, J.M.; Golshani, A.; Gargac, S.; Goswami, T. Biomechanics of the ankle joint and clinical outcomes of total ankle replacement. J. Mech. Behave. Biomed. Mater. 2008, 1, 276–294. [Google Scholar] [CrossRef] [PubMed]
- Perren, S.M. Evolution of the internal fixation of long bone fractures: The scientific basis of biological internal fixation: Choosing a new balance between stability and biology. Bone Jt. J. 2002, 84, 1093–1110. [Google Scholar] [CrossRef]
- Goswami, T.; Gundapaneni, D.; Slocum, M.; Paul, P.; Christof, S. Failure investigation of a tibiotalocalcaneal arthrodesis system. Eng. Fail. Anal. 2016, 59, 588–604. [Google Scholar] [CrossRef]
- Egol, K.A.; Kubiak, E.N.; Fulkerson, E.; Kummer, F.J.; Koval, K.J. Biomechanics of locked plates and screws. J. Orthop. Trauma 2004, 18, 488–493. [Google Scholar] [CrossRef] [PubMed]
- Borgeaud, M.; Cordey, J.; Leyvraz, P.F.; Perren, S.M. Mechanical analysis of the bone to plate interface of the LC-DCP and of the PC-FIX on human femora. Injury 2000, 31, C29–C36. [Google Scholar] [CrossRef]
- Narayan, R.; Burt, V.; Lampman, S.; Marken, K.; Marquard, E.; Riley, B. ASM Handbook. In Materials for Medical Devices; ASM International: Materials Park, OH, USA, 2012; Volume 23. [Google Scholar]
- Majid, K.; Crowder, T.; Baker, E.; Baker, K.; Koueiter, D.; Shields, E.; Herkowitz, H.N. Analysis of in vivo corrosion of 316 L stainless steel posterior thoracolumbar plate systems: A retrieval study. Clin. Spine Surg. 2011, 24, 500–505. [Google Scholar]
- Sivakumar, M.; Mudali, U.K.; Rajeswari, S. Investigation of failures in stainless steel orthopaedic implant devices: Fatigue failure due to improper fixation of a compression bone plate. J. Mater. Sci. Lett. 1994, 13, 142–145. [Google Scholar] [CrossRef]
- Thapa, N.; Prayson, M.; Goswami, T. A failure study of a locking compression plate implant. Case Stud. Eng. Fail. Anal. 2015, 3, 68–72. [Google Scholar] [CrossRef]

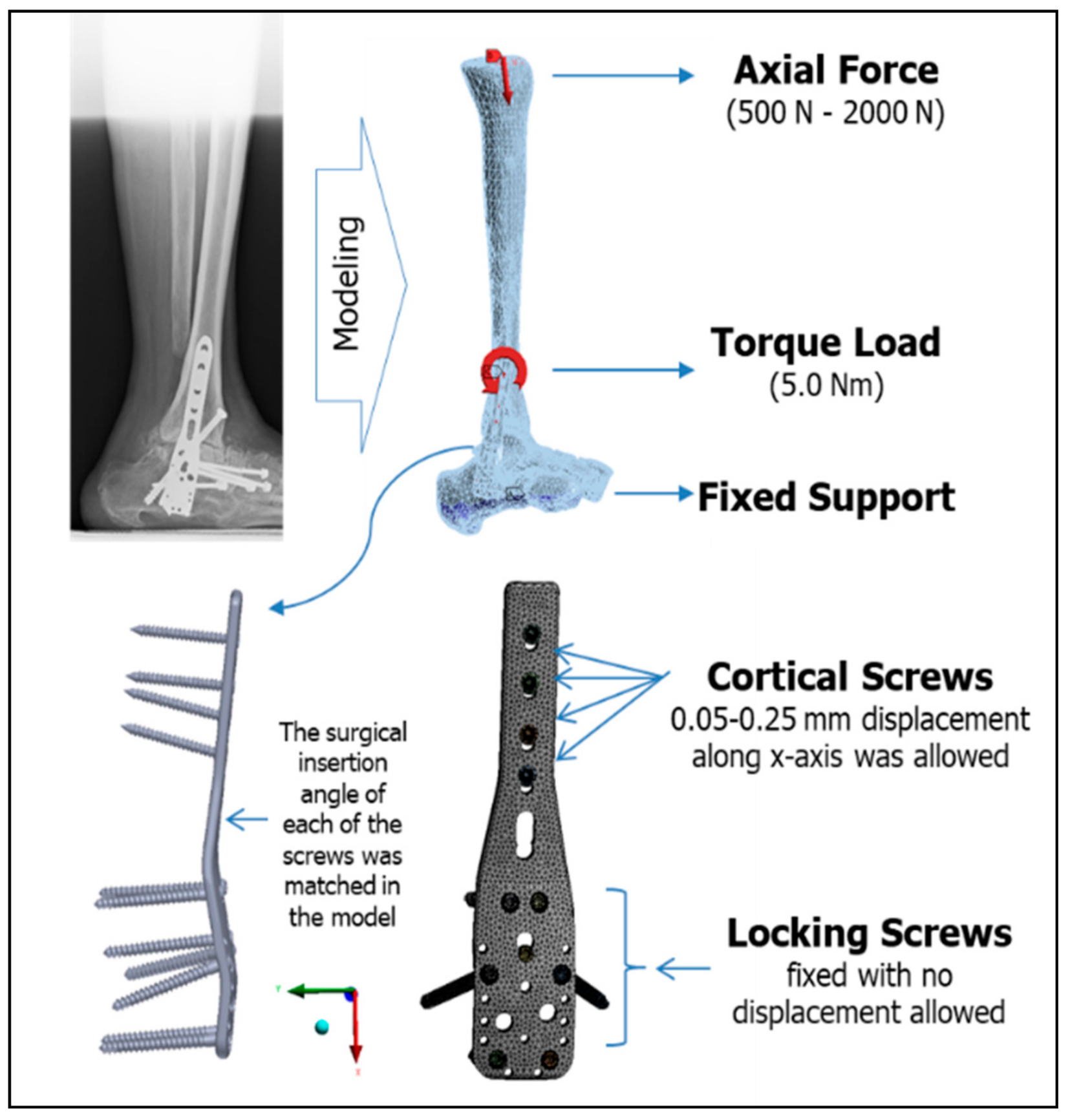



| Authors | Year | Title | Age | Gender Male:Female | Details |
|---|---|---|---|---|---|
| Ahmad, J., Pour, A.E., and Raikin, S.M. [1] | 2007 | The modified use of a proximal humeral locking plate for tibiotalocalcaneal arthrodesis | 22–72 years Mean: 54.2 | 11:6 | 18 patients showed that 94.4% (17 of 18) of the patients had successful fusion after approximately 20 weeks when the proximal humeral locking plates were used for obtaining tibiotalocalcaneal arthrodesis. |
| Shi, Z., Zhang, C., Gu, W., Zhang, C., and Zeng, B. [15] | 2011 | Ankle arthrodesis by lateral malleolus osteotomy and internal fixation with locking proximal humeral plate | 36–67 years Mean: 48 | 10:8 | Reported successful results when the same plate was used for ankle arthrodesis. |
| Haider Twaij and Dev Damany | 2013 | PHILOS humerus plate for a distal tibial fracture | 51 | 1:0 | A successful result for the case. |
| Shearman, A.D., Eleftheriou, K.I., Patel, A., Pradhan, R., and Rosenfeld, P.F. [4] | 2016 | Use of a Proximal Humeral Locking Plate for Complex Ankle and Hindfoot Fusion | 25–74 years Mean: 56.1 | 11:10 | 17 of 21 patients (81%) had satisfactory results when proximal locking plates were used for obtaining tibiotalocalcaneal arthrodesis. |
| Name of Device | Size | Company | Serial No. | Date of Insertion | Failure First Noticed |
|---|---|---|---|---|---|
| LCP Proximal Humerus Locking Plate | 3.5 mm | DePuy Synthes | N/A | 08/2008 | 2014 |
| Cortical Screws | 3.5 mm | DePuy Synthes | N/A | 08/2008 | 2010–2014 |
| Locking Screws | 3.5 mm | DePuy Synthes | N/A | 08/2008 | 2011–2014 |
| Cannulated Screw | 6.5 mm | Zimmer | N/A | 08/2008 | 2013 |
| Composition | ASTM Standards F138-03 and F139-03 | Screw | |||
|---|---|---|---|---|---|
| (Min–Max) | Area 1 | Area 2 | Area 3 | Average | |
| %Mn | 0–2.04 | 1.63 | 1.51 | 1.62 | 1.57 |
| %Si | 0–0.80 | 0.62 | 0.63 | 0.42 | 0.56 |
| %Cr | 16.80–19.20 | 18.57 | 18.68 | 18.71 | 18.65 |
| %Mo | 2.15–3.10 | 2.97 | 3.09 | 2.36 | 2.81 |
| %Ni | 12.85–15.15 | 14.83 | 14.94 | 14.63 | 14.8 |
| Material Properties | 316L Stainless Steel |
|---|---|
| Elastic Modulus (GPa) | 200 |
| Shear Modulus (GPa) | 82 |
| Poisson’s Ratio | 0.265 |
| Mass Density (g/m3) | 8.027 |
| Tensile Strength (N/mm2) | 860 |
| Yield Strength (N/mm2) | 690 |
| Axial Force (N) | Coefficient of Friction | Design A | Design B | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Non-Locking Screws Displacement (mm) | |||||||||||
| 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | ||
| 500 | 0.10 | 219.81 | 221.90 | 224.19 | 226.72 | 229.49 | 220.86 | 222.95 | 225.24 | 227.76 | 230.54 |
| 0.20 | 210.54 | 211.70 | 212.97 | 214.38 | 215.92 | 211.59 | 212.75 | 214.02 | 215.42 | 216.97 | |
| 0.30 | 205.39 | 206.03 | 206.74 | 207.52 | 208.38 | 206.44 | 207.08 | 207.79 | 208.57 | 209.43 | |
| 0.40 | 202.53 | 202.88 | 203.28 | 203.71 | 204.19 | 203.58 | 203.93 | 204.33 | 204.76 | 205.24 | |
| 0.50 | 200.93 | 201.13 | 201.35 | 201.59 | 201.86 | 201.99 | 202.19 | 202.40 | 202.64 | 202.91 | |
| 750 | 0.10 | 330.26 | 333.39 | 336.83 | 340.62 | 344.78 | 331.29 | 334.42 | 337.86 | 341.65 | 345.81 |
| 0.20 | 316.35 | 318.09 | 320.00 | 322.10 | 324.42 | 317.38 | 319.12 | 321.03 | 323.14 | 325.45 | |
| 0.30 | 308.62 | 309.59 | 310.65 | 311.82 | 313.11 | 309.66 | 310.62 | 311.69 | 312.85 | 314.14 | |
| 0.40 | 304.33 | 304.87 | 305.46 | 306.11 | 306.82 | 305.37 | 305.90 | 306.49 | 307.14 | 307.85 | |
| 0.50 | 301.95 | 302.24 | 302.57 | 302.93 | 303.33 | 302.98 | 303.28 | 303.61 | 303.97 | 304.36 | |
| 1000 | 0.10 | 440.70 | 444.87 | 449.46 | 454.50 | 460.06 | 441.72 | 445.89 | 450.48 | 455.53 | 461.08 |
| 0.20 | 422.15 | 424.47 | 427.02 | 429.82 | 432.91 | 423.18 | 425.49 | 428.04 | 430.85 | 433.93 | |
| 0.30 | 411.85 | 413.14 | 414.56 | 416.11 | 417.83 | 412.88 | 414.16 | 415.58 | 417.14 | 418.85 | |
| 0.40 | 406.13 | 406.84 | 407.63 | 408.50 | 409.45 | 407.15 | 407.87 | 408.66 | 409.52 | 410.47 | |
| 0.50 | 402.95 | 403.35 | 403.78 | 404.26 | 404.79 | 403.97 | 404.37 | 404.81 | 405.29 | 405.82 | |
| 1500 | 0.10 | 551.13 | 556.34 | 562.08 | 568.39 | 575.33 | 552.15 | 557.36 | 563.10 | 569.41 | 576.35 |
| 0.20 | 527.95 | 530.85 | 534.04 | 537.54 | 541.40 | 528.97 | 531.87 | 535.06 | 538.56 | 542.42 | |
| 0.30 | 515.08 | 516.68 | 518.46 | 520.40 | 522.55 | 516.10 | 517.70 | 519.48 | 521.42 | 523.56 | |
| 0.40 | 507.92 | 508.82 | 509.80 | 510.88 | 512.07 | 508.94 | 509.84 | 510.82 | 511.90 | 513.09 | |
| 0.50 | 503.95 | 504.44 | 504.99 | 505.59 | 506.25 | 504.97 | 505.46 | 506.01 | 506.61 | 507.27 | |
| 2000 | 0.10 | 661.56 | 667.82 | 674.70 | 682.28 | 690.61 | 662.58 | 668.84 | 675.72 | 683.29 | 691.62 |
| 0.20 | 633.75 | 637.23 | 641.05 | 645.26 | 649.88 | 634.77 | 638.24 | 642.07 | 646.27 | 650.90 | |
| 0.30 | 618.30 | 620.23 | 622.35 | 624.69 | 627.26 | 619.31 | 621.25 | 623.37 | 625.71 | 628.28 | |
| 0.40 | 609.71 | 610.79 | 611.97 | 613.27 | 614.69 | 610.73 | 611.80 | 612.98 | 614.28 | 615.71 | |
| 0.50 | 604.94 | 605.54 | 606.20 | 606.92 | 607.71 | 605.96 | 606.56 | 607.21 | 607.93 | 608.73 | |
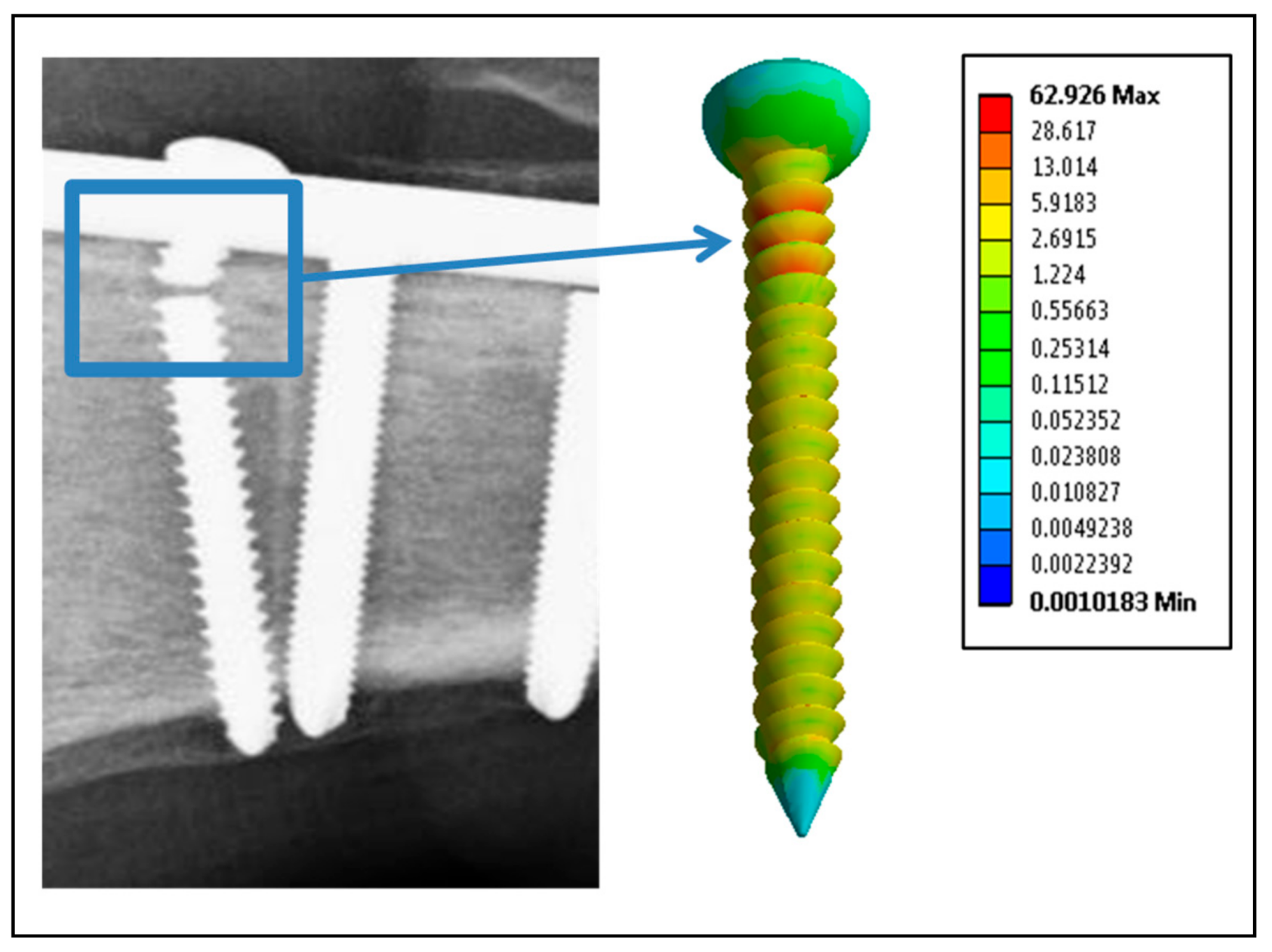
| Description | Cortical Screws | Locking Screws | |||||||
|---|---|---|---|---|---|---|---|---|---|
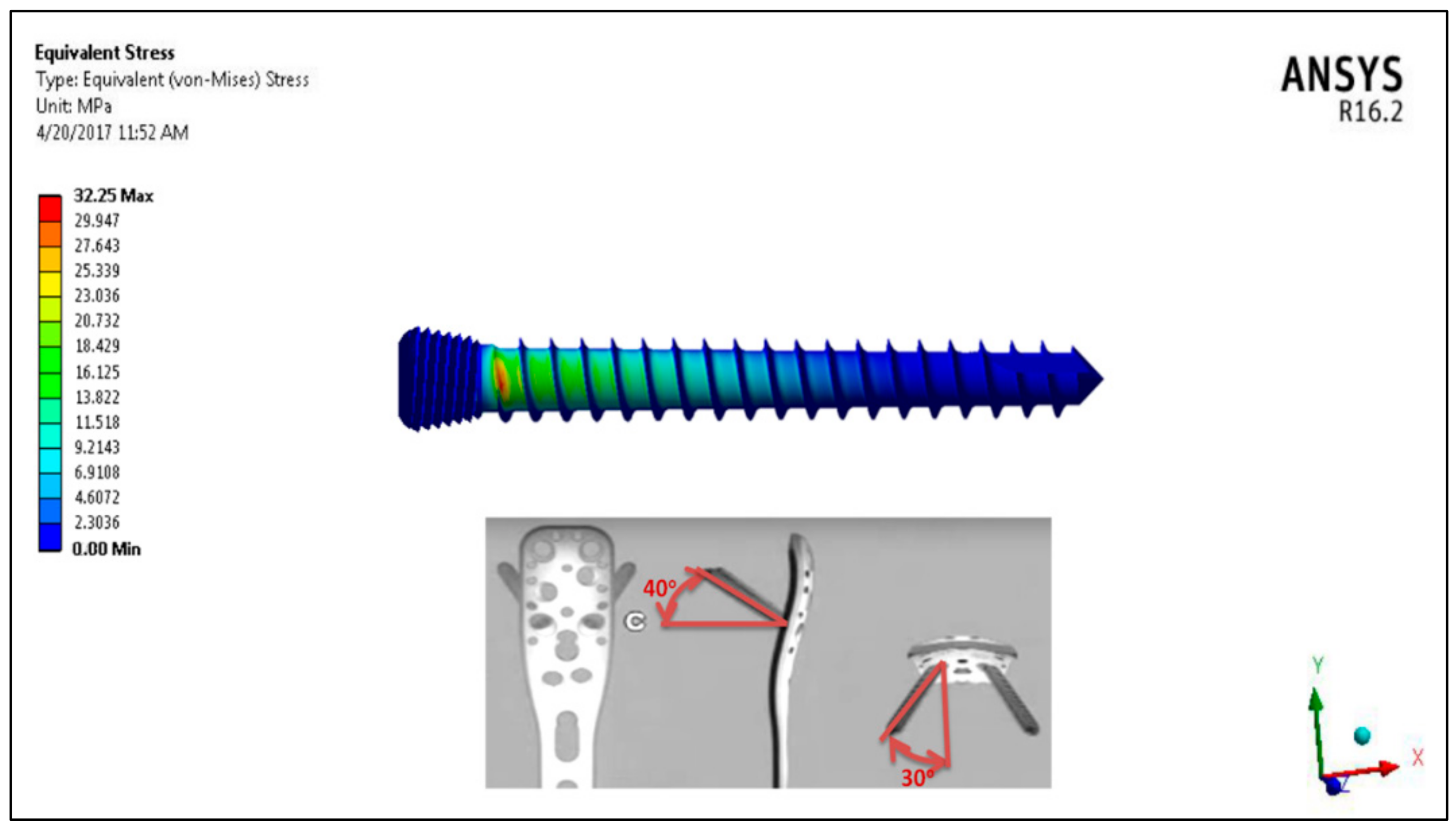
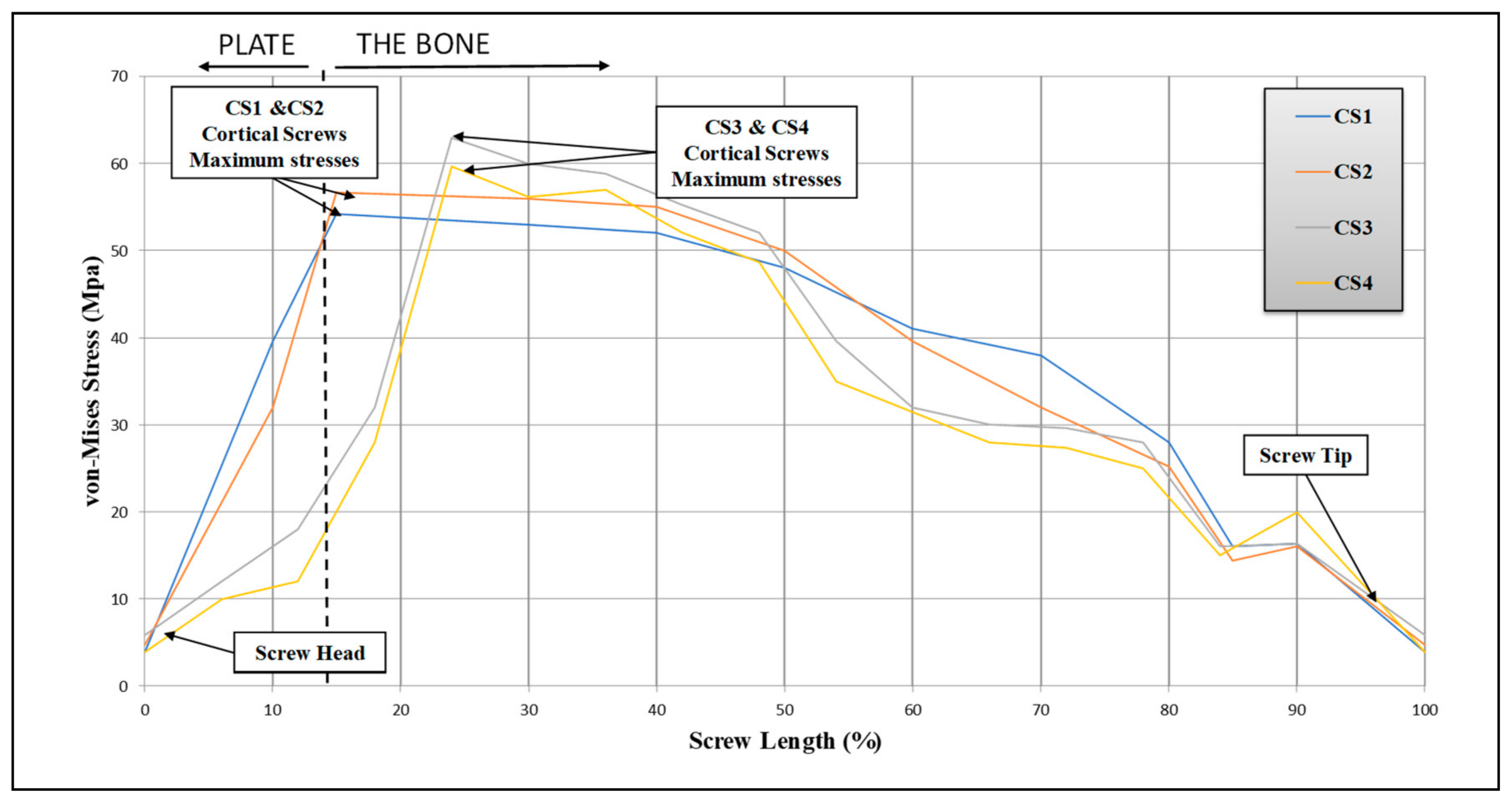
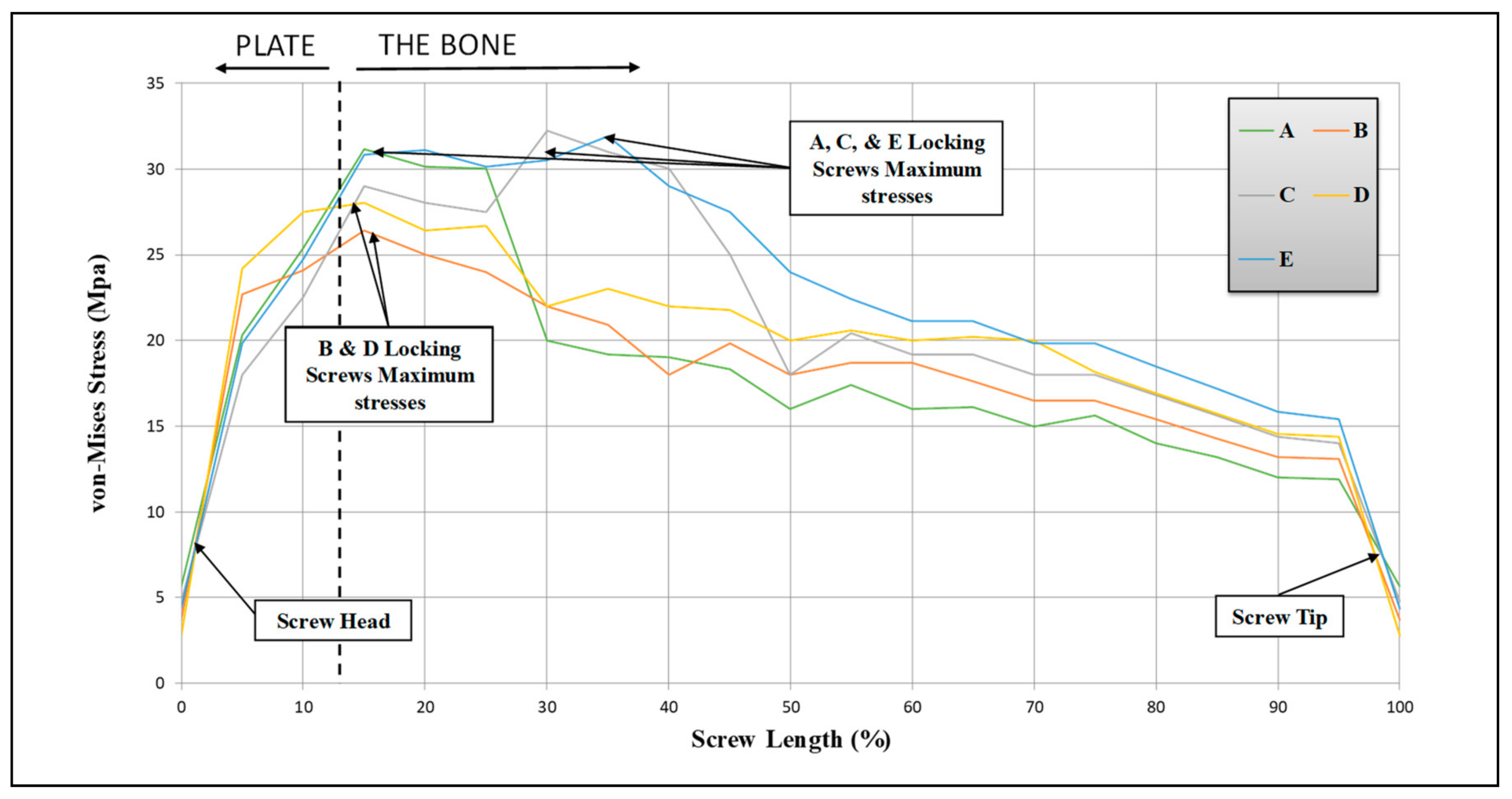
| The Screw | CS1 | CS2 | CS3 | CS4 | A | B | C | D | E |
| Maximum Stress (MPa) | 54.164 | 56.6316 | 62.926 | 59.627 | 31.138 | 26.4 | 32.25 | 28.04 | 31.9 |
| Screw | Visual Examination | Fractographic Examination | Quantitative Examination | |
|---|---|---|---|---|
Cortical Screws | CS1 | Plastic deformation, failed into two pieces X-ray image shows it was failed after two years of insertion | Fatigue striations Microcracks A rubbed surface | The maximum von Mises stresses were near the head of the screw |
| CS2 | No noticeable failure | N/A | The maximum von Mises stresses were near the head of the screw | |
| CS3 | Plastic deformation, failed into two pieces X-ray image shows it was failed after five years of insertion | N/A | The maximum von Mises stresses s were near the middle of the screw | |
| CS4 | Plastic deformation, failed into two pieces X-ray image shows it was failed after six years of insertion | Inclusion particles displaying ductile fracture Fatigue striations | The maximum von Mises stresses s were near the middle of the screw | |
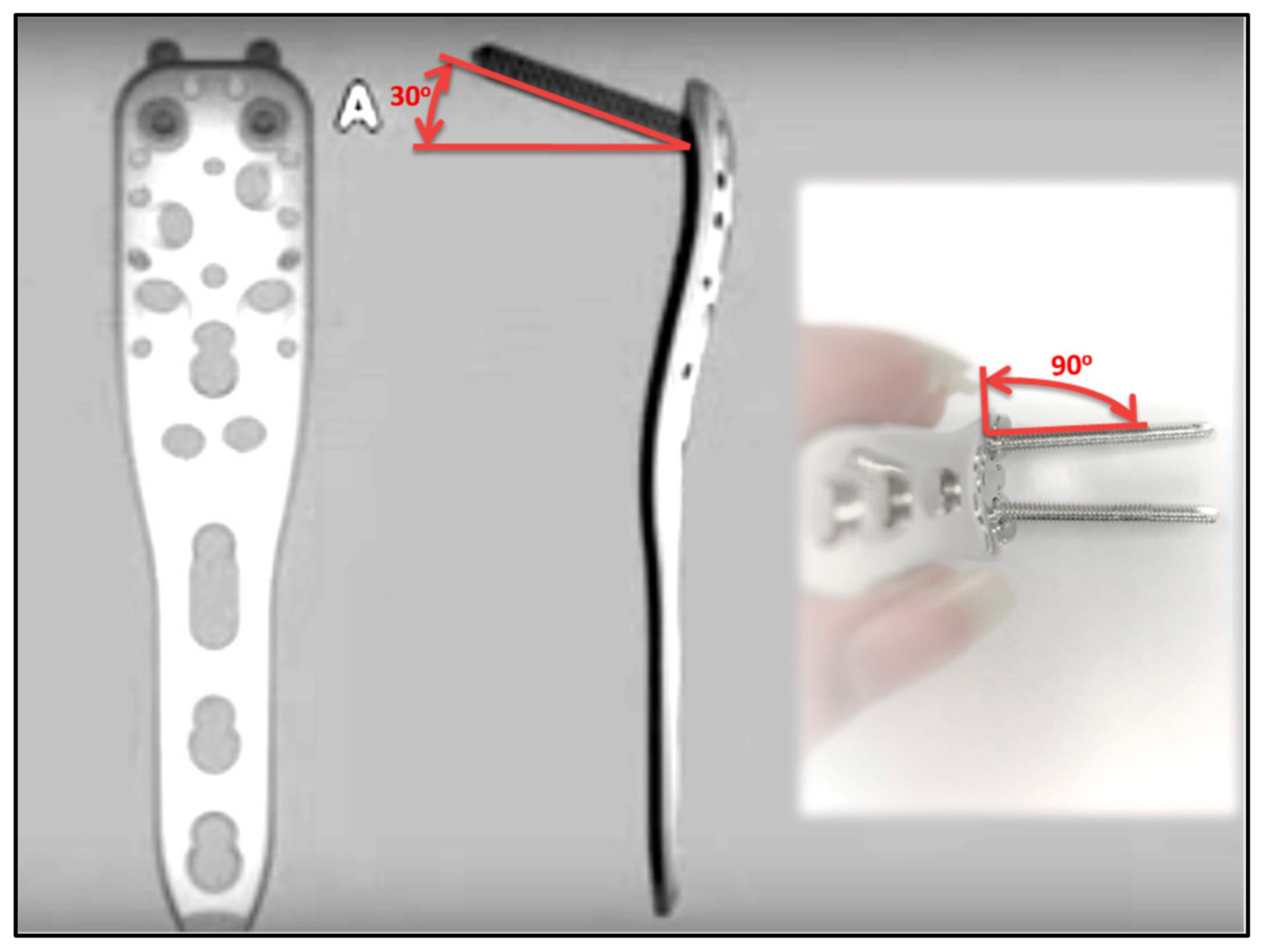
Locking Screws | LA | Inserted slightly upward with 30° angle and parallel to the other screw. One screw failed and fractured into two pieces | N/A | The von Mises stresses distributed between 20–40% the screw length Higher than levels b and d |
| LB | Inserted perpendicular to the plate and inward 30° angle. No noticeable failure | N/A | The von Mises stresses distributed near the head of the screw Lower than levels a, c, and e | |
| LC | Inserted upward with a 40° angle and outward 30° angle. One screw failed and fractured into two pieces | Inclusions Fatigue striations | The von Mises stresses distributed between 20–40% the screw length Higher than levels b and d | |
| LD | Inserted slightly upward with a10° angle. No noticeable failure | N/A | The von Mises stresses distributed near the head of the screw Lower than levels a, c, and e | |
| LE | Inserted upward with a 30° angle and slightly outward. One screw failed and fractured into two pieces | Inclusions Fatigue striations | The von Mises stresses distributed between 20–40% the screw length Higher than levels b and d | |
Cannulated Screw | Plastic deformation, failed into two pieces X-ray image shows it was failed after six years of insertion | N/A | The stresses were higher in the shaft of the screw | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamandi, F.; Laughlin, R.; Goswami, T. Failure Analysis of PHILOS Plate Construct Used for Pantalar Arthrodesis Paper II—Screws and FEM Simulations. Metals 2018, 8, 279. https://doi.org/10.3390/met8040279
Hamandi F, Laughlin R, Goswami T. Failure Analysis of PHILOS Plate Construct Used for Pantalar Arthrodesis Paper II—Screws and FEM Simulations. Metals. 2018; 8(4):279. https://doi.org/10.3390/met8040279
Chicago/Turabian StyleHamandi, Farah, Richard Laughlin, and Tarun Goswami. 2018. "Failure Analysis of PHILOS Plate Construct Used for Pantalar Arthrodesis Paper II—Screws and FEM Simulations" Metals 8, no. 4: 279. https://doi.org/10.3390/met8040279
APA StyleHamandi, F., Laughlin, R., & Goswami, T. (2018). Failure Analysis of PHILOS Plate Construct Used for Pantalar Arthrodesis Paper II—Screws and FEM Simulations. Metals, 8(4), 279. https://doi.org/10.3390/met8040279






