Mean Stress Effect on the Axial Fatigue Strength of DIN 34CrNiMo6 Quenched and Tempered Steel
Abstract
:1. Introduction
1.1. Historical Background
1.2. Empirical Methods
1.3. Methods Based on Physical Principles
- Gough hypothesis [7]: This theory states that effect of the mean stresses is due only to the damage produced by the maximum stress reached during the cycle, with no regard for the mean stress itself. This assumption led to the Crossland method [30], which uses the maximum hydrostatic stress during the cycle as the damage parameter.
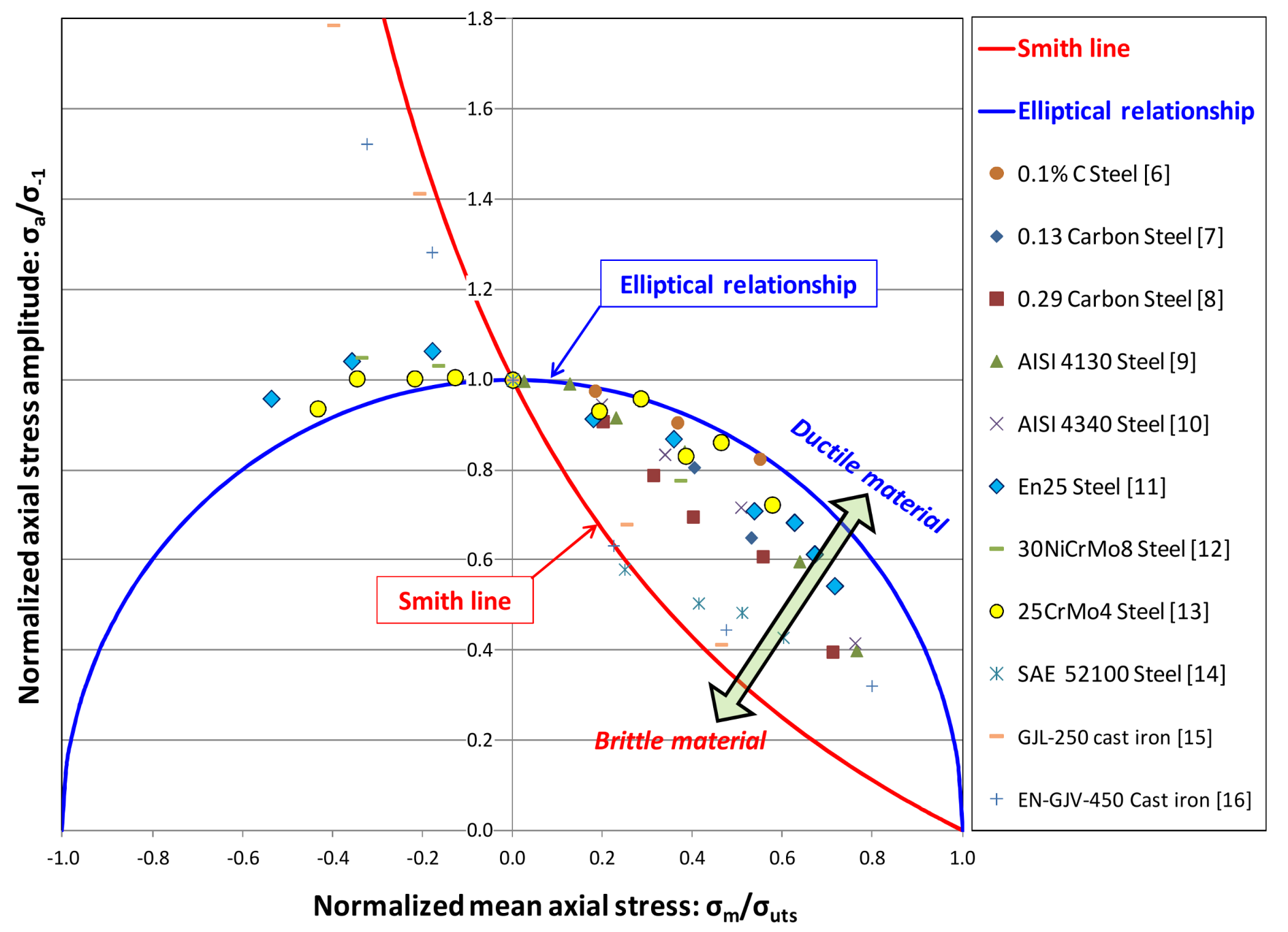
- Distortion energy theory [17]: In a theoretical material of von Mises, the effect of the normal stress to the critical plane is quadratic, without any influence of the hydrostatic stress. Moreover, equating the energies produced in N cycles in the case of completely reversed alternating stresses and the case of superimposed static stresses to a variable stress, an elliptic relationship between the mean and alternating stresses is obtained. This theory can be expressed analytically through the Marin multiaxial fatigue method.
- Total strain energy theory [31]: The effect of the mean stresses is related to the total elastic deformation energy stored. This hypothesis leads to the Froustey method, which leads to an elliptic relationship between the mean and alternating stresses, as in the Marin method.
- Findley critical plane [32]: The normal stress to high shear stress amplitudes planes allow the propagation of a micro-crack initiated by shear stresses. As Findley remarks [33], this effect is approximately linear in some materials, being clearly non-linear in others. For simplicity purposes, a linear normal maximum stress to the critical plane was selected by Findley as one of the damage parameters for the formulation of the Findley critical plane method.
2. Testing Procedure
2.1. Material
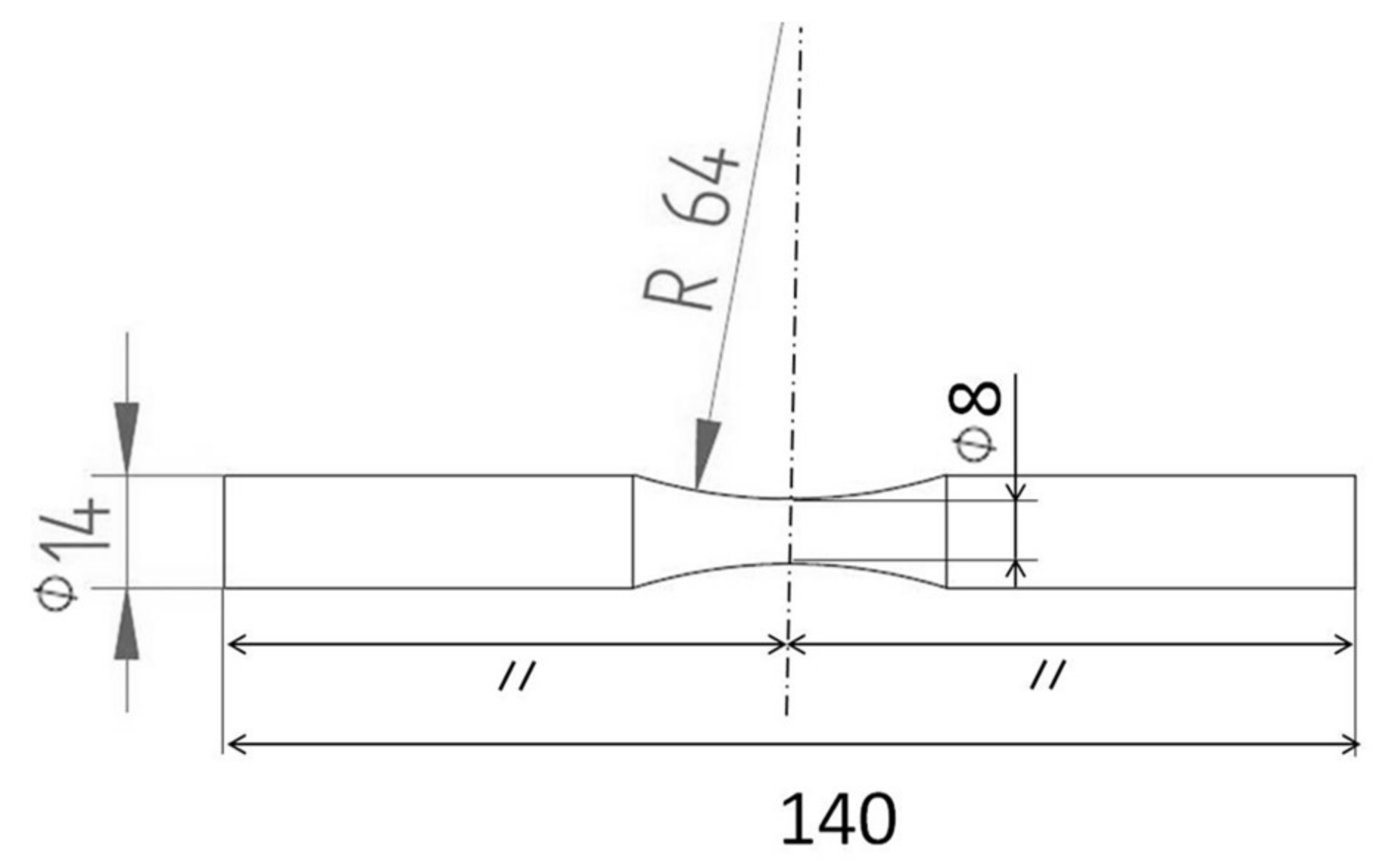
2.2. Specimens and Testing Machine
3. Results and Experimental Correlation with Empirical and Physical Models
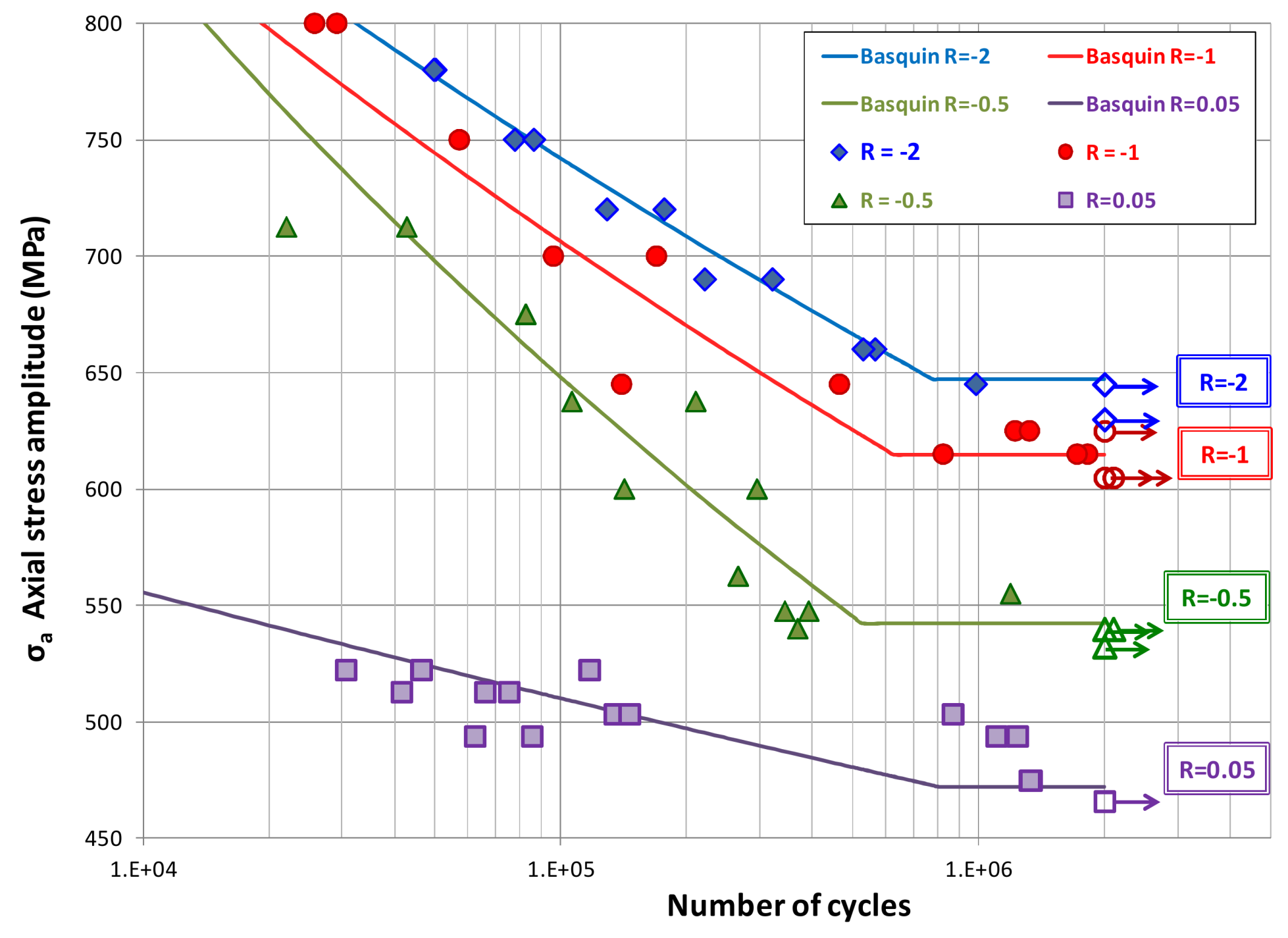
3.1. Fatigue Test Results
3.2. Fractographic Analysis of the Specimens
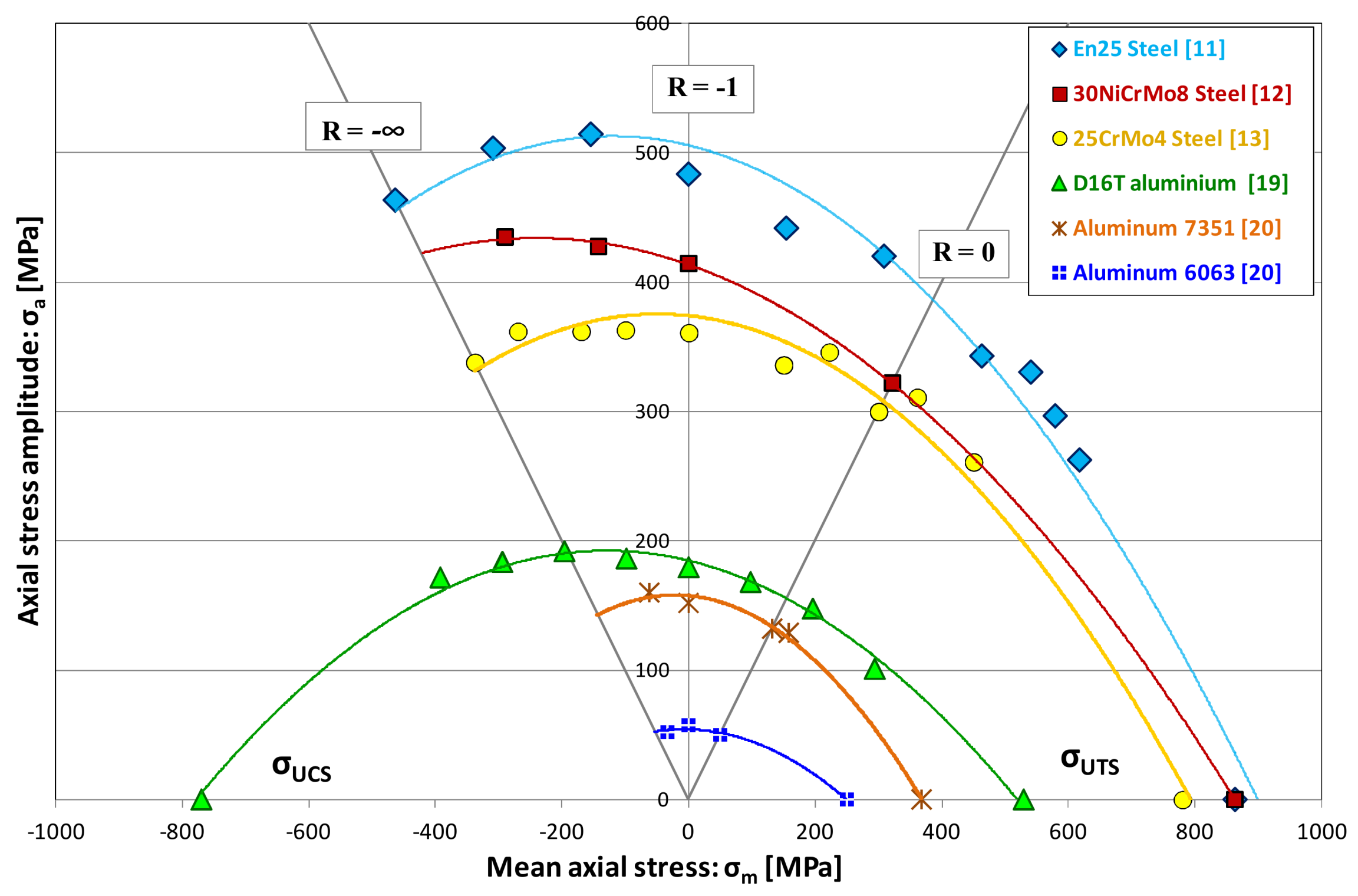
3.3. Correlation of the Experimental Results with Empirical and Physical Models
3.3.1. Empirical Models
3.3.2. Physical-Based Models
4. Development of an Energetic Fatigue Criterion for a DIN 34CrNiMo6 Quenched and Tempered Steel
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Derivation of the Parameters of the Proposed Physical Method
Appendix A.1. Fully Reversed Torsion Fatigue Test
Appendix A.2. Repeated Torsion Fatigue Test
Appendix A.3. Fully Reversed Axial Fatigue Test
Appendix A.4. Repeated Axial Fatigue Test
References
- Wöhler, A. Über die Festigkeits-Versuche mit Eisen und Stahl; Zeitschrift für Bauwesen: Frankfurt (Oder), Prussia, 1870; Volume 20, pp. 73–106. [Google Scholar]
- Papuga, J. A survey on evaluating the fatigue limit under multiaxial loading. Int. J. Fatigue 2011, 33, 153–165. [Google Scholar] [CrossRef]
- Smith, J.O. The Effect of Range of Stress on the Fatigue Strength of Metals; Bulletin Series No. 334; University of Illinois Engineering Experiment Station: Champaign, IL, USA, 1942. [Google Scholar]
- Weibull, W. Chapter VIII: Presentation of Results. In Fatigue Testing and Analysis of Results; Pergamon Press Oxford: London, UK; Paris, France, 1961; p. 153. [Google Scholar]
- Lüpfert, H.P.; Spies, H.J. Fatigue strength of heat-treated steel under static multiaxial compression stress. Adv. Eng. Mater. 2004, 6, 544–550. [Google Scholar] [CrossRef]
- Ukrainetz, P.R. The Effect of the Mean Stress on the Endurance Limit. Master’s Thesis, The University of Columbia, New York, NY, USA, August 1960. [Google Scholar]
- Gough, H.J. The Fatigue of Metals; Scott, Greenwood & Son: London, UK, 1924. [Google Scholar]
- Forrest, P.G. Fatigue of Metals; Pergamon Press Inc.: London, UK, 1962. [Google Scholar]
- Grover, H.J.; Bishop, S.M.; Jackson, L.R. Axial Load Fatigue Tests of Unnotched Sheet Specimens of 24S-T3 and 75S-T6 Aluminum Alloys and SAE 4130 Steels; Technical Note; National Advisory Committee for Aeronautics: Columbia, SC, USA, 1951.
- Trapp, W.J.; Schwartz, R.T. Elevated Temperature Fatigue Properties of SAE 4340 Steel. Proc. Am. Soc. Test. Mater. 1953, 53, 825–838. [Google Scholar]
- O’Connor, H.C.; Morrison, J.L.M. The Effect of Mean Stress on the Push-Pull Fatigue Properties of an Alloy Steel. In Proceedings of the International Conference on Fatigue of Metals, London, UK, 10–14 September 1956; Institution of Mechanical Engineers: London, UK, 1956; pp. 102–109. [Google Scholar]
- Grün, P.; Troost, A.; Akin, O.; Klubberg, F. Langzeitund Dauerschwingfestigkeit des Vergütungsstahls 25CrMo4 bei mehrachsiger Beanspruchung durch dreischwingende Lastspannungen. Materialwissenschaft Werkstofftechnik 1991, 22, 73–80. [Google Scholar] [CrossRef]
- Klubberg, F.; Schäfer, H.J.; Hempen, M.; Beiss, P. Mittelspannungsempfindlichkeit metallischer Werkstoffe bei schwingender Beanspruchung. In Roell Amsler Symposium 2001 World of Dynamic Testing; Verlag Mainz: Aachen, Germany, 2001; ISBN 3-89653-983-3. [Google Scholar]
- Bomas, H.; Bacher-Hoechst, M.; Kienzler, R.; Kunow, S.; Loewisch, G.; Muehleder, F.; Schroeder, R. Crack initiation and endurance limit of a hard steel under multiaxial cyclic loads. Fatigue Fract. Eng. Mater. Struct. 2009, 33, 126–139. [Google Scholar] [CrossRef]
- Rausch, T. Zum Schwingfestigkeitsverhalten von Gusseisenwerkstoffen unter Einachsiger und Mehrachsiger Beanspruchung am Beispiel von EN-GJV-450. Ph.D. Thesis, Aachen University, Aachen, Germany, 2011. [Google Scholar]
- Klubberg, P.; Beiss, P.; Broeckmann, C. Schwingfestigkeit von Gusseisen mit Lamellengraphit. Gießtechnik Motorenbau 2009, 2061, 107–118. [Google Scholar]
- Marin, J. Interpretation of fatigue strengths for combined stresses. In Proceedings of the International Conference on Fatigue of Metals, London, UK, 10–14 September 1956; Institution of Mechanical Engineers: London, UK, 1956; pp. 184–195. [Google Scholar]
- Gerber, H. Bestimmung der zulassigen Spannungen in Eisenkonstructionen. Z. Bayerischen Architeckten Ingenieur-Vereins 1874, 6, 101–110. [Google Scholar]
- Sochava, A.I. Approximating the diagram of limiting amplitudes taking into consideration the area of medium compressive stresses. Strength Mater. 1977, 9, 1169–1173. [Google Scholar] [CrossRef]
- Beiss, P.; Klubberg, F.; Schäfer, H.J.; Krug, P.; Weiß, H. Fatigue Behaviour of High Performance Spray-Compacted Aluminium Alloys. In Proceedings of the 11th International Conference on Aluminium Alloys, Aachen, Germany, 22–26 September 2008; Wiley-VCH: Weinheim, Germany, 2008; Volume 2, pp. 1583–1588. [Google Scholar]
- Klubberg, F.; Klopfer, I.; Broeckmann, C.; Berchtold, R.; Beiss, P. Fatigue testing of materials and components under mean load conditions. Anales Mecánica Fractura 2011, 1, 419–424. [Google Scholar]
- Goodman, J. Mechanics Applied to Engineering; Longmans Green: London, UK, 1899. [Google Scholar]
- Haigh, B.P. Elastic and Fatigue Fracture in Metals. Metal Ind. 1922, 21, 466. [Google Scholar]
- Morrow, J. Fatigue properties of metals, Section 3.2. In Fatigue Design Handbook; Pub. No. AE-4; SAE: Warrendale, PA, USA, 1968. [Google Scholar]
- Bridgman, P.W. Studies in Large Plastic Flow and Fracture with Special Emphasis on the Effects of Hydrostatic Pressure, 1st ed.; McGraw-Hill Book Company: New York, NY, USA, 1952; pp. 38–86. ISBN 0674731336. [Google Scholar]
- Dowling, N.E.; Calhoun, C.A.; Arcari, A. Mean stress effects in stress-life fatigue and the Walker equation. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 163–179. [Google Scholar] [CrossRef]
- Dowling, N.E. Mean stress effects in strain-life fatigue. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 1004–1019. [Google Scholar] [CrossRef]
- Dietmann, H. Festigkeitsberechnung bei Mehrachsiger Schwingbeansoruchung. Konstruktion 1973, 25, 181–189. [Google Scholar]
- Susmel, L.; Tovo, R.; Lazzarin, P. The mean stress effect on the high-cycle fatigue strength from a multiaxial fatigue point of view. Int. J. Fatigue 2005, 27, 928–943. [Google Scholar] [CrossRef]
- Crossland, B. Effect of Large Hydrostatic Pressure on the Torsional Fatigue Strength of an Alloy Steel. In Proceedings of the International Conference on Fatigue of Metals, London, UK, 10–14 September 1956; Institution of Mechanical Engineers: London, UK, 1956; pp. 138–149. [Google Scholar]
- Froustey, C. Fatigue multiaxiale en endurance de l’acier 30 NCD 16. Ph.D. Thesis, École Nationale Supérieure d’Arts et Métiers, Bordeaux, France, September 1987. [Google Scholar]
- Findley, W.N.; Coleman, J.J.; Hanley, B.C. Theory for Combined Bending and Torsion Fatigue with Data for SAE 4340 Steel. In Proceedings of the International Conference on Fatigue of Metals, London, UK, 10–14 September 1956; Institution of Mechanical Engineers: London, UK, 1956; pp. 150–157. [Google Scholar]
- Findley, W.N. A theory for the effect of mean stress on fatigue of metals under combined torsion and axial load or bending. J. Eng. Ind. Trans. ASME 1959, 81, 301–306. [Google Scholar]
- Avilés, R.; Albizuri, J.; Rodríguez, A.; López de Lacalle, L.N. Influence of low-plasticity ball burnishing on the high-cycle fatigue strength of medium carbon AISI 1045 steel. Int. J. Fatigue 2013, 55, 230–244. [Google Scholar] [CrossRef]
- Branco, R.; Costa, J.D.; Antunes, F.V. Low-cycle fatigue behaviour of 34CrNiMo6 high strength steel. Theor. Appl. Fract. Mech. 2012, 58, 28–34. [Google Scholar] [CrossRef]
- Branco, R.; Costa, J.D.M.; Antunes, F.V.; Perdigão, S. Monotonic and Cyclic Behavior of Din 34CrNiMo6 Tempered Alloy Steel. Metals 2016, 6, 98. [Google Scholar] [CrossRef]
- Davoli, P.; Bernasconi, A.; Filippini, M.; Foletti, S.; Papadopoulos, I.V. Independence of the torsional fatigue limit upon a mean shear stress. Int. J. Fatigue 2003, 25, 471–480. [Google Scholar] [CrossRef]
- ASTM. ASTM E466-15, Standard Practice for Conducting Force Controlled Constant Amplitude Axial Fatigue Tests of Metallic Materials; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]
- Sonsino, C.M. Course of SN-curves especially in the high-cycle fatigue regime with regard to component design and safety. Int. J. Fatigue 2007, 29, 2246–2258. [Google Scholar] [CrossRef]
- Li, C.; Li, S.; Duan, F.; Wang, Y.; Zhang, Y.; He, D.; Li, Z.; Wang, W. Statistical Analysis and Fatigue Life Estimations for Quenched and Tempered Steel at Different Tempering Temperatures. Metals 2017, 7, 312. [Google Scholar] [CrossRef]
- Gaur, V.; Doquet, V.; Persent, E.; Mareau, C.; Roguet, E.; Kittel, J. Surface versus internal fatigue crack initiation in steel: Influence of mean stress. Int. J. Fatigue 2016, 82, 437–448. [Google Scholar] [CrossRef]
- Sakai, T.; Nakagawa, A.; Oguma, N.; Nakamura, Y.; Ueno, A.; Kikuchi, S.; Sakaida, A. A review on fatigue fracture modes of structural metallic materials in very high cycle regime. Int. J. Fatigue 2016, 93, 339–351. [Google Scholar] [CrossRef]
- Papadopoulos, I.V.; Davoli, P.; Gorla, C.; Filippini, M.; Bernasconi, A. A comparative study of multiaxial high-cycle fatigue for metals. Int. J. Fatigue 1997, 19, 219–235. [Google Scholar] [CrossRef]
- Morrison, J.L.M. Session 2: Stress Distribution. In Proceedings of the International Conference on Fatigue of Metals, London, UK, 10–14 September 1956; Institution of Mechanical Engineers: London, UK, 1956; pp. 741–742. [Google Scholar]
- Gurson, A. Continuum theory of ductile rupture by void nucleation and growth: Part I yield criteria and flow rules for porous ductile media. J. Eng. Mater. Technol. 1977, 99, 2–15. [Google Scholar] [CrossRef]
- Zenner, H.; Simbürger, A.; Liu, J. On the fatigue limit of ductile metals under complex multiaxial loading. Int. J. Fatigue 2000, 22, 137–145. [Google Scholar] [CrossRef]
- Nishijima, S. Basic Properties of JIS Steels for Machine Structural Use; NRIM Special Report (Technical Report) No. 93-02; National Research Institute for Metals: Tokyo, Japan, 1993. [Google Scholar]





| Element | C | Cr | Ni | Mo | Mn | Si | P | S | Fe |
|---|---|---|---|---|---|---|---|---|---|
| Weight (%) | 0.345 | 1.565 | 1.565 | 0.237 | 0.710 | 0.275 | 0.0075 | 0.003 | Balance |
| Monotonic Properties | Symbol | Value |
|---|---|---|
| Yield strength | σyp | 1084 MPa |
| Ultimate tensile strength | σuts | 1210 MPa |
| Reduction of area | Z | 60.2% |
| Elongation at fracture | A | 12.2% |
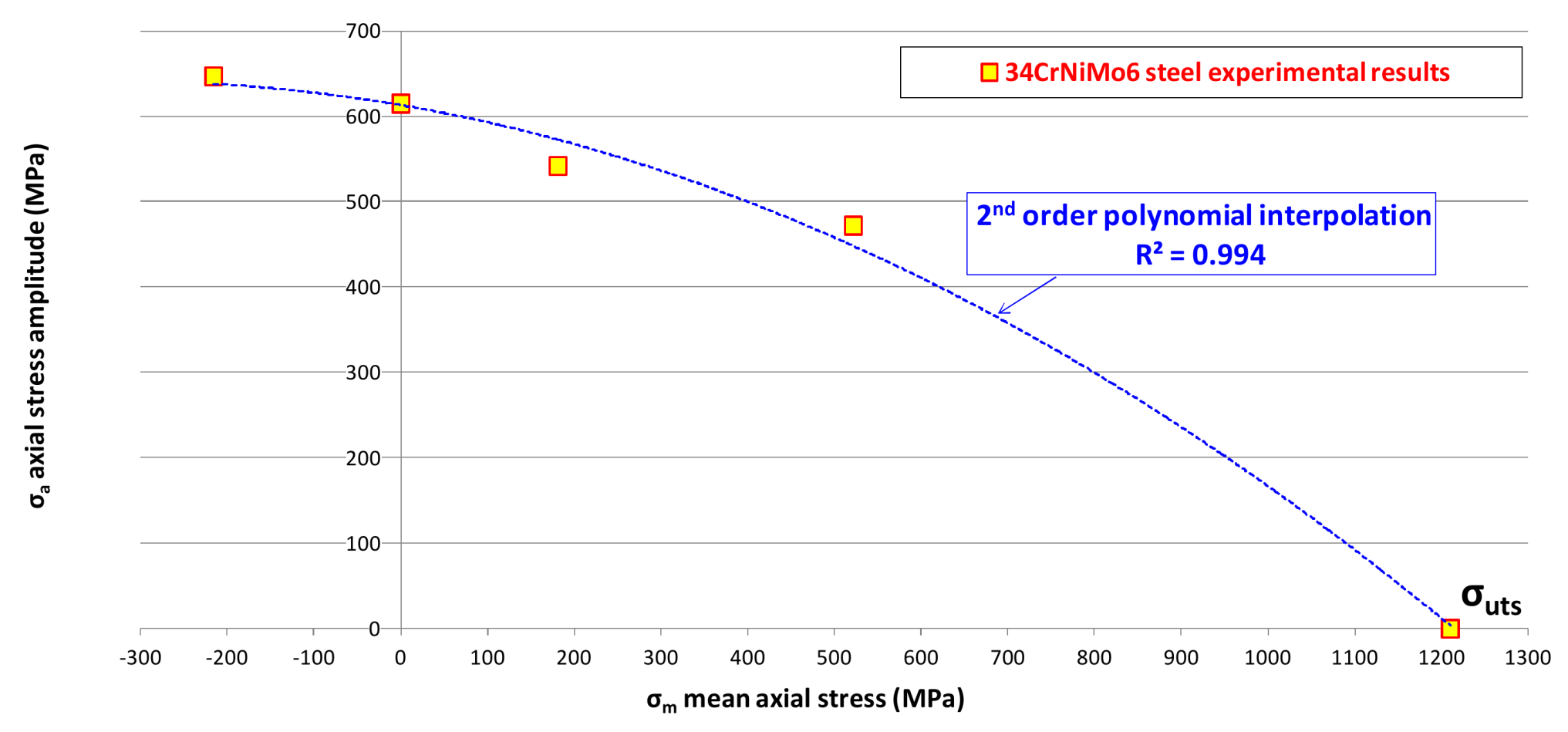
| σm (MPa) | σa (MPa) | R (Stress Ratio) | α | β |
|---|---|---|---|---|
| −216 | 647 | −2 | 1.14 × 1048 | −15.000 |
| 0 | 615 | −1 | 4.61 × 1042 | −13.220 |
| 181 | 542 | −0.5 | 1.79 × 1031 | −9.338 |
| 522 | 472 | 0.05 | 6.37 × 1077 | −26.889 |
| R (σmin/σmax) | σm (MPa) | Gerber | Goodman | Morrow | Dietmann |
|---|---|---|---|---|---|
| −2 | −216 | 8.0 | −12.0 | −8.3 | −3.2 |
| −0.5 | 181 | −10.9 | 3.5 | −0.3 | −4.6 |
| 0.05 | 522 | −6.1 | −25.9 | 13.4 | 1.7 |
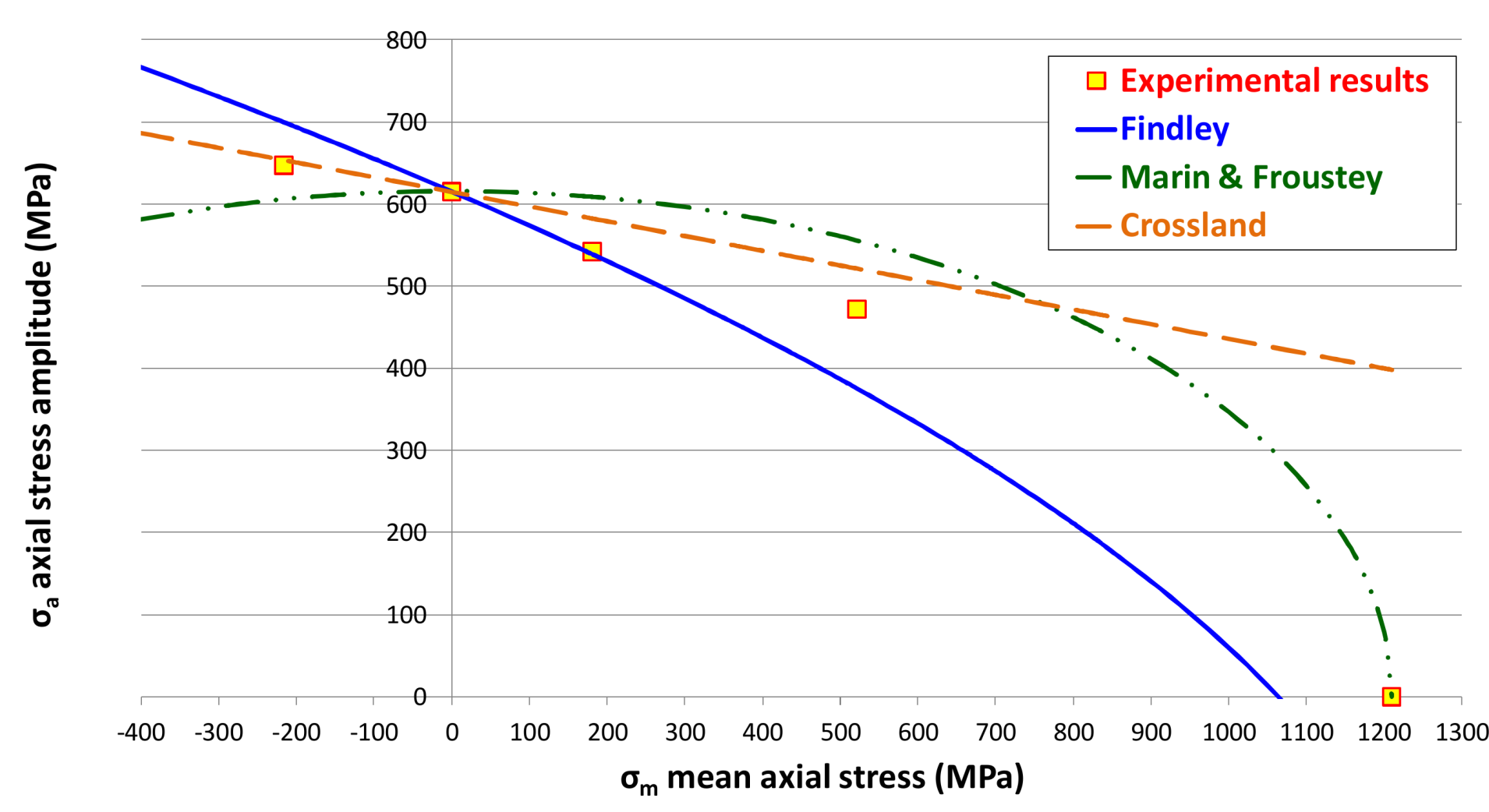
| R (σmin/σmax) | σm (MPa) | Crossland | Marin, Froustey | Findley |
|---|---|---|---|---|
| −2 | −216 | −1.0 | 6.5 | −8.1 |
| −0.5 | 181 | −7.5 | −12.2 | 0.6 |
| 0.05 | 522 | −10.5 | −17.6 | 20.5 |
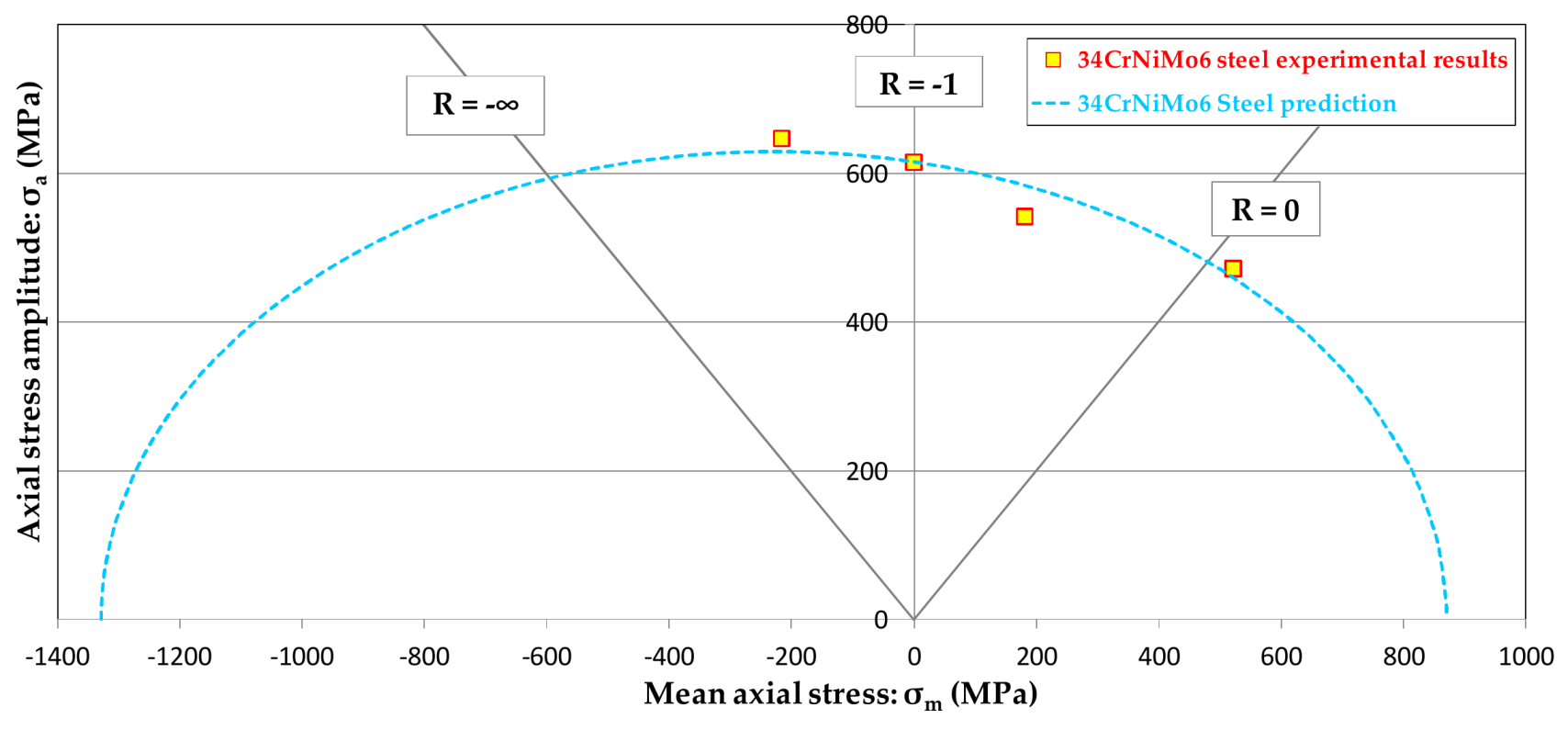
| Parameters | σ−1 | τ−1 | σ0 | τ0 | a | b | c | Λ |
|---|---|---|---|---|---|---|---|---|
| Values for 34CrNiMo6 steel | 615 | 433 | 961 | 765 | 433 | 819 | 4092 | 2337 |
| R (σmin/σmax) | σm (MPa) | Proposed Theory (Equation (17)) |
|---|---|---|
| −2 | −216 | 2.6 |
| −0.5 | 181 | −7.5 |
| 0.05 | 522 | 2.6 |
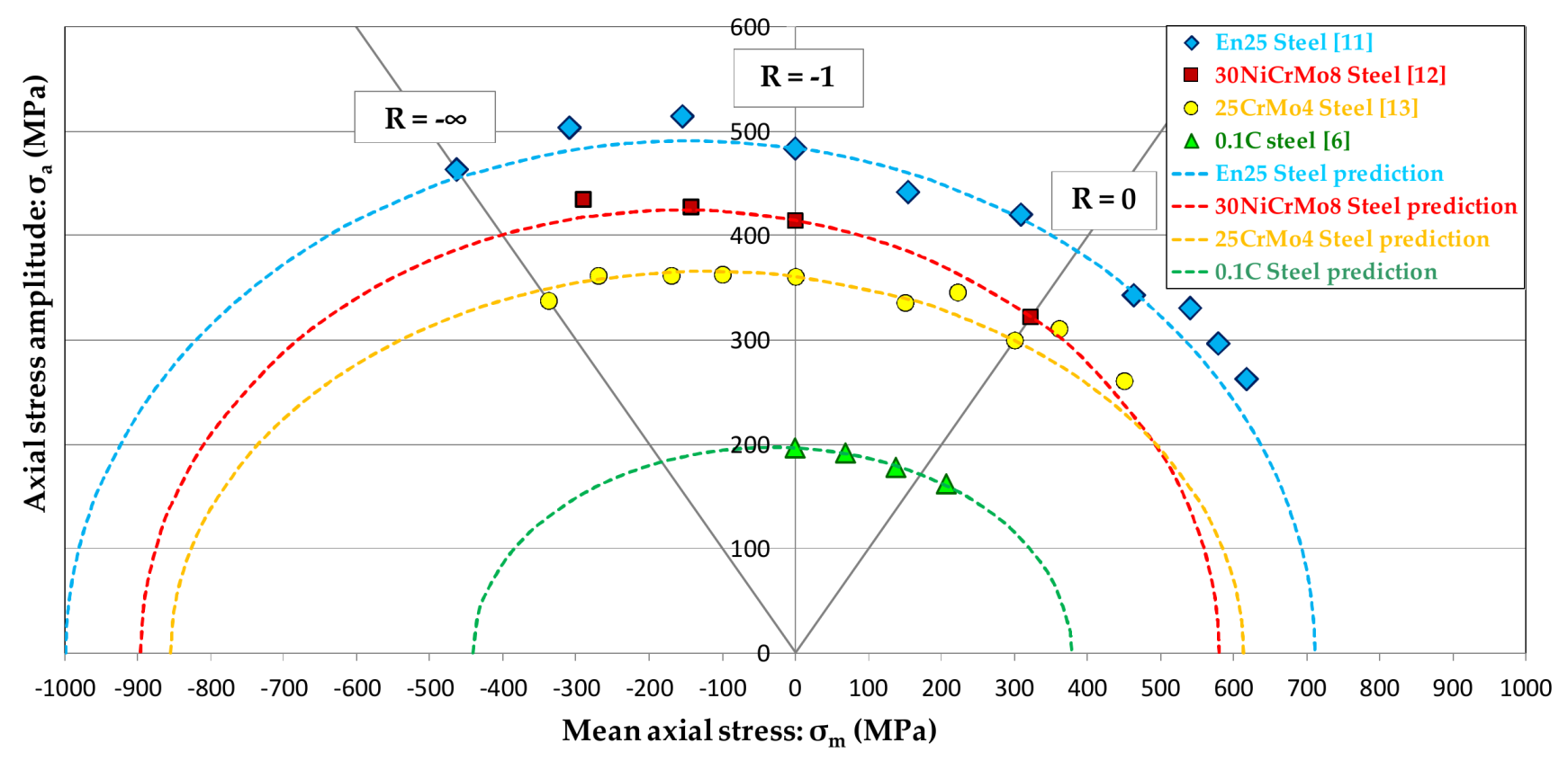
| Parameter | σ−1 | τ−1 | σ0 | τ0 | a | b | c | Λ |
|---|---|---|---|---|---|---|---|---|
| Values for En25 steel [11] | 483 | 301 | 770 | 534 | 301 | 578 | 2163 | 813 |
| Values for 30NiCrMo8 steel [12] | 414 | 311 | 644 | 543 | 311 | 560 | 3528 | 2251 |
| Values for 25CrMo4 steel [13] | 361 | 228 | 600 | 414 | 228 | 493 | 2113 | 857 |
| Values for 0.1C steel [6] | 197 | 114 | 343 | 213 | 114 | 293 | 709 | 94 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pallarés-Santasmartas, L.; Albizuri, J.; Avilés, A.; Avilés, R. Mean Stress Effect on the Axial Fatigue Strength of DIN 34CrNiMo6 Quenched and Tempered Steel. Metals 2018, 8, 213. https://doi.org/10.3390/met8040213
Pallarés-Santasmartas L, Albizuri J, Avilés A, Avilés R. Mean Stress Effect on the Axial Fatigue Strength of DIN 34CrNiMo6 Quenched and Tempered Steel. Metals. 2018; 8(4):213. https://doi.org/10.3390/met8040213
Chicago/Turabian StylePallarés-Santasmartas, Luis, Joseba Albizuri, Alexander Avilés, and Rafael Avilés. 2018. "Mean Stress Effect on the Axial Fatigue Strength of DIN 34CrNiMo6 Quenched and Tempered Steel" Metals 8, no. 4: 213. https://doi.org/10.3390/met8040213
APA StylePallarés-Santasmartas, L., Albizuri, J., Avilés, A., & Avilés, R. (2018). Mean Stress Effect on the Axial Fatigue Strength of DIN 34CrNiMo6 Quenched and Tempered Steel. Metals, 8(4), 213. https://doi.org/10.3390/met8040213





