A Combined Hybrid 3-D/2-D Model for Flow and Solidification Prediction during Slab Continuous Casting
Abstract
:1. Introduction
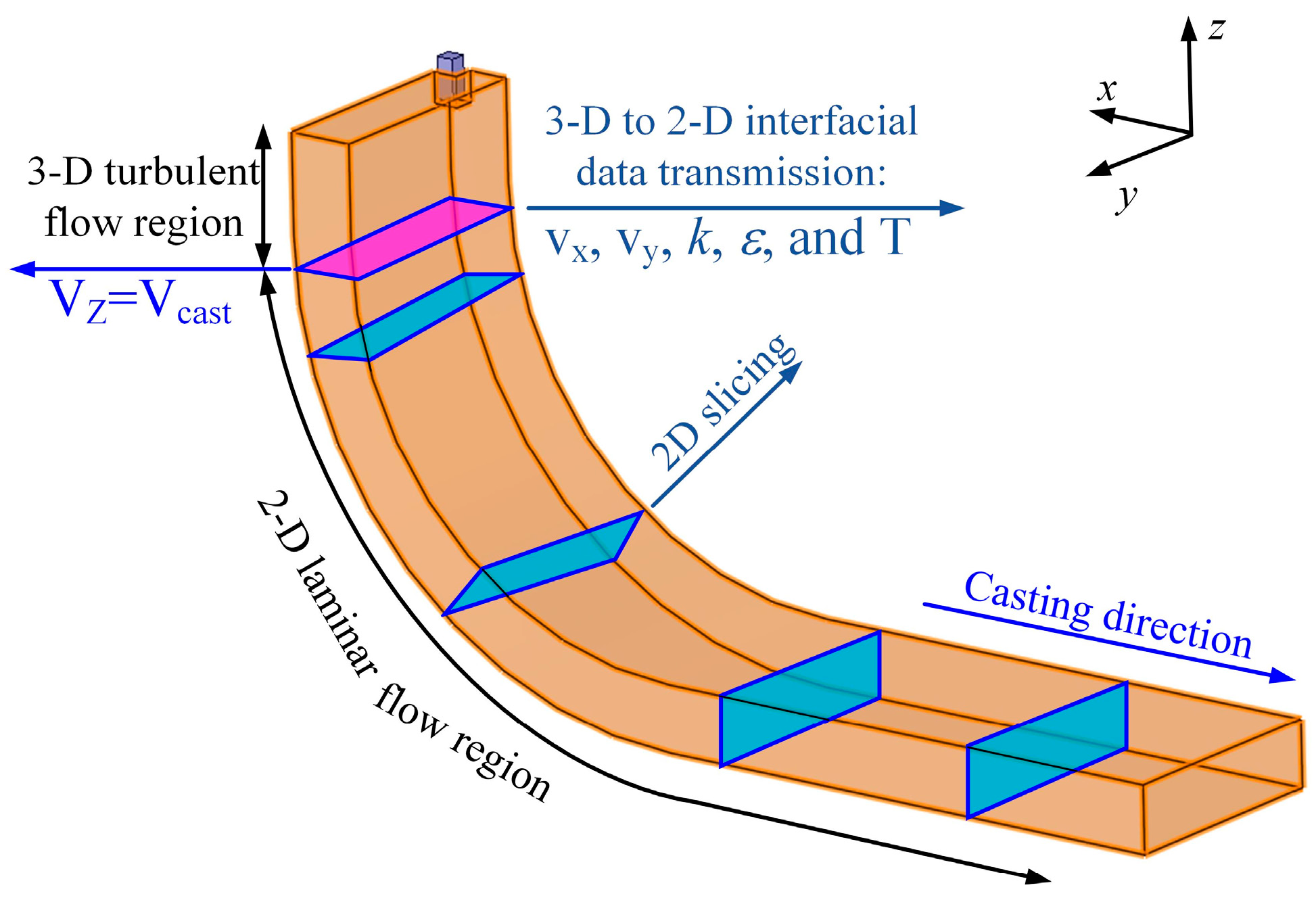
2. Model Description
2.1. Mathematical Formulation
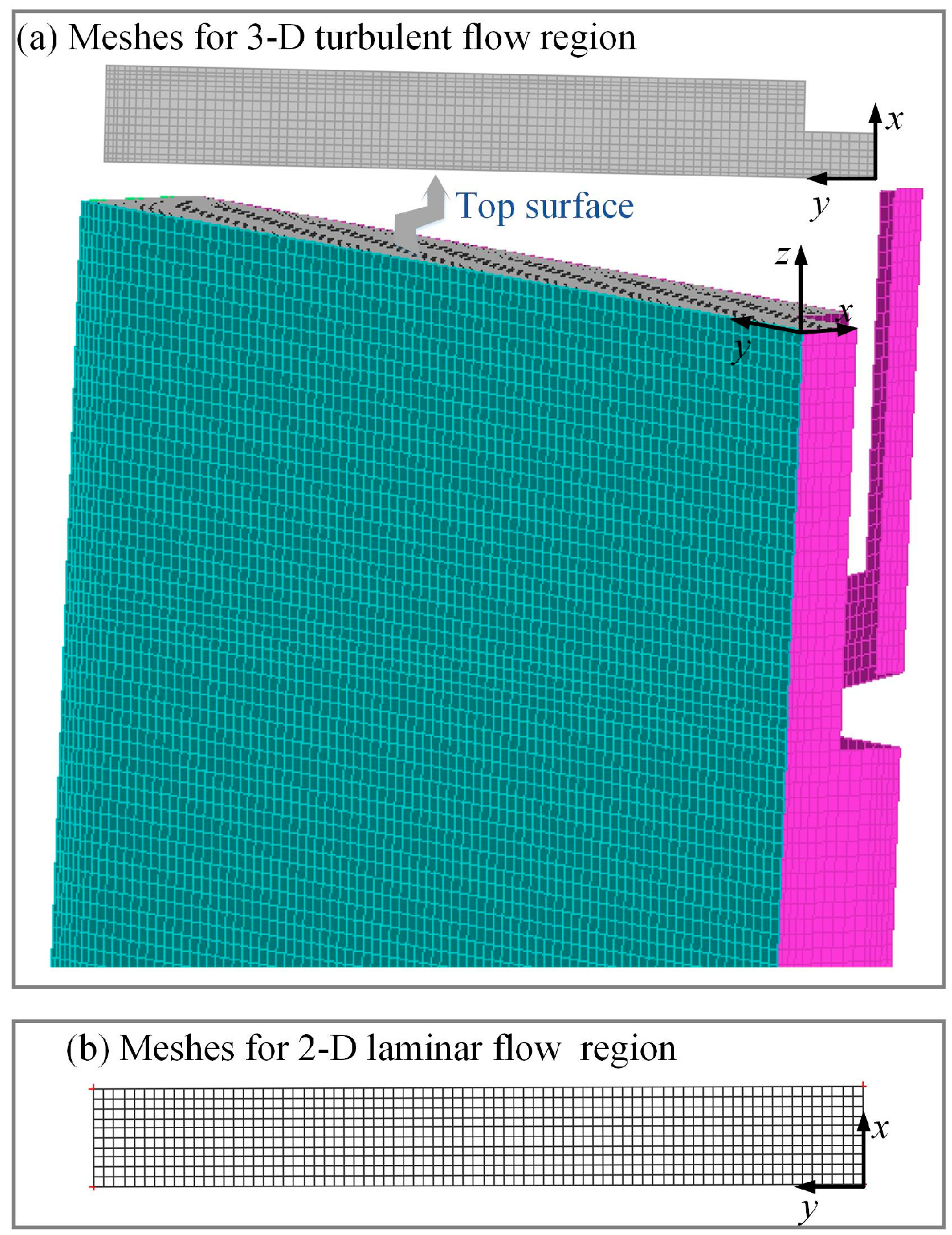
2.2. Computational Domain
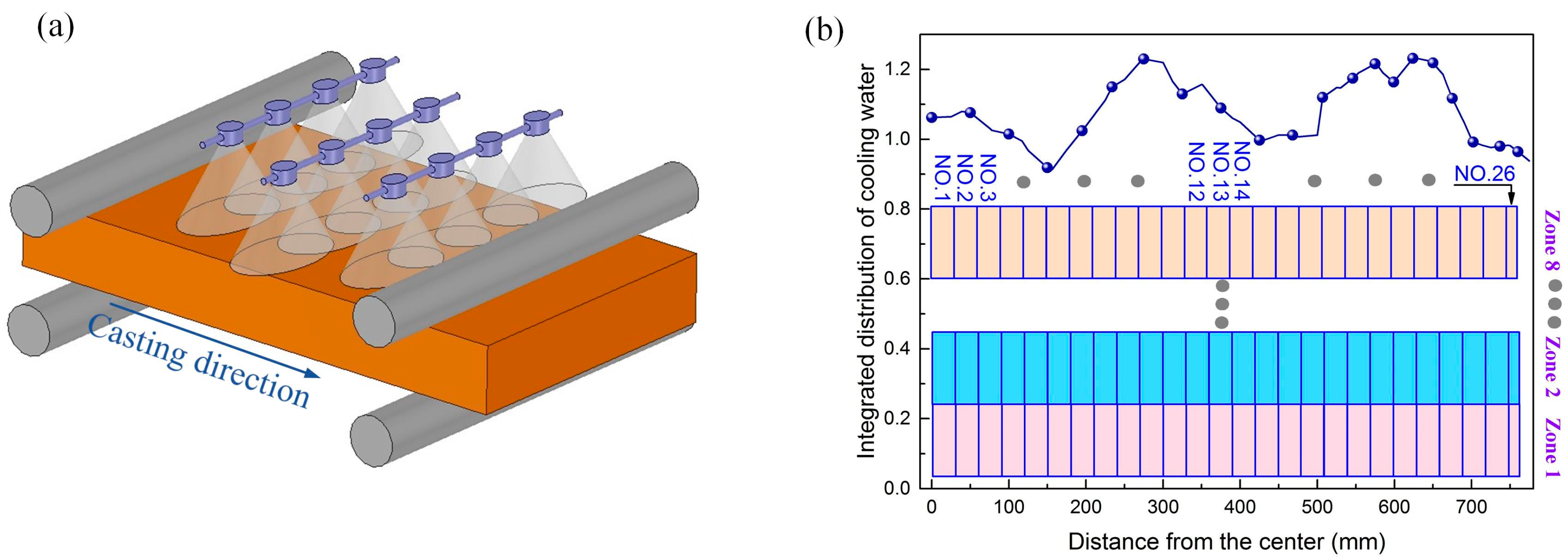
2.3. Boundary Conditions and Physical Properties
2.4. Solution Procedure
3. Results and Discussion
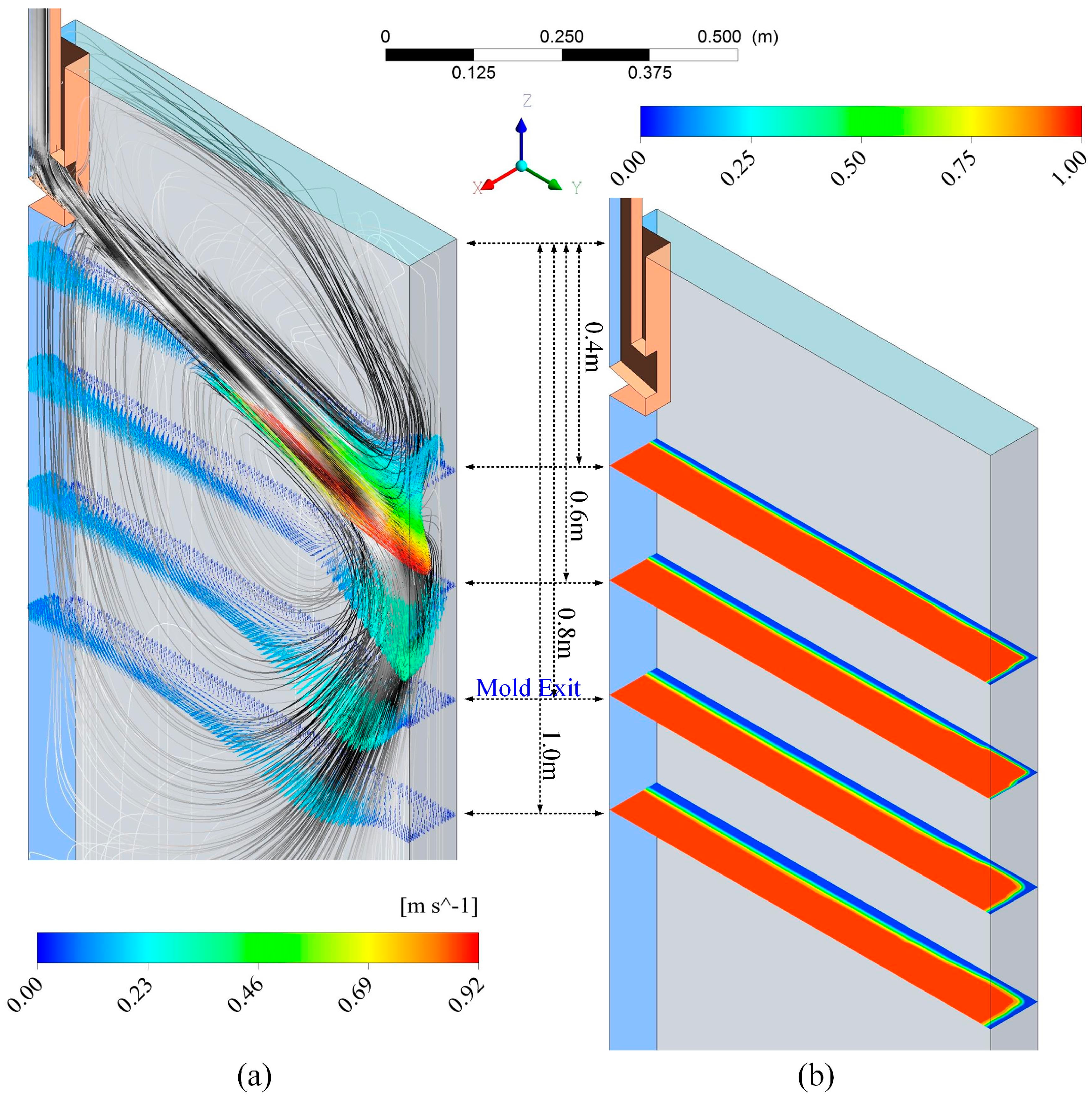
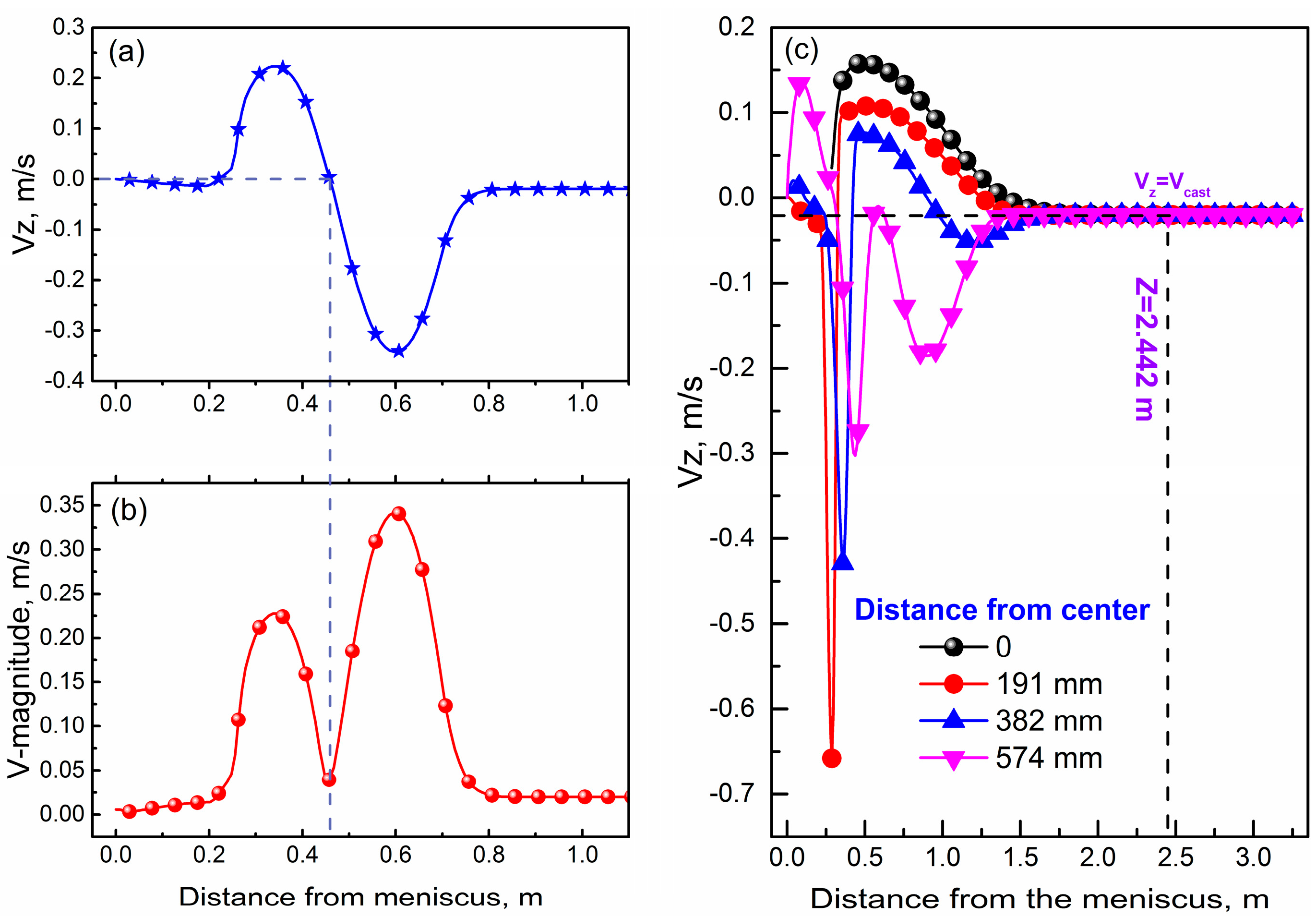
3.1. Flow and Solidification Phenomena in the Turbulent Flow Region
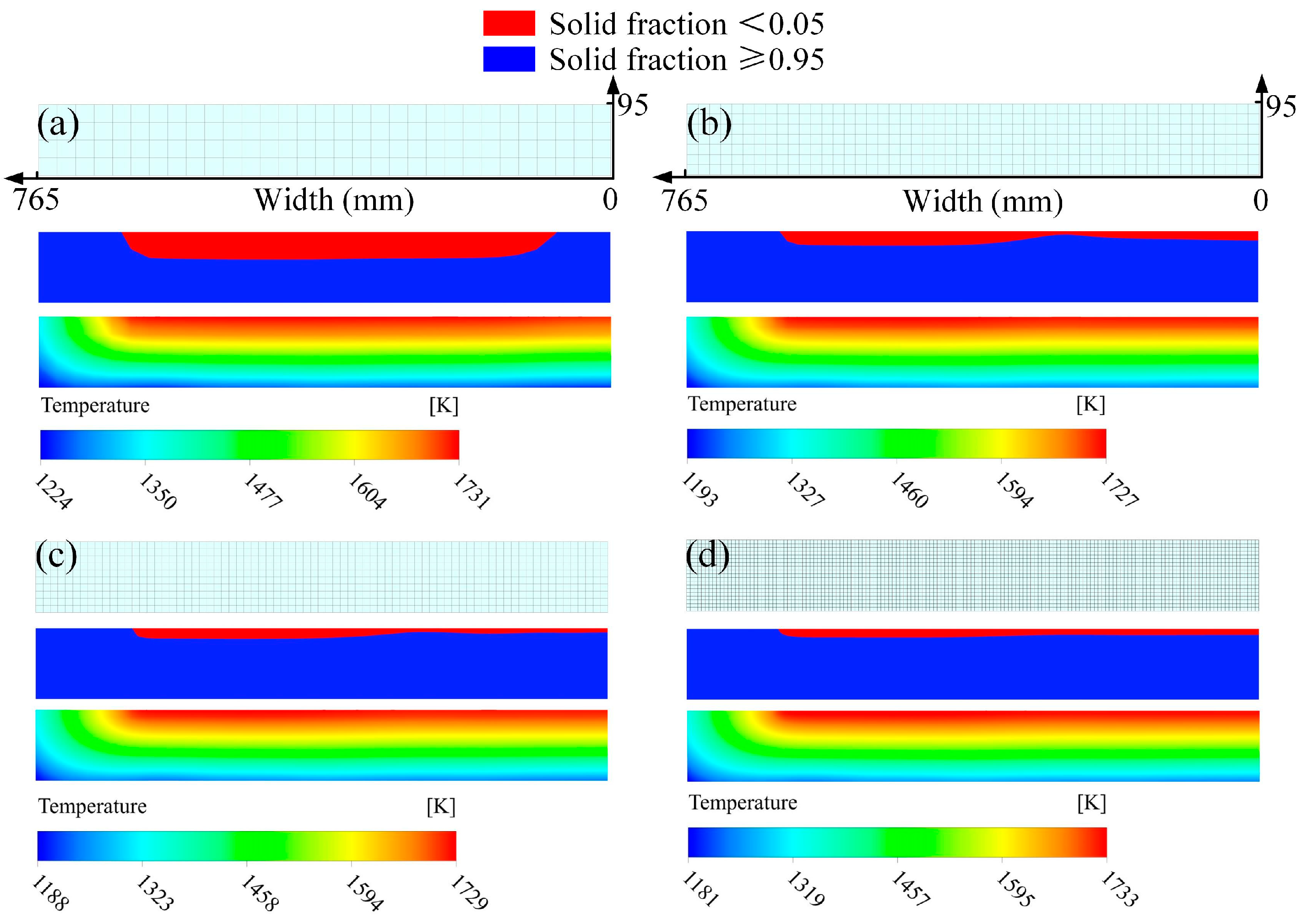
3.2. Grid Independence Tests for the Laminar Flow Region
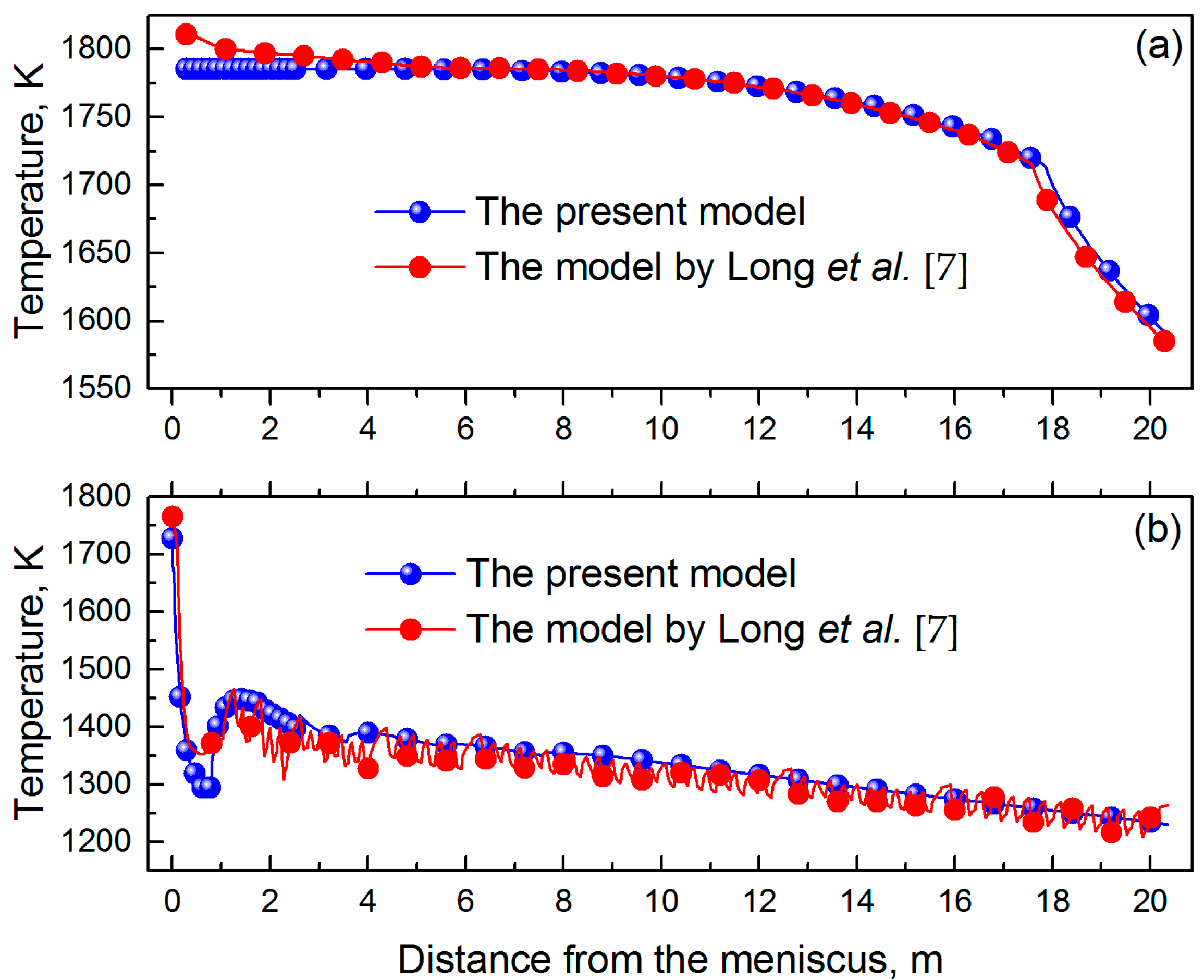
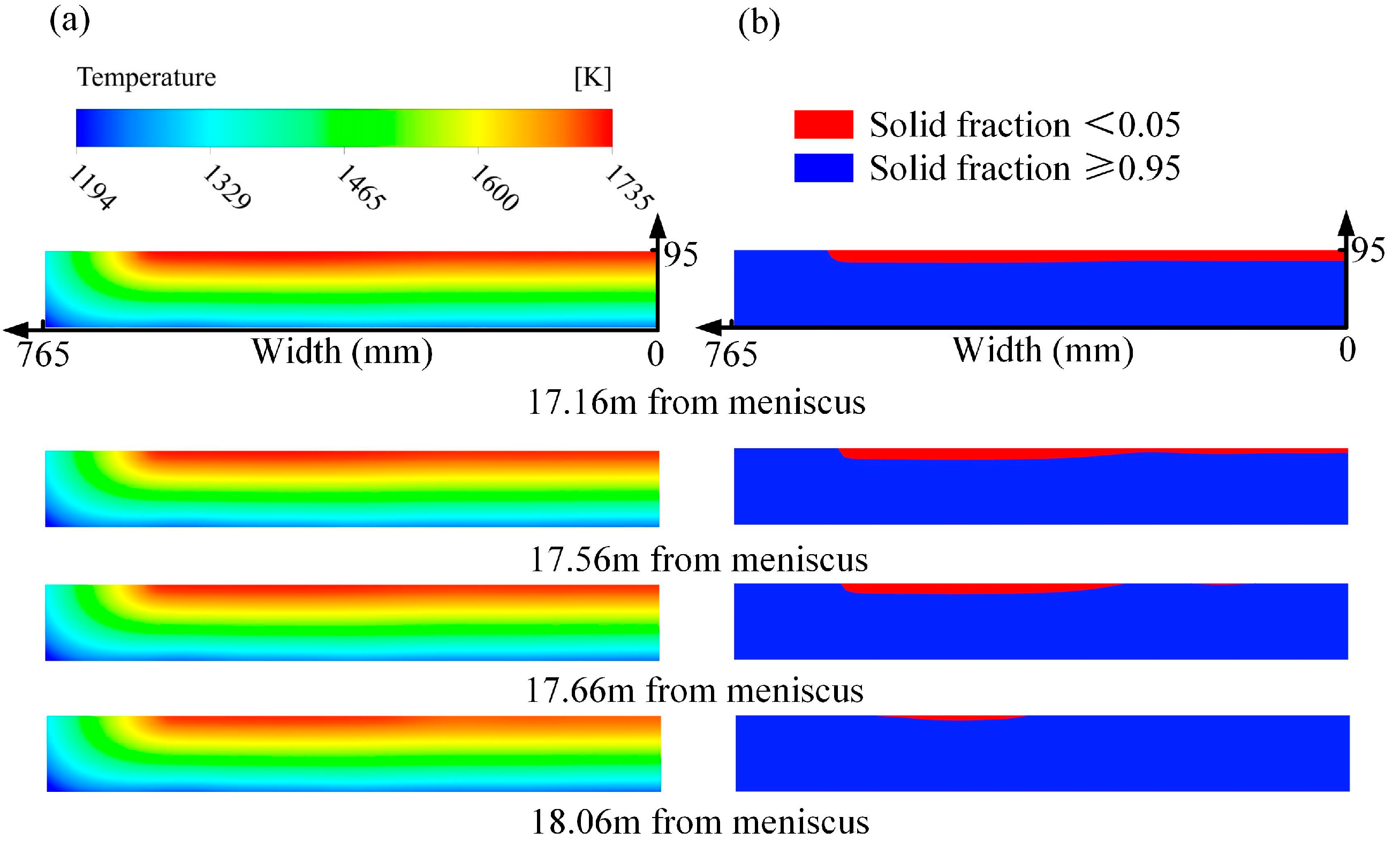
3.3. Temperature Field and Solidification Profile
4. Conclusions
- (1)
- The impact effect caused by the molten steel jet on the formation of a solidification shell is significant. The impact point is at the position 457 mm below the meniscus, and the plug flow is formed 2442 mm below the meniscus.
- (2)
- For the simulation of the laminar flow region, the grids with a cell size of 10 × 10 mm2 are sufficient to attain a precise temperature distribution and solidification profile.
- (3)
- The solidification profile of the strand is not entirely uniform. The final solidification points, roughly being at the position from 400–500 mm in the width direction, are 17.66 m away from the meniscus.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ma, J.C.; Xie, Z.; Ci, Y.; Jia, G.L. Simulation and application of dynamic heat transfer model for improvement of continuous casting process. Mater. Sci. Technol. 2009, 25, 636–639. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, D.F.; Long, M.J.; Shen, J.L.; Qin, R.S. Two-dimensional heat transfer model for secondary cooling of continuously cast beam blanks. Ironmak. Steelmak. 2014, 41, 377–386. [Google Scholar] [CrossRef]
- Ma, J.C.; Lu, C.S.; Yan, Y.T.; Chen, L.Y. Design and application of dynamic secondary cooling control based on real time heat transfer model for continuous casting. Int. J. Cast Met. Res. 2014, 27, 135–140. [Google Scholar] [CrossRef]
- He, D.F.; Chang, S.; Wang, H.B. Controlling transverse cracks of slab based on edge control technology. J. Iron Steel Res. Int. 2015, 22, 42–47. [Google Scholar] [CrossRef]
- Chen, S.D.; Hu, Z.F.; Yuan, Y.Y.; Luo, Y.Z. Study on intermediate crack in continuous casting slab of medium carbon steel. J. Iron Steel Res. Int. 2011, 18, 383–388. [Google Scholar]
- Long, M.J.; Chen, D.F.; Wang, Q.X.; Luo, D.H.; Han, Z.W.; Liu, Q.; Gao, W.X. Determination of CC slab solidification using nail shooting technique. Ironmak. Steelmak. 2012, 39, 370–377. [Google Scholar] [CrossRef]
- Long, M.J.; Dong, Z.H.; Chen, D.F.; Liao, Q.; Ma, Y.G. Effect of uneven solidification on the quality of continuous casting slab. Int. J. Mater. Prod. Technol. 2013, 47, 216–232. [Google Scholar] [CrossRef]
- Shen, H.F.; Hardin, R.A.; MacKenzie, R.; Beckermann, C. Simulation using realistic spray cooling for the continuous casting of multi-component steel. J. Mater. Sci. Technol. 2002, 18, 311–314. [Google Scholar]
- Long, M.J.; Chen, D.F. Study on mitigating center macro-segregation during steel continuous casting process. Steel Res. Int. 2011, 82, 847–856. [Google Scholar] [CrossRef]
- Ji, C.; Luo, S.; Zhu, M.; Sahai, Y. Uneven solidification during wide-thick slab continuous casting process and its influence on soft reduction zone. ISIJ Int. 2014, 54, 103–111. [Google Scholar] [CrossRef]
- Xie, X.; Chen, D.F.; Long, H.J.; Long, M.J.; Lv, K. Mathematical modeling of heat transfer in mold copper coupled with cooling water during the slab continuous casting process. Metall. Mater. Trans. B 2014, 45, 2442–2452. [Google Scholar] [CrossRef]
- Hardin, R.A.; Liu, K.; Kapoor, A.; Beckermann, C. A transient simulation and dynamic spray cooling control model for continuous steel casting. Metall. Mater. Transf. B 2003, 34, 297–306. [Google Scholar] [CrossRef]
- Wang, Q.Q.; Zhang, L.F. Influence of FC-mold on the full solidification of continuous casting slab. JOM 2016, 68, 2170–2179. [Google Scholar] [CrossRef]
- Shamsi, M.R.R.I.; Ajmani, S.K. Three dimensional turbulent fluid flow and heat transfer mathematical model for the analysis of a continuous slab caster. ISIJ Int. 2007, 47, 433–442. [Google Scholar] [CrossRef]
- Shamsi, M.R.R.I.; Ajmani, S.K. Analysis of mould, spray and radiation zones of continuous billet caster by three-dimensional mathematical model based on a turbulent fluid flow. Steel Res. Int. 2010, 81, 132–141. [Google Scholar] [CrossRef]
- Yang, J.W.; Du, Y.P.; Shi, R.; Cui, X.C. Fluid flow and solidification simulation in beam blank continuous casting process with 3d coupled model. Iron Steel Res. Int. 2006, 13, 17–21. [Google Scholar] [CrossRef]
- Seyedein, S.H.; Hasan, M. A three-dimensional simulation of coupled turbulent flow and macroscopic solidification heat transfer for continuous slab casters. Int. J. Heat Mass Transf. 1997, 40, 4405–4423. [Google Scholar] [CrossRef]
- Sun, H.B.; Zhang, J.Q. Study on the macrosegregation behavior for the bloom continuous casting: Model development and validation. Metall. Mater. Transf. B 2014, 45, 1133–1149. [Google Scholar] [CrossRef]
- Cai, K.K. Continuous Casting Mold; Metallurgical Industry Press: Beijing, China, 2008; p. 6. ISBN 978-7-5024-4635-2. [Google Scholar]
| Parameters | Values | Secondary Cooling | Length (mm) | Cooling Water Flow Rate (L/min) |
|---|---|---|---|---|
| Mold section | 1530 × 190 mm2 | Zone 1 | 405 | 155 |
| Mold length | 800 mm | Zone 2 | 555 | 84 |
| Inside size of SEN | 86 × 45 mm2 | Zone 3 | 800 | 54 |
| Outside size of SEN | 141 × 100 mm2 | Zone 4 | 1730 | 65 |
| Port size of SEN | 45 × 73 mm2 | Zone 5 | 1927 | 52 |
| Port angle | −15 degrees | Zone 6 | 3854 | 86 |
| Casting speed | 1.2 m/min | Zone 7 | 5806 | 86 |
| Casting temperature | 1811 K | Zone 8 | 4485 | 59 |
| Steel grade | Q345 | - | - | - |
| Physical Properties | Values | Physical Properties | Values |
|---|---|---|---|
| Density, kg/m3 | 7330 | Viscosity, kg·(m·s)−1 | 0.0062 |
| Specific heat, J (kg·K)−1 | 319.59 + 0.1934 × T (K) | Thermal conductivity, W (m·K)−1 | 57.524 − 0.0164 × T (K) |
| Liquidus, K | 1786 | Solidus, K | 1715 |
| Latent heat, J/kg | 255,500 | - | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, M.; Chen, H.; Chen, D.; Yu, S.; Liang, B.; Duan, H. A Combined Hybrid 3-D/2-D Model for Flow and Solidification Prediction during Slab Continuous Casting. Metals 2018, 8, 182. https://doi.org/10.3390/met8030182
Long M, Chen H, Chen D, Yu S, Liang B, Duan H. A Combined Hybrid 3-D/2-D Model for Flow and Solidification Prediction during Slab Continuous Casting. Metals. 2018; 8(3):182. https://doi.org/10.3390/met8030182
Chicago/Turabian StyleLong, Mujun, Huabiao Chen, Dengfu Chen, Sheng Yu, Bin Liang, and Huamei Duan. 2018. "A Combined Hybrid 3-D/2-D Model for Flow and Solidification Prediction during Slab Continuous Casting" Metals 8, no. 3: 182. https://doi.org/10.3390/met8030182
APA StyleLong, M., Chen, H., Chen, D., Yu, S., Liang, B., & Duan, H. (2018). A Combined Hybrid 3-D/2-D Model for Flow and Solidification Prediction during Slab Continuous Casting. Metals, 8(3), 182. https://doi.org/10.3390/met8030182




