Distinct Fracture Patterns in Construction Steels for Reinforced Concrete under Quasistatic Loading— A Review
Abstract
1. Introduction
2. Experimental Results on Steel Specimens under Tensile Loading
2.1. Stress–Strain Diagrams
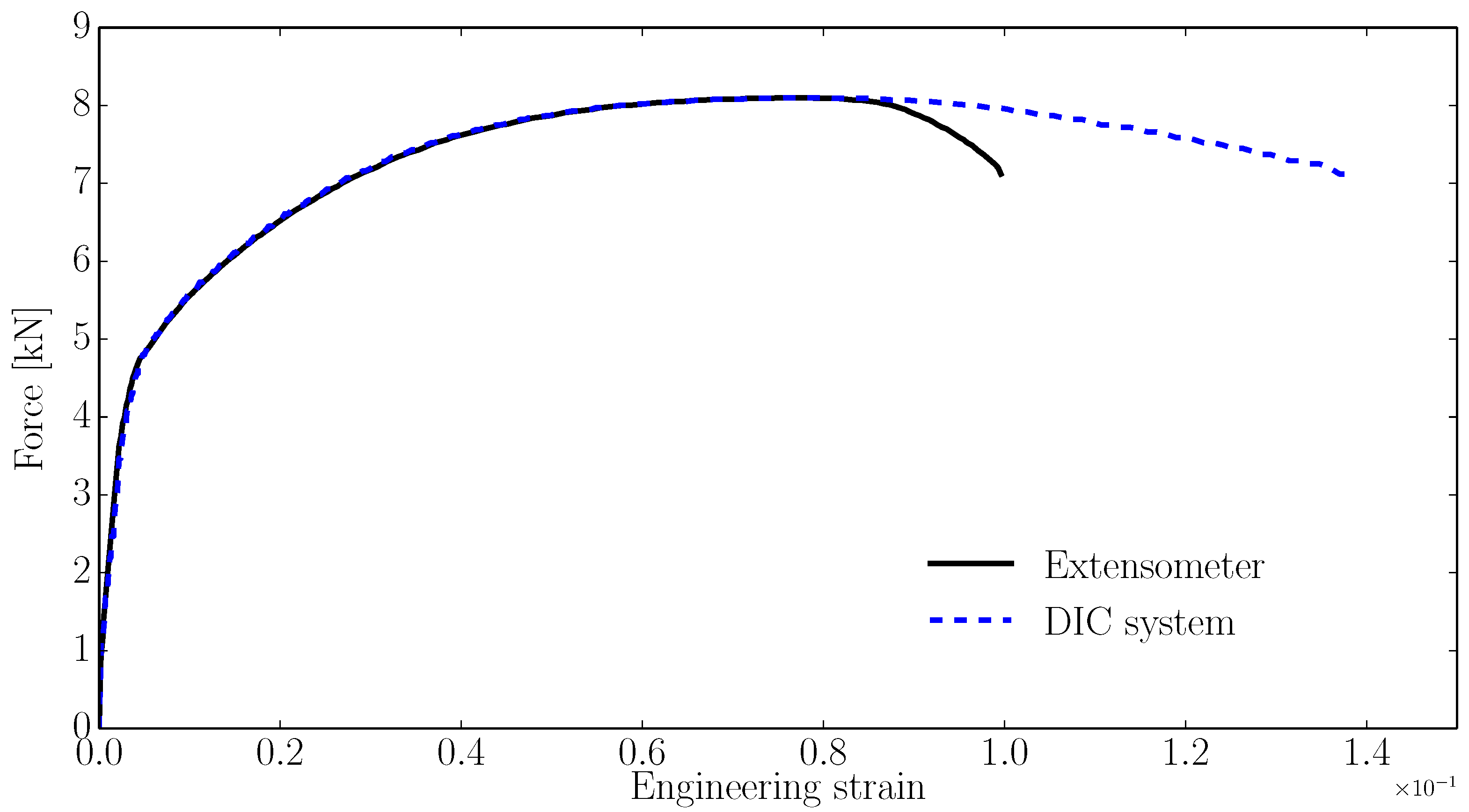
2.1.1. Strain Measuring Technique
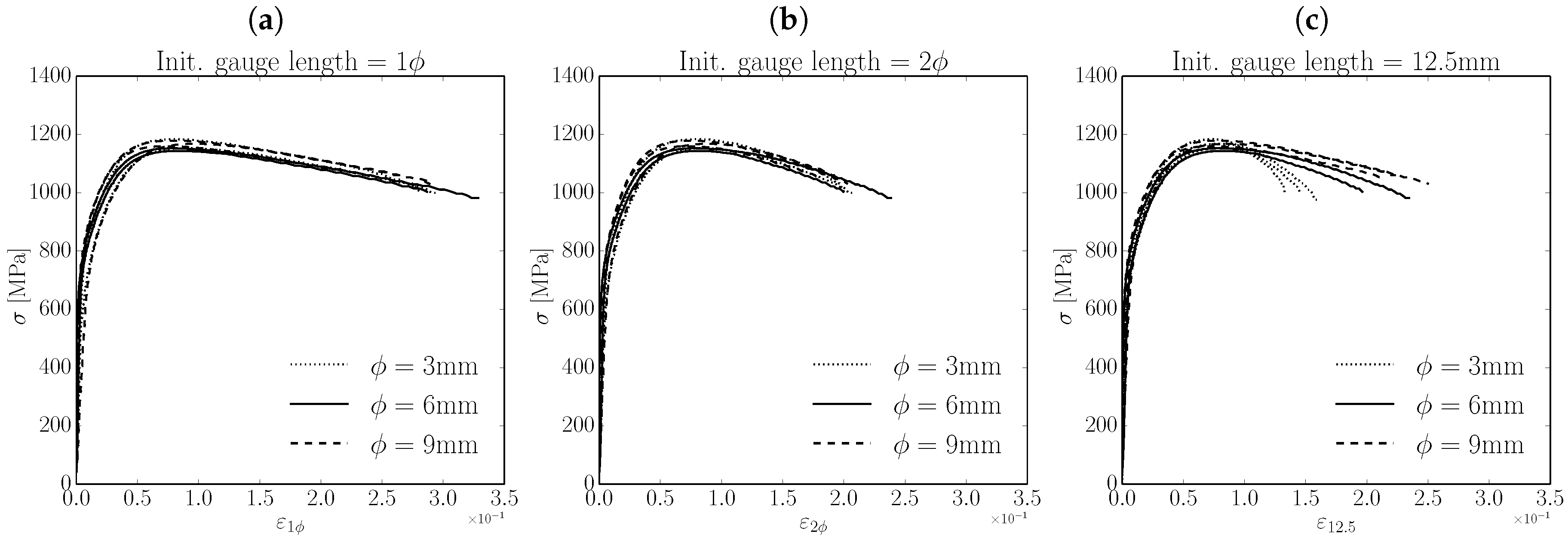
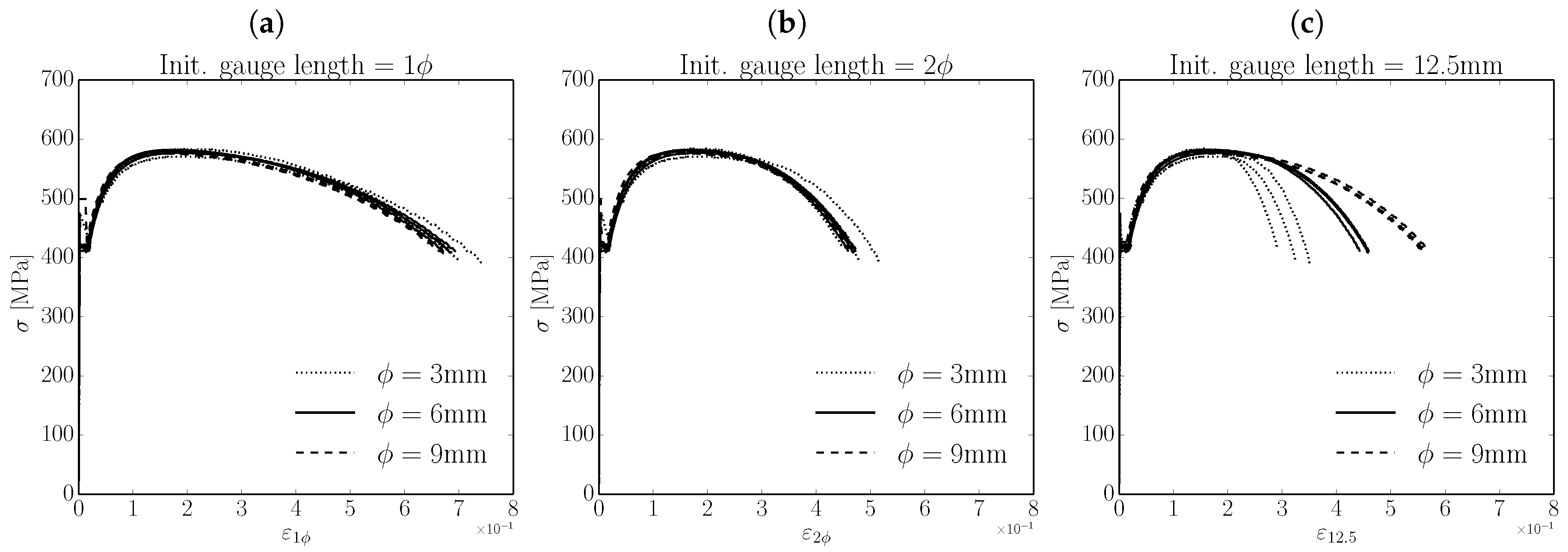
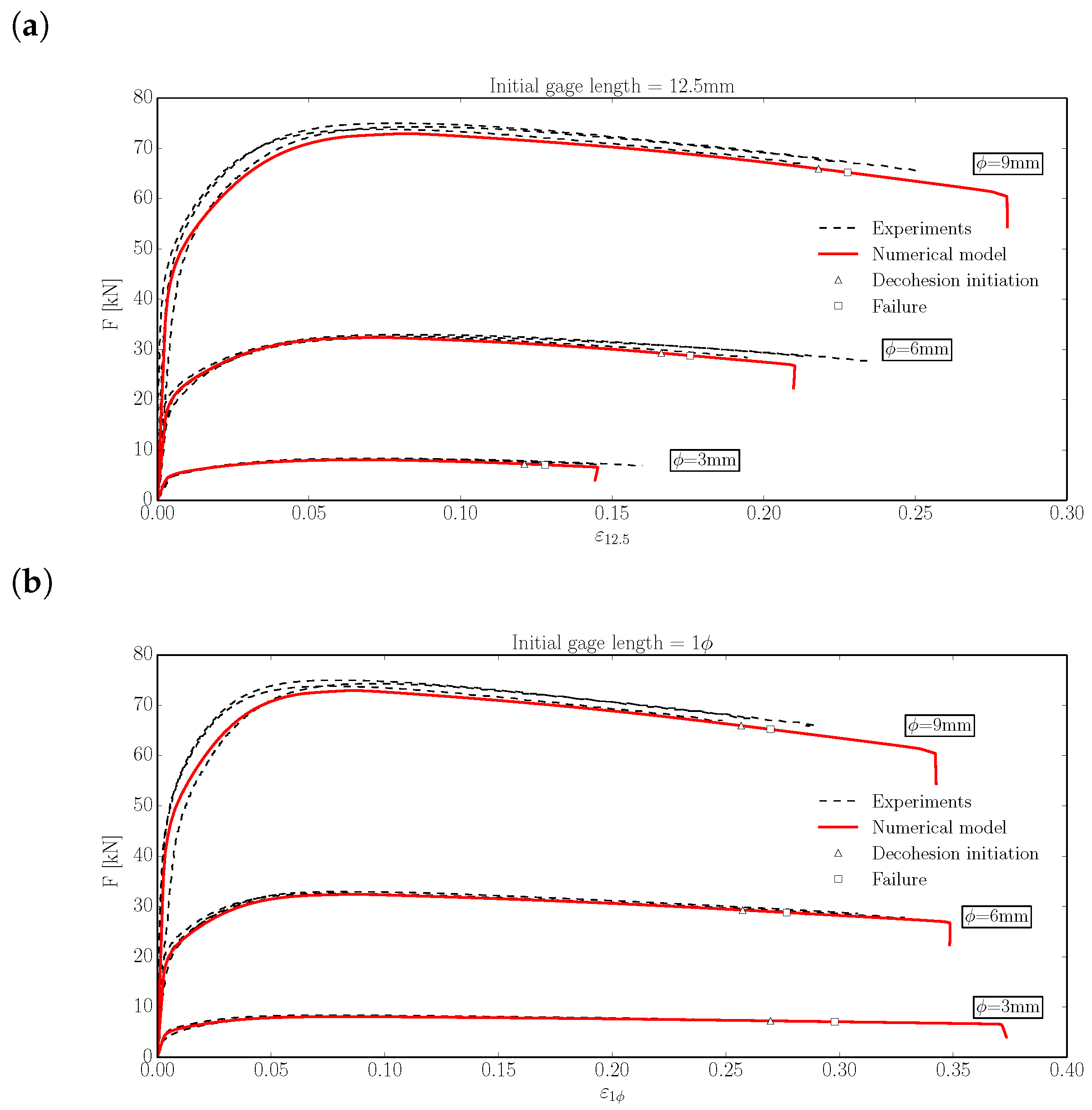
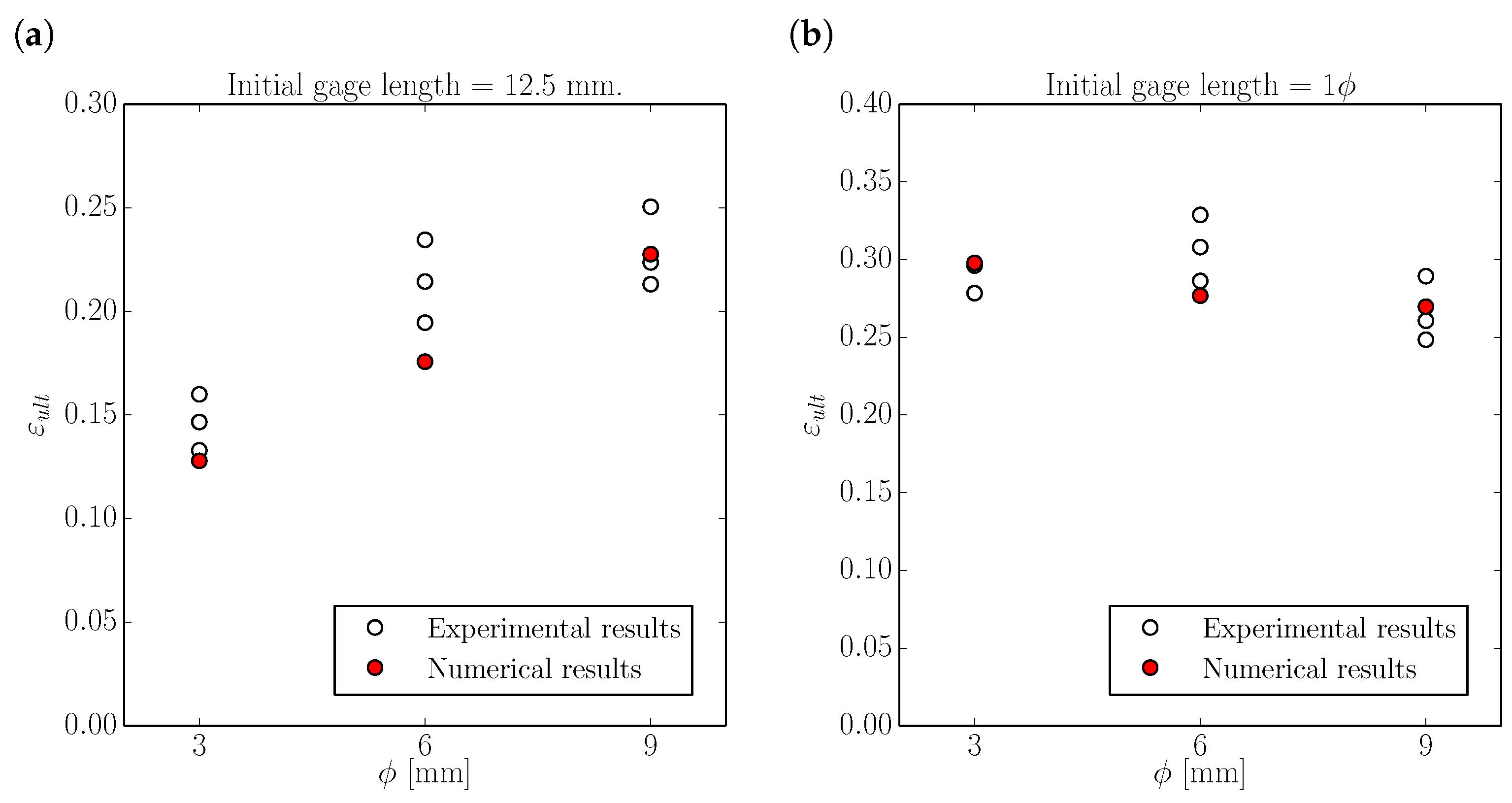
2.1.2. Influence of the Specimen Radius and the Initial Gauge Length
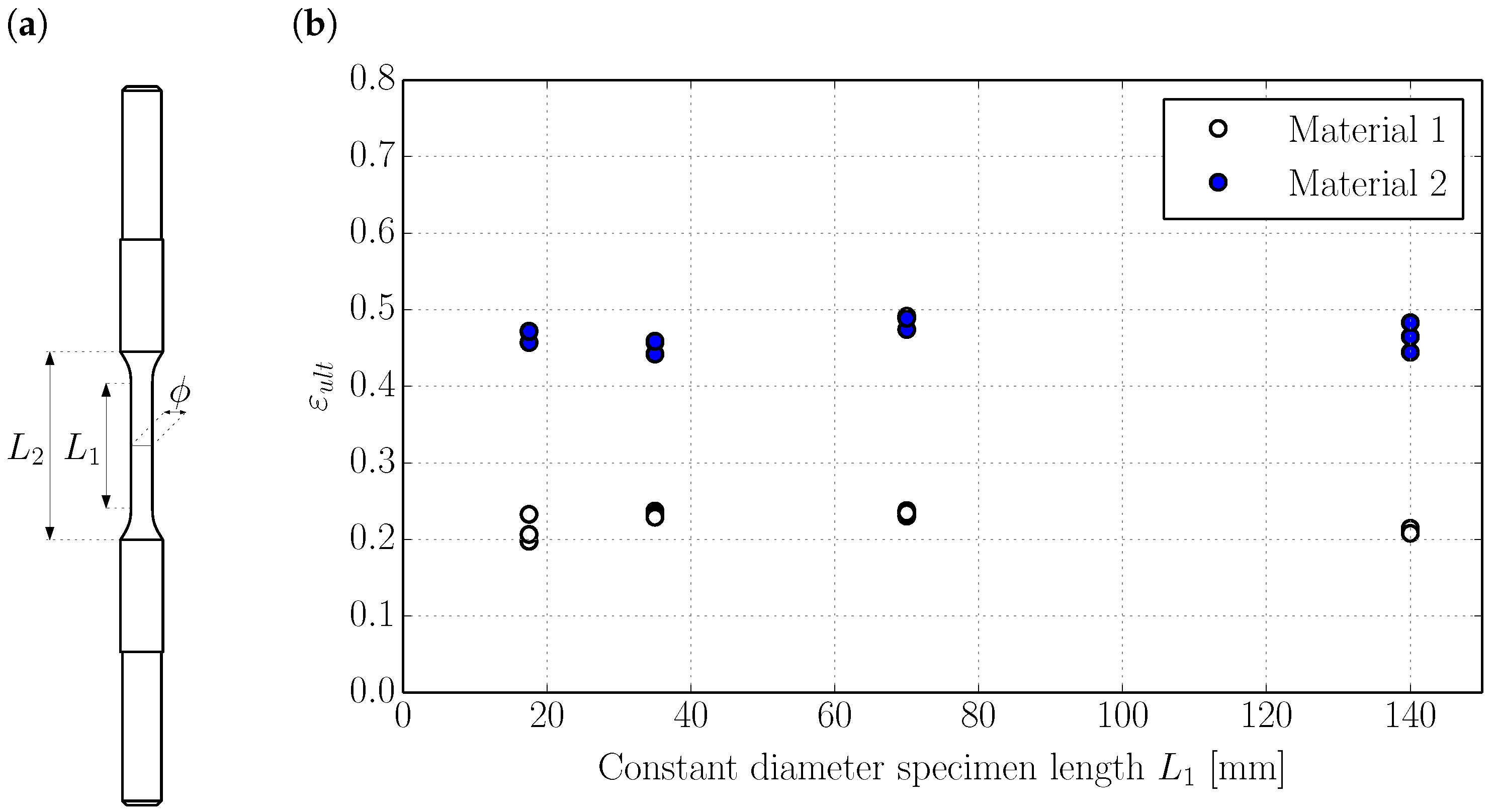
2.1.3. Influence of the Specimen Length
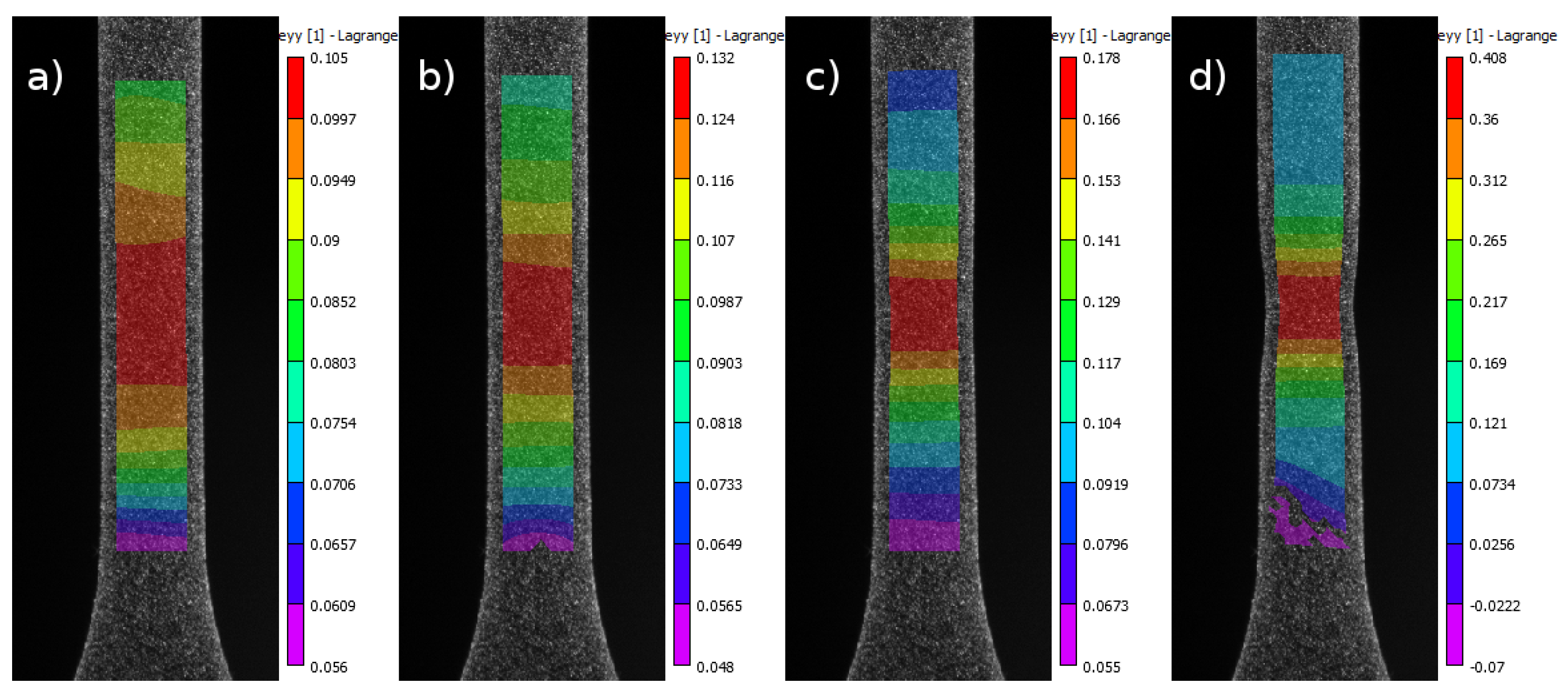
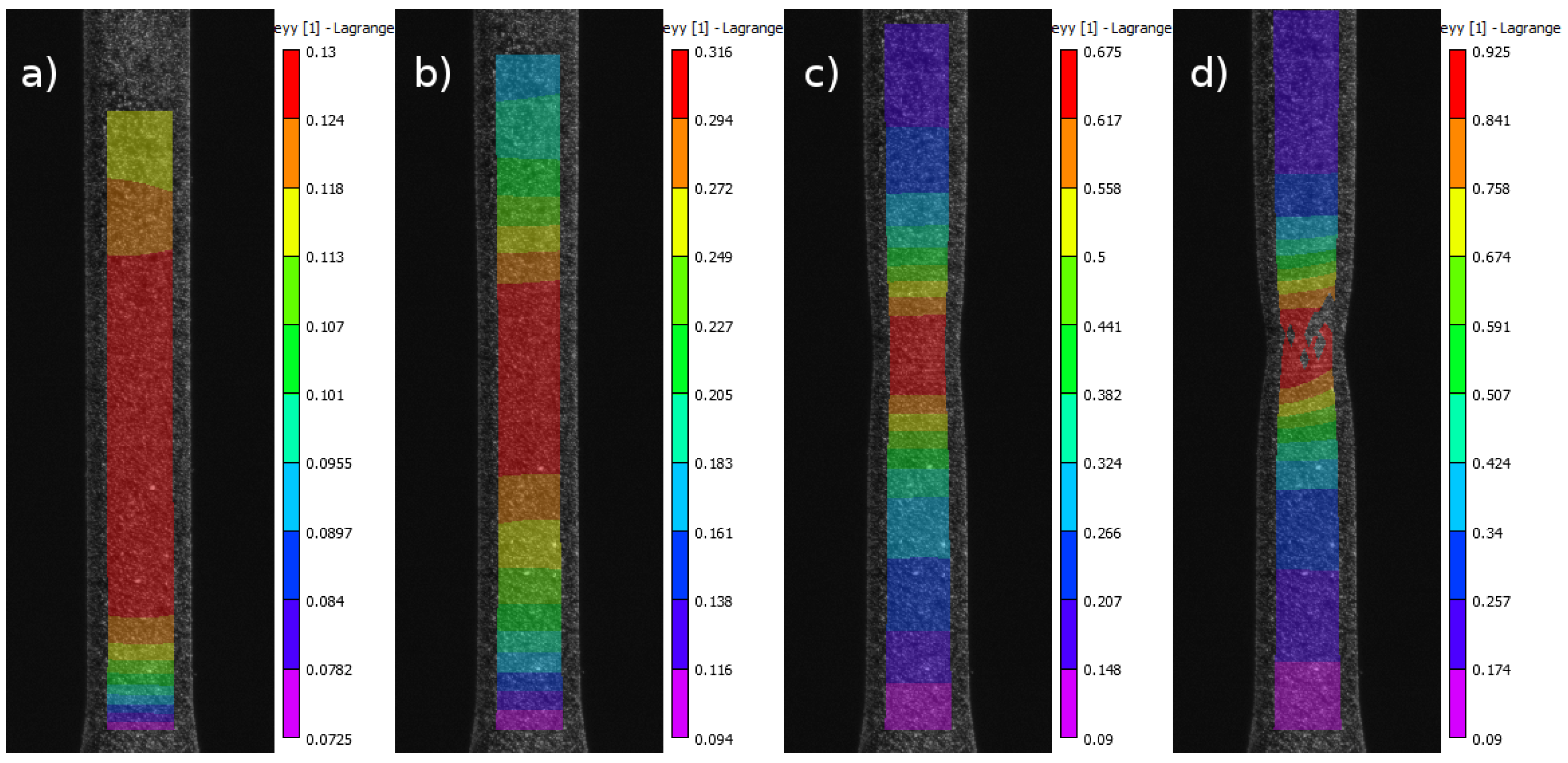
2.2. Strain Fields Maps
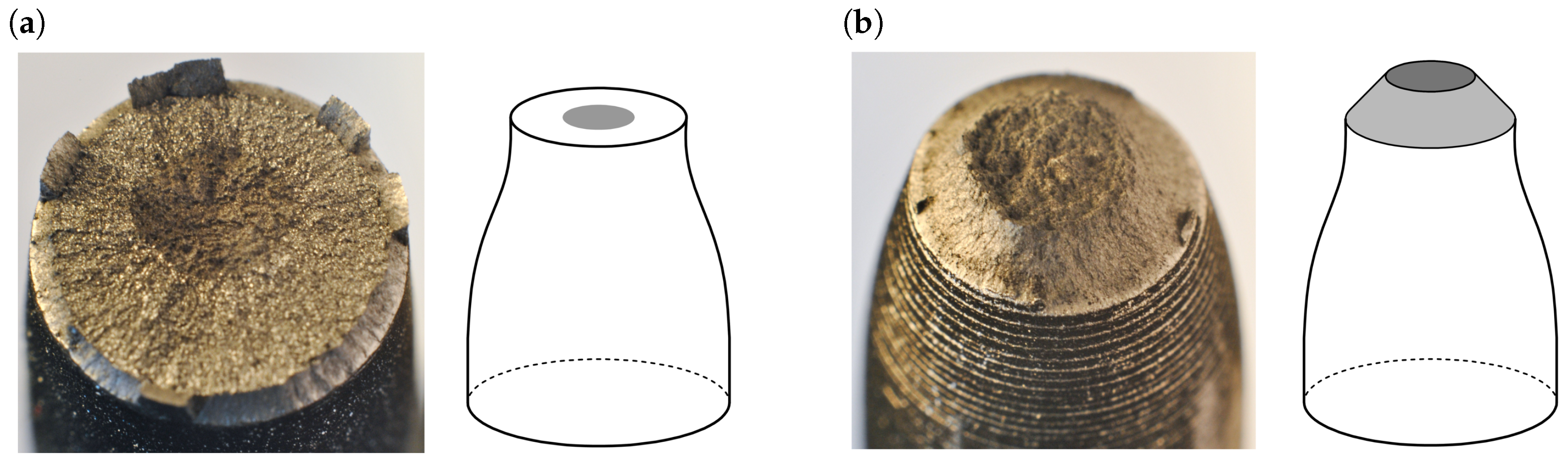
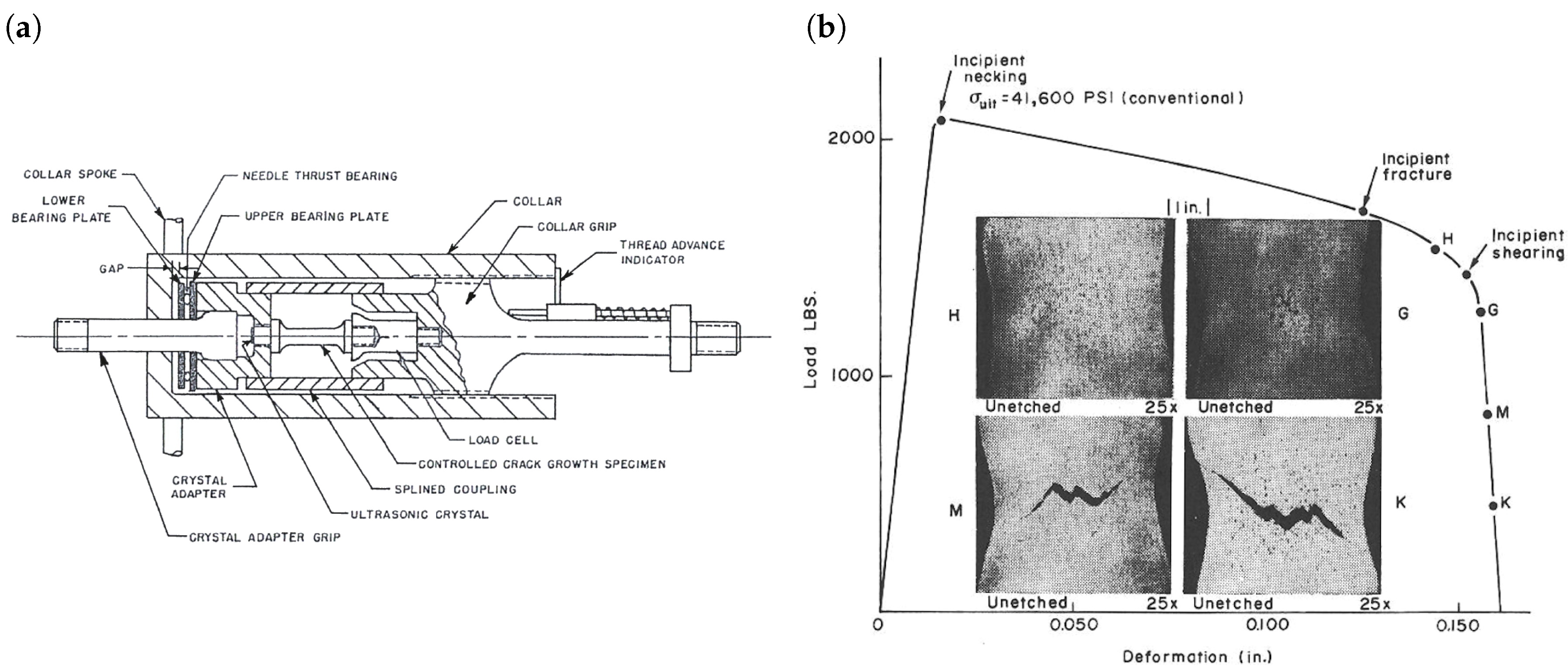
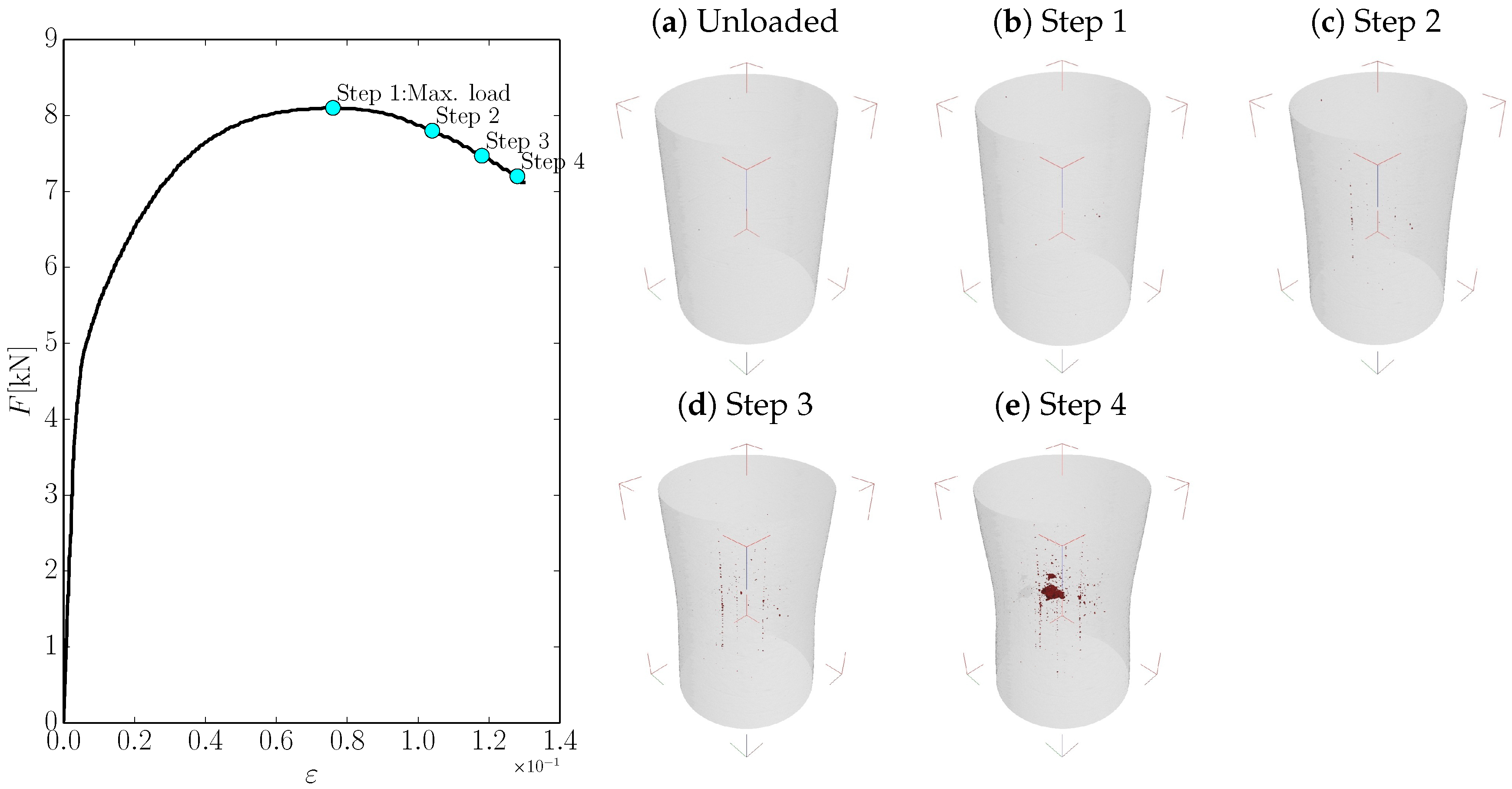
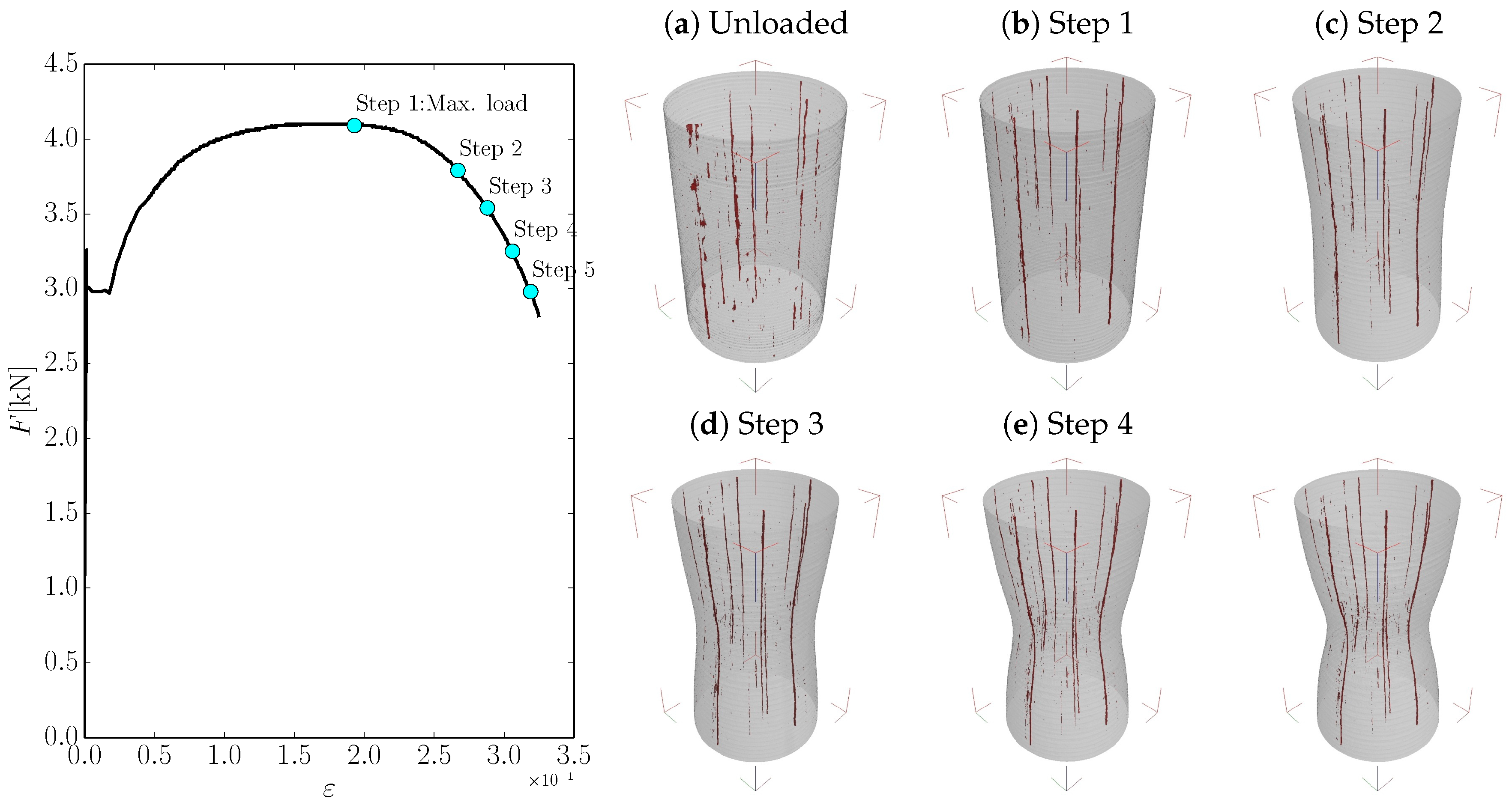
2.3. Analysis of the Fracture Surface
- After necking localises, small microvoids develop, interfacial non-connected cracks at inclusions appear, as well as short intercrystalline cracks.
- Later, as strain increases, the volume of voids and cracks also increase, weakening the material matrix in the center of the necking region. Around this weakened zone, an esentially non-fractured region remains under a low hydrostatic stress state, thus being under high shear stresses that eventually lead to cracking out of the initial fracture plane, which are the so-called shear lips.
2.3.1. Fractographs
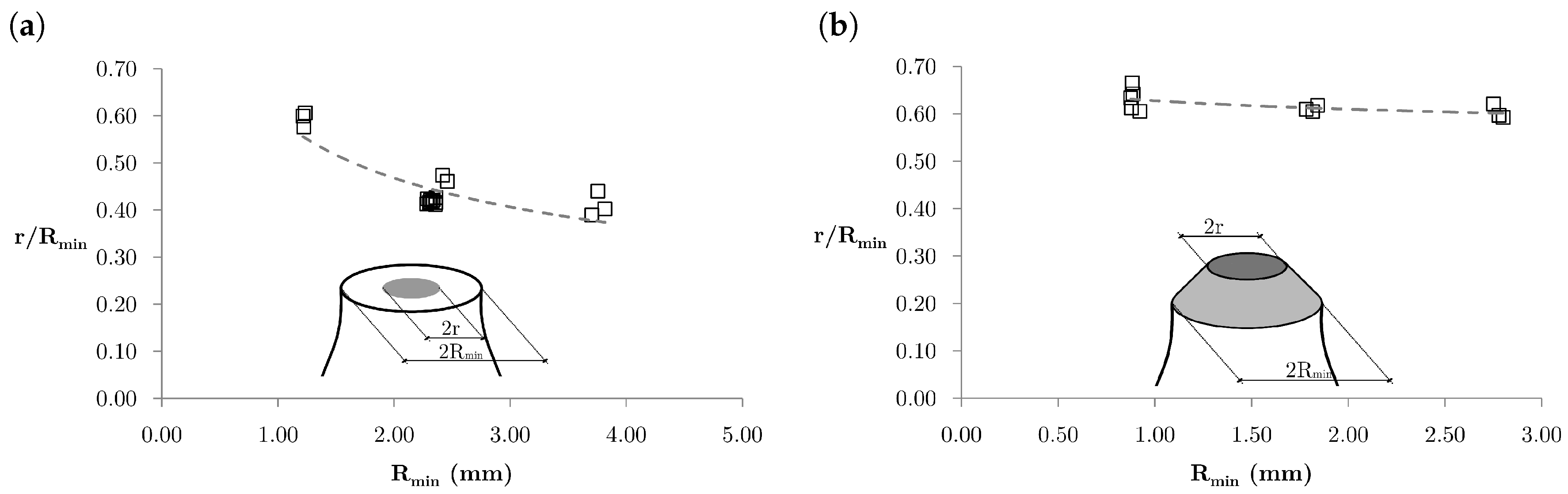
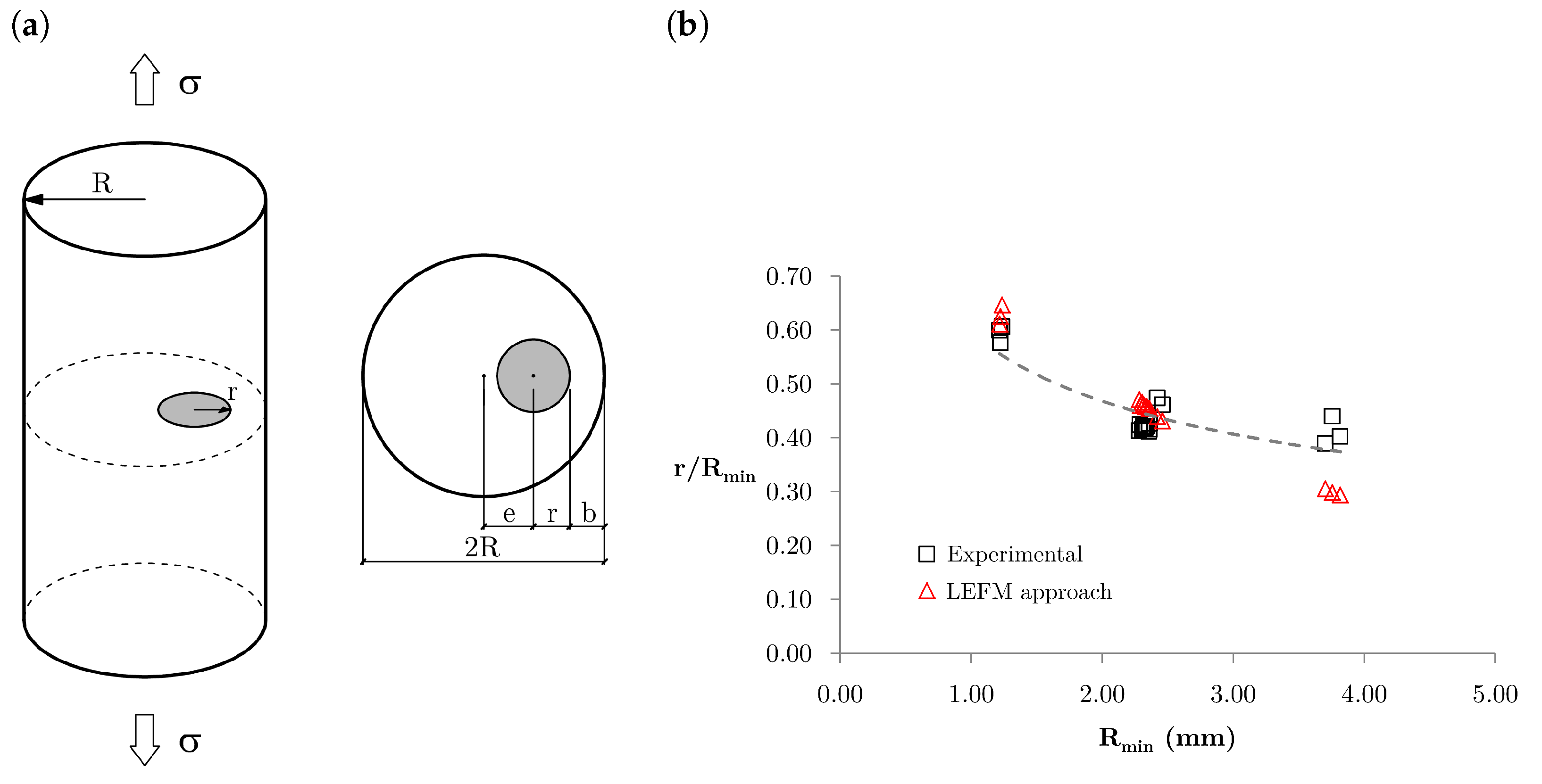
2.3.2. Size of the Internal Damage
- is the stress intensity factor.
- b stands for the smaller distance between the crack boundary and the specimen boundary.
- r is the internal crack radius.
- R is the specimen radius.
- is the tensile stress away from the fracture zone.
- are the coefficients defined in Table 2.
2.4. Evolution of Damage
2.4.1. Tests on Embrittled Specimens by Means of Liquid Nitrogen
2.4.2. Tests Analysed with X-ray Computed Tomography
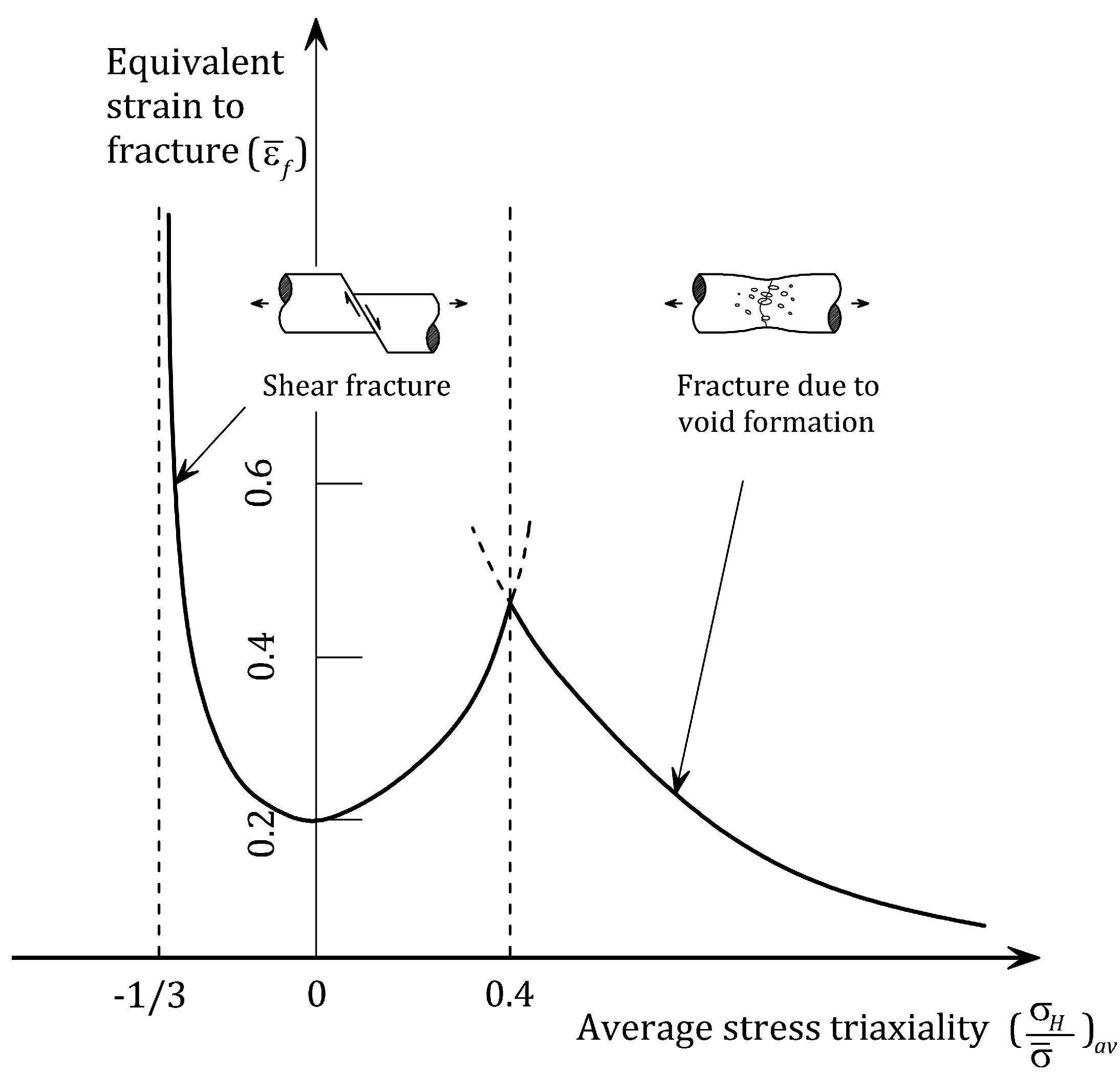
2.5. Influence of Stress Triaxiality on Ductile Fracture
- Zone I: low triaxialities, where fracture is mainly due to shearing.
- Zone II: medium triaxialities, where fracture is the result of a combination of shearing and the nucleation-growth-coalescence mechanism.
- Zone III: high triaxialities, where the nucleation-growth-coalescence mechanism drives fracture.
The Lode Angle
3. Numerical Models
3.1. Models Usually Employed with Metals
3.1.1. Uncoupled Models
Johnson–Cook Model
Wilkins et al. Model.
Bai–Wierzbicki Model
3.1.2. Coupled Models
Lemaitre’s Model
Xue–Wierzbicki Model
Modified Johnson–Cook Model
Gurson-Like Models
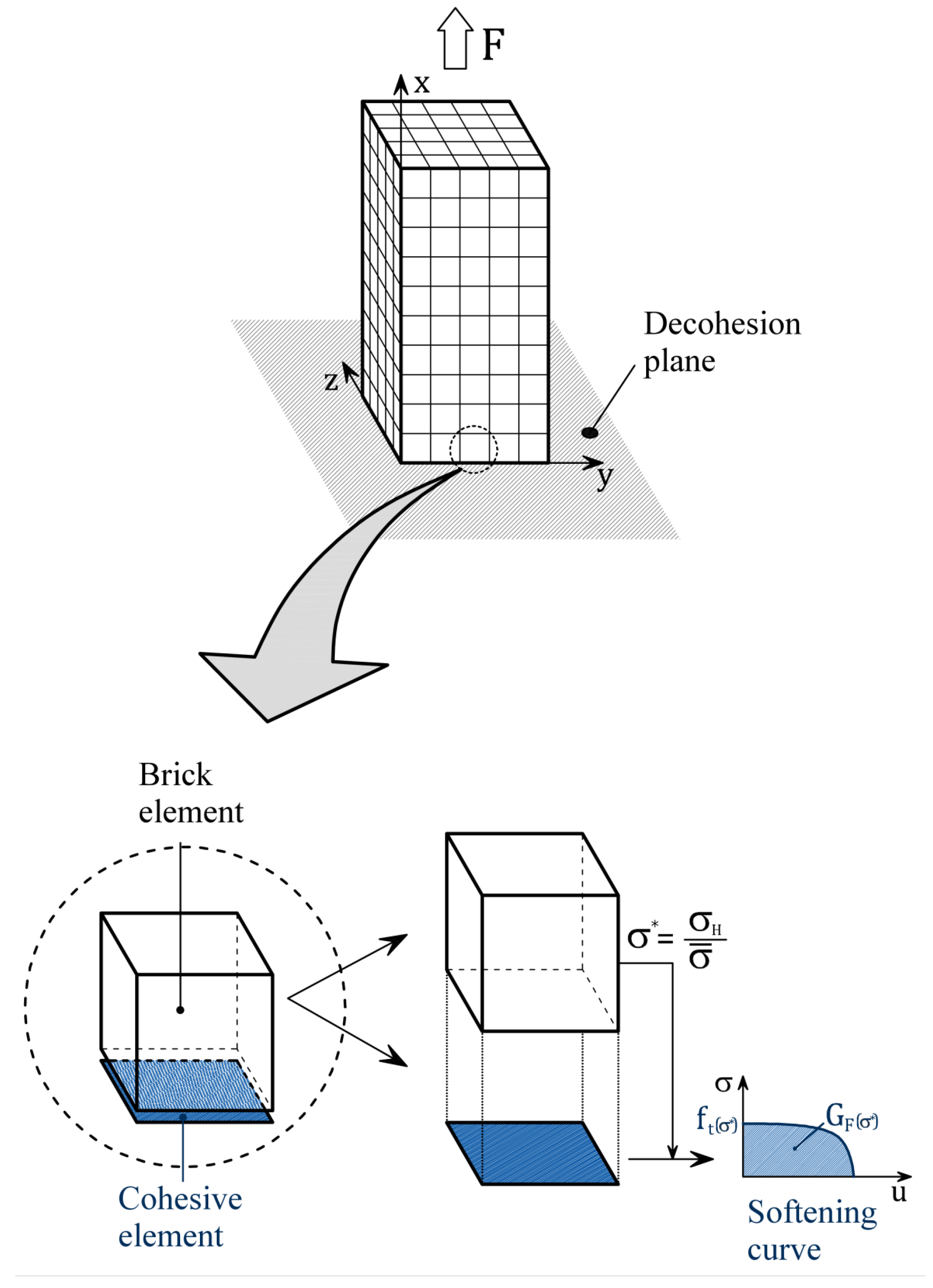
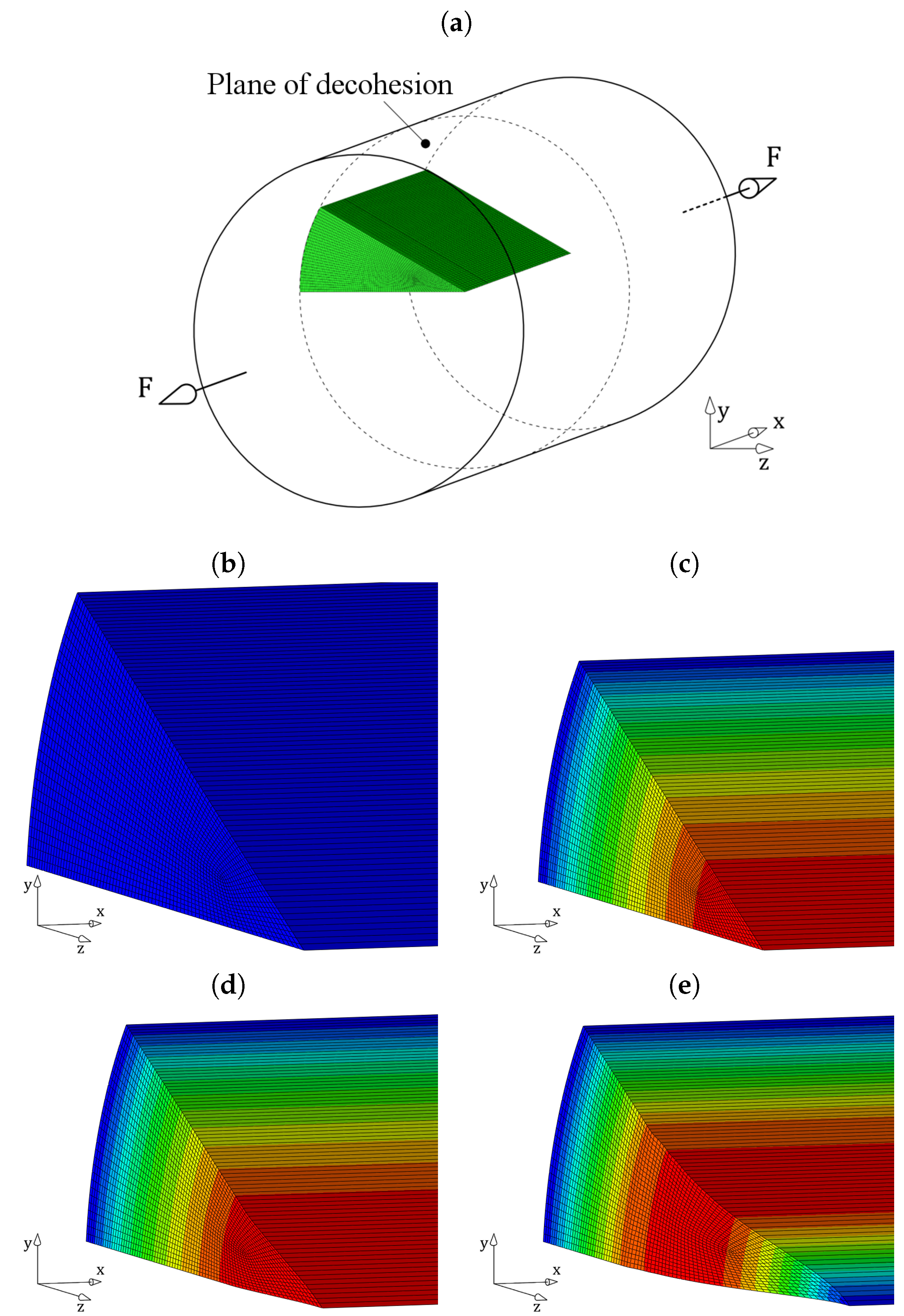
3.2. Triaxiality-Dependent Cohesive Model
4. Conclusions
- If specimens of different radii are to be compared, a proportional-to-the-radius initial gauge length should be considered.
- The reference gauge length must be centered with the eventual fracture plane, otherwise the strain gradient would affect the measurements; this can be accomplished by using a digital image correlation system and not with conventional extensometers.
- If reliable values of the stress–strain curve beyond the maximum engineering stress are to be obtained, digital image correlation extensometry is preferred. The gauge length must be proportional to the specimen radius and placed so its midpoint is coincident with the fracture plane.
- X-ray computed tomography helps to identify internal damage in steel specimens, at least if thin enough specimens are used.
- Triaxiality must always be considered as a key factor when numerically reproducing fracture in steel. The Lode parameter can also be important in some cases.
- A triaxiality-dependent cohesive model is able to successfully reproduce fracture in eutectoid steel bars under tension.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- International Organization for Standardization. E. 6892-1. Metallic Materials-Tensile Testing-Part 1: Method of Test at Room Temperature; ISO: Geneva, Switzerland, 2009. [Google Scholar]
- Bluhm, J.I.; Morrissey, R.J. Fracture in a Tensile Specimen; Defense Technical Information Center: Fort Belvoir, VA, USA, 1966.
- Tvergaard, V.; Needleman, A. Analysis of the cup–cone fracture in a round tensile bar. Acta Metall. 1984, 32, 157–169. [Google Scholar] [CrossRef]
- Besson, J.; Steglich, D.; Brocks, W. Modeling of crack growth in round bars and plane strain specimens. Int. J. Solids Struct. 2001, 38, 8259–8284. [Google Scholar] [CrossRef]
- Scheider, I.; Brocks, W. Simulation of cup–cone fracture using the cohesive model. Eng. Fract. Mech. 2003, 70, 1943–1961. [Google Scholar] [CrossRef]
- Barsoum, I.; Faleskog, J. Rupture mechanisms in combined tension and shear—Micromechanics. Int. J. Solids Struct. 2007, 44, 5481–5498. [Google Scholar] [CrossRef]
- Barsoum, I.; Faleskog, J. Rupture mechanisms in combined tension and shear—Experiments. Int. J. Solids Struct. 2007, 44, 1768–1786. [Google Scholar] [CrossRef]
- Huespe, A.E.; Needleman, A.; Oliver, J.; Sánchez, P.J. A finite thickness band method for ductile fracture analysis. Int. J. Plast. 2009, 25, 2349–2365. [Google Scholar] [CrossRef]
- Huespe, A.E.; Needleman, A.; Oliver, J.; Sánchez, P.J. A finite strain, finite band method for modeling ductile fracture. Int. J. Plast. 2012, 28, 53–69. [Google Scholar] [CrossRef]
- Hutchinson, J.W.; Tvergaard, V. Shear band formation in plane strain. Int. J. Solids Struct. 1981, 17, 451–470. [Google Scholar] [CrossRef]
- Ayaso, J.; González, B.; Matos, J.C.; Vergara, D.; Lorenzo, M.; Toribio, J. Análisis fractográfico cuantitativo del comportamiento en fractura de aceros perlíticos progresivamente trefilados. Anal. Mech. Fract. 2005, 22, 128–133. [Google Scholar]
- González, B.; Matos, J.C.; Toribio, J. Relación microestructura-propiedades mecánicas en acero perlítico progresivamente trefilado. Anal. Mech. Fract. 2009, 1, 142–147. [Google Scholar]
- Rodríguez, R.; Toribio, J.; Ayaso, F.J. Defectos microestructurales que gobiernan la fractura anisótropa en aceros fuertemente trefilados. Anal. Mech. Fract. 2009, 1, 148–153. [Google Scholar]
- Suárez, F.; Gálvez, J.C.; Cendón, D.A.; Atienza, J.M. Fracture of eutectoid steel bars under tensile loading: Experimental results and numerical simulation. Eng. Fract. Mech. 2016, 158, 87–105. [Google Scholar] [CrossRef]
- Suárez, F. Estudio de la Rotura en Barras de Acero: Aspectos Experimentales y Numéricos. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2013. [Google Scholar]
- Peters, W.; Ranson, W. Digital imaging techniques in experimental stress analysis. Opt. Eng. 1982, 21, 213427. [Google Scholar] [CrossRef]
- Chu, T.; Ranson, W.; Sutton, M.A. Applications of digital-image-correlation techniques to experimental mechanics. Exp. Mech. 1985, 25, 232–244. [Google Scholar] [CrossRef]
- Hung, P.C.; Voloshin, A. In-plane strain measurement by digital image correlation. J. Braz. Soc. Mech. Sci. Eng. 2003, 25, 215–221. [Google Scholar] [CrossRef]
- Sutton, M.A.; Orteu, J.J.; Schreier, H. Image Correlation for Shape, Motion and Deformation Measurements: Basic Concepts, Theory and Applications; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Pan, B.; Wang, Z.; Lu, Z. Genuine full-field deformation measurement of an object with complex shape using reliability-guided digital image correlation. Opt. Express 2010, 18, 1011–1023. [Google Scholar] [CrossRef] [PubMed]
- Pan, B.; Dafang, W.; Yong, X. Incremental calculation for large deformation measurement using reliability-guided digital image correlation. Opt. Lasers Eng. 2012, 50, 586–592. [Google Scholar] [CrossRef]
- Suárez, F.; Gálvez, J.C.; Cendón, D.A.; Atienza, J.M. Study of the last part of the stress-deformation curve of construction steels with distinct fracture patterns. Eng. Fract. Mech. 2016, 166, 43–59. [Google Scholar] [CrossRef]
- Guinea, G.; Rojo, F.; Elices, M. Stress intensity factors for internal circular cracks in fibers under tensile loading. Eng. Fract. Mech. 2004, 71, 365–377. [Google Scholar] [CrossRef]
- Rojo, F. Aplicación de la Mecánica de la Fractura a la Rotura Frágil de Fibras De sémola. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2003. [Google Scholar]
- ASTM. E 399-90: Standard Test Method for Plane-Strain Fracture Toughness of Metallic Materials; Annual Book of ASTM Standards: West Conshohocken, PA, USA, 1997; Volume 3, pp. 506–536. [Google Scholar]
- Mirza, M.S.; Barton, D.C.; Church, P.; Sturges, J.L. Ductile Fracture of Pure Copper : An Experimental and Numerical Study. J. Phys. IV France 1997, 7, 891–896. [Google Scholar] [CrossRef]
- Toribio, J. A fracture criterion for high-strength steel notched bars. Eng. Fract. Mech. 1997, 57, 39–404. [Google Scholar] [CrossRef]
- Toribio, J.; Ayaso, F. Anisotropic fracture behaviour of cold drawn steel: A materials science approach. Mater. Sci. Eng. A 2003, 343, 265–272. [Google Scholar] [CrossRef]
- Toribio, J.; Vergara, D.; Lorenzo, M. Hydrogen effects in multiaxial fracture of cold-drawn pearlitic steel wires. Eng. Fract. Mech. 2017, 174, 243–252. [Google Scholar] [CrossRef]
- Gurson, A.L. Continuum Theory of Ductile Rupture by Void Nucleation and Growth: Part I. Yield Criteria and Flow Rules for Porous Ductile Media; Number Part 1 in Technical Report; Division of Engineering, Brown University: Providence, RI, USA, 1977. [Google Scholar]
- Bridgman, P.W. Studies in Large Plastic Flow and Fracture: With Special Emphasis on the Effects of Hydrostatic Pressure; Metallurgy and Metallurgical Engineering Series; Harvard University Press: Cambridge, MA, USA, 1952. [Google Scholar]
- Johnson, G.; Cook, W. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. In Proceedings of the Seventh International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983. [Google Scholar]
- Bao, Y. Prediction of Ductile Crack Formation in Uncracked Bodies. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2003. [Google Scholar]
- Bao, Y.; Wierzbicki, T. On fracture locus in the equivalent strain and stress triaxiality space. Int. J. Mech. Sci. 2004, 46, 81–98. [Google Scholar] [CrossRef]
- Bao, Y. Dependence of ductile crack formation in tensile tests on stress triaxiality, stress and strain ratios. Eng. Fract. Mech. 2005, 72, 505–522. [Google Scholar] [CrossRef]
- Borvik, T.; Langseth, M.; Hopperstad, O.; Malo, K. Ballistic penetration of steel plates. Int. J. Impact Eng. 1999, 22, 855–886. [Google Scholar] [CrossRef]
- Lode, W. Versuche über den Einfluß der mittleren Hauptspannung auf das Fließen der Metalle Eisen, Kupfer und Nickel. Z. Phys. A Hadron. Nuclei 1926, 36, 913–939. [Google Scholar]
- Zhang, Z.L.; Thaulow, C.; Ødegård, J. A complete Gurson model approach for ductile fracture. Eng. Fract. Mech. 2000, 67, 155–168. [Google Scholar] [CrossRef]
- Xue, L.; Wierzbicki, T. Ductile fracture initiation and propagation modeling using a new fracture criterion. In Proceedings of the 9th European Mechanics of Materials Conference (EMMC9), Moret sur Loing, France, 9–12 May 2006; pp. 181–186. [Google Scholar]
- Bai, Y.; Wierzbicki, T. A new model of metal plasticity and fracture with pressure and Lode dependence. Int. J. Plast. 2008, 24, 1071–1096. [Google Scholar] [CrossRef]
- Erice, B. Flow and Fracture Behaviour of High Performance Alloys. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2012. [Google Scholar]
- Erice, B.; Gálvez, F. A coupled elastoplastic-damage constitutive model with Lode angle dependent failure criterion. Int. J. Solids Struct. 2014, 51, 93–110. [Google Scholar] [CrossRef]
- Mirone, G.; Corallo, D. A local viewpoint for evaluating the influence of stress triaxiality and Lode angle on ductile failure and hardening. Int. J. Plast. 2010, 26, 348–371. [Google Scholar] [CrossRef]
- Barsoum, I.; Faleskog, J. Micromechanical analysis on the influence of the Lode parameter on void growth and coalescence. Int. J. Solids Struct. 2011, 48, 925–938. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Sharma, P.; Chandel, P.; Bhardwaj, V.; Singh, M.; Mahajan, P. Ballistic impact response of high strength aluminium alloy 2014-T652 subjected to rigid and deformable projectiles. Thin-Walled Struct. 2017. [Google Scholar] [CrossRef]
- Ouyang, Q.; Weng, G.; Soh, A.; Guo, X. Influences of nanotwin volume fraction on the ballistic performance of coarse-grained metals. Theor. Appl. Mech. Lett. 2017, 7. [Google Scholar] [CrossRef]
- Holmen, J.K.; Hopperstad, O.S.; Børvik, T. Influence of yield-surface shape in simulation of ballistic impact. Int. J. Impact Eng. 2017, 108, 136–146. [Google Scholar] [CrossRef]
- Sharma, P.; Chandel, P.; Mahajan, P.; Singh, M. Quasi-Brittle Fracture of Aluminium Alloy 2014 under Ballistic Impact. Procedia Eng. 2017, 173, 206–213. [Google Scholar] [CrossRef]
- Burley, M.; Campbell, J.; Dean, J.; Clyne, T. Johnson–Cook parameter evaluation from ballistic impact data via iterative FEM modelling. Int. J. Impact Eng. 2018, 112, 180–192. [Google Scholar] [CrossRef]
- Morales-Alonso, G.; Cendón, D.; Gálvez, F.; Sánchez-Gálvez, V. Influence of the softening curve in the fracture patterns of concrete slabs subjected to blast. Eng. Fract. Mech. 2015, 140, 1–16. [Google Scholar] [CrossRef]
- Imbalzano, G.; Tran, P.; Ngo, T.D.; Lee, P.V. A numerical study of auxetic composite panels under blast loadings. Compos. Struct. 2016, 135, 339–352. [Google Scholar] [CrossRef]
- Gambirasio, L.; Rizzi, E. An enhanced Johnson–Cook strength model for splitting strain rate and temperature effects on lower yield stress and plastic flow. Comput. Mater. Sci. 2016, 113, 231–265. [Google Scholar] [CrossRef]
- Liang, X.; Wang, Z.; Wang, R. Deformation model and performance optimization research of composite blast resistant wall subjected to blast loading. J. Loss Prev. Process Ind. 2017, 49, 326–341. [Google Scholar] [CrossRef]
- Wilkins, M.; Streit, R.; Reaugh, J. Cumulative-Strain-Damage Model of Ductile Fracture: Simulation and Prediction of Engineering Fracture Tests; Technical Report; Lawrence Livermore National Lab.: Livermore, CA, USA; Science Applications, Inc.: San Leandro, CA, USA, 1980.
- Lemaitre, J. Coupled elasto-plasticity and damage constitutive equations. Comput. Methods Appl. Mech. Eng. 1985, 51, 31–49. [Google Scholar] [CrossRef]
- Lemaitre, J. A continuous damage mechanics model for ductile fracture. Trans. ASME J. Eng. Mater. Technol. 1985, 107, 83–89. [Google Scholar] [CrossRef]
- Xue, L. Damage accumulation and fracture initiation in uncracked ductile solids subject to triaxial loading. Int. J. Solids Struct. 2007, 44, 5163–5181. [Google Scholar] [CrossRef]
- Xue, L.; Wierzbicki, T. Ductile fracture initiation and propagation modeling using damage plasticity theory. Eng. Fract. Mech. 2008, 75, 3276–3293. [Google Scholar] [CrossRef]
- Børvik, T.; Hopperstad, O.; Berstad, T.; Langseth, M. A computational model of viscoplasticity and ductile damage for impact and penetration. Eur. J. Mech.-A/Solids 2001, 20, 685–712. [Google Scholar] [CrossRef]
- Rice, J.R.; Tracey, D.M. On the ductile enlargement of voids in triaxial stress fields. J. Mech. Phys. Solids 1969, 17, 201–217. [Google Scholar] [CrossRef]
- Nègre, P.; Steglich, D.; Brocks, W. Crack extension in aluminium welds: A numerical approach using the Gurson–Tvergaard–Needleman model. Eng. Fract. Mech. 2004, 71, 2365–2383. [Google Scholar] [CrossRef]
- Fei, H.; Yazzie, K.; Chawla, N.; Jiang, H. The effect of random voids in the modified Gurson model. J. Electron. Mater. 2012, 41, 177–183. [Google Scholar] [CrossRef]
- Li, H.; Fu, M.W.; Lu, J.; Yang, H. Ductile fracture: Experiments and computations. Int. J. Plast. 2011, 27, 147–180. [Google Scholar] [CrossRef]
- Needleman, A.; Tvergaard, V. Numerical modeling of the ductile-brittle transition. Int. J. Fract. 2000, 101, 73–97. [Google Scholar] [CrossRef]
- Hao, S.; Brocks, W. The Gurson–Tvergaard–Needleman-model for rate and temperature-dependent materials with isotropic and kinematic hardening. Comput. Mech. 1997, 20, 34–40. [Google Scholar] [CrossRef]
- Steglich, D.; Siegmund, T.; Brocks, W. Micromechanical modeling of damage due to particle cracking in reinforced metals. Comput. Mater. Sci. 1999, 16, 404–413. [Google Scholar] [CrossRef]
- Nahshon, K.; Hutchinson, J.W. Modification of the Gurson Model for shear failure. Eur. J. Mech.- A/Solids 2008, 27, 1–17. [Google Scholar] [CrossRef]
- Nielsen, K.L.; Tvergaard, V. Effect of a shear modified Gurson model on damage development in a FSW tensile specimen. Int. J. Solids Struct. 2009, 46, 587–601. [Google Scholar] [CrossRef]
- Nahshon, K.; Xue, Z. A modified Gurson model and its application to punch-out experiments. Eng. Fract. Mech. 2009, 76, 997–1009. [Google Scholar]
- Jackiewicz, J. Use of a modified Gurson model approach for the simulation of ductile fracture by growth and coalescence of microvoids under low, medium and high stress triaxiality loadings. Eng. Fract. Mech. 2011, 78, 487–502. [Google Scholar] [CrossRef]
- Nielsen, K.L.; Tvergaard, V. Ductile shear failure or plug failure of spot welds modelled by modified Gurson model. Eng. Fract. Mech. 2010, 77, 1031–1047. [Google Scholar] [CrossRef]
- Xu, F.; Zhao, S.; Han, X. Use of a modified Gurson model for the failure behaviour of the clinched joint on Al6061 sheet. Fatigue Fract. Eng. Mater. Struct. 2014, 37, 335–348. [Google Scholar] [CrossRef]
- Morgeneyer, T.F.; Besson, J. Flat to slant ductile fracture transition: Tomography examination and simulations using shear-controlled void nucleation. Scr. Mater. 2011, 65, 1002–1005. [Google Scholar] [CrossRef]
- Vadillo, G.; Reboul, J.; Fernández-Sáez, J. A modified Gurson model to account for the influence of the Lode parameter at high triaxialities. Eur. J. Mech.-A/Solids 2016, 56, 31–44. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modéer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Vandewalle, L.; Dupont, D. Bending Test and Interpretation; RILEM Publication PRO: Bagneux, France, 2003; Volume 31, pp. 1–14. [Google Scholar]
- RILEM-TCS. Determination of the fracture energy of mortar and concrete by means of three-point bend tests on notched beams. Mater. Struct. 1985, 18, 285–290. [Google Scholar]
- Bažant, Z.P.; Planas, J. Fracture and Size Effect in Concrete and Other Quasibrittle Materials; New Directions in Civil Engineering; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Bažant, Z.P.; Bittnar, Z.; Jirásek, M.; Mazars, J. Fracture and Damage in Quasibrittle Structures: Experiment, Modeling and Computation; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- García-Álvarez, V.O.; Carol, I.; Gettu, R. Numerical simulation of fracture in concrete using joint elements. Anal. Mech. Fract. 1994, 11, 75–80. [Google Scholar]
- Xie, M.; Gerstle, W. Energy-based cohesive crack propagation modeling. J. Eng. Mech. 1995, 121, 1349–1358. [Google Scholar] [CrossRef]
- Carol, I.; Prat, P.C.; López, C.M. Normal/Shear Cracking Model: Application to Discrete Crack Analysis. J. Eng. Mech. 1997, 123, 765–773. [Google Scholar] [CrossRef]
- Cendón, D. Estudio de la Fractura en Modo Mixto de Hormigones y Morteros. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2001. [Google Scholar]
- Gálvez, J.C.; Cendón, D.A.; Planas, J.; Elices, M. Fractura en modo mixto de probetas de hormigón con doble entalla bajo solicitación de compresión: simulación numérica. Anal. Mech. Fract. 2001, 18, 219–225. [Google Scholar]
- Gálvez, J.C.; Cervenka, J.; Cendón, D.A.; Saouma, V. A discrete crack approach to normal/shear cracking of concrete. Cem. Concr. Res. 2002, 32, 1567–1585. [Google Scholar] [CrossRef]
- Gálvez, J.C.; Cendón, D.A. Simulación de la fractura del hormigón en modo mixto. Rev. Int. Metodos Numér. 2002, 18, 31–58. [Google Scholar]
- Rashid, Y. Ultimate strength analysis of prestressed concrete pressure vessels. Nuclear Eng. Des. 1968, 7, 334–344. [Google Scholar] [CrossRef]
- Suidan, M.; Schnobrich, W.C. Finite element analysis of reinforced concrete. J. Struct. Div. 1973, 99, 2109–2122. [Google Scholar]
- Gupta, A.K.; Akbar, H. Cracking in reinforced concrete analysis. J. Struct. Eng. 1984, 110, 1735–1746. [Google Scholar] [CrossRef]
- De Borst, R.; Nauta, P. Non-orthogonal cracks in a smeared finite element model. Eng. Comput. 1985, 2, 35–46. [Google Scholar] [CrossRef]
- Jirásek, M.; Zimmermann, T. Rotating crack model with transition to scalar damage. J. Eng. Mech. 1998, 124, 277–284. [Google Scholar] [CrossRef]
- Simo, J.; Oliver, J. A new approach to the analysis and simulation of strain softening in solids. In Proceedings of the Conference on Fracture and Damage in Quasibrittle Structures; CRC Press: New York, NY, USA, 1994; pp. 25–39. [Google Scholar]
- Larsson, R.; Runesson, K.; Sture, S. Embedded localization band in undrained soil based on regularized strong discontinuity–theory and FE-analysis. Int. J. Solids Struct. 1996, 33, 3081–3101. [Google Scholar] [CrossRef]
- Reyes, E. Rotura de la Fábrica de Ladrillo Bajo Solicitaciones de Tracción y Cortante. Ph.D. Thesis, Universidad de Castilla la Mancha, Ciudad Real, Spain, 2004. [Google Scholar]
- Sancho, J.M.; Planas, J.; Cendón, D.A.; Reyes, E.; Gálvez, J.C. An embedded crack model for finite element analysis of concrete fracture. Eng. Fract. Mech. 2007, 74, 75–86. [Google Scholar] [CrossRef]
- Sancho, J.M.; Planas, J.; Fathy, A.M.; Gálvez, J.C.; Cendón, D.A. Three-dimensional simulation of concrete fracture using embedded crack elements without enforcing crack path continuity. Int. J. Numer. Anal. Methods Geomech. 2007, 31, 173–187. [Google Scholar] [CrossRef]
- Reyes, E.; Gálvez, J.C.; Casati, M.J.; Cendón, D.A.; Sancho, J.M.; Planas, J. An embedded cohesive crack model for finite element analysis of brickwork masonry fracture. Eng. Fract. Mech. 2009, 76, 1930–1944. [Google Scholar] [CrossRef]
- Gálvez, J.C.; Planas, J.; Sancho, J.M.; Reyes, E.; Cendón, D.A.; Casati, M.J. An embedded cohesive crack model for finite element analysis of quasi-brittle materials. Eng. Fract. Mech. 2012, 109, 369–386. [Google Scholar] [CrossRef]
- Siegmund, T.; Brocks, W. A numerical study on the correlation between the work of separation and the dissipation rate in ductile fracture. Eng. Fract. Mech. 2000, 67, 139–154. [Google Scholar] [CrossRef]
- Scheider, I. Derivation of separation laws for cohesive models in the course of ductile fracture. Eng. Fract. Mech. 2009, 76, 1450–1459. [Google Scholar] [CrossRef]
- ASTM. ASTM E 1820-01. Standard Test Method for Measurement of Fracture Toughness; Technical Report; ASTM: West Conshohocken, PA, USA, 2001. [Google Scholar]
- Cendón, D.; Jin, N.; Liu, Y.; Berto, F.; Elices, M. Numerical Assessment of Gray Cast Iron Notched Specimens by Using a Triaxiality-Dependent Cohesive Zone Model. Theor. Appl. Fract. Mech. 2017, 90, 259–267. [Google Scholar] [CrossRef]




| Mat. | C | Si | Mn | P | S | Cr | Mo | Ni | Cu | Al | Ti | Nb | V | N |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.83 | 0.25 | 0.72 | 0.012 | 0.004 | 0.24 | <0.01 | 0.02 | 0.01 | <0.003 | <0.005 | <0.005 | <0.01 | 0.0097 |
| 2 | 0.22 | 0.18 | 1.00 | 0.024 | 0.042 | 0.08 | 0.03 | 0.14 | 0.46 | <0.003 | <0.005 | <0.0r 05 | <0.01 | 0.0113 |
| C | C | C | |
|---|---|---|---|
| i = 1 | 0.01242 | −0.3097 | 1.185 |
| i = 2 | −6.388 | 1.547 | −3.723 |
| i = 3 | 16.89 | −0.8769 | 2.628 |
| i = 4 | −9.838 | - | - |
| i = 5 | −1.228 | - | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suárez, F.; Gálvez, J.C.; Cendón, D.A.; Atienza, J.M. Distinct Fracture Patterns in Construction Steels for Reinforced Concrete under Quasistatic Loading— A Review. Metals 2018, 8, 171. https://doi.org/10.3390/met8030171
Suárez F, Gálvez JC, Cendón DA, Atienza JM. Distinct Fracture Patterns in Construction Steels for Reinforced Concrete under Quasistatic Loading— A Review. Metals. 2018; 8(3):171. https://doi.org/10.3390/met8030171
Chicago/Turabian StyleSuárez, Fernando, Jaime C. Gálvez, David A. Cendón, and José M. Atienza. 2018. "Distinct Fracture Patterns in Construction Steels for Reinforced Concrete under Quasistatic Loading— A Review" Metals 8, no. 3: 171. https://doi.org/10.3390/met8030171
APA StyleSuárez, F., Gálvez, J. C., Cendón, D. A., & Atienza, J. M. (2018). Distinct Fracture Patterns in Construction Steels for Reinforced Concrete under Quasistatic Loading— A Review. Metals, 8(3), 171. https://doi.org/10.3390/met8030171





