Numerical Simulation of Transient Multiphase Flow in a Five-Strand Bloom Tundish during Ladle Change
Abstract
:1. Introduction
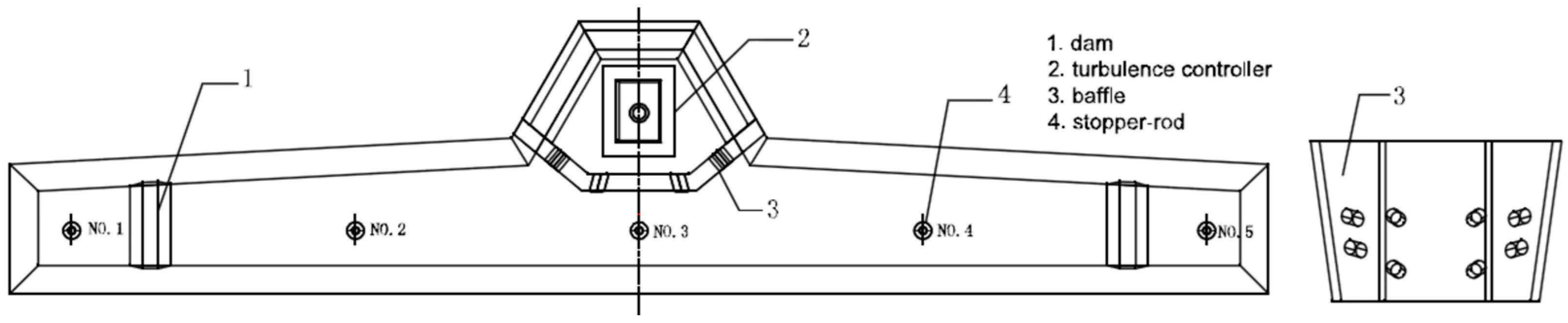
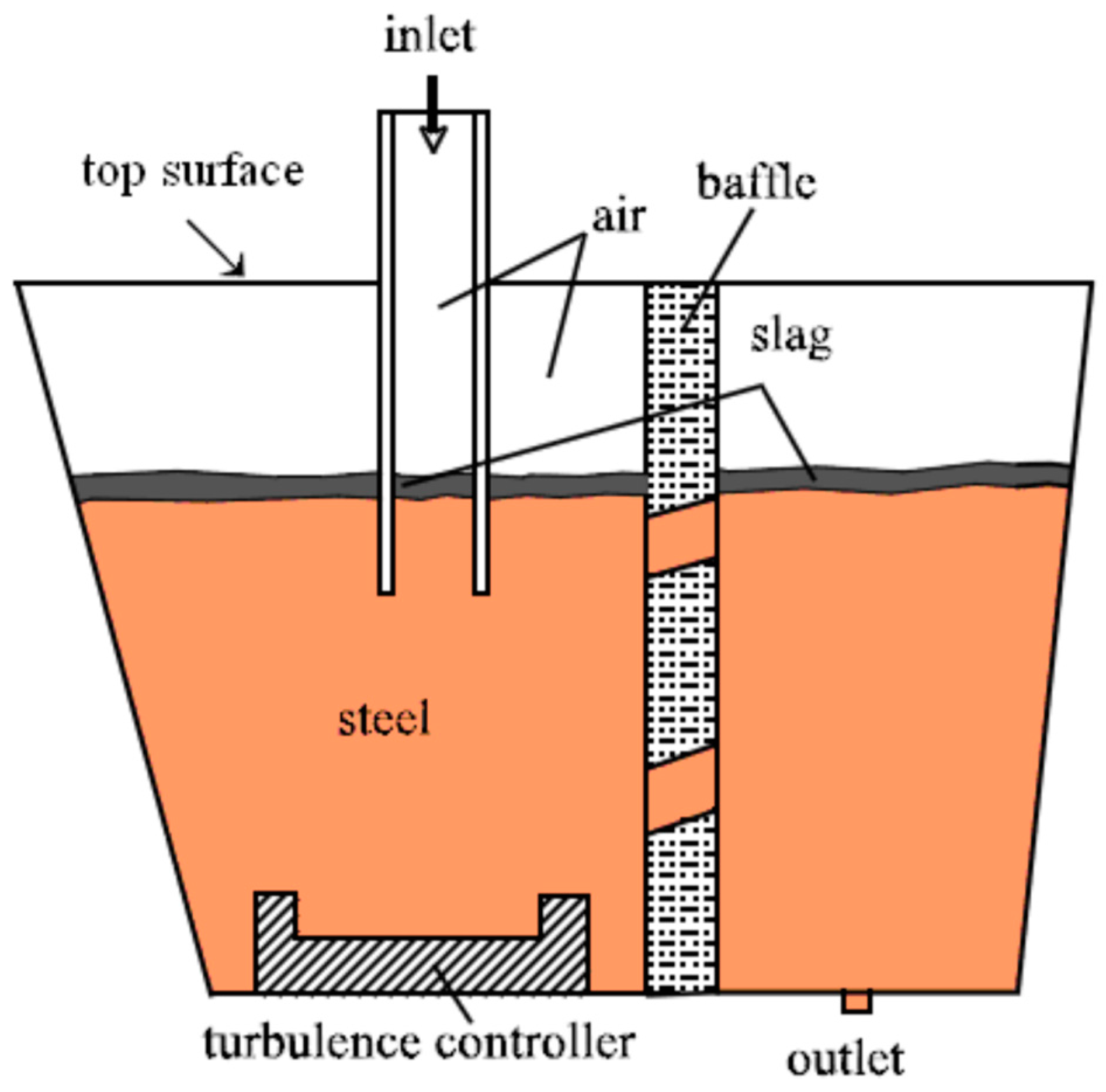
2. Model Descriptions
2.1. Basic Assumptions
- (1)
- There are no chemical reactions among the phases in a molten bath;
- (2)
- The cover slag is regarded completely as a liquid in the tundish;
- (3)
- Air, slag and molten steel are treated as incompressible viscous fluids with the fixed physical properties;
- (4)
- There is no slip and interpenetration among the fluids;
- (5)
- The influence of temperature on the flow field in the tundish is ignored.
2.2. Governing Equations
- (1)
- The multiphase VOF model [1] can be expressed as follows:
- (2)
- The fluid flow in the tundish is a complicated turbulent flow, and turbulence modeling is expressed through the standard k-ε model.
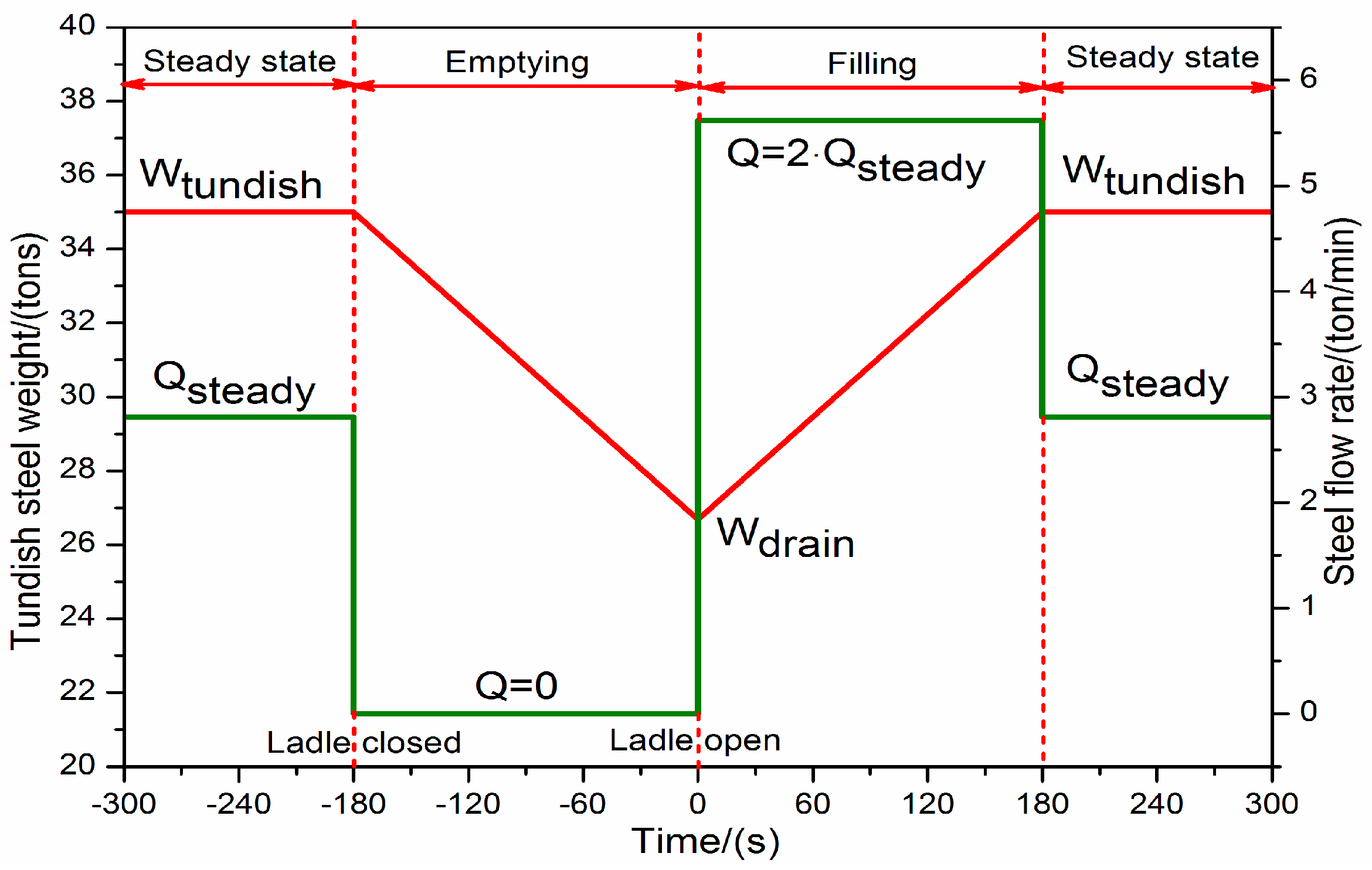
2.3. Boundary Conditions
2.4. Numerical Method
3. Results and Discussion
3.1. Model Validations
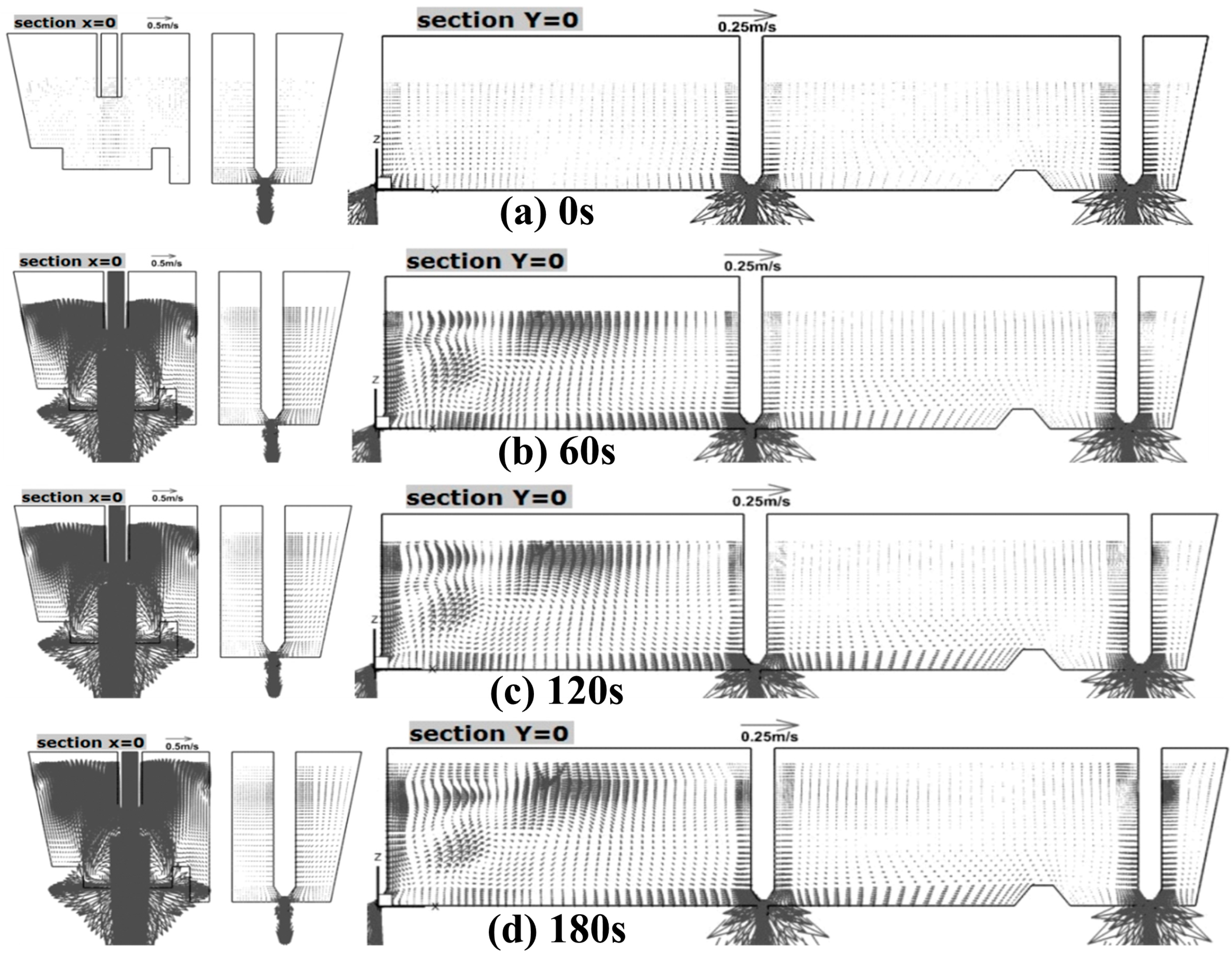
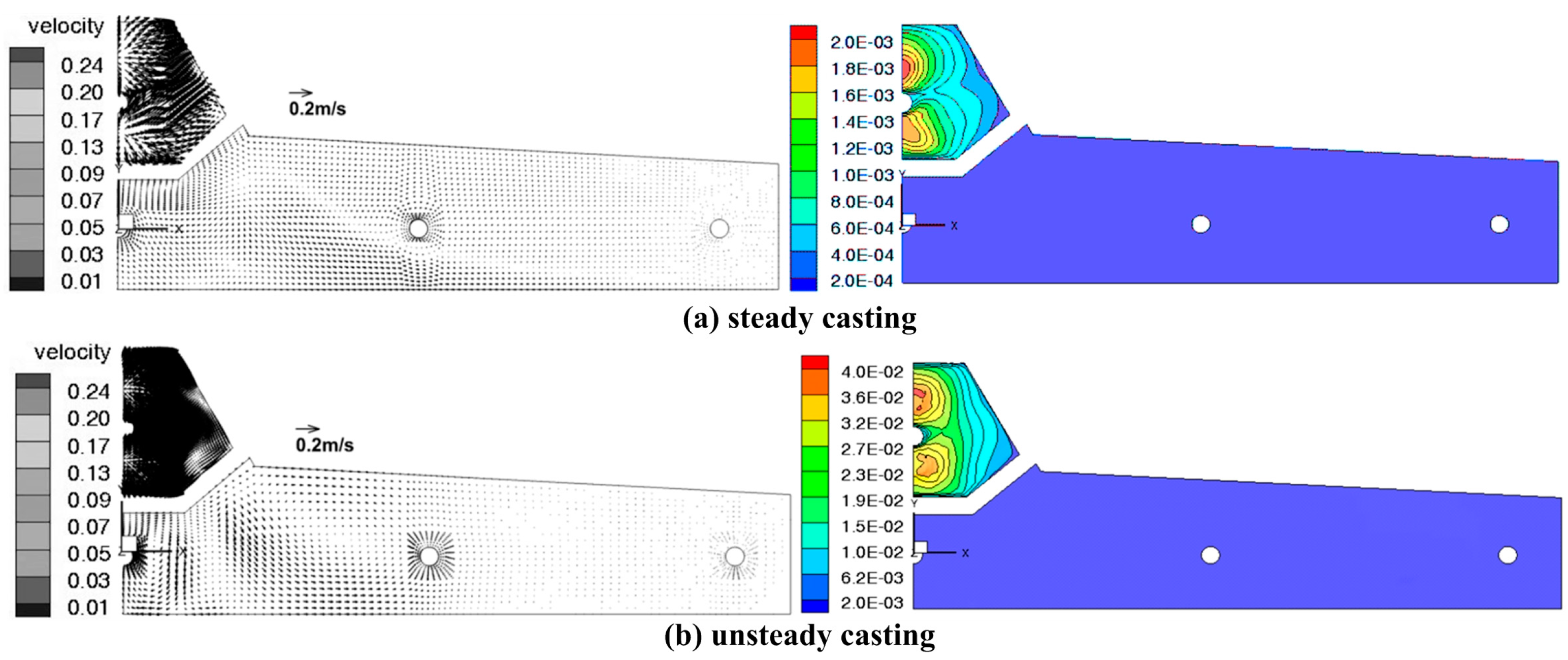
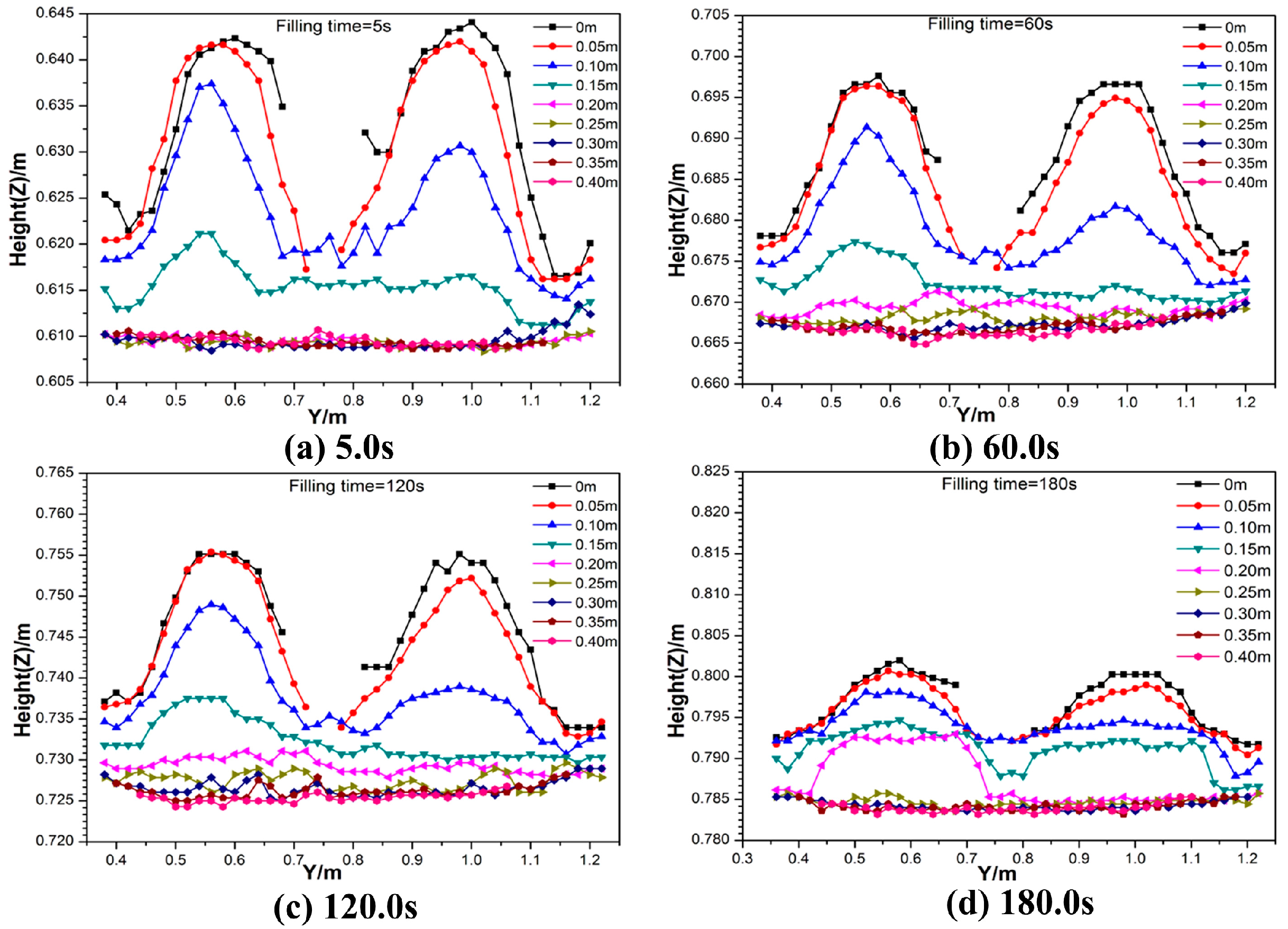
3.2. The Flow Field of Molten Steel in the Tundish
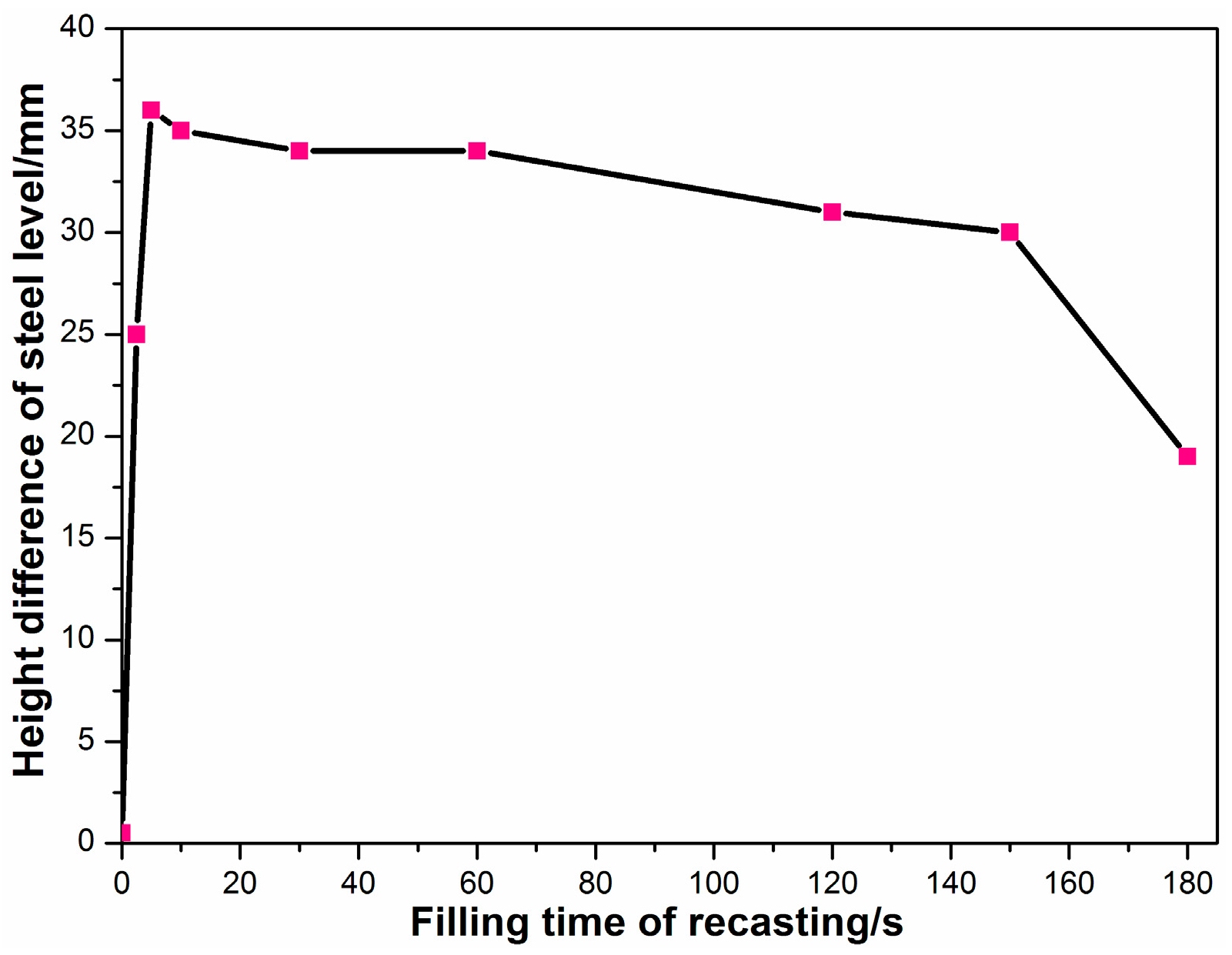
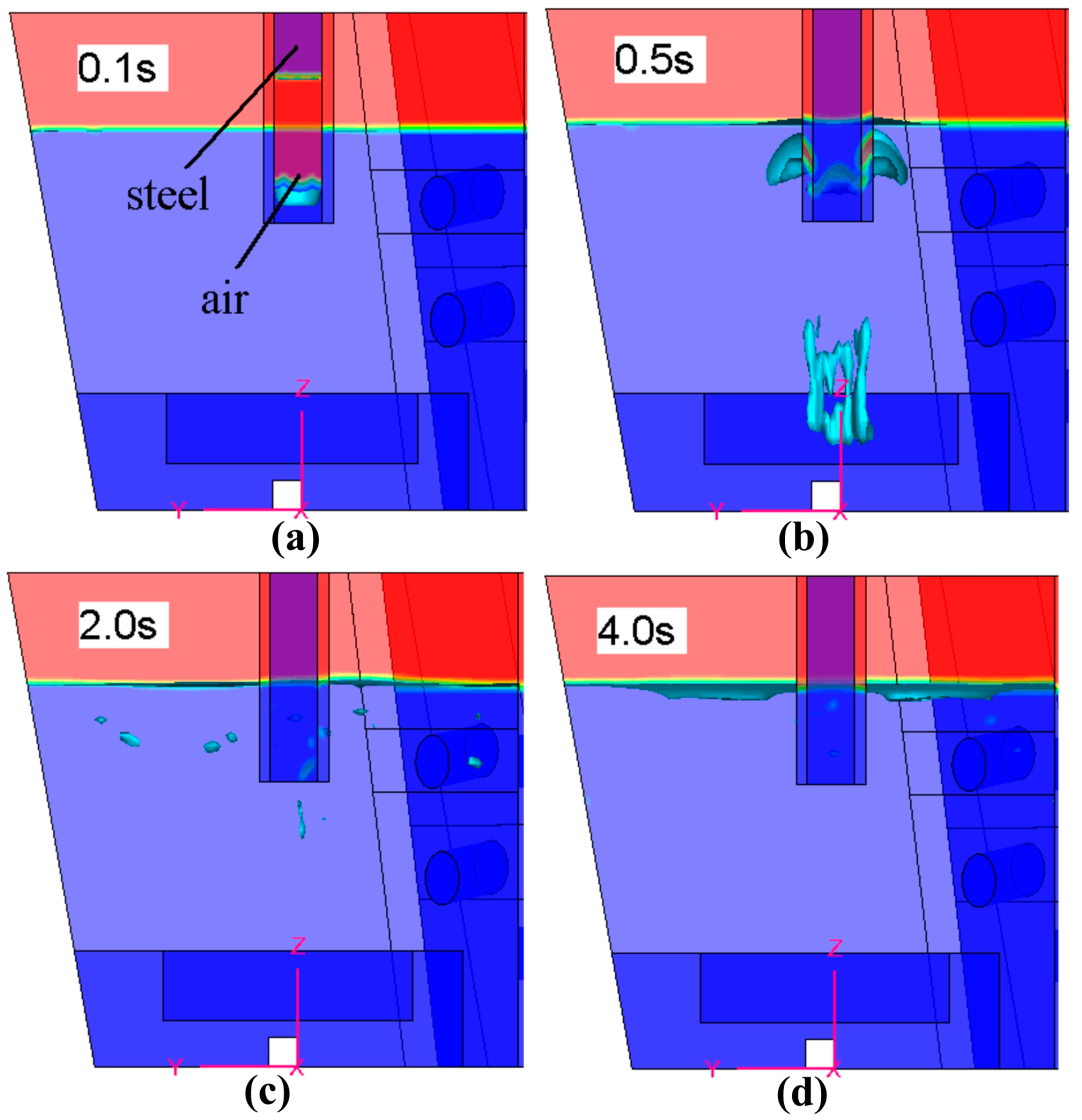
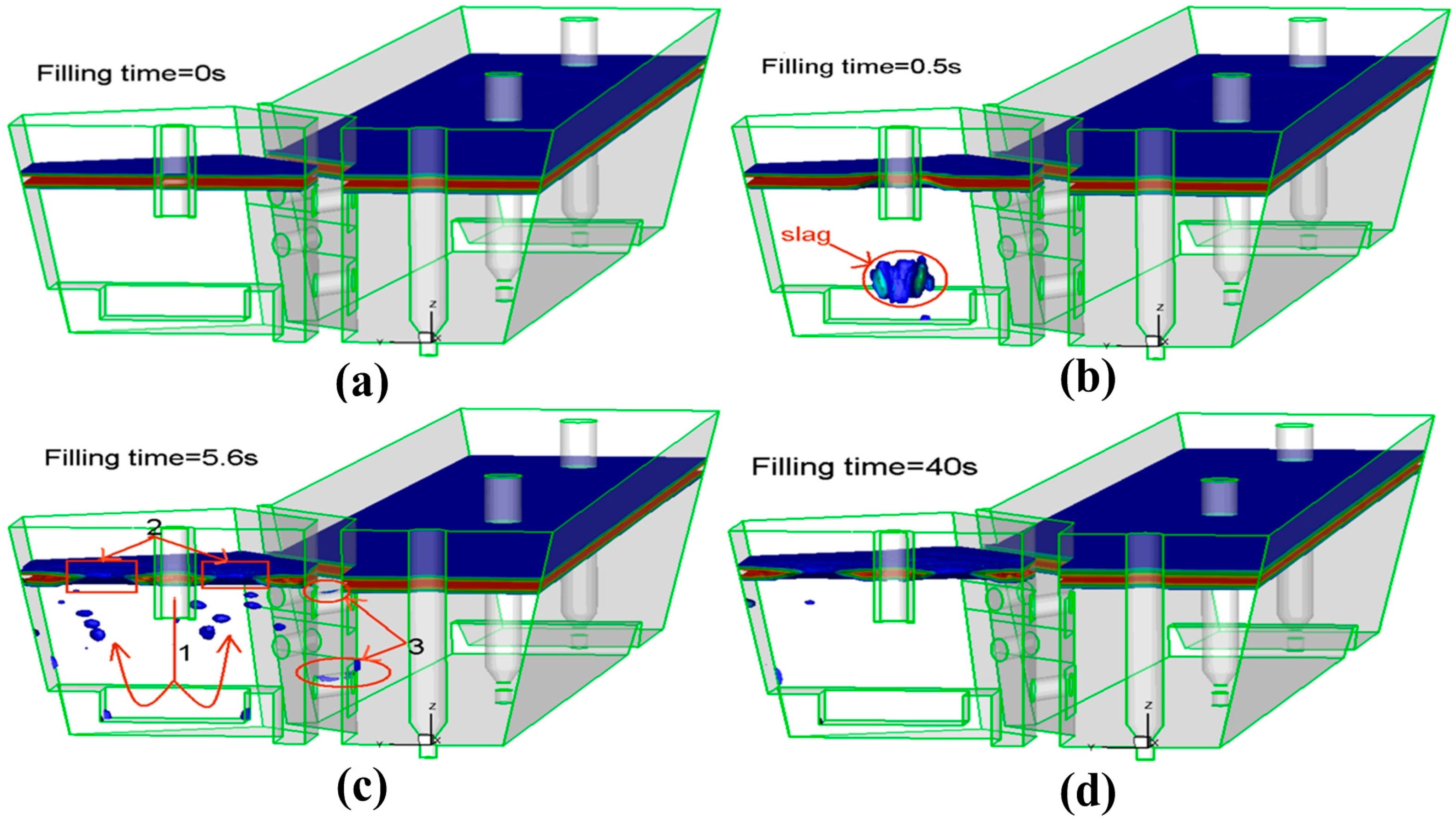
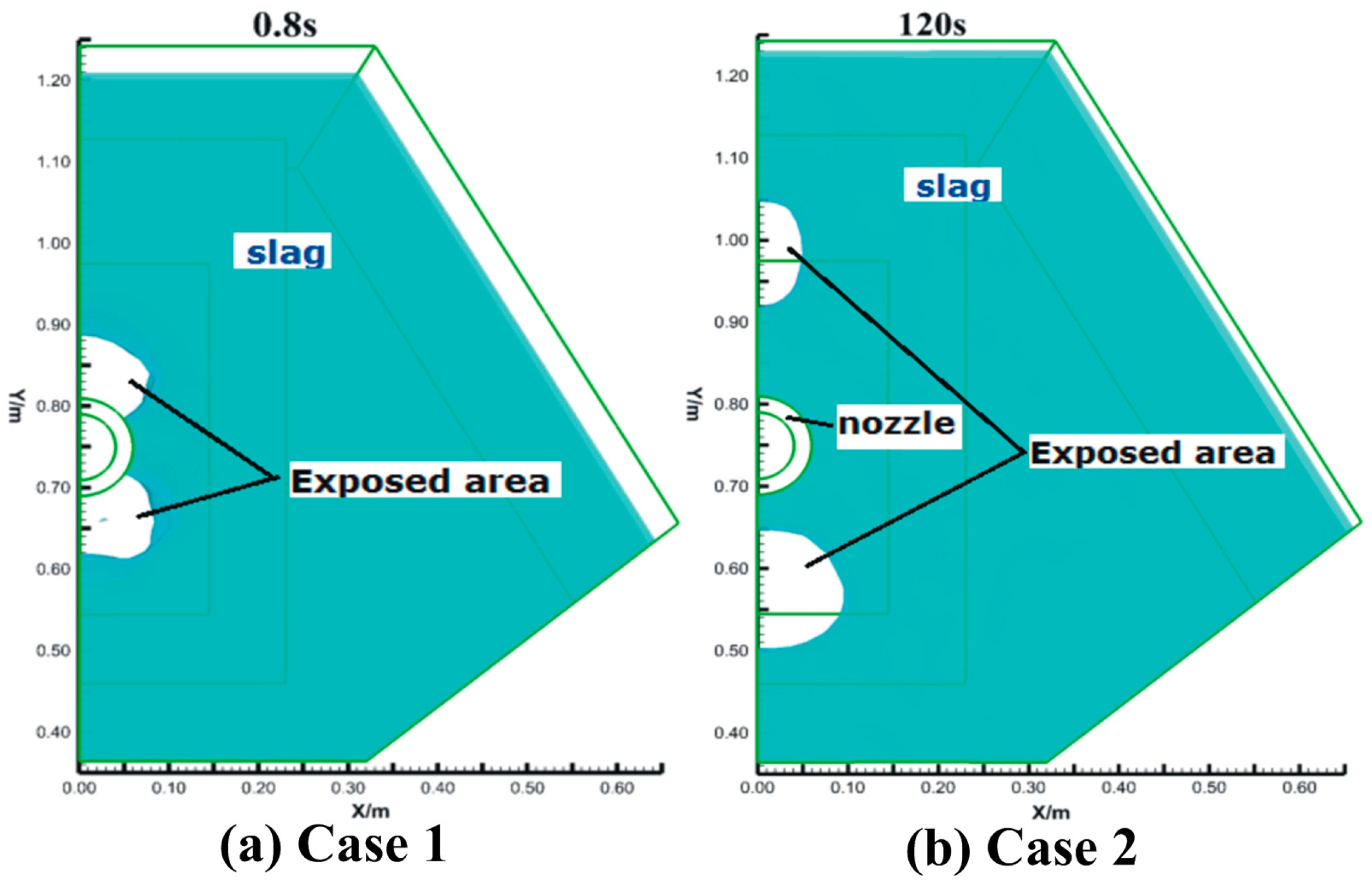
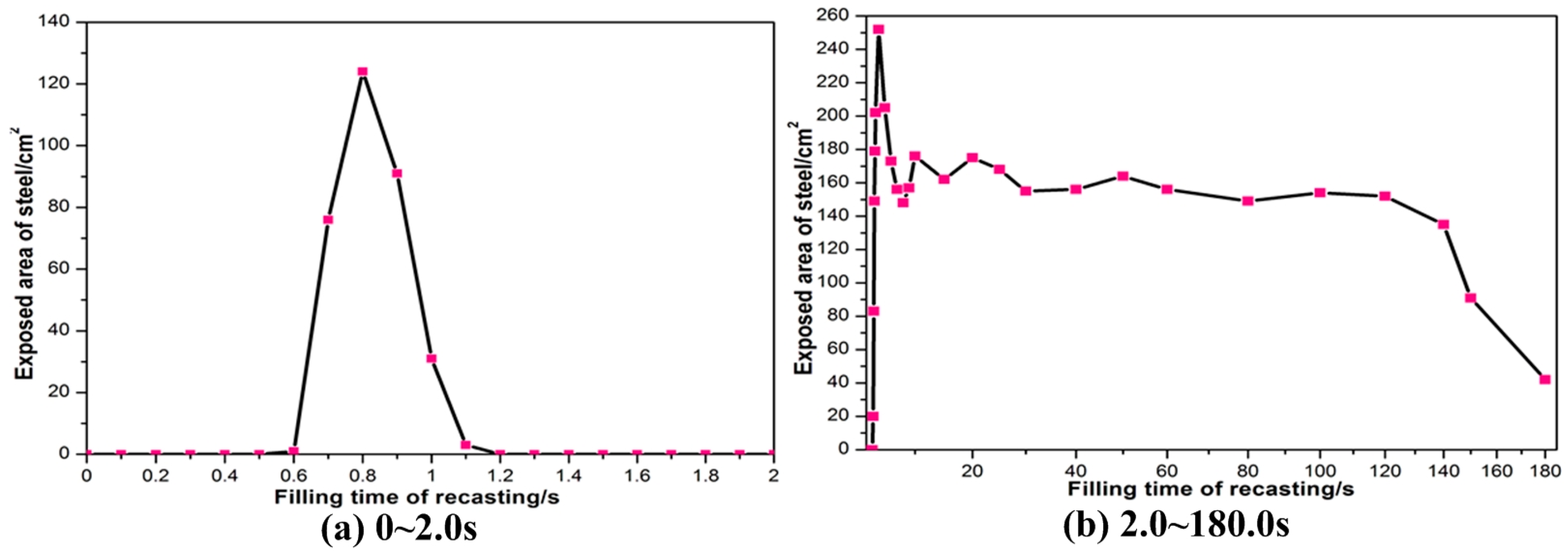
3.3. Steel-Slag-Air Multiphase Behavior
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bolling, R.; Odenthal, H.; Pfeifer, H. Transient fluid flow in a continuous casting tundish during ladle change and steady-state casting. Steel Res. Int. 2005, 76, 71–80. [Google Scholar] [CrossRef]
- Sahai, Y. Tundish technology for casting clean steel: A review. Metall. Mater. Trans. B 2016, 47, 2095–2106. [Google Scholar] [CrossRef]
- Liu, Z.; Li, B.; Zhang, L.; Xu, G. Analysis of transient transport and entrapment of particle in continuous casting mold. ISIJ Int. 2014, 54, 2324–2333. [Google Scholar] [CrossRef]
- Ling, H.; Zhang, L. Numerical simulation of the growth and removal of inclusions in the molten steel of a two-strand tundish. JOM 2013, 65, 1155–1163. [Google Scholar] [CrossRef]
- Cho, S.M.; Kim, S.H.; Thomas, B.G. Transient fluid flow during steady continuous casting of steel slabs: Part Ⅰ. Measurements and modeling of two-phase flow. ISIJ Int. 2014, 54, 845–854. [Google Scholar] [CrossRef]
- Alaei, A.R.; Edris, H.; Shirani, E. Upward molten flow for optimization of fluid flow in continuous casting tundish. J. Iron Steel Res. Int. 2010, 17, 34–39. [Google Scholar] [CrossRef]
- Takahashi, K.; Ando, M.; Ishii, T. Numerical investigation of unsteady molten steel flow and inclusion behavior in the tundish in the ladle change period. ISIJ Int. 2014, 54, 304–310. [Google Scholar] [CrossRef]
- Warzecha, M. Numerical and physical modelling of steel flow in a one-strand continuous casting tundish. Metalurgija 2011, 50, 147–150. [Google Scholar]
- Zhang, L. Transient fluid flow phenomena in continuous casting tundishes. Iron Steel Technol. 2010, 7, 55–69. [Google Scholar]
- Ling, H.; Zhang, L.; Li, H. Mathematical modeling on the growth and removal of non-metallic inclusions in the molten steel in a two-strand continuous casting tundish. Metall. Mater. Trans. B 2016, 47, 2991–3012. [Google Scholar] [CrossRef]
- Ling, H.; Zhang, L.; Wang, H. Effect of different removal conditions on the growth and removal of inclusions in the molten steel in a two-strand tundish. Metall. Res. Technol. 2017, 114, 516. [Google Scholar] [CrossRef]
- Fernandez, J.M.O.; Morros, C.S.; Somoano, J.R.; Ordieres, M.A. Multiphase modelling of the steel grade transition in a continuous casting tundish. In Proceedings of the ASME 2009 Fluids Engineering Division Summer Meeting, Vail, CO, USA, 2–6 August 2009; pp. 2183–2194. [Google Scholar]
- Siddiqui, M.I.H.; Jha, P.K. Multi-phase analysis of steel-air-slag system during ladle change-over process in CC tundish steelmaking process. In Proceedings of the Asia Steel International Conference, Yokohama, Japan, 5–8 October 2015. [Google Scholar]
- Youngs, D.L. Time-dependent multi-material flow with large fluid distortion. In Numerical Methods in Fluid Dynamics; Morton, K.W., Baines, M.J., Eds.; Academic Press: Cambridge, MA, USA, 1982; pp. 273–285. [Google Scholar]
- Odenthal, H.J.; Bölling, R.; Pfeifer, H. Three-dimensional LDA and DPIV investigations of tundish water models. In Proceedings of the 2nd International Conference on the Science & Technology of Steelmaking, Swansea, UK, 10–11 April 2001; pp. 499–517. [Google Scholar]
- Sahai, Y.; Emi, T. Physical modeling of melt flow in continuous casting tundishes. In Proceedings of the International Conference on Modelling and Simulation in Metallurgical Engineering and Materials Science, Beijing, China, 11–13 June 1996. [Google Scholar]


| Casting Condition | Value |
|---|---|
| Working capacity of tundish, t | 35 |
| Bloom cross section, mm2 | 280 × 380 |
| Casting speed, m/min | 0.63 |
| Height of molten steel, mm | 800 |
| Inner diameter of nozzle, mm | 81 |
| Submergence depth of nozzle, mm | 310 |
| Thickness of slag layer, mm | 40 |
| Property | Air | Slag | Steel |
|---|---|---|---|
| Density, kg/m3 | 1.225 | 2700 | 7000 |
| Viscosity, pa∙s | 1.79 × 10−5 | 0.6 | 0.0065 |
| Time, s | Numerical Results, cm2 | Experimental Results, cm2 | Errors, % |
|---|---|---|---|
| 1.3 | 167 | 174 | 4.2 |
| 5 | 188 | 197 | 4.6 |
| 20 | 163 | 168 | 3.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Luo, R.; Fang, Q.; Ni, H.; Song, X. Numerical Simulation of Transient Multiphase Flow in a Five-Strand Bloom Tundish during Ladle Change. Metals 2018, 8, 146. https://doi.org/10.3390/met8020146
Zhang H, Luo R, Fang Q, Ni H, Song X. Numerical Simulation of Transient Multiphase Flow in a Five-Strand Bloom Tundish during Ladle Change. Metals. 2018; 8(2):146. https://doi.org/10.3390/met8020146
Chicago/Turabian StyleZhang, Hua, Ronghua Luo, Qing Fang, Hongwei Ni, and Xiao Song. 2018. "Numerical Simulation of Transient Multiphase Flow in a Five-Strand Bloom Tundish during Ladle Change" Metals 8, no. 2: 146. https://doi.org/10.3390/met8020146
APA StyleZhang, H., Luo, R., Fang, Q., Ni, H., & Song, X. (2018). Numerical Simulation of Transient Multiphase Flow in a Five-Strand Bloom Tundish during Ladle Change. Metals, 8(2), 146. https://doi.org/10.3390/met8020146





