Sensitivity Analysis of Oxide Scale Influence on General Carbon Steels during Hot Forging
Abstract
:1. Introduction
2. Materials and Methods
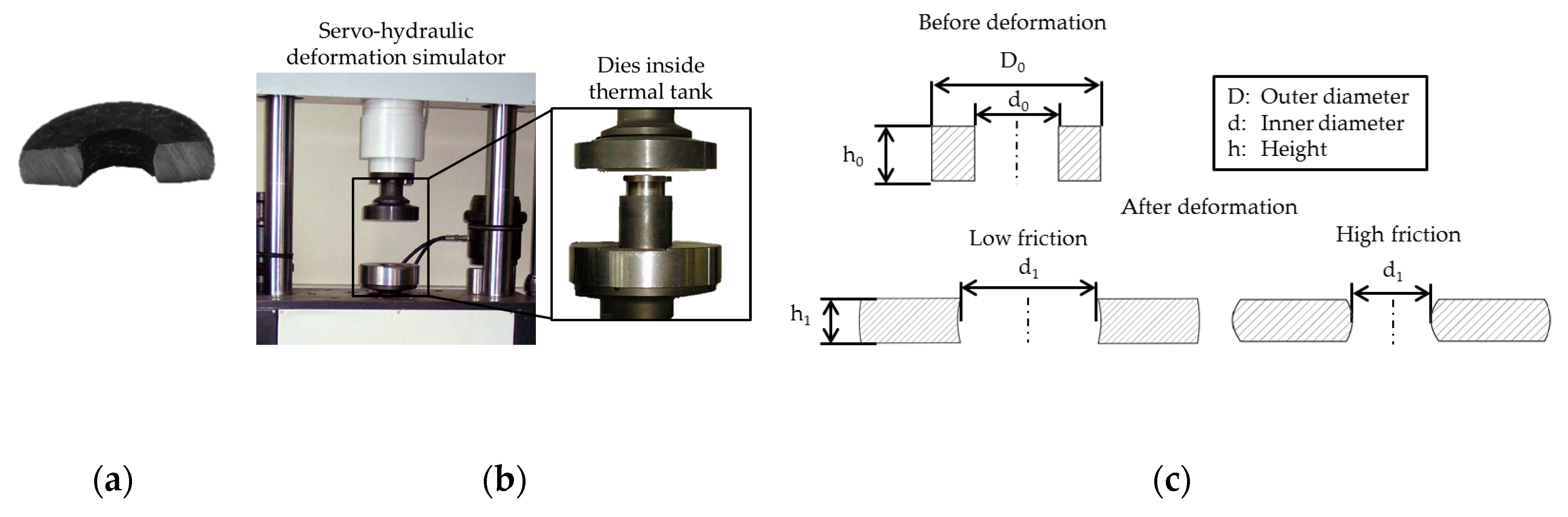
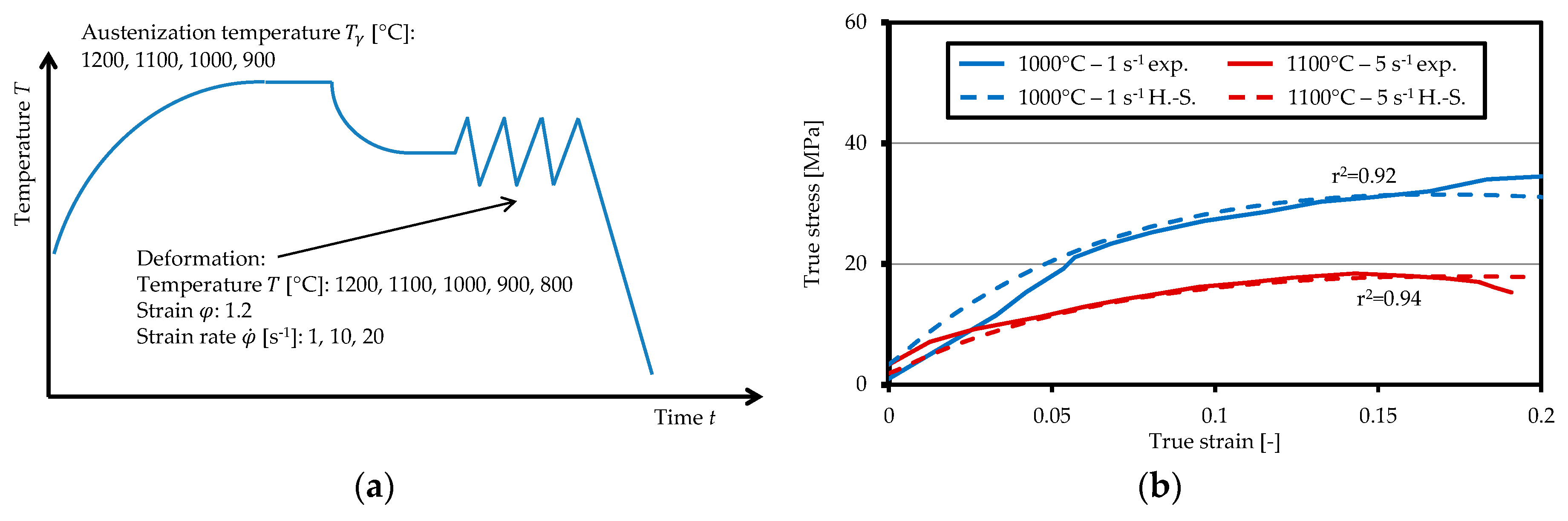
2.1. Experimental Procedure
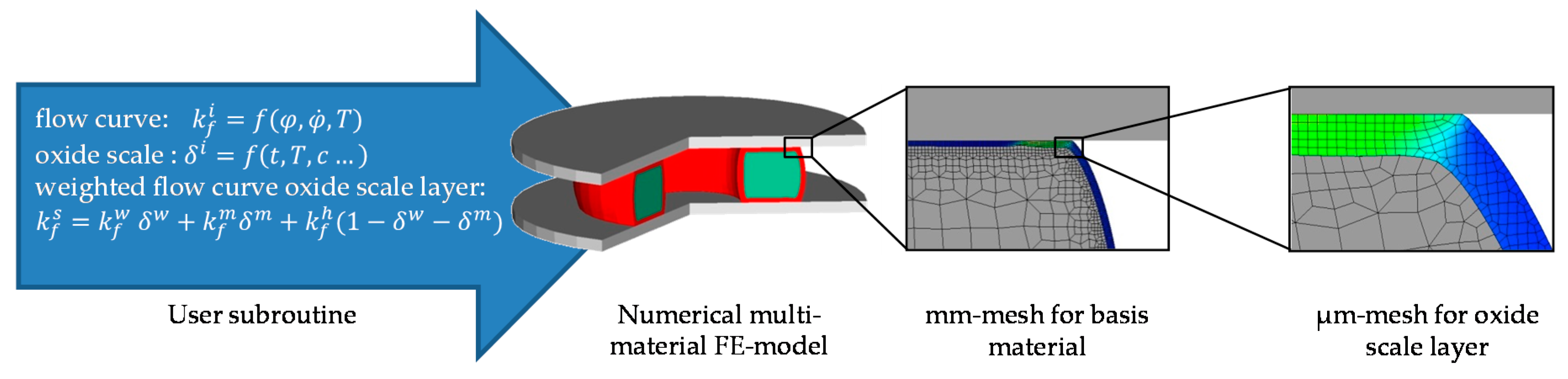
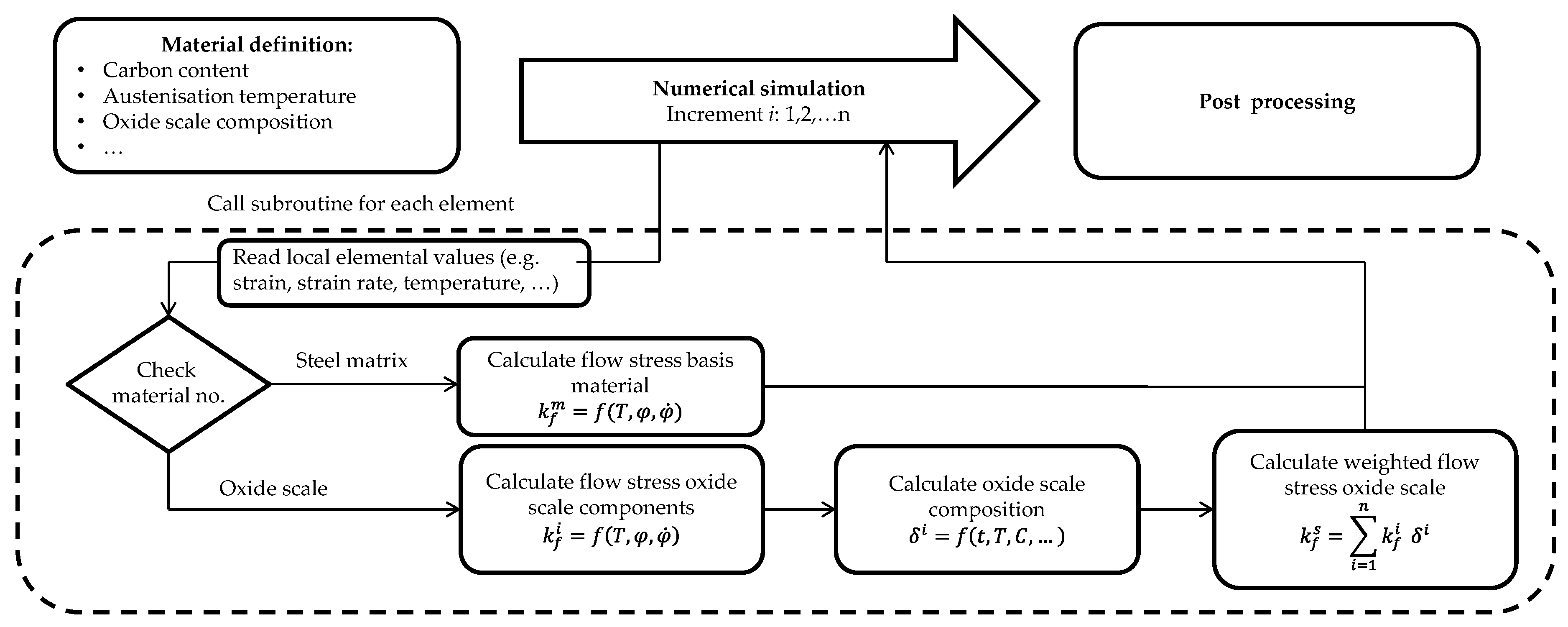
2.2. Aspects of the Numerical Model and Its Implementation
3. Results and Discussions
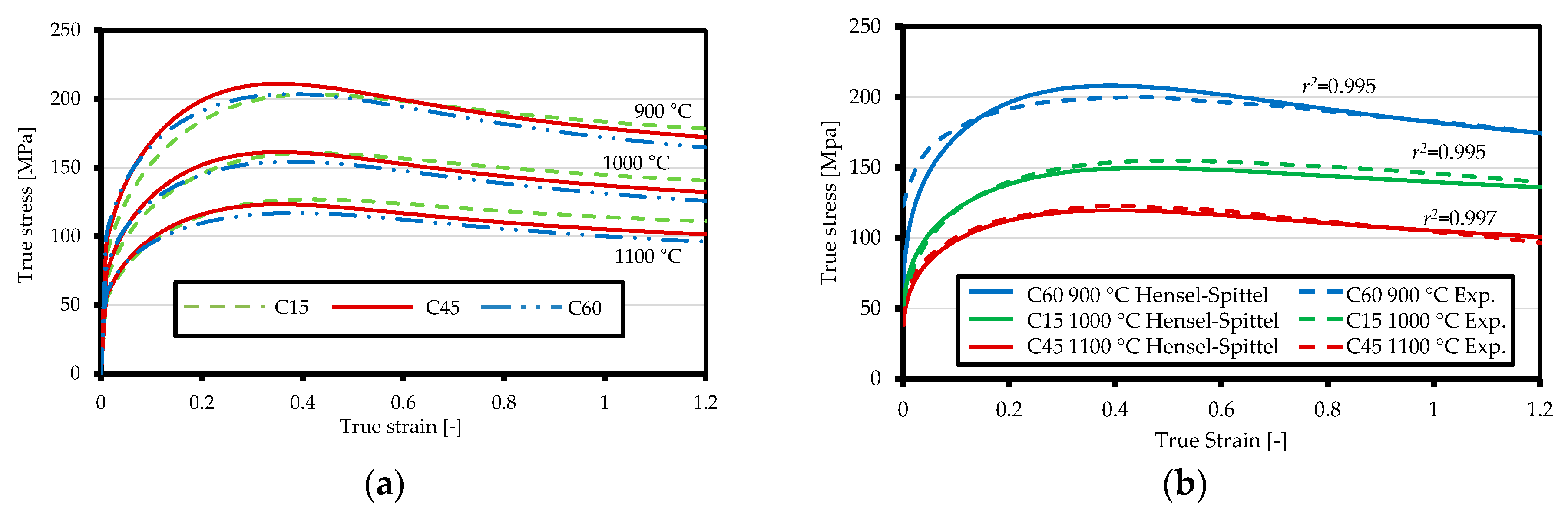
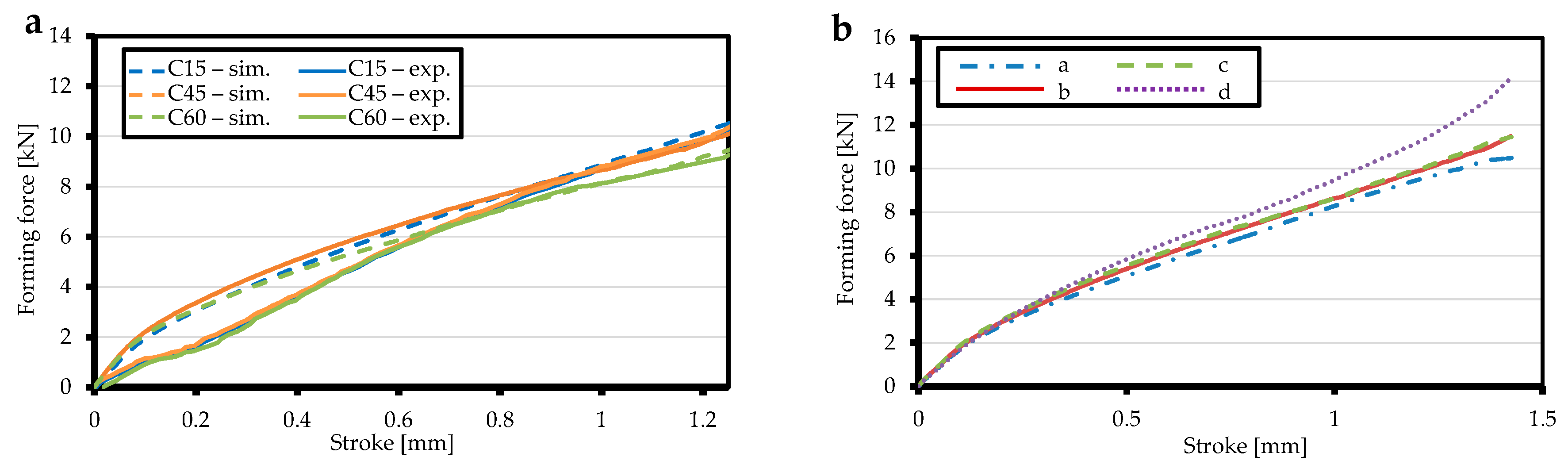
3.1. Ring Compression Test and Model Validation
3.2. Sensitivity Analysis
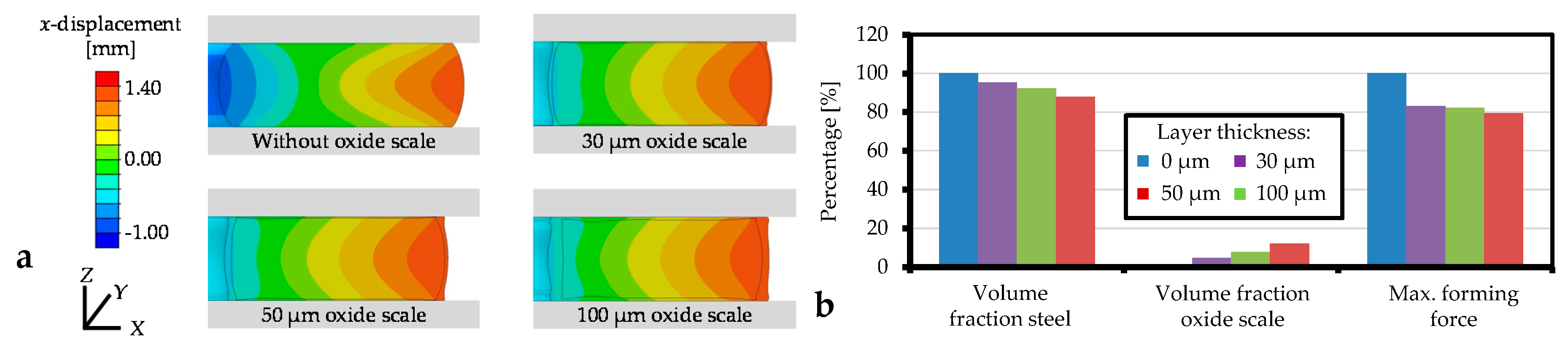
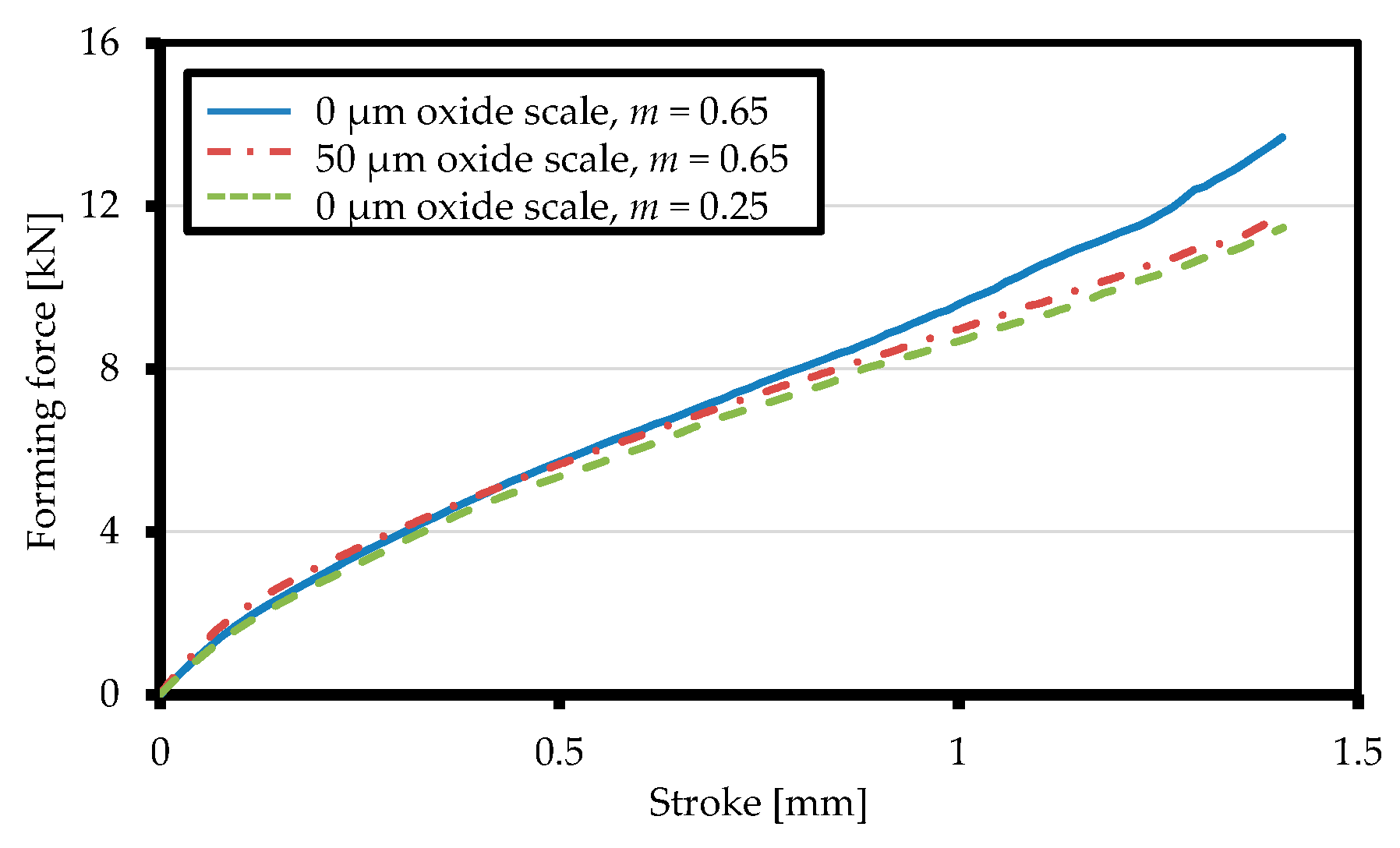
3.2.1. Layer Thickness
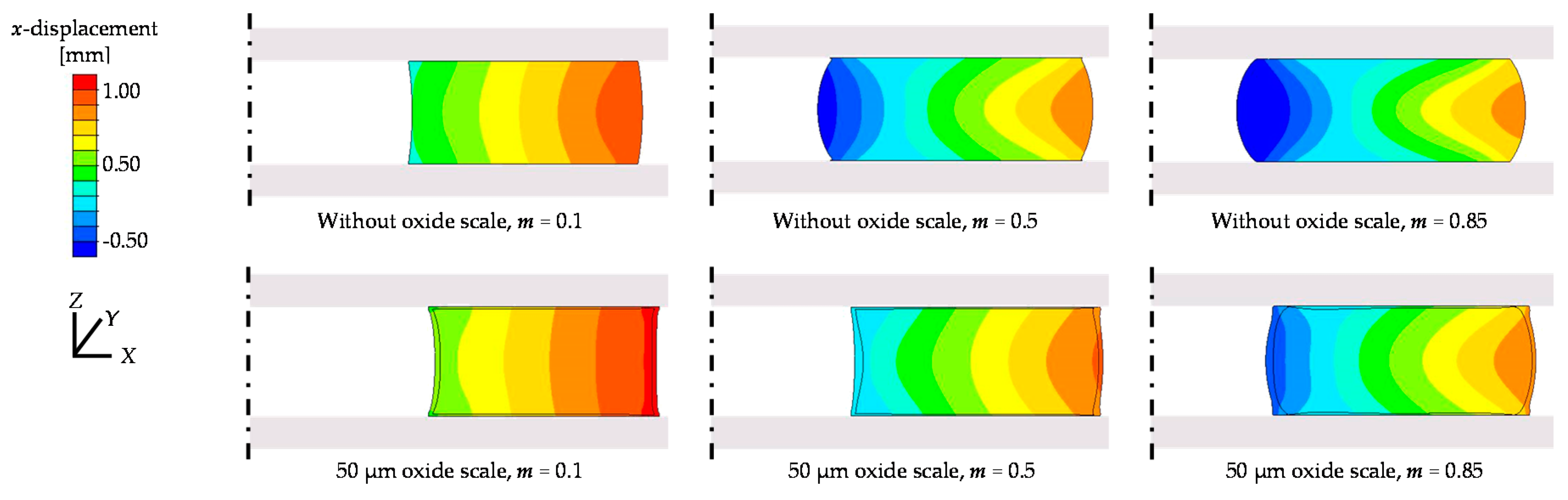
3.2.2. Friction Conditions
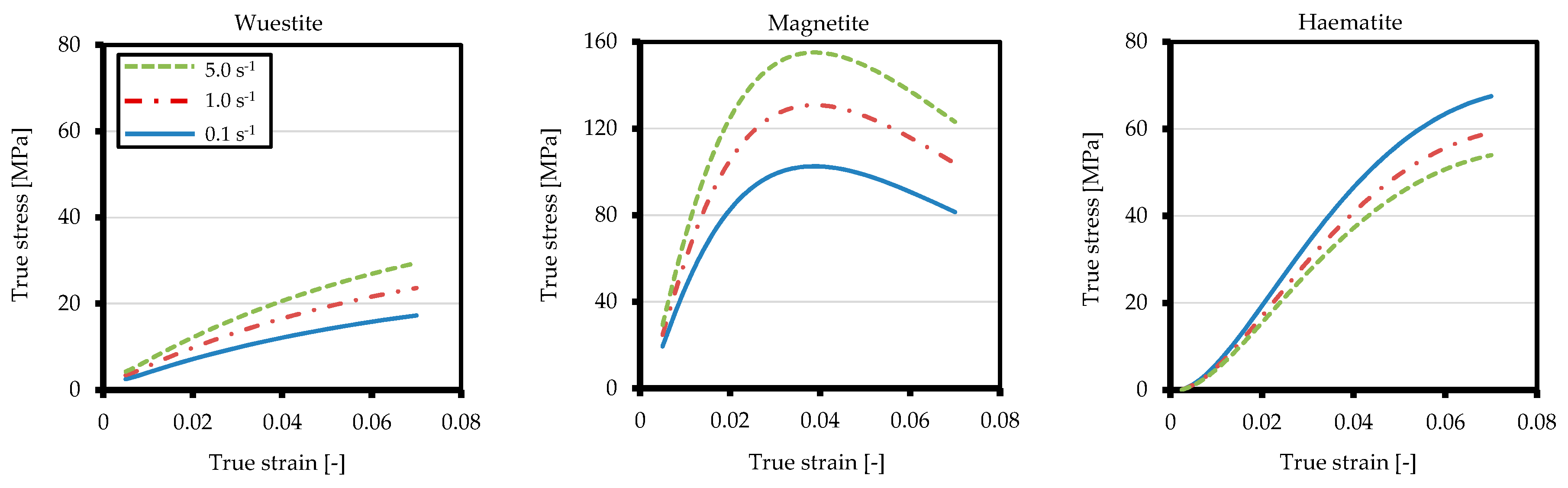
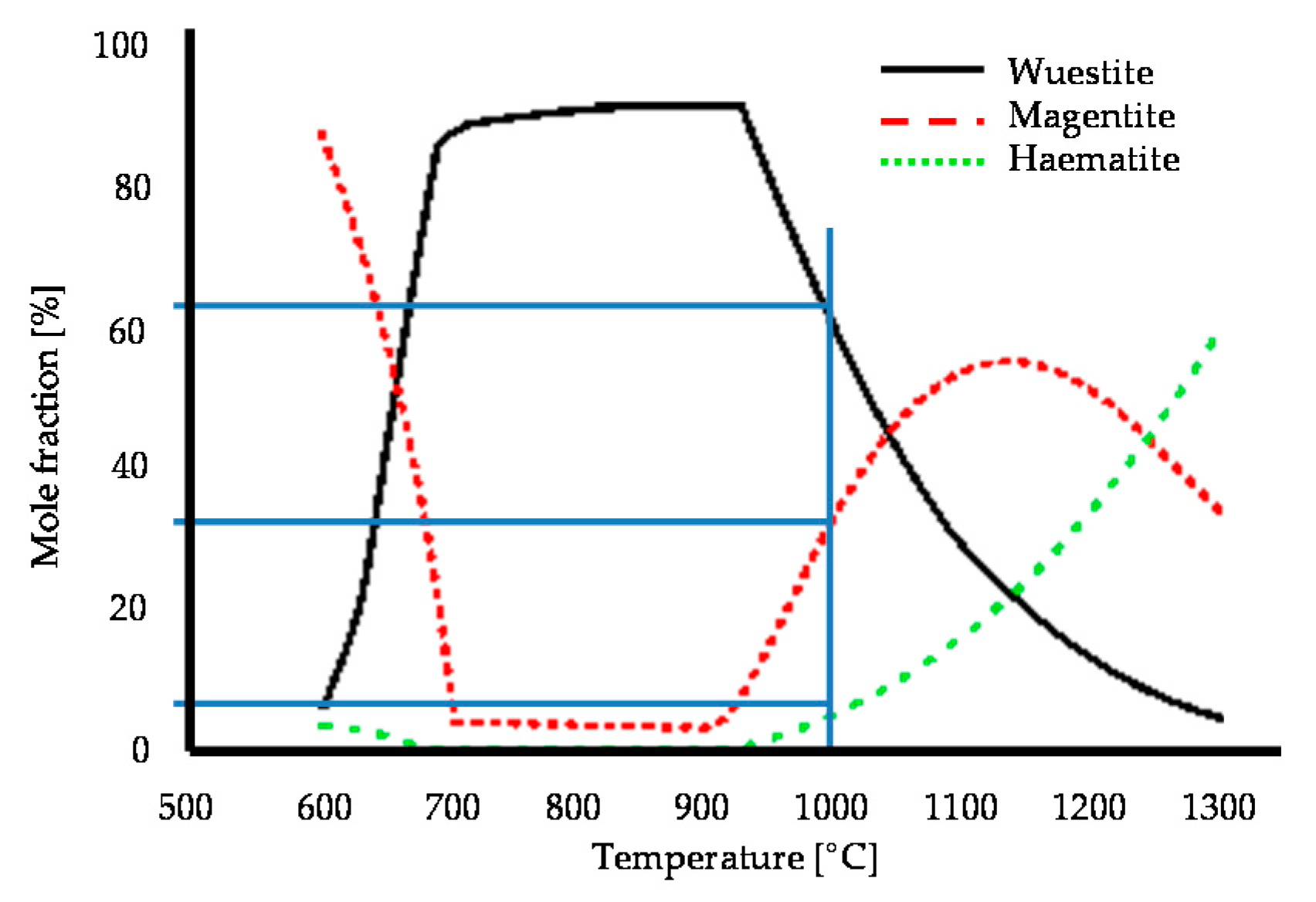
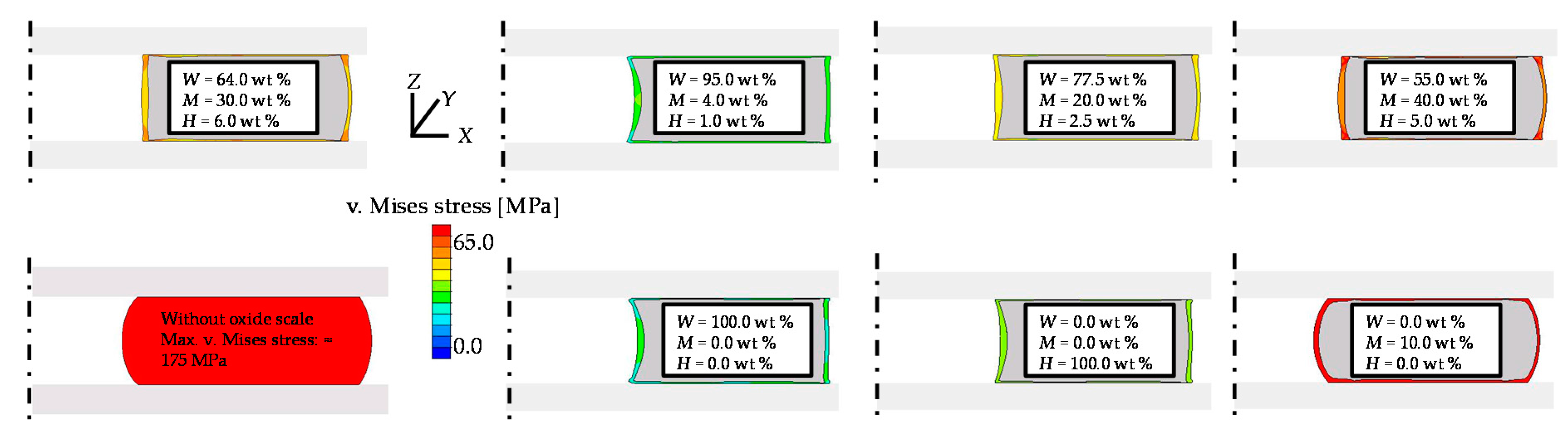
3.2.3. Oxide Scale Composition
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fischer, M.U.A.; Dickert, H.H.; Bleck, W.; Huskic, A.; Kazhai, M.; Hadifi, T.; Bouguecha, A.; Behrens, B.-A.; Labanove, N.; Felde, N.; et al. EcoForge: Energieeffiziente Prozesskette zur Herstellung von Hochleistungs-Schmiedebauteilen. HTM J. Heat Treat. Mater. 2014, 69, 209–219. (In German) [Google Scholar] [CrossRef]
- Luong, L.; Heijkoop, T. The influence of scale on friction in hot metal working. Wear 1981, 71, 93–102. [Google Scholar] [CrossRef]
- Behrens, B.-A.; Bouguecha, A.; Vucetic, M.; Chugreev, A. Advanced wear simulation for bulk metal forming processes. In Proceedings of the Numiform 2016: The 12th International Conference on Numerical Methods in Industrial Forming Processes, Troyes, France, 4–7 July 2016; Volume 80. [Google Scholar] [CrossRef]
- Behrens, B.-A. Finite element analysis of die wear in hot forging processes. CIRP Ann. Manuf. Technol. 2008, 57, 305–308. [Google Scholar] [CrossRef]
- Kawalla, R.; Steinert, F. Untersuchung des Einflusses von Prozessparametern in der Fertigstraße auf die Tertiärzunderausbildung. Mat.-wiss. u. Werkstofftech. 2007, 38, 36–42. [Google Scholar] [CrossRef]
- Krzyzanowski, M.; Beynon, J.; Farrugia, D. Oxide Scale Behavior in High Temperature Metal Processing; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2010; ISBN 978-35-2-732518-4. [Google Scholar]
- Malik, A.U.; Whittle, D.P. Oxidation of Fe-C alloys in the temperature range 600–850 °C. Oxid. Met. 1981, 16, 339–353. [Google Scholar] [CrossRef]
- Birks, N.; Frederik, S.; Meier, G.H. Introduction to High Temperature Oxidation of Metals, 2nd ed.; Cambridge University Press: Cambridge, UK, 2006; ISBN 978-05-2-148517-3. [Google Scholar]
- Kubaschewski, O.; Hopkins, B.E. Oxidation of metals and alloys. Mater. Corros. 1954, 11, 108–114. [Google Scholar] [CrossRef]
- Brauns, E.; Rahmel, A.; Christmann, H. Die Verschiebung des Nonvarianzpunktes zwischen Eisen, Wüstit, Magnetit und Sauerstoff im System Eisen—Sauerstoff durch Legierungselemente oder fremde Oxyde—Auswirkungen auf das Verhalten von Eisenlegierungen beim Verzundern. Arch. Eisenhttenwes. 1959, 30, 553–564. [Google Scholar] [CrossRef]
- Garnaud, G.; Rapp, R.A. Thickness of the oxide scale layers formed during the oxidation of iron. Oxid. Met. 1977, 11, 193–198. [Google Scholar] [CrossRef]
- Graf, M.; Kawalla, R. Scale behaviour and deformation properties of oxide scale during hot rolling of steel. Key Eng. Mater. 2012, 504–506, 546–551. [Google Scholar] [CrossRef]
- Graf, M. Modellierung des Zunderverhaltens Entlang der Prozesskette Warmband, TU Bergakademie Freiberg; Freiberger Forschungsheft B353: Freiberg, Germany, 2013; ISBN 978-38-6-012480-2. [Google Scholar]
- Takeda, M.; Onishi, T.; Nakakubo, S.; Fujimoto, S. Physical properties of iron-oxide scales on Si-containing steels at high temperature. Mater. Trans. 2009, 50, 2242–2246. [Google Scholar] [CrossRef]
- Behrens, B.-A.; Bouguecha, A.; Hadifi, T.; Mielke, J. Advanced friction modeling for bulk metal forming processes. Prod. Eng. 2011, 5, 621–627. [Google Scholar] [CrossRef]
- Barnes, D.J.; Wilson, J.E.; Stott, F.H. The influence of oxide films on the friction and wear of Fe-5% Cr alloy in controlled environments. Wear 1977, 45, 161–176. [Google Scholar] [CrossRef]
- Vergne, C.; Boher, C.; Gras, R.; Levailant, C. Influence of oxides on friction in hot rolling: Experimental investigations and tribological modelling. Wear 2000, 260, 957–975. [Google Scholar] [CrossRef]
- Hinsley, C.F.; Male, A.T.; Rowe, G.W. Frictional properties of metal oxides at high temperatures. Wear 1968, 11, 233–238. [Google Scholar] [CrossRef]
- Munther, P.A.; Lenard, J.G. The effect of scaling on interfacial friction in hot rolling of steels. J. Mater. Process. Technol. 1993, 37, 3–36. [Google Scholar] [CrossRef]
- Tingle, E.D. The importance of surface oxide films in the friction and lubrication of metals. Trans. Faraday Soc. 1950, 46, 93–102. [Google Scholar] [CrossRef]
- Matsumoto, R.; Osumi, Y.; Utsunomiya, H. Reduction of friction of steel covered with oxide scale in hot forging. J. Mater. Process. Technol. 2014, 214, 651–659. [Google Scholar] [CrossRef]
- Graf, M.; Ullmann, M.; Korpalla, G.; Kawalla, R. Materialkennwerte als Basis für die nummerische simulation von Warmumformprozessen. In Proceedings of the 22. Verformungskundliches Kolloquium, Planneralm, Germany, February 2013; pp. 49–55. [Google Scholar]
- Wray, P.J. Effect of carbon content on the plastic flow of plain carbon steels at elevated temperatures. Metall. Trans. A 1982, 13, 125–134. [Google Scholar] [CrossRef]
- Korpała, G.; Ullmann, M.; Graf, M.; Wester, H.; Bouguecha, A.; Awiszus, B.; Behrens, B.-A.; Kawalla, R. Modelling the influence of carbon content on material behavior during forging. AIP Conf. Proc. 2017, 1896, 190013. [Google Scholar] [CrossRef]
- Behrens, B.-A.; Kawalla, R.; Awiszus, B.; Bouguecha, A.; Ullmann, M.; Graf, M.; Bonk, C.; Chugreev, A.; Wester, H. Numerical investigation of the oxide scale deformation behaviour with consideration of carbon content during hot forging. Procedia Eng. 2017, 207, 526–531. [Google Scholar] [CrossRef]
- Korpala, G. Einfluss der Chemischen Zusammensetzung auf die Mechanischen Eigenschaften von Unlegiertem Bainitischen Stahl mit Restaustenit; Freiberger Forschungshefte: Freiberg, Germany, 2016. [Google Scholar]
- Tominaga, J.; Wakimoto, K.; Mori, T.; Murakami, M.; Yoshimura, T. Manufacture of wire rods with good descaling property. Trans. Iron Steel Inst. Jpn. 1982, 22, 646–656. [Google Scholar] [CrossRef]
- Sun, W. A Study on the Characteristics of Oxide Scale in Hot Rolling of Steel. University of Wollongong Thesis Collection. 2005. Available online: http://ro.uow.edu.au/theses/440 (accessed on 13 February 2018).
- Male, A.T.; Cockcroft, M.G. A method for the determination of the coefficient of friction of metals under conditions of bulk plastic deformation. J. Inst. Met. 1964, 93, 38–46. [Google Scholar]
- Krzyzanowski, M.; Beyon, J.H. Oxide Behaviour in hot rolling. In Metal Forming Science and Practice; Lenard, J., Ed.; Elsevier: Amsterdam, The Netherlands, 2002; pp. 259–295. ISBN 978-00-8-053631-6. [Google Scholar]
- Frolish, M.F.; Krzyzanowski, M.; Beyon, J.H. Oxide scale behaviour on aluminium and steel under hot working conditions. J. Mater. Process. Technol. 2006, 177, 36–40. [Google Scholar] [CrossRef]
- Koch, S.; Vucetic, M.; Hübner, S.; Bouguecha, A.; Behrens, B.-A. Superimposed oscillating and non-oscillating ring compression tests for sheet-bulk metal forming technology. Appl. Mech. Mater. 2015, 794, 89–96. [Google Scholar] [CrossRef]

| Steel Grade | C | Si | Mn | P | S | Cr | Mo | Ni | Cu | Al |
|---|---|---|---|---|---|---|---|---|---|---|
| C15 | 0.160 | 0.210 | 0.420 | 0.001 | <0.001 | 0.100 | 0.045 | 0.087 | 0.108 | 0.017 |
| C45 | 0.490 | 0.200 | 0.420 | 0.001 | 0.001 | 0.100 | 0.034 | 0.081 | 0.096 | 0.021 |
| C60 | 0.63 | 0.200 | 0.420 | <0.001 | <0.001 | 0.100 | 0.035 | 0.076 | 0.100 | 0.017 |
| 3275 | 0.03662 | 0.0027 | 0.41618 | −0.0421 | −0.08004 | 0.07959 | 894 | −0.01367 | 0.00276 | 0.00236 | 0.17777 |
| 1.83501 | 0.00015 | 0.13325 | 0.048 | 0.15951 |
| Oxidation Temperature Oxide Scale Thickness | Steel Grade | Experimental (mm) | Simulation (mm) | Deviation (%) | |||
|---|---|---|---|---|---|---|---|
| Inner Diameter | Height | Inner Diameter | Height | Inner Diameter | Height | ||
| Oxidation temperature: 1000 °C Oxide scale thickness 50 µm | C15 | 3.7 | 1.61 | 3.91 | 1.63 | 5.1 | 1.2 |
| C45 | 3.75 | 1.67 | 3.86 | 1.7 | 2.9 | 1.8 | |
| C60 | 3.8 | 1.68 | 3.77 | 1.66 | −0.79 | −1.2 | |
| Oxidation temperature: 900 °C Oxide scale thickness: 30 µm | C15 | 3.65 | 1.59 | 3.74 | 1.59 | 2.47 | 1.89 |
| C45 | 3.71 | 1.82 | 4.00 | 1.82 | 7.82 | −1.1 | |
| C60 | 3.8 | 1.67 | 3.81 | 1.68 | 0.26 | 0.6 | |
| Variant | Height (mm) | Inner Diameter (mm) |
|---|---|---|
| Experimental ring compression test (averaged) | 1.62 | 3.7 |
| Simulation; W = 64.0 wt %; M = 30.0 wt %; H = 6.0 wt % (calculated composition for 1000 °C based on [28]) | 1.63 | 3.91 |
| Simulation; W = 55.0 wt %; M = 40.0 wt %; H = 5.0 wt % | 1.63 | 3.89 |
| Simulation; W = 77.50 wt %; M = 20.0 wt %; H = 2.5 wt % | 1.63 | 4.25 |
| Simulation; W = 95.0 wt %; M = 4.0 wt %; H = 1.0 wt % | 1.63 | 4.41 |
| Simulation; without oxide scale | 1.62 | 2.67 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behrens, B.-A.; Chugreev, A.; Awiszus, B.; Graf, M.; Kawalla, R.; Ullmann, M.; Korpala, G.; Wester, H. Sensitivity Analysis of Oxide Scale Influence on General Carbon Steels during Hot Forging. Metals 2018, 8, 140. https://doi.org/10.3390/met8020140
Behrens B-A, Chugreev A, Awiszus B, Graf M, Kawalla R, Ullmann M, Korpala G, Wester H. Sensitivity Analysis of Oxide Scale Influence on General Carbon Steels during Hot Forging. Metals. 2018; 8(2):140. https://doi.org/10.3390/met8020140
Chicago/Turabian StyleBehrens, Bernd-Arno, Alexander Chugreev, Birgit Awiszus, Marcel Graf, Rudolf Kawalla, Madlen Ullmann, Grzegorz Korpala, and Hendrik Wester. 2018. "Sensitivity Analysis of Oxide Scale Influence on General Carbon Steels during Hot Forging" Metals 8, no. 2: 140. https://doi.org/10.3390/met8020140
APA StyleBehrens, B.-A., Chugreev, A., Awiszus, B., Graf, M., Kawalla, R., Ullmann, M., Korpala, G., & Wester, H. (2018). Sensitivity Analysis of Oxide Scale Influence on General Carbon Steels during Hot Forging. Metals, 8(2), 140. https://doi.org/10.3390/met8020140









