The Role of Glide during Creep of Copper at Low Temperatures
Abstract
1. Introduction
2. The Creep Mobility
3. Dislocation Dynamics Method
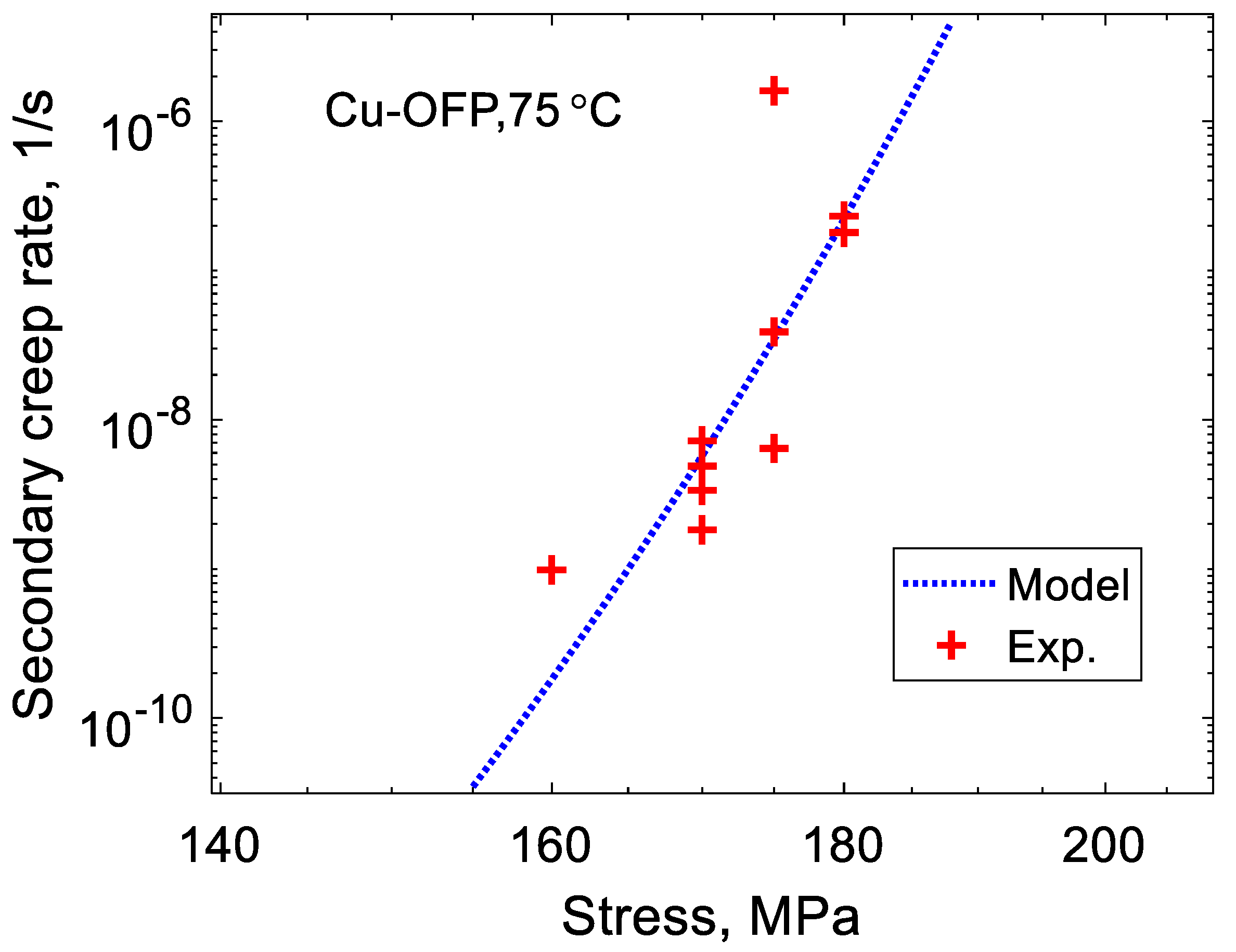
4. Glide Controlled Creep of Copper at 75 °C
4.1. Dislocation Mobility
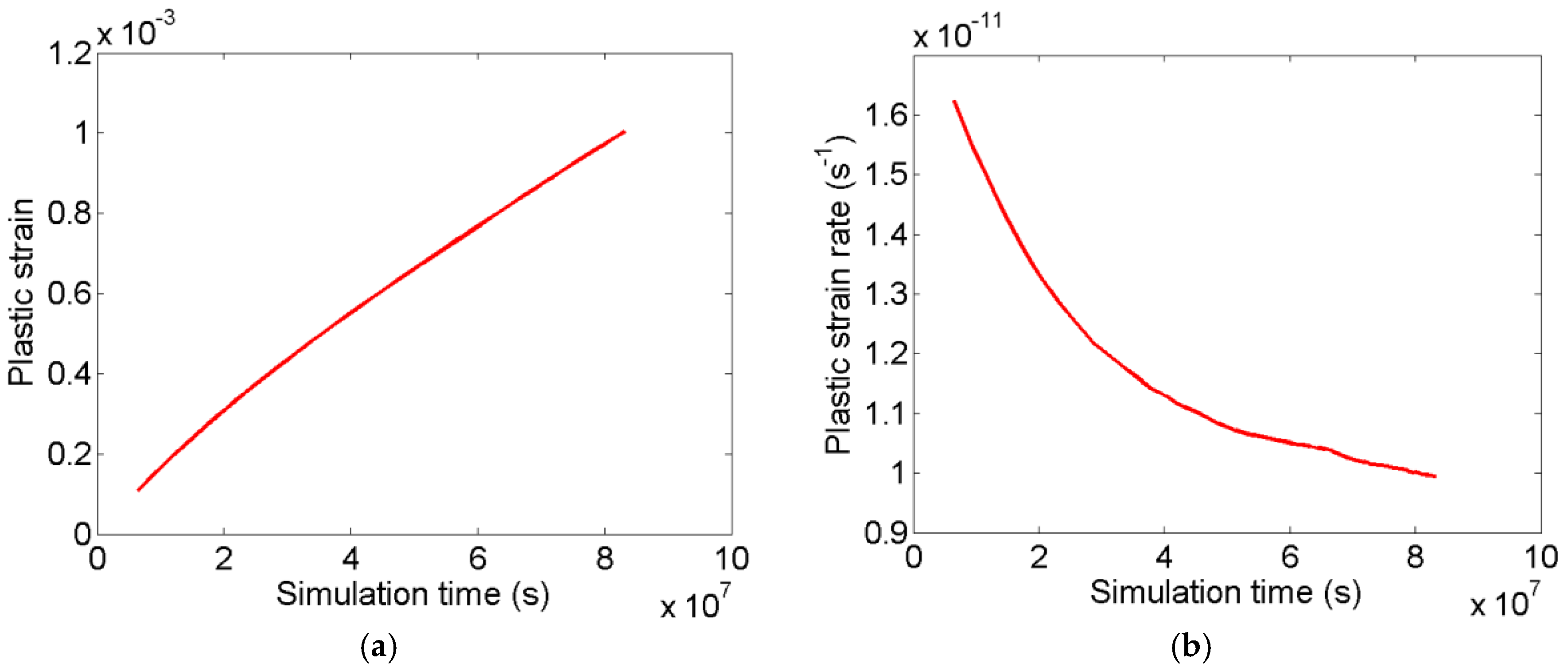
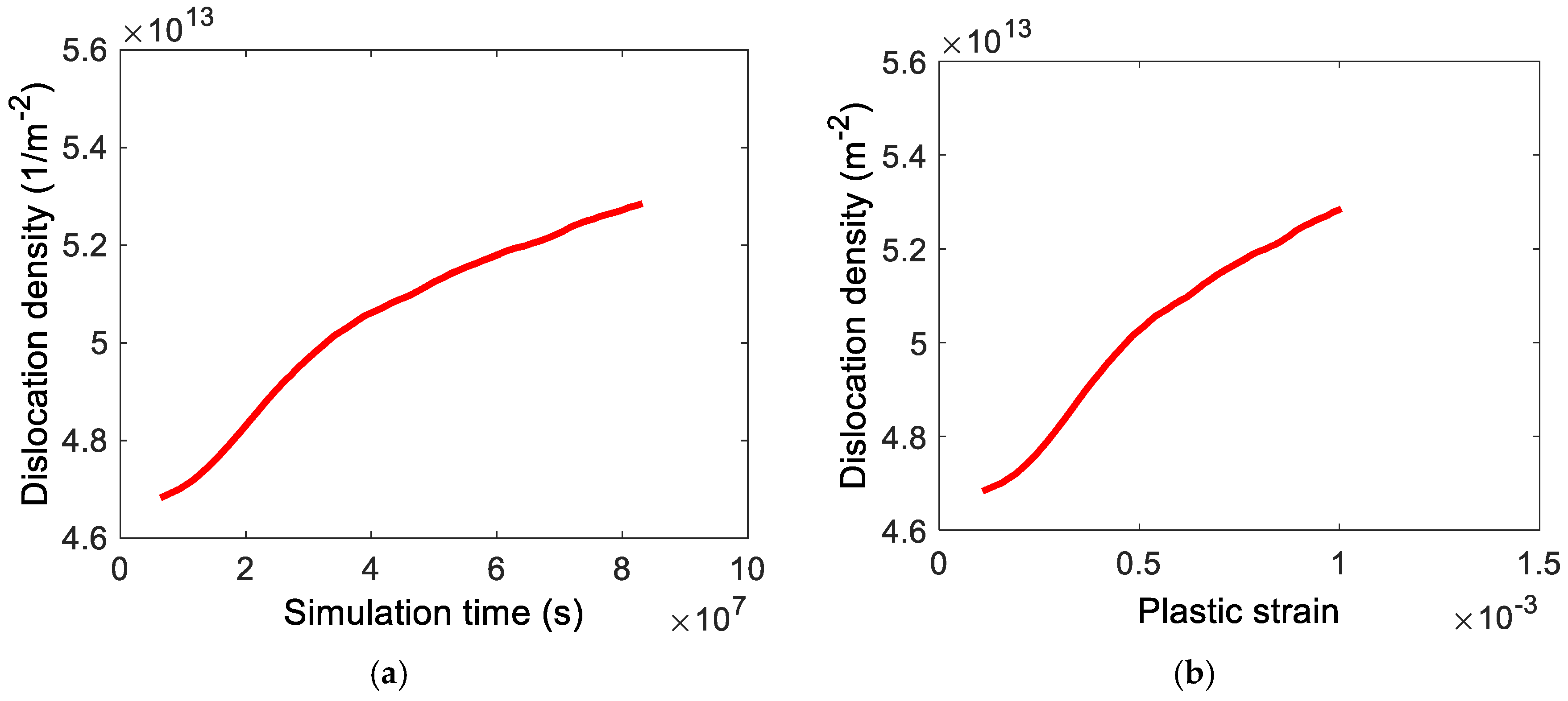
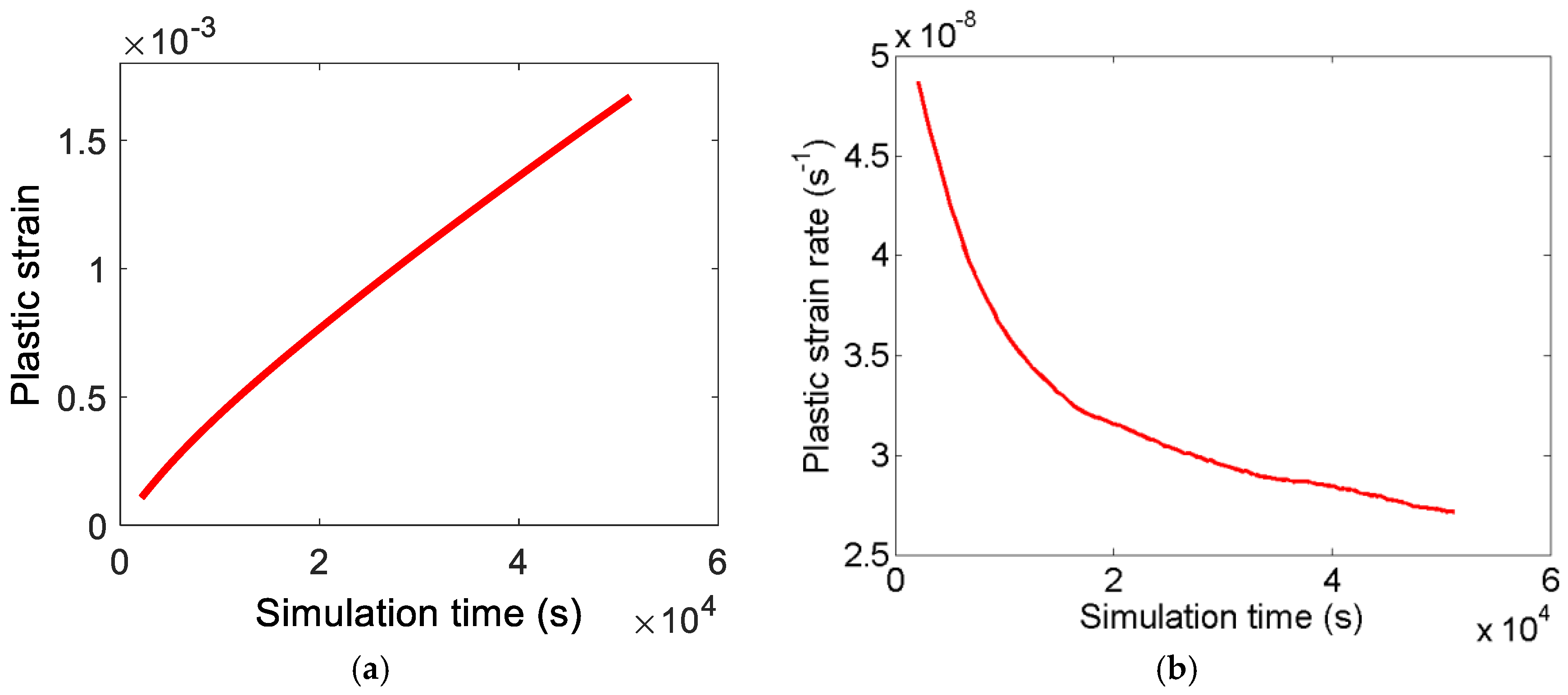
4.2. Dislocation Dynamics Simulation
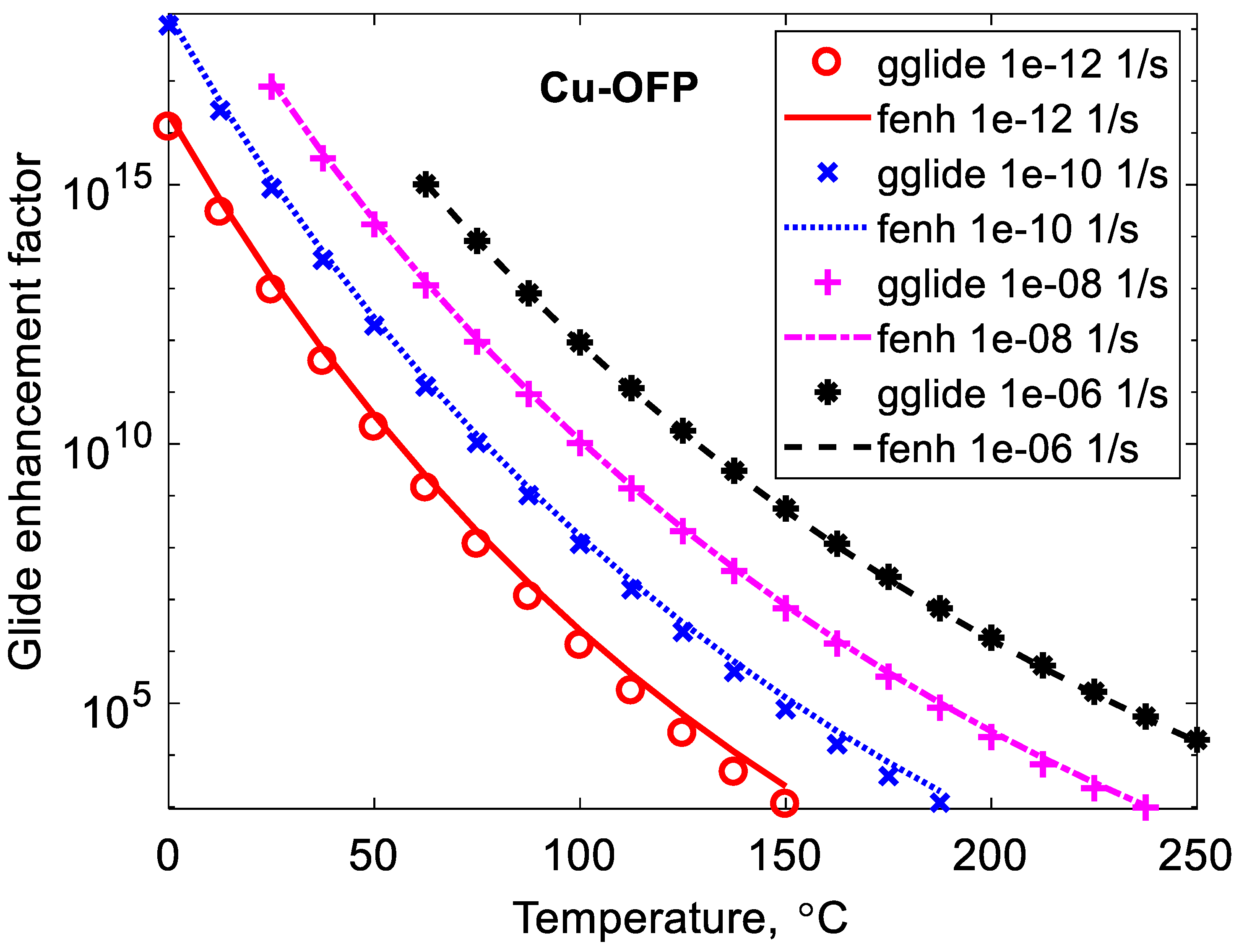
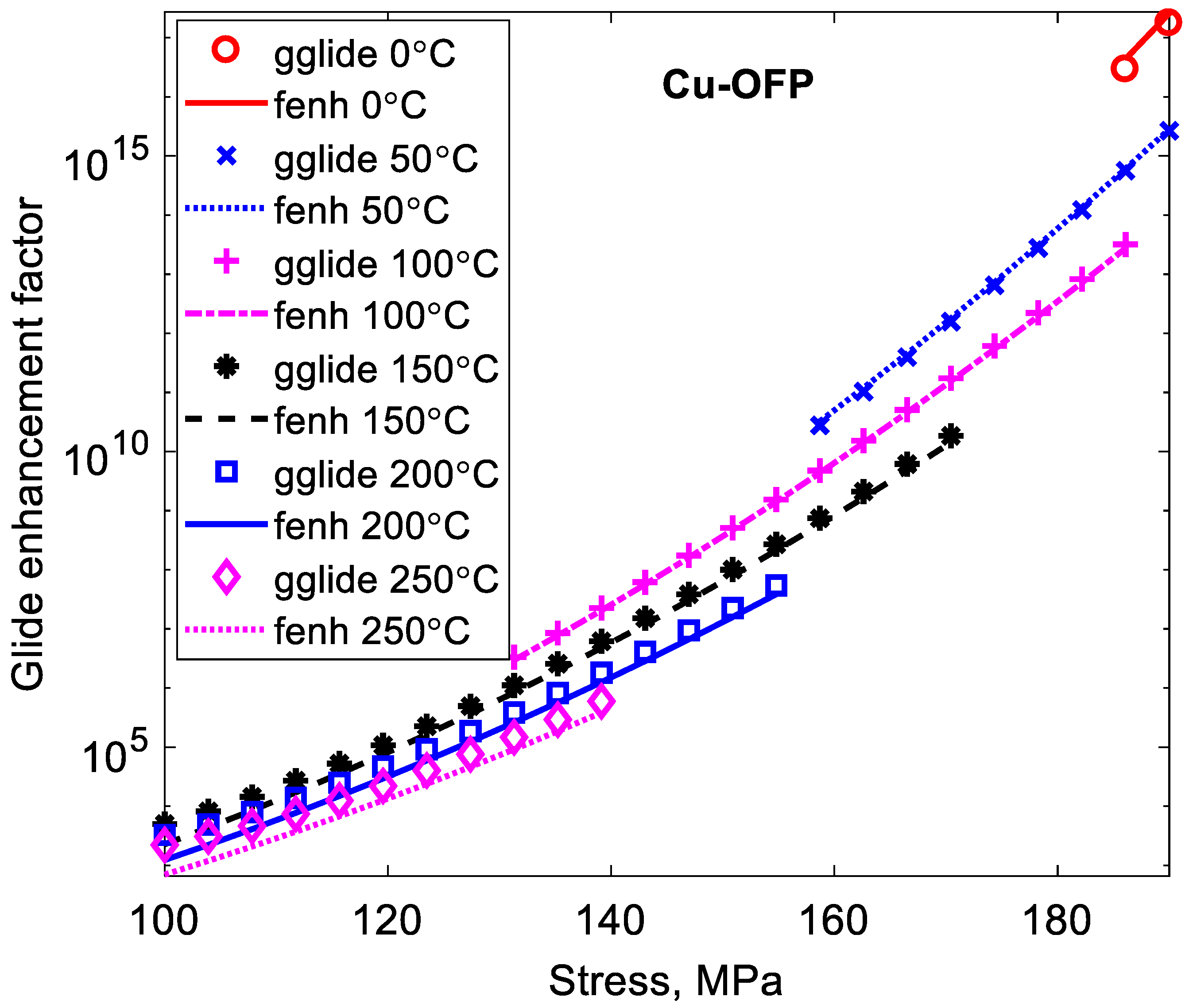
5. Evaluation of Effective Stresses
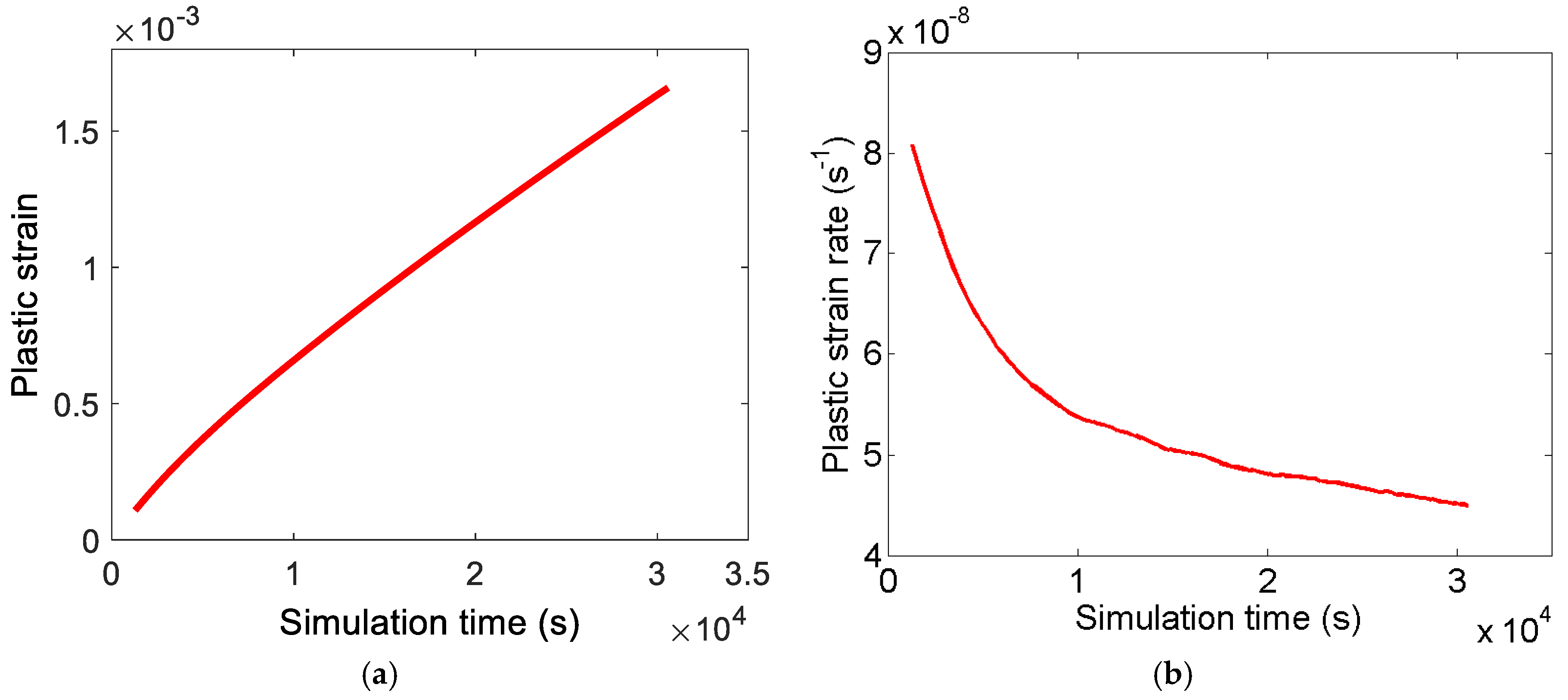
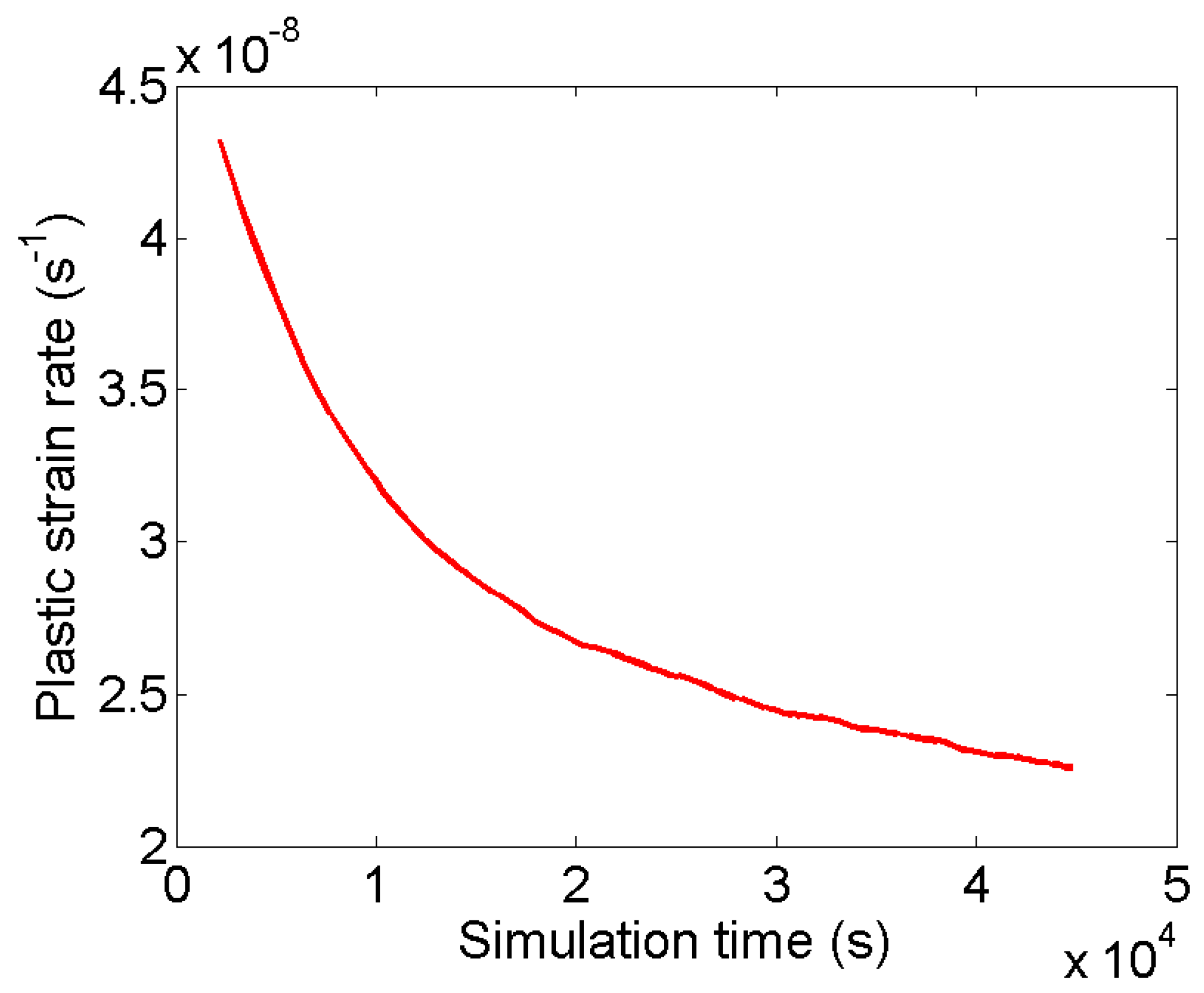
6. Effect of Change in the Applied Stress
7. Discussion
8. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Parameter Values Used in the Computations
| Parameter Description | Parameter | Value | Reference |
|---|---|---|---|
| Coefficient for self-diffusion | Ds0 | 1.31 × 10−5 m2/s | [37] |
| Activation energy for self-diffusion | Q | 198,000 J/mol | [37] |
| Burgers vector | b | 2.56 × 10−10 m | |
| Atomic volume | Ω0 | = 1.18× 10−29 m3 | |
| Lattice misfit for P atom | ε | 0.055 | [22] |
| Taylor factor | m | 3.06 | |
| Constant in Taylor’s equation describing the influence of dislocation density on the strength | α | (1 − ν/2)/2π(1 − ν) = 0.19 | [38,39] |
| Max back stress | σimax | 257 MPa | [1] |
| Dislocation line tension | τL | Gb2/2 = 7.94∙× 10−16 MN | |
| Subgrain stress constant | Ksub | 11 | [40] |
| Max interaction energy between P solute and dislocation | 8220 J/mol | [22] | |
| Boltzmann’s constant | kB | 1.381 × 10−23 J/grad | |
| Grain size | dgrain | 100 μm | [2] |
| Shear modulus | G | 45,400 × (1 − 7.1 × 10−4 × (T − 20)), MPa, T in °C | [41] |
| Yield strength | σy | 75 MPa for as hot worked in reference condition. For value at other temperatures and strain rates, see Ref. | [19] |
| Work hardening constant | cL | 28–31 | [19] |
References
- Sandstrom, R.; Andersson, H.C.M. Creep in phosphorus alloyed copper during power-law breakdown. J. Nucl. Mater. 2008, 372, 76–88. [Google Scholar] [CrossRef]
- Sandstrom, R. Basic model for primary and secondary creep in copper. Acta Mater. 2012, 60, 314–322. [Google Scholar] [CrossRef]
- Hirth, J.P.; Lothe, J. Theory of Dislocations; Krieger: Malabar, FL, USA, 1982. [Google Scholar]
- Blum, W.; Rosen, A.; Cegielska, A.; Martin, J.L. Two mechanisms of dislocation motion during creep. Acta Metall. 1989, 37, 2439–2453. [Google Scholar] [CrossRef]
- Kocks, U.F. A statistical theory of flow stress and work-hardening. Philos. Mag. 1966, 13, 541–566. [Google Scholar] [CrossRef]
- Lagneborg, R. Dislocation mechanisms in creep. Int. Metall. Rev. 1972, 17, 130–146. [Google Scholar]
- Sandström, R. The role of cell structure during creep of cold worked copper. Mater. Sci. Eng. A 2016, 674, 318–327. [Google Scholar] [CrossRef]
- Cottrell, A.H. Logarithmic and andrade creep. Philos. Mag. Lett. 1997, 75, 301–307. [Google Scholar] [CrossRef]
- Nabarro, F.R.N. The time constant of logarithmic creep and relaxation. Mater. Sci. Eng. A 2001, 309–310, 227–228. [Google Scholar] [CrossRef]
- Spigarelli, S.; Sandström, R. Basic creep modelling of aluminium. Mater. Sci. Eng. A 2018, 711, 343–349. [Google Scholar] [CrossRef]
- Sandström, R. Fundamental Modelling of Creep Properties. In Creep; Tanski, T., Zieliński, A., Eds.; inTech: London, UK, 2017. [Google Scholar]
- Biberger, M.; Gibeling, J.C. Analysis of creep transients in pure metals following stress changes. Acta Metall. Mater. 1995, 43, 3247–3260. [Google Scholar] [CrossRef]
- Chen, B.; Flewitt, P.E.J.; Cocks, A.C.F.; Smith, D.J. A review of the changes of internal state related to high temperature creep of polycrystalline metals and alloys. Int. Mater. Rev. 2015, 60, 1–29. [Google Scholar] [CrossRef]
- Ahlquist, C.N.; Nix, W.D. The measurement of internal stresses during creep of al and Al-Mg alloys. Acta Metall. 1971, 19, 373–385. [Google Scholar] [CrossRef]
- Cuddy, L.J. Internal stresses and structures developed during creep. Metall. Mater. Trans. B 1970, 1, 395–401. [Google Scholar] [CrossRef]
- Davies, P.W.; Williams, K.R. Cavity growth by grain-boundary sliding during creep of copper. Met. Sci. 1969, 3, 220–221. [Google Scholar] [CrossRef]
- Henderson, P.J.; Sandstrom, R. Low temperature creep ductility of OFHC copper. Mater. Sci. Eng. A 1998, 246, 143–150. [Google Scholar] [CrossRef]
- Sandström, R.; Wu, R. Influence of phosphorus on the creep ductility of copper. J. Nucl. Mater. 2013, 441, 364–371. [Google Scholar] [CrossRef]
- Sandström, R.; Hallgren, J. The role of creep in stress strain curves for copper. J. Nucl. Mater. 2012, 422, 51–57. [Google Scholar] [CrossRef]
- Sandström, R. Fundamental Models for Creep Properties of Steels and Copper. Trans. Indian Inst. Met. 2016, 69, 197–202. [Google Scholar] [CrossRef]
- Wu, R.; Sandström, R.; Jin, L.Z. Creep crack growth in phosphorus alloyed oxygen free copper. Mater. Sci. Eng. A 2013, 583, 151–160. [Google Scholar] [CrossRef]
- Sandstrom, R.; Andersson, H.C.M. The effect of phosphorus on creep in copper. J. Nucl. Mater. 2008, 372, 66–75. [Google Scholar] [CrossRef]
- Sandström, R. Influence of phosphorus on the tensile stress strain curves in copper. J. Nucl. Mater. 2016, 470, 290–296. [Google Scholar] [CrossRef]
- Korzhavyi, P.A.; Sandström, R. First-principles evaluation of the effect of alloying elements on the lattice parameter of a 23Cr25NiWCuCo austenitic stainless steel to model solid solution hardening contribution to the creep strength. Mater. Sci. Eng. A 2015, 626, 213–219. [Google Scholar] [CrossRef]
- Nes, E.; Marthinsen, K. Modeling the evolution in microstructure and properties during plastic deformation of f.c.c.-metals and alloys—An approach towards a unified model. Mater. Sci. Eng. A 2002, 322, 176–193. [Google Scholar] [CrossRef]
- Kocks, U.F.; Argon, A.S.; Ashby, M.F. Thermodynamics and kinetics of slip. Prog. Mater. Sci. 1975, 19, 291. [Google Scholar]
- Chandler, H.D. Effect of unloading time on interrupted creep in copper. Acta Metall. Mater. 1994, 42, 2083–2087. [Google Scholar] [CrossRef]
- Mecking, H.; Estrin, Y. The effect of vacancy generation on plastic deformation. Scr. Metall. 1980, 14, 815–819. [Google Scholar] [CrossRef]
- Sandström, R. The role of microstructure in the prediction of creep rupture of austenitic stainless steels. In Proceedings of the ECCC Creep & Fracture Conference, Düsseldorf, Germany, 10–14 September 2017. [Google Scholar]
- Arsenlis, A.; Cai, W.; Tang, M.; Rhee, M.; Oppelstrup, T.; Hommes, G. Enabling strain hardening simulations with dislocation dynamics. Model. Simul. Mater. Sci. Eng. 2007, 15, 553–595. [Google Scholar] [CrossRef]
- Haghighat, S.M.H.; Eggeler, G.; Raabe, D. Effect of climb on dislocation mechanisms and creep rates in γ′-strengthened Ni base superalloy single crystals: A discrete dislocation dynamics study. Acta Mater. 2013, 61, 3709–3723. [Google Scholar] [CrossRef]
- Delandar, A.H.; Haghighat, S.M.H.; Korzhavyi, P.; Sandström, R. Dislocation dynamics modeling of plastic deformation in single-crystal copper at high strain rates. Int. J. Mater. Res. 2016, 107, 988–995. [Google Scholar] [CrossRef]
- Bulatov, V.V.; Cai, W. Computer Simulations of Dislocations; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Matsuo, T.; Nakajima, K.; Terada, Y.; Kikuchi, M. High temperature creep resistance of austenitic heat-resisting steels. Mater. Sci. Eng. A 1991, 146, 261–272. [Google Scholar] [CrossRef]
- Hausselt, J.; Blum, W. Dynamic recovery during and after steady state deformation of Al-11wt%Zn. Acta Metall. 1976, 24, 1027–1039. [Google Scholar] [CrossRef]
- Magnusson, H.; Sandstrom, R. Creep strain modeling of 9 to 12 Pct Cr steels based on microstructure evolution. Metall. Mater. Trans. A 2007, 38, 2033–2039. [Google Scholar] [CrossRef]
- Neumann, G.; Tölle, V.; Tuijn, C. Monovacancies and divacancies in copper Reanalysis of experimental data. Phys. B Condens. Matter 1999, 271, 21–27. [Google Scholar] [CrossRef]
- Horiuchi, R.; Otsuka, M. Mechanism of high temperature creep of aluminum-magnesium solid solution alloys. Trans. Jpn. Inst. Met. 1972, 13, 284–293. [Google Scholar] [CrossRef]
- Orlová, A. On the relation between dislocation structure and internal stress measured in pure metals and single phase alloys in high temperature creep. Acta Metall. Mater. 1991, 39, 2805–2813. [Google Scholar] [CrossRef]
- Wu, R.; Pettersson, N.; Martinsson, Å.; Sandström, R. Cell structure in cold worked and creep deformed phosphorus alloyed copper. Mater. Charact. 2014, 90, 21–30. [Google Scholar] [CrossRef]
- Ledbetter, H.M.; Naimon, E.R. Elastic Properties of Metals and Alloys. II. Copper. J. Phys. Chem. Ref. Data 1974, 3, 897–935. [Google Scholar] [CrossRef]


| Mglide (Pa·s)−1 | Three Stages of Deformation | |||
|---|---|---|---|---|
| 2.89 × 10−13 | Early | 1.22 × 105 | −0.92 × 105 | 0.81 × 105 |
| Intermediate | 0.09 × 105 | −1.96 × 105 | 0.89 × 105 | |
| Final | −0.61 × 105 | −1.58 × 105 | 0.54 × 105 | |
| 8.67 × 10−10 | Early | 1.29 × 105 | −1.12 × 105 | 1.01 × 105 |
| Intermediate | −0.86 × 105 | −0.71 × 105 | 0.81 × 105 | |
| Final | −0.82 × 105 | −1.45 × 105 | −2.39 × 105 | |
| 1.44 × 10−9 | Early | 1.32 × 105 | −1.15 × 105 | 0.85 × 105 |
| Intermediate | 0.40 × 105 | −0.71 × 105 | −0.41 × 105 | |
| Final | −1.06 × 105 | −0.61 × 105 | −1.42 × 105 |
| Mglide (Pa·s)−1 | Illustrated Points | |||
|---|---|---|---|---|
| 8.67 × 10−10 | 1 | −0.86 × 105 | −0.71 × 105 | −0.81 × 105 |
| 2 | −0.39 × 105 | −0.92 × 105 | −0.33 × 105 | |
| 3 | −1.06 × 105 | −0.72 × 105 | −1.84 × 105 | |
| 1.44 × 10−9 | 1 | −1.57 × 105 | −1.15 × 105 | −1.47 × 105 |
| 2 | −0.73 × 105 | −0.75 × 105 | −0.54 × 105 | |
| 3 | −1.18 × 105 | −0.96 × 105 | −1.95 × 105 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosseinzadeh Delandar, A.; Sandström, R.; Korzhavyi, P. The Role of Glide during Creep of Copper at Low Temperatures. Metals 2018, 8, 772. https://doi.org/10.3390/met8100772
Hosseinzadeh Delandar A, Sandström R, Korzhavyi P. The Role of Glide during Creep of Copper at Low Temperatures. Metals. 2018; 8(10):772. https://doi.org/10.3390/met8100772
Chicago/Turabian StyleHosseinzadeh Delandar, Arash, Rolf Sandström, and Pavel Korzhavyi. 2018. "The Role of Glide during Creep of Copper at Low Temperatures" Metals 8, no. 10: 772. https://doi.org/10.3390/met8100772
APA StyleHosseinzadeh Delandar, A., Sandström, R., & Korzhavyi, P. (2018). The Role of Glide during Creep of Copper at Low Temperatures. Metals, 8(10), 772. https://doi.org/10.3390/met8100772






