Quadratic Midpoint Integration Method for J2 Metal Plasticity
Abstract
:1. Introduction
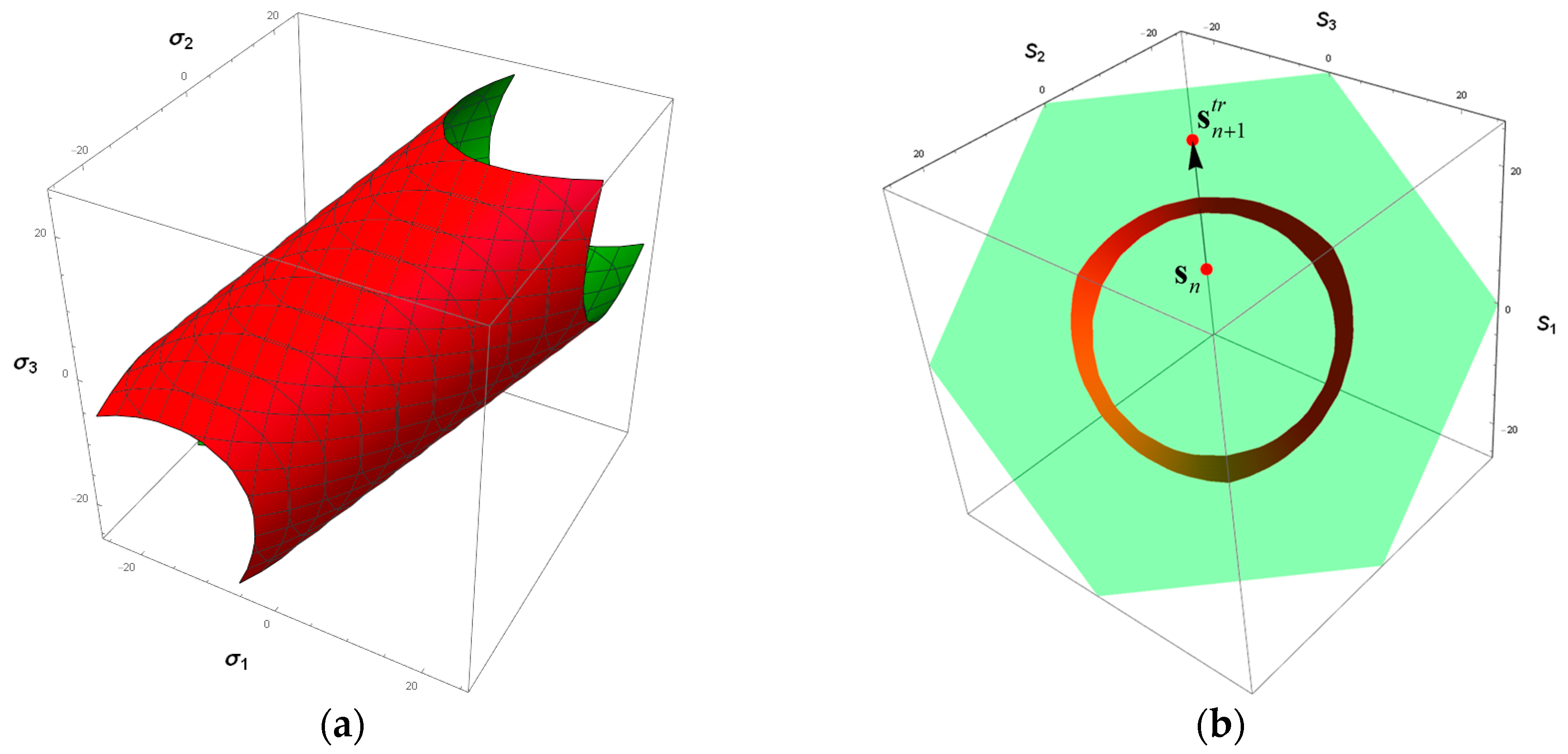
2. J2 Metal Plasticity
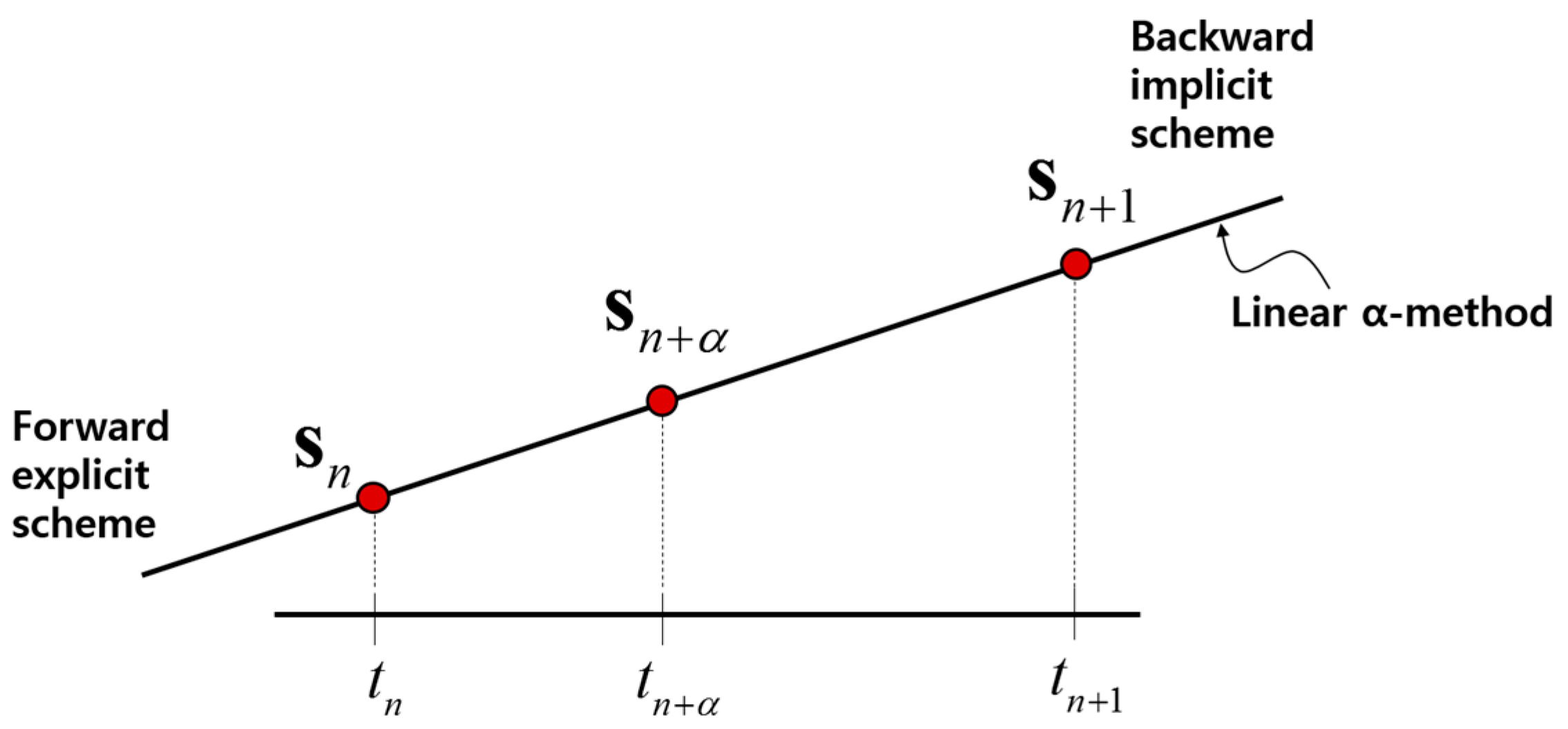
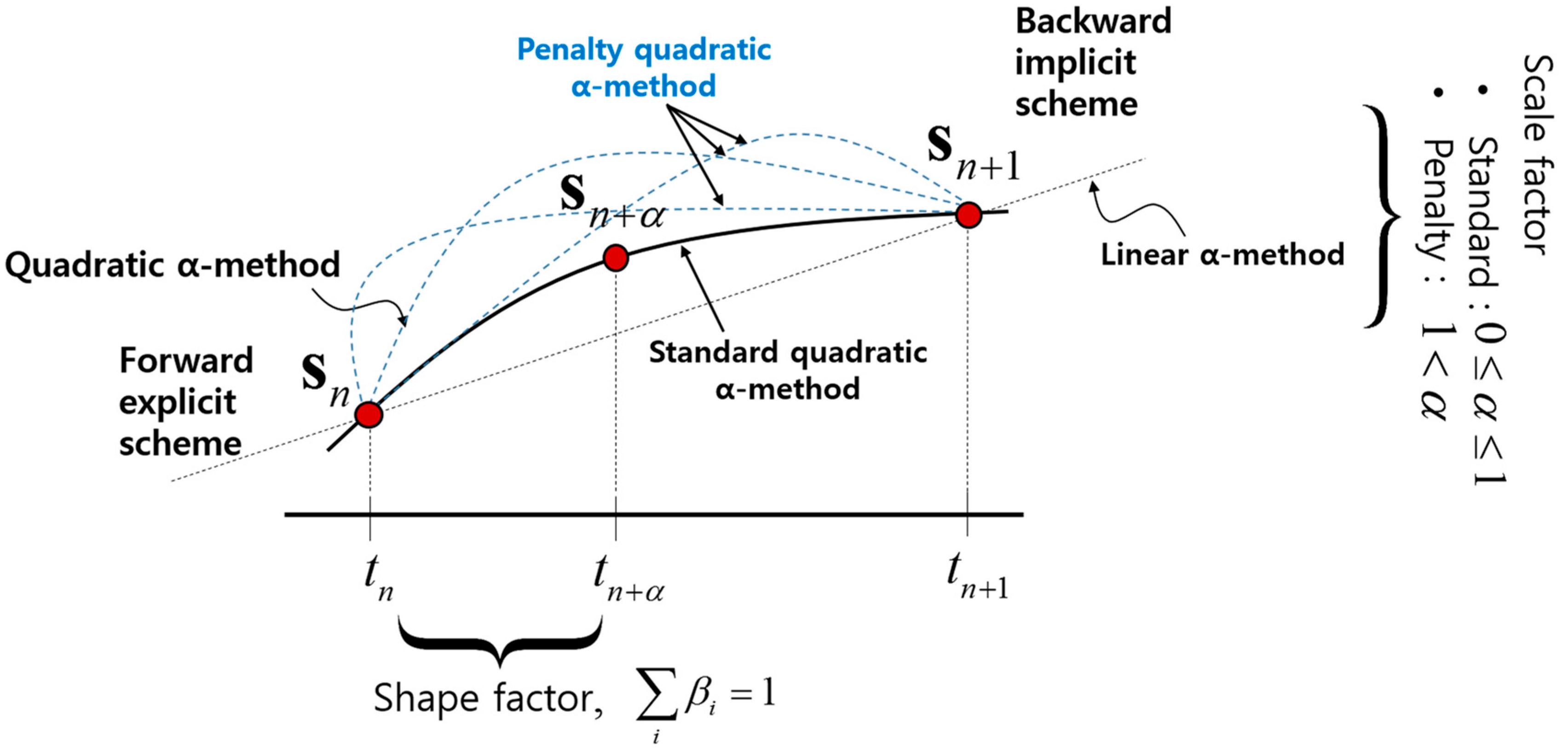
3. J2 Metal Plasticity with Linear α Method
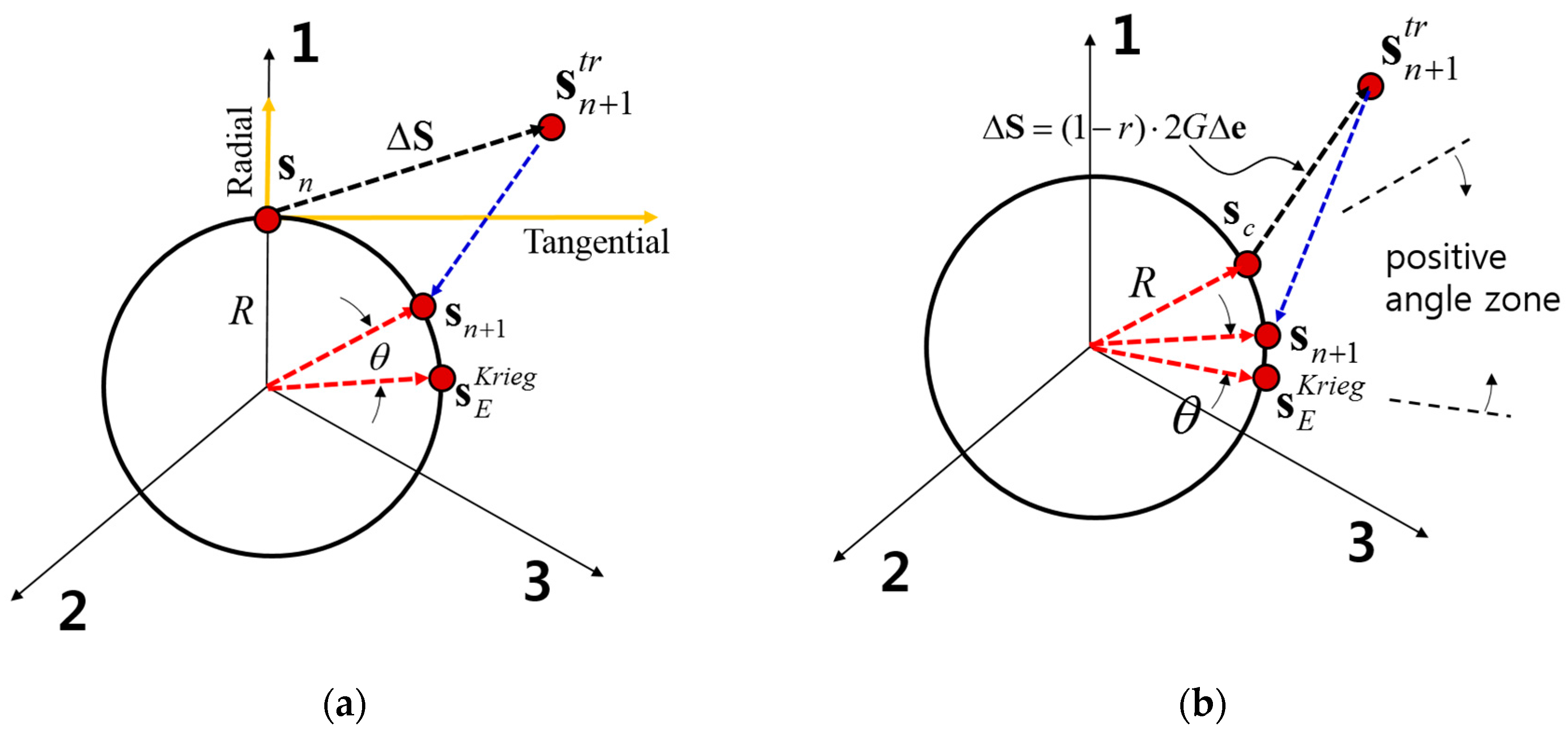
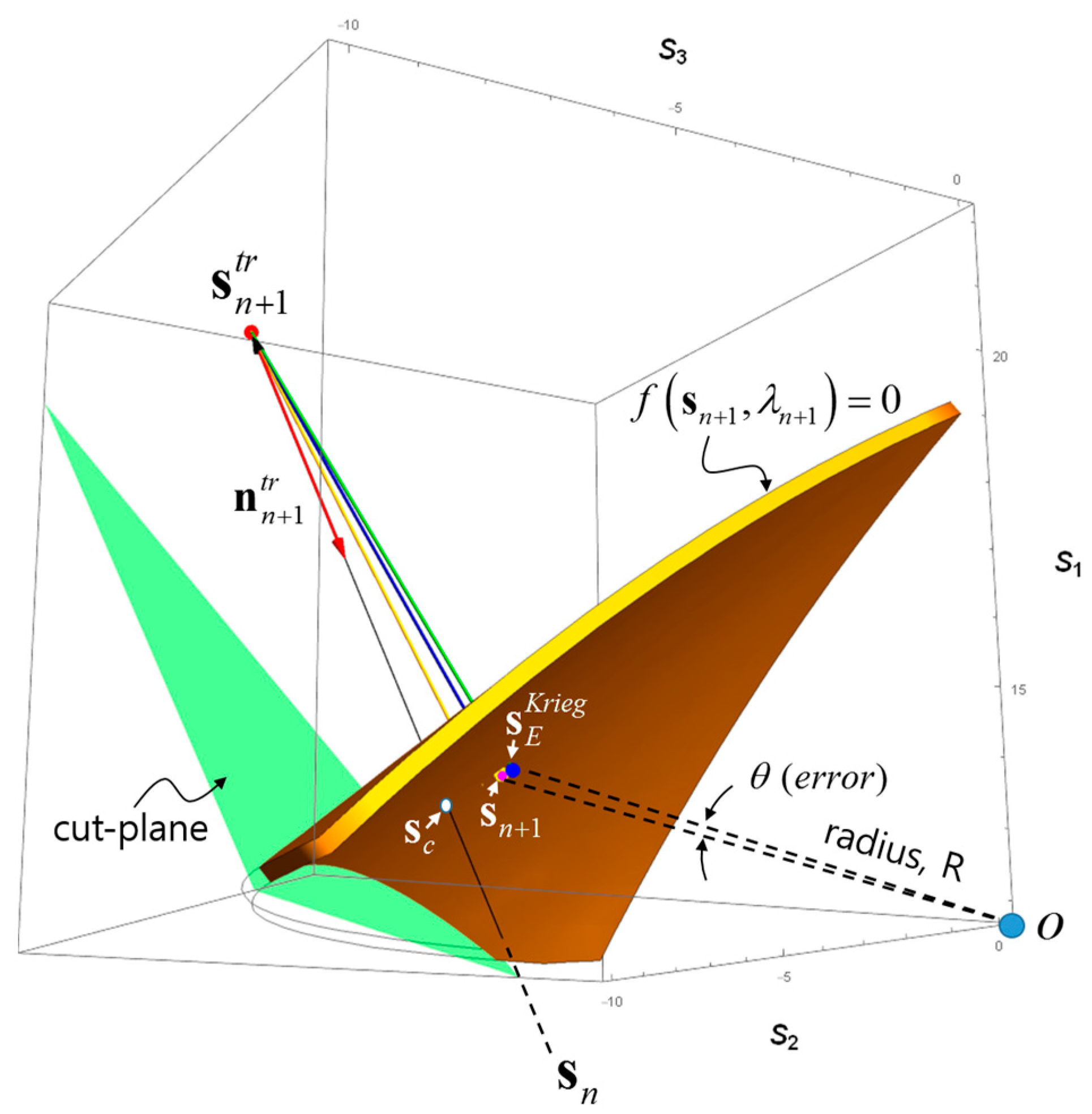
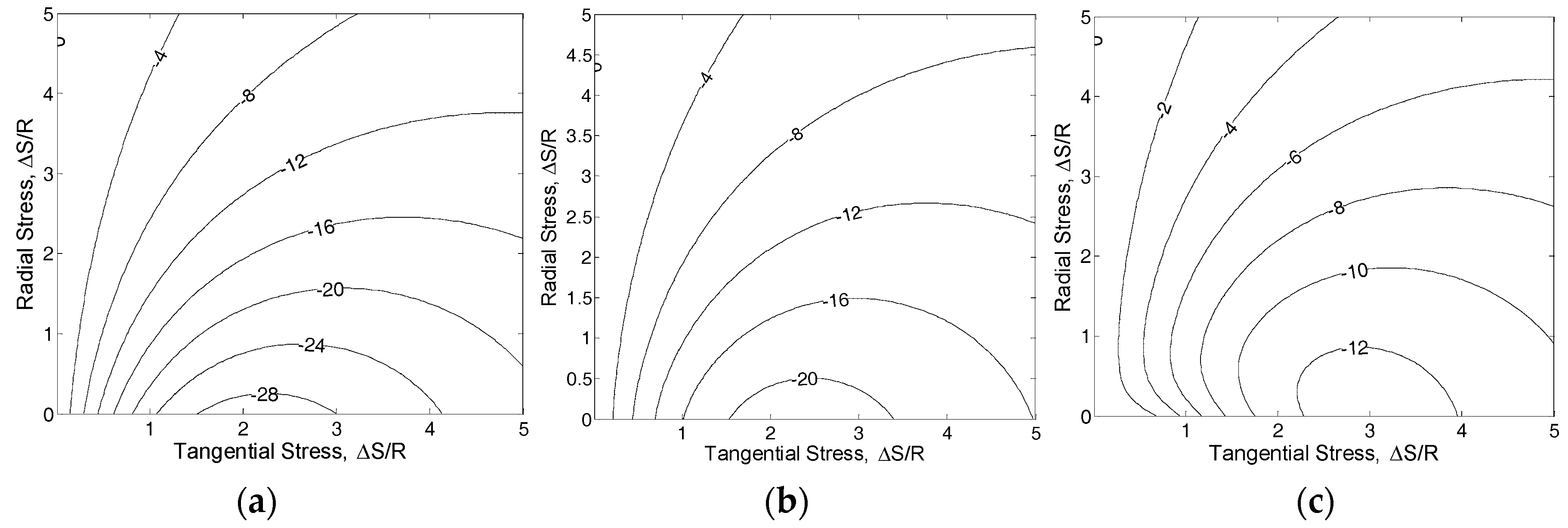
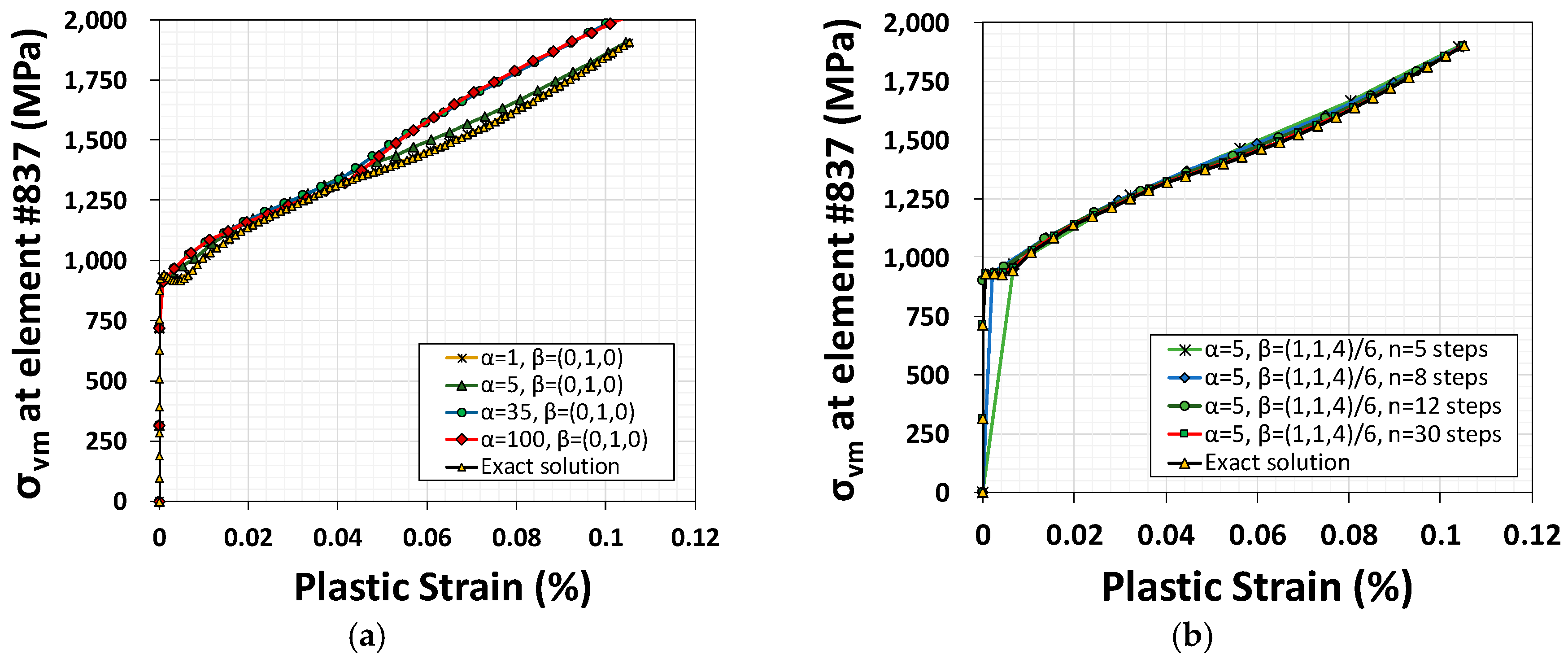
4. Accuracy of Quadratic Midpoint Integration Method
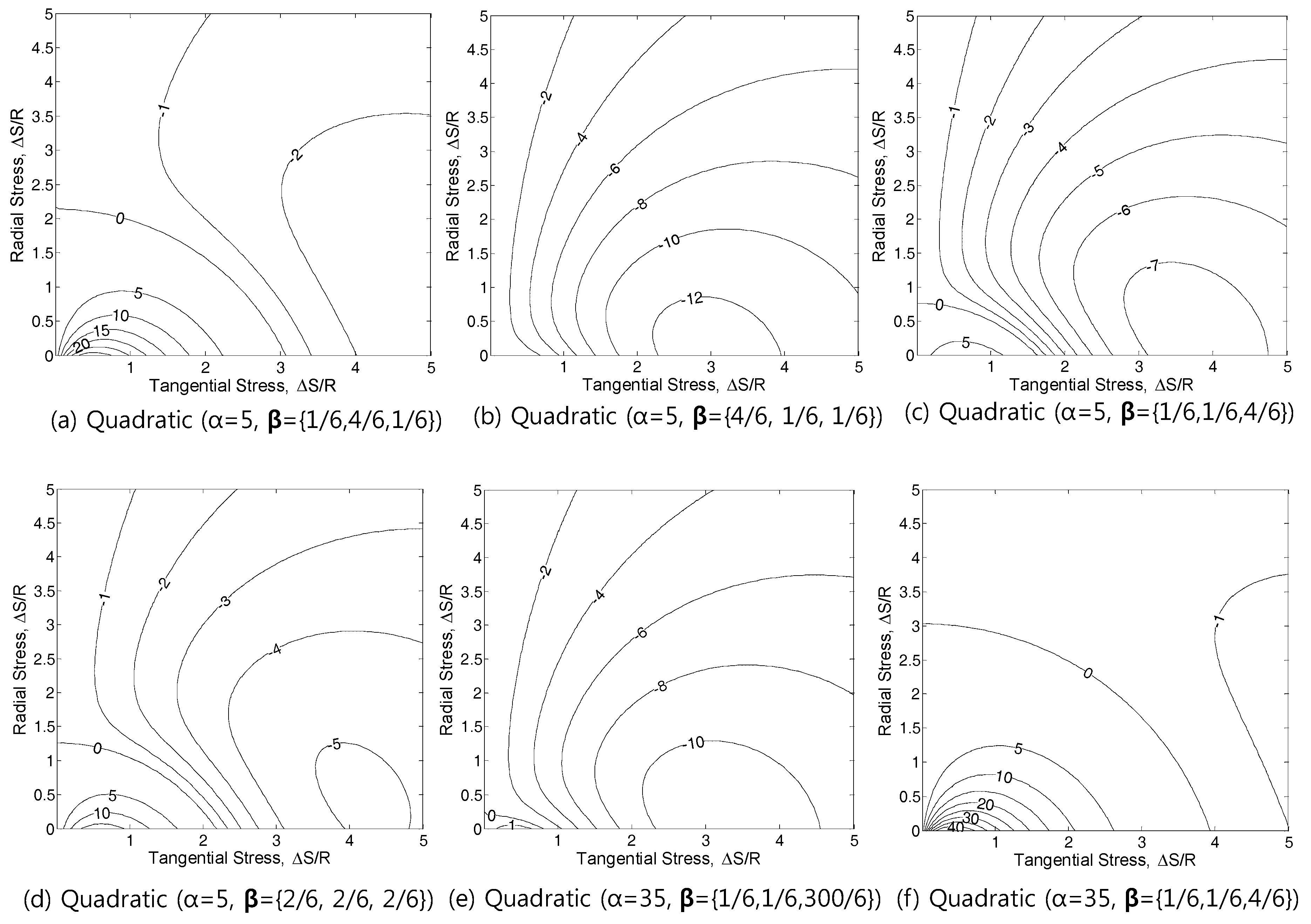
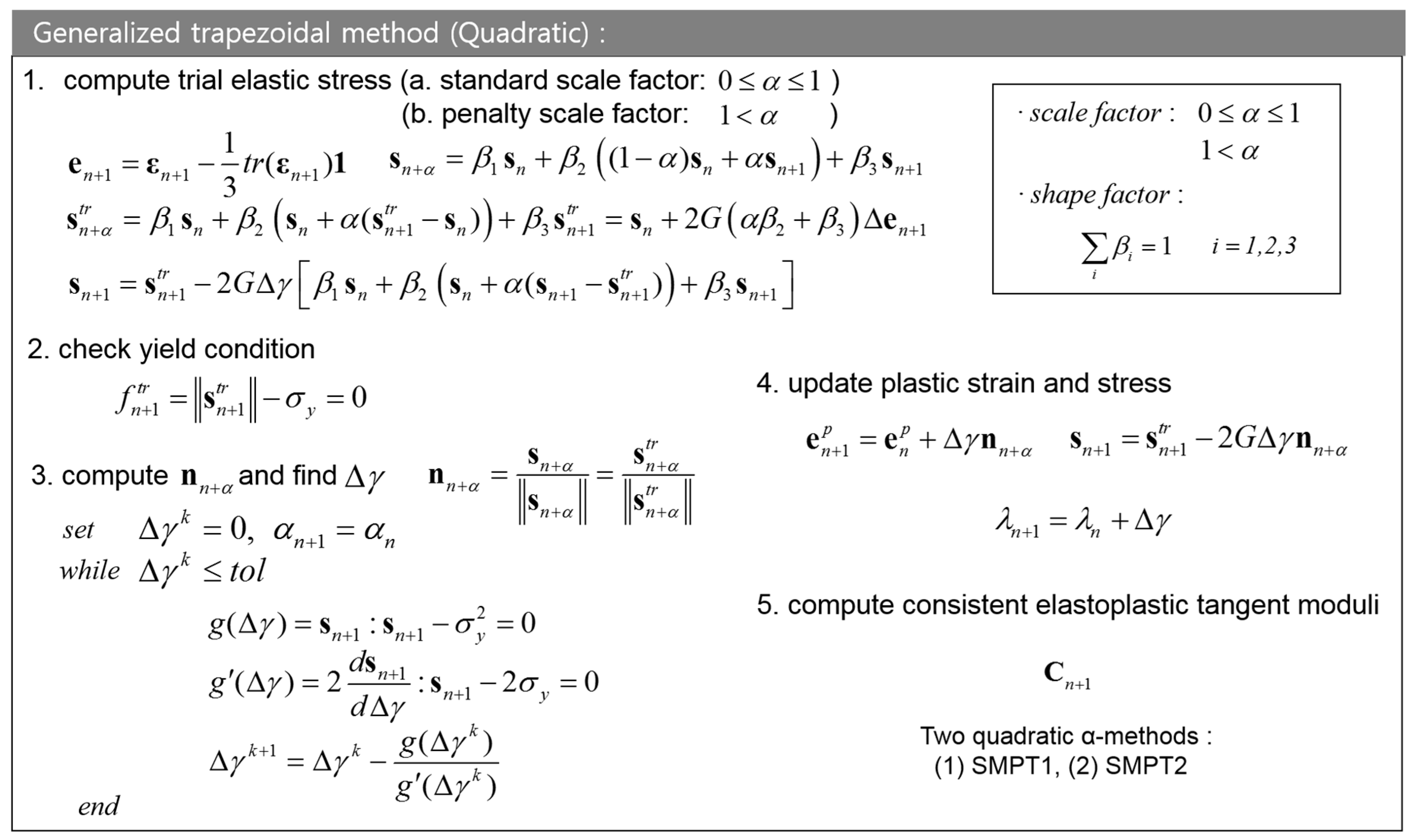
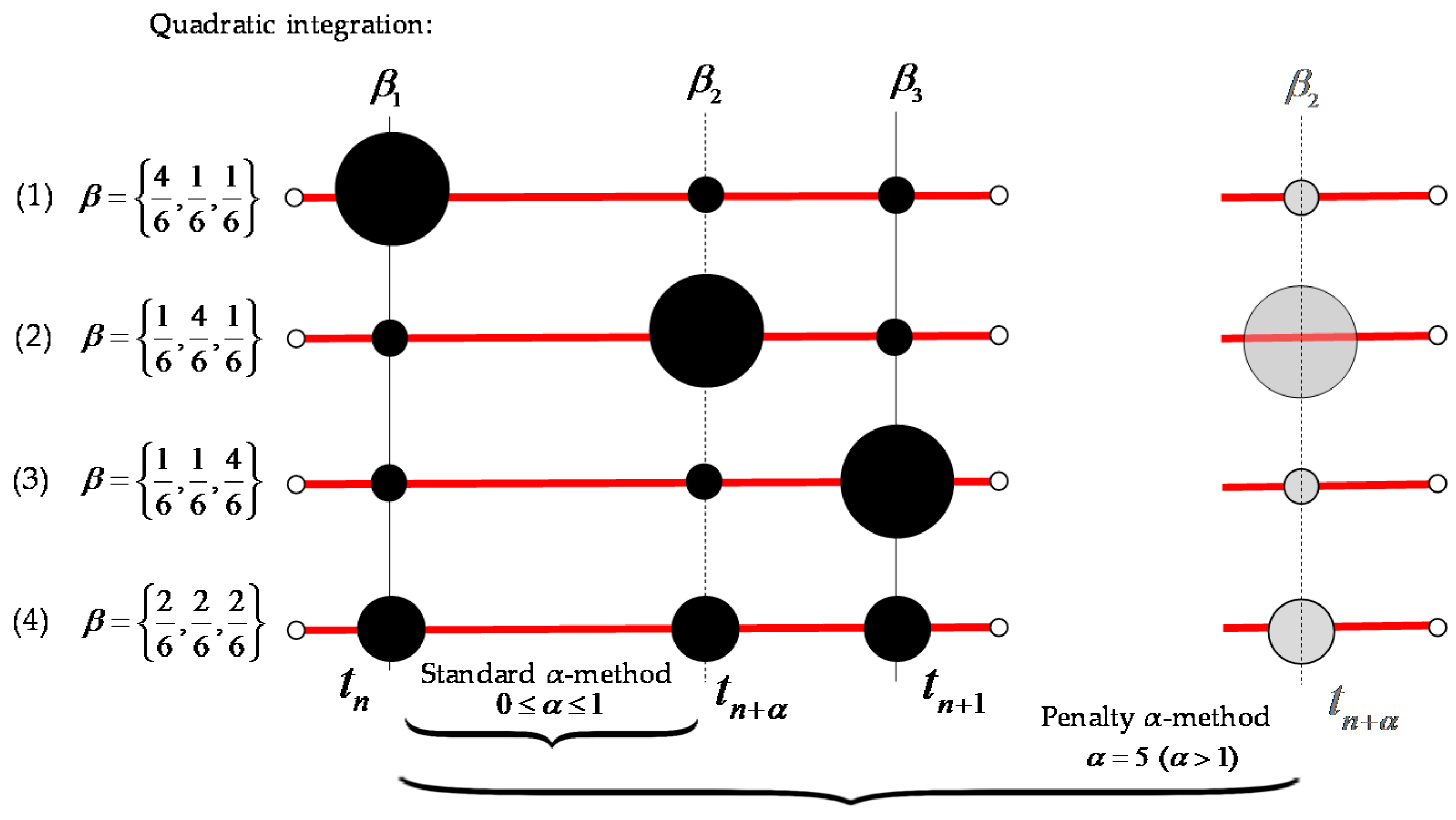
5. Implementation for Quadratic α Method
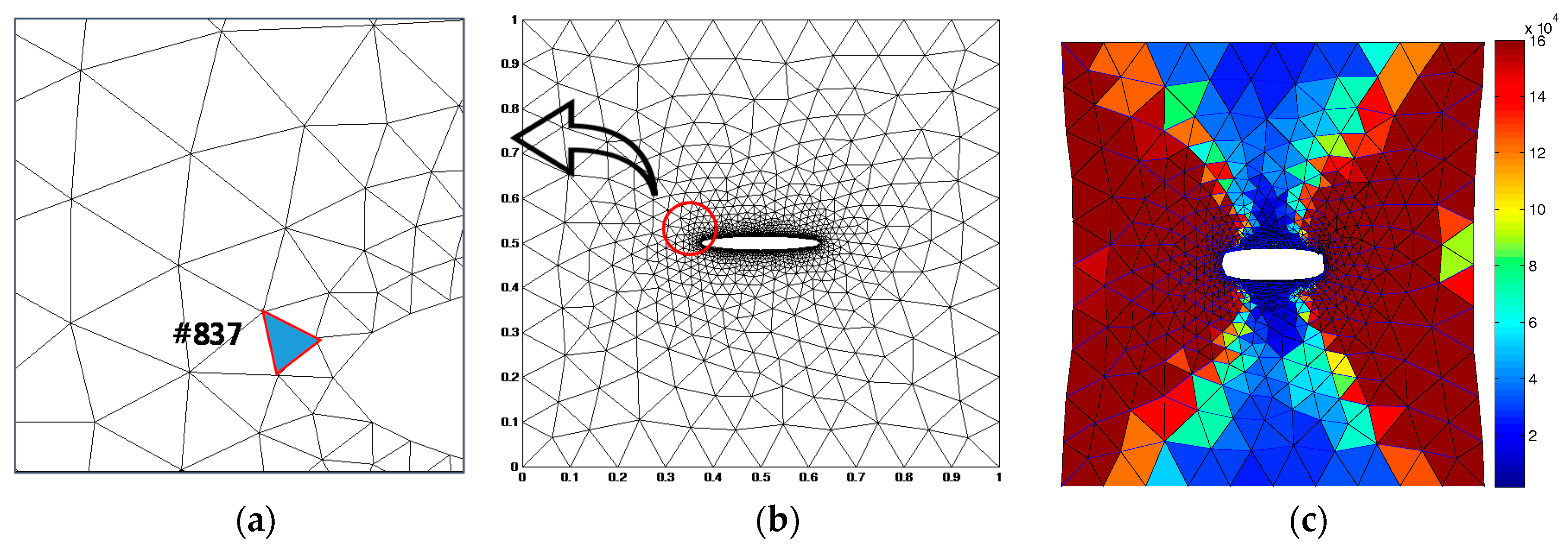
6. 2D Metal Panel Problem with Slit-Like Defect
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rice, J.R.; Tracey, D.M. Computational fracture mechanics. In Numerical and Computer Methods in Structural Mechanics; Academic Press, Inc.: New York, NY, USA, 1973; pp. 585–623. [Google Scholar]
- Krieg, R.D.; Krieg, D.B. Accuracies of numerical solution methods for the elastic-perfectly plastic model. Trans. ASME 1977, 99, 510–515. [Google Scholar] [CrossRef]
- Ortiz, M.; Popov, E.P. Accuracy and stability of integration algorithms for elastoplastic constitutive relations. Int. J. Numer. Methods Eng. 1985, 21, 1561–1576. [Google Scholar] [CrossRef]
- Simo, J.C.; Taylor, R.L. A return mapping algorithm for plane stress elastoplasticity. Int. J. Numer. Methods Eng. 1986, 22, 649–670. [Google Scholar] [CrossRef]
- Simo, J.C.; Hughes, T.J.R. Computational Inelasticity; Springer: Berlin, Germany, 1998; pp. 1–392. ISBN 0-387-97520-9. [Google Scholar]
- Willam, K.J. Computational Mechanics of Solids and Structures (Class Note); University of Colorado: Boulder, CO, USA, 2002. [Google Scholar]
- Shim, H. Higher-order α-method in computational plasticity. KSCE J. Civ. Eng. 2005, 9, 255–259. [Google Scholar] [CrossRef]
- Artioli, E.; Auricchio, F.; Beirão da Veiga, L. Generalized midpoint integration algorithms for J2 plasticity with linear hardening. Int. J. Numer. Methods Eng. 2007, 72, 422–463. [Google Scholar] [CrossRef]
- Jahanshahi, M. Second order integration algorithms for J2 plasticity with generalized isotropic/kinematic hardening. Asian J. Civ. Eng. 2012, 13, 203–232. [Google Scholar]
- Tresca, H. Mémoire sur l’écoulement des corps solides soumis à de fortes pressions. C. R. Hebd. Séances Acad. Sci. 1864, 59, 754–758. [Google Scholar]
- Von Mises, R. Mechanik der festen Körper im plastisch-deformablen Zustand, Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen. Math.-Phys. Kl. 1913, 1, 582–592. [Google Scholar]
- Boerja, R.I. Plasticity: Modeling & Computation; Springer: Berlin, Germany, 2013; pp. 31–40. [Google Scholar]
- Ballani, J. Three Solution Methods for Perfect Plasticity. 2008. Available online: http://m2matlabdb.ma.tum.de (accessed on 1 August 2017).
- Persson, P.-O.; Strang, G. A simple mesh generator in Matlab. SIAM Rev. 2004, 46, 329–345. [Google Scholar] [CrossRef]


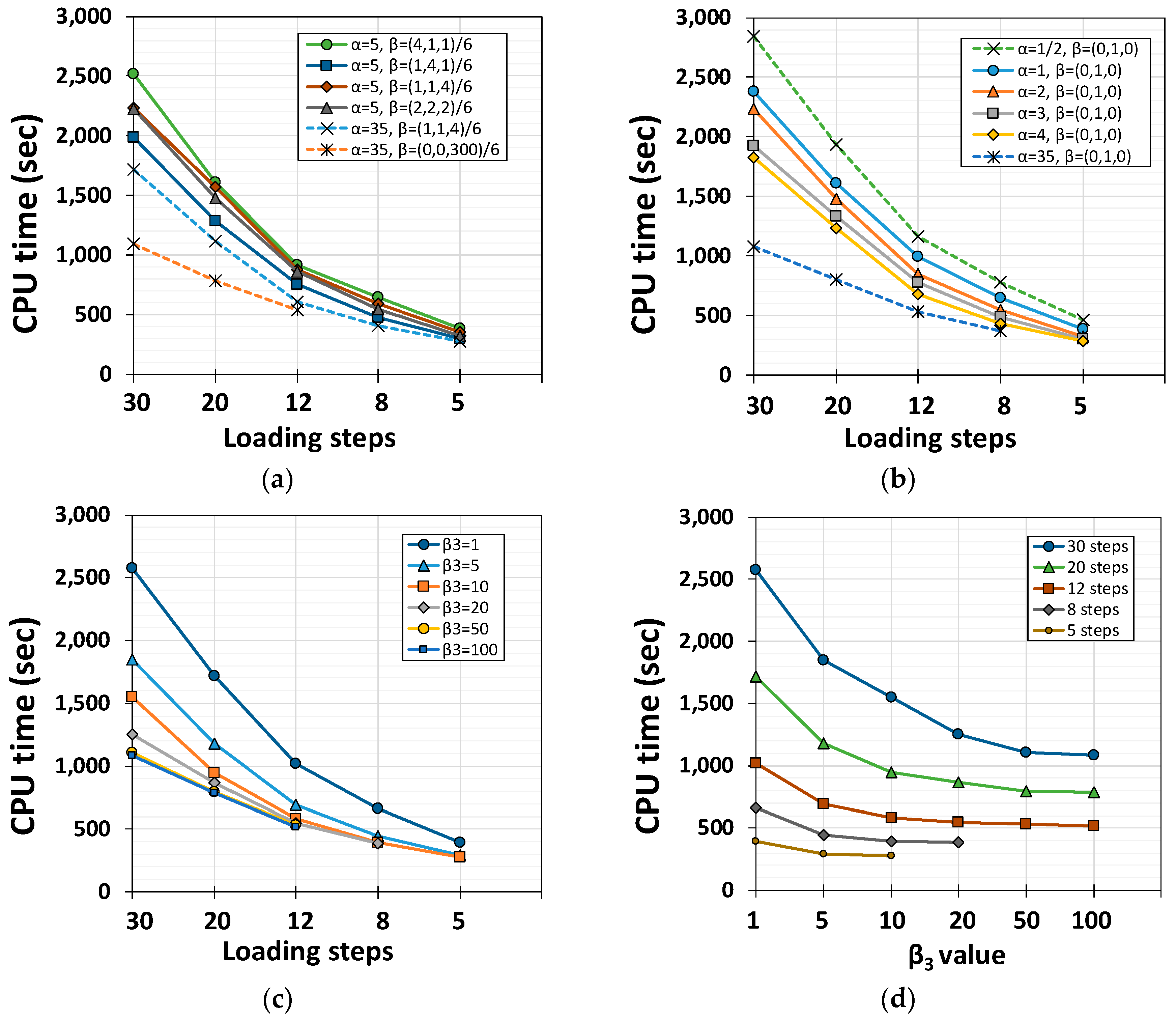
| Time Integration Schemes | 30 Steps | 12 Steps | 8 Steps | 5 Steps | ||
|---|---|---|---|---|---|---|
| Quadratic -SMPT1 | All | 2578.4 | 1019.6 | 660.8 | 392.1 | |
| 2377.6 | 998.3 | 648.2 | 385.4 | |||
| 2235.1 | 846.8 | 549.3 | 323.2 | |||
| 1925.9 | 781.5 | 488.2 | 305.3 | |||
| 1823.1 | 678.5 | 436.0 | 285.0 | |||
| 1533.0 | 575.7 | diverged 1 | 263.1 | |||
| 1082.1 | 530.3 | 367.3 | diverged 1 | |||
| 1984.4 | 754.3 | 479.4 | 303.2 | |||
| 2521.9 | 918.4 | 651.5 | 387.0 | |||
| 2234.2 | 878.9 | 591.2 | 358.3 | |||
| 2228.9 | 860.5 | 549.2 | 326.4 | |||
| 1717.3 | 606.0 | 411.4 | 276.7 | |||
| 1092.7 | 542.3 | diverged 1 | diverged 1 | |||
| Quadratic -SMPT2 | 2523.1 | 992.8 | 640.3 | 378.1 | ||
| 2256.8 | 868.4 | 552.4 | 319.2 | |||
| 2055.7 | 753.2 | 486.2 | 303.0 | |||
| 1833.7 | 682.1 | 422.1 | 266.7 | |||
| 1541.8 | 543.1 | diverged 1 | diverged 1 | |||
| 1137.9 | diverged 1 | diverged 1 | diverged 1 | |||
| 2011.6 | 693.8 | 476.6 | 297.4 | |||
| 2540.2 | 990.2 | 638.5 | 378.7 | |||
| 2206.7 | 884.0 | 594.2 | 352.0 | |||
| 2285.7 | 858.0 | 552.0 | 319.2 | |||
| 1728.6 | 610.4 | diverged 1 | 270.4 | |||
| diverged 1 | diverged 1 | diverged 1 | diverged 1 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rhee, I.; Kim, W. Quadratic Midpoint Integration Method for J2 Metal Plasticity. Metals 2018, 8, 66. https://doi.org/10.3390/met8010066
Rhee I, Kim W. Quadratic Midpoint Integration Method for J2 Metal Plasticity. Metals. 2018; 8(1):66. https://doi.org/10.3390/met8010066
Chicago/Turabian StyleRhee, Inkyu, and Woo Kim. 2018. "Quadratic Midpoint Integration Method for J2 Metal Plasticity" Metals 8, no. 1: 66. https://doi.org/10.3390/met8010066
APA StyleRhee, I., & Kim, W. (2018). Quadratic Midpoint Integration Method for J2 Metal Plasticity. Metals, 8(1), 66. https://doi.org/10.3390/met8010066





