Abstract
The paper deals with a theoretical and experimental study of the relationship between the microstructural parameters, mechanical properties, and impact deformation and fracture of steels using the example of 17Mn1Si pipe steel. A model for the behavior of a polycrystalline grain conglomerate under impact loading at different temperatures was proposed within a cellular automata framework. It was shown that the intensity of dissipation processes explicitly depends on temperature and these processes play an important role in stress relaxation at the boundaries of structural elements. The Experimental study reveals the relationship between pendulum impact test temperature and the deformation/fracture energy of the steel. The impact toughness was shown to decrease almost linearly with the decreasing test temperature, which agrees with the fractographic analysis data confirming the increase in the fraction of brittle fracture in this case. It was shown with the aid of the proposed model and numerical simulations that the use of the excitable cellular automata method and an explicit account of test temperature through the possibility of energy release at internal interfaces help to explain the experimentally observed features of impact failure at different temperatures.
1. Introduction
The study of the deformation behavior of structurally heterogeneous materials within the physical mesomechanics framework [1] involves the formulation of hierarchical models that take into account the relationship between different-scale processes. Of particular importance is the study of the local material response at the mesoscale level where stresses and strains are distributed very inhomogeneously. This is stress/strain heterogeneity is caused by a large number of interface/grain boundaries as well as by specific heterogeneous nucleation and storage of deformation defects [2,3,4,5,6,7,8]. Structural heterogeneities serve as preferred sites for plastic flow initiation, generation of lattice and boundary defects and discontinuities of various types [9,10,11]. A pre-defined structural level of deformation is associated naturally with a free surface where deformation takes place first [12,13,14,15,16]. The nonlinearity of the deformation processes can be taken into account by considering an independent 2D subsystem (surface layer and internal interfaces) and a 3D crystalline subsystem (grain interior).
Structural steel 17Mn1Si is widely used in oil and gas pipelines. Its microstructure and properties have been studied and documented in detail [17]. The steel has relatively low tensile strength which is paired with high ductility and fracture toughness according to in-filed pneumatic test results. Besides, it shows high resistance to structural and mechanical degradation during long-term operation [18,19]. Tensile stress-strain curves of this steel do not always exhibit a yield plateau. Instead, rapid strain hardening is observed on early stages of deformation, which leads to partial ductility exhaustion in individual regions or in grain conglomerates, thus causing a trend to strain localization. Physical reasons for strain instabilities based on dislocation kinetics have been re-considered recently in [20,21].
Owing to the microstructural inhomogeneity on a meso-scale, the reliability of the pipeline as an engineering structure under service conditions is likely determined by the “weakest link” in the microstructure and not by the integral properties of steel [22,23].
Although the results of the present work on the deformation and fracture of the specific steel 17Mn1Si cannot be directly extended to all pipe steels used in oil and gas pipeline industry, the common property for all these steels is high fracture toughness (or the ability to resist ductile crack initiation and growth). The fracture toughness is determined by the amount of the work of plastic deformation in the fracture zone, which depends on the type of the microstructure formed during thermomechanical processing of the initial hot-rolled sheet [24,25,26]. Unlike other steels, the pipeline steels have a well-defined ratio of strength, ductility and fracture toughness, which is specified by the thermomechanical processing scheme [27,28,29]. The simulation results of this study were verified for 17Mn1Si pipe steel because of its widespread use. Nevertheless, the proposed approach and model assumptions can be extended with certain restrictions to other pipe steels.
It is known that the ductility and fracture toughness of pipe steels is determined by the microstructure, which is first of all characterized by the distribution of phases and grain sizes. In the case of mixed or brittle fracture, first microcracks appear most commonly at grain boundaries. It is therefore very important to optimize the grain sizes and analyze the mechanical behavior of grains under dynamic loads. Based on pneumatic test results, it was found that the high fracture toughness (or the ability to terminate a prolonged ductile crack) is governed by the volume and intensity of plastic deformation in front of the growing crack [27,28,29]. At the stage of stable ductile crack growth, the volume of plastically deformed metal in front of the crack tip depends on the dimensions of structural elements of the material. The larger is the metal volume at the growing crack tip, which is involved in plastic deformation resistance, the higher the fracture energy is and the shorter the fracture length is in a real oil or gas pipeline. In laboratory conditions, these characteristics are usually evaluated in the first approximation based on impact toughness [23,28,29].
Another essential aspect of the formulated problem is to find the relationship between the impact toughness and the grain size as has been proposed, for example, in [30] for ferrite-pearlite steels. Although important, this issue is beyond the scope of the present paper and will be addressed in forthcoming publications. There is also a technology factor associated with the fact that the mechanical properties and the deformation behavior of pipe steels are determined, in addition to grain size, by the quantitative ratio of ferrite and pearlite phases, their dimensions, the presence, size and type of non-metallic inclusions, grain shape, crystallographic texture, etc. Considering materials science aspects based on the microstructure and properties relationships, it would be ideal to take all the above structural factors into explicit consideration, which is an extremely challenging task (see, for example, Ref. [31], where it was shown that the grain size reduction did not always result in the impact toughness increase). Therefore, these microstructural factors are not considered in the present first approximation work because our major objective is to formulate a constitutive deformation behavior model, which can be then potentially extended to account for the mentioned microstructural features.
A large number of studies have been devoted to understanding of phenomenology and microscopic mechanisms of plastic deformation at the grain scale or at the scale of grain conglomerates [32,33,34]. The effect of microscopic deformation mechanisms in these works is taken into account through the use of appropriate phenomenological dependences. However, multiscale studies of processes occurring under impact loading conditions are still scarce. In addition, the finding of the relationship between the microstructural parameters and mechanical (macroscopic) properties of pipeline materials is a relevant topic of considerable scientific and practical interest [31,35,36].
This paper presents a theoretical and experimental study of the relationship between the microstructural parameters, mechanical properties, and impact deformation and fracture of steels using the example of 17Mn1Si pipe steel.
2. Experimental Procedure
Impact deformation remains the most common and effective method of assessing the ductility of steels under dynamic loading at different temperatures and determining their fracture energy. Charpy impact test specimens measuring 10 mm × 10 mm × 55 mm with a concentrator of depth a = 2 mm were spark cut from a steel sheet of thickness 30 mm. The specimens had a V-notch machined on a milling machine Blacks Charpy CNM (RJW Ltd., Kent, UK) with a flat milling cutter of suitable shape. The impact toughness was determined on an Instron 450MPX motorized pendulum impact tester equipped with an instrumented striker (Instron, Buckinghamshire, UK). The deformation and failure behavior was studied using fracture surface images obtained with a LEO EVO 50 scanning electron microscope (Zeiss, Oberkochen, Germany).
3. Theoretical Procedure
The simulation method developed and used here is based on the theory of evolution of couple stress fields that induce reversible structural-phase transformations and the formation of vortex structures at interfaces. This theory has been successfully expanded within the physical mesomechanics framework [1,3,12]. The material within the multilevel approach of physical mesomechanics is considered as a set of structural elements in a 3D-crystalline and 2D-planar subsystems along which rotational wave flows of mass and energy transfer occur. The rotational wave flows must particularly occur under dynamic (and localized) loading conditions. In this case, rotational modes of deformation arise under the action of local moments of forces. Note that the given approach was specifically developed to model processes, which had not been described in the framework of classical methods. This applies, first of all, to processes in open systems with a continuous energy supply. Such systems are known for their ability to self-organize and generate new deformation structures.
There are well-proven and experimentally validated classical approaches for describing thermodynamically quasi-equilibrium quasi-static processes. Nevertheless, it was shown that the Stochastic Excitable Cellular Automata SECA method does not contradict the linear theory of elasticity and, moreover, the fundamental transfer equation (modified Turnbull equation) in the limiting case coincides with the classical Hooke’s law [3]. The method also includes an explicit account of porosity and nanocrystalline structure of the material, and algorithms for calculating the local moments of forces and angular velocities of microrotations occurring in a structurally heterogeneous medium.
For analyzing the effect of temperature on the dynamic deformation behavior of ductile steel specimens with the characteristics resembling those of steel 17Mn1Si, we performed a series of numerical simulations based on a modified hybrid discrete-continuous approach that combines excitable cellular automata (ECA) methods. Each active element of an automaton is characterized by a particular set of neighbors in the first coordination sphere and by numerical parameters corresponding to the material contained in the simulated volume of space. These parameters are the elastic modulus, density, shear modulus, dislocation density, thermal conductivity, specific heat capacity, thermal expansion coefficient, and others. The interaction with neighboring elements can lead to changes in the thermal and mechanical energy components and associated physical parameters (temperature, entropy, stress, deformation, density, etc.).
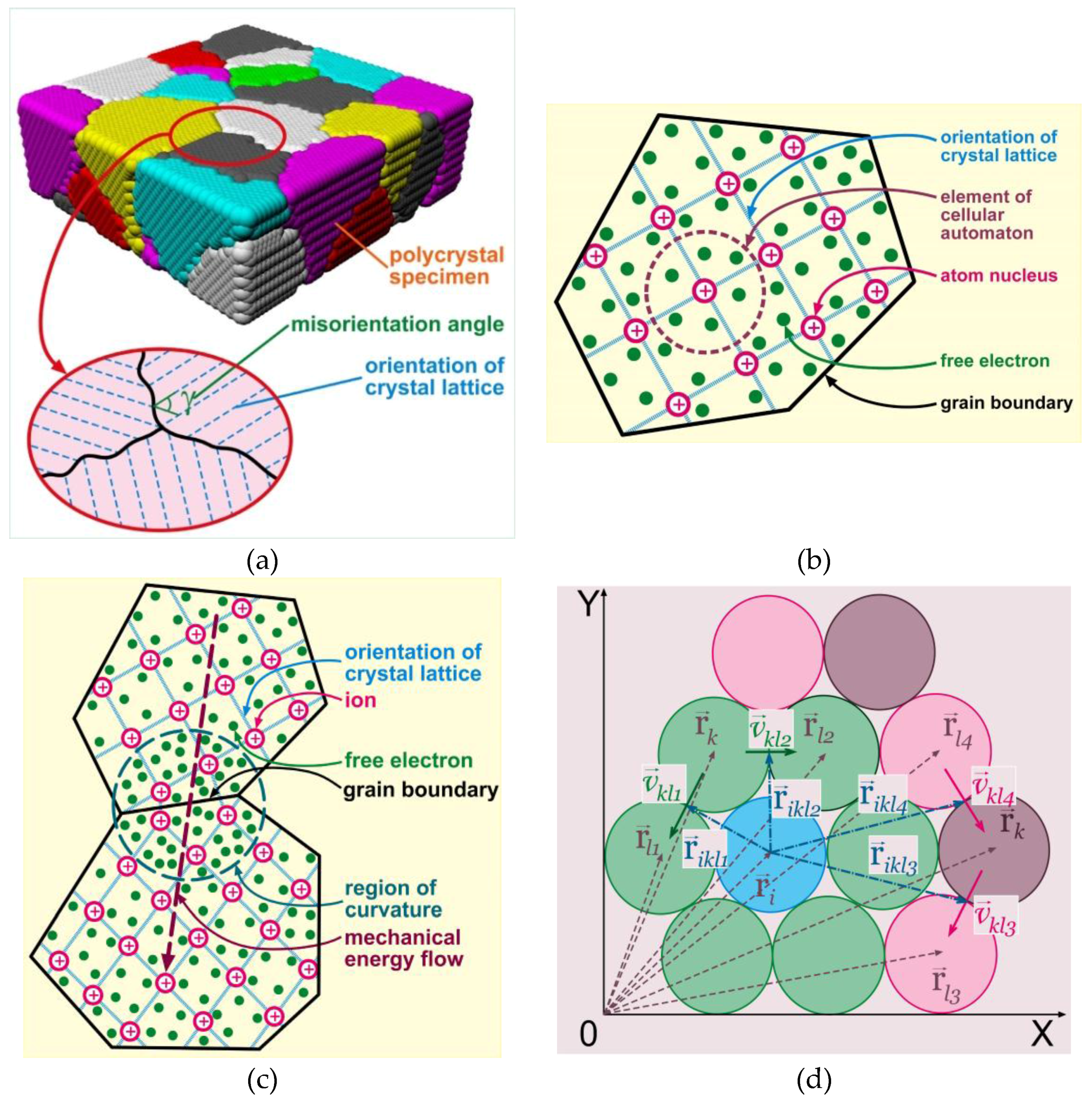
The object of simulation is the mechanical energy distribution in a specimen subjected to external mechanical load (e.g., tension, compression, etc.). The simulated specimen is represented as a cellular automaton that is a network of interconnected elements (Figure 1a). This network is divided into clusters, each of which corresponds to an individual grain (Figure 1b) with its own lattice orientation vector and vector coordinates given by the Euler angles. The boundary energy depending on the lattice misorientation angle is also taken into account in an explicit form (Figure 1c).
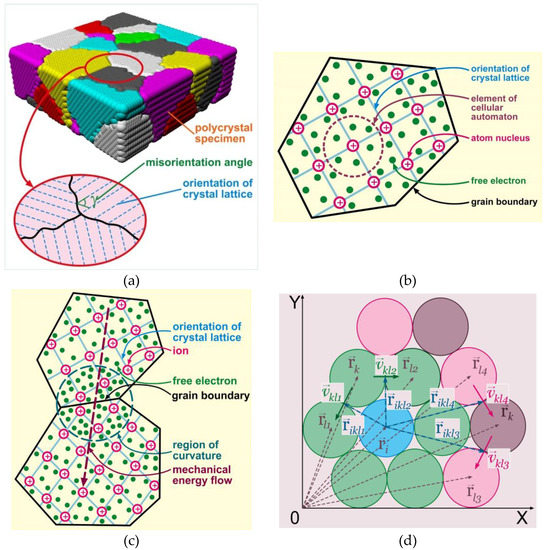
Figure 1.
Schematic illustrations: (a) polycrystalline specimen as a cellular automaton; (b) grains with crystal lattice; (c) neighboring grains with different lattice orientations; (d) calculation scheme for the angular velocity of material microrotation in the active element of the cellular automaton.
The results of simulation are represented as the calculated spatial distribution of such quantities as the specific elastic energy, local moments of forces, angular velocities and linear mass transfer rates, specific torsion energy, and the density of defect structures in the material. Here and below, the defect means any isolated region of the crystal in which the translational and rotational symmetry of the lattice is broken. A more detailed description of the method can be found elsewhere [3].
The input parameters of the model are the initial values of hydrostatic pressure p, density ρ, and temperature T of each element. The mechanical energy value of the i-th element at the n-th time step depends on its energy value at the (n − 1)-th time step and the total energy influx from the nearest neighbors, i.e., elements in its first coordination sphere. The energy fluxes are calculated by the following algorithm.
- The stress at the interface boundary of the i-th element and its k-th neighbor at the (n − 1)-th time step is calculated as the difference of hydrostatic pressures acting from each element of the considered pair:
- A relation analogous to the Newtonian viscous flow assuming he proportionality between the force and velocity [3] is used to calculate the average velocity of material points moving through a virtual boundary between fixed elements of space under the action of stress :Here, is the material mobility at the boundary between the i-th element and its k-th neighbor:where , are the elastic moduli of the i-th element and its k-th neighbor, is the number of defects in the active element and is the number of atoms in the active element, c is the effective rate of material response to external mechanical load, is the Boltzmann constant, and is the temperature at the boundary. Here, is the activation energy of the motion of the boundary between the i-th element and its k-th neighbor, which is calculated according to the Read–Shockley approximation, which tacitly assumes that all grain boundaries are of low-angle origin (this is a serious limitation of the model which has yet to be elaborated in the future research) [37]:where is the maximum boundary energy corresponding to the maximum lattice misorientation angle , and is the function that determines the lattice misorientation angle of grains containing the i-th element and its k-th neighbor, 0 ≤ ≤ (Figure 1c). We may conclude from this definition of mobility that the boundary mobility is the reciprocal of the specific (over the volume) momentum of reaction force of the material contained in the neighboring element. Then, we calculate the volume fraction of the substance transferred to the neighboring element () and the mechanical energy change in the i-th element as a result of interaction with its k-th neighbor ():Here, Δτ is the time step, is the element size and is the element volume.
- The total relative volume change () and the mechanical energy change () of the i-th element are found as a result of its interaction with all of nearest neighbors:
In this case, > 0 if the amount of matter in the i-th element decreases in comparison with the previous time step. Otherwise, > 0. The relative material volume () and the total mechanical energy () of the i-th element at the n-th time step are calculated as follows:
where is the energy dissipation term due to microrotations of cellular automaton elements determined as:
Here, is the increment of the vector angle of rotation of the active element, is the shear modulus, is the dissipation coefficient that can be measured experimentally and is the radius of the active element.
Knowing the density and the volume change , we can estimate the mass change and its updated value for the i-th element:
The updated density values of the material contained in the i-th element () and its hydrostatic pressure () are defined by the equations:
The increment of the vector angle of rotation of the i-th element at the n-th step () is proportional to the total angular velocity of the i-th element at the n-th step ():
The angular velocity of the i-th element in Figure 1d under the action of the flow of matter through the boundary between the k-th and l-th elements (each k-th element lies in the first coordination sphere of the i-th element, and each l-th element lies at the intersection of the first coordination spheres of the i-th and corresponding k-th elements) is found as follows:
The total angular velocity of the i-th element is defined as the sum:
where K is the number of elements in the first coordination sphere of the i-th element, and L is the number of elements at the intersection of the first coordination spheres of the i-th and each k-th neighboring elements.
The change in the moment of force acting on the i-th element during the time interval τ () is calculated as:
where G is the shear modulus of the material contained in the i-th element, and is the element radius. Thus, since local moments of forces generate rotation structures in the field of mass transfer rates under high-rate loading, it is very useful to calculate the vorticity vector defined as the curl of velocity:
The vorticity vector components are expressed as;
where Ω is the vorticity tensor defined by its components as:
The angular velocity calculated using Equations (18) and (19) is physically similar to the vorticity vector. Taking into account Equation (20), the following relations are derived for the vorticity vector components:
Thus, the vorticity tensor Ω can be expressed as:
The change in the number of defects in the i-th element () during its rotation through the angle is determined on the basis of the number of unit cells of the crystal lattice falling within the sector corresponding to this angle:
where is the volume of the sector corresponding to the angle , is the unit cell volume, and k is the proportionality coefficient depending on the type of the atomic packing and material. It is known from the “first principles” that each material has its own interatomic interaction energy and therefore the coefficient k for different materials is different. However, it depends not only on the magnitude of this energy but also on many other factors such as, e.g., the dislocation density, the concentration and type of impurities at grain boundaries, and others.
The sector volume is defined as:
Substituting Equation (27) into Equation (26), we obtain:
Using Equation (28), we can estimate the change in the number of defects in the material during curvature formation under the action of the local moment of force:
It should be noted that the form of Equation (2) was chosen based on the idea that a plastically deformable solid under high-rate dynamic loading behaves like a viscous liquid. This assumption was discussed and analyzed in more detail in [3].
As was shown earlier, active elements of the cellular automaton are fixed regions of the space occupied by the mesoscopic volume of the material flowing through virtual boundaries between these elements. We must therefore distinguish real boundaries between structural elements of the material from virtual boundaries between active elements in the model. Real boundaries can move along with material mass transfer. To describe the transformation of real grain boundaries, we have developed an algorithm of bistable cellular automata using a fuzzy set theory.
Earlier, we derived Equation (6) for that is the volume fraction of the material transferred from the i-th element through the boundary with its k-th neighbor due to the passage of the mechanical energy front during the n-th time step. The propagation of mechanical energy is thus accompanied by mass transfer between elements, which can induce changes in the shape of the grains making up the simulated medium. In reality, boundaries between grains are not always represented by a clearly defined crystallographic plane, and the crystal lattice near the grain boundary is not always ideal. The motion of such boundary regions, which are often refereed to as non-equilibrium brain boundaries, can be described using probabilistic models.
The index of the grain that will contain the i-th element at the (n + 1)-th time step can be determined using the fuzzy set theory, which is an extension of classical set theory and which assumes that the membership function of an element in a set may take non-integral values. Each such value can be interpreted as the probability of the element membership in one or another set.
Suppose that at each n-th time step for each i-th element there is a set of quantities (k = 1, ..., K), K is the number of elements in the first coordination sphere. Let the i-th element. as well as every k-th element in the first coordination sphere of the i-th element, be characterized by finite sets of membership functions for each of the existing grains:
where g is the grain number, and NG is the total number of grains. At the same time, the following conditions must be satisfied at the zero time step:
Depending on the fraction of the substance that left the i-th element () or flowed into it () as a result of interaction with each k-th neighbor at the n-th time step, the value of the membership function of the i-th element in the grain with number g at the (n + 1)-th step is defined as follows:
The second term on the right-hand side of this equation is responsible for the “outflow” of matter from the i-th element, while the third term is responsible for the matter “inflow” into the i-th element from elements in the first coordinationsphere. With the thus calculated values of for each i-th element and for each grain with number g, we have the set . Based on the values of the parameter , we may stochastically determine the grain to which the i-th element belongs at the (n + 1)-th step and, depending on this choice, the physical parameters of the material contained in it.
The stochastic choice of the number of the i-th element grain at the n-th time step is made as follows. First, the sum of the values of all membership functions is calculated for this element:
Then, using a random number generator that delivers real numbers uniformly distributed on the interval [0; ] we find the value of . The interval [0; ] is represented as a union of disjoint sets:
where = 0, ., g = 1,…, .
Depending on which of the intervals the value belongs to, the grain number is determined. The function that makes this choice has the form:
where
As a result of the choice made, a certain set of the i-th element parameters at the n-th time step is assigned values characterizing the grain with number . The values of all element parameters computed at the n-th time step become input parameters for the (n + 1)-th time step. The output parameters of the simulated specimen are the final values of the element parameters calculated at the last time step.
4. Results and Discussion
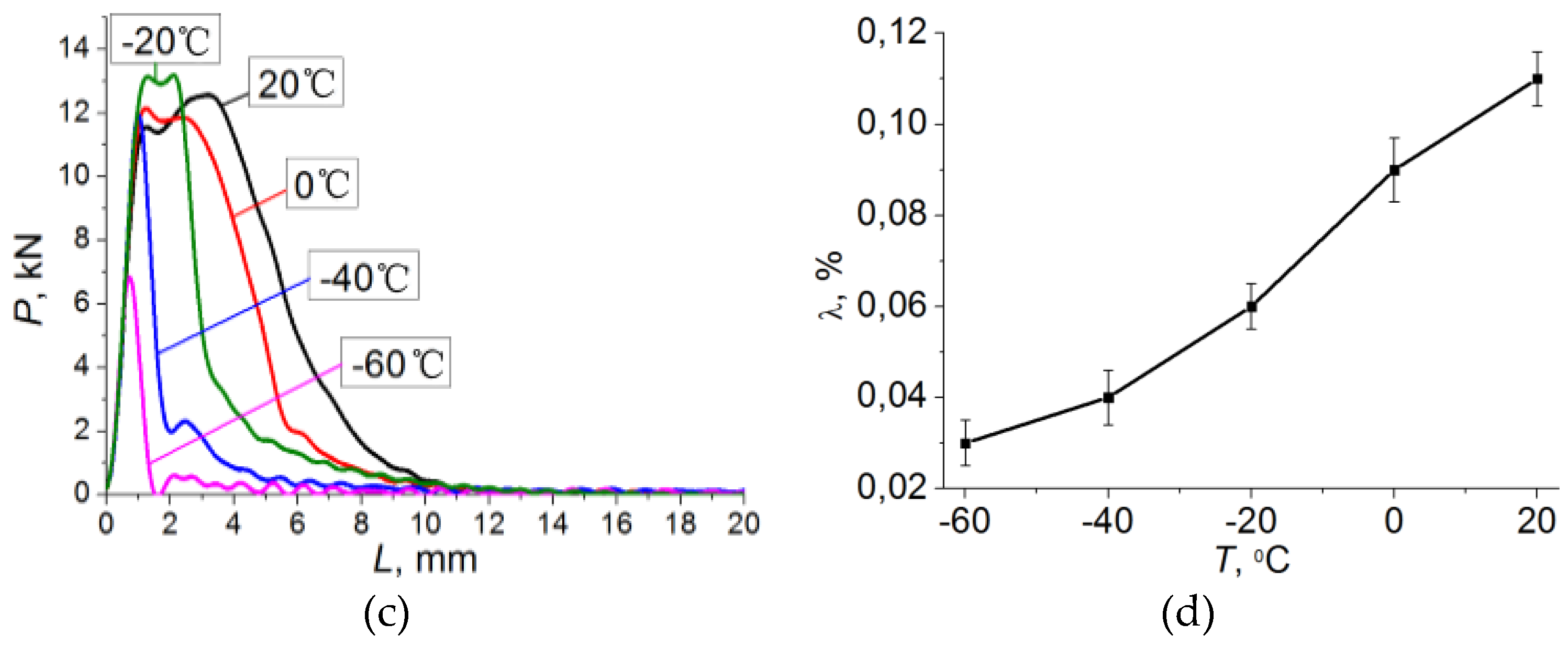
Test specimens in the as-delivered state had ferrite-pearlite structure with an average grain size of 13 ± 3 μm (Figure 2a,b). Ferrite grains are mostly globular. The microhardness of 17Mn1Si steel was 1.57 ± 0.06 GPa. Impact bending tests were conducted with recording fracture diagrams of specimens at different temperatures (Figure 2c) and with measuring the maximum contraction ratio of the specimens λ (%) in the crack growth region (Figure 2d). The obtained data were used to calculate their impact toughness KCV (Table 1). It has been shown that a decrease in the test temperature causes a decrease in the fracture energy. Additionally, the temperature decrease leads to a decrease in the amount of ductility because plastic flow of metal becomes less homogeneous (at the microscopic level). In the literature this effect is often termed as “cold brittleness”. It is most typical for materials with the least densely packed bcc lattice and is not observed in more densely packed Face Cubic Centered fcc and Hexagonal Closed packed (hcp) lattices [38].

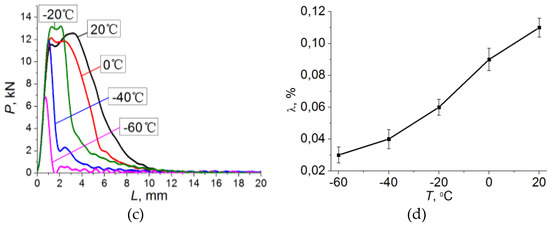
Figure 2.
(a,b) Optical images of 17Mn1Si steel microstructure in the as-delivered state, (c) impact loading curves in the “load–displacement” coordinates for the specimens with the V-notch tested at different temperatures shown in the legend, (d) dependence of the maximum contraction ratio of specimens λ (%) in the crack growth region on the test temperature T, °C for specimens with different concentrator shapes

Table 1.
Impact toughness and maximum contraction ratio of specimens λ (%) in the crack growth region.
The fracture energy decrease in 17Mn1Si steel is due to the growing density of dislocations in the microstructure of the material and their constrained relaxation, which leads to the formation of micro-defects (cracks) [38,39]. The motion of dislocations during plastic flow of solids is impeded at low test temperatures due to their low mobility, restricted mass transfer, etc.
The relaxation capacity of the material with the decreasing test temperature at the macroscopic level can be quantitatively defined using the maximum contraction ratio of the specimen λ (%) in the crack growth region (see Table 1). The maximum contraction ratio is the ratio of the reduced cross-sectional area of the fractured specimen to the initial cross-sectional area, expressed as a percentage [20,21]. According to the literature, the decrease in the work of plastic deformation in specimen fracture directly depends on the change in the mobility of dislocations. The activation of plastic deformation with the test temperature increase from T = −60 to 20 °C at the crack tip and contraction λ (%) (see Table 1) must also contribute to the elimination of other microdefects that reduce the mobility of dislocations (dislocation barriers, dispersed second phase particles, etc.), thus leading to an increase in the impact toughness.
As noted above, the boundaries of structural elements, first of all grains, play several functional roles during plastic deformation. From the viewpoint of strain hardening, especially under static loading, the grain boundaries are obstacles to dislocation glide and thereby they contribute to the increase the flow stress as deformation proceeds. This effect is known as the Hall–Petch hardening according to which the flow (yield) stress is inversely proportional to the square root of the grain size [40]. On the other hand, especially under high-rate loading, the boundaries can be the regions whose deformation promotes an efficient dissipation of energy rapidly supplied to the material. For example, the grain boundaries serve as efficient sinks for incoming lattice dislocations. As a result, the fracture energy and impact fracture toughness should increase [41]. It is rather difficult to check the validity of this hypothesis only in experiments, so we used numerical simulations.
4.1. Simulation of Impact Loading Meso-Dynamics at Different Temperatures
Five numerical simulations on cyclic impact loading were performed using the SECA method aiming at analyzing the deformation behavior of the specimens (having mesoscopic volumes) subjected to impact loading at different temperatures (T = −60, −40, −20, 0, 20 °C). A model material was simulated to have a microstructure and properties similar to those of 17Mn1Si steel. In the simulations, we explicitly took into account energy dissipation during local rotations of the material. The mechanical energy change in each element of the cellular automaton causes an increase in the torsion energy of the element material proportionally to the dissipation coefficient according to Equation (17). This coefficient is the increasing function of the material temperature and its values are given in Table 2.

Table 2.
Dissipation coefficient adopted for 17Mn1Si steel at different temperatures.
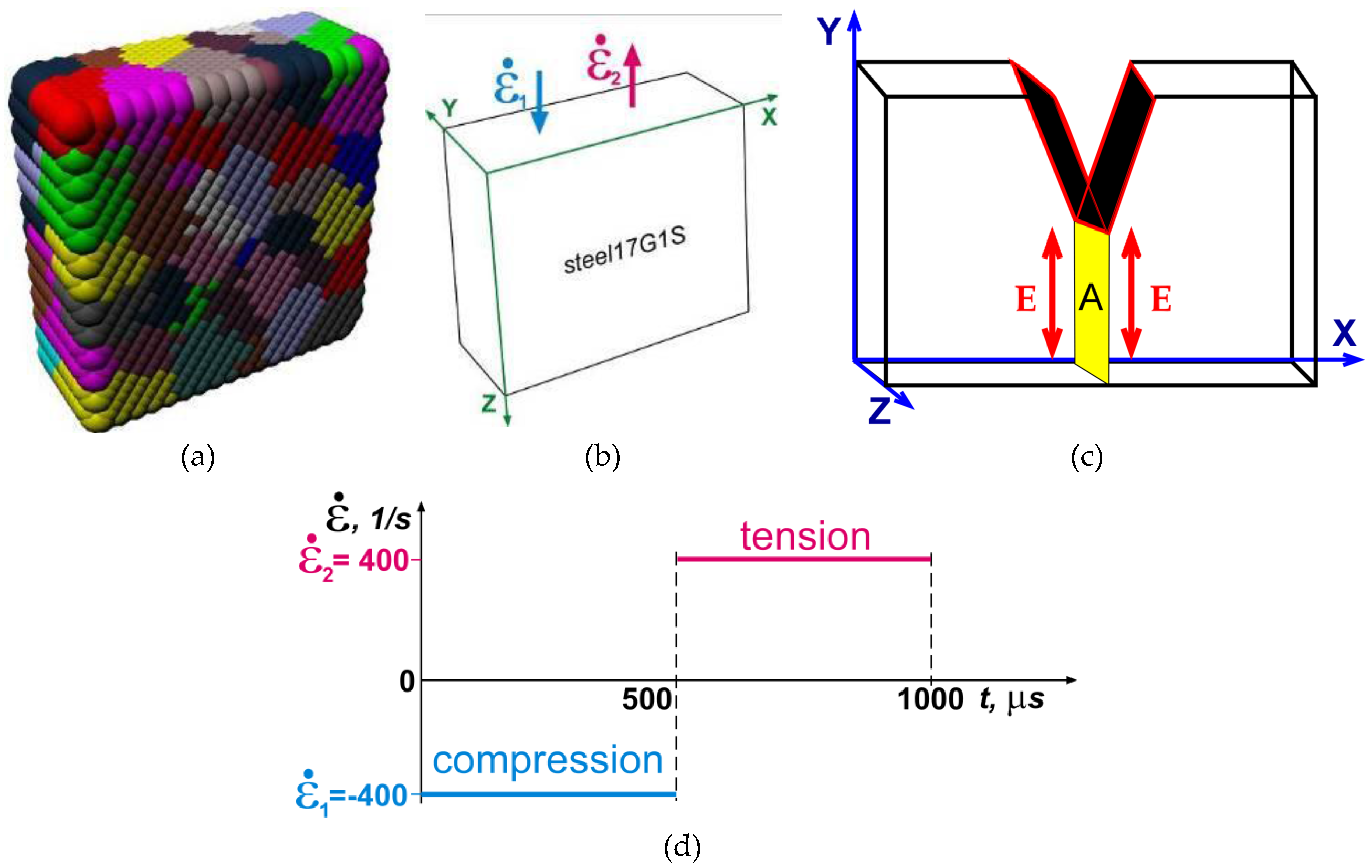
We analyzed the behavior of a prismatic specimen (having a representative mesoscopic volume) with the grain structure typical of 17Mn1Si steel. Each specimen has 30 μm × 10 μm × 30 μm dimensions and is represented as a cellular automaton with an fcc packing of elements of 1 μm each; the grain size is set at 5 μm (Figure 3a). The simulation time step is 10 ns. The initial stress and strain are zero. The upper face is compressed at a rate of 400 s−1 during the first 500 μs and then extended at the same rate during the next 500 μs (Figure 3b,d). There is no energy exchange through other boundaries.
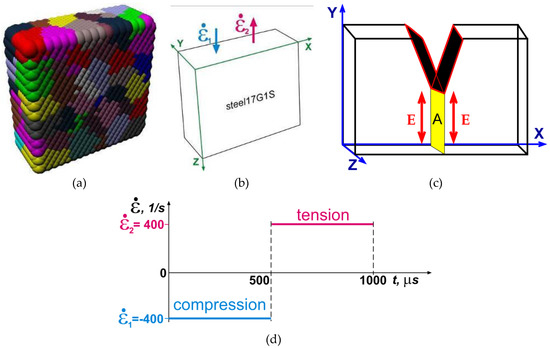
Figure 3.
Schematic of the specimen or simulated mesoscopic volume (a); deformation scheme (b); position of the simulated specimen (plane A) in the simulated system (c); and time—load dependence (d). E in (c) means residual cross section in the notch tip vicinity.
The simulated mesoscopic volume mimics the space occupied by the material in the immediate vicinity of the notch, as shown in Figure 3c. The loaded face of the simulated specimen is thus in contact with the geometric stress concentrator, which is the source of elastic energy flows. In contrast to the way it is usually done in the simulation of macroscopic systems, in our case the loading is induced not through an indenter but the notch tip that locally accumulates a large part of the indenter energy in its vicinity. The energy accumulation mechanisms near notches of different shape were earlier discussed using the method of excitable cellular automata in Ref. [3].
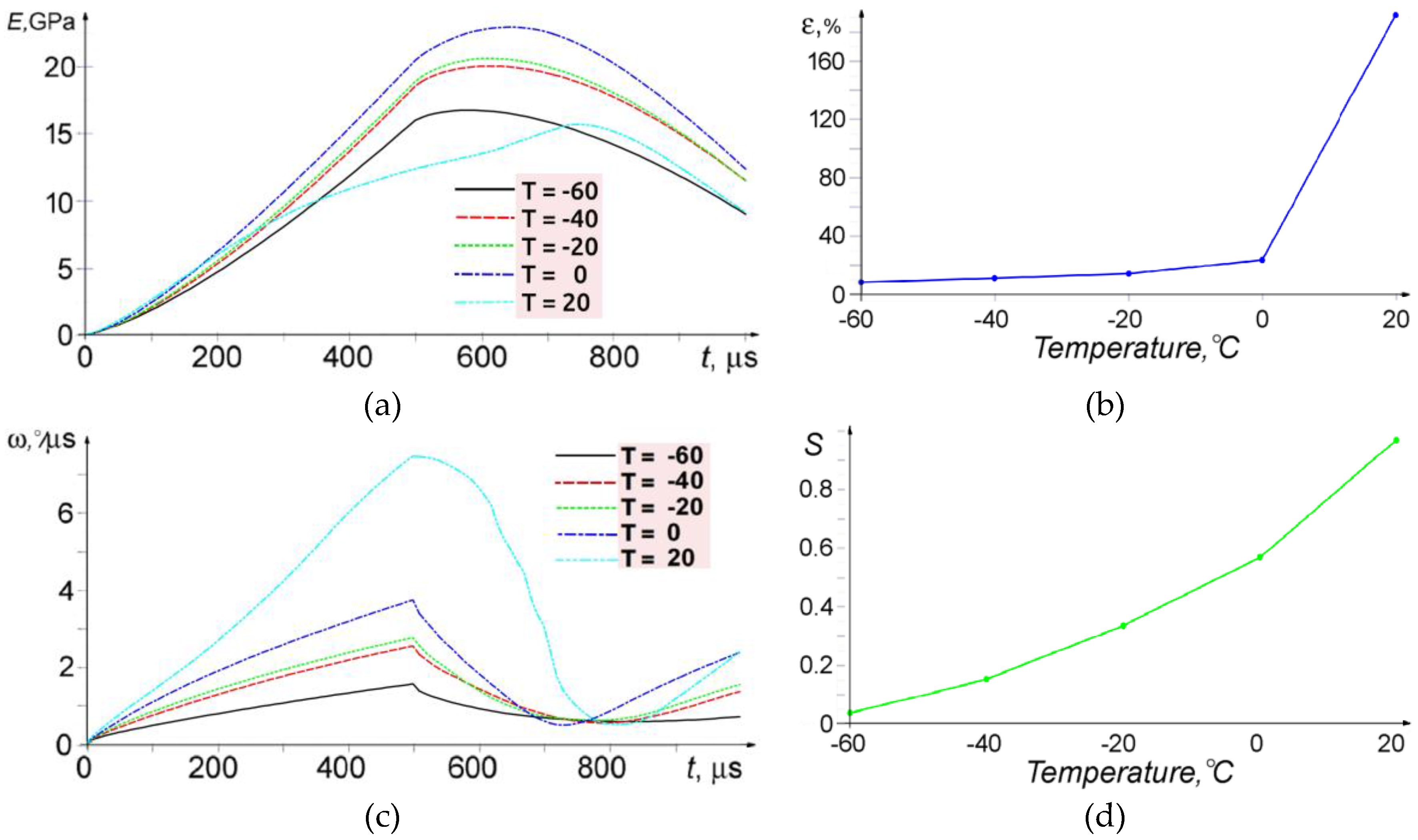
Figure 4 shows the time dependences of the specific (over the volume) elastic energy, rotation energy, relative rotation energy (the ratio of rotation energy to total mechanical energy), and the average magnitude of local angular velocity of the material in the element. Besides, it shows the dependence of the specific elastic energy on the total deformation of the specimen. These dependences are determined for the entire specimen volume, with the exception of 1 μm-thick boundary layers. Let us analyze these dependencies in some details.
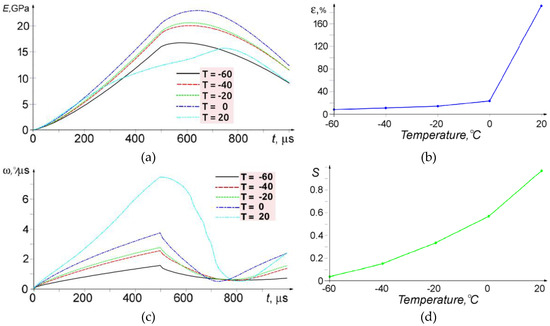
Figure 4.
Specific elastic energy of specimens vs. time (a); total strain vs. test temperature (500 µm) (b); average angular velocity of microrotations vs. time (c); and fraction of microrotation energy in the total elastic energy supplied vs. test temperature (500 µm) (d). The legends show the temperatures T in °C.
As one can see, the specimen response to the applied (alternating) load is generally similar but differs in absolute values within the temperature range T = −60–0 °C. The higher the temperature, the higher the specific elastic energy is. Moreover, the specific elastic energy increases nonlinearly with temperature. At the room temperature T = 20 °C and the loading time t ~ 280 μs, the rate of increase in the specific elastic energy decreases noticeably. Then, in contrast to all others test temperatures, it continues increasing even after the beginning of the tension half-cycle (until t ~ 720 μs), after which it decreases like in all other specimens. This means that the test temperature rise to T = 20 °C activates elastic energy relaxation due to plastic deformation and hence the level of energy in the studied specimens reduces significantly. The observed effect is most likely associated with the possible release of stresses at the structural boundaries, which should promote relaxation.
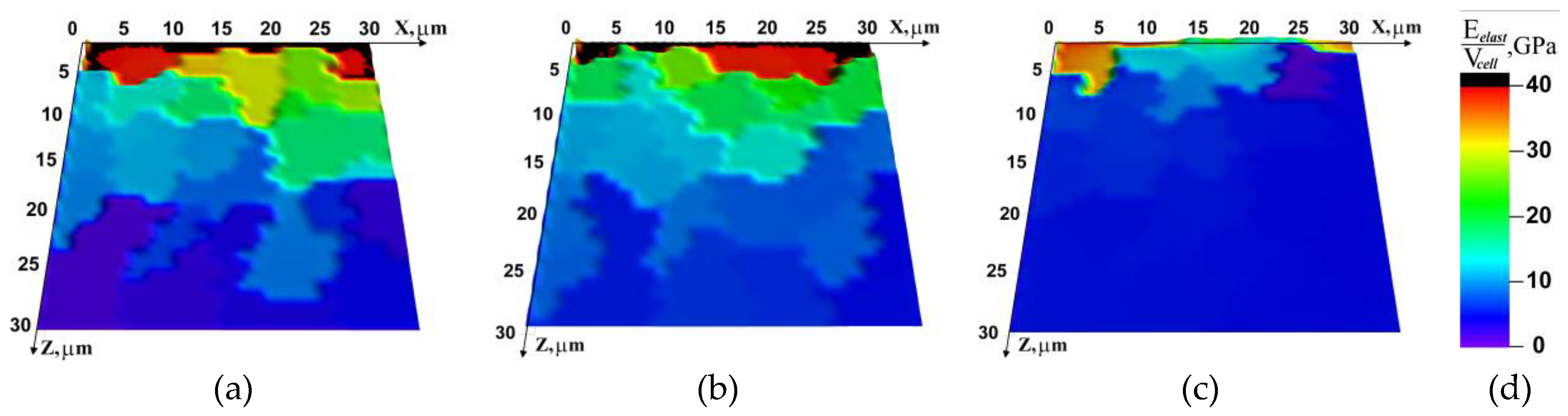
The distribution patterns of the specific elastic energy shown in Figure 5 demonstrate that the extreme values of the elastic energy at room temperature are observed only in the layer adjacent to the plane where the load applies. At lower temperatures, this parameter is seen to increase throughout the analyzed mesoscopic volume, which also confirms the assumption that relaxation is retarded in this case.
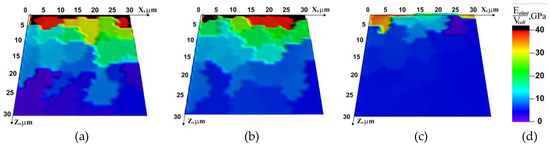
Figure 5.
Specific elastic energy distribution on specimen faces at different temperatures at 500 μs after the beginning of loading. (a) −60 °C; (b) −20 °C; (c) 20 °C; (d) color legend.
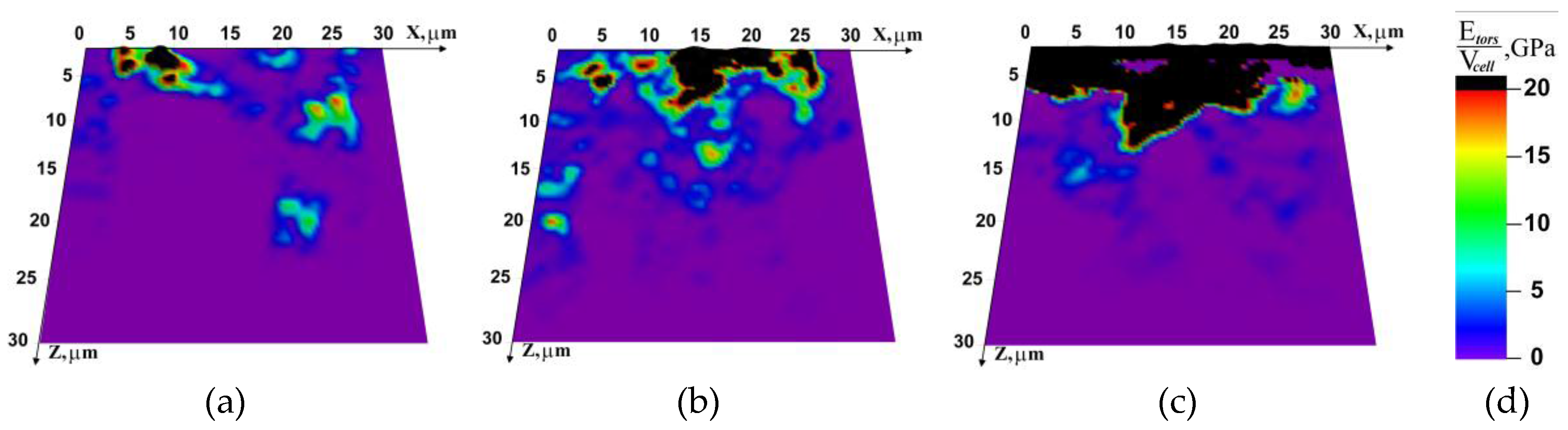
The observed effects can be explained by the distribution patterns of specific rotation energy shown in Figure 6. The maximum change in the analyzed parameter is observed in the upper layer of thickness about 5–7 cellular automaton elements. The specific rotation energy in the upper layer of the studied mesoscopic volume, through which the load is transmitted, is much higher at high test temperatures. It was also found that irrespective of the test temperature the pattern formed at the instant of time when the load direction alters (t = 500 μs) remains almost unchanged in the subsequent t = 205 μs of loading.
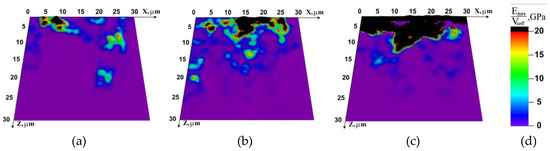
Figure 6.
Specific rotation energy distribution on specimen faces at different temperatures at 500 μs after the beginning of loading. (a) −60 °C; (b) −20 °C; (c) 20 °C; (d) color legend.
As has been noted above, the boundaries between structural elements are a 2D subsystem in which deformation begins first. This is particularly important under high-rate loading when the dissipation of the elastic energy supplied into the specimen can significantly increase the impact fracture energy [42,43]. This is confirmed by the temperature dependences of specific rotation energy (Figure 6). The active involvement of rotational deformation modes in dissipation at room temperature allows for energy absorption and thereby increases the fracture resistance.
In our opinion, the localized change of the specific rotation energy only in the upper layers of the cellular automaton is first of all associated with the account for the grain structure of the studied mesoscopic volume in the model. The relaxation of stresses arising under localized high-rate load applied from the upper face occurs mostly due to deformation in the upper layer of the mesoscopic volume. The effect of test temperature on the observed difference agrees well with the above analysis of elastic deformation characteristics.
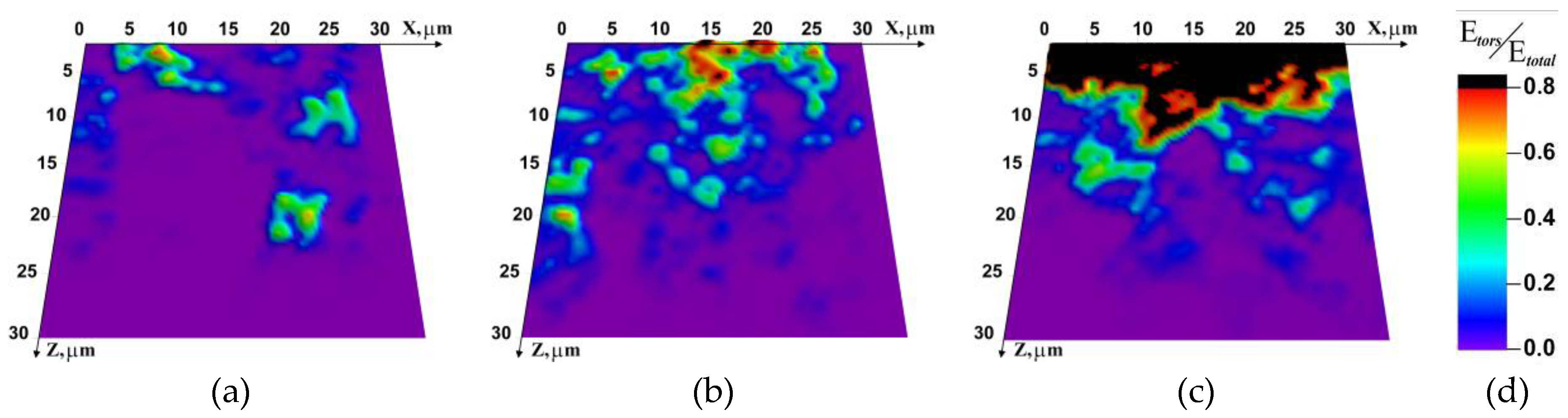
Figure 7 shows the distribution of the relative rotation energy. The distribution remains almost unchanged with time at the lowest test temperature (T = −60 °C), even despite the change in the direction of applied external load. As relaxation becomes more probable with the growing temperature (T = −20 °C), the size of the region involved in inelastic deformation increases, including the distribution in Z direction (Figure 7b). At room temperature (Figure 7c), inelastic deformation revealed from the rotation energy distribution is mostly localized in the upper layer, again apparently due to the activation of dissipation at the boundaries of structural elements (grains).
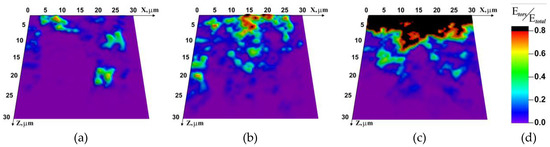
Figure 7.
Relative rotation energy distribution on specimen faces at different temperatures at 500 μs after the beginning of loading. (a) −60 °C; (b) −20 °C; (c) 20 °C; (d) color legend.
This assumption is convincingly supported by the variation curves of the average magnitude of local angular velocity shown in Figure 4. This parameter is seen to increase proportionally to the test temperature and achieves its maximum value when the direction of applied load is changed (t = 500 μs), for all test temperatures. On the other hand, the minimum value of this parameter is observed at t = 750–800 μs (then it increases again, probably due to the oscillating character of elastic energy accumulation and its subsequent release at the structural element boundaries).
This fact was confirmed by analyzing the distribution of accumulated relative rotation energy at test room temperature (Figure 7c). It was found that at t = 750 sec the distribution pattern of the analyzed quantity is nearly the same as the pattern at t = 500 μs, despite the fact that the applied load direction changed. On the other hand, at the lowest test temperature T = −60 °C for the same loading time, the local angular velocities are almost zero. Notice once again that the explicit account of the grain structure at the test temperature T = 20 °C caused localized dissipation in the cellular automaton surface layer of thickness 5–7 μm, while (for the same reason) at T = 0 °C and lower the elastic energy dissipation in these layers was much less pronounced (Figure 7a,b). Thus, we have illustrated both the explicit temperature dependence of dissipation intensity and the important role of dissipation for stress relaxation at the boundaries of structural elements.
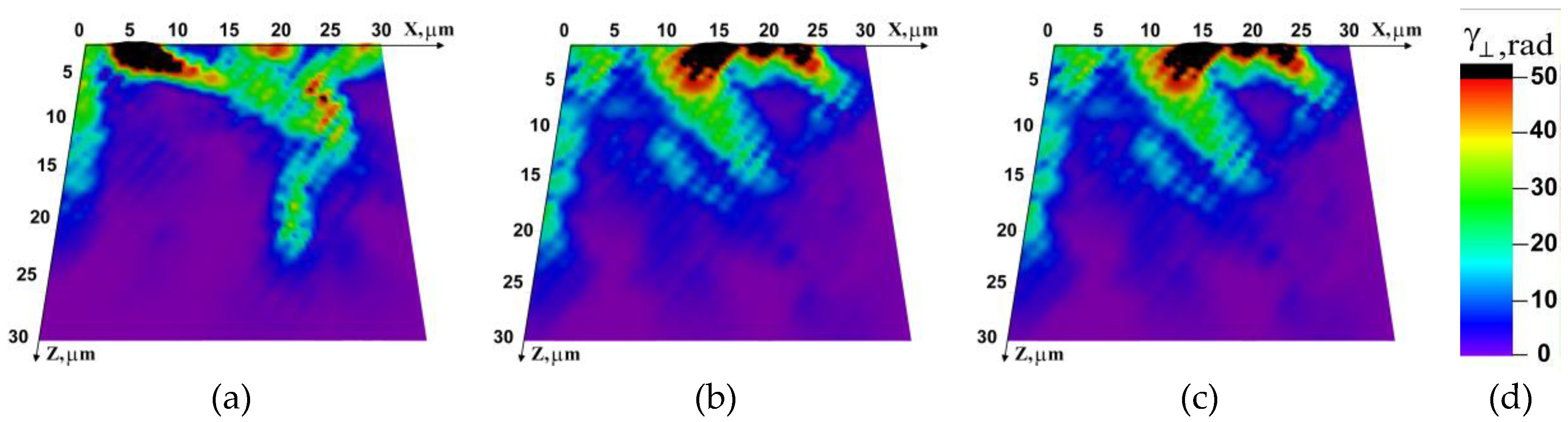
The discussed effect can also be demonstrated by the distribution patterns of accumulated strain in the direction perpendicular to the fracture surface as a result of microrotations. Figure 8 shows the distribution of ( is the accumulated angle of local material rotation) on the specimen faces at different temperatures at 500 μs after the start of loading. The quantity is responsible for the formation of the deformation relief in the XOZ coordinate plane, i.e., on the future fracture surface. At lower test temperatures, the accumulated rotation value is much lower and reaches limiting values in individual crystallites only (Figure 8a,b).
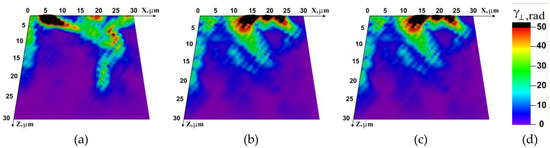
Figure 8.
Distribution of the accumulated angle of local material rotation on specimen faces at different temperatures at 500 μs after the start of loading: (a) −60 °C; (b) −20 °C; (c) 20 °C; (d) color legend.
4.2. Fracture Micromechanisms
As was shown above, the deformation of metals at the micro- and mesoscopic levels in pendulum impact tests leads to a continuous formation and evolution of structural microdefects. Their initiation and evolution from the standpoint of micromechanics are associated with the motion of dislocations induced by plastic deformation and interaction of stress fields in regions surrounding dislocations. An integral evaluation of the effect of loading conditions on deformation and failure mechanisms can be performed by fractographic analysis (Figure 9).

Figure 9.
Scanning Electron Microscope (SEM) images of the fracture surface of impact bending specimens tested at different temperatures. (a) T = 20 °C; (b) T = −20 °C; (c) T = −60 °C.
T = 20 °C: The surface of the crack initiation region has all signs of ductile fracture (Figure 9a). It has typical macropits surrounded by conglomerates of smaller pits.
T = −20 °C: The fracture mechanism is similar to that at T = 20 °C. The size of ductile fracture pits is slightly smaller (Figure 9b) [44,45].
T = −60 °C: The major fracture mechanism at this temperature was cleavage. The fracture surface is covered by “river lines” (Figure 9c) and fracture ridges formed by microcrack coalescence on parallel facets (surface areas) under the influence of plastic deformation in the surrounding material.
Thus, the whole set of experimental and numerical simulation data obtained in variable temperature conditions under high-rate loading suggests that dissipation processes develop with the involvement of 2D subsystems in the form of internal interfaces. Undoubtedly, the dissipation coefficient value used in the model should be further refined and adjusted both within phenomenological and microscopic model and experimental approaches. In our subsequent study, the impact loading of notched Charpy specimens will be numerically simulated with the aim of accounting for the inelastic processes occurring under constrained conditions and localization. Nevertheless, we have shown with the aid of the proposed model and numerical simulations that the use of the excitable cellular automata method and an explicit account of test temperature through the possibility of energy release at internal interfaces allow the method to be successfully applied for explaining the experimentally observed regularities.
5. Conclusions
A model for the behavior of a grain conglomerate under impact loading at different temperatures was proposed within a cellular automata framework. The model takes into account energy dissipation due to local rotations of material fragments. The mechanical energy change in each element of a cellular automaton causes an increase in the rotation energy of the element material proportionally to the dissipation coefficient, which is the increasing function of the material temperature.
The deformation behavior of model material specimens (having mesoscopic dimensions) with the microstructure and properties resembling those of 17Mn1Si steel was numerically analyzed at different test temperatures. It was shown that the intensity of dissipation processes depends on temperature and these processes play an important role in stress relaxation at the boundaries of structural elements.
The microstructural parameters and the effect of test temperature on the impact toughness of 17Mn1Si steel were studied. The relationship between pendulum impact test temperature and the deformation and fracture energy of the steel was investigated. The characteristics of structural deformation energy of 17Mn1Si steel were obtained, and their physical and mechanical nature was discussed. The impact toughness was shown to decrease almost linearly with the decreasing test temperature, which agrees with the fractographic analysis data confirming the increase in the fraction of brittle fracture in this case.
It was shown with the aid of the proposed model and numerical simulations that the use of the excitable cellular automata method and an explicit account of test temperature through the possibility of energy release at internal interfaces help to explain the experimentally observed regularities of impact failure at different temperatures.
Acknowledgments
The work was performed in the framework of fundamental research projects of the Russian State Academies of Sciences (2013–2020), and with a partial support of RFBR Grant No. 15-08-05818_a, Project of the Headquarter of the Russian Academy of Sciences on Arctic research, and Grant No. 11.2 of the Russian Academy of Sciences (Department of Power Engineering, Mechanical Engineering, Mechanics, and Control Processes). The authors are grateful to Shared Use Center “Nanotech” of ISPMS SB RAS for the assistance in conducting fractographic studies.
Author Contributions
Dmitry Moiseenko and Pavel Maksimov conceived, designed and performed the numerical experiments; Ilya Vlasov performed the experiments; Dmitry Moiseenko, Pavlo Maruschak and Sergey Panin analyzed the data; Dmitry Moiseenko, Pavlo Maruschak, Filippo Berto, Siegfried Schmauder and Alexey Vinogradov wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Panin, V.E.; Egorushkin, V.E. Basic Physical Mesomechanics of Plastic Deformation and Fracture of Solids as Hierarchically Organized Nonlinear Systems. Phys. Mesomech. 2015, 18, 377–390. [Google Scholar] [CrossRef]
- Panin, V.E.; Panin, A.V.; Moiseenko, D.D. Physical mesomechanics of a deformed solid as a multilevel system. II. Chessboard-like mesoeffect of the interface in heterogeneous media in external fields. Phys. Mesomech. 2007, 10, 5–14. [Google Scholar] [CrossRef]
- Moiseenko, D.D.; Panin, V.E.; Elsukova, T.F. Role of local curvature in grain boundary sliding in a deformed polycrystal. Phys. Mesomech. 2013, 16, 335–347. [Google Scholar] [CrossRef]
- Makarov, P.V.; Schmauder, S.; Cherepanov, O.I.; Smolin, I.Y.; Romanova, V.A.; Balokhonov, R.R.; Saraev, D.Y.; Soppa, E.; Kizler, P.; Fischer, G.; et al. Simulation of elastic-plastic deformation and fracture of materials at micro-, meso- and macrolevels. Theor. Appl. Fract. Mech. 2001, 37, 183–244. [Google Scholar] [CrossRef]
- Shilkrot, L.E.; Curtin, W.A.; Miller, R.E. A coupled atomistic/continuum model of defects in solids. J. Mech. Phys. Solids 2002, 50, 2085–2106. [Google Scholar] [CrossRef]
- Olson, G.B. Computational Design of Hierarchically Structured Materials. Science 1997, 277, 1237–1242. [Google Scholar] [CrossRef]
- Mura, R.; Ting, T.C.T. Micromechanics of Defects in Solids (2nd rev. ed.). J. Appl. Mech. 1989, 56, 487. [Google Scholar] [CrossRef]
- Ohashi, T.; Kawamukai, M.; Zbib, H. A multiscale approach for modeling scale-dependent yield stress in polycrystalline metals. Int. J. Plast. 2007, 23, 897–914. [Google Scholar] [CrossRef]
- Kouznetsova, V.; Geers, M.G.D.; Brekelmans, W.A.M. Multi-scale constitutive modelling of heterogeneous materials with a gradient-enhanced computational homogenization scheme. Int. J. Numer. Methods Eng. 2002, 54, 1235–1260. [Google Scholar] [CrossRef]
- Kouznetsova, V.G.; Geers, M.G.D.; Brekelmans, W.A.M. Multi-scale second-order computational homogenization of multi-phase materials: A nested finite element solution strategy. Comput. Methods Appl. Mech. Eng. 2004, 193, 5525–5550. [Google Scholar] [CrossRef]
- Miehe, C. Computational micro-to-macro transitions discretized micro-structures of heterogeneous materials at finite strains based on the minimization of averaged incremental energy. Comput. Methods Appl. Mech. Eng. 2003, 192, 559–591. [Google Scholar] [CrossRef]
- Panin, V.E.; Egorushkin, V.E.; Panin, A.V.; Chernyavskii, A.G. Plastic distortion as a fundamental mechanism in nonlinear mesomechanics of plastic deformation and fracture. Phys. Mesomech. 2016, 19, 255–258. [Google Scholar] [CrossRef]
- McDowell, D.L. A perspective on trends in multiscale plasticity. Int. J. Plast. 2010, 26, 1280–1309. [Google Scholar] [CrossRef]
- Zhu, T.; Li, J.; Samanta, A.; Leach, A.; Gall, K. Temperature and strain-rate dependence of surface dislocation nucleation. Phys. Rev. Lett. 2008, 100. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.Y.; He, M.; Shin, J.; Richter, G.; Gianola, D.S. Measuring surface dislocation nucleation in defect-scarce nanostructures. Nat. Mater. 2015, 14, 707–713. [Google Scholar] [CrossRef] [PubMed]
- Nicola, L.; Bower, A.F.; Kim, K.S.; Needleman, A.; Van der Giessen, E. Surface versus bulk nucleation of dislocations during contact. J. Mech. Phys. Solids 2007, 55, 1120–1144. [Google Scholar] [CrossRef]
- Gale, W.F.; Totemeir, T.C. Smithells Metals Reference Book; Elsevier Butterworth-Heinemann: Oxford, UK, 2004. [Google Scholar]
- Pyshmintsev, I.Y.; Struin, A.O.; Gervasyev, A.M.; Lobanov, M.L.; Rusakov, G.M.; Danilov, S.V.; Arabey, A.B. Effect of bainite crystallographic texture on failure of pipe steel sheets made by controlled thermomechanical treatment. Metallurgist 2016, 60, 405–412. [Google Scholar] [CrossRef]
- Nykyforchyn, H.; Lunarska, E.; Tsyrulnyk, O.T.; Nikiforov, K.; Genarro, M.E.; Gabetta, G. Environmentally assisted “in-bulk” steel degradation of long term service gas trunkline. Eng. Fail. Anal. 2010, 17, 624–632. [Google Scholar] [CrossRef]
- Yasnikov, I.S.; Vinogradov, A.; Estrin, Y. Revisiting the Considère Criterion from the Viewpoint of Dislocation Theory Fundamentals. Scr. Mater. 2014, 76, 37–40. [Google Scholar] [CrossRef]
- Vinogradov, A. Mechanical Properties of ultrafine grained metals: New challenges and perspectives. Adv. Eng. Mater. 2015, 17, 1710–1722. [Google Scholar] [CrossRef]
- Lehto, P.; Remes, H.; Saukkonen, T.; Hänninen, H.; Romanoff, J. Influence of grain size distribution on the Hall-Petch relationship of welded structural steel. Mater. Sci. Eng. A 2014, 592, 28–39. [Google Scholar] [CrossRef]
- Zhuang, Z.; O’Donoghu, P.E. The recent development of analysis methodology for rapid crack propagation and arrest in gas pipelines. Int. J. Fract. 2000, 101, 269–290. [Google Scholar] [CrossRef]
- Han, Y.; Shi, J.; Xu, L.; Cao, W.Q.; Dong, H. Effect of hot rolling temperature on grain size and precipitation hardening in a Ti-microalloyed low-carbon martensitic steel. Mater. Sci. Eng. A 2012, 553, 192–199. [Google Scholar] [CrossRef]
- Farber, V.M.; Pyshmintsev, I.Yu.; Arabei, A.B.; Selivanova, O.V.; Polukhina, O.N. Contributions of structural factors to the strength of K65 steels. Steel Transl. 2012, 42, 687–690. [Google Scholar] [CrossRef]
- Bhattacharjee, D.; Knott, J.F.; Davis, C.L. Charpy-impact-toughness prediction using an “Effective” grain size for thermomechanically controlled rolled microalloyed steels. Metall. Mater. Trans. A 2004, 35, 121–130. [Google Scholar] [CrossRef]
- Smirnov, M.A.; Pyshmintsev, I.Y.; Maltseva, A.N.; Mushina, O.V. Effect of ferrite-bainite structure on the properties of high-strength pipe steel. Metallurgist 2012, 56, 43–51. [Google Scholar] [CrossRef]
- O’Donoghue, P.E.; Kanninen, M.F.; Lueng, C.P.; Demofonti, G.; Venzi, S. The development and validation of a dynamic fracture propagation model for gas transmission pipelines. Int. J. Press. Vessels Pip. 1997, 70, 11–25. [Google Scholar] [CrossRef]
- Pyshmintsev, I.Y.; Boryakova, A.N.; Smirnov, M.A.; Krainov, V.I. Influence of the plastic-deformation temperature on the structure and properties of low-carbon pipe steel. Steel Transl. 2010, 40, 21–26. [Google Scholar] [CrossRef]
- Tsuji, N.; Okuno, S.; Koizumi, Y.; Minamino, Y. Toughness of Ultrafine Grained Ferritic Steels Fabricated by ARB and Annealing Process. Mater. Trans. 2004, 45, 2272–2281. [Google Scholar] [CrossRef]
- Safarov, I.M.; Korznikov, A.V.; Galeyev, R.M.; Sergeev, S.N.; Gladkovsky, S.V.; Pyshmintsev, I.Y. An anomaly of the temperature dependence of the impact strength of low-carbon steel with an ultrafine-grain structure. Dokl. Phys. 2016, 61, 15–18. [Google Scholar] [CrossRef]
- Zhao, R.; Han, J.Q.; Liu, B.B.; Wan, M. Interaction of forming temperature and grain size effect in micro/meso-scale plastic deformation of nickel-base superalloy. Mater. Des. 2016, 94, 195–206. [Google Scholar] [CrossRef]
- Kouznetsova, V.; Brekelmans, W.A.M.; Baaijens, F.P.T. Approach to micro-macro modeling of heterogeneous materials. Comput. Mech. 2001, 27, 37–48. [Google Scholar] [CrossRef]
- Armstrong, R. The influence of polycrystal grain size on several mechanical properties of materials. Metall. Mater. Trans. B 1970, 1, 1169–1176. [Google Scholar] [CrossRef]
- Hwang, B.; Kim, Y.G.; Lee, S.; Kim, Y.M.; Kim, N.J.; Yoo, J.Y. Effective grain size and charpy impact properties of high-toughness X70 pipeline steels. Metall. Mater. Trans. A 2005, 36, 2107–2114. [Google Scholar] [CrossRef]
- Mirzaev, D.A.; Schastlivtsev, V.M.; Yakovleva, I.L.; Tereshchenko, N.A.; Shaburov, D.V. The formation of delamination cracks in impact-toughness tests as a cause of the increase in the impact toughness of steels with bcc structure. Phys. Met. Metallogr. 2015, 116, 1253–1258. [Google Scholar] [CrossRef]
- Priester, L. Grain Boundaries; Springer Series in Materials Science 172; Springer Science+Business Media: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Chernov, V.M.; Kardashev, B.K.; Moroz, K.A. Low-temperature embrittlement and fracture of metals with different crystal lattices—Dislocation mechanisms. Nucl. Mater. Energy 2016, 9, 496–501. [Google Scholar] [CrossRef]
- Benac, D.J.; Cherolis, N.; Wood, D. Managing Cold Temperature and Brittle Fracture Hazards in Pressure Vessels. J. Fail. Anal. Prev. 2016, 16, 55–66. [Google Scholar] [CrossRef]
- Hansen, N. Hall-petch relation and boundary strengthening. Scr. Mater. 2004, 51, 801–806. [Google Scholar] [CrossRef]
- Shin, S.Y.; Hwang, B.; Lee, S.; Kim, N.J.; Ahn, S.S. Correlation of microstructure and charpy impact properties in API X70 and X80 line-pipe steels. Metall. Mater. Trans. A 2007, 458, 281–289. [Google Scholar] [CrossRef]
- Panin, S.; Vinogradov, A.; Moiseenko, D.; Maksimov, P.; Berto, F.; Byakov, A.; Eremin, A.; Narkevich, N. Numerical and Experimental Study of Strain Localization in Notched Specimens of a Ductile Steel on Meso- and Macroscales. Adv. Eng. Mater. 2016, 18, 2095–2106. [Google Scholar] [CrossRef]
- Margolin, B.Z.; Shvetsova, V.A. Brittle fracture criterion: Structural mechanics approach. Strength Mater. 1992, 24, 115–131. [Google Scholar] [CrossRef]
- Goritskii, V.M.; Shneyderov, G.R.; Lushkin, M.A. Nature of anisotropy of impact toughness of structural steels with ferrite-pearlite structure. Phys. Met. Metall. 2013, 114, 877–883. [Google Scholar] [CrossRef]
- Panin, S.V.; Maruschak, P.O.; Vlasov, I.V.; Moiseenko, D.D.; Berto, F.; Vinogradov, A. Effect of temperature-force factors and concentrator shape on impact fracture mechanisms of 17Mn1Si steel. Adv. Mater. Sci. Eng. 2017, 2017, 12. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).