Morphology and Crystallography of Ausferrite in Austempered Ductile Iron
Abstract
:1. Introduction
2. Materials and Methods
3. Results
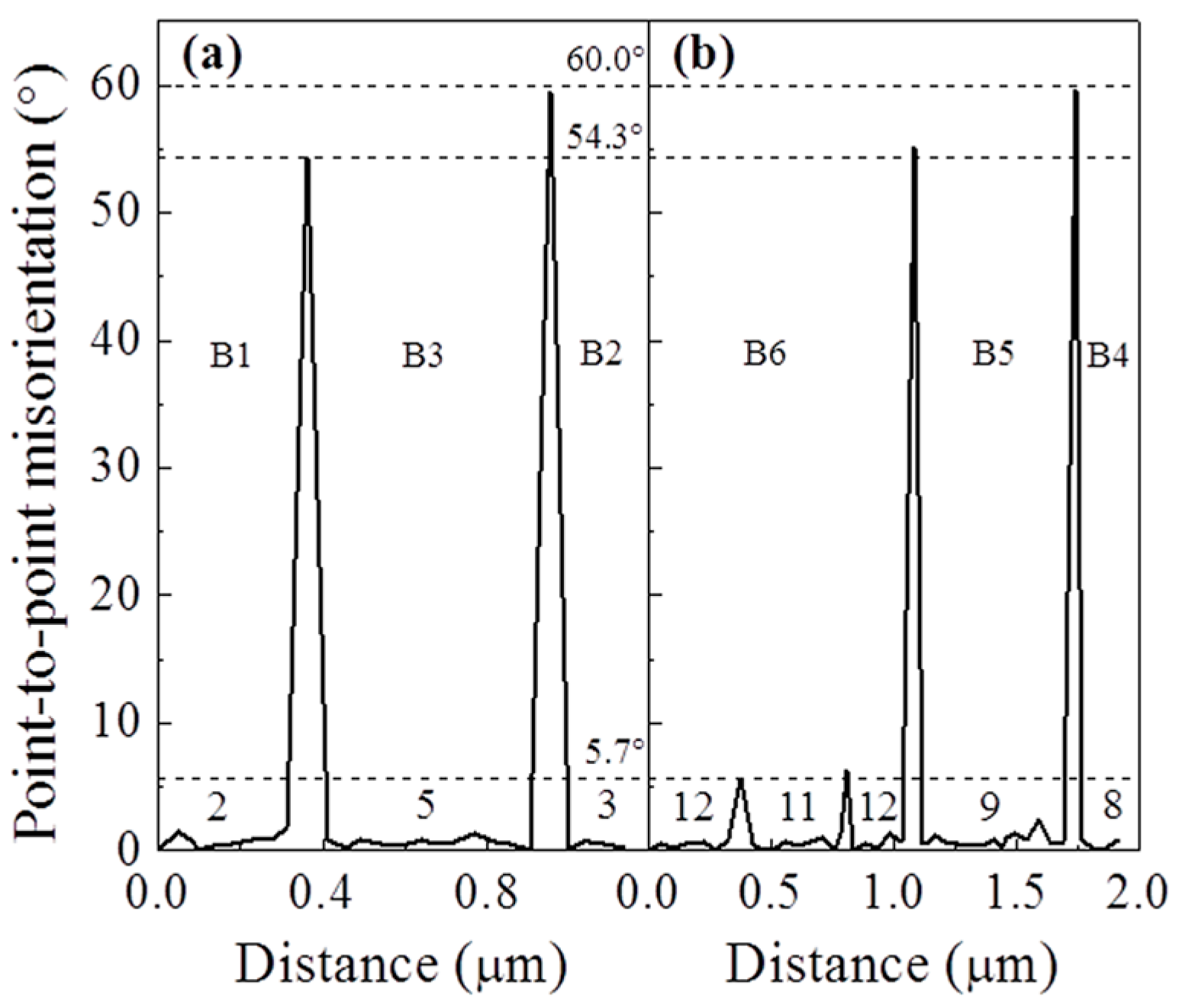
3.1. Analysis of Ferrite/Austenite
3.2. Ferrite/Austenite Boundaries
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Humbert, M.; Germain, L.; Gey, N.; Boucard, E. Evaluation of the orientation relations from misorientation between inherited variants: Application to ausformed martensite. Acta Mater. 2015, 82, 137–144. [Google Scholar] [CrossRef]
- Guo, Z.; Lee, C.S.; Morris, J.W., Jr. On coherent transformations in steel. Acta Mater. 2004, 52, 5511–5518. [Google Scholar] [CrossRef]
- Kitahara, H.; Ueji, R.; Tsuji, N.; Minamino, Y. Crystallographic features of lath martensite in low-carbon steel. Acta Mater. 2006, 54, 1279–1288. [Google Scholar] [CrossRef]
- He, Y.; Godet, S.; Jonas, J.J. Observations of the Gibeon meteorite and the inverse Greninger–Troiano orientation relationship. J. Appl. Cryst. 2006, 39, 72–81. [Google Scholar] [CrossRef]
- Morito, S.; Huang, X.; Furuhara, T.; Maki, T.; Hansen, N. The morphology and crystallography of lath martensite in alloy steels. Acta Mater. 2006, 54, 5323–5331. [Google Scholar] [CrossRef]
- Sato, H.; Zaefferer, S. A study on the formation mechanisms of butterfly-type martensite in Fe–30% Ni alloy using EBSD-based orientation microscopy. Acta Mater. 2009, 57, 1931–1937. [Google Scholar] [CrossRef]
- Kurdjumov, G.; Sachs, G. Über den mechanismus der stahlhärtung. Z. Phys. 1930, 64, 325–343. [Google Scholar] [CrossRef]
- Nishiyama, Z. X-ray investigation of the mechanism of the transformation from face-centered cubic lattice to body-centered cubic. Sci. Rep. Tohoku Univ. 1934, 23, 637–664. [Google Scholar]
- Wassermann, G. Uder den mechanismus der α-γ-umwandlung des eisens. Verl. Stahleisen 1935, 17, 149–155. [Google Scholar]
- Greninger, A.B.; Troiano, A.R. The mechanism of martensite formation. Met. Trans. 1949, 185, 590–598. [Google Scholar]
- Pitsch, W. The martensite transformation in thin foils of ironnitrogen alloys. Philos. Mag. 1959, 4, 577–584. [Google Scholar] [CrossRef]
- Morito, S.; Tanaka, H.; Konishi, R.; Furuhara, T.; Maki, T. The morphology and crystallography of lath martensite in Fe–C alloys. Acta Mater. 2003, 51, 1789–1799. [Google Scholar] [CrossRef]
- Ferry, M.; Xu, W. Microstructural and crystallographic features of ausferrite in as-cast gray iron. Mater. Charact. 2004, 53, 43–49. [Google Scholar] [CrossRef]
- Zhang, S.; Morito, S.; Komizo, Y. Variant selection of low carbon high alloy steel in an austenite grain during martensite transformation. ISIJ Int. 2012, 52, 510–515. [Google Scholar] [CrossRef]
- Miyamoto, G.; Iwata, N.; Takayama, N.; Furuhara, T. Quantitative analysis of variant selection in ausformed lath martensite. Acta Mater. 2012, 60, 1139–1148. [Google Scholar] [CrossRef]
- Kinney, C.C.; Pytlewski, K.R.; Khachaturyan, A.G.; Morris, J.W., Jr. The microstructure of lath martensite in quenched 9Ni steel. Acta Mater. 2014, 69, 372–385. [Google Scholar] [CrossRef]
- Furuhara, T.; Kawata, H.; Morito, S.; Maki, T. Crystallography of upper bainite in Fe–Ni–C alloys. Mater. Sci. Eng. A 2006, 431, 228–236. [Google Scholar] [CrossRef]
- Pancholi, V.; Krishnan, M.; Samajdar, I.S.; Yadav, V.; Ballal, N.B. Self-accommodation in the bainitic microstructure of ultra-high-strength steel. Acta Mater. 2008, 56, 2037–2050. [Google Scholar] [CrossRef]
- Takayama, N.; Miyamoto, G.; Furuhara, T. Effects of transformation temperature on variant pairing of bainitic ferrite in low carbon steel. Acta Mater. 2012, 60, 2387–2396. [Google Scholar] [CrossRef]
- Suikkanen, P.P.; Cayron, C.; DeArdo, A.J.; Karjalainen, L.P. Crystallographic analysis of isothermally transformed bainite in 0.2C–2.0Mn–1.5Si–0.6Cr steel using EBSD. J. Mater. Sci. Technol. 2013, 29, 359–366. [Google Scholar] [CrossRef]
- Shibata, A.; Murakami, T.; Morito, S.; Furuhara, T.; Maki, T. The origin of midrib in lenticular martensite. Mater. Trans. 2008, 49, 1242–1248. [Google Scholar] [CrossRef]
- Kelly, P.M.; Jostsons, A.; Blake, R.G. The orientation relationship between lath martensite and austenite in low carbon, low alloy steels. Acta Metall. Mater. 1990, 38, 1075–1081. [Google Scholar] [CrossRef]
- Pham, A.H.; Ohba, T.; Morito, S.; Hayashi, T. An advanced fitting method for crystallographic and morphological analyses of EBSD data applied for low-carbon steel martensite. Mater. Trans. 2013, 54, 1396–1402. [Google Scholar] [CrossRef]
- Wang, C.; Qiu, H.; Kimura, Y.; Inoue, T. Morphology, crystallography, and crack paths of tempered lath martensite in a medium-carbon low-alloy steel. Mater. Sci. Eng. A 2016, 669, 48–57. [Google Scholar] [CrossRef]
- Zhang, M.X.; Kelly, P.M. Accurate orientation relationship between ferrite and austenite in low carbon martensite and granular bainite. Scr. Mater. 2002, 47, 749–755. [Google Scholar] [CrossRef]
- Qi, L.; Khachaturyan, A.G.; Morris, J.W., Jr. The microstructure of dislocated martensitic steel: Theory. Acta Mater. 2014, 76, 23–39. [Google Scholar] [CrossRef]
- Hsu, C.-H.; Chuang, T.-L. Influence of stepped austempering process on the fracture toughness of austempered ductile iron. Metall. Mater. Trans. A 2001, 32, 2509–2513. [Google Scholar] [CrossRef]
- Francucci, G.; Sikora, J.; Dommarco, R. Abrasion resistance of ductile iron austempered by the two-step process. Mater. Sci. Eng. A 2008, 485, 46–54. [Google Scholar] [CrossRef]
- Han, C.F.; Wang, Q.Q.; Sun, Y.F.; Li, J. Effects of molybdenum on the wear resistance and corrosion resistance of carbidic austempered ductile iron. Metallogr. Microstruct. Anal. 2015, 4, 298–304. [Google Scholar] [CrossRef]
- Yang, J.; Putatunda, S.K. Improvement in strength and toughness of austempered ductile cast iron by a novel two-step austempering process. Mater. Des. 2004, 25, 219–230. [Google Scholar] [CrossRef]
- Erić, O.; Rajnović, D.; Zec, S.; Sidjanin, L.; Jovanović, M.T. Microstructure and fracture of alloyed austempered ductile iron. Mater. Charact. 2006, 57, 211–217. [Google Scholar] [CrossRef]
- Elsayed, A.H.; Megahed, M.M.; Sadek, A.A.; Abouelela, K.M. Fracture toughness characterization of austempered ductile iron produced using both conventional and two-step austempering processes. Mater. Des. 2009, 30, 1866–1877. [Google Scholar] [CrossRef]
- Wu, K.M. Three-dimensional analysis of acicular bainitic ferrite in a low-carbon steel containing titanium. Scr. Mater. 2006, 54, 569–574. [Google Scholar] [CrossRef]
- GB/T 24733-2009. Austempered Ductile Iron (ADI) Castings; China Standard Press: Beijing, China, 2009. [Google Scholar]
- Wang, C.; Qiu, H.; Inoue, T. Delaminating crack paths in ultrafine, elongated ferritic steel. ISIJ Int. 2009, 53, 2272–2274. [Google Scholar] [CrossRef]
- Germain, L.; Gey, N.; Mercier, R.; Blaineau, P.; Humbert, M. An advanced approach to reconstructing parent orientation maps in the case of approximate orientation relations: Application to steels. Acta Mater. 2012, 60, 4551–4562. [Google Scholar] [CrossRef]
- Cayron, C. EBSD imaging of orientation relationships and variant groupings in different martensitic alloys and Widmanstätten iron meteorites. Mater. Charact. 2014, 94, 93–110. [Google Scholar] [CrossRef]





| G–T Variant | {111}γ | {011}α | Bain Variant | Packet | ||
|---|---|---|---|---|---|---|
| GT1 | () | () | [] | [] | X | P1 |
| GT2 | () | () | [] | [] | X | |
| GT3 | () | () | [] | [] | Y | |
| GT4 | () | () | [] | [] | Y | |
| GT5 | () | () | [] | [] | Z | |
| GT6 | () | () | [] | [] | Z | |
| GT7 | () | () | [] | [] | X | P2 |
| GT8 | () | () | [] | [] | X | |
| GT9 | () | () | [] | [] | Y | |
| GT10 | () | () | [] | [] | Y | |
| GT11 | () | () | [] | [] | Z | |
| GT12 | () | () | [] | [] | Z | |
| GT13 | () | () | [] | [] | X | P3 |
| GT14 | () | () | [] | [] | X | |
| GT15 | () | () | [] | [] | Y | |
| GT16 | () | () | [] | [] | Y | |
| GT17 | () | () | [] | [] | Z | |
| GT18 | () | () | [] | [] | Z | |
| GT19 | () | () | [] | [] | X | P4 |
| GT20 | () | () | [] | [] | X | |
| GT21 | () | () | [] | [] | Y | |
| GT22 | () | () | [] | [] | Y | |
| GT23 | () | () | [] | [] | Z | |
| GT24 | () | () | [] | [] | Z |
| Group | Variant Pair | Misorientation Angle | Number Percentage |
|---|---|---|---|
| 1 | GT7-GT8, GT9-GT10, GT11-GT12 | 5.7° | 20% |
| 2 | GT7-GT10, GT8-GT11, GT9-GT12 | 54.3° | 20% |
| 3 | GT7-GT9, GT7-GT11, GT7-GT12 | 60° | 60% |
| GT8-GT9, GT8-GT10, GT8-GT12 | |||
| GT9-GT11, GT10-GT11, GT10-GT12 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Du, X.; Li, S.; Sun, Y.; Yang, P. Morphology and Crystallography of Ausferrite in Austempered Ductile Iron. Metals 2017, 7, 238. https://doi.org/10.3390/met7070238
Wang C, Du X, Li S, Sun Y, Yang P. Morphology and Crystallography of Ausferrite in Austempered Ductile Iron. Metals. 2017; 7(7):238. https://doi.org/10.3390/met7070238
Chicago/Turabian StyleWang, Chengduo, Xueshan Du, Songjie Li, Yufu Sun, and Peixu Yang. 2017. "Morphology and Crystallography of Ausferrite in Austempered Ductile Iron" Metals 7, no. 7: 238. https://doi.org/10.3390/met7070238
APA StyleWang, C., Du, X., Li, S., Sun, Y., & Yang, P. (2017). Morphology and Crystallography of Ausferrite in Austempered Ductile Iron. Metals, 7(7), 238. https://doi.org/10.3390/met7070238






