Experimental Analysis of the Behaviour of Aluminium Alloy EN 6082AW T6 at High Temperature
Abstract
:1. Introduction
1.1. Research Motivation
1.2. Previous Research
2. Test Study and Comparison of Results
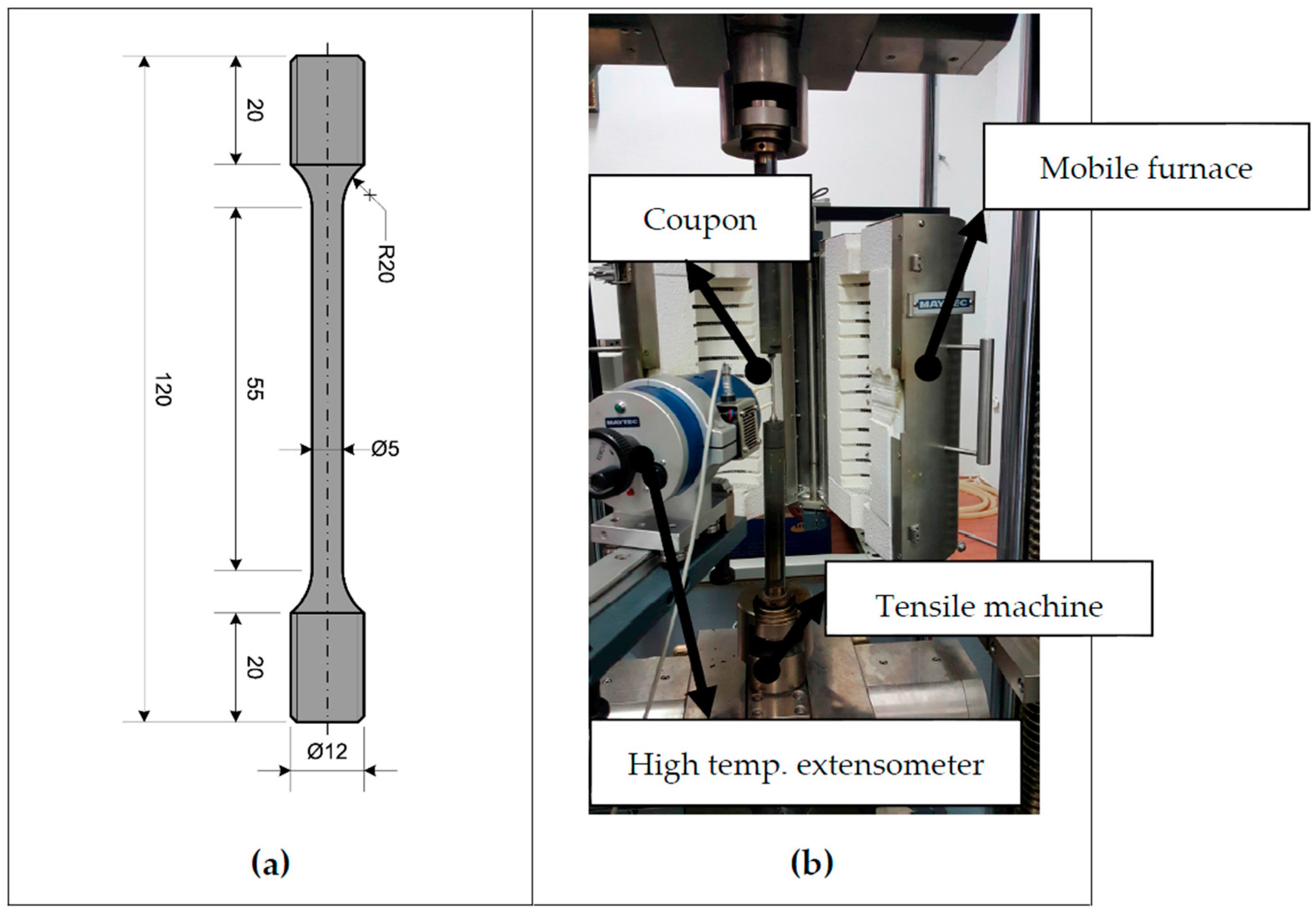
2.1. Test Setup
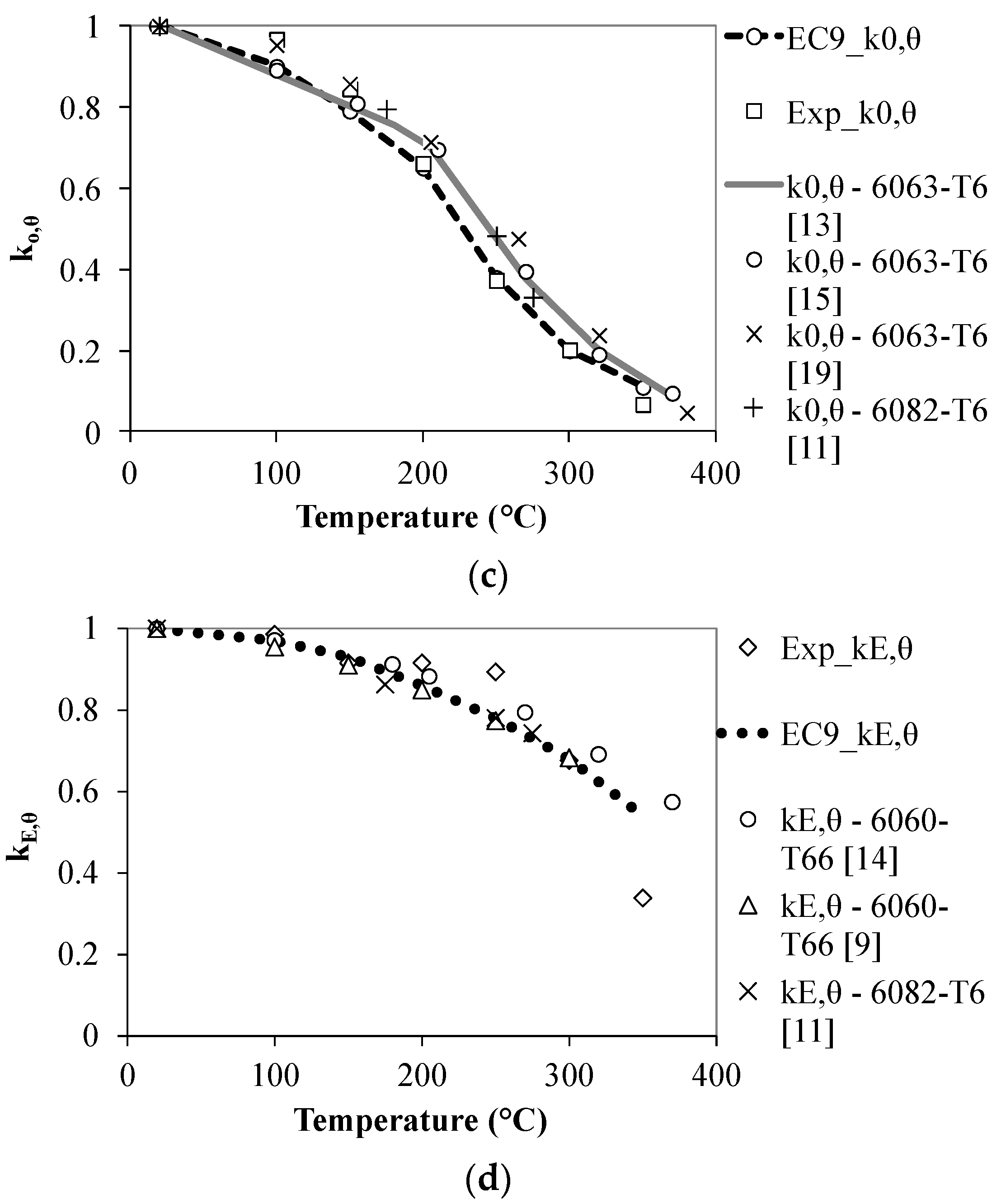
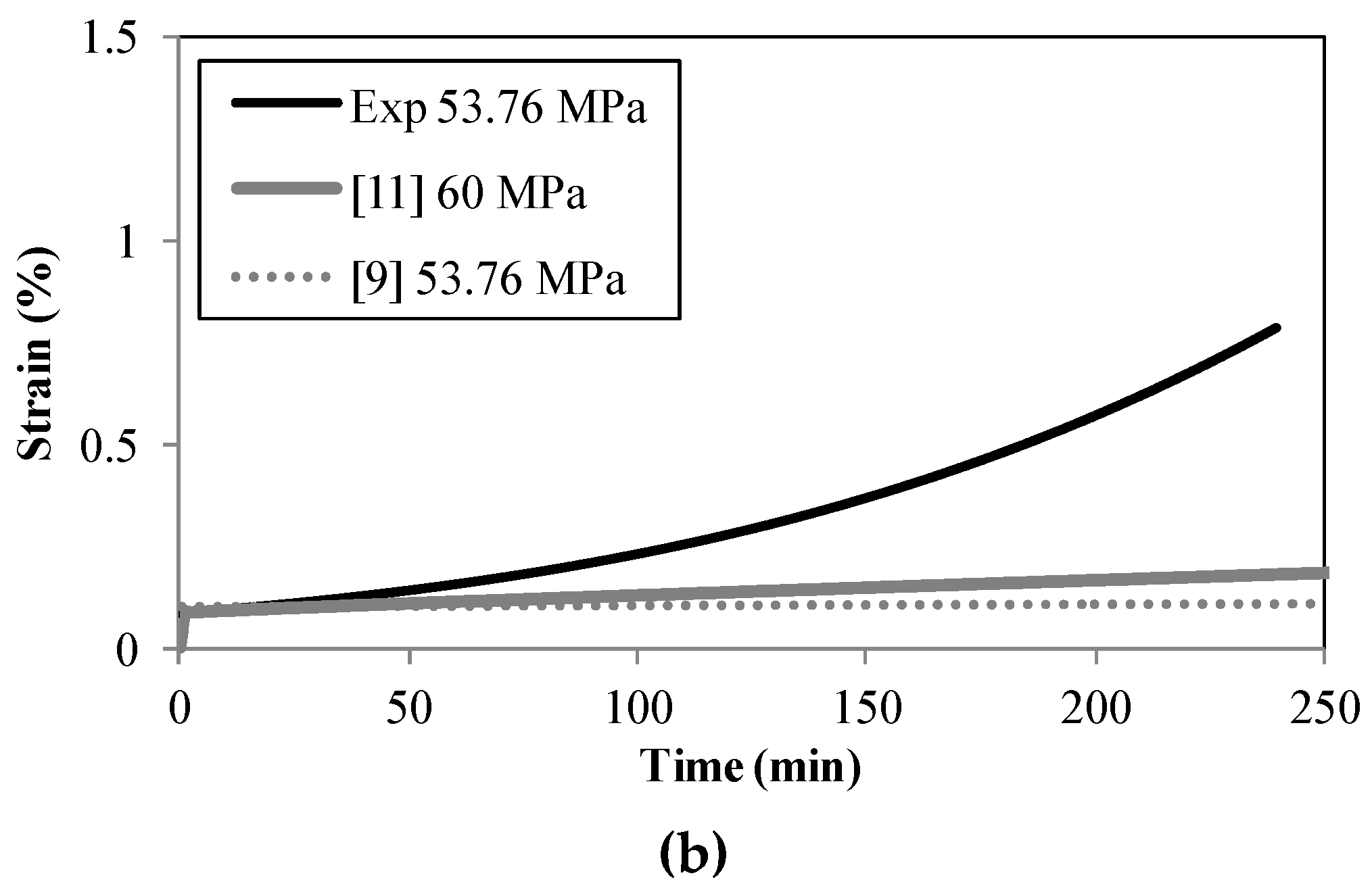
2.2. Comparison with EC9 and Other Studies
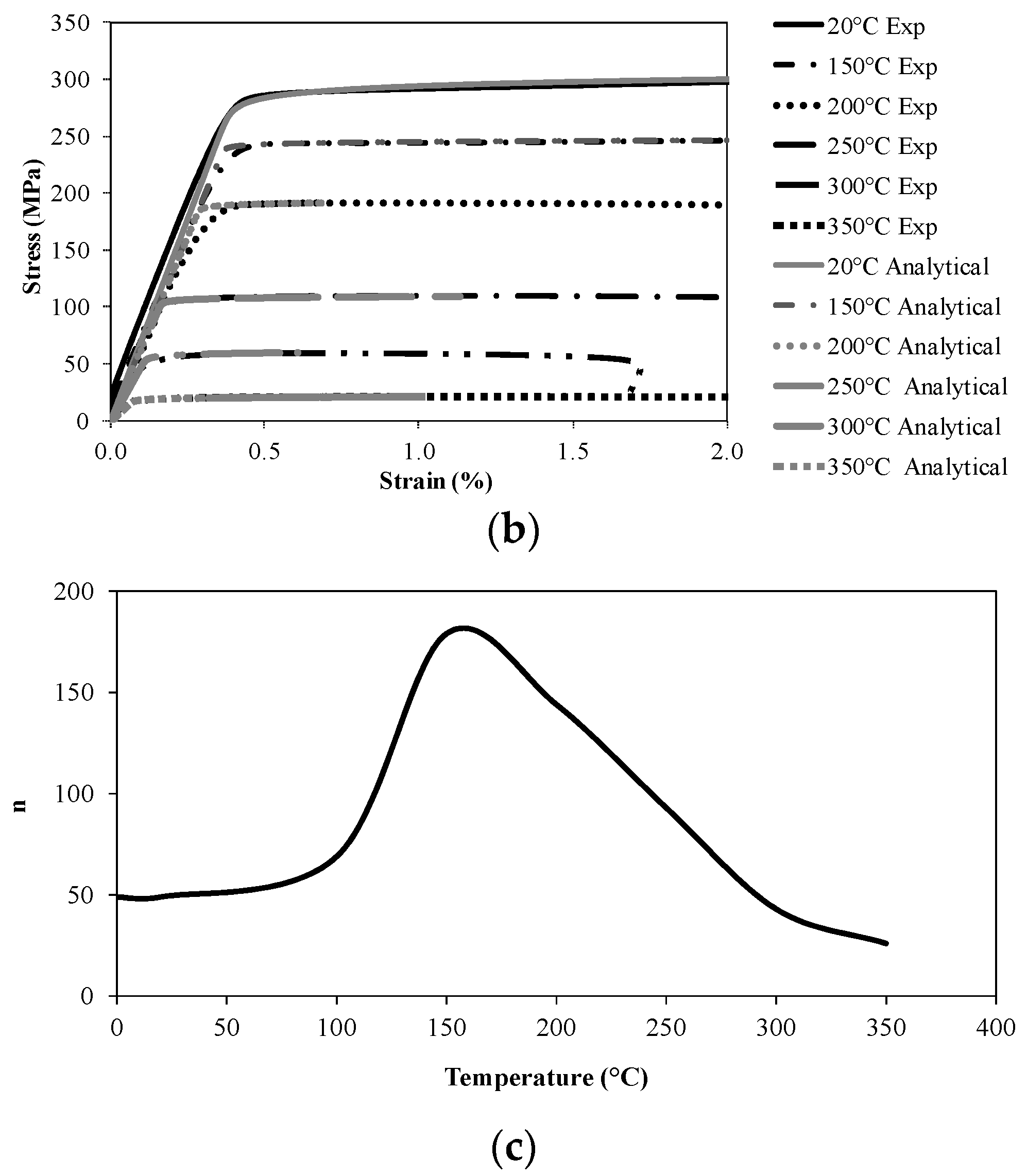
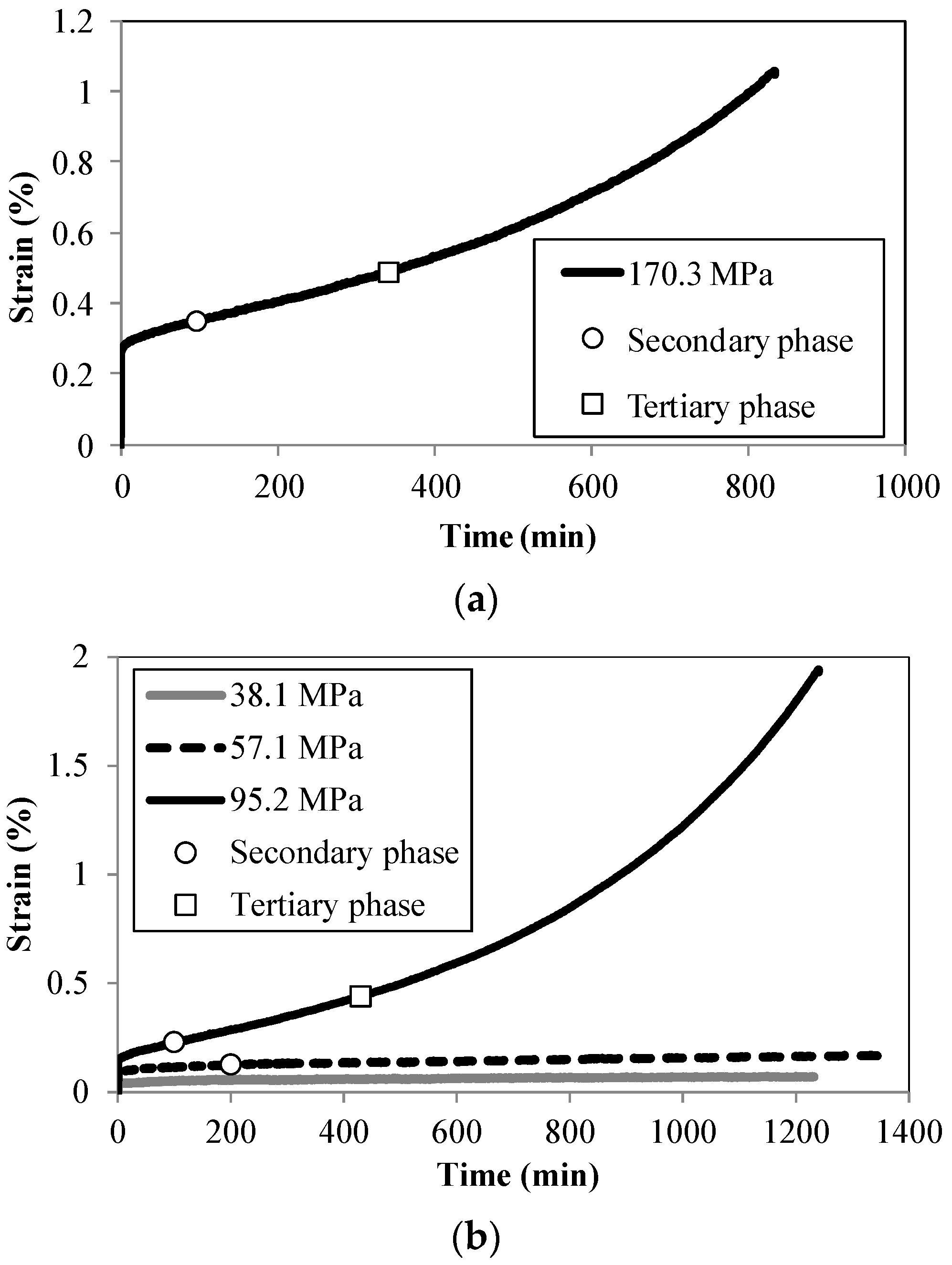
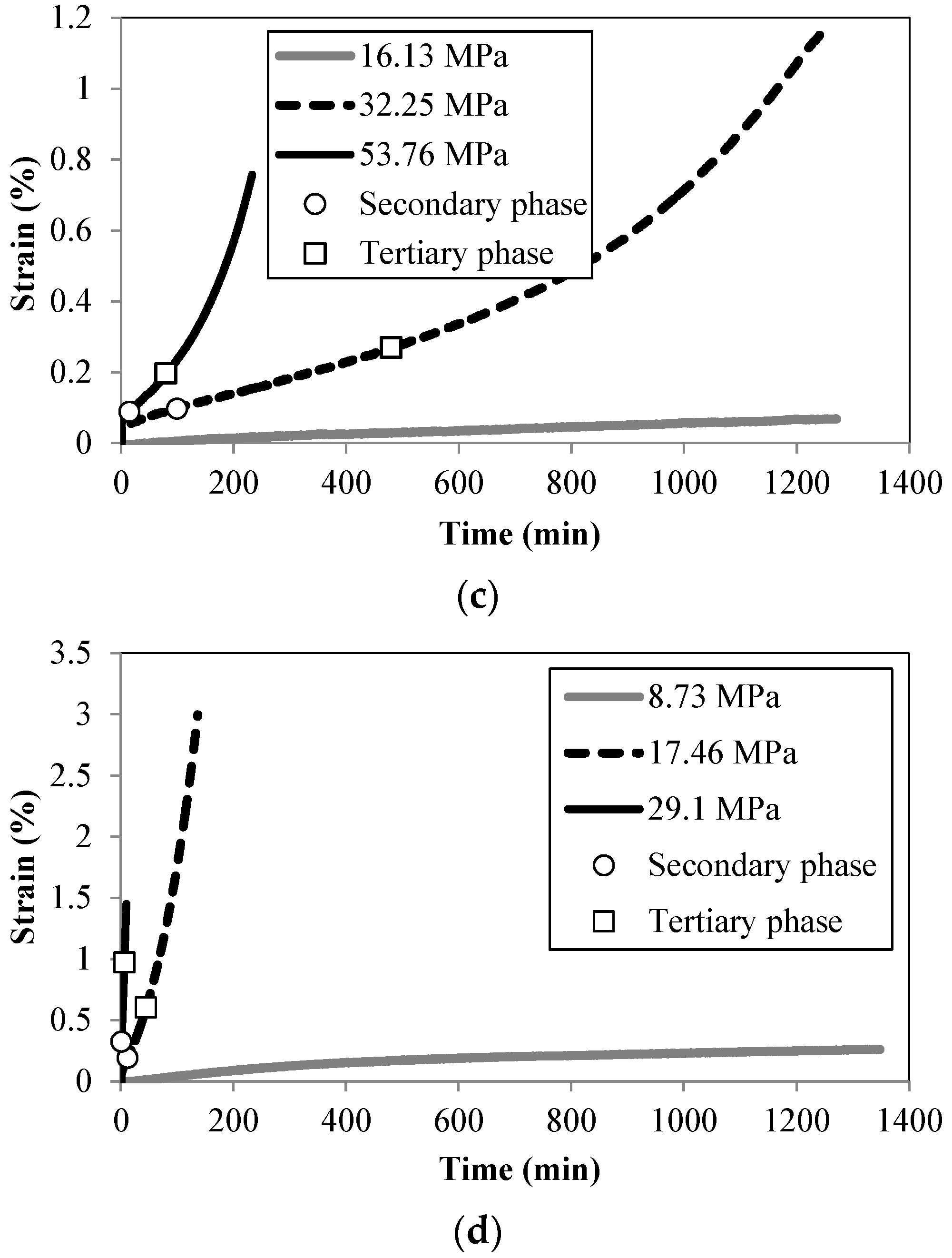
2.3. Test Results and Comparison
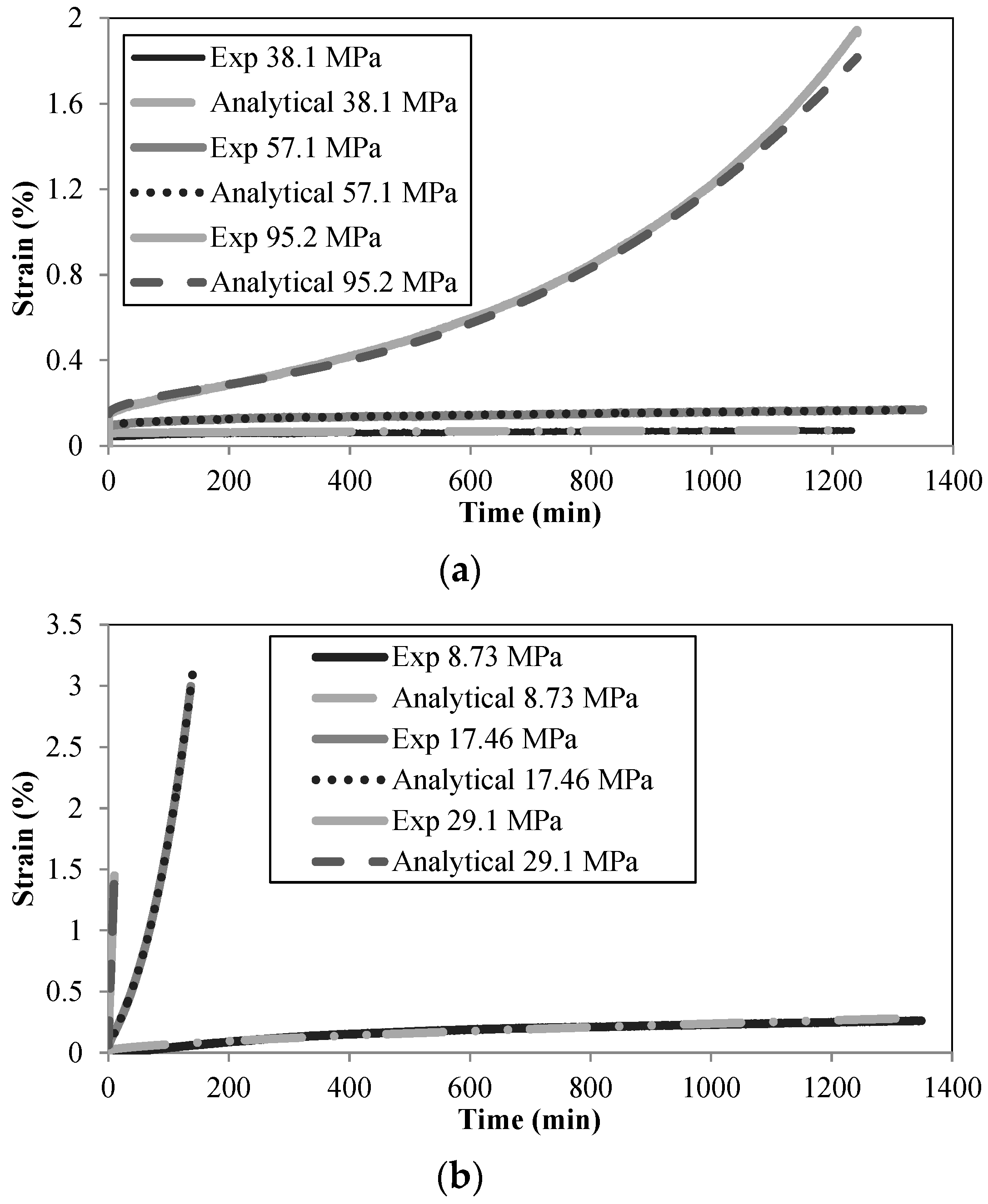
2.4. Analytical Creep Model
2.5. Microstructure of Aluminium
3. Discussion of Results
3.1. Constant Stress-Rate Tests
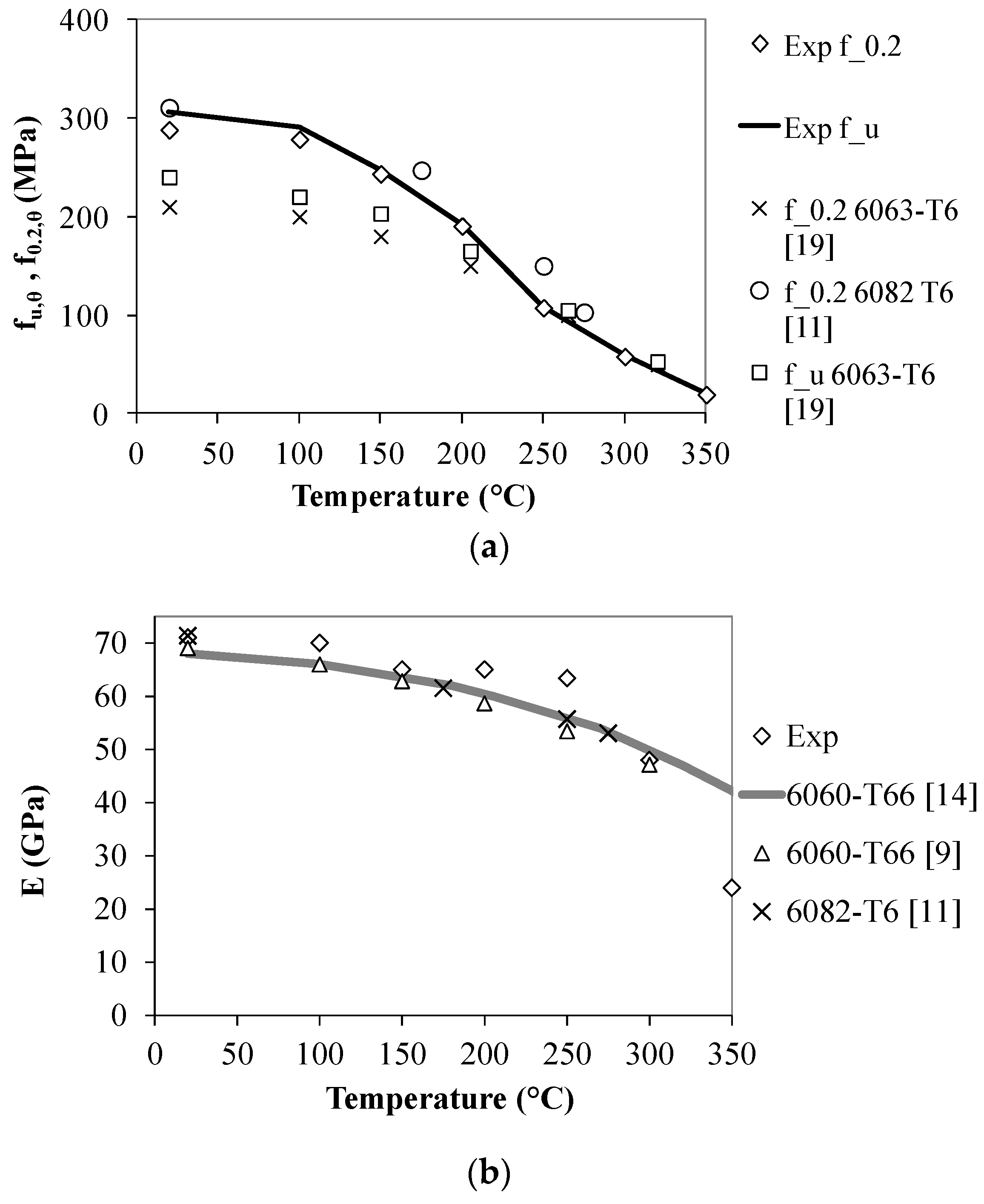
3.2. Stress at 0.2% Strain and Modulus of Elasticity
3.3. Creep Development
3.4. Time of Occurrence of Creep Phases
3.5. Accuracy of the Analytical Creep Model
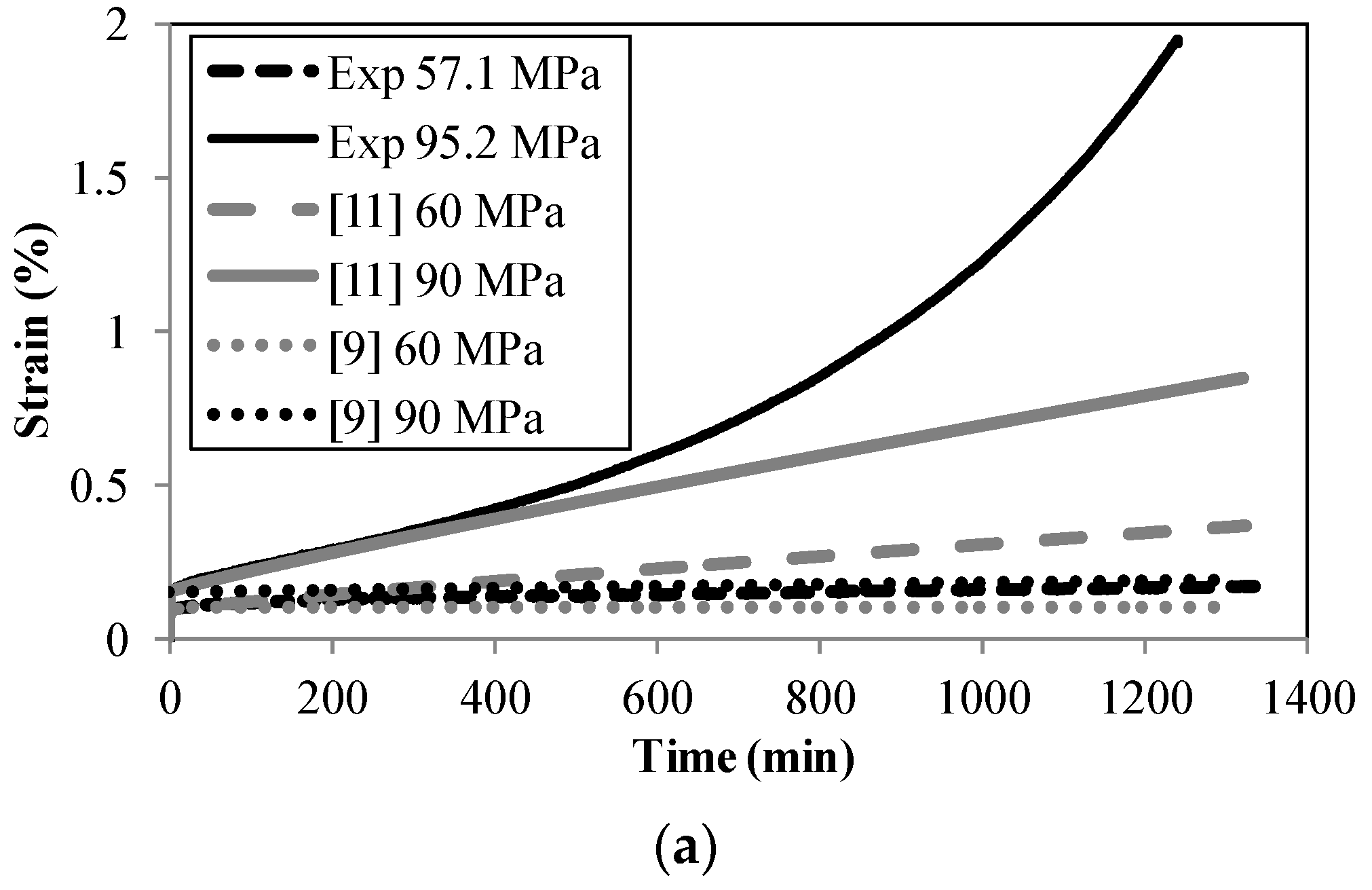
3.6. Comparison with Existing Creep Models
4. Conclusions
- Mechanical properties of the analysed alloy correlate well with the proposal from Eurocode 9 and study [11] which is based on the same alloy type;
- The critical temperature interval for creep manifestation of the analysed alloy lies within the range 200 °C–300 °C;
- The analytical creep model proposed is sufficiently accurate to represent the creep test results;
- Creep test results correlate well with results from the study by Langhelle [11] for the primary and secondary phases.
Acknowledgements
Author Contributions
Conflicts of Interest
Nomenclature
| total strain in fire conditions | |
| temperature dependent thermal strain | |
| stress-related strain | |
| stress-, temperature-, and time-dependent creep strain | |
| strain value at fu,θ | |
| εt | ultimate strain |
| f0.2 | stress at 0.2% strain at normal temperature |
| f0.2,θ | stress at 0.2% strain at temperature θ |
| fu | ultimate strength at normal temperature |
| fu, θ | ultimate strength at temperature θ |
| Ey,20 | modulus of elasticity at normal temperature |
| Ey,θ | modulus of elasticity at temperature θ |
| kE,θ | reduction factor for modulus of elasticity at temperature θ |
| k0,θ | reduction factor for stress at 0.2% strain at temperature θ |
References
- Mazzolani, F.M. Aluminium Alloy Structures, 2nd ed.; E & FN SPON, Chapman & Hall: London, UK, 1994. [Google Scholar]
- Skejić, D.; Boko, I.; Torić, N. Aluminium as a modern material for structures. Građevinar 2015, 67, 1075–1085. [Google Scholar]
- European Committee for Standardization. EN 1999-1-1:2007, Eurocode 9—Design of Aluminium Structures—Part 1-1: General Structural Rules; European Committee for Standardization: Brussels, Belgium, 2007. [Google Scholar]
- Purkiss, J.A. Fire Safety Engineering Design of Structures, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2007. [Google Scholar]
- Maljaars, J.; Soetens, F.; Katgerman, L. Constitutive model for aluminium alloys exposed to fire conditions. Metall. Mater. Trans. A 2008, 39, 778–789. [Google Scholar] [CrossRef]
- Maljaars, J. Literature Study on Aluminium Structures Exposed to Fire, Report 1; Netherlands Institute for Metals Research, Technical University of Eindhoven, TNO Built Environment and Geosciences: Eindhoven, The Netherlands, 2005. [Google Scholar]
- Maljaars, J.; Twilt, L.; Fellinger, J.H.H.; Snijder, H.H.; Soetens, F. Aluminium structures exposed to fire conditions—An overview. Heron 2010, 55, 85–122. [Google Scholar]
- Maljaars, J.; Soetens, F.; Snijder, H.H. Local buckling of aluminium structures exposed to fire Part 1: Tests. Thin Walled Struct. 2009, 47, 1404–1417. [Google Scholar] [CrossRef]
- Maljaars, J.; Soetens, F.; Snijder, H.H. Local buckling of aluminium structures exposed to fire Part 2: Finite element models. Thin Walled Struct. 2009, 47, 1418–1428. [Google Scholar] [CrossRef]
- Zheng, Y.Q.; Zhang, Z. The fire performance and fire-resistance design of aluminium alloy I-beams. Fire Mater. 2016, 40, 141–157. [Google Scholar] [CrossRef]
- Langhelle, N.K. Experimental Validation and Calibration of Nonlinear Finite Element Models for Use in Design of Aluminium Structures Exposed to Fire. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, April 1999. [Google Scholar]
- Eberg, E.; Amdahl, J.; Langhelle, N.K. Experimental Investigation of Creep Behaviour of Aluminium at Elevated Temperatures, SINTEF Report No. STF22 F96713; SINTEF: Trondheim, Norway, 1996.
- Fogle, E.J.; Lattimer, B.Y.; Feih, S.; Kandare, E.; Mouritz, A.P.; Case, S.W. Compression load failure of aluminium plates due to fire. Eng. Struct. 2012, 34, 155–162. [Google Scholar] [CrossRef]
- Kaufman, J.G. Properties of Aluminium Alloys—Tensile, Creep and Fatigue Data at High and Low Temperatures; ASM International: Materials Park, OH, USA, 1999. [Google Scholar]
- Voorhees, H.R.; Freeman, J.W. Report on the Elevated-Temperature Properties of Aluminium and Magnesioum Alloys; STP No. 291; American Society of Testing Materials: West Conshohocken, PA, USA, 1960. [Google Scholar]
- Anderberg, Y. Modelling Steel Behaviour. Fire Saf. J. 1988, 13, 17–26. [Google Scholar] [CrossRef]
- American Society for Testing and Materials (ASTM). ASTM E8/E8M-11, Standard Test Methods for Tension Testing of Metallic Materials; ASTM International: West Conshohocken, PA, USA, 2011. [Google Scholar]
- American Society for Testing and Materials (ASTM). ASTM E21–09, Standard Test Methods for Elevated Temperature Tension Tests of Metallic Materials; ASTM International: West Conshohocken, PA, USA, 2009. [Google Scholar]
- Metallnormcentralen (MNC). Aluminium Konstruksjonsbock Materiallaera; MNC Handbook 12; MNC: Stockholm, Sweden, 1983. [Google Scholar]
- Shepherd, P. The Performance in Fire of Restrained Columns in Steel-Framed Construction. Ph.D. Thesis, University of Sheffield, Sheffield, UK, July 1999. [Google Scholar]
- Faggiano, B.; De Matteis, G.; Landolfo, R.; Mazzolani, F. Behaviour of aluminium alloy structures under fire. J. Civ. Eng. Manag. 2004, 10, 183–190. [Google Scholar] [CrossRef]
- Harmathy, T.Z. Creep Deflections of Metal Beams in Transient Heating Processes, with Particular Reference to Fire. Can. J. Civ. Eng. 1976, 3, 219–228. [Google Scholar] [CrossRef]


| Temperature (°C) | Modulus of Elasticity Ey,θ (GPa) | Yield Strength f0.2,θ (MPa) | Ultimate Strength fu,θ (MPa) | εt (%) |
|---|---|---|---|---|
| 20 | 71.0 | 288.0 | 306.2 | 7.1 |
| 100 | 70.0 | 278.4 | 290.8 | 9.7 |
| 150 | 65.0 | 243.3 | 246.9 | 12.3 |
| 200 | 65.0 | 190.4 | 191.3 | 3.1 |
| 250 | 63.4 | 107.5 | 109.4 | 2.8 |
| 300 | 48.0 | 58.2 | 59.4 | 1.7 |
| 350 | 24.0 | 19.5 | 20.7 | 19.3 |
| Temperature (°C) | Stationary Creep Test Parameters | |||
|---|---|---|---|---|
| Stress σ (MPa) | σ/f0.2,θ | Time of the Occurrence of Secondary Phase (min) | Time of the Occurrence of Tertiary Phase (min) | |
| 150 | 170.3 | 0.7 | 95 | 340 |
| 200 | 38.10 57.10 95.20 | 0.20 0.30 0.50 | - 200 100 | - - 430 |
| 250 | 16.13 32.25 53.76 | 0.15 0.30 0.50 | - 100 15 | - 480 80 |
| 300 | 8.73 17.46 29.10 | 0.15 0.30 0.50 | - 12 1.4 | - 45 6.4 |
| Temperature (°C) | Reduction Factors | |||
|---|---|---|---|---|
| Exp f0.2,θ/f0.2 | EC9 [3] f0.2,θ/f0.2 | Exp Ey,θ/Ey,20 | EC9 [3] Ey,θ/Ey,20 | |
| 100 | 0.97 | 0.90 | 0.99 | 0.97 |
| 150 | 0.84 | 0.79 | 0.92 | 0.93 |
| 200 | 0.66 | 0.65 | 0.92 | 0.86 |
| 250 | 0.37 | 0.38 | 0.89 | 0.78 |
| 300 | 0.20 | 0.20 | 0.68 | 0.68 |
| 350 | 0.07 | 0.11 | 0.34 | 0.54 |
| Temperature (°C) | n |
|---|---|
| 20 | 49 |
| 100 | 69 |
| 150 | 179 |
| 200 | 144 |
| 250 | 93 |
| 300 | 43 |
| 350 | 26 |
| Temperature (°C) | Coefficient | Stress Level (MPa) | ||
|---|---|---|---|---|
| 38.10 (0.20f0.2,θ) | 57.10 (0.30f0.2,θ) | 95.20 (0.50f0.2,θ) | ||
| 200 | a | 3.378 × 10−4 | 5.133 × 10−3 | 8.619 × 10−3 |
| b | 0.5200 | 0.3729 | 0.5115 | |
| c | 0.0586 | 0.0879 | 0.1465 | |
| e | - | 6.650 × 10−10 | 1.000 × 10−8 | |
| f | - | 2.1770 | 2.6270 | |
| 16.13 (0.15f0.2,θ) | 32.25 (0.30f0.2,θ) | 53.76 (0.50f0.2,θ) | ||
| 250 | a | 2.187 × 10−4 | 1.742 × 10−3 | 5.641 × 10−4 |
| b | 0.7468 | 0.7377 | 1.1460 | |
| c | 2.544 × 10−2 | 5.087 × 10−2 | 0.0848 | |
| e | - | 5.523 × 10−10 | 7.583 × 10−8 | |
| f | - | 2.9500 | 2.8270 | |
| 8.73 (0.15f0.2,θ) | 17.46 (0.30f0.2,θ) | 29.10 (0.50f0.2,θ) | ||
| 300 | a | 2.513 × 10−3 | 0.0183 | 0.1697 |
| b | 0.6470 | 0.8291 | 0.9000 | |
| c | 0.0182 | 0.0364 | 0.0606 | |
| e | - | 1.633 × 10−5 | 5.861 × 10−5 | |
| f | - | 2.3690 | 3.1200 | |
| Study | Al | Cu | Si | Fe | Mn | Mg | Zn2 | Cr | Ca | Pb | Ti2 | Sn2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6082-T6–Exp | 96.49 | 0.099 | 1.281 | 0.708 | 0.523 | 0.767 | 0.0615 | 0.0141 | 0.0011 | 0.0034 | 0.0108 | 0.0173 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torić, N.; Brnić, J.; Boko, I.; Brčić, M.; Burgess, I.W.; Uzelac, I. Experimental Analysis of the Behaviour of Aluminium Alloy EN 6082AW T6 at High Temperature. Metals 2017, 7, 126. https://doi.org/10.3390/met7040126
Torić N, Brnić J, Boko I, Brčić M, Burgess IW, Uzelac I. Experimental Analysis of the Behaviour of Aluminium Alloy EN 6082AW T6 at High Temperature. Metals. 2017; 7(4):126. https://doi.org/10.3390/met7040126
Chicago/Turabian StyleTorić, Neno, Josip Brnić, Ivica Boko, Marino Brčić, Ian W. Burgess, and Ivana Uzelac. 2017. "Experimental Analysis of the Behaviour of Aluminium Alloy EN 6082AW T6 at High Temperature" Metals 7, no. 4: 126. https://doi.org/10.3390/met7040126
APA StyleTorić, N., Brnić, J., Boko, I., Brčić, M., Burgess, I. W., & Uzelac, I. (2017). Experimental Analysis of the Behaviour of Aluminium Alloy EN 6082AW T6 at High Temperature. Metals, 7(4), 126. https://doi.org/10.3390/met7040126







.JPG)


