Experimental and Numerical Simulation Investigation on Laser Flexible Shock Micro-Bulging
Abstract
:1. Introduction
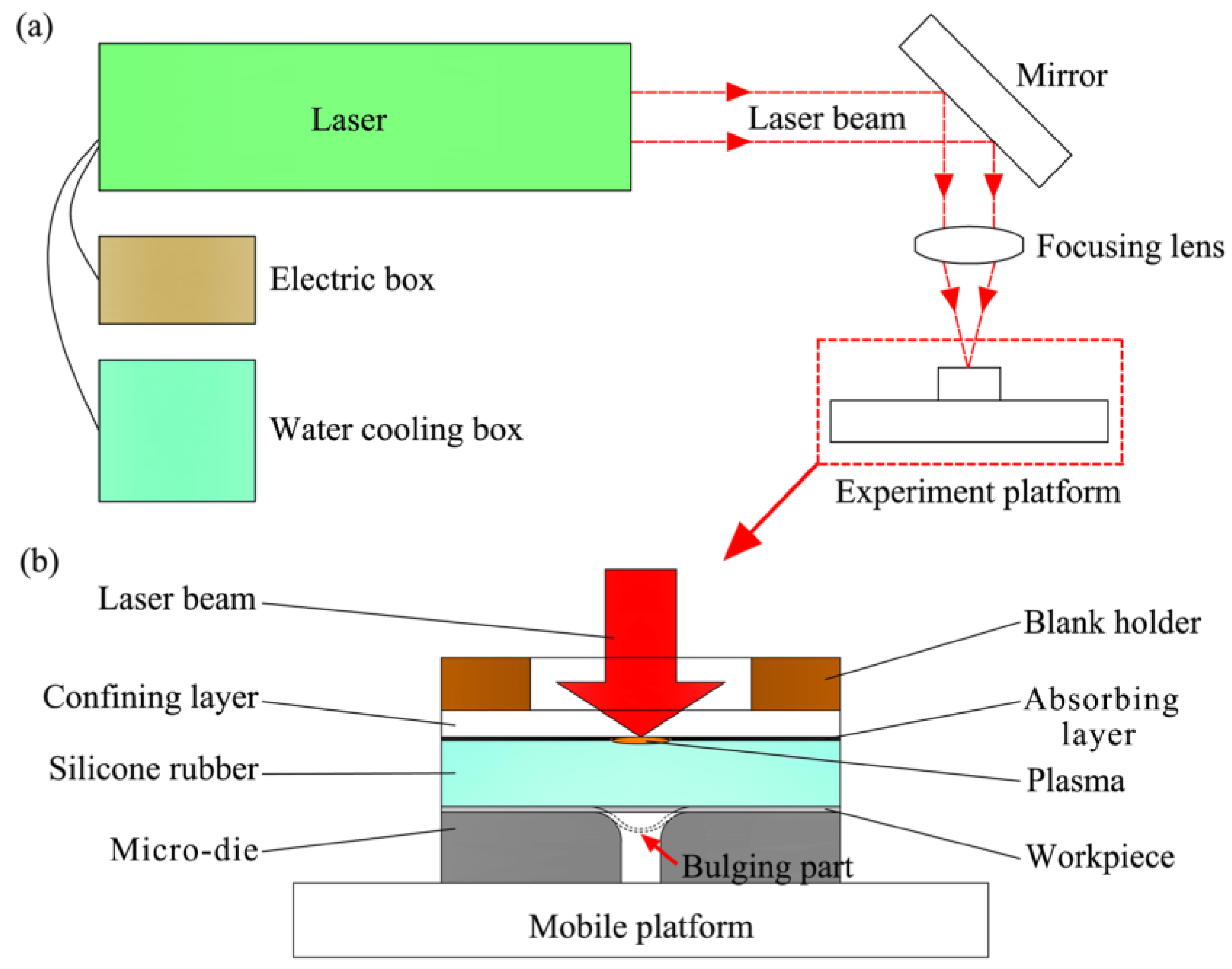
2. Mechanism of Laser Flexible Shock Micro-Bulging
3. Experiment
3.1. Experimental Material
3.2. Micro-Die
3.3. Experimental Parameters
3.4. TEM Methodology
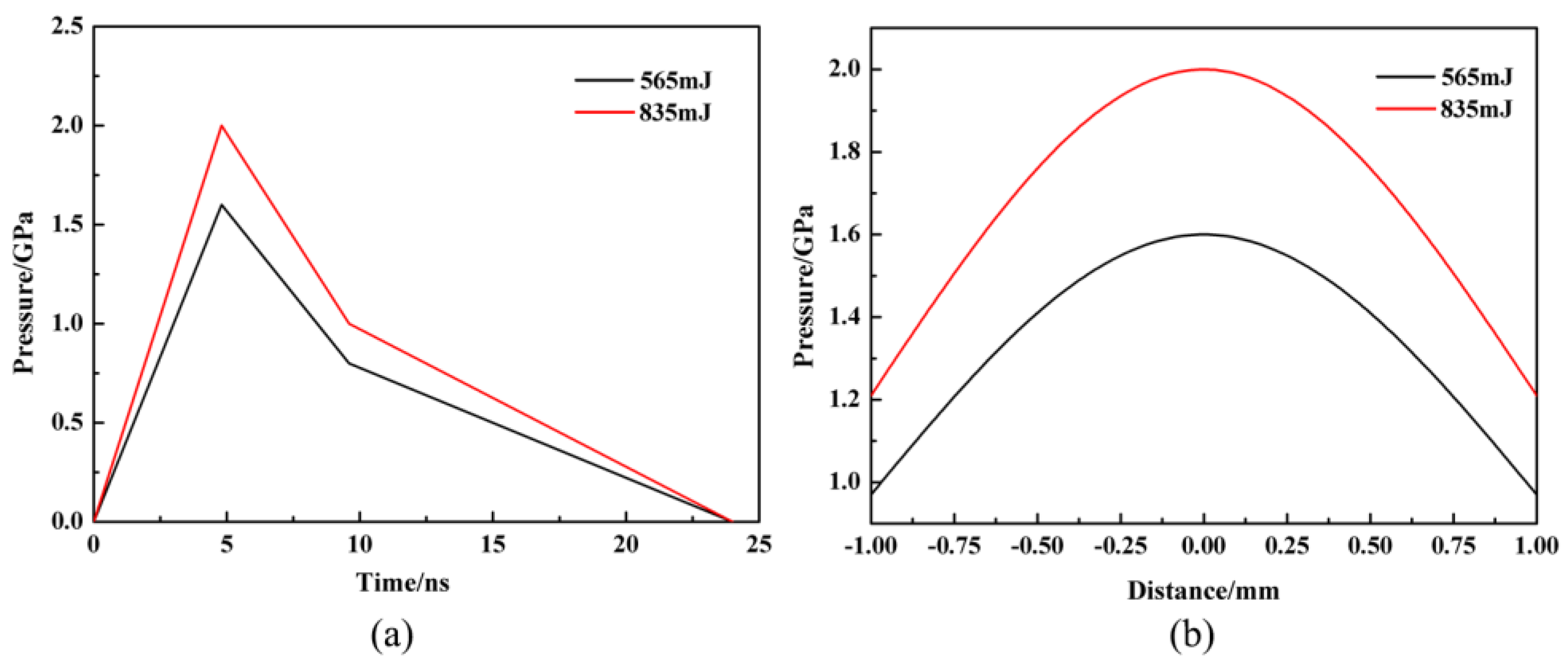
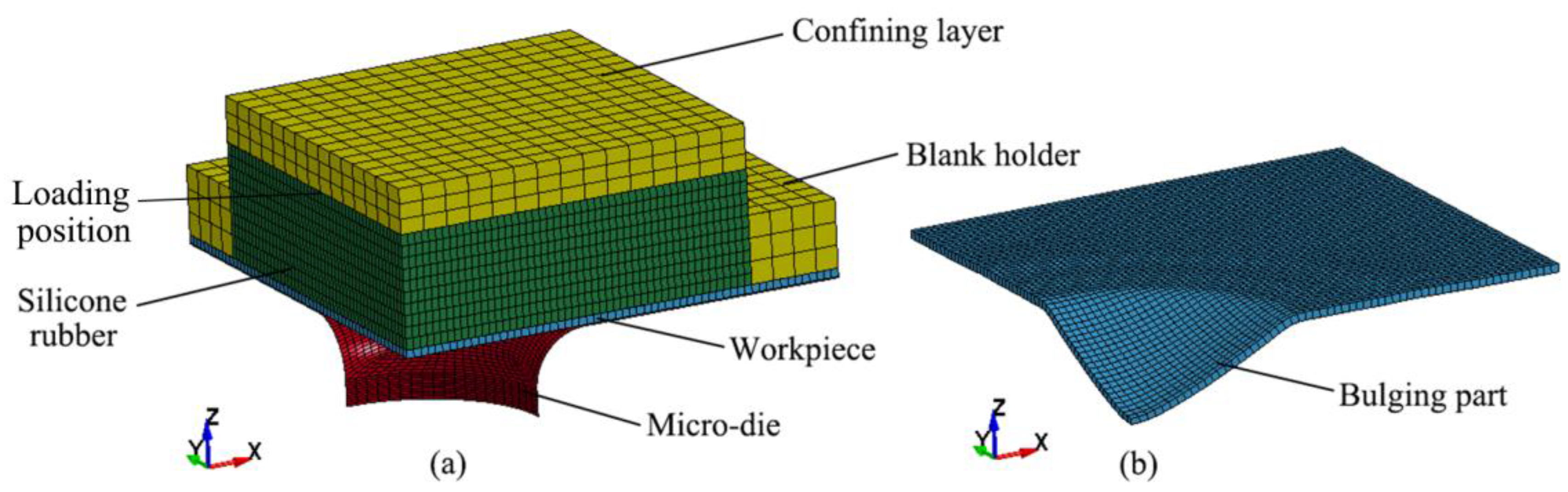
4. Numerical Simulation
5. Results and Discussions
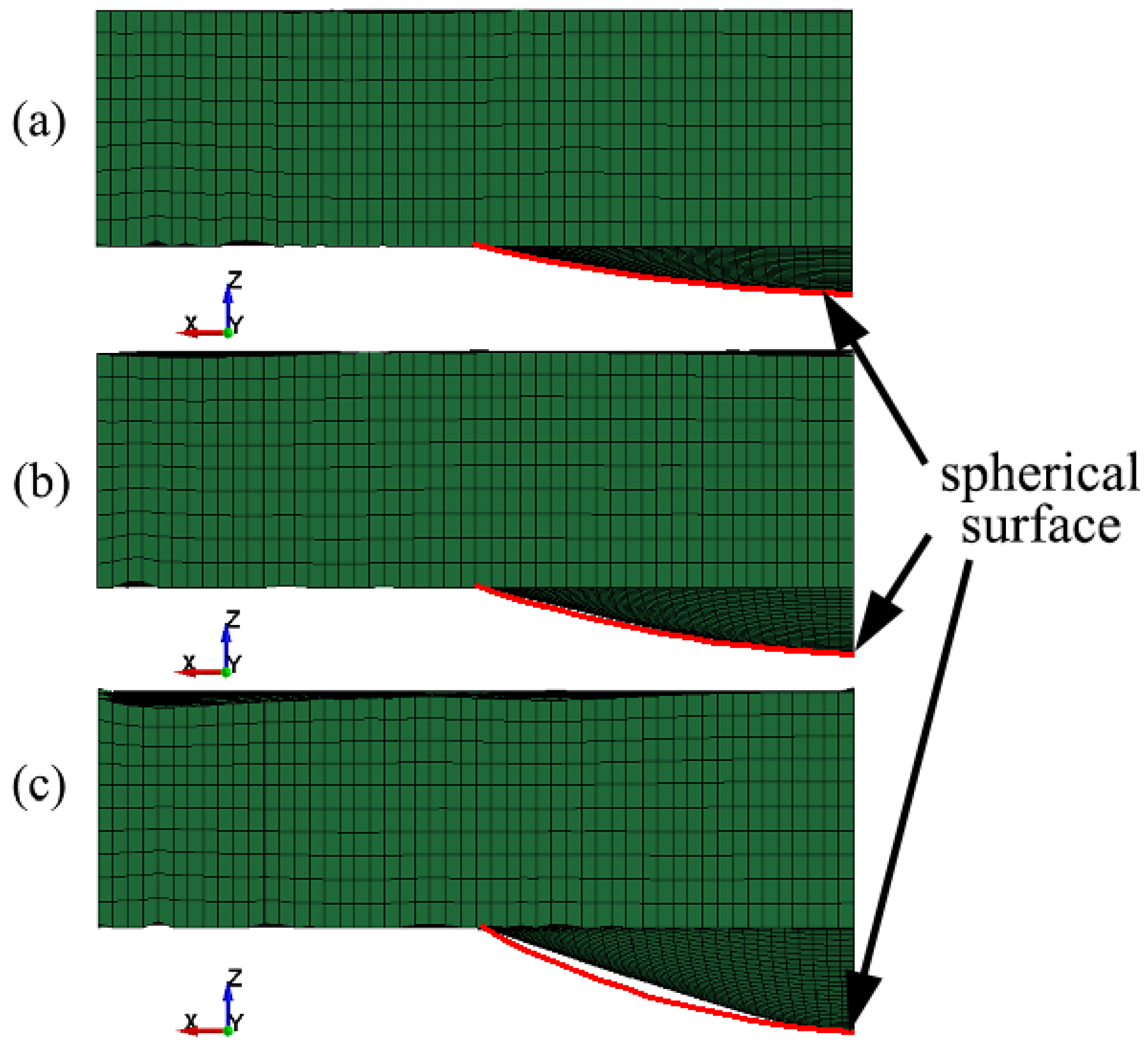
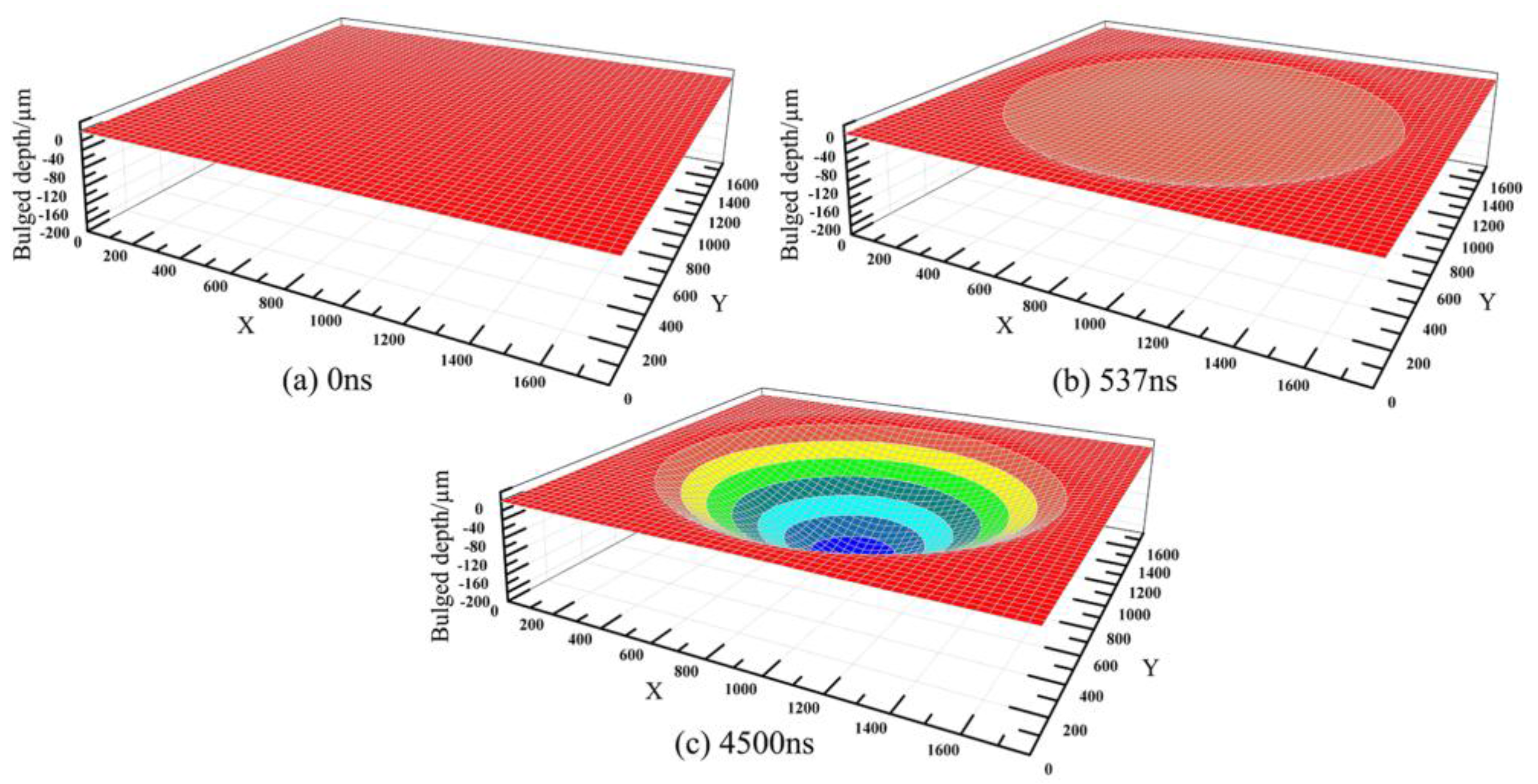
5.1. Surface Morphology
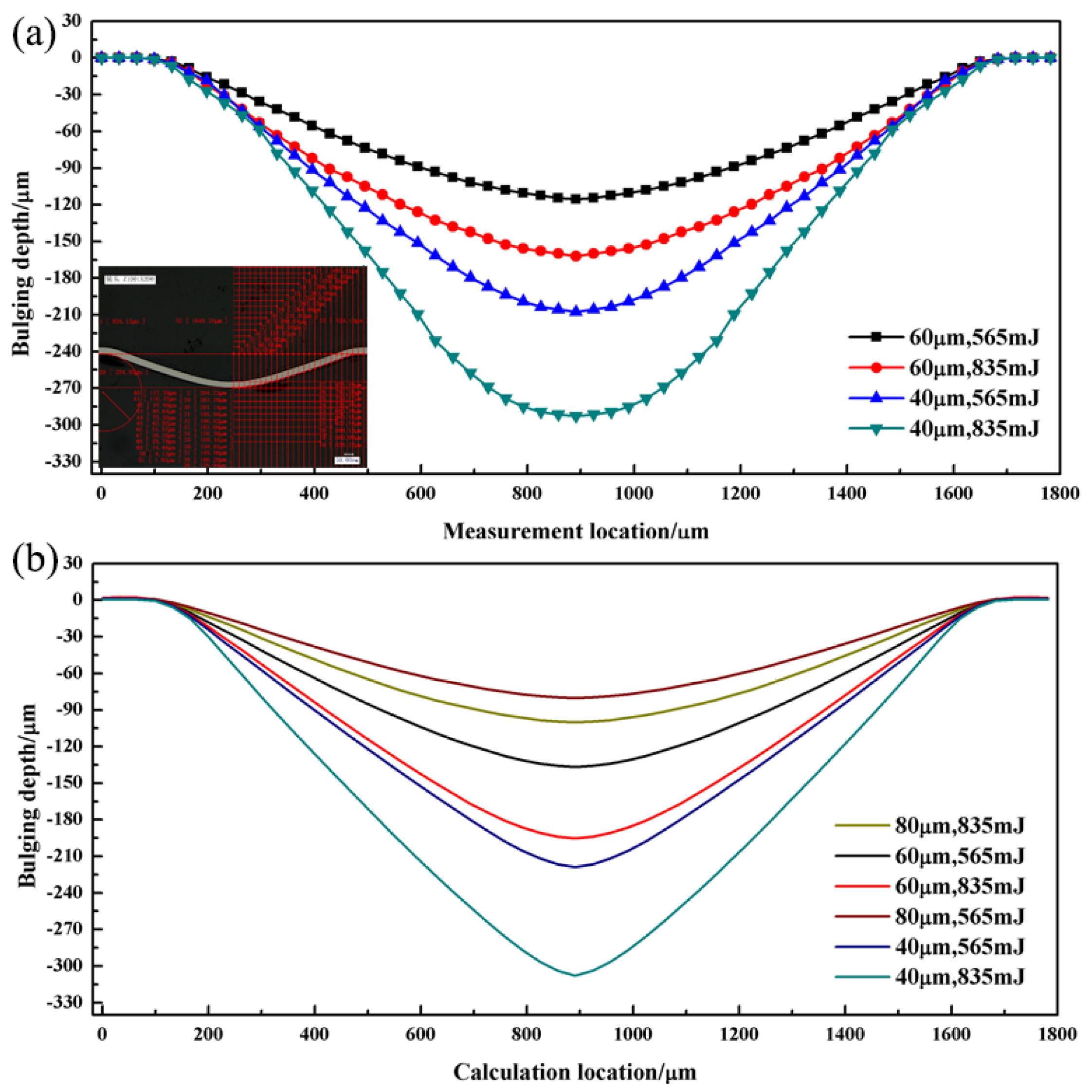
5.2. Bulging Depth
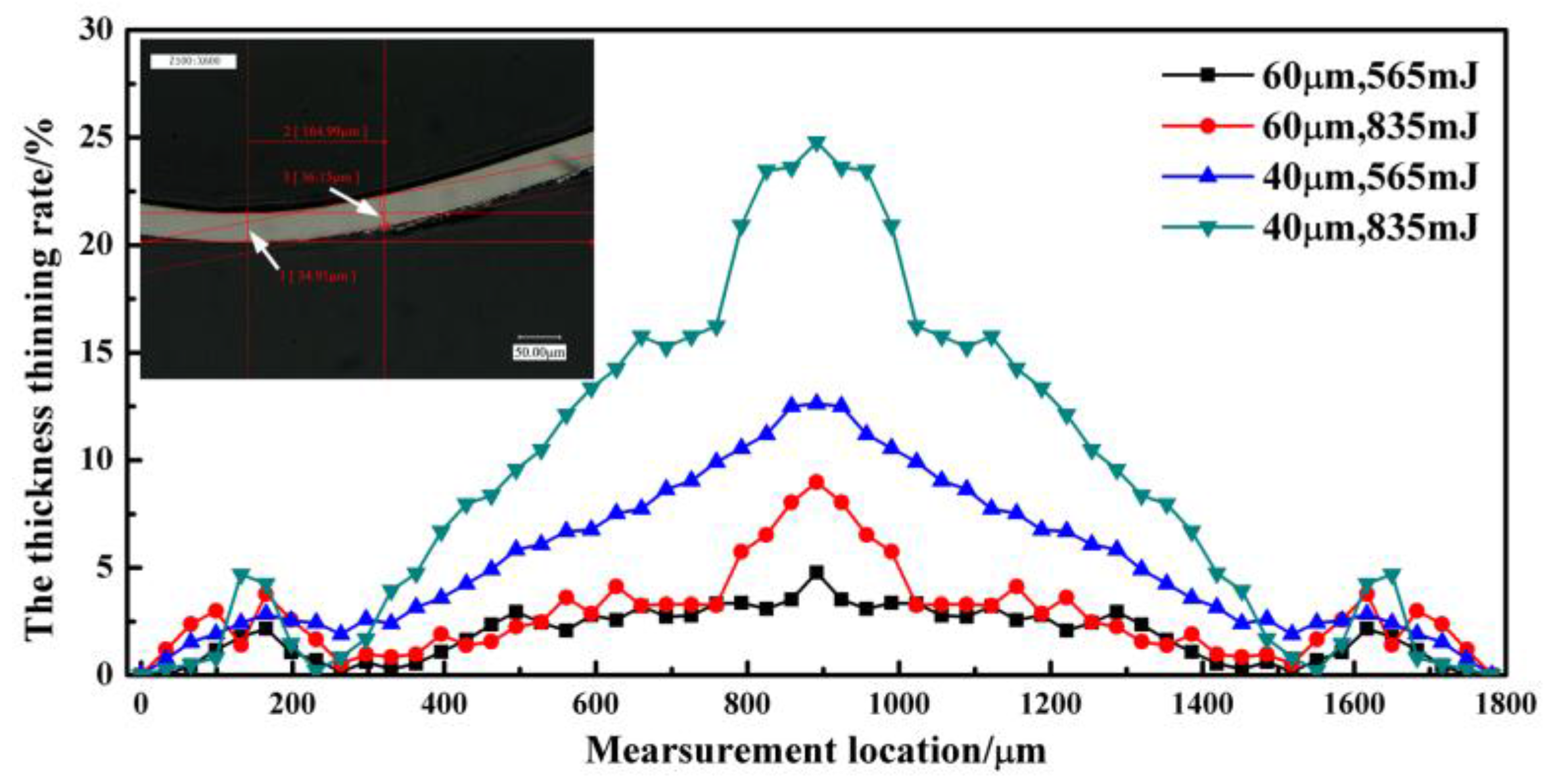
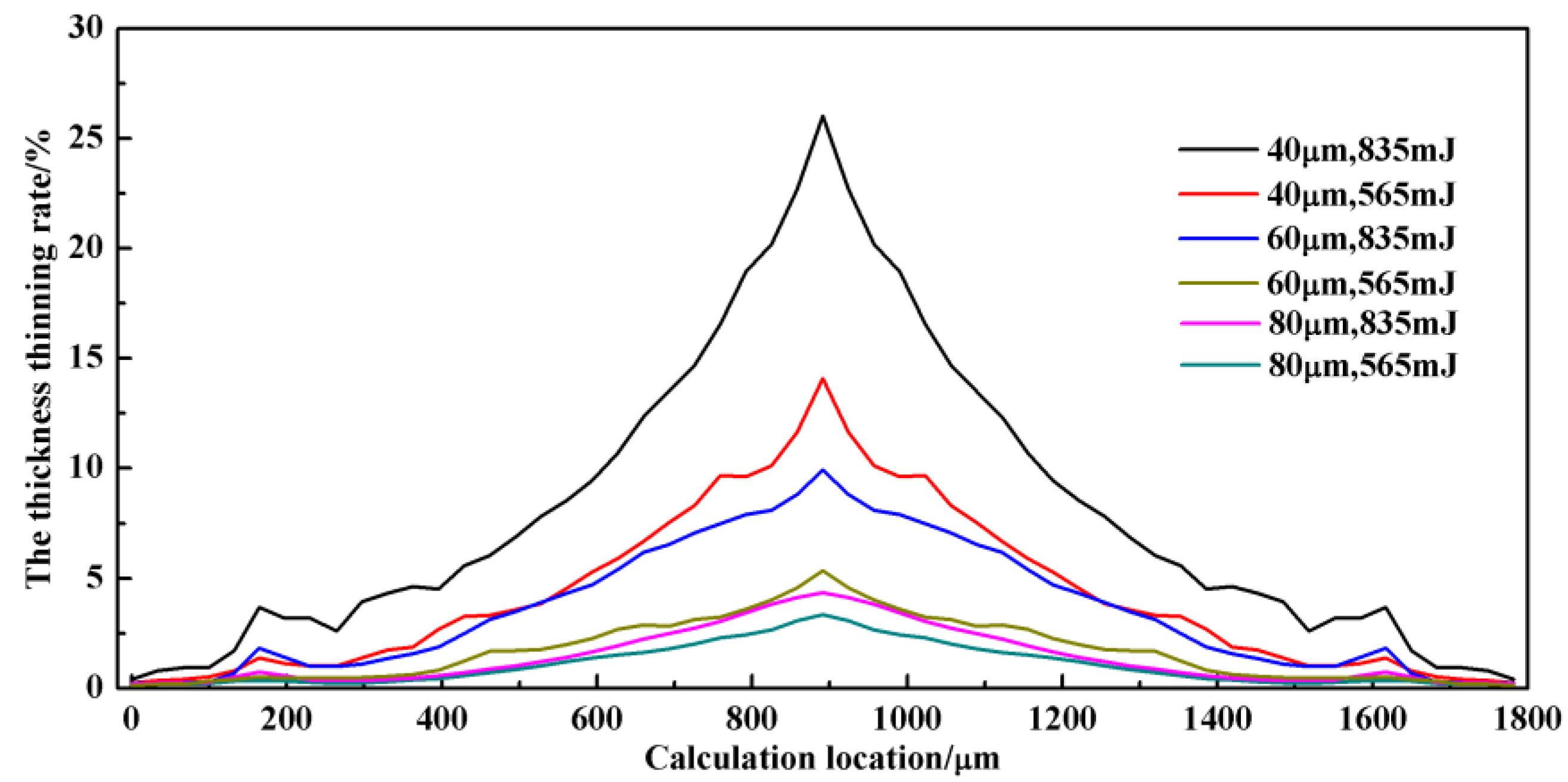
5.3. Thickness Thinning Rate
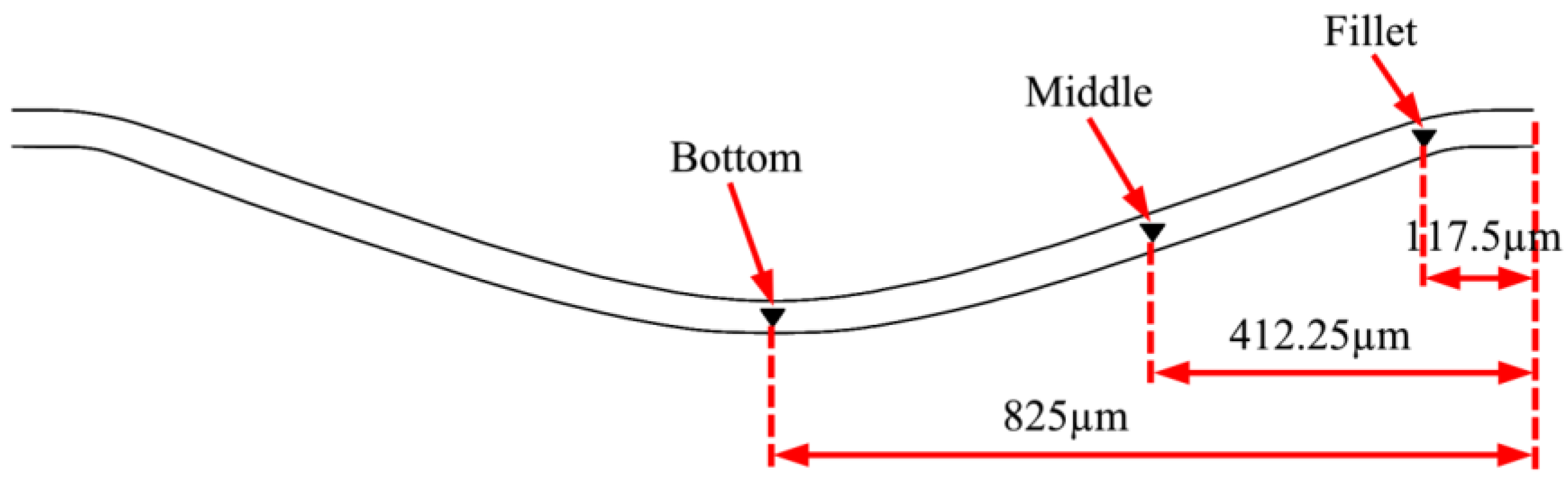
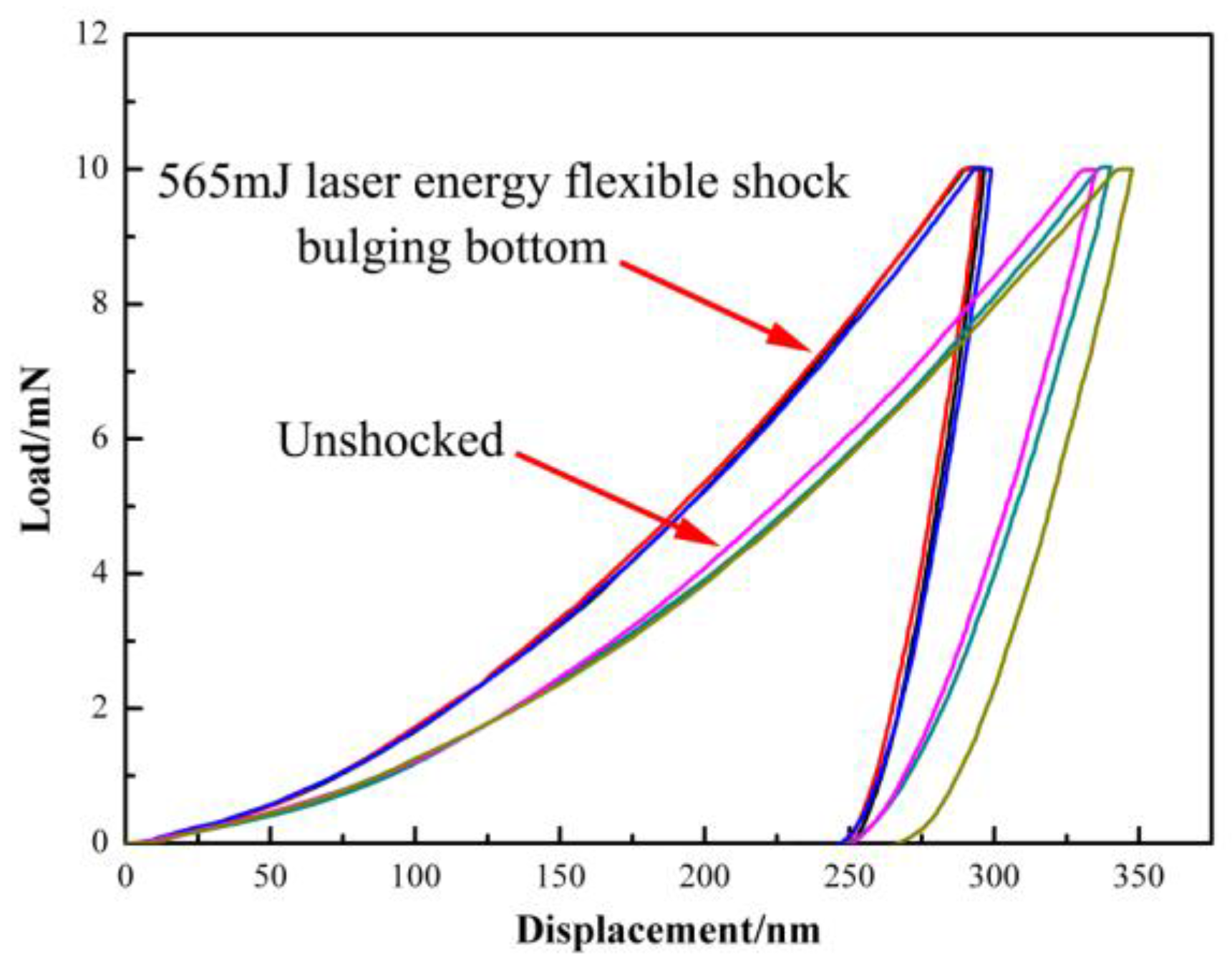
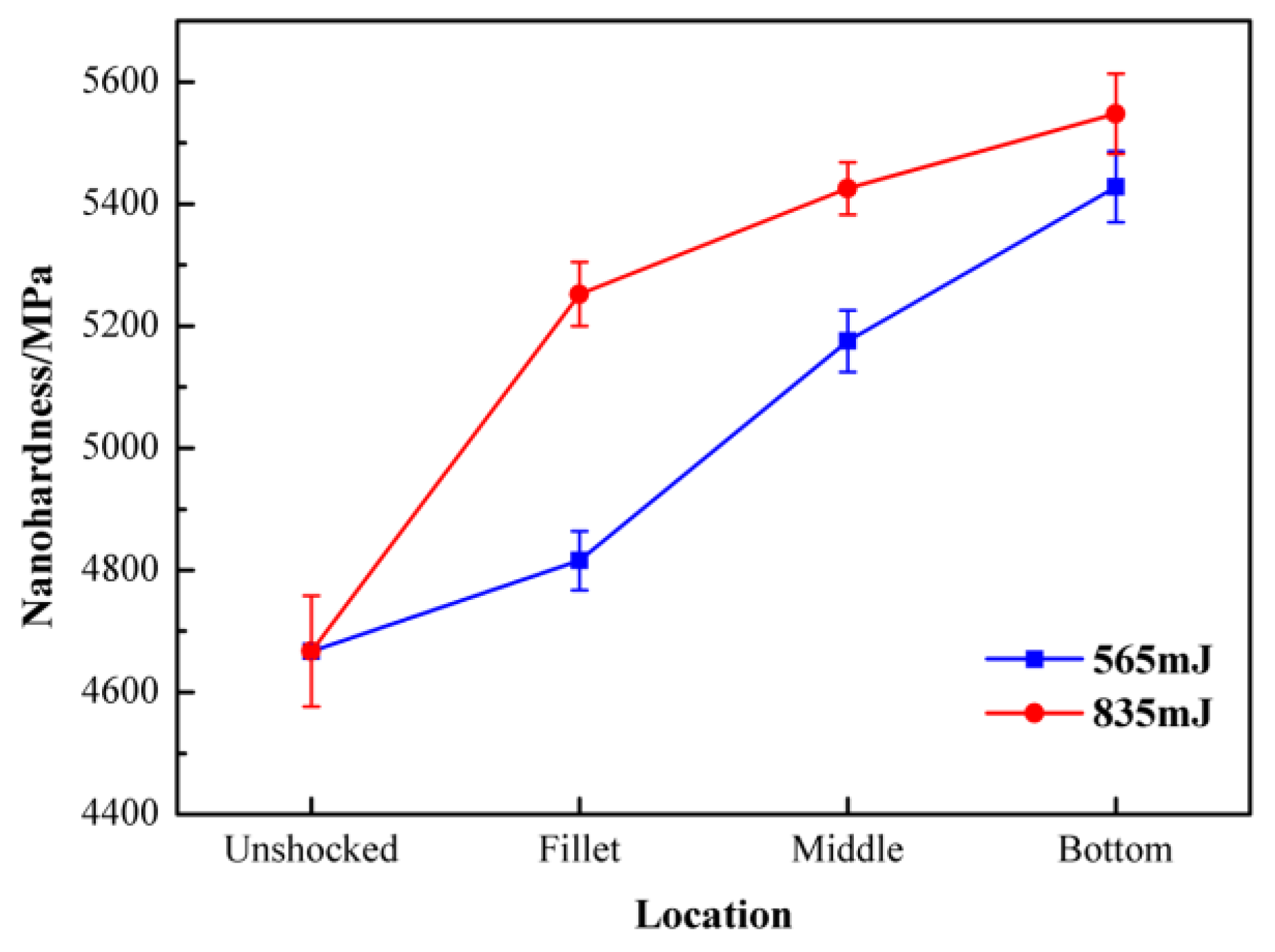
5.4. Hardness Distribution of the Cross Section
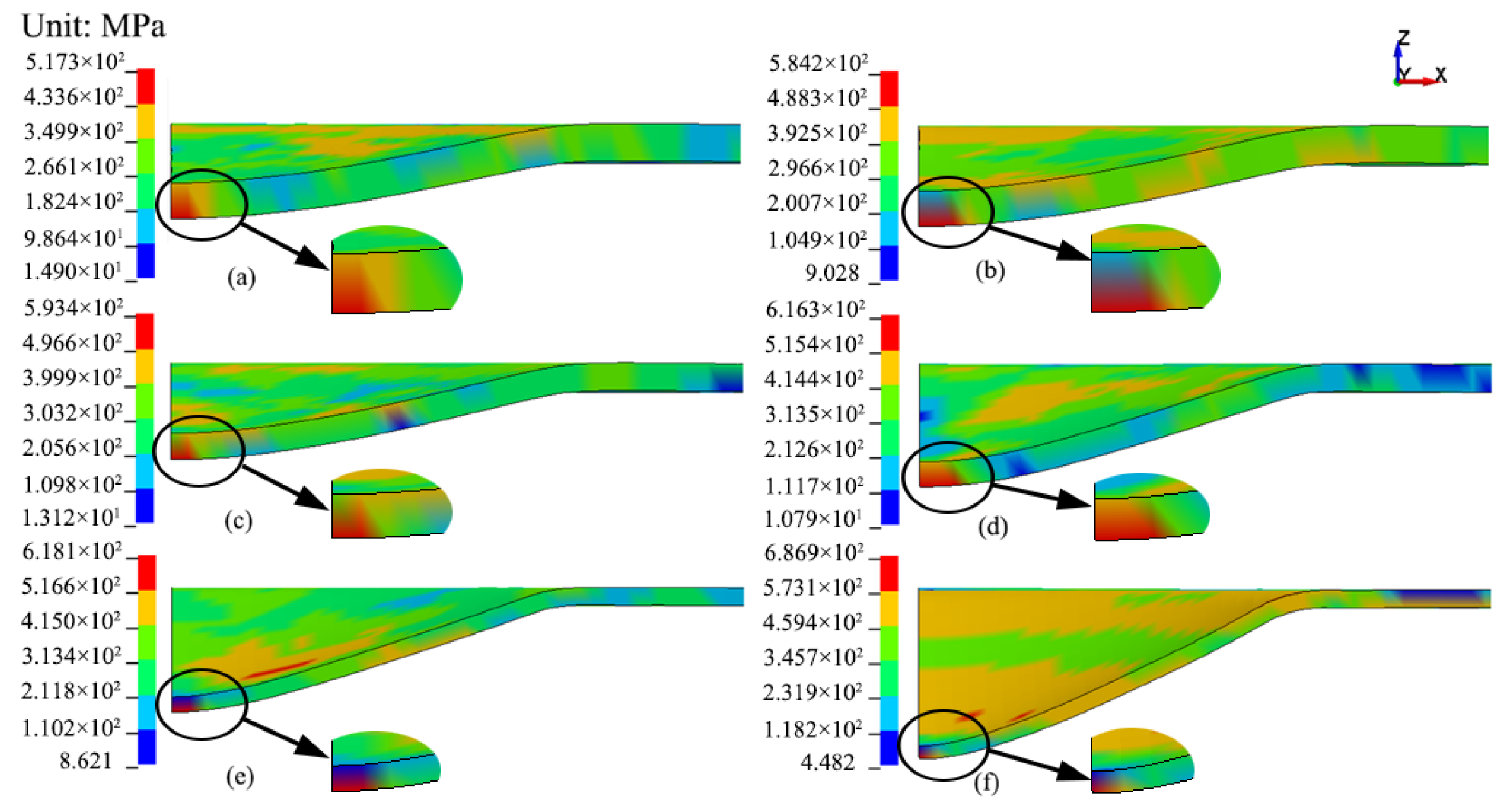
5.5. Equivalent Stress and Plastic Strain Distribution
6. Conclusions
- (1)
- The shape of the micro bulging parts was closely related to the deformation of silicone rubber according to the Gaussian laser model in the LFSB process. The surface integrity of the micro bulging parts was good with a decrease of the laser energy and workpiece thickness.
- (2)
- As the workpiece thickness decreased and laser energy increased, the bulging depth and thickness thinning rate of the micro bulging parts increased. This was similar to traditional micro forming.
- (3)
- The grains were refined and the nano-hardness of the workpiece in the cross section increased obviously after the laser flexible shock effect.
- (4)
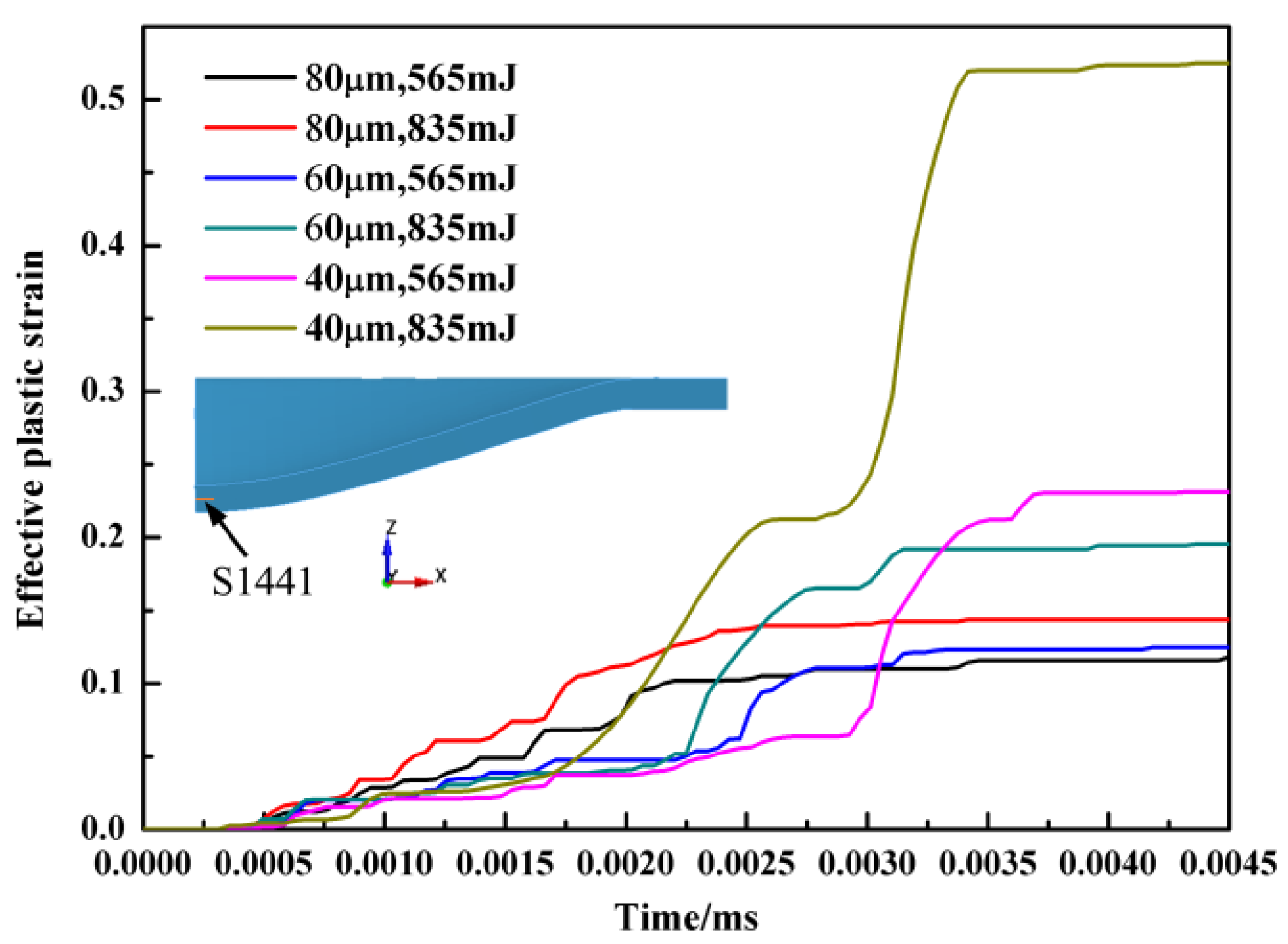
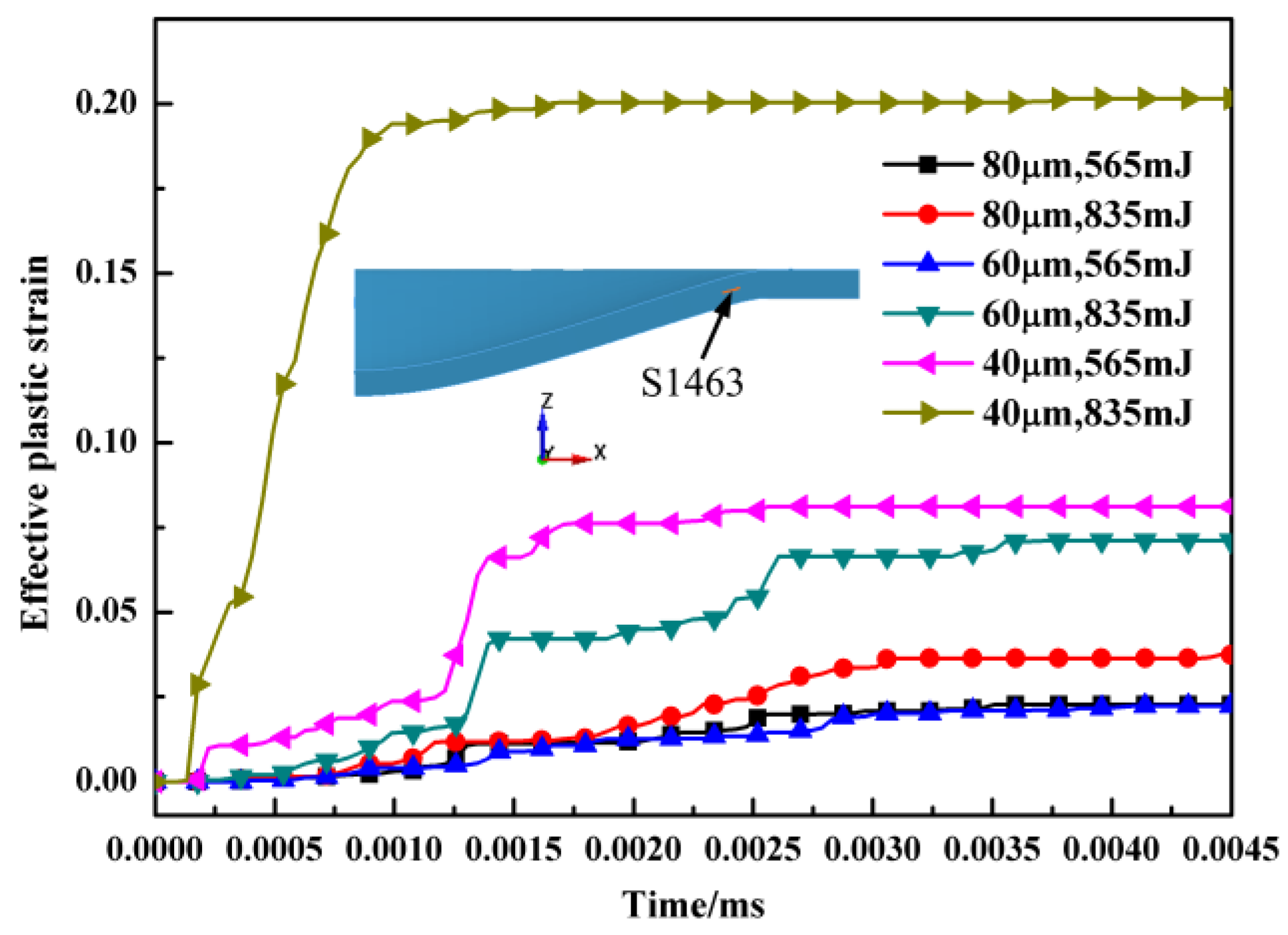
- The equivalent stress and plastic strain was concentrated at the bottom of the micro bulging parts. The maximum equivalent stress and plastic strain increased with an increase of the laser energy and a decrease of the workpiece thickness. The variation of the equivalent plastic strain of the elements S1441 and S1463 presented a significantly increasing trend under a thinner workpiece and larger laser energy.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Geiger, M.; Kleiner, M. Microforming. CIRP Ann. Manuf. Technol. 2001, 50, 445–462. [Google Scholar] [CrossRef]
- Joo, B.Y.; Oh, S.I. Forming of Micro Channels with Ultra Thin Metal Foils. CIRP Ann. Manuf. Technol. 2004, 53, 243–246. [Google Scholar] [CrossRef]
- Gau, J.T.; Principe, C. Springback behavior of brass in micro sheet forming. J. Mater. Process. Technol. 2007, 191, 7–10. [Google Scholar] [CrossRef]
- Fu, M.W.; Yang, B. Experimental and simulation studies of micro blanking and deep drawing compound process using copper sheet. J. Mater. Process. Technol. 2013, 213, 101–110. [Google Scholar] [CrossRef]
- Peng, L.F.; Hu, P. Investigation of micro/meso sheet soft punch stamping process—Simulation and experiments. Mater. Des. 2009, 30, 783–790. [Google Scholar] [CrossRef]
- Irthiea, I.K.; Green, G. Evaluation of micro deep drawing technique using soft die-simulation and experiments. Int. J. Adv. Manuf. Technol. 2017, 89, 2363–2374. [Google Scholar] [CrossRef]
- Wang, X.; Qian, Q. Numerical simulation of flexible micro-bending processes with consideration of grain structure. Comput. Mater. Sci. 2015, 110, 134–143. [Google Scholar] [CrossRef]
- Gao, Y.K. Improvement of fatigue property in 7050–T7451 aluminum alloy by laser peening and shot peening. Mater. Sci. Eng. A 2011, 528, 3823–3828. [Google Scholar] [CrossRef]
- López de Lacalle, L.N.; Lamikiz, A. The effect of ball burnishing on heat-treated steel and Inconel 718 milled surfaces. Int. J. Adv. Manuf. Technol. 2007, 32, 958–968. [Google Scholar] [CrossRef]
- Avilés, R.; Albizuri, J. Influence of laser polishing in an inert atmosphere on the high cycle fatigue strength of AISI 1045 steel. Int. J. Fatigue 2014, 68, 67–79. [Google Scholar] [CrossRef]
- Martínez, S.; Lamikiz, A. Analysis of the regimes in the scanner-based laser hardening process. Opt. Lasers Eng. 2017, 90, 72–80. [Google Scholar] [CrossRef]
- Tabernero, I.; Lamikiz, A. Numerical simulation and experimental validation of powder flux distribution in coaxial laser cladding. J. Mater. Process. Technol. 2010, 210, 2125–2134. [Google Scholar] [CrossRef]
- Niehoff, S.H.; Hu, Z.Y. Mechanical and Laser Micro Deep Drawing. Key Eng. Mater. 2007, 344, 799–806. [Google Scholar] [CrossRef]
- Zhou, M.; Huang, T. The novel nanosecond laser micro-manufacturing of three-dimensional metallic structures. Appl. Phys. A 2008, 90, 293–297. [Google Scholar] [CrossRef]
- Ocaña, J.L.; Morales, M. Laser shock microforming of thin metal sheets. Appl. Surf. Sci. 2009, 255, 5633–5636. [Google Scholar] [CrossRef] [Green Version]
- Gao, H.; Cheng, G.J. Laser-Induced High-Strain-Rate Superplastic 3-D Microforming of Metallic Thin Films. J. Microelectromech. Syst. 2010, 19, 273–281. [Google Scholar] [CrossRef]
- Zheng, C.; Sun, S. Numerical simulation and experimentation of micro scale laser bulge forming. Int. J. Mach. Tools Manuf. 2010, 50, 1048–1056. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, D. Micro scale laser shock forming of pure copper and titanium sheet with forming/blanking compound die. Opt. Lasers Eng. 2015, 67, 83–93. [Google Scholar] [CrossRef]
- Nagarajan, B.; Castagne, S. Mold-free fabrication of 3D microfeatures using laser-induced shock pressure. Appl. Surf. Sci. 2013, 268, 529–534. [Google Scholar] [CrossRef]
- Zhang, D.; Lin, Y. A mold-free laser shock micro-drawing forming process using Plasticine as the flexible support. Int. J. Adv. Manuf. Technol. 2015, 79, 265–272. [Google Scholar] [CrossRef]
- Wang, X.; Du, D. Investigation of microscale laser dynamic flexible forming process—Simulation and experiments. Int. J. Mach. Tools Manuf. 2013, 67, 8–17. [Google Scholar] [CrossRef]
- Liu, H.X.; Li, J.W. Experimental and Numerical Simulation Research on Micro-Gears Fabrication by Laser Shock Punching Process. Micromachines 2015, 6, 969–983. [Google Scholar] [CrossRef]
- Zheng, C.; Ji, Z. Variation of fracture mode in micro-scale laser shock punching. Opt. Laser Technol. 2015, 72, 25–32. [Google Scholar] [CrossRef]
- Fabbro, R.; Fournier, J. Physical study of laser-produced plasma in confined geometry. J. Appl. Phys. 1990, 68, 775–784. [Google Scholar] [CrossRef]
- Zhou, J.Z.; Yang, J.C. Experimental study on the effects of overlay properties on laser-induced shock waves. Chin. J. Lasers 2002, 11, 1041–1044. [Google Scholar]
- Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 541–547.
- Dirikolu, M.H.; Akdemir, E. Computer aided modelling of flexible forming process. J. Mater. Process. Technol. 2004, 148, 376–381. [Google Scholar] [CrossRef]
- Peyre, P.; Fabbro, R. Laser shock processing: A review of the physics and applications. Opt. Quantum Electron. 1995, 27, 1213–1229. [Google Scholar]
- Zhou, J.Z.; Ni, M.X. Theoretical investigation and finite element simulation of laser peen forming of metal plate. Chin. J. Lasers 2007, 34, 288–294. [Google Scholar]
- Wang, H.J.; Liu, H.X. Numerical simulations of the spall damage of the target material induced by laser driven flyer impacting. Adv. Mater. Res. 2011, 156–157, 1305–1312. [Google Scholar] [CrossRef]
- Geiger, M.; Vollertsen, F. Fundamentals on the Manufacturing of Sheet Metal Microparts. CIRP Ann. Manuf. Technol. 1996, 45, 277–282. [Google Scholar] [CrossRef]
- Cheng, G.J.; Pirzada, D. Microstructure and mechanical property characterizations of metal foil after microscale laser dynamic forming. J. Appl. Phys. 2007, 101, 063108. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
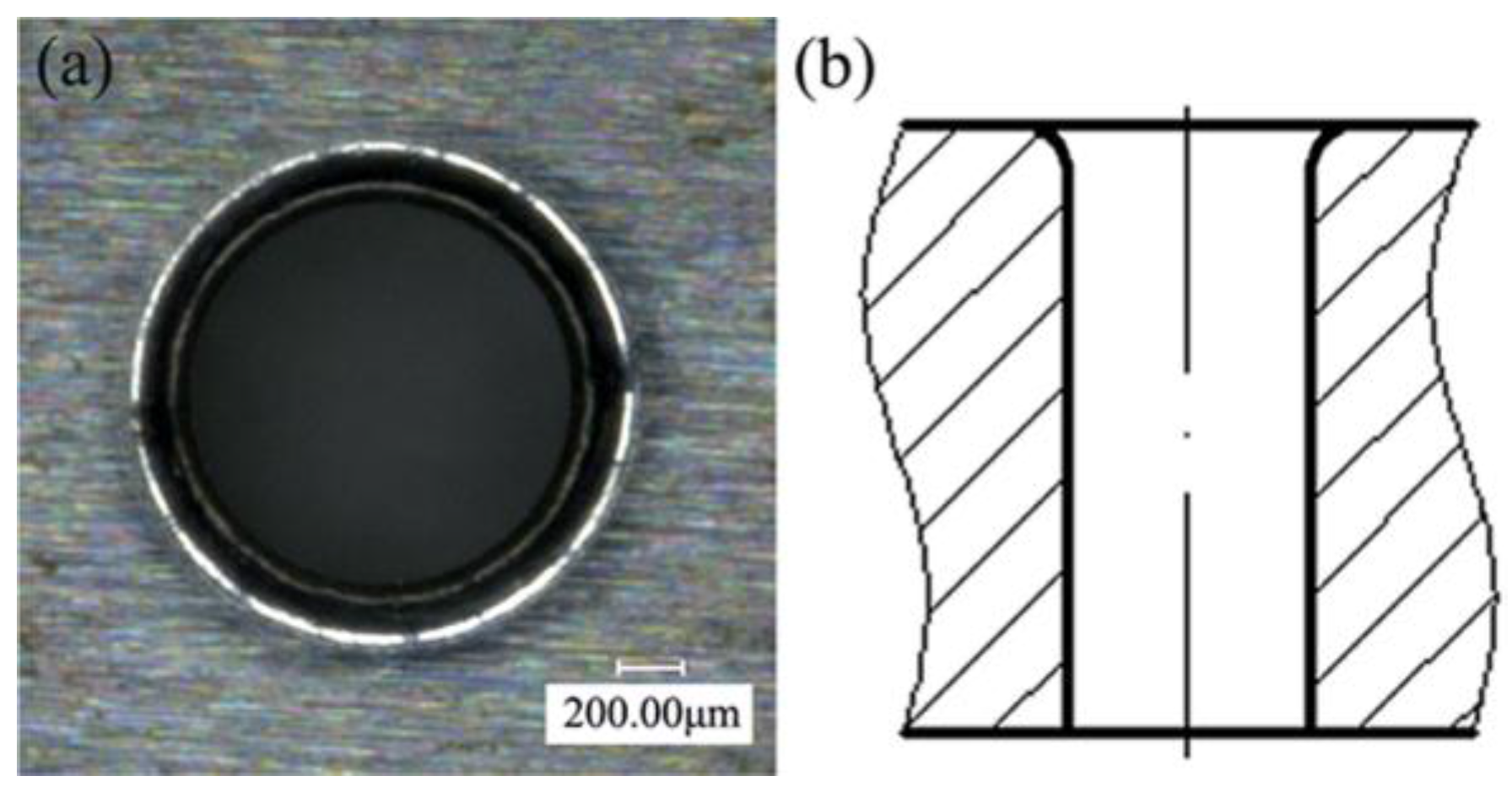




| Parameter | Design Dimensions/mm | Actual Dimensions/mm | Error/% |
|---|---|---|---|
| Diameter/d | 1.2 | 1.18 | 1.67 |
| Fillet radius/r | 0.24 | 0.235 | 2.08 |
| Technical Parameters | Value |
|---|---|
| Single pulse energy | 80–2000 mJ |
| Pulse width | 8 ns |
| Wave length | 1064 nm |
| Energy stability | <±1% |
| Exit spot diameter | 9 mm |
| Parameter | Value |
|---|---|
| Laser energy/mJ | 565, 835 |
| 304 stainless steel foil/µm | 40, 60 |
| Spot diameter/mm | 2 |
| PMMA/mm | 3 |
| Silicone rubber/mm | 0.5 |
| Blank holder force/N | 12 |
| Material | A (MPa) | B (MPa) | C | n | ε0 (s−1) |
|---|---|---|---|---|---|
| 304 stainless steel foil | 350 | 275 | 0.022 | 0.36 | 1 |
| Material | Hardness Shore A (°) | M-R Constant C10 (MPa) | M-R Constant C01 (MPa) | Poisson’s Ratio (v) |
|---|---|---|---|---|
| Silicone rubber | 70 | 0.736 | 0.184 | 0.49997 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Sun, X.; Shen, Z.; Li, L.; Sha, C.; Ma, Y.; Gau, J.-T.; Wang, X. Experimental and Numerical Simulation Investigation on Laser Flexible Shock Micro-Bulging. Metals 2017, 7, 93. https://doi.org/10.3390/met7030093
Liu H, Sun X, Shen Z, Li L, Sha C, Ma Y, Gau J-T, Wang X. Experimental and Numerical Simulation Investigation on Laser Flexible Shock Micro-Bulging. Metals. 2017; 7(3):93. https://doi.org/10.3390/met7030093
Chicago/Turabian StyleLiu, Huixia, Xianqing Sun, Zongbao Shen, Liyin Li, Chaofei Sha, Youjuan Ma, Jenn-Terng Gau, and Xiao Wang. 2017. "Experimental and Numerical Simulation Investigation on Laser Flexible Shock Micro-Bulging" Metals 7, no. 3: 93. https://doi.org/10.3390/met7030093
APA StyleLiu, H., Sun, X., Shen, Z., Li, L., Sha, C., Ma, Y., Gau, J.-T., & Wang, X. (2017). Experimental and Numerical Simulation Investigation on Laser Flexible Shock Micro-Bulging. Metals, 7(3), 93. https://doi.org/10.3390/met7030093







