Comparison of Single Ti6Al4V Struts Made Using Selective Laser Melting and Electron Beam Melting Subject to Part Orientation
Abstract
:1. Introduction
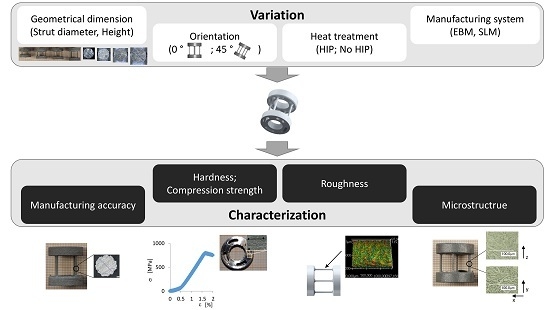
2. Materials and Methods
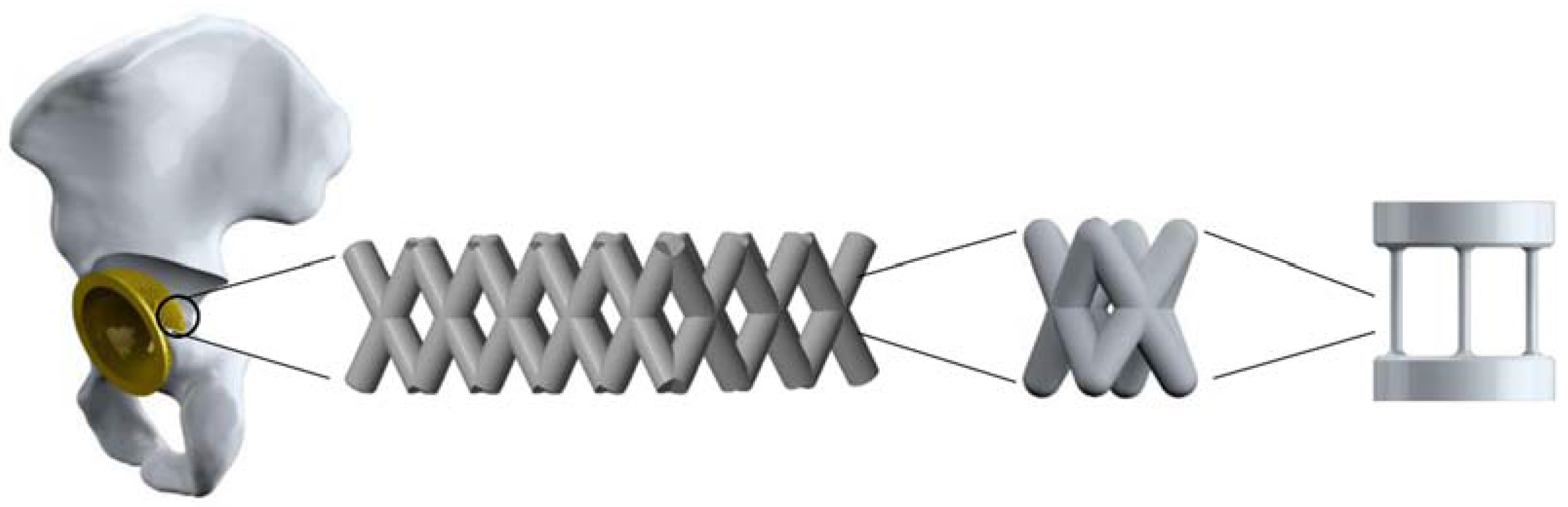
2.1. Parts Design and Configuration
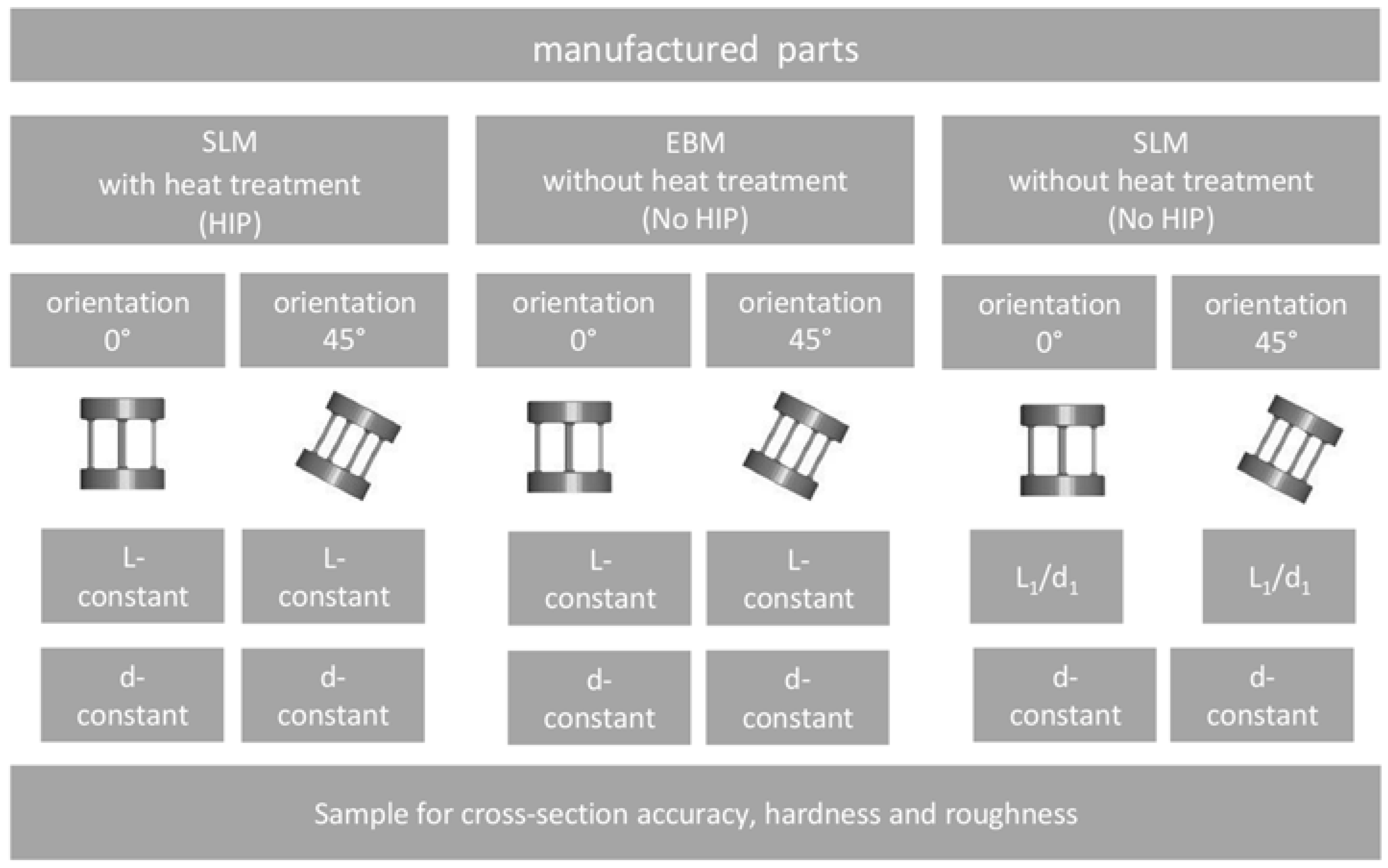
2.2. Fabrication of the Scaffolds via the SLM Process and the EBM Process
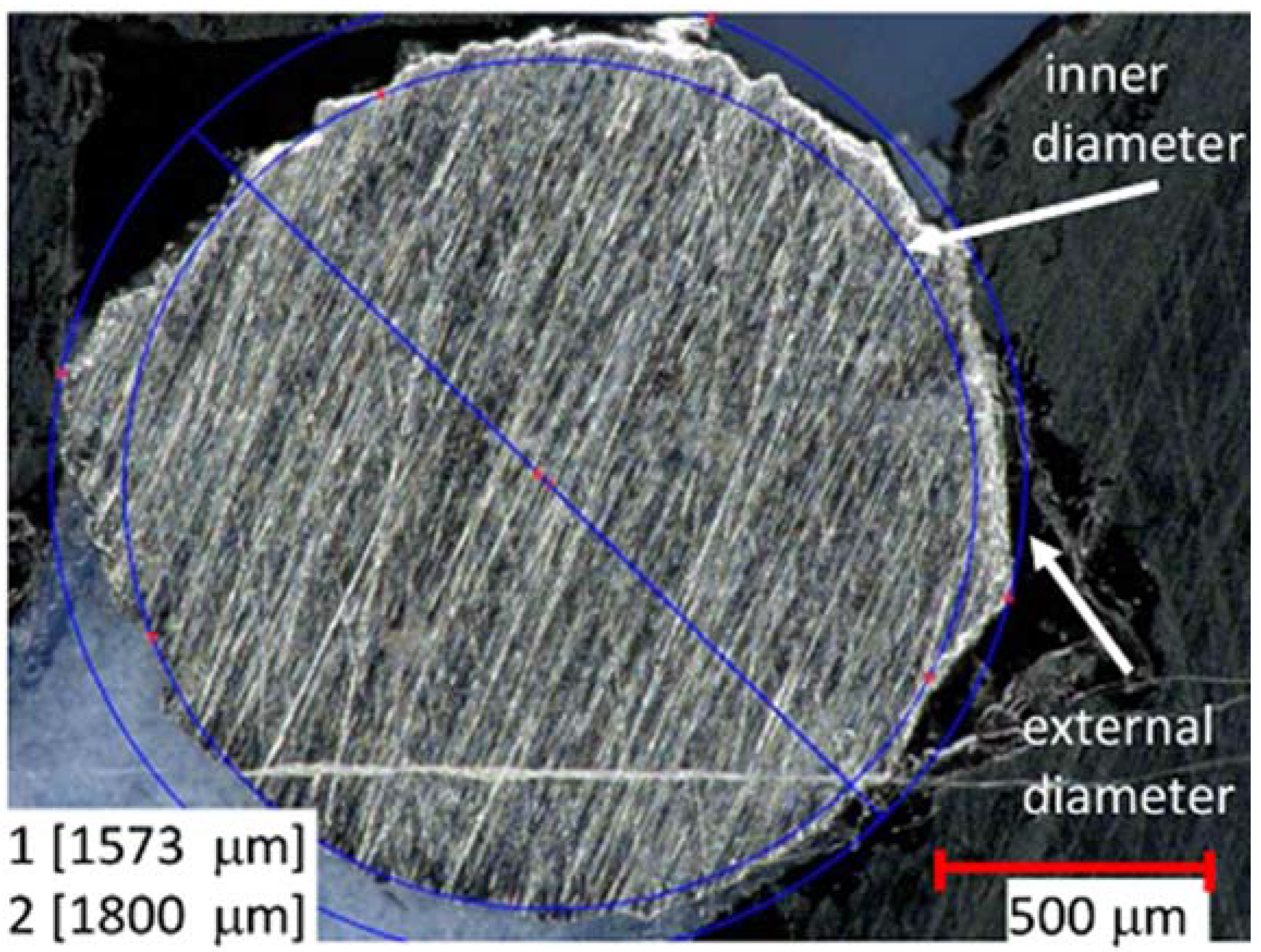
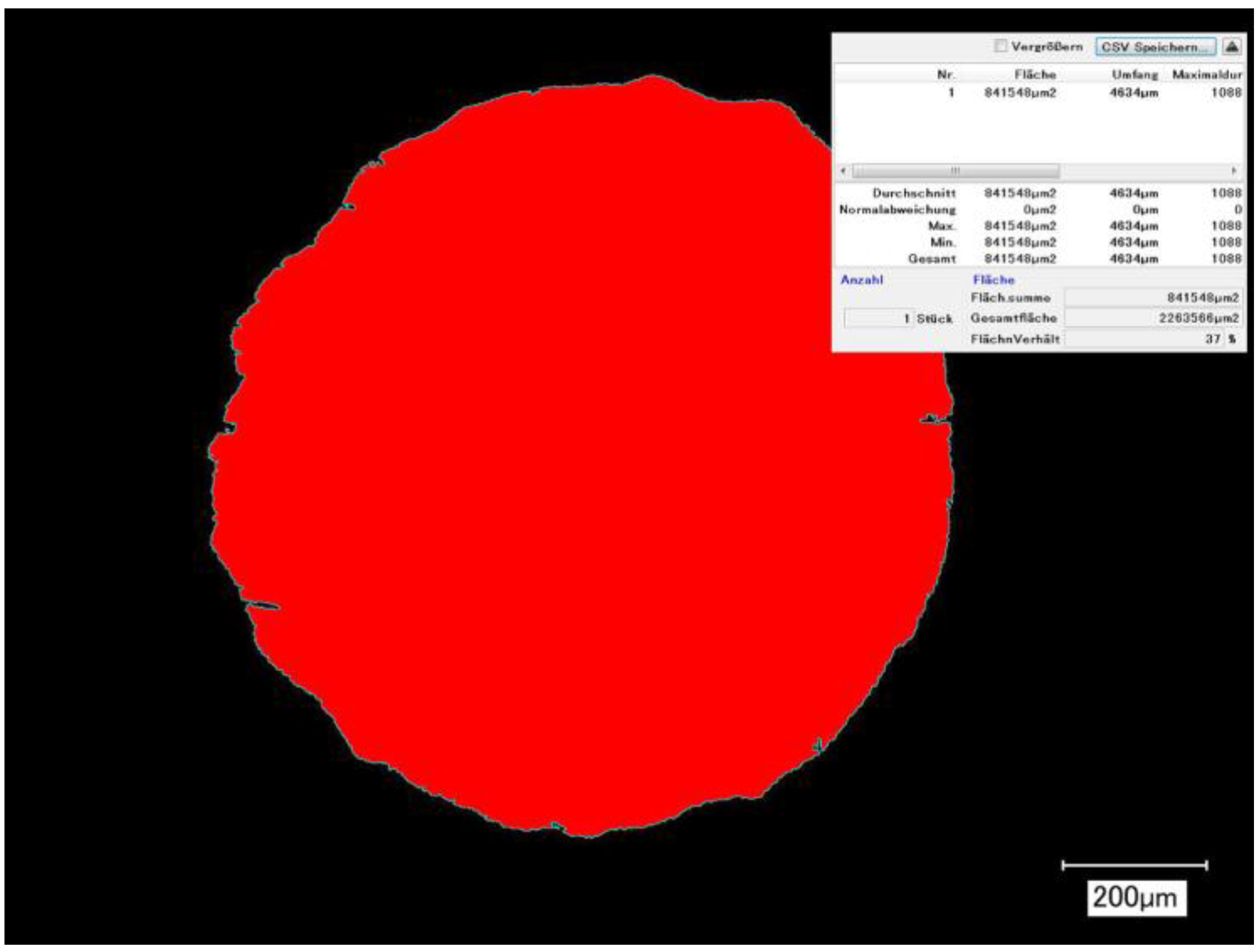
2.3. Measurements
2.4. Statistical Analysis
3. Results and Discussion
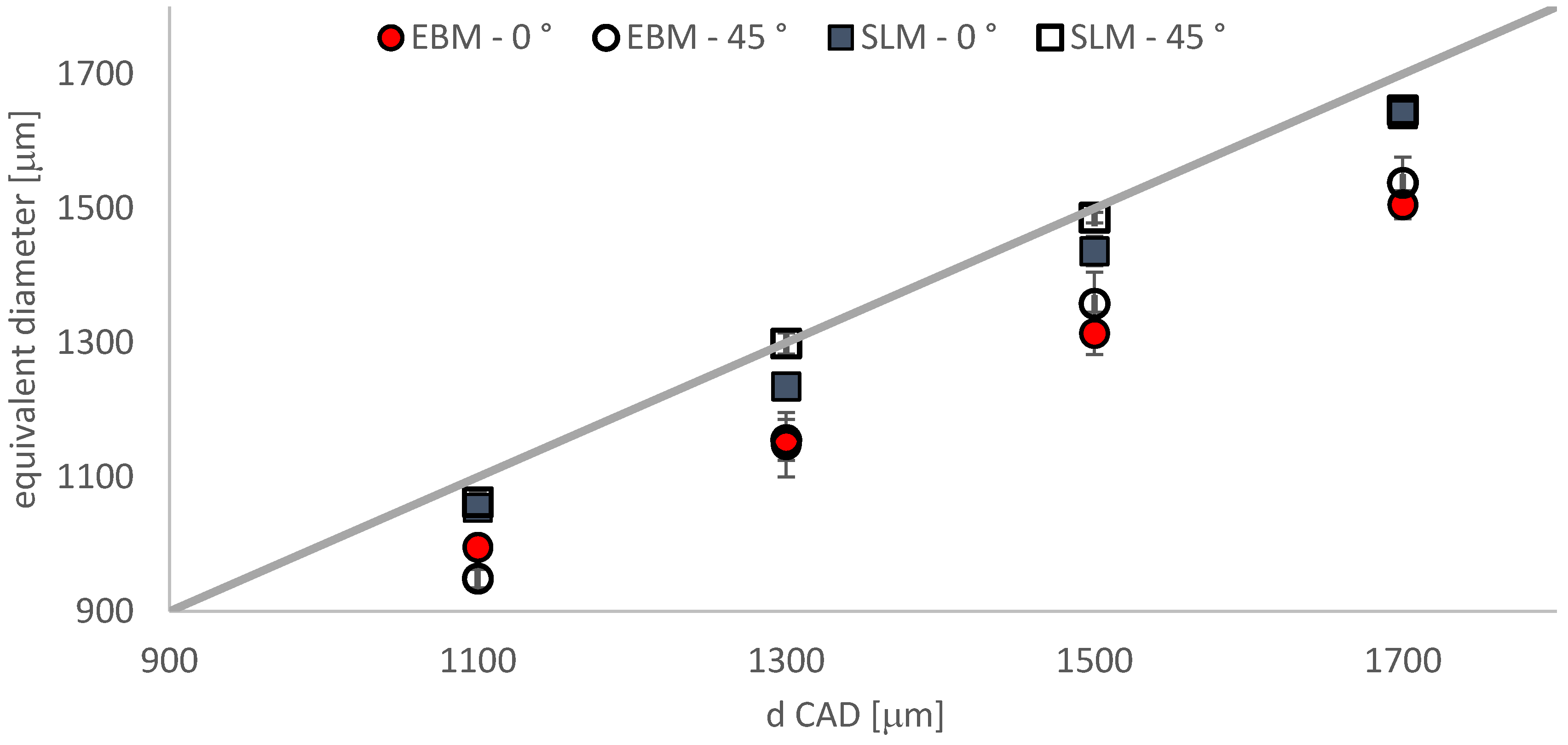
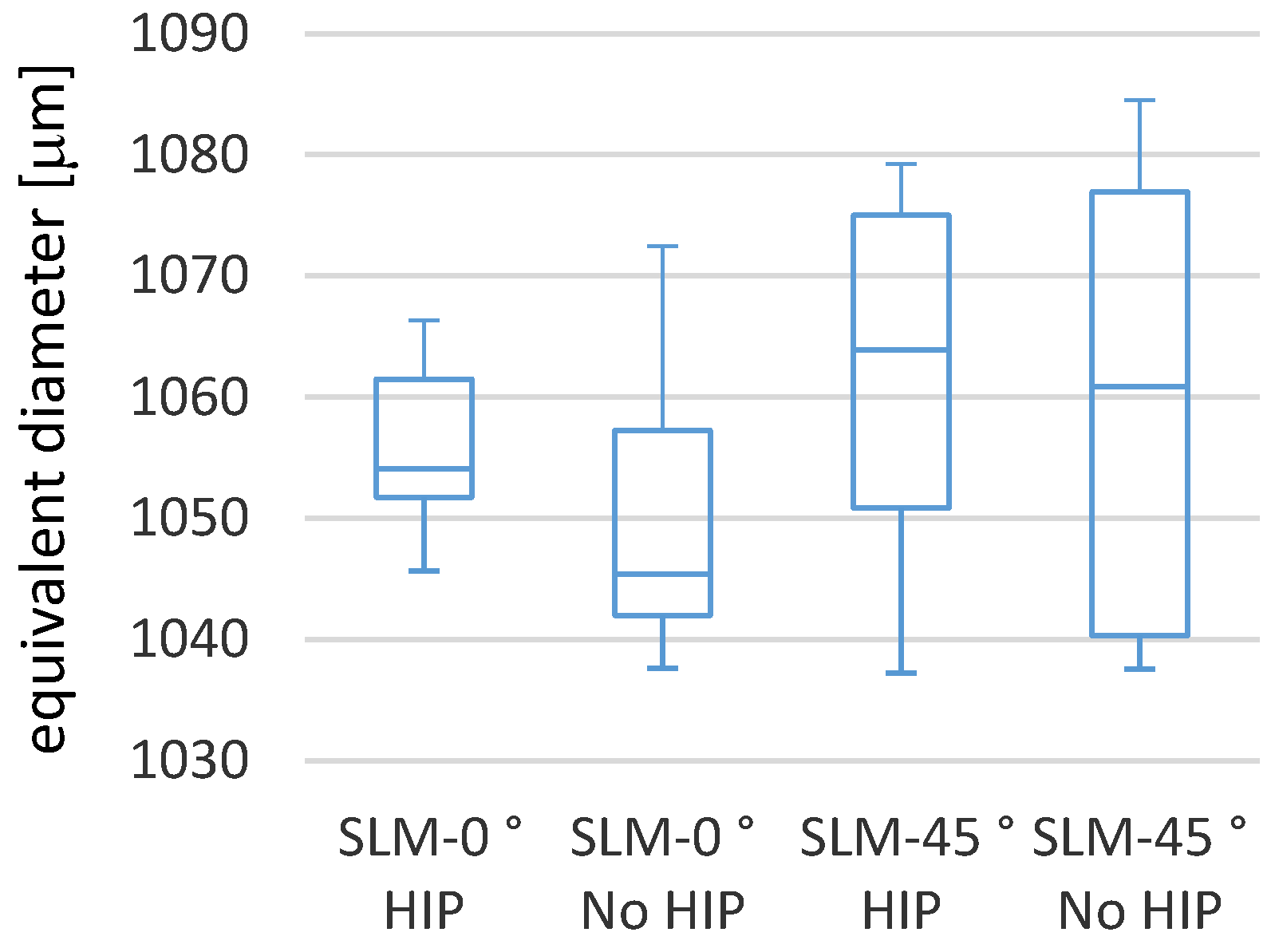
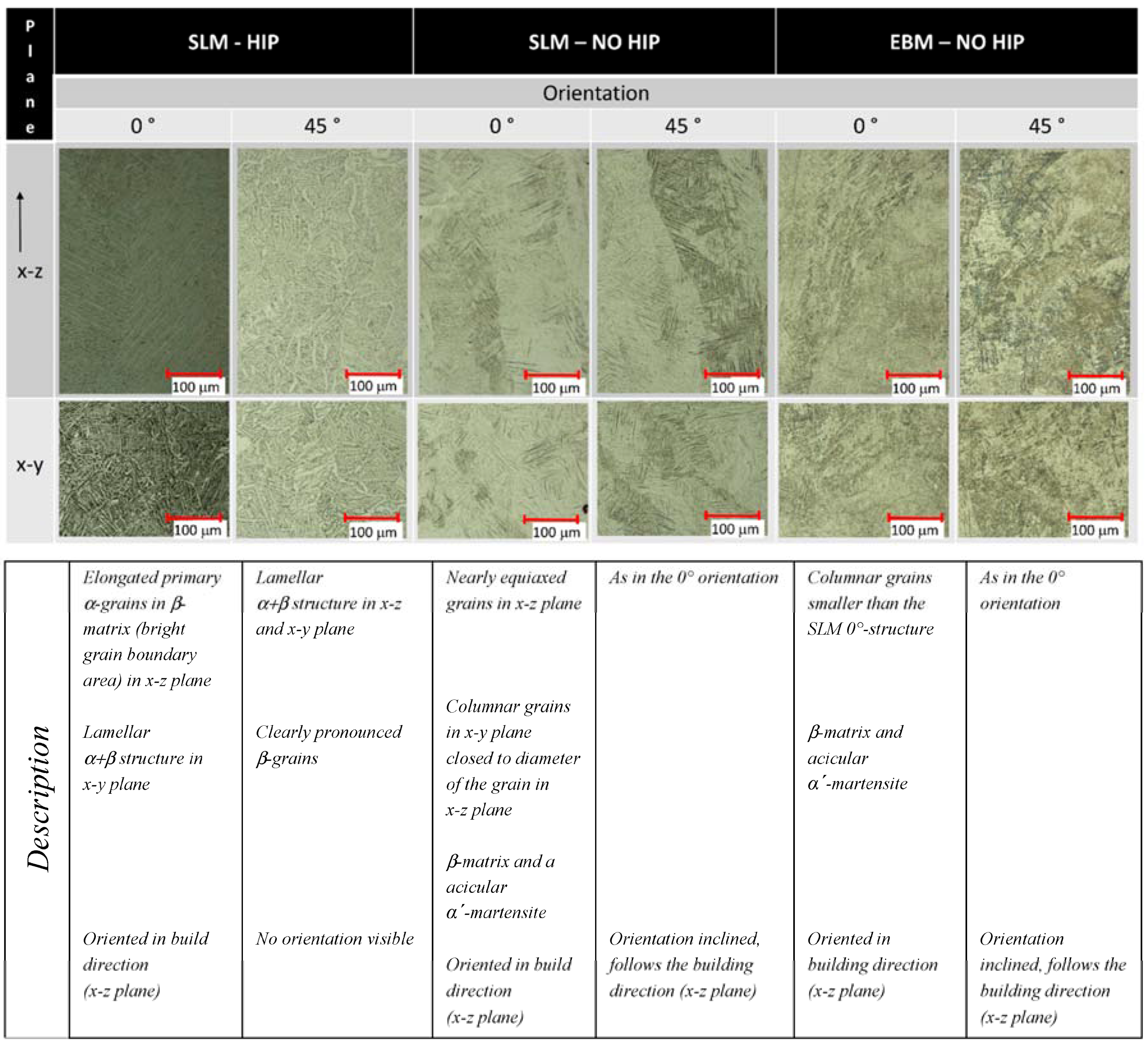
3.1. Cross-Section Accuracy of Fabricated Struts
Comparison of SLM Manufactured Parts with and without Heat Treatment
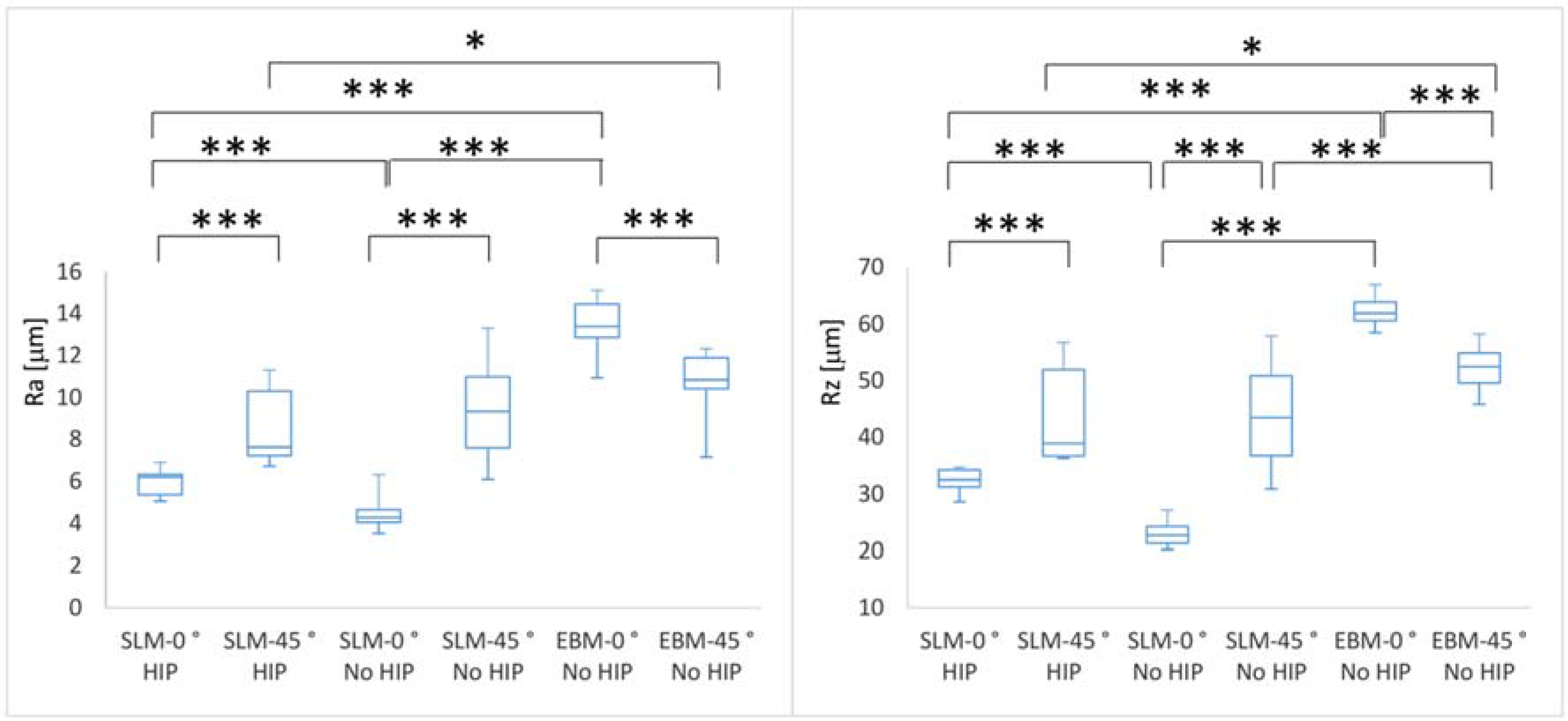
3.2. Surface Quality
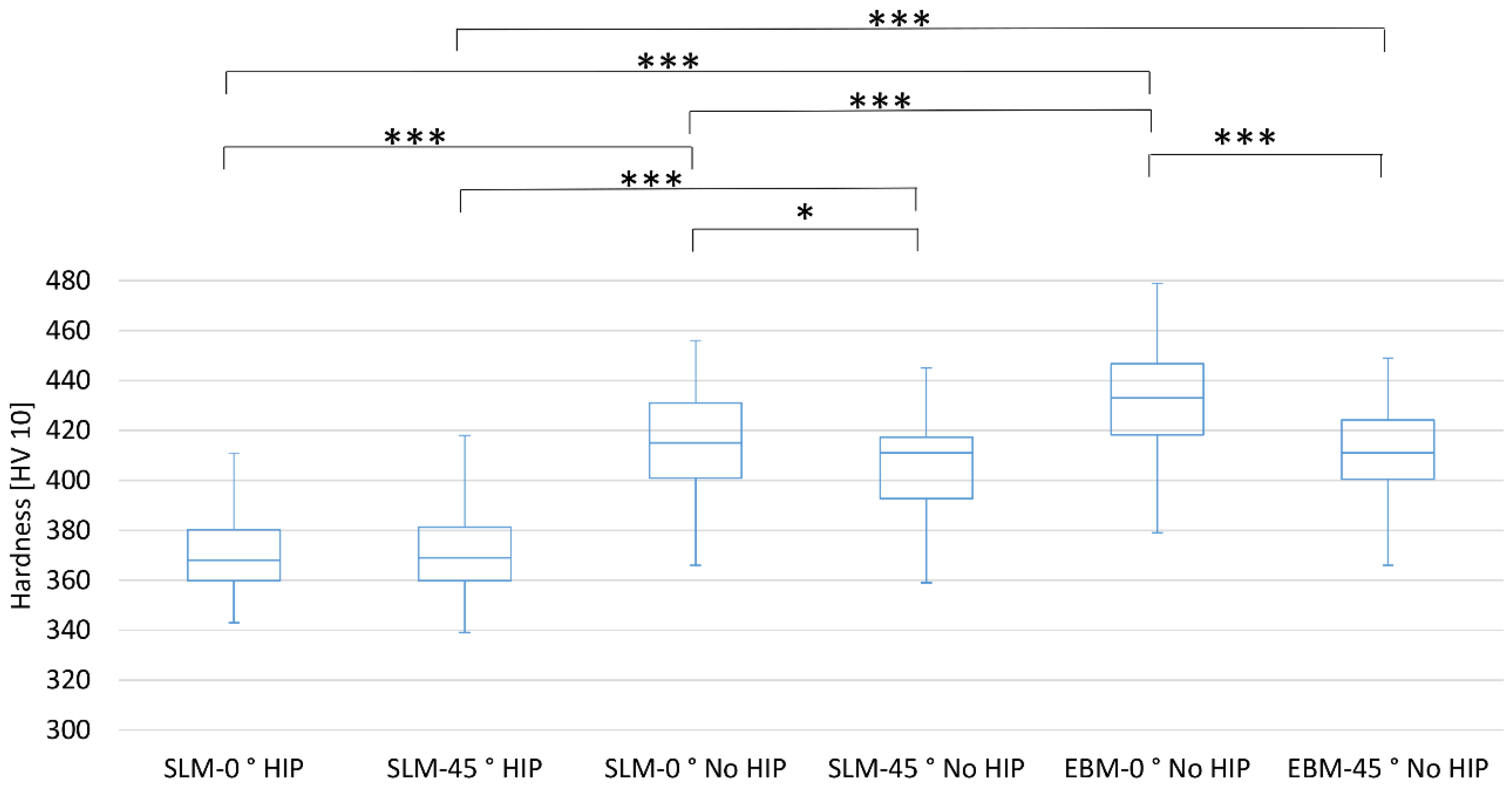
3.3. Vickers Hardness
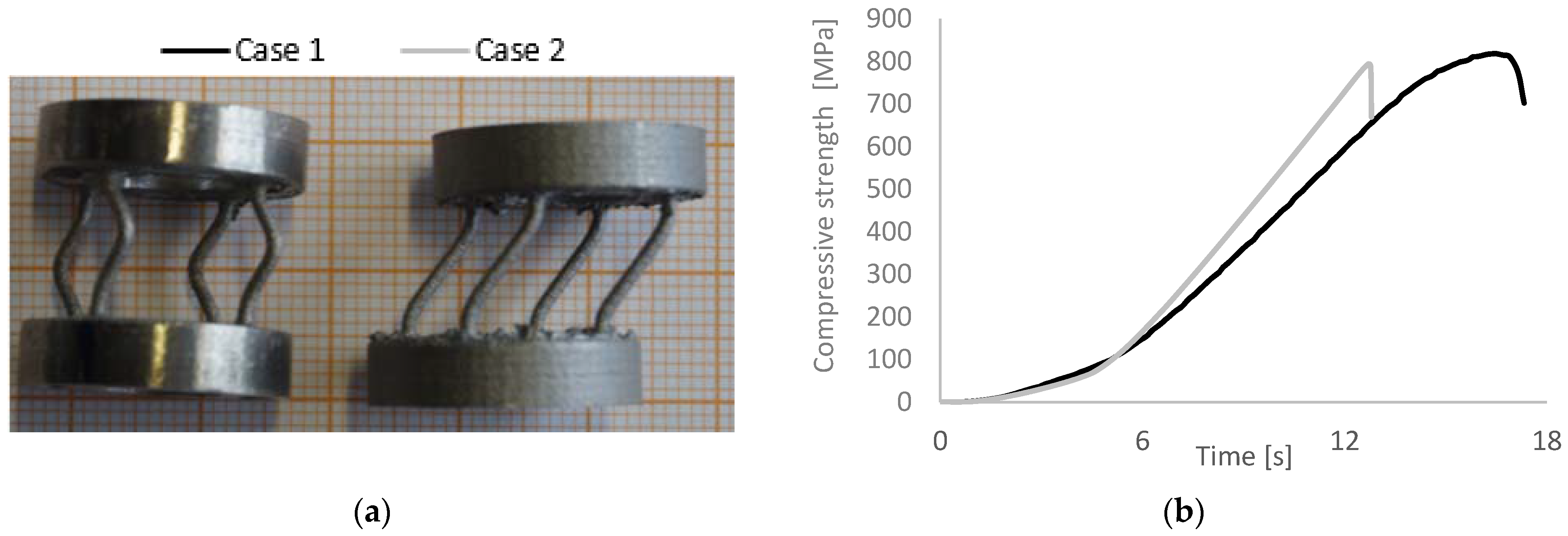
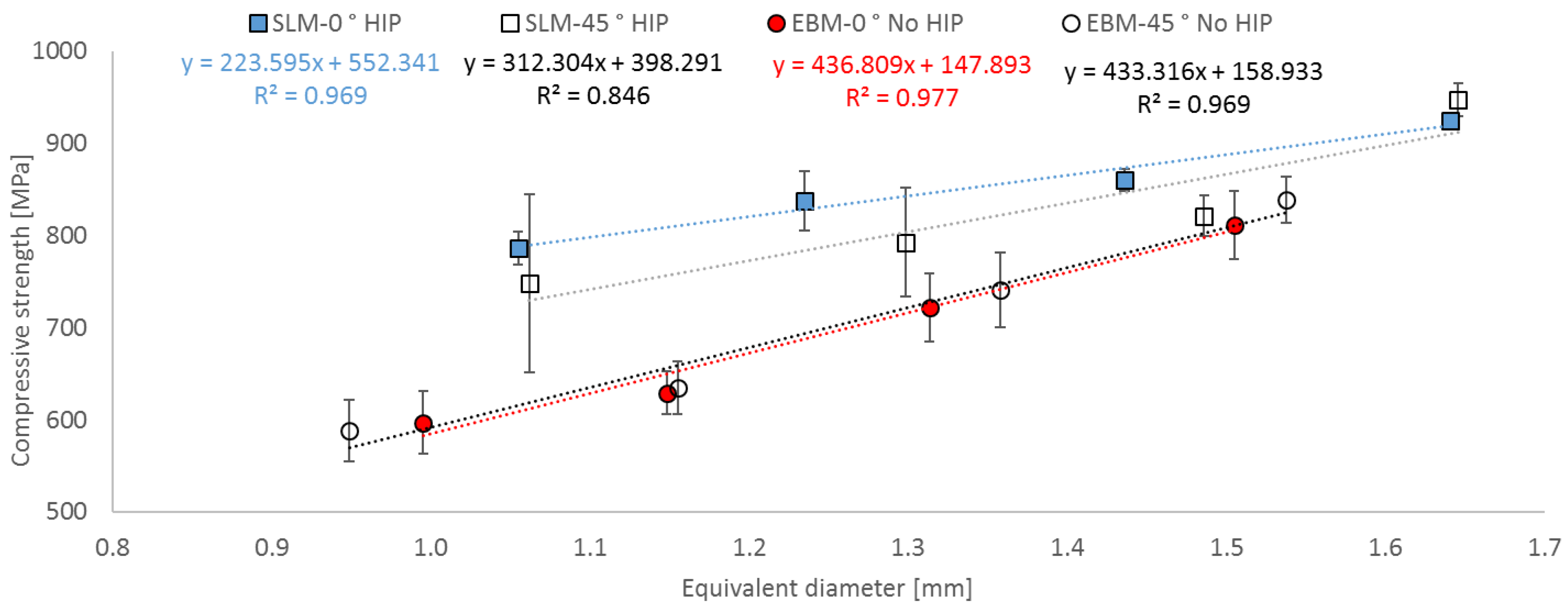
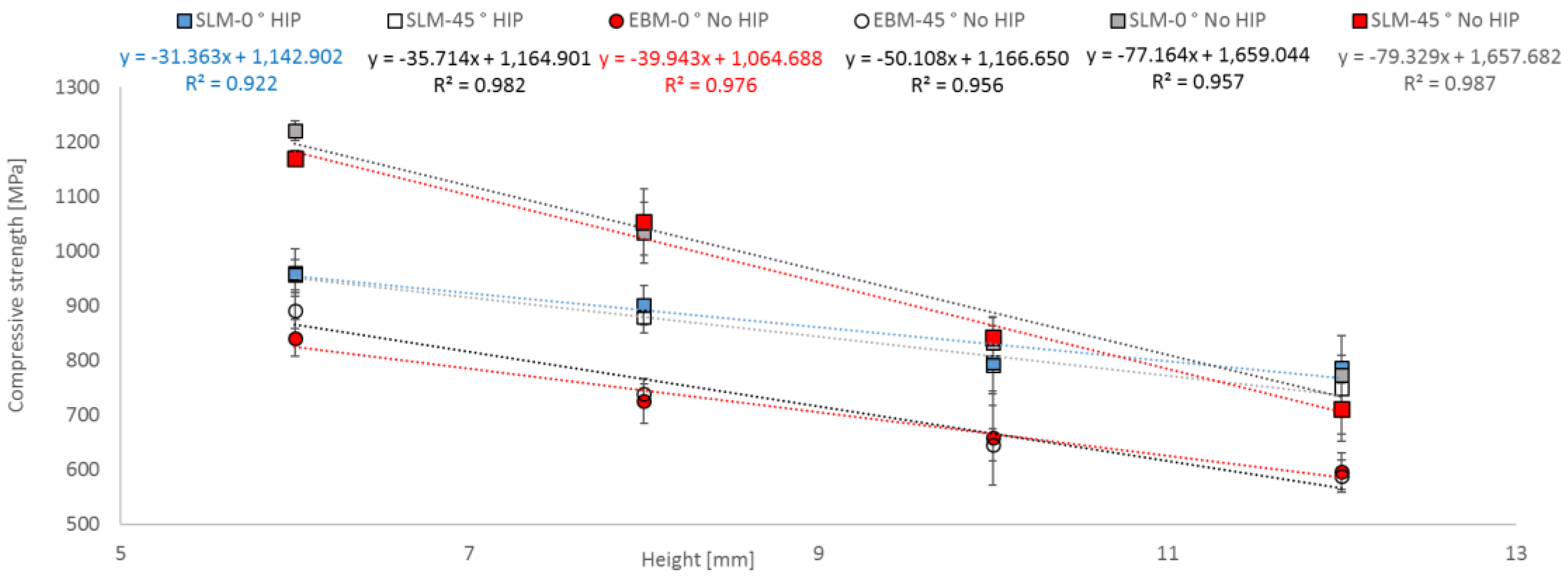
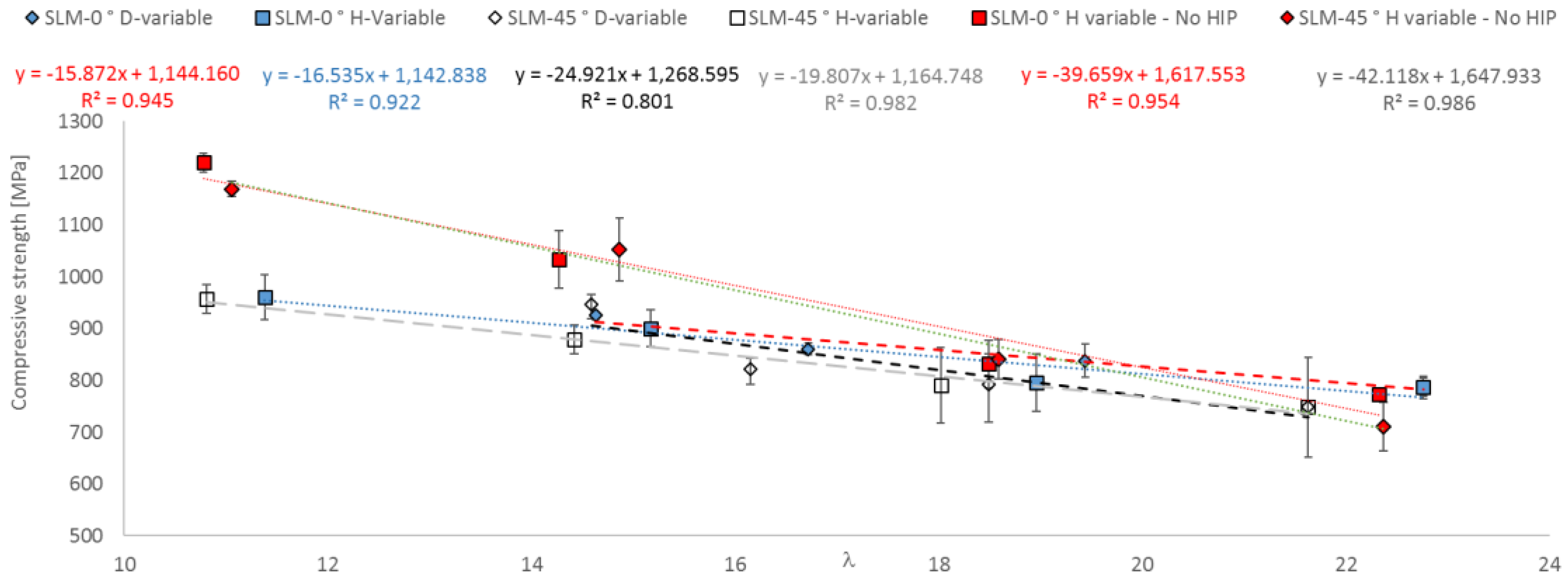
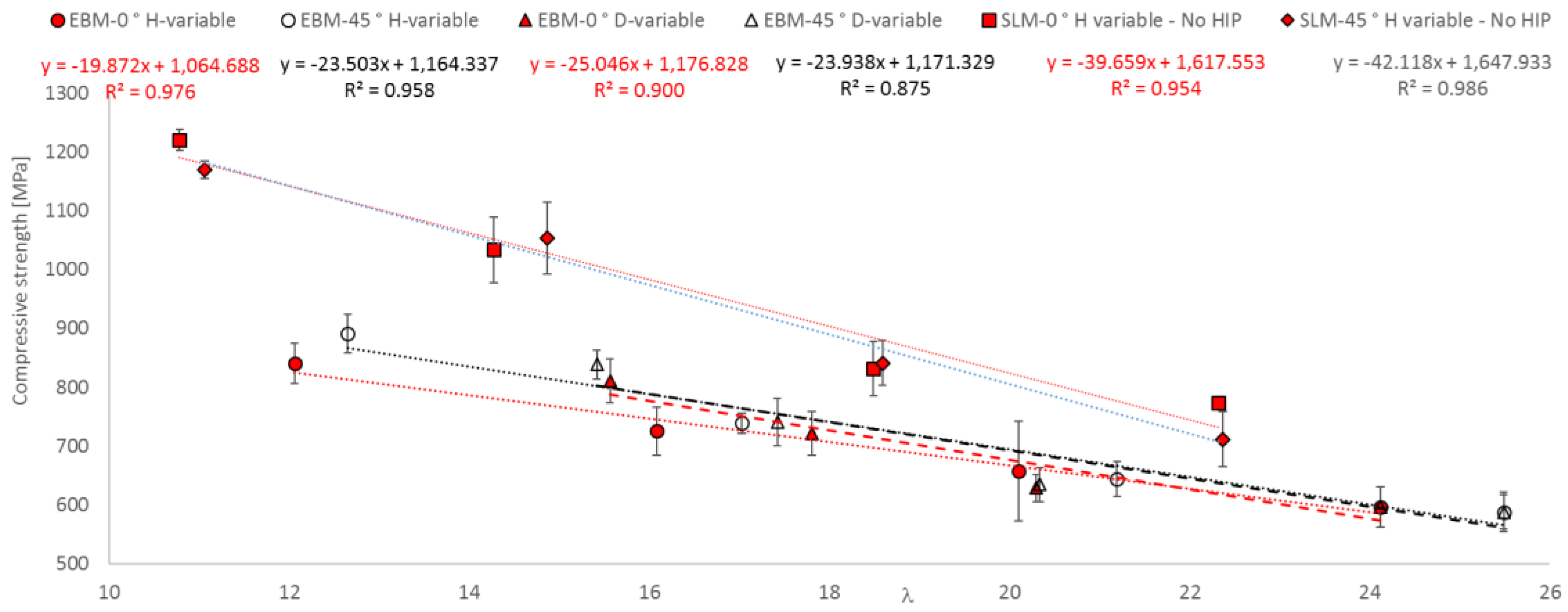
3.4. Compressive Strength as a Function of Geometrical Parameter
Case 1: (long curve)
Case 2: (steep abrupt decrease)
4. Conclusions
- Cross-section accuracy of fabricated struts
- ○
- All manufactured struts deviate from the given diameter from CAD data.
- ○
- The SLM parts show a higher accuracy than the EBM parts.
- ○
- No geometric differences could be determined between the HIPed and NO HIPed SLM parts.
- The values of roughness obtained for SLM- and EBM-manufactured Ti6Al4V parts correspond to those from the literature. The SLM parts have significantly lower Ra and RZ values in both orientations.
- Different hardness values between EBM and SLM were determined and supported by their different respective microstructures. The No HIPed EBM parts showed the highest values for hardness. The HIPed SLM parts showed the lowest values according to microstructure. The hardness of the 45° oriented parts without heat treatment was significantly lower than of the 0° oriented parts. Heat-treated parts showed no differences in dependence on the orientation.
- Based on tests under uniaxial loading conditions, the influence of strut orientation on compression strength was demonstrated.
- ○
- A functional correlation between compressive strength and slenderness ratio (λ) as well as between equivalent diameter (d) and height (L) of EBM and SLM parts could be established.
- ○
- Modifications in diameter lead to a larger influence on compressive strength than modifications in height.
- ○
- A strut orientation of 45 degrees leads to a moderate decrease in the compression strength of EBM and SLM parts.
- ○
- Both the microstructure and the cross-section accuracy of fabricated struts as well as roughness are responsible for differences in compressive strength.
- ○
- The specimens produced show 2 types of stability failure—symmetric and antimetric buckling—at the same compressive strength levels.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Heinl, P.; Müller, L.; Körner, C.; Singer, R.F.; Müller, F.A. Cellular Ti-6Al-4V structures with interconnected macro porosity. Acta Biomater. 2008, 4, 1536–1544. [Google Scholar] [CrossRef] [PubMed]
- Geetha, M.; Singh, A.K.; Asokamani, R.; Gogia, A.K. Ti based biomaterials, the ultimate choice for orthopaedic implants—A review. Prog. Mater. Sci. 2009, 54, 397–425. [Google Scholar] [CrossRef]
- Hazlehurst, K.; Wang, C.J.; Stanford, M. Evaluation of the stiffness characteristics of square pore CoCrMo cellular structures manufactured using laser melting technology for potential orthopaedic applications. Mater. Des. 2013, 51, 949–955. [Google Scholar] [CrossRef]
- Attar, H.; Calin, M.; Zhang, L.C.; Scudino, S.; Eckert, J. Manufacture by selective laser melting and mechanical behavior of commercially pure titanium. Mater. Sci. Eng. A 2014, 593, 170–177. [Google Scholar] [CrossRef]
- Attar, H.; Löber, L.; Funk, A.; Calin, M.; Zhang, L.C.; Prashanth, K.G. Mechanical behavior of porous commercially pure Ti and Ti–TiB composite materials manufactured by selective laser melting. Mater. Sci. Eng. A 2015, 625, 350–356. [Google Scholar] [CrossRef]
- Wauthle, R.; van der Stok, J.; Yavari, S.A.; van Humbeeck, J.; Kruth, J.P.; Zadpoor, A.A.; Weinans, H.; Mulier, M.; Schrooten, J. Additively manufactured porous tantalum implants. Acta Biomater. 2015, 14, 217–225. [Google Scholar] [CrossRef] [PubMed]
- Thijs, L.; Sistiaga, M.L.M.; Wauthle, R.; Qingge, X.; Kruth, J.-P.; Humbeeck, J.V. Strong morphological and crystallographic texture and resulting yield strength anisotropy in selective laser melted tantalum. Acta Mater. 2013, 61, 4657–4668. [Google Scholar] [CrossRef]
- Öhmann, C.; Baleani, M.; Pani, C.; Taddei, F.; Alberghini, M.; Viceconti, M.; Manfrini, M. Compressive behaviour of child and adult cortical bone. Bone 2011, 49, 2011. [Google Scholar] [CrossRef] [PubMed]
- Grimal, Q. Assessment of cortical bone elasticity and strength: Mechanical testing and ultrasound provide complementary data. Med. Eng. Phys. 2009, 31, 1140–1147. [Google Scholar] [CrossRef] [PubMed]
- Lewis, G. Properties of open-cell porous metals and alloys for orthopaedic applications. J. Mater. Sci. Mater. Med. 2013, 24, 2293–2325. [Google Scholar] [CrossRef] [PubMed]
- Abele, E.; Stoffregen, H.A.; Kniepkamp, M.; Lang, S. Selective laser melting for manufacturing of thin-walled porous elements. J. Mater. Process. Technol. 2015, 215, 114–122. [Google Scholar] [CrossRef]
- Guo, C.; Ge, W.; Lin, F. Effects of scanning parameters on material deposition during Electron Beam Selective Melting of Ti-6Al-4V powder. J. Mater. Process. Technol. 2015, 217, 148–157. [Google Scholar] [CrossRef]
- Song, B.; Dong, S.; Zhang, B.; Liao, H.; Coddet, C. Effects of processing parameters on microstructure and mechanical property. Mater. Des. 2012, 35, 120–125. [Google Scholar] [CrossRef]
- Yadroitsev, I.; Krakhmalev, P.; Yadroitsava, I. Selective laser melting of Ti6Al4V alloy for biomedical applications temperature monitoring and microstructural evolution. J. Alloy. Compd. 2014, 583, 404–409. [Google Scholar] [CrossRef]
- Vrancken, B.; Thijs, L.; Kruth, J.P.; van Humbeeck, J. Heat treatment of Ti6Al4V produced by Selective Laser Melting: Microstructure and mechanical properties. J. Alloy. Compd. 2012, 541, 177–185. [Google Scholar] [CrossRef]
- Luxner, M.H.; Stampfl, J.; Pettermann, H.E. Finite element modeling concepts and linear analyses of 3D regular open cell structures. J. Mater. Sci. 2005, 40, 5859–5866. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F.; Schajer, G.S.; Robertson, C.I. Mechanics of two-dimensional cellular materials. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1982, 382, 25–42. [Google Scholar] [CrossRef]
- Campoli, G.; Borleffs, M.S.; Yavari, S.A.; Wauthle, R.; Weinans, H.; Zadpoor, A.A. Mechanical properties of open-cell metallic biomaterials manufactured using additive manufacturing. Mater. Des. 2013, 49, 957–965. [Google Scholar] [CrossRef]
- Weißmann, V.; Bader, R.; Hansmann, H.; Laufer, N. Influence of the structural orientation on the mechanical properties of selective laser melted Ti6Al4V open-porous scaffolds. Mater. Des. 2016, 95, 188–197. [Google Scholar] [CrossRef]
- Challis, V.J.; Roberts, A.P.; Grotowski, J.F.; Zhang, L.C.; Sercombe, T.B. Prototypes for Bone Implant Scaffold Designed via Topolgy Optimation and Manufactured by Solid Freeform Fabrication. Adv. Eng. Mater. 2010, 12, 1106–1110. [Google Scholar] [CrossRef]
- Weißmann, V.; Wieding, J.; Hansmann, H.; Laufer, N.; Wolf, A.; Bader, R. Specific Yielding of Selective Laser-Melted Ti6Al4V Open-Porous Scaffolds as a Function of Unit Cell Design and Dimensions. Metals 2016, 6, 166. [Google Scholar] [CrossRef]
- Mahshid, R.; Hansen, H.N.; Højbjerre, K.L. Strength analysis and modeling of cellular lattice structures manufactured using selective laser melting for tooling applications. Mater. Des. 2016, 104, 276–283. [Google Scholar] [CrossRef]
- Xu, S.; Shen, J.; Zhou, S.; Huang, X.; Xie, Y.M. Design of lattice structures with controlled anisotropy. Mater. Des. 2016, 93, 443–447. [Google Scholar] [CrossRef]
- Rashed, M.G.; Ashraf, M.; Mines, R.A.; Hazell, P.J. Metallic microlattice materials a current state of the art on manufacturing, mechanical properties and applications. Mater. Des. 2016, 95, 518–533. [Google Scholar] [CrossRef]
- Wauthle, R.; Vrancken, B.; Beynaerts, B.; Jorisson, K.; Schrooten, J.; Kruth, J.P.; van Humbeeck, J. Effects of build orientation and heat treatment on the microstructure and mechanical properties of selective laser melted Ti6Al4V lattice structures. Addit. Manuf. 2015, 5, 77–84. [Google Scholar] [CrossRef]
- Cain, V.; Thijs, L.; van Humbeeck, J.; van Hooreweder, B.; Knutsen, R. Crack propagation and fracture toughness of Ti6Al4V alloy produced by selective laser melting. Addit. Manuf. 2015, 5, 68–76. [Google Scholar] [CrossRef]
- Wu, M.-W.; Lai, P.-H.; Chen, J.-K. Anisotropy in the impact toughness of selective laser leted Ti6Al4V alloy. Mater. Sci. Eng. A 2015, 650, 295–299. [Google Scholar] [CrossRef]
- De Wild, M.; Schumacher, R.; Mayer, K.; Schkommodau, E.; Thoma, D.; Bredell, M.; Gujer, A.K.; Grätz, K.W.; Weber, F.E. Bone regeneration by the osteoconductivity of porous titanium implants manufactured by selective laser melting: A histological and micro computed tomography study in the rabbit. Tissue Eng. Part A 2013, 19, 2645–2654. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Nune, K.C.; Murr, L.E.; Misra, R.K. Biocompatibility and Mechanical Behaviour of 3D Scaffolds for biomedical devices: Process-structure-property paradigm. Int. Mater. Rev. 2016, 61, 20–45. [Google Scholar] [CrossRef]
- Taniguchi, N.; Fukibayashi, S.; Takemoto, M.; Sasaki, K.; Otsuki, B.; Nakamara, T.; Matsuhita, T.; Kokubo, T.; Matsuda, S. Effect of pore size on bone ingrowth into porous titanium implants fabricated by dditive manufacturing an invivo experiment. Mater. Sci. Eng. C 2015, 59, 690–701. [Google Scholar] [CrossRef] [PubMed]
- Labeas, G.N.; Sunaric, M.M. Investigation on the Static Response and Failure Process of Metallic Open Lattice Cellular Structures. Strain 2010, 46, 195–204. [Google Scholar] [CrossRef]
- Ahmadi, S.M.; Campoli, G.; Yavari, S.A.; Sajadi, B.; Wauthle, R.; Schrooten, J.; Weinans, H.; Zadpoor, A.A. Mechanical behavior of regular open-cellporous biomaterials made of diamond lattice unit cells. J. Mech. Behav. Biomed. Mater. 2014, 34, 106–115. [Google Scholar] [CrossRef] [PubMed]
- Ushijima, K.; Cantwell, W.J.; Mines, R.A.; Tsopanos, S.; Smith, M. An investigation into the compressive properties of stainless steel micro-lattice structures. J. Sandw. Struct. Mater. 2010, 13, 303–329. [Google Scholar] [CrossRef]
- Suard, M.; Martin, G.; Lhuissier, P.; Dendievel, R.; Vignat, F.; Blandin, J.-J. Mechanical equivalent diameter of single struts for the stiffness prediction of lattice structures produced by electron beam melting. Addit. Manuf. 2015, 8, 124–131. [Google Scholar] [CrossRef]
- Desphande, V.S.; Ashby, M.F.; Fleck, N.A. Foam topology bending versus stretching dominated architectures. Acta Mater. 2001, 49, 1035–1040. [Google Scholar]
- Mazur, M.; Leary, M.; Sun, S.; Vcelka, M.; Shidid, D.; Brandt, M. Deformation and failure behaviour of Ti-6Al-4V lattice structures manufactured by selective laser melting (SLM). Int. J. Adv. Manuf. Technol. 2016, 84, 1391–1411. [Google Scholar] [CrossRef]
- McKnown, S.; Shen, Y.; Brooks, W.K.; Sutcliffe, C.J.; Cantwell, W.J.; Langdon, G.S.; Nurrick, G.N.; Theobald, M.D. The quasi-static and blast loading response of lattice structures. Int. J. Impact Eng. 2008, 35, 795–810. [Google Scholar] [CrossRef]
- Gong, H.; Rafi, K.; Gu, H.; Ram, G.J.; Starr, T.; Strucker, B. Influence of defects on mechanical properties of Ti–6Al–4V components produced by selective laser melting and electron beam melting. Mater. Des. 2015, 86, 545–554. [Google Scholar] [CrossRef]
- Simonelli, M.; Tse, Y.; Tuck, C. Effect of the build orientation on the Mechanical Properties and Fracture Modes of SLM Ti-6Al-4V. Mater. Sci. Eng. A 2014, 616, 1–11. [Google Scholar] [CrossRef]
- Qiu, C.; Adkins, N.; Attalah, M. Microstructure and tensile properties of selectively laser-melted and of HIPed laser-melted Ti-6Al-4V. Mater. Sci. Eng.A 2013, 578, 230–239. [Google Scholar] [CrossRef]
- Bartolomeu, F.; Faria, S.; Carvalho, O.; Pinto, E.; Alves, N.; Silva, F.S.; Miranda, G. Predictive models for physical and mechanical properties of Ti6Al4V produced by selective laser melting. Mater. Sci. Eng. A 2016, 663, 181–192. [Google Scholar] [CrossRef]
- Sigl, M.; Lutzmann, S.; Zaeh, M.F. Transient Physical Effects in Electron Beam Sintering. In Proceedings of the Solid Freeform Fabrication Symposium, Austin, Texas, 7–9 August 2006.
- Drescher, P.; Reimann, T.; Seitz, H. Investigation of powder removal of net-structured titanium parts made from electron beam melting. Int. J. Rapid Manuf. 2014, 4, 81–89. [Google Scholar] [CrossRef]
- Fox, J.C.; Moylan, S.P.; Lane, B.M. Effect of process parameters on the surface roughness of overhanging structures in laser powder bed fusion additive manufacturing. Procedia CIRP 2016, 45, 131–134. [Google Scholar] [CrossRef]
- Triantaphyllou, A.; Giusca, C.L.; Macaulay, G.D.; Roerig, F.; Hoebel, M.; Leach, R.K.; Tomita, B.; Milne, K.A. Surface texture measurement for additive manufacturing. Surf. Topogr. Metrol. Prop. 2015, 3, 024002. [Google Scholar] [CrossRef]
- Kasperovich, G.; Hausmann, J. Improvement of fatigue resistance and ductility of TiAl6V4 processed by selective laser melting. J. Mater. Process. Technol. 2015, 220, 202–214. [Google Scholar] [CrossRef]
- Campanelli, S.L.; Contuzzi, N.; Ludovico, A.D.; Caiazzo, F.; Cardaropoli, F.; Sergi, V. Manufacturing and characterization of Ti6Al4V lattice components manufactured by selective laser melting. Materials 2014, 7, 4803–4822. [Google Scholar] [CrossRef]
- Murr, L.E.; Quinones, S.A.; Gaytan, S.M.; Lopez, M.I.; Rodela, A.; Martinez, E.Y.; Hernandez, D.H.; Martinez, E.; Medina, F.; Wicker, R.B. Microstructure and mechanical behavior of Ti-6Al-4V produced by rapid layer manufacturing, for biomedical applications. J. Mech. Behav. Biomed. Mater. 2009, 2, 20–32. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.-W.; Lai, P.-H. The positive effect of hot isostatic pressing on improving the anisotropies of bending and impact properties in selective laser melted Ti6Al4V alloy. Mater. Sci. Eng. A 2016, 658, 429–438. [Google Scholar] [CrossRef]
- Sattler, K. Lehrbuch der Statik: Theorie und ihre Anwendungen. Erster Band: Grundlagen und Fundamentale Berechnungsverfahren; Springer Verlag GmbH: Heidelberg/Berlin, Germany, 1969; p. 132. [Google Scholar]
- Leuders, S.; Thöne, M.; Riemer, A.; Niendorf, T.; Tröster, T.; Richard, H.A.; Maier, H.J. On the mechanical behaviour of titanium alloy TiAl6V4 manufactured by selective laser melting Fatigue resistance and crack growth performance. Int. J. Fatigue 2013, 48, 300–307. [Google Scholar] [CrossRef]
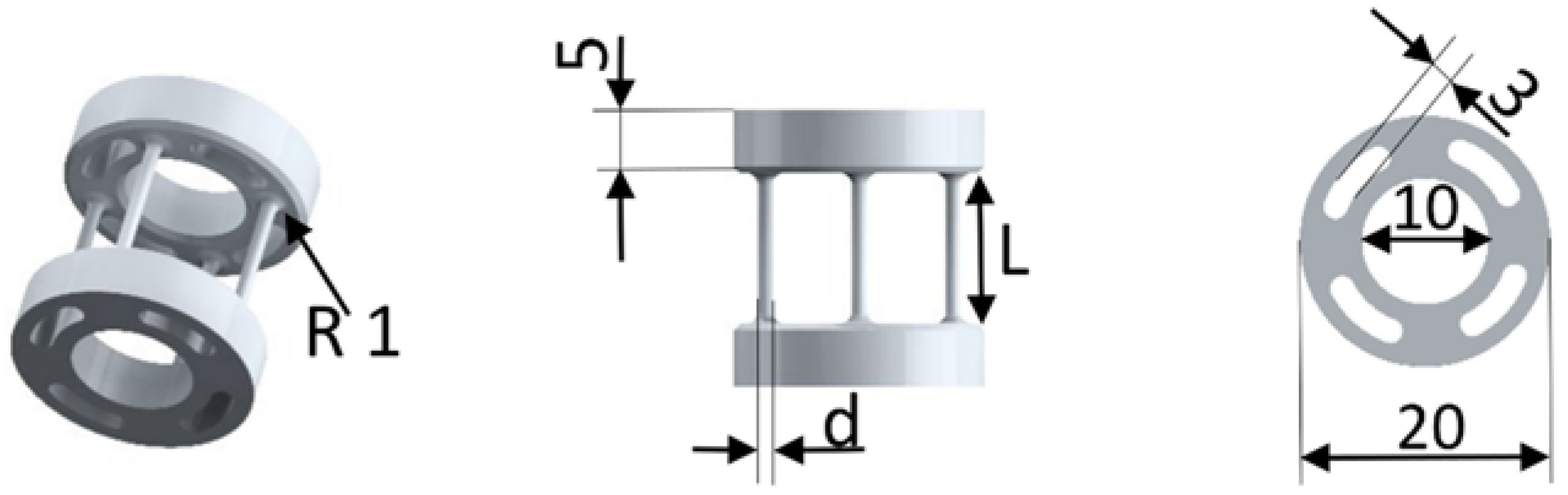



| Variation 1 | Variation 2 | ||||||
|---|---|---|---|---|---|---|---|
| Height L (mm) | Height L (mm) | ||||||
| 12 | 10 | 8 | 6 | 12 | |||
| Diameter d (mm) | Diameter d (mm) | ||||||
| 1.1 | 1.1 | 1.3 | 1.5 | 1.7 | |||
| Parameter | Description | Unit | Process Parameter |
|---|---|---|---|
| P | Laser Power | W | 275 |
| v | Scan speed | mm/s | 805 |
| d | Hatch spacing | µm | 120 |
| t | Layer thickness | µm | 50 |
| Parameter | Description | Unit | Process Parameter |
|---|---|---|---|
| P | Beam current | mA | ~21 |
| Acceleration voltage | kV | 60 | |
| v | Scan speed | mm/s | ~4530 |
| d | Hatch spacing | µm | 100 |
| t | Layer thickness | µm | 50 |
| dCAD–Orientation | EBM (μm) | SLM (μm) |
|---|---|---|
| 1.1 mm 0° | 995 ± 7 | 1057 ± 7 |
| 1.1 mm 45° | 949 ± 14 | 1063 ± 14 |
| 1.3 mm 0° | 1148 ± 48 | 1235 ± 17 |
| 1.3 mm 45° | 1155 ± 30 | 1299 ± 16 |
| 1.5 mm 0° | 1314 ± 32 | 1436 ± 22 |
| 1.5 mm 45° | 1358 ± 47 | 1486 ± 8 |
| 1.7 mm 0° | 1505 ± 21 | 1640 ± 9 |
| 1.7 mm 45° | 1538 ± 38 | 1646 ± 10 |
| Dimension | SLM HIP 0° | SLM No HIP 0° | EBM No HIP 0° | SLM HIP 45° | SLM No HIP 45° | EBM No HIP 45° | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| dCAD (mm] | LCAD (mm] | σ (MPA) | λ | σ (MPA) | λ | σ (MPA) | λ | σ (MPA) | λ | σ (MPA) | λ | σ (MPA) | λ |
| 1.7 | 12 | 925 ± 8 | 14.6 ± 0.1 | 811 ± 37 | 15.6 ± 0.1 | 947 ± 18 | 14.6 ± 0.1 | 838 ± 25 | 15.4 ± 0.1 | ||||
| 1.5 | 860 ± 11 | 16.7 ± 0.1 | 722 ± 37 | 17.8 ± 0.1 | 821 ± 22 | 16.2 ± 0.2 | 741 ± 40 | 17.4 ± 0.1 | |||||
| 1.3 | 838 ± 32 | 19.4 ± 0.1 | 629 ± 23 | 20.3 ± 0.2 | 793 ± 59 | 18.5 ± 0.1 | 634 ± 29 | 20.3 ± 0.1 | |||||
| 1.1 | 12 | 787 ± 22 | 22.8 ± 0.1 | 773 ± 10 | 22.3 ± 0.1 | 597 ± 34 | 24.1 ± 0.2 | 748 ± 97 | 21.6 ± 0.1 | 711 ± 47 | 22.4 ± 0.1 | 588 ± 33 | 25.5 ± 0.1 |
| 10 | 795 ± 56 | 19.0 ± 0.1 | 832 ± 46 | 18.5 ± 0.1 | 658 ± 85 | 20.1 ± 0.2 | 791 ± 73 | 18.0 ± 0.1 | 841 ± 38 | 18.6 ± 0.1 | 645 ± 30 | 21.2 ± 0.1 | |
| 8 | 900 ± 36 | 15.2 ± 0.1 | 1033 ± 56 | 14.3 ± 0.1 | 726 ± 41 | 16.1 ± 0.2 | 879 ± 28 | 14.4 ± 0.1 | 1053 ± 61 | 14.9 ± 0.1 | 739 ± 18 | 17.0 ± 0.1 | |
| 6 | 961 ± 43 | 11.4 ± 0.1 | 1220 ± 18 | 10.8 ± 0.1 | 841 ± 39 | 12.1 ± 0.2 | 960 ± 28 | 10.8 ± 0.1 | 1169 ± 15 | 11.1 ± 0.1 | 891 ± 33 | 12.7 ± 0.1 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weißmann, V.; Drescher, P.; Bader, R.; Seitz, H.; Hansmann, H.; Laufer, N. Comparison of Single Ti6Al4V Struts Made Using Selective Laser Melting and Electron Beam Melting Subject to Part Orientation. Metals 2017, 7, 91. https://doi.org/10.3390/met7030091
Weißmann V, Drescher P, Bader R, Seitz H, Hansmann H, Laufer N. Comparison of Single Ti6Al4V Struts Made Using Selective Laser Melting and Electron Beam Melting Subject to Part Orientation. Metals. 2017; 7(3):91. https://doi.org/10.3390/met7030091
Chicago/Turabian StyleWeißmann, Volker, Philipp Drescher, Rainer Bader, Hermann Seitz, Harald Hansmann, and Nico Laufer. 2017. "Comparison of Single Ti6Al4V Struts Made Using Selective Laser Melting and Electron Beam Melting Subject to Part Orientation" Metals 7, no. 3: 91. https://doi.org/10.3390/met7030091
APA StyleWeißmann, V., Drescher, P., Bader, R., Seitz, H., Hansmann, H., & Laufer, N. (2017). Comparison of Single Ti6Al4V Struts Made Using Selective Laser Melting and Electron Beam Melting Subject to Part Orientation. Metals, 7(3), 91. https://doi.org/10.3390/met7030091