Thermo-Viscoplastic Behavior of Ni-Based Superalloy Haynes 282 and Its Application to Machining Simulation

Abstract

Ni-based superalloys are extensively used in high-responsibility applications in components of aerospace engines and gas turbines with high temperature service lives. The wrought, γ’-strengthened superalloy Haynes 282 has been recently developed for applications similar to other common superalloys, such as Waspaloy or Inconel 718, with improved creep behavior, thermal stability, and fabrication ability. Despite the potential of Haynes 282, there are still important gaps in the knowledge of the mechanical behavior of this alloy. In fact, it was not possible to find information concerning the mechanical behavior of the alloy under impulsive loading. This paper focuses on the mechanical characterization of the Haynes 282 at strain rates ranging from 0.1 to 2800 s⁻¹ and high temperatures ranging from 293 to 523 K using Hopkinson bar compression tests. The experimental results from the thermo-mechanical characterization allowed for calibration of the Johnson–Cook model widely used in modeling metallic alloy’s responses under dynamic loading. Moreover, the behavior of Haynes 282 was compared to that reported for Inconel 718, and the results were used to successfully model the orthogonal cutting of Haynes 282, being a typical case of dynamic loading requiring previous characterization of the alloy.

1. Introduction

Aerospace engines and gas turbine operations involve elevated temperatures during the components’ service lives. Ni-based superalloys (being about 50% of the weight in an aerospace engine) offer high strength at high temperatures, fatigue strength, thermal stability, and resistance to corrosion under aggressive environmental conditions [1], being widely used in aerospace engines and gas turbines. However, due to their good mechanical properties, nickel-based superalloys are difficult to machine and expensive (see, for instance, [2,3]).

Nickel-based superalloys commonly used in these applications, such as Inconel 718, Waspalloy, and others, have been analyzed in the literature, covering both the mechanical behavior and fabrication ability of this family of alloys [4,5,6].

Haynes 282 is a γ’-strengthened Ni-based superalloy developed at the beginning of the present century with the aim of obtaining excellent creep behavior, thermal stability, fabrication ability, and strain-age cracking improvement [7]. Manufacturers demonstrated the increased creep strength, when compared to 263 and Waspaloy alloys at high temperatures (923–1200 K), as being equivalent to R-41 alloy in the range 1089–1200 K. The ductility decrement after long exposure times to elevated temperatures exhibited by R-41 and Waspaloy alloys was significantly improved.

In the solution-annealed condition, Haynes 282 alloy presented improved formability characteristics in terms of lower yield strength, when compared to higher γ’-containing alloys, such as R-41 and Waspaloy alloys.

Moreover, the formability of Haynes 282 was evaluated in terms of room temperature tensile properties indicating good cold formability, and also through controlled heating rate tensile (CHRT) properties [8], showing good resistance to strain-age cracking. Finally, the oxidation resistance of Haynes 282 alloy at 1200 K was similar to, or even better than, other Ni superalloys [7].

Haynes 282 is remarkably easier to weld than other γ’ alloys of similar strength due to its greater resistance to strain-age cracking, in spite of its γ’ content, and high strength at temperatures up to 1173 K [9,10]. The advantages of the Haynes 282 alloy have motivated its increasing use in hot section parts in gas turbines for aircrafts and power generation [9,10,11], and also the study of this alloy in the scientific literature.

Joseph et al. [12] studied the influence of heat treatment on the microstructure and mechanical properties of Ni-based superalloy Haynes 282. The authors found that grain boundary γ’ and a bi-modal intragranular γ’ distribution, dependent on the heat treatment, can be used to tailor the mechanical properties to be appropriate for specific applications.

The sensitivity of Haynes 282 to a hydrogen environment was analyzed in [13]. Tensile tests in hydrogen and argon atmospheres were carried out at room-temperature, showing significant hydrogen embrittlement of this alloy.

The effect of dynamic strain aging (DSA) on the deformation behavior of Haynes 282 during monotonic and cyclic loading was studied by Hörnqvist et al. [14]. The strong influence of DSA on the development of stress during cycling at intermediate temperatures was observed, resulting in cyclic hardening and serrated yielding. Despite these effects, the tensile properties were only slightly affected and no clear effects on the fatigue life could be observed.

He et al. [15] performed low-cycle fatigue (LCF) tests for Haynes 282 at temperatures between 298 and 1023 K with total strain ranges from 0.7% to 1.7%, showing an improved number of cycles to failure at high temperatures. Moreover, Haynes 282 showed better LCF properties at high temperatures when compared to two other types of low γ’ volume fraction nickel-based superalloys. This behavior seems to be related to the prevalence of transgranular fractures occurring in Haynes 282, while a mixture of intergranular and transgranular fractures were observed in the other alloys.

Most contributions in the literature are focused on cyclic loading behavior since fatigue phenomena are crucial for aeronautical applications. Additionally, the formability of Haynes 282, commonly used in forging, was studied by Joseph et al. [16]. The authors analyzed room-temperature ductility in the longitudinal transverse (LT) and short transverse (ST) directions in several specimens from forgings. Significant anisotropy in ductility, varying from approximately 25% in the LT direction to 12% in the ST direction, was found with different failure mechanisms (ductile with intergranular fracture in LT, cracking of carbides in ST).

Despite efforts to improve knowledge concerning the mechanical responses of Haynes 282 to different conditions, it is difficult to find works dealing with the thermo-mechanical behavior of this alloy at high strain rates and temperatures. It is worth noting that the dynamic characterization of Haynes 282 is of considerable interest for different applications. Firstly, knowledge of the response of this material under high strain rates is necessary for the design of components susceptible to experiencing impact loading. This is the case in aeroengine components, which could suffer impact loading. Moreover, component design requires finite element analysis due to the complexity of the geometries and loading conditions. Accurate predictions of component responses are strongly related to proper mechanical characterization of the alloy, allowing for the calibration of constitutive models. On the other hand, the machining commonly required for finishing superalloy components is a manufacturing process involving high strains, high strain rates, and elevated temperatures [17,18]. The analysis of the machinability of this alloy is strongly related to dynamic mechanical behavior.

The present work is focused on the dynamic characterization of the Haynes 282 superalloy. The thermo-mechanical behavior of the alloy was characterized by compression at a large range of strain rates and temperatures. The behavior of Haynes 282 was compared to the Inconel 718 alloy. The 718 alloy is widely used in aeroengines and has been soundly analyzed in the literature, thus, it was used as a reference for comparison with the behavior of the Haynes 282 alloy. Significant differences between both alloys were observed. The thermo-viscoplastic response under dynamic loading has been used to calibrate the Johnson–Cook constitutive model. This model is typically used in the simulation of metal alloy responses under dynamic loading. The resultant constitutive equation was applied to model the orthogonal cutting of Haynes 282, being a case of dynamic loading requiring proper characterization. The model was validated by comparing it to machining tests performed on Haynes 282 and it showed good accuracy when predicting cutting forces.

2. Materials

A Haynes 282 alloy bar, manufactured as per specification AMS5951, annealed at 1408 K, and age-hardened, was used in this study. According to the manufacturer, the Haynes 282 alloy was provided in the solution-annealed condition, in which it is readily formable. The typical solution annealing temperature is in the range of 1394–1422 K. After component fabrication, a two-step age-hardening treatment was required to make the alloy into high-strength condition. The treatment includes 1283 K/two hours/AC (air cool) + 1061 K/eight hours/AC. The chemical composition of the Haynes 282 used in this work is provided in Table 1. The nickel content is slightly higher than that found in other superalloys such as Inconel 718. The Fe content is considerably lower in Haynes 282 than in Inconel 718; however, the other main difference between the two superalloys is in cobalt content, where Haynes 282 contains a greater quantity than Inconel 718.

Table 1. Chemical composition of Inconel 718 and Haynes 282 superalloys (wt %) [19].

Element %	Ni	Cr	Fe	Nb	Mo	Ti	Al	Co.	Si	Cu	Mn	C
Inconel 718	53.02	18.49	18.12	5.40	3.06	0.96	0.55	0.10	0.06	0.05	0.06	0.03
Haynes 282	57	19.40	0.87	<0.01	8.52	2.22	1.41	10.2	<0.05	<0.01	0.06	0.062

3. Methods

3.1. Experimental Characterization of the Thermo-Viscoplastic Behavior of Haynes 282

Compression tests at different strain rates and temperatures were carried out. Compression specimens were made from the alloy bar using an electrodischarge machine model CUT E 350 (GF Machining Solutions, Geneva, Switzerland). The cylindrical compression samples, considered in both quasi-static and dynamic tests, had the following dimensions: diameter φ = 8 mm and thickness t = 4 mm. The aspect ratio t/φ = 0.5 prevented significant friction and inertia effects and it was defined according to the critical slenderness ratio to avoid size effects established by Bertholf and Karnes [20]. Additionally, the sample ends were lubricated to reduce friction effects during the tests. Three specimens per test condition were performed to ensure the repeatability of the experimental data. The figures only show the average of the three tests.

3.1.1. Quasi-Static Compression Testing

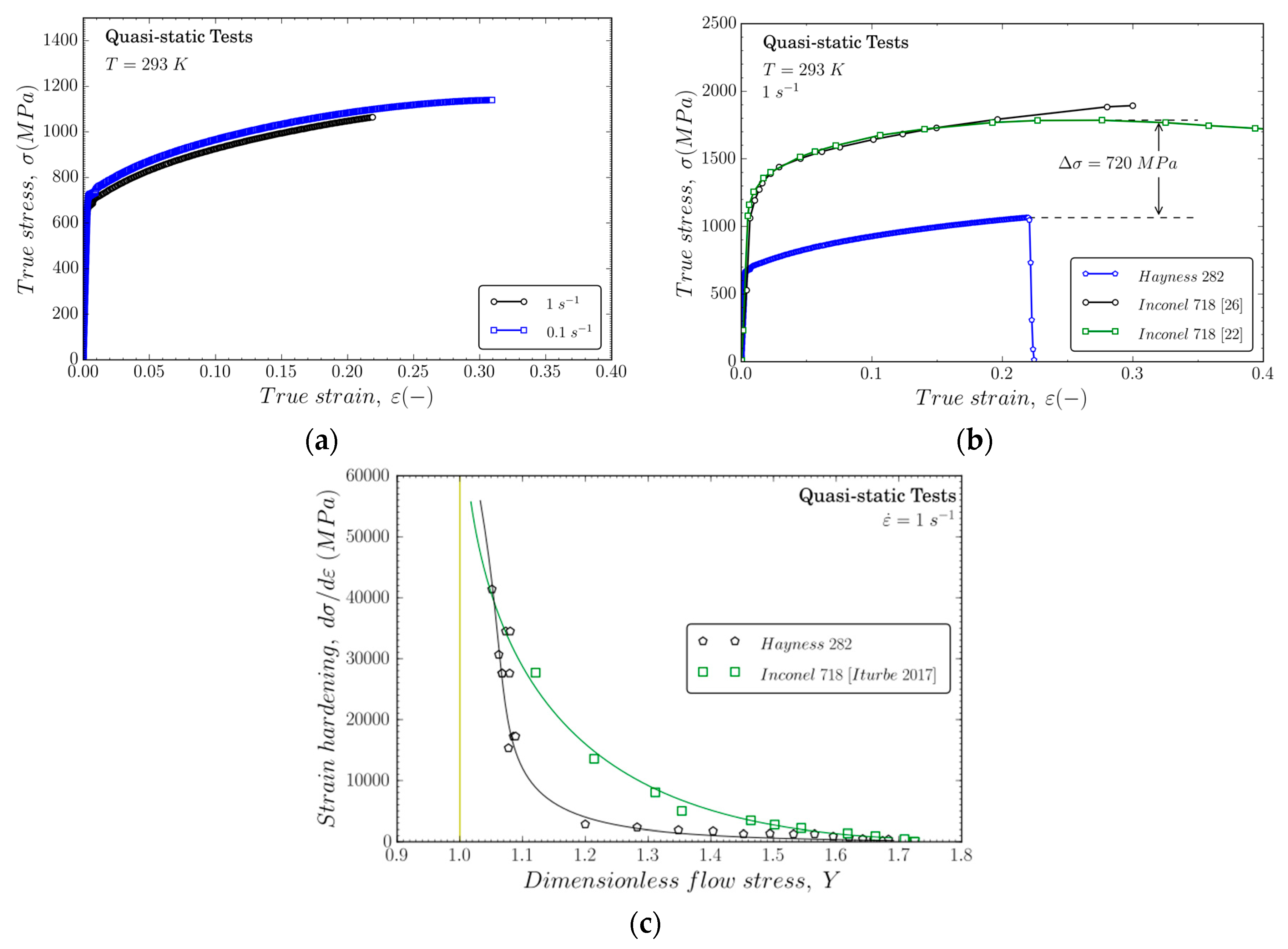
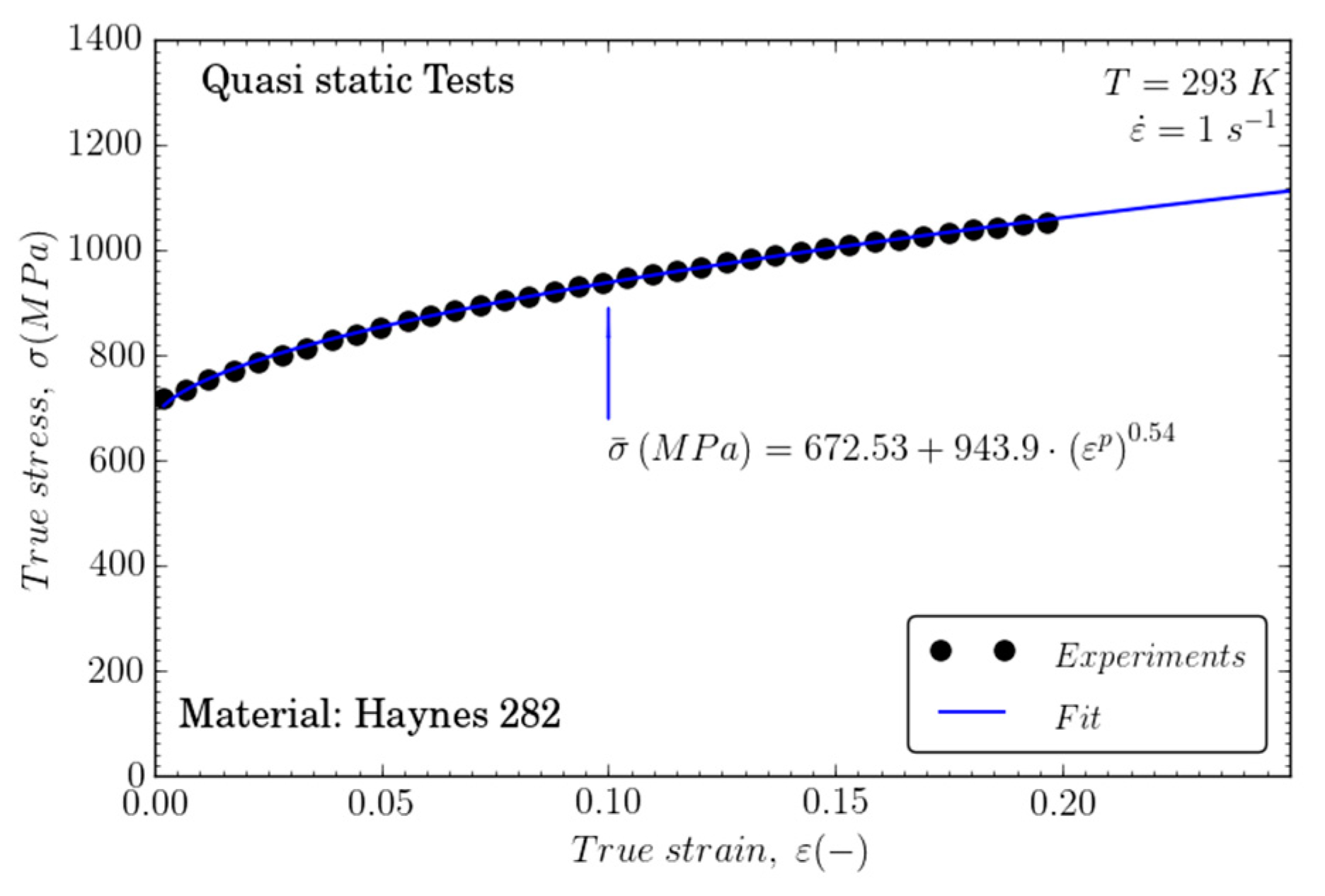
The tests were performed using an INSTRON servo-electric testing machine (INSTRON, Cerdanyola, Barcelona, Spain) instrumented with a 100 kN load cell. Two low loading speeds (2.4 and 24 mm/min) were imposed in order to ensure quasi-static loading conditions. Low-rate compression tests were conducted within the range of strain rates $0.1{\mathrm{s}}^{-1}<\dot{\epsilon }<1{\mathrm{s}}^{-1}$. Figure 1a shows the representative quasi-static compression stress–strain curves for Haynes 282. The rate sensitivity is negligible within this range of strain rates, which is a common characteristic of other metallic alloys [21]. Figure 1b compares the quasi-static behavior of Inconel 718, obtained from literature, and the experimental results in the present work for Haynes 282. Inconel 718 presents larger yield stress (1100 MPa) than Haynes 282 (710 MPa). Moreover, the strain hardening is also greater for Inconel 718. Figure 1c shows the strain hardening parameter θ = ∂σ/∂ε versus the normalized flow stress Y = σ/σ₀, σ₀ being the material yield stress at the onset of plastic deformation for each alloy. The remarkable strain hardening exhibited by Inconel 718 boosts the material flow stress; however, Haynes 282 and Inconel 718 show the same flow saturation condition (θ = 0).

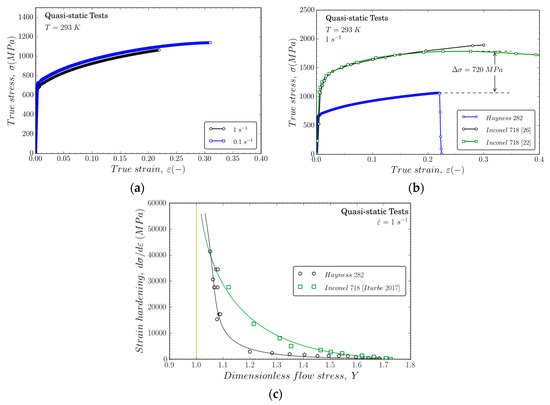
Figure 1. (a) Representative quasi-static compression stress–strain curves for Haynes 282; (b) Comparison of mechanical behavior for Haynes 282 and Inconel 718; (c) Strain hardening parameter θ = ∂σ/∂ε versus the dimensionless flow stress Y = σ/σ₀ for both alloys [22].

3.1.2. Dynamic Compression Testing

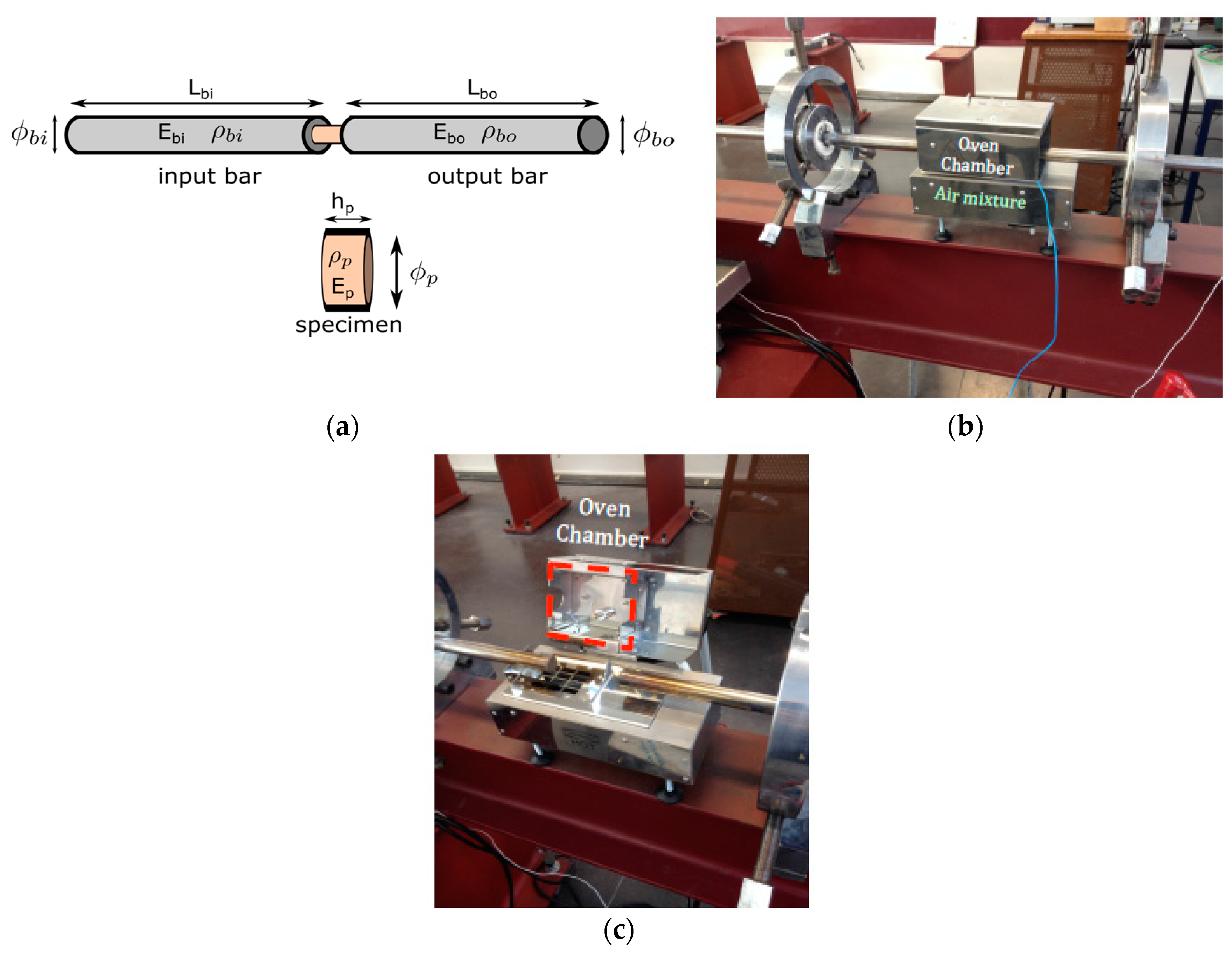
Dynamic compression experiments with strain rates ranging from $800 {\mathrm{s}}^{-1} < \dot{\epsilon }< 2800 {\mathrm{s}}^{-1}$ were carried out using a conventional Kolsky apparatus (LEM3, Metz, France) (see Figure 2). The split Hopkinson pressure bar (SPHB) consisted of high strength steel. A furnace was coupled at the testing zone in order to analyze temperature behavior. Table 2 summarizes the main parameters of the split Hopkinson pressure bar setup.

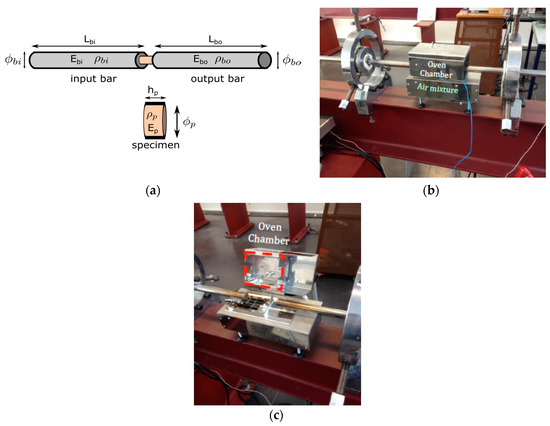
Figure 2. (a) Scheme of the experimental device, including relevant properties of the input and output bars and specimens (E, Young modulus; ρ, density), and dimensions (length; diameter); (b) Split Hopkinson pressure bars used during dynamic tests with the furnace coupled for temperature testing; (c) Details of the furnace.

Table 2. Parameters of the split Hopkinson pressure bar.

Lbi (m)	Lbo (m)	Φbi (m)	Φbo (m)	${\mathit{\rho }}_{\mathit{b}\mathit{i}}$ (kg/m3)	${\mathit{\rho }}_{\mathit{b}\mathit{o}}$ (kg/m3)	hp (m)	Φp (m)	${\mathit{\rho }}_{\mathit{b}\mathit{i}}$ (kg/m3)
0.30	0.30	0.018	0.018	7800	7800	0.004	0.008	8270

The strain rate depends on the projectile impact velocity $V_p$ and the yield stress of the tested material. When the projectile impacts the input bar, an incident stress elastic wave, ${\sigma }_I$, is created and travels along the impact bar with an elastic wave speed $C_0$, dependent on Young’s modulus and the density of the material $\rho \left(C_0=\sqrt{E/\rho }\right)$. The incident wave intensity,${\sigma }_I$, is proportional to the speed of the projectile $V_p$ in the following form ${\sigma }_I={\rho }_0{C}_0{V}_p/2$. When the incident strain wave ${\epsilon }_I={\sigma }_I/E$ reaches the specimen interface, a part of it is reflected (${\epsilon }_R,{\sigma }_R$) and a part is transmitted (${\epsilon }_T,{\sigma }_T$) along the output bar.

Based on the assumptions of uniaxial wave propagation and uniform stress distribution in the specimen, the stresses, strains, and strain rates can be calculated in the case of dynamic forces equilibrium using the following equations [23]:

$$\begin{array}{c}\sigma (t)=\frac{E_b}{2}\frac{{\varphi }_b}{{\varphi }_s}({\epsilon }_I+{\epsilon }_R+{\epsilon }_T)\\ \epsilon \left(t\right)=\frac{C_0}{L_0}\int \left({\epsilon }_I+{\epsilon }_R+{\epsilon }_T\right)d\psi \\ \dot{\epsilon }\left(t\right)=\frac{C_0}{L_0}\left({\epsilon }_I+{\epsilon }_R+{\epsilon }_T\right)\end{array}\left\}\stackrel{}{\to }{\epsilon }_T={\epsilon }_I+{\epsilon }_R\to \right\{\begin{array}{c}\sigma \left(t\right)=E_b{\left(\frac{{\varphi }_b}{{\varphi }_s}\right)}^2\left|{\epsilon }_T\right|\\ \epsilon \left(t\right)=\frac{2C_0}{L_0}{\int }_0^t\left|{\epsilon }_R\right(\psi \left)\right|d\psi \\ \dot{\epsilon }(t)=\frac{2C_0}{L_0}\left|{\epsilon }_R\left(t\right)\right|\end{array}$$

(1)

From these equations, the thermo-viscoplastic behavior σ(ε) for an imposed strain rate ($\dot{\epsilon }$) can be defined. Note that in order to determine the stress–strain curves, dynamic specimen equilibrium (force equilibrium, energy balance) was verified for each sample, and corrections for wave dispersion and friction effects were applied using a homemade program developed at the Lab of LEM3, called the Waves Analysis and Study Program (WASP), according to conventional wave analysis. The software allows for the rebuilding of the thermo-viscoplastic behavior of the material tested under dynamic loading in terms of the stress–strain curve from the record of the three waves (incident, reflected, and transmitted). In addition, the software allows correcting friction and adiabatic effects to determine the behavior of the material tested. All details for the theory of SHPB testing and the analytical approach presented previously can be found in [24].

The device allows for conducting dynamic compression testing at different temperatures (from room temperature up to 523 K) using a furnace, ensuring a constant temperature in the specimen through the use of a fan for the hot air stream flow. The estimated time to achieve this uniform temperature is 30 min. This level of temperature (523 K) is intermediate when considering the service temperature range for the component (typically up to 1073 K), however, the experimental tests allow for the characterization of the thermal softening terms in the constitutive equation. On the other hand, testing at a higher temperature is extremely difficult since the bar alloy also experiences degradation of its mechanical properties due to high temperature. More details concerning the development of the experimental device are reported in [25].

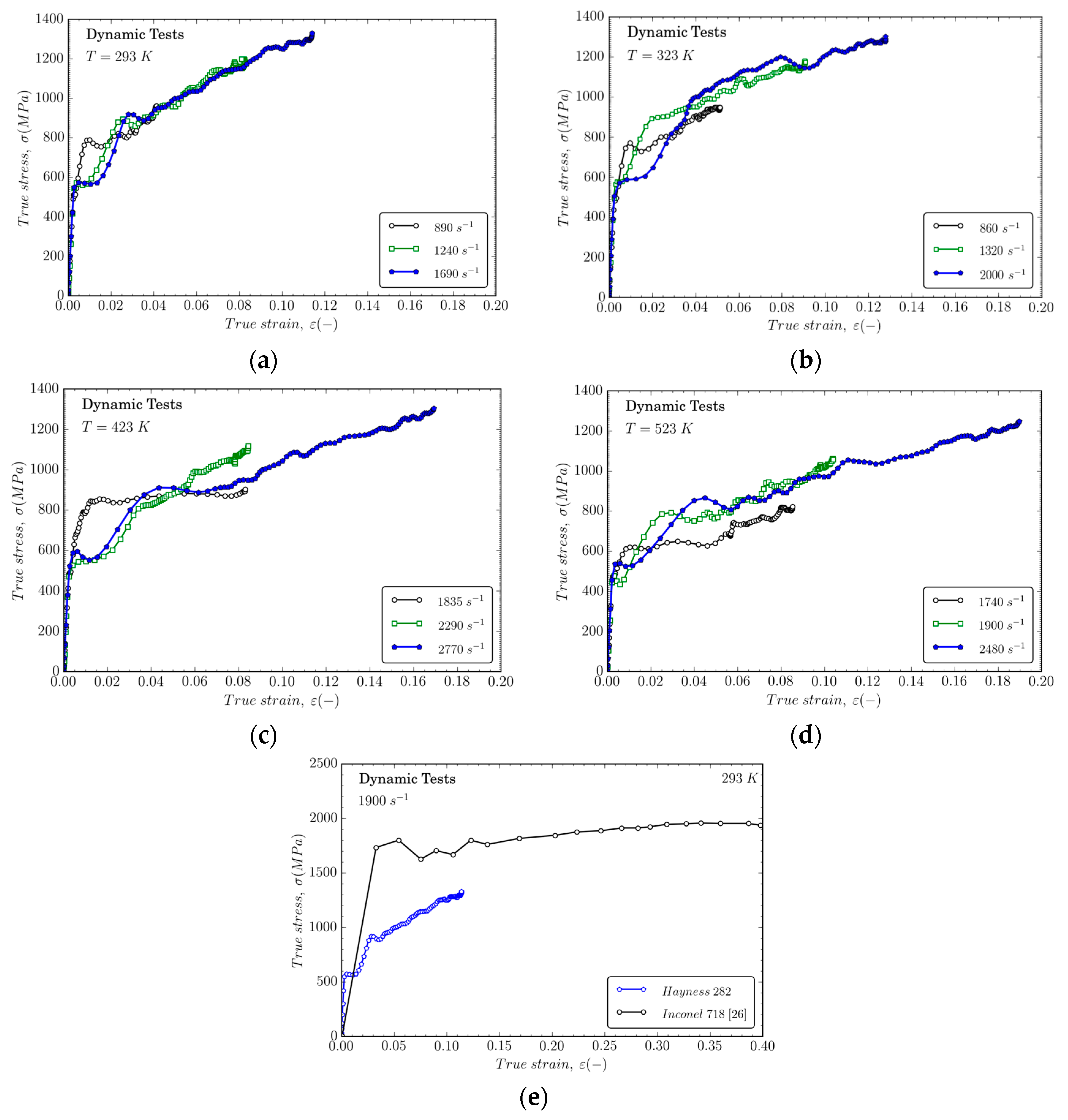
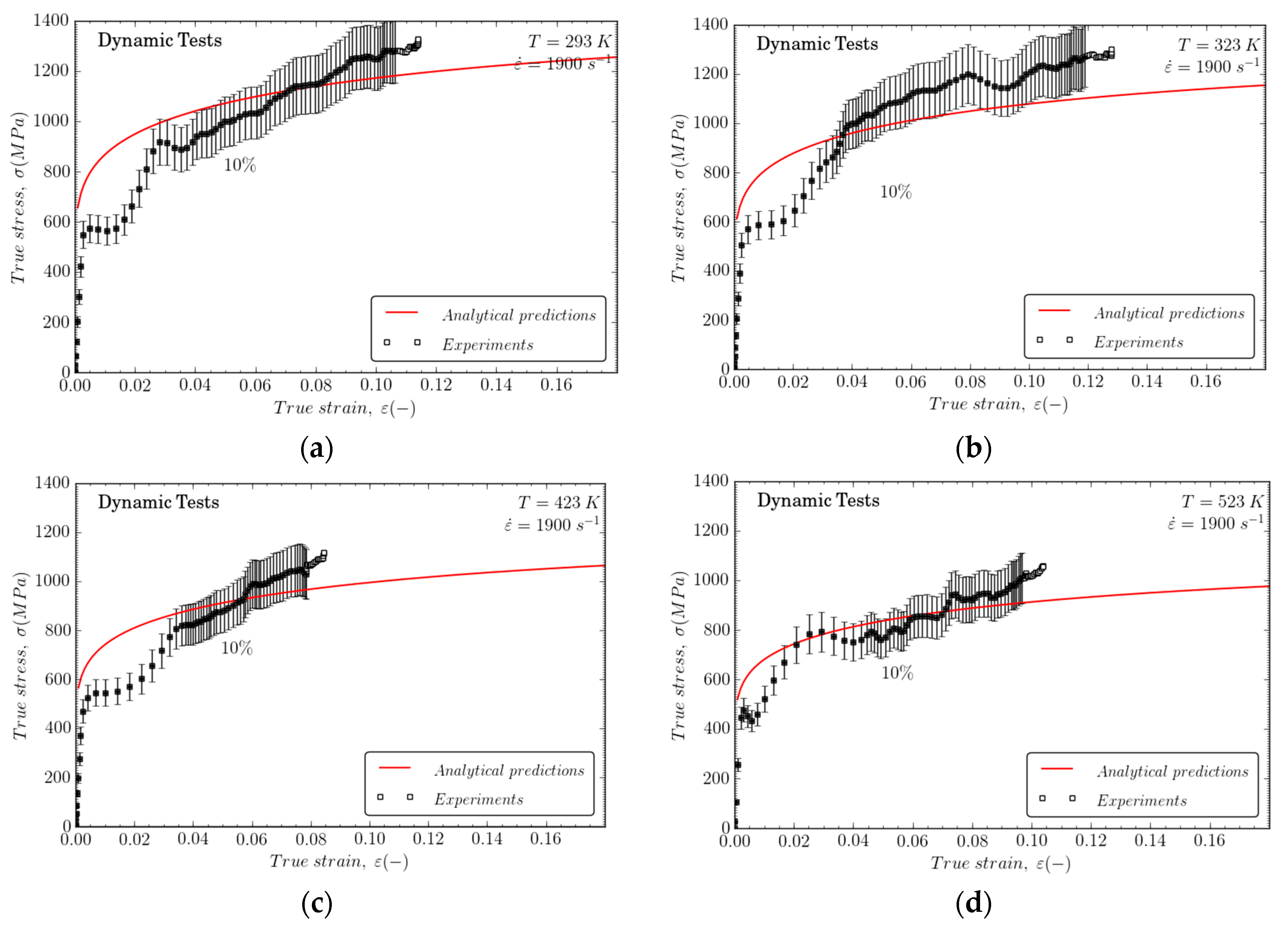
Figure 3 shows some of the dynamic compression stress–strain curves obtained from the tests. The strain hardening seems to be nearly independent of the loading rate at room temperature (Figure 3a) as it was previously observed from the low-rate experiments. Strain rate hardening is slightly increased for higher temperatures, as can be observed in Figure 3b–d. Figure 3e shows large differences between Haynes 282 and Inconel 718 alloy for a deformation rate of 1900 s⁻¹ with a higher level of tension for the second material. This behavior is related to the better formability of Haynes 282, especially when dynamic loading is involved during the manufacturing route.

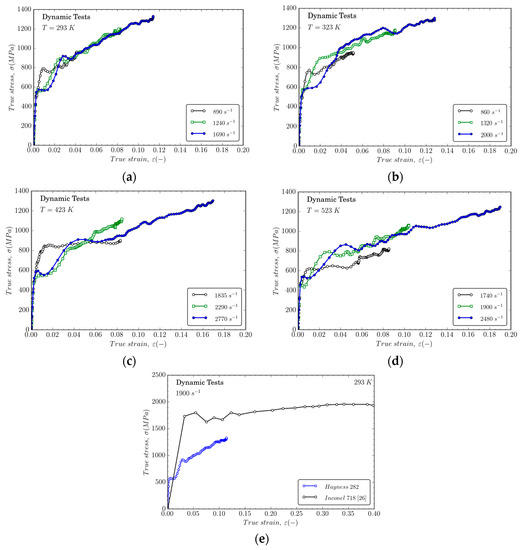
Figure 3. Flow stress evolution versus true strain for different strain rates at different temperatures: (a) 293 K; (b) 323 K; (c) 423 K; and (d) 523 K; (e) Comparison of mechanical behavior for Haynes 282 and Inconel 718 at 1900 s⁻¹ and at room temperature [26].

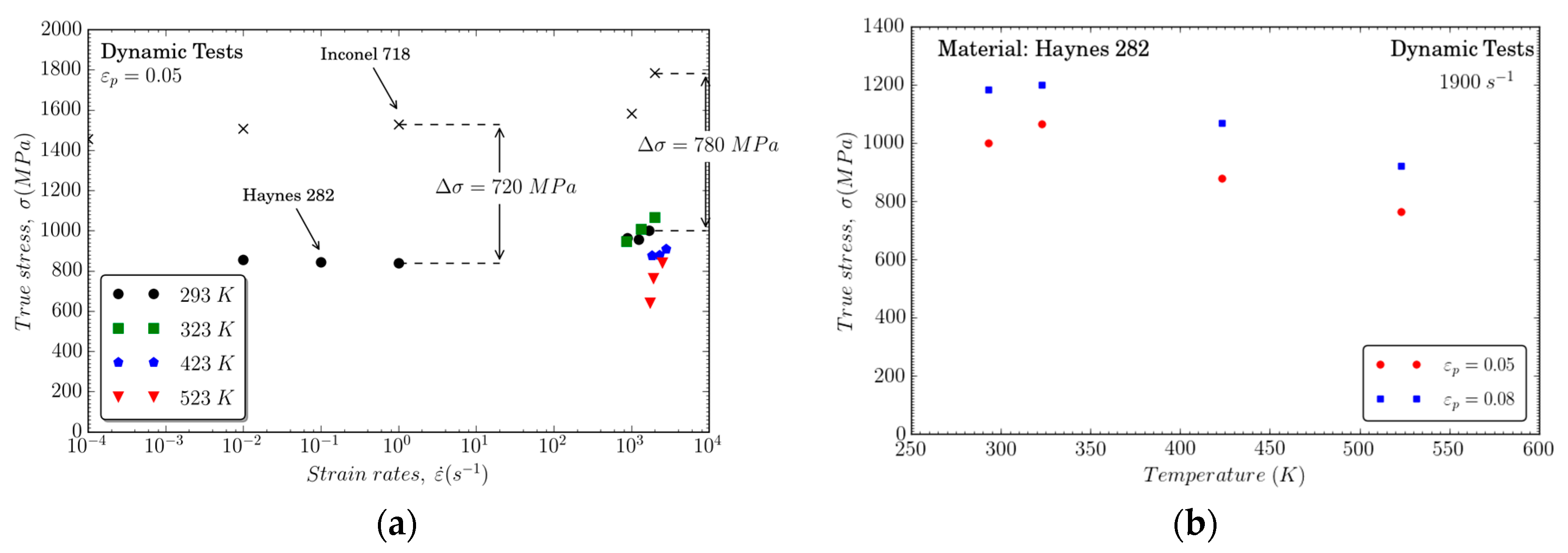
Figure 4a illustrates the flow stress evolution at plastic strains equal to 0.05 versus the strain rate for different temperatures. For the range of strain rates considered, the difference between Haynes 282 and Inconel 718 alloys is roughly constant between 720 and 780 MPa.

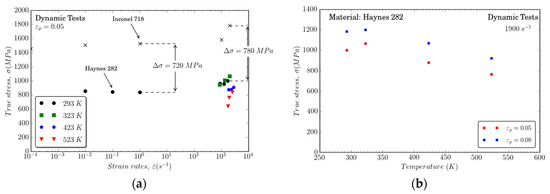
Figure 4. Flow stress evolution versus: (a) strain rate and (b) temperature for different plastic strain levels.

The dependence of flow stress on strain rate is negligible until $\dot{\epsilon }\approx 1000 {\mathrm{s}}^{-1}$. Beyond this strain rate value, strain rate hardening is observed for all temperatures considered. Furthermore, a remarkable decrease is observed at a temperature of 523 K.

This last observation is highlighted in Figure 4b, showing, for $\dot{\epsilon }\approx 1900 {\mathrm{s}}^{-1}$, that the flow stress depending on temperature for different levels of plastic strain (for ${\epsilon }_p=0.05$ and ${\epsilon }_p=0.08$) is almost parallel, corresponding to a constant temperature sensitivity. Beyond T ≈ 400 K, an incipient decrease in flow stress is displayed. This is in agreement with experiments published for Haynes 282 [9] and for Ni superalloys (as Haynes 188 [27] and Inconel 718 [22]).

3.2. Modelling of the Thermo-Viscoplastic Behavior

Based on experiments previously presented, the thermo-viscoplastic behavior of Haynes 282 is modeled using the Johnson–Cook constitutive relation [28], based on a phenomenological formulation and successfully used in modeling the machining and impact process of metals.

This constitutive law defines the effective flow stress following the expression given in Equation (2). The first term of Equation (2) defines the strain hardening due to plastic deformation (${\bar{\epsilon }}^p$) depending on the reference yield stress A and the material constants B and n. The second term accounts for strain rate sensitivity (${\dot{\bar{\epsilon }}}^p$) through the material parameter C and the reference strain rate ${\dot{\bar{\epsilon }}}_0$. Regarding the third term, it captures the thermal softening of the material using the thermal sensitivity parameter m:

$$\bar{\sigma }({\bar{\epsilon }}^p,{\dot{\bar{\epsilon }}}^p,T)=\left[A+B{\left({\bar{\epsilon }}^p\right)}^n\right]\left[1+C\ln \left(\frac{{\dot{\bar{\epsilon }}}^p}{{\dot{\bar{\epsilon }}}_0}\right)\right] \left[1-{\Theta }^m\right]$$

(2)

where $\Theta$ depends on the current temperature T, the melting temperature T_m, and a reference temperature T₀ as:

$$\Theta =\frac{T-T_0}{T_m-T_0}$$

(3)

The initial temperature T₀ was set to 293 K, and the melting temperature T_m for this alloy is 1573 K [29].

The Johnson–Cook model, being a phenomenological and decoupled model, allows for isolation of each part of the equation to obtain the constants of the model. The procedure for obtaining the parameters of Equation (1) is detailed below.

3.2.1. Strain Hardening

The strain hardening term of the JC model is defined as ${\bar{\sigma }}_{\epsilon }\left({\bar{\epsilon }}_p\right)= A+B\cdot {\bar{\epsilon }}_p{}^n$. These parameters are usually fitted using quasi-static tests at room temperature, as described in Section 2, Figure 5. The parameters obtained for Haynes 282 are compared to those obtained for Inconel 718 from the literature [22] (see Table 3). The yield stress is about 50% of that given for Inconel 718 and the strain hardening coefficient is slightly lower than that found in the quasi-static test.

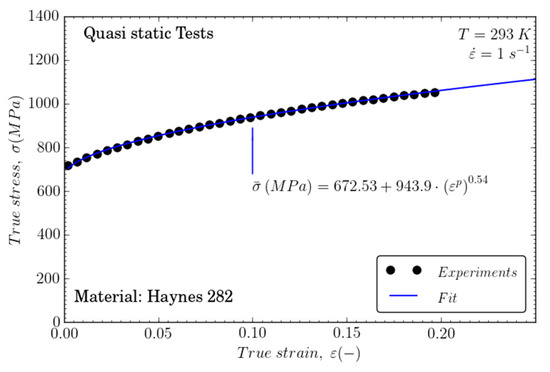
Figure 5. Flow stress evolution versus strain rate and fitting to obtain A, B, and n.

Table 3. Parameters obtained for strain hardening-softening and comparison with Inconel 718 [22].

Material	A (MPA)	B (MPA)	$\mathit{n} (-)$
Haynes 282	672.53	943.9	0.54
Inconel 718 [22]	1377	1243.5	0.6767

3.2.2. Strain Rate Hardening

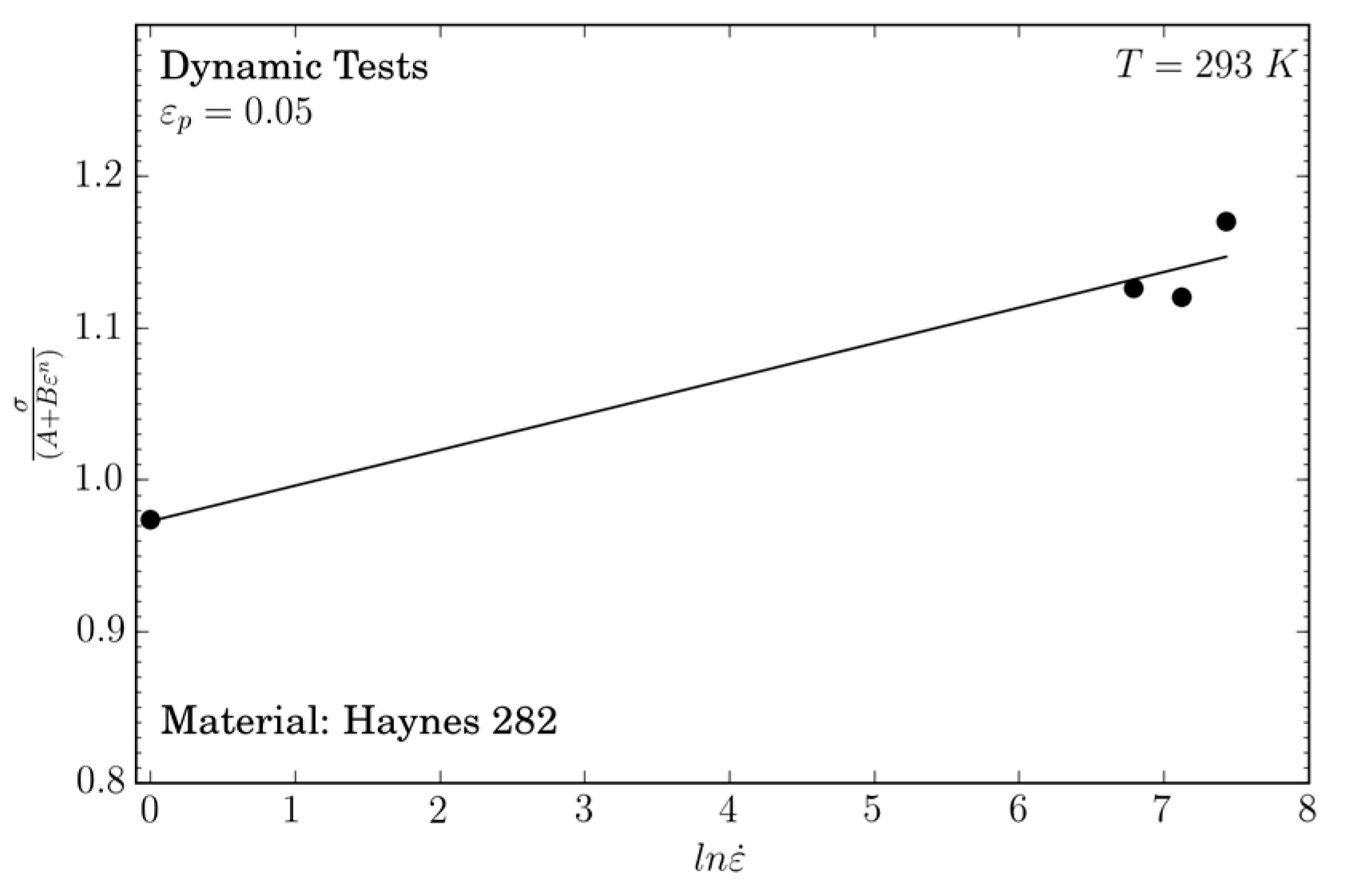
The term corresponding to strain rate sensitivity is $1+C·\ln \left(\dot{\bar{\epsilon }}/{\dot{\bar{\epsilon }}}_0\right)$. The Johnson–Cook model can be simplified for T = T_ref = 293 K and rearranged as:

$$\frac{{\bar{\sigma }}_{\epsilon }\left({\bar{\epsilon }}_p\right)}{A+B\cdot {\bar{\epsilon }}_p^n} =1+C\ln \left(\frac{{\dot{\bar{\epsilon }}}^p}{{\dot{\bar{\epsilon }}}_0}\right)$$

(4)

Using the values of $B$ and $n$ obtained above, a linear curve $\frac{{\bar{\sigma }}_{\epsilon }\left({\bar{\epsilon }}_p\right)}{A+B\cdot {\epsilon }_p^n}$ vs. $\ln \left(\frac{{\dot{\bar{\epsilon }}}^p}{{\dot{\bar{\epsilon }}}_0}\right)$ is plotted in Figure 6. Equation (4) allows for the defining of the value of the strain rate sensitivity $C=0.023$. This value is higher compared to the one obtained for Inconel 718 and published by Iturbe et al. [22], $C_{inconel}=0.0045.$ Therefore, Inconel 718 shows a lower strain rate sensitivity than Haynes 282.

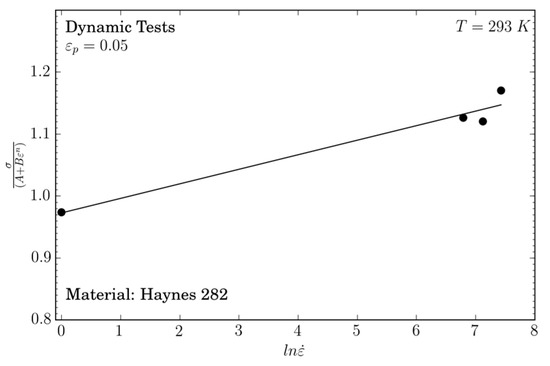
Figure 6. Dimensionless flow stress evolution versus the logarithm strain rate and linear fitting to obtain C.

3.2.3. Temperature Softening

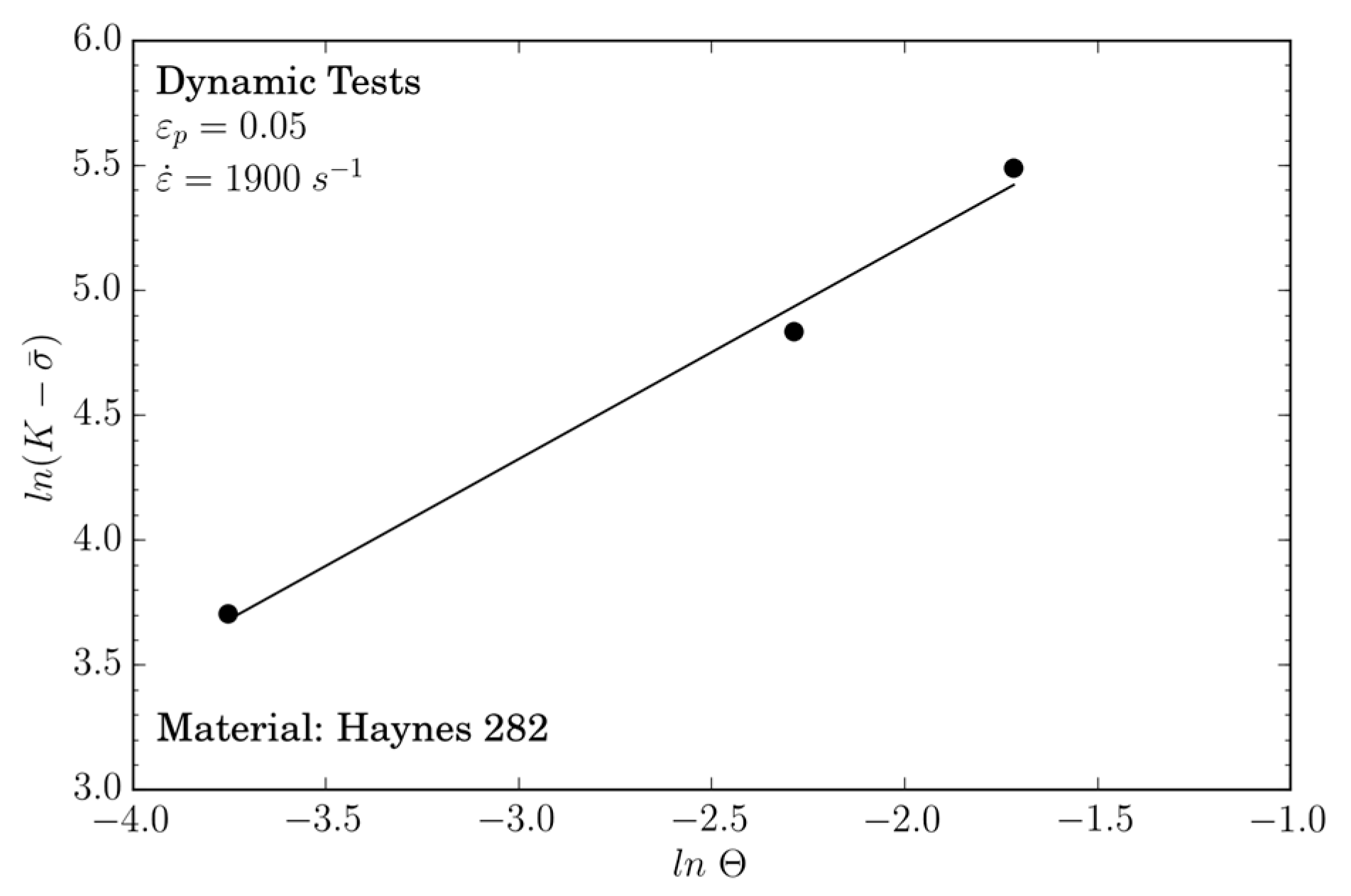
The temperature sensitivity parameter $m$ is defined using experiments performed at ${\dot{\bar{\epsilon }}}_{}=1900{\mathrm{s}}^{-1}$, corresponding to dynamic strain rate. The temperature sensitivity approach is expressed as: $\left[1-{\Theta }^m\right]$. Therefore, the equivalent stress is as follows in Equation (5):

$$\bar{\sigma }({\bar{\epsilon }}^p,{\dot{\bar{\epsilon }}}^p,T)=K \left[1-{\Theta }^m\right]$$

(5)

where $K=\left[A+B{\left({\bar{\epsilon }}^p\right)}^n\right]\left[1+C\ln \left(\frac{{\dot{\bar{\epsilon }}}^p}{{\dot{\bar{\epsilon }}}_0}\right)\right]$. Using the natural logarithm on both sides, Equation (5) may be rewritten as:

$$\ln \left(K-\bar{\sigma }\right)= m\ln \left(\Theta \right)+\ln K$$

(6)

Applying a linear fitting method coupled to an optimization method, such as the least squares method, as shown in Figure 7, the temperature sensitivity is equal to $m=0.855$ for the range of temperatures considered in this work: $293\mathrm{K}<T<523\mathrm{K}$. It has to be noted that it would be interesting to perform some tests for temperatures ranging from 523 to 973 K since atypical behaviours were observed in this range for Inconel 718. Thus, below this temperature, Inconel 718 was not so sensitive to temperature increases. The mechanical properties in the temperature range between 294 and 973 K decreased by 20% [22]. For Haynes 282, this decrease was 30% for the temperature range $293 \mathrm{K}<T<523 \mathrm{K}$ (see Figure 4b).

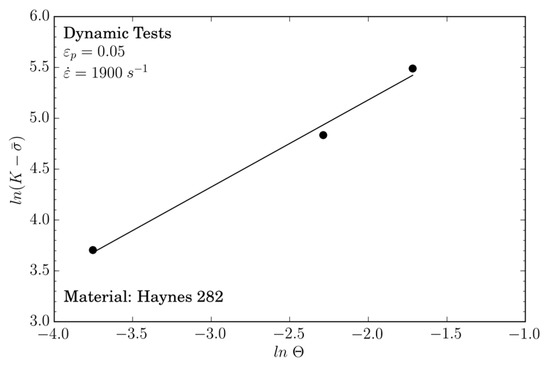
Figure 7. $\ln \left(K-\bar{\sigma }\right)-\ln \left(\Theta \right)$ curve and linear fitting to obtain $m$.

Finally, the set of material constants found, and the physical constants of Haynes 282, are listed in Table 4.

Table 4. Physical properties and Johnson–Cook parameters of Haynes 282 at room temperature.

Elasticity		Thermo-Viscoplastic Behavior
$E \left(\mathrm{GPa}\right)$	$\nu (-)$	$A \left(\mathrm{MPa}\right)$	$B \left(\mathrm{MPa}\right)$	$n (-)$	$\dot{{\epsilon }_{0 }}\left({\mathrm{s}}^{-1}\right)$	$C (-)$	$m (-)$
217	0.319	672.53	943.9	0.54	1	0.023	0.855
Other Physical Constants
$\rho \left(\mathrm{kg}/{\mathrm{m}}^3\right)$		$\beta (-)$		$T_0\left(\mathrm{K}\right)$		$T_m\left(\mathrm{K}\right)$
8270		0.9		293		1573

3.2.4. Analysis of Thermo-Viscoplastic Behavior under Different Strain Rates and Temperatures

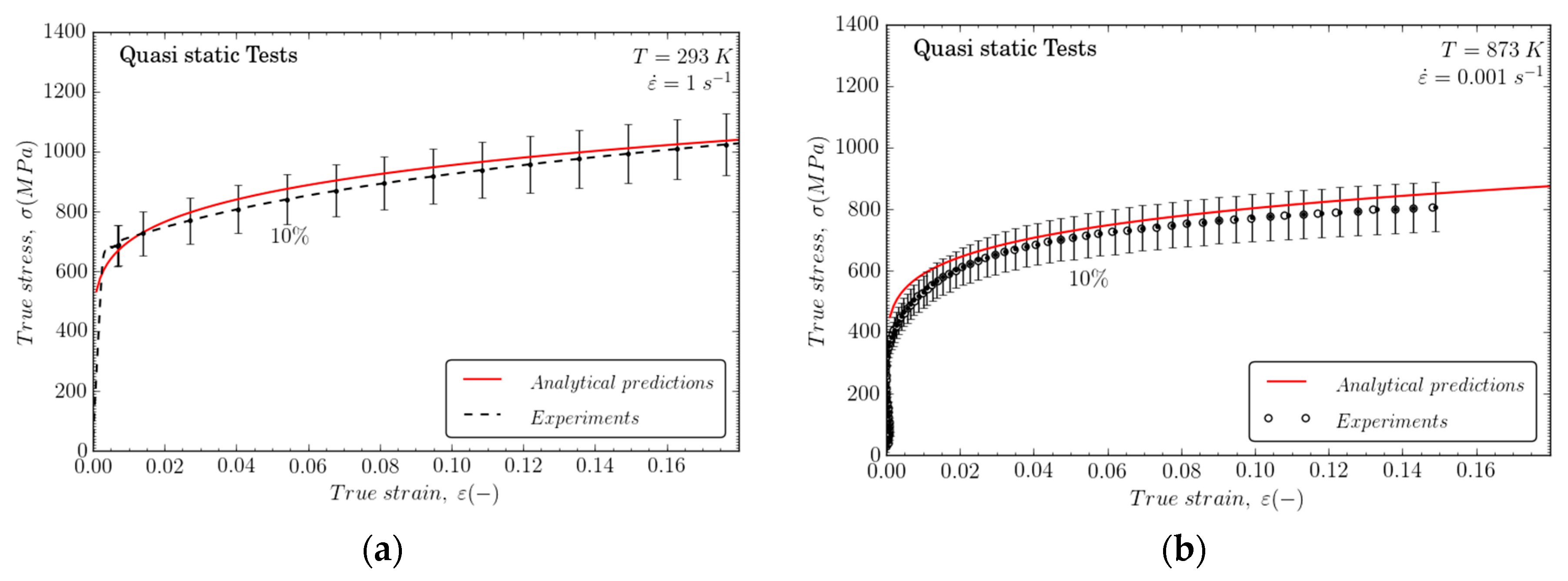
The calibrated model is correlated with experiments for different strain rate levels at different temperatures. The constitutive description is suitable for defining the flow stress, as well as the strain hardening rate of the material for the loading conditions considered (the induced error is, in any case, less than 10%). Figure 8a displays a good correlation between experimental results and predictions. In order to validate the parameters of the Johnson–Cook model, an additional test at 873 K and 0.001 s⁻¹ was been carried out, as shown in Figure 8b.

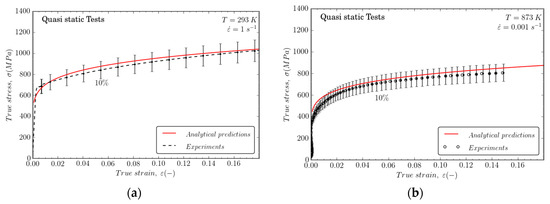
Figure 8. (a) Comparison between analytical predictions of the Johnson–Cook model and experiments at $T_0=293 \mathrm{K}$ and ${\dot{\bar{\epsilon }}}_0=1 {\mathrm{s}}^{-1}$; (b) Analytical predictions of the constitutive model within wide ranges of strains and strain rates at T₀ = 873 K.

The Johnson–Cook model reproduces work hardening and material flow stress within a wide range of temperatures, 293 K < T₀ < 523 K, with an error of 10% for large deformations, making it suitable for numerical simulation of mechanical behavior for machining or impact problems, as shown in Figure 9. It is remarkable that strain rate influences material strain hardening; in the same manner, it must be highlighted that temperature also strongly influences work hardening.

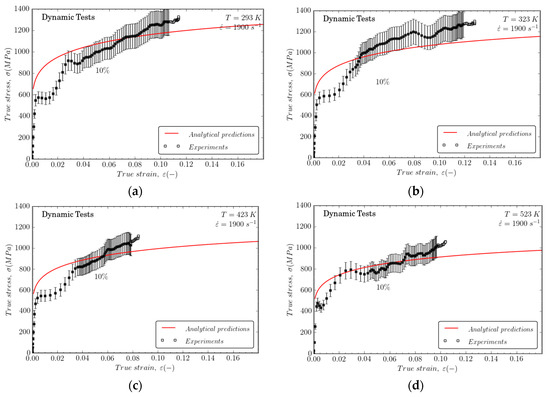
Figure 9. Comparisons between analytical predictions of the constitutive model and experiments at 1900 s⁻¹ and (a) T₀ = 293 K; (b) T₀ = 323 K; (c) T₀ = 423 K; and (d) T₀ = 523 K.

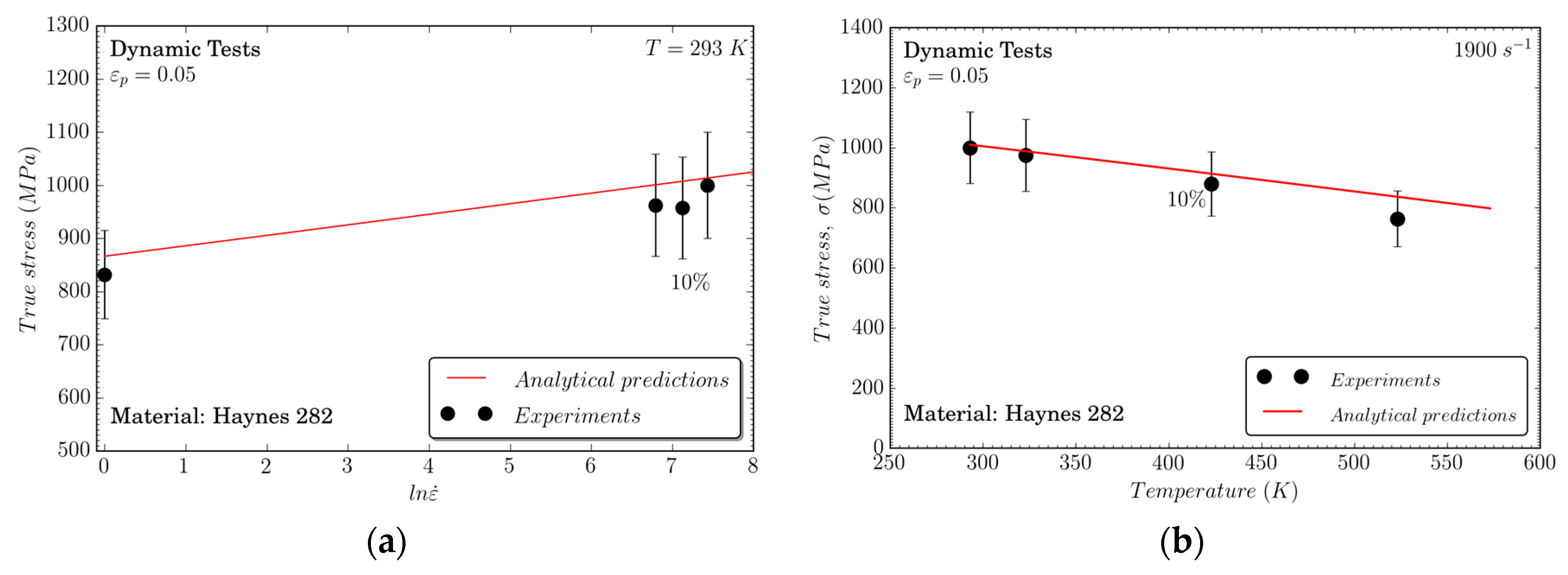
Moreover, it is remarkable that the Johnson–Cook model exhibits the capability for properly describing the rate sensitivity of the material, as shown in Figure 10a. The material temperature sensitivity is also well defined by the model predictions, as shown in Figure 10b. These facts are of primary relevance for aeronautical applications where Haynes 282 is widely used.

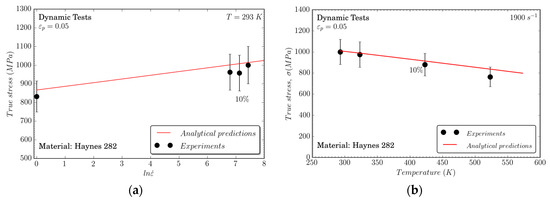
Figure 10. Comparison between the analytical predictions of the constitutive model and experiments at 1900 s⁻¹ to analyze the influence of (a) strain rates and (b) temperatures.

The Johnson–Cook model is, therefore, revealed as suitable for describing the thermo-viscoplastic response of the material within wide ranges of strain, strain rates, and temperatures.

4. Modeling Orthogonal Cutting of Haynes 282

In order to validate the thermo-mechanical characterization of Haynes 282, orthogonal cutting tests were conducted and a numerical model based on finite elements was developed.

4.1. Experimental Setup

A Pinacho Smart Lathe 6/165, instrumented with a model Kistler 9257B dynamometer to measure the cutting forces, was used to perform the tests. In Figure 11 the setup of the experiments can be observed, where the workpiece is attached to the lathe through a mandrel and the tool is oriented assuring that the cutting edge is parallel to the spindle axis.

Figure 11. Test setup.

A hollow disc with an external diameter of 89 mm and a thickness of 2 mm was used as the specimen. Triangular uncoated carbide tool inserts (TCMW 16 T3 08 H13A) with a rake angle of 0°, a clearance angle of 7°, and a honing radius of 25 μm were used in the tests. All tests were performed under dry conditions. Three trials per test condition were performed to ensure repeatability of the experimental data. The cutting parameters selected for the test are listed in Table 5. Although the type of tool selected is not suitable for the machining of materials in this study, the tests took three seconds to warranty the integrity of the cutting edge.

Table 5. Cutting parameters in turning tests.

Depth of Pass (mm)	Feed Rate (mm/rev)	Cutting Speed (m/min)
2	0.15	180; 120; 90; 60
	0.10	180; 120; 90; 60
	0.05	180; 120; 90; 60

4.2. Numerical Model

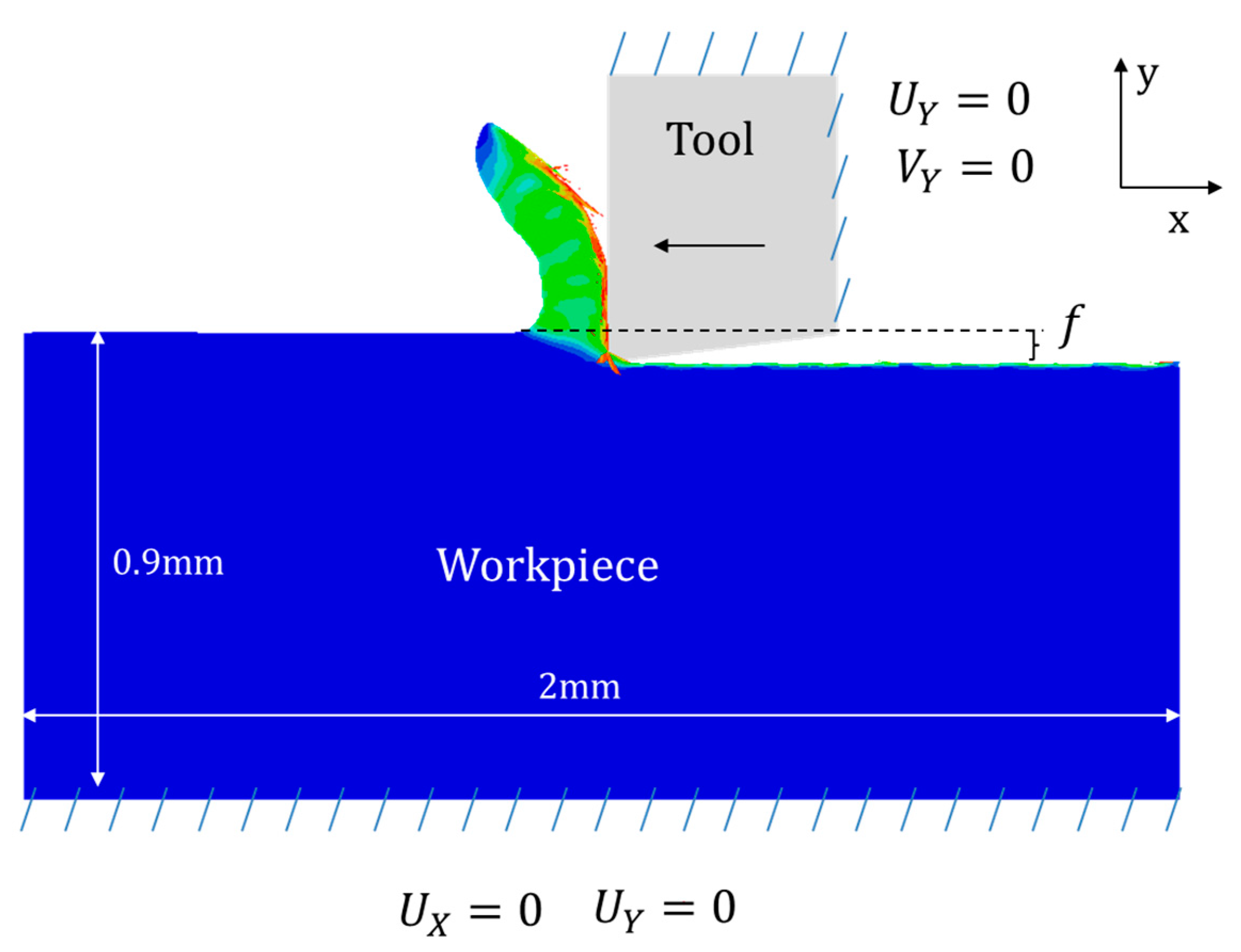
A two-dimensional numerical model was developed to simulate the orthogonal cutting tests on Haynes 282. The workpiece was modelled as a plate with a length equal to 2 mm (ensuring steady state conditions concerning cutting force predictions and chip morphology), a height of 0.9 mm (enough to avoid thermal interference of the boundaries), and a thickness of 2 mm (equal to that tested during turning). The Johnson–Cook model was used to model the thermo-viscoplastic behaviour of Haynes 282. The parameters are listed in Table 4, and Table 6, Table 7 and Table 8 summarize the rest of the properties defined in the model to simulate the material behavior.

Table 6. Temperature dependence of thermal conductivity [19].

Thermal Conductivity of Haynes 282 (W/m/K)	Temperature (K)
10.3	293
12.0	373
14.1	473
18.5	673
22.6	873
26.1	1073

Table 7. Temperature dependence of specific heat capacity [19].

Specific Heat Capacity of Haynes 282 (J/kg K)	Temperature (K)
436	293
463	373
494	473
544	673
581	873
650	1073

Table 8. Temperature dependence of thermal expansion for Haynes 282 [19].

Thermal Expansion of Haynes 282 (K−1)	Temperature (K)
1.21 × 10−5	293
1.21 × 10−5	373
1.24 × 10−5	473
1.31 × 10−5	673
1.42 × 10−5	973

In addition, the numerical model implemented in this work takes into account the temperature evolution assuming adiabatic heating. This was computed along the deformation process though the expression:

$$\Delta T\left({\bar{\epsilon }}^p,{\dot{\bar{\epsilon }}}^p,T\right)=\frac{\beta }{\rho C_p}{\int }_{{\epsilon }^e }^{{\bar{\epsilon }}^p}\bar{\sigma }\left({\bar{\epsilon }}^p,{\dot{\bar{\epsilon }}}^p,T\right) d{\bar{\epsilon }}^p$$

(7)

where the Quinney–Taylor coefficient, which defines the percentage of plastic work converted into heat, was taken to be equal to $\beta$ = 0.9 [30,31].

The tool was modelled as a rigid body with rake and clearance angles of 0° and 7°, respectively, with a honing radius of 25 μm. CPE4RT elements with a size about 5 µm were used in order to mesh the tool.

A constant friction coefficient of 0.4 was used at the tool–workpiece interface. A detailed scheme of the numerical model and the boundary conditions are shown in Figure 12.

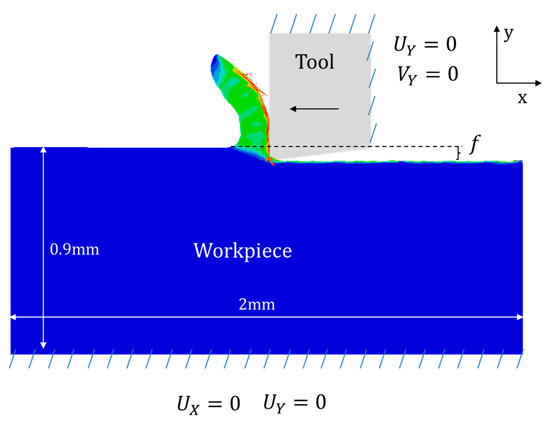
Figure 12. Model boundary conditions.

4.3. Experimental and Numerical Results

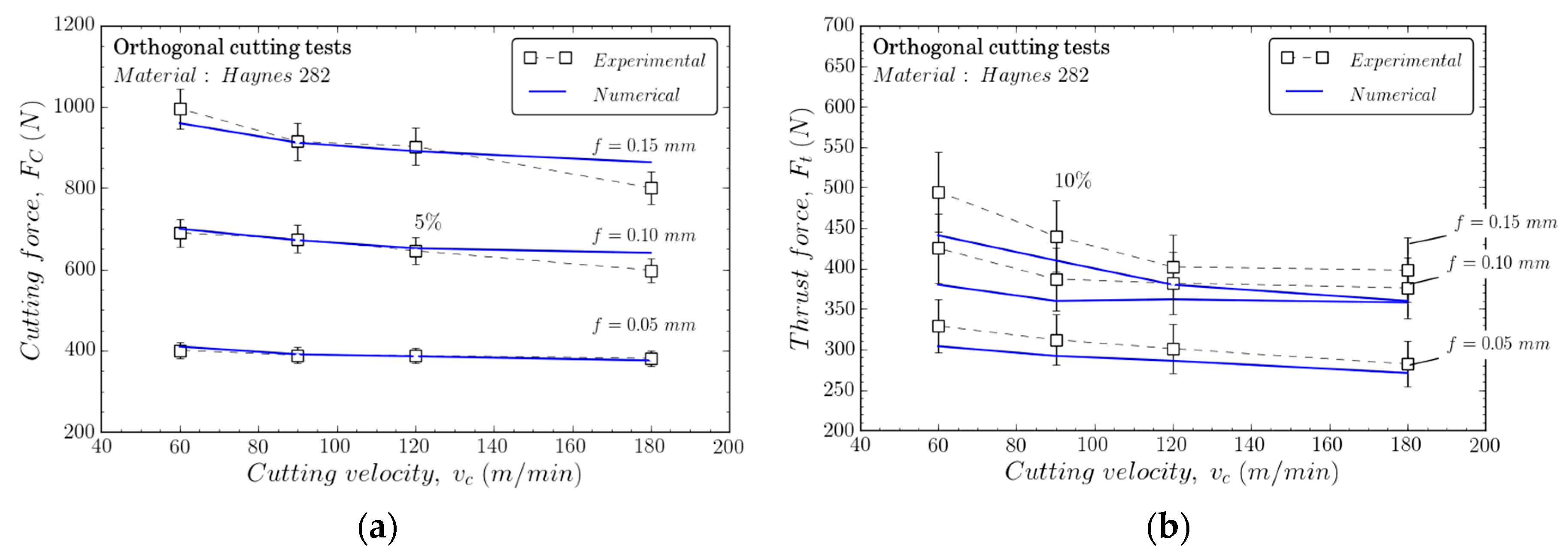
In Figure 13, the tendency of the experimental thrust and cutting forces measured during cutting and the predicted values obtained with the numerical model tests are plotted versus the cutting speed.

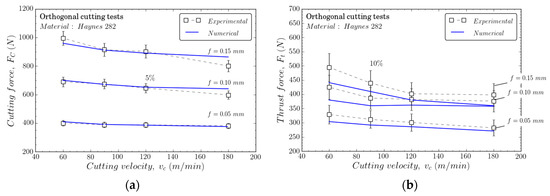
Figure 13. Numerical (a) and experimental (b) cutting forces for Haynes 282.

Reasonable agreement between experimental and numerical results was found, and a maximum error of the cutting and thrust forces of 5% and 10%, respectively, was obtained. Johnson–Cook parameters seem to be suitable for machining simulations. The thermal softening term characterized at an intermediate temperature seemed to properly represent the mechanical behavior during cutting, although the primary and secondary cutting zone typically reaches a high temperature.

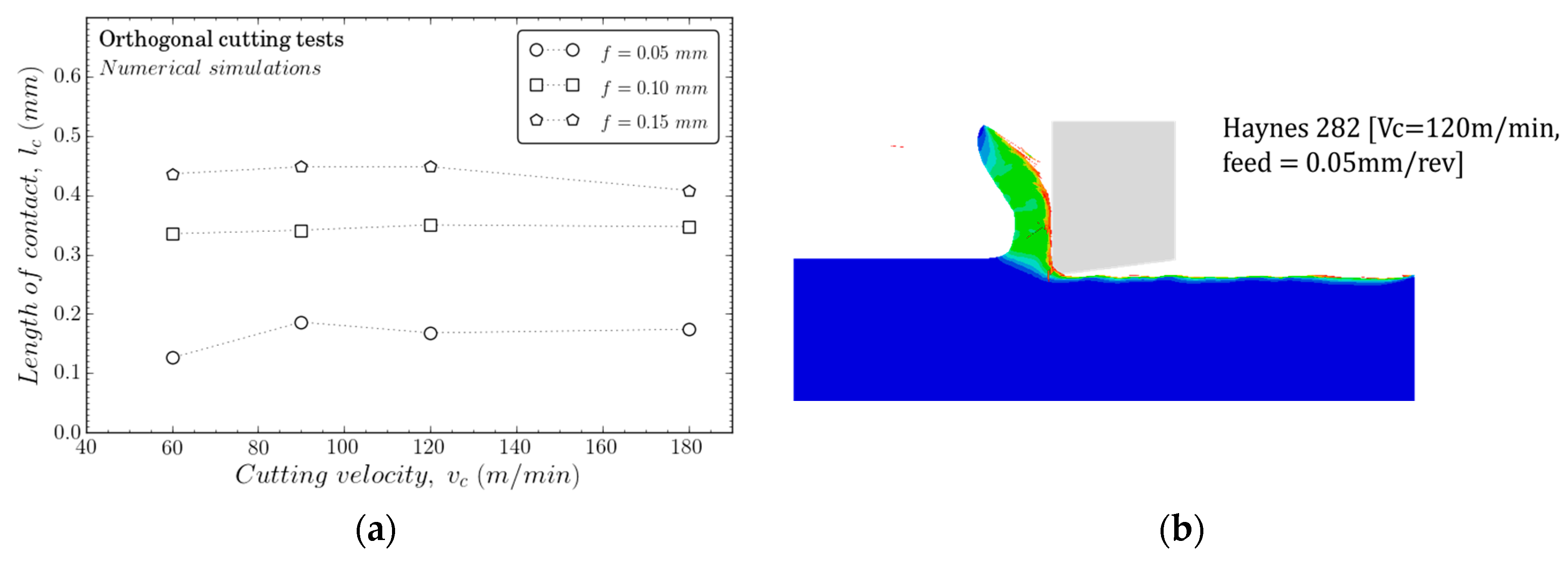
The morphology of the chip contact length at the tool–workpiece interface is an interesting parameter to analyse because of its relationship with wear evolution. The contact lengths for the different feeds considered in the study are presented in Figure 14a. As is well known, the contact length increased with the feed, although no linear effect was observed due to the dominant influence of the cutting-edge radius at lower values of the feed. There was a slight trend to diminish the contact length with the cutting velocity; however, this effect is more commonly accused in high-speed machining, while the range of velocities considered was relatively low. This trend, observed with the numerical results, agrees with other studies [32]. The morphology of the chip tended to be continuous in the range of velocities analyzed (see Figure 14b).

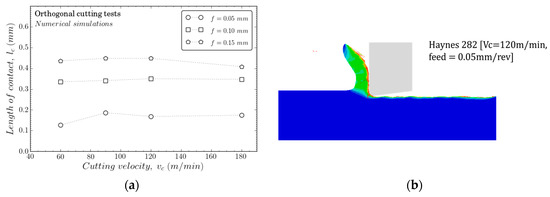
Figure 14. (a) Contact length as a function of the cutting speed and (b) chip morphology of Haynes 282 as a function of the cutting speed.

5. Conclusions

In this paper, dynamic characterization of Haynes 282 alloy under a wide range of strain rates and temperatures has been conducted. Haynes 282 is compared to a reference Ni alloy, Inconel 718. The analysis allowed the identification of parameters in the Johnson–Cook model in order to simulate orthogonal cutting of Haynes 282, a case of dynamic loading. The main conclusions are summarized below:

• Haynes 282 presented lower mechanical properties than Inconel 718 for the range of strain rates considered–around 720–780 MPa. The Haynes 282 alloy has deformation hardening slightly higher than Inconel 718 and higher sensitivity to strain rates.
• For the temperature range considered (293–523 K), Haynes 282 experienced elevated thermal softening with a decrease in plastic flow rate of about 30%, while this parameter decreased by about 20% for Inconel 718.
• The parameters of the Johnson–Cook model were obtained from the characterization, and the proposed expression successfully fitted the experimental data for Haynes 282.
• The constitutive model was applied to simulation of the orthogonal cutting of Haynes 282. The simulations were validated with experiments in terms of measured cutting forces. Good agreement was observed, showing the ability of the constitutive model proposed to simulate this dynamic process.