Electromagnetic Forming Rules of a Stiffened Panel with Grid Ribs
Abstract
:1. Introduction
2. Foundations of Modeling
2.1. Basic Equations
2.1.1. Electromagnetic Forces
- (1)
- the voltage in the symmetric plane is considered to be zero;
- (2)
- the magnetic vector potential is zero at Y = 0;
- (3)
- an infinite flag is set in the infinite surface for the far field air region.
2.1.2. Deformation Equation of Workpiece
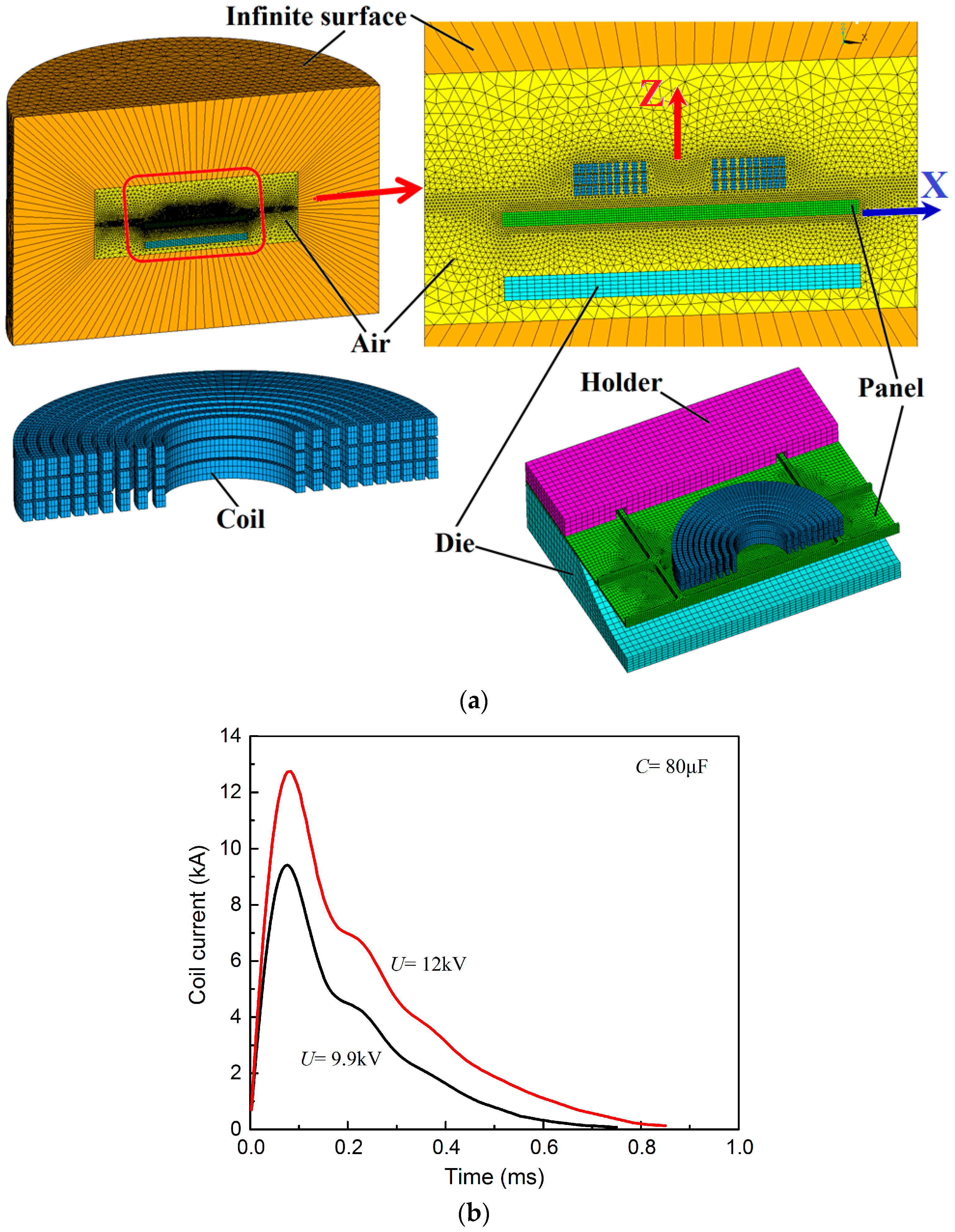
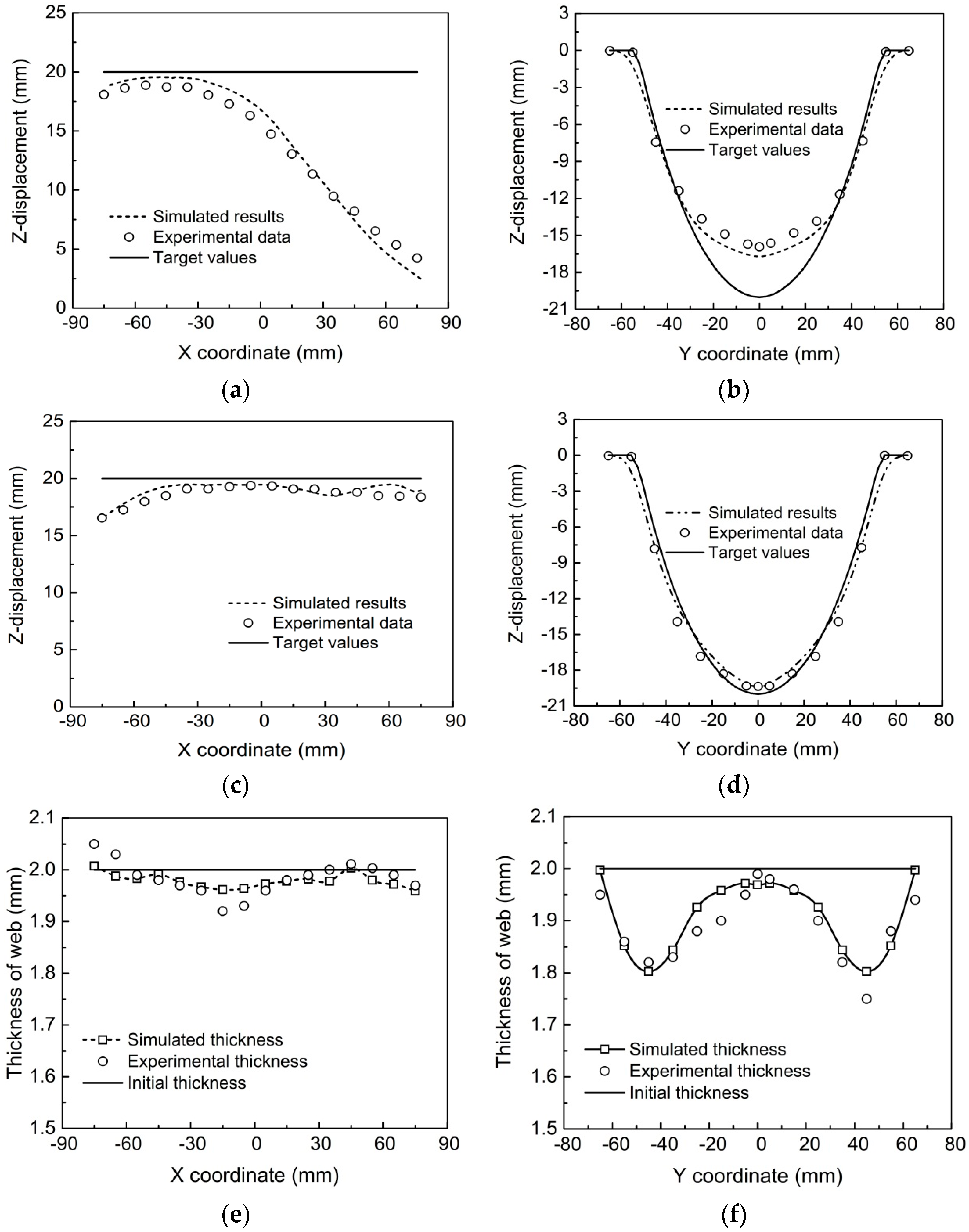
2.2. Model Preparations
3. Forming Rules of Stiffened Panels during EMIF Process
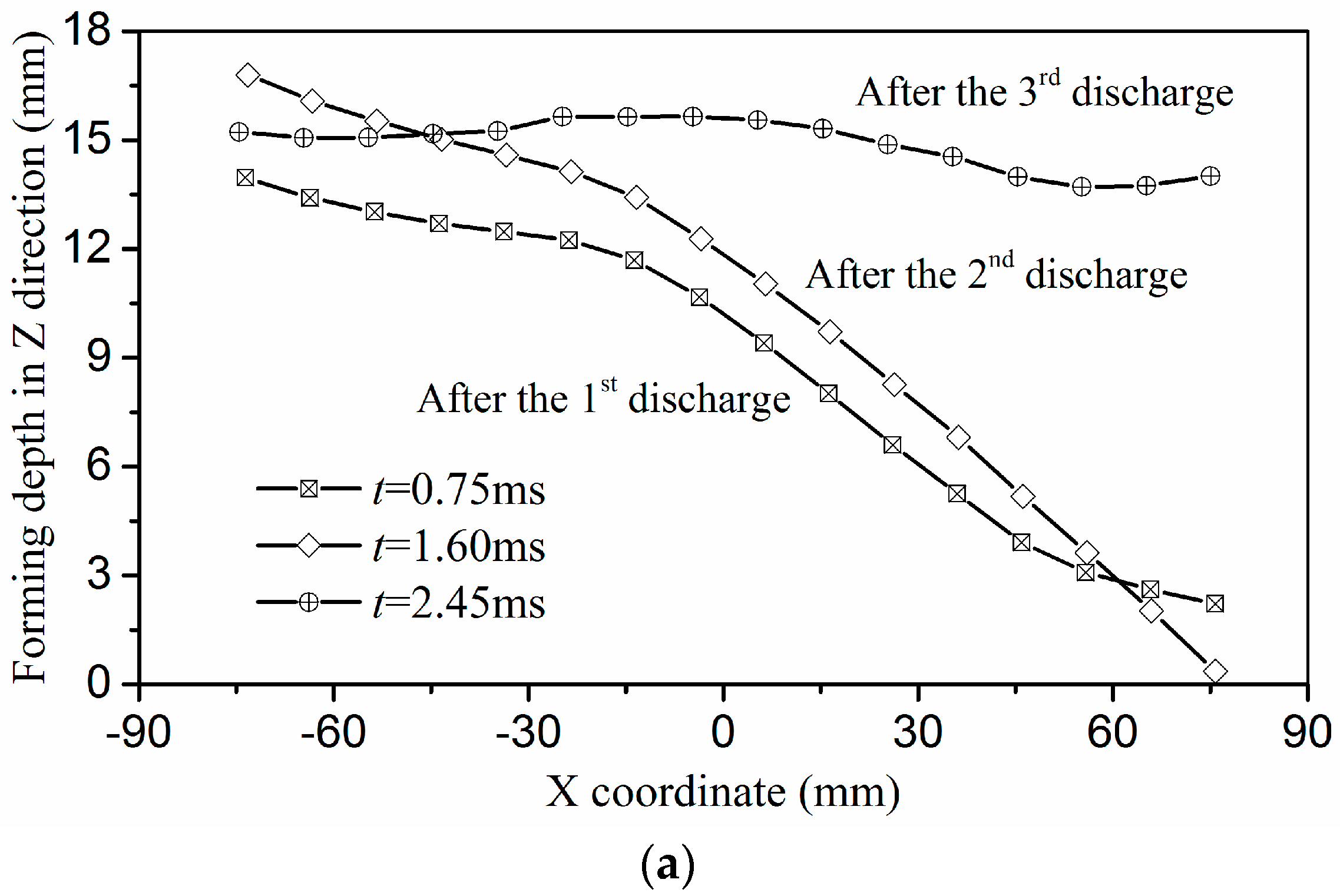
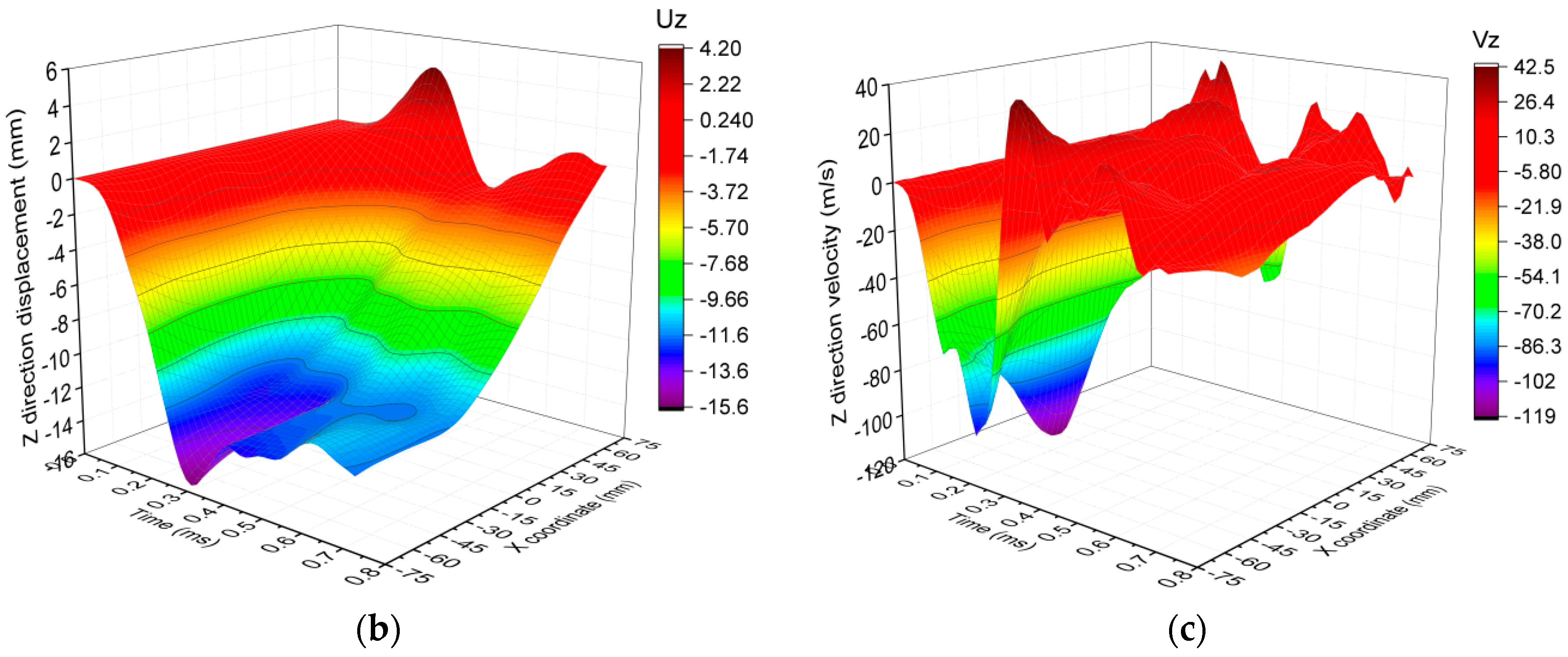
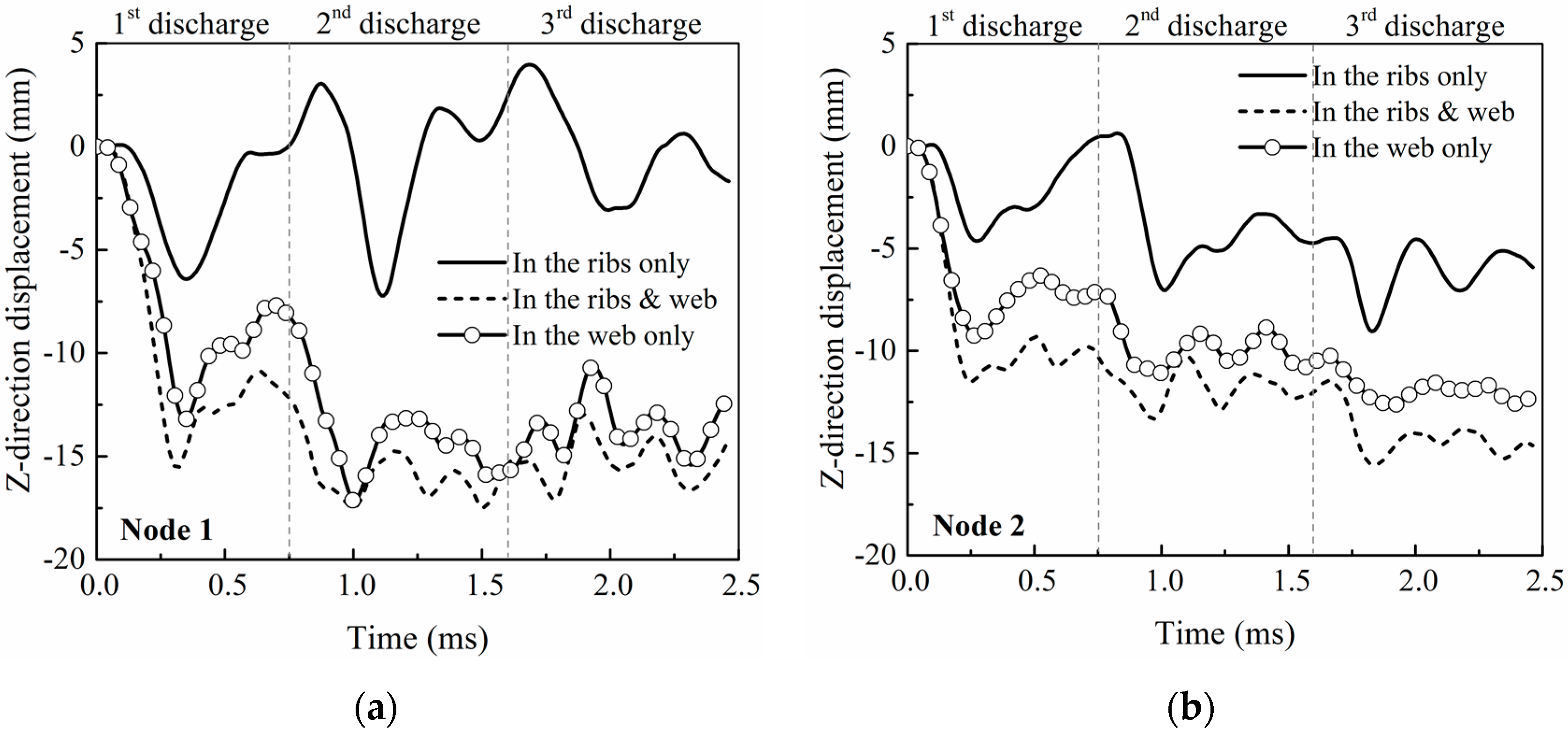
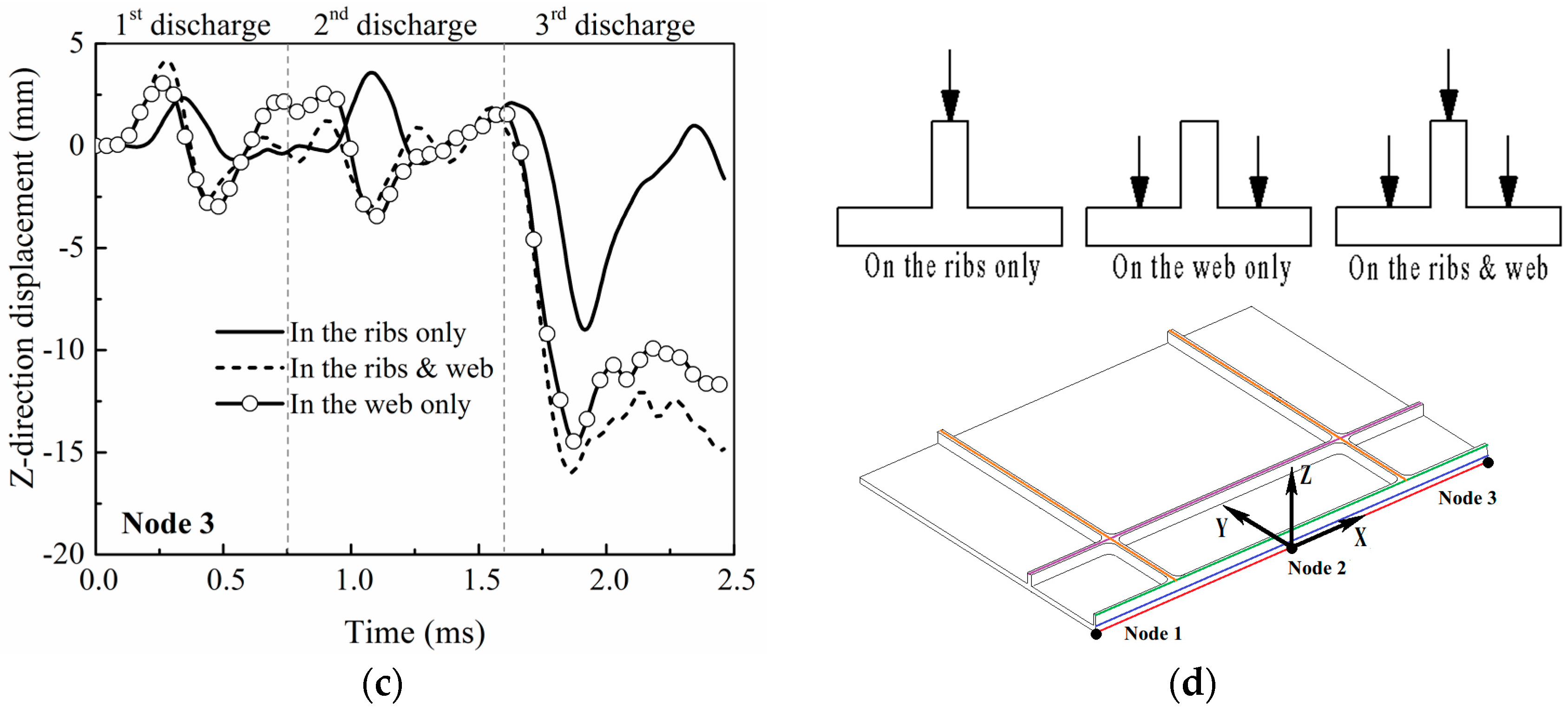
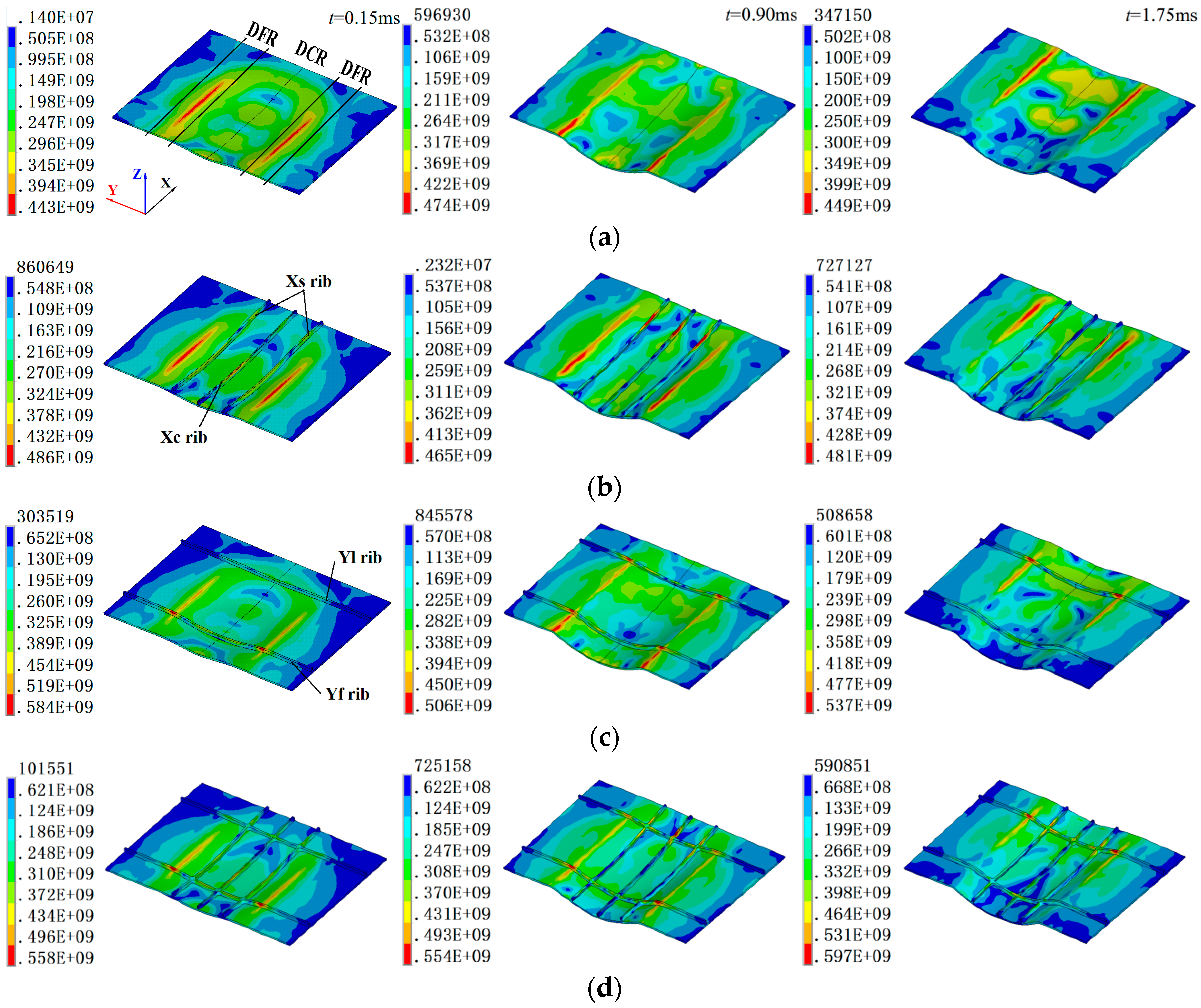
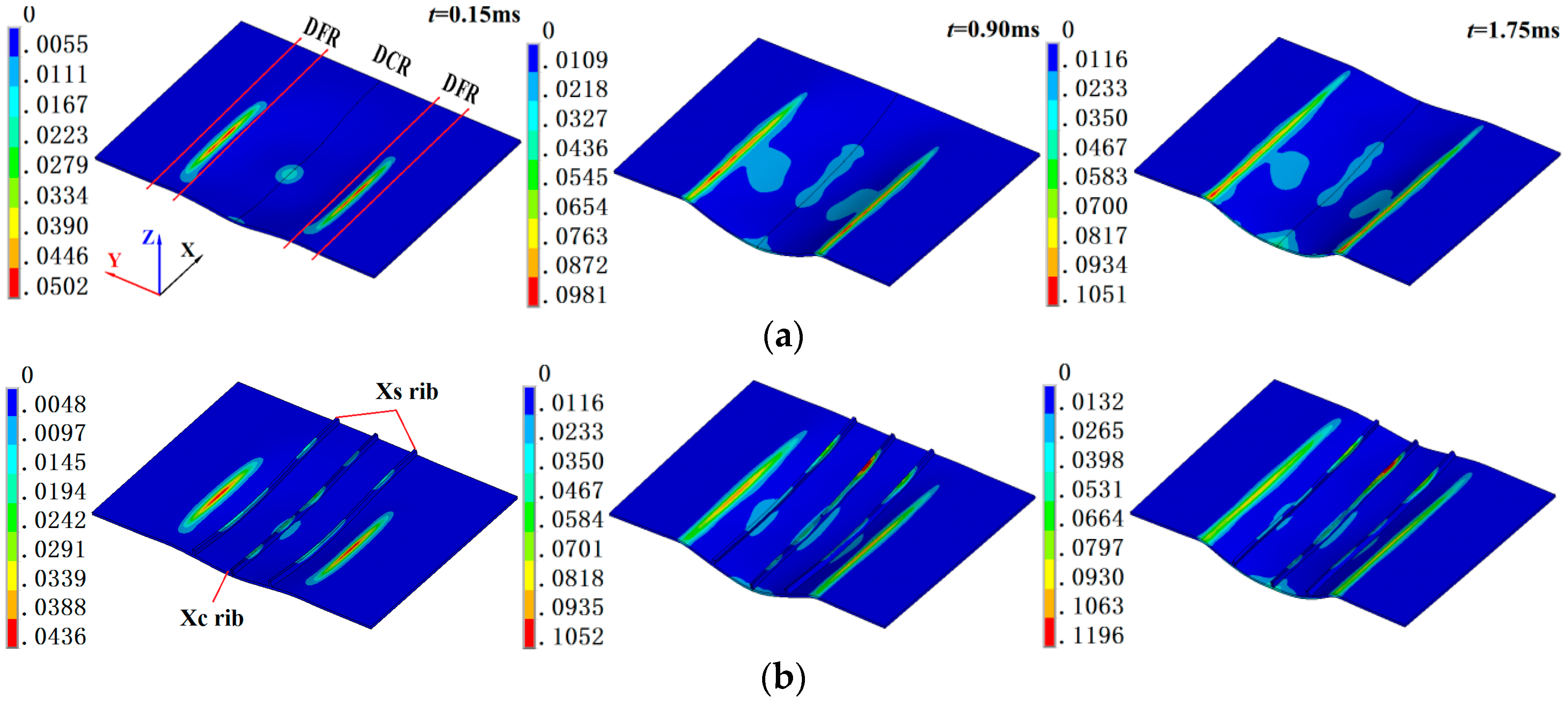
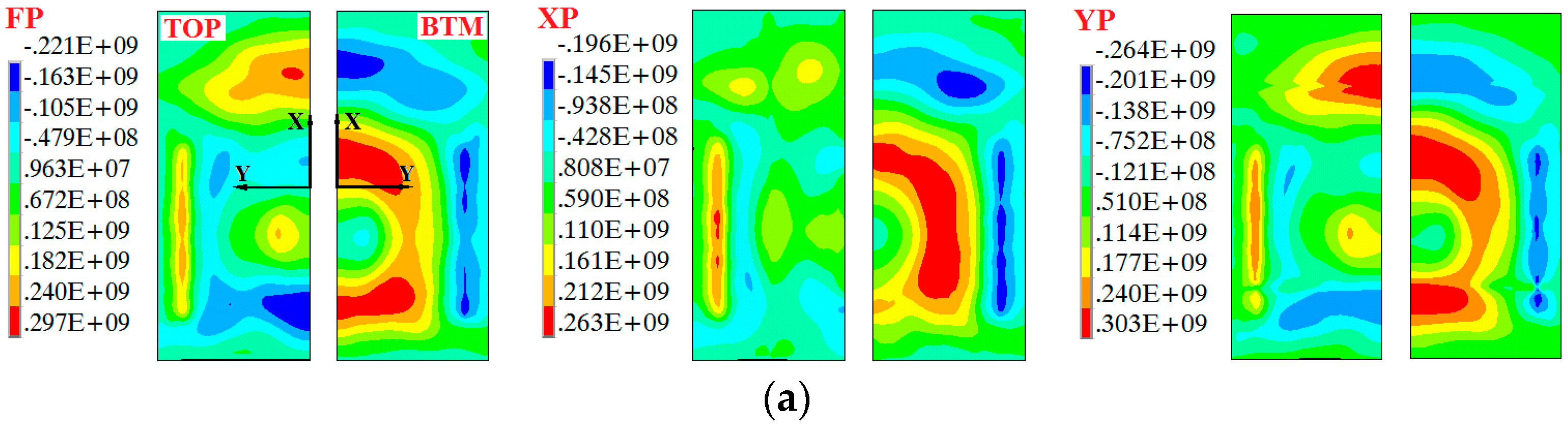
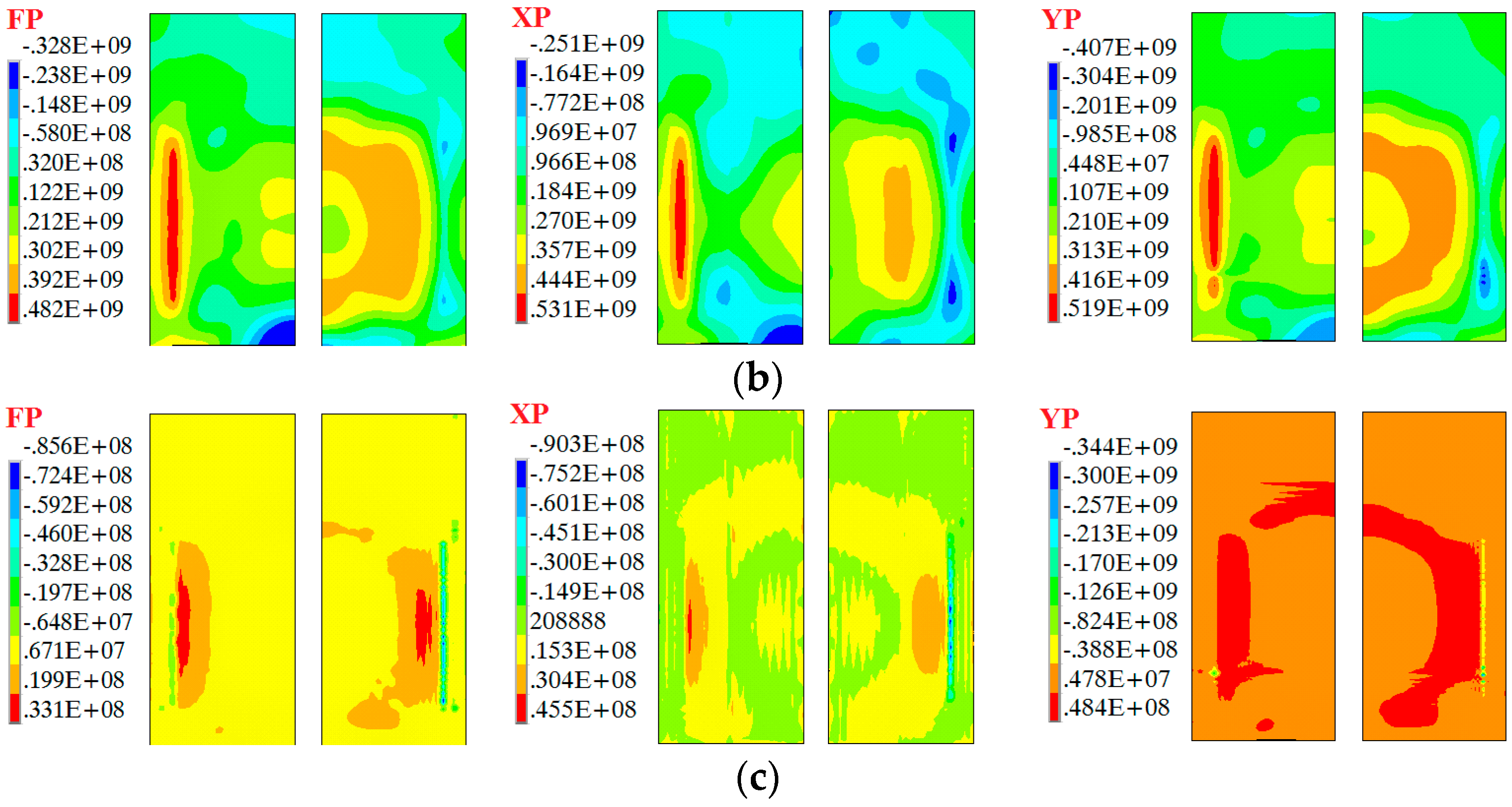
3.1. Characteristic of Force
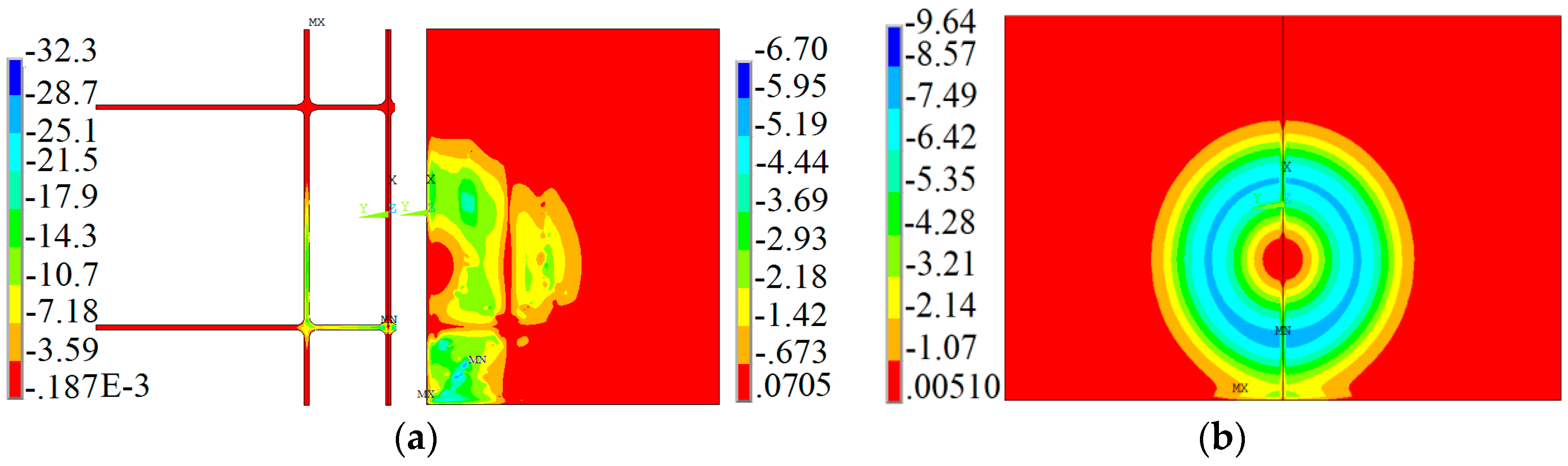
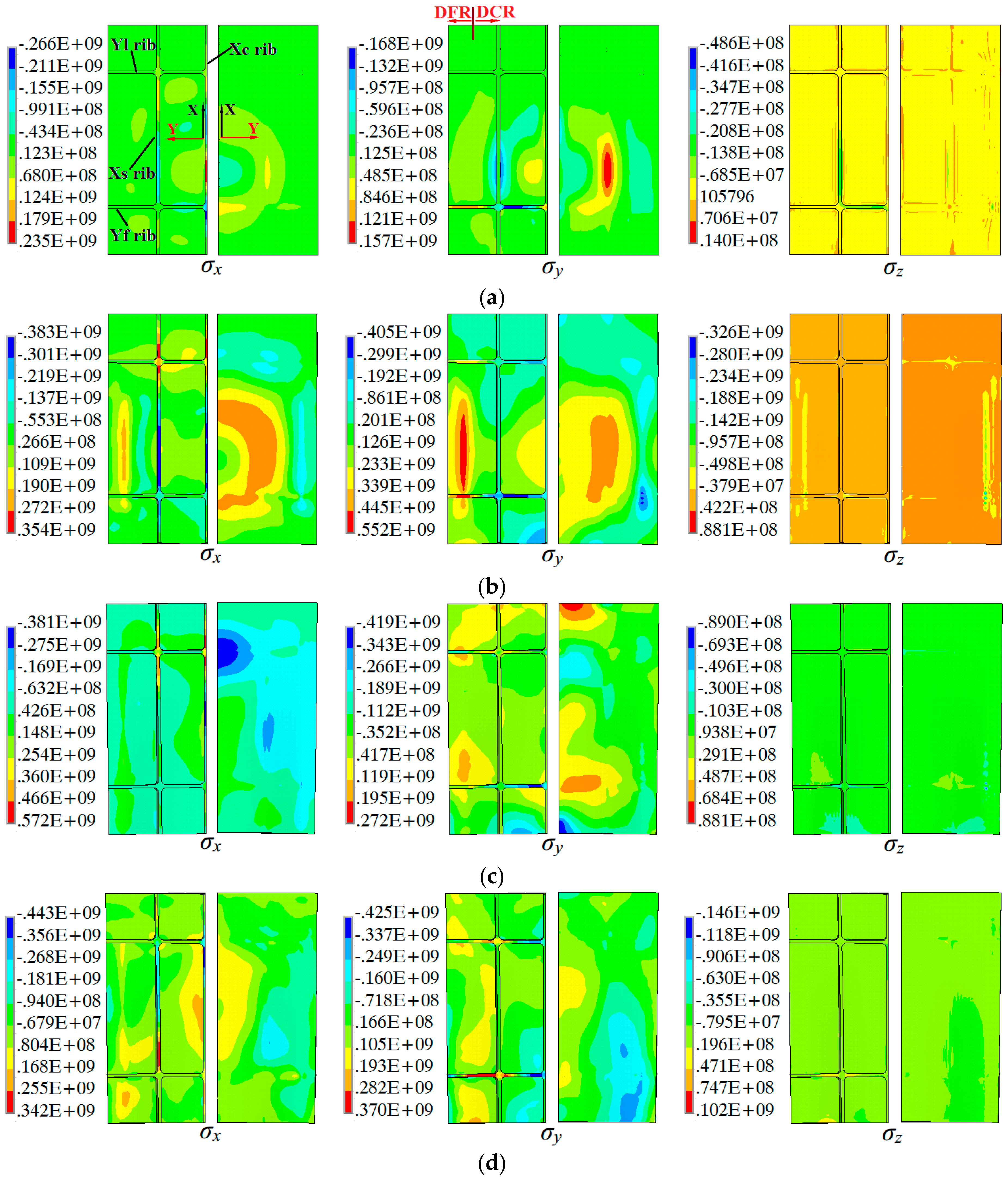
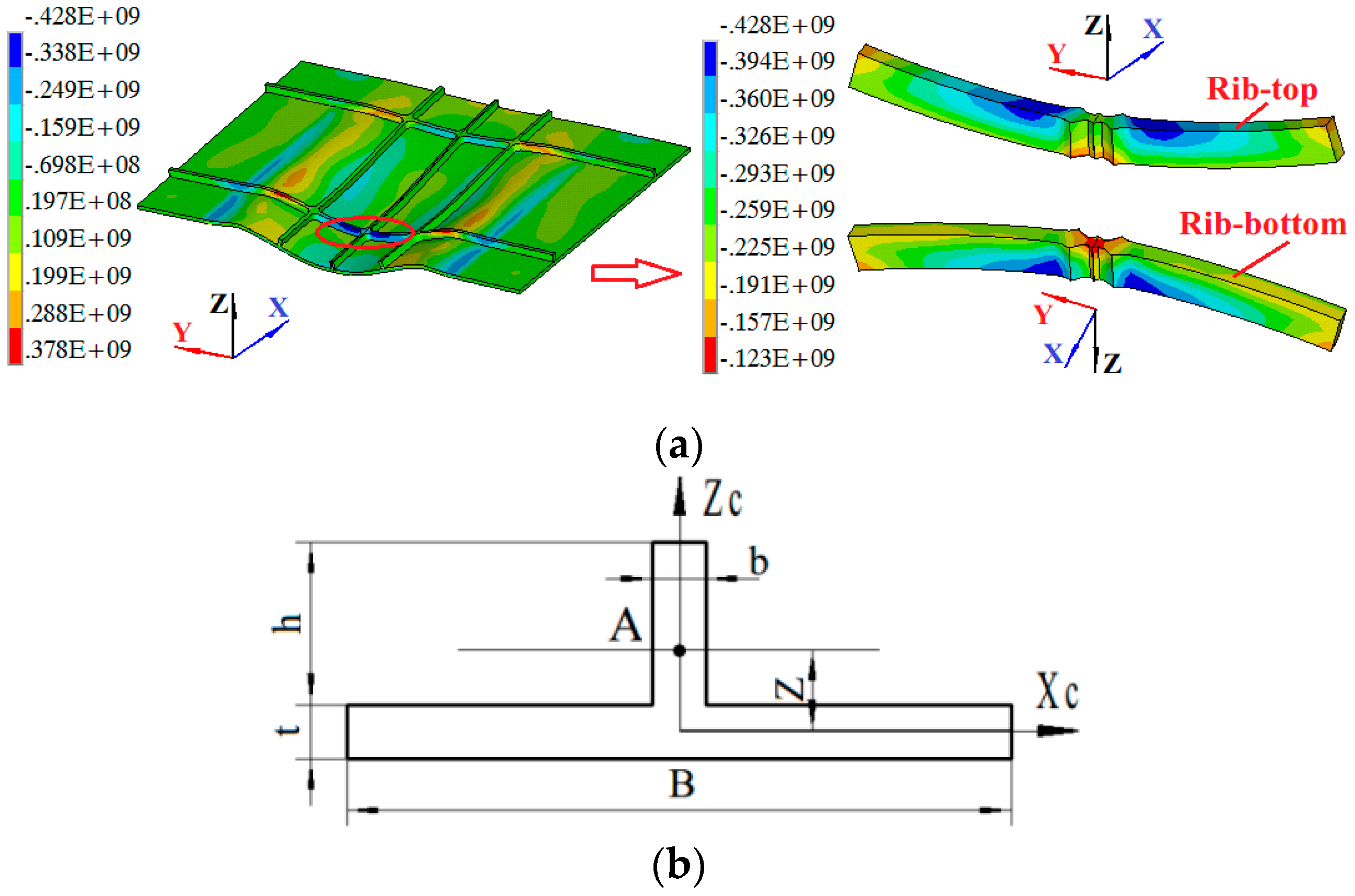
3.2. Evolution of Stress
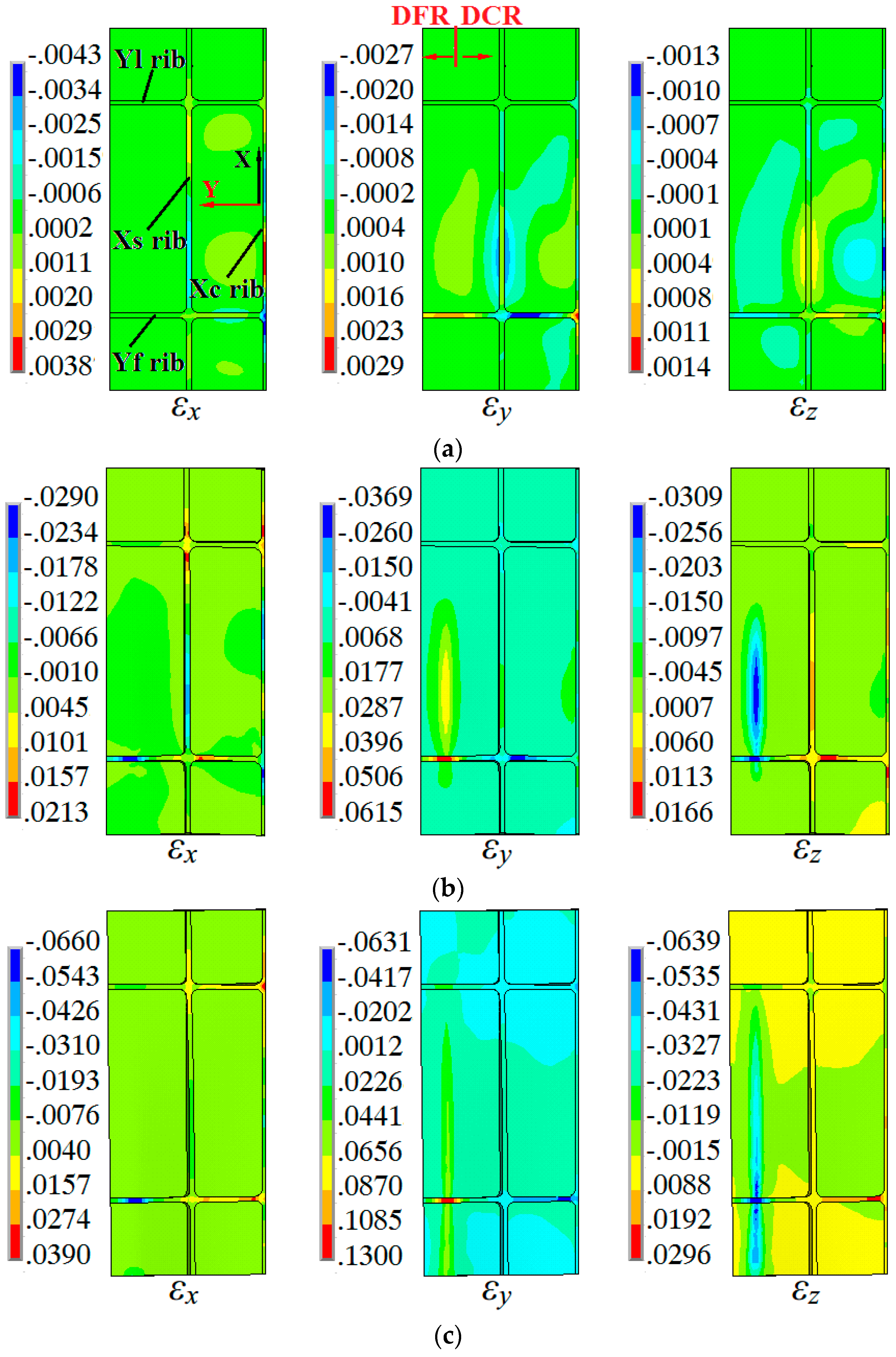
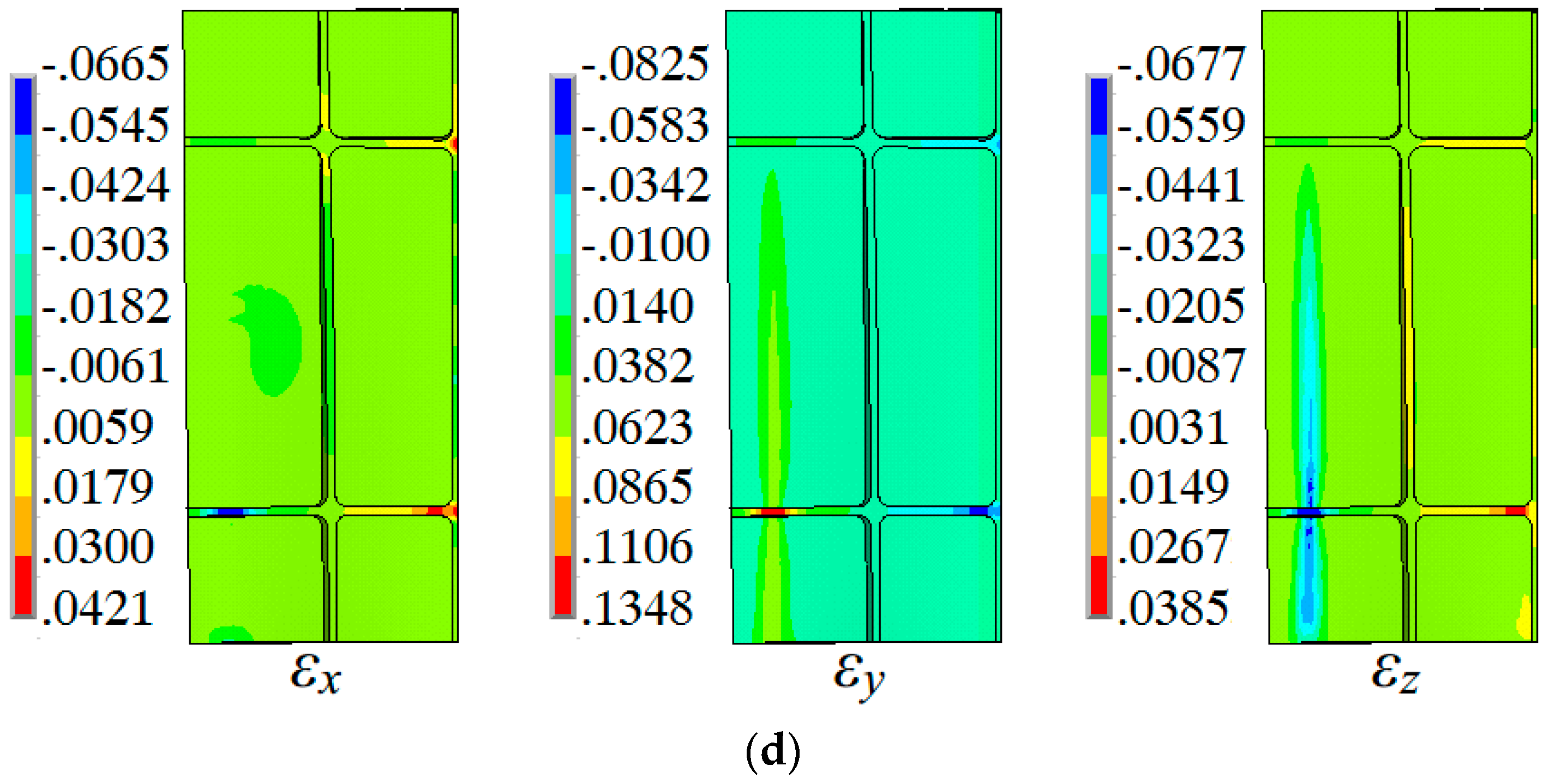
3.3. Evolution of Strain
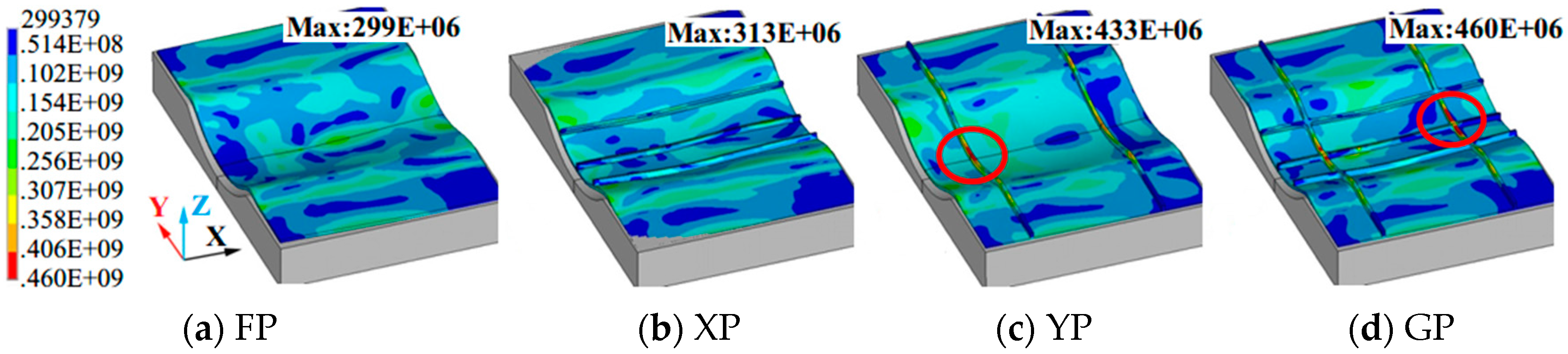
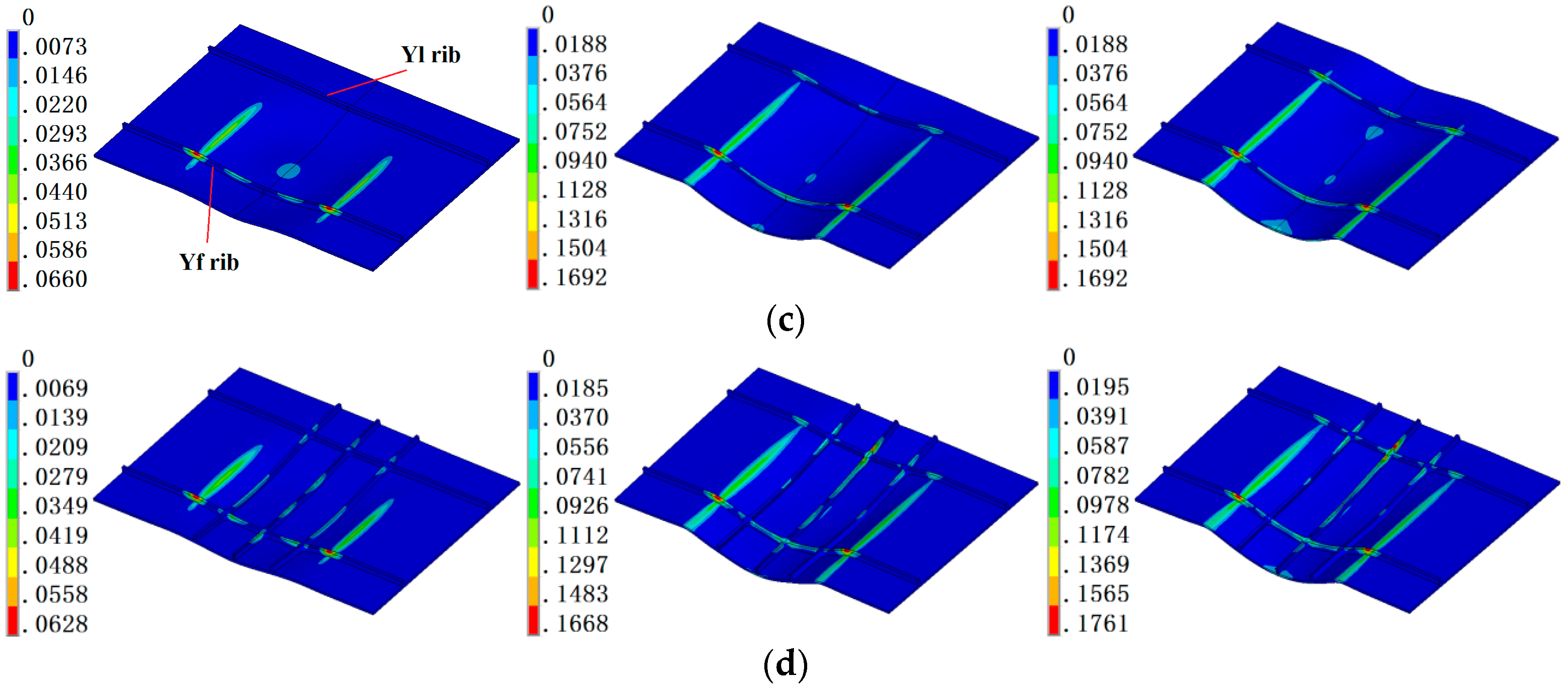
3.4. Influence of Rib Configuration on the Web
4. Conclusions
- (1)
- The forming depth of the stiffened panels is largely due to the forces on the web, not the ribs, due to the fact that the area and the structural stiffness of the web is larger than that of the ribs, although the electromagnetic forces are applied on both the ribs and the web and mainly concentrate on the ribs.
- (2)
- The ribs are subjected to the uniaxial stress parallel to the rib directions, and the web is subjected to plane stress in the die cavity region and three-directional stress in the die fillet region. There are both compressive stresses along the rib direction at the top and bottom of the Y-direction ribs because the stress neutral layer locates in the web. Reasonable parameters should be designed carefully if there are X direction ribs due to large stress which also concentrates in these ribs.
- (3)
- The Y direction ribs are subjected to three-directional strain with tensile deformation in the die fillet region and compressive deformation in the die cavity region. Large strain in the web concentrates in the die fillet region with plane strain. Large tensile plastic deformation in the die fillet region inclines to thin easily, and compressive strain in the Y-direction ribs of the die cavity region easily inclines to wrinkling.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pettit, R.G.; Wang, J.J.; Toh, C. Validated Feasibility Study of Integrally Stiffened Metallic Fuselage Panels for Reducing Manufacturing Costs; NASA/CR-2000-209342; Boeing Commercial Airplane Group: Seattle, WA, USA, 2000. [Google Scholar]
- Munroe, J.; Wilkins, K.; Gruber, M. Integral Airframe Structures (IAS)—Validated Feasibility Study of Integrally Stiffened Metallic Fuselage Panels for Reducing Manufacturing Costs; NASA/CR-2000-209337; Boeing Commercial Airplane Group: Seattle, WA, USA, 2000. [Google Scholar]
- Gariépy, A.; Miao, H.; Lévesque, M. Peen Forming. Compr. Mater. Process. 2014, 3, 295–329. [Google Scholar]
- Miao, H.Y.; Demers, D.; Larose, S.; Perron, C.; Levesque, M. Experimental study of shot peening and stress peen forming. J. Mater. Proc. Technol. 2010, 210, 2089–2102. [Google Scholar] [CrossRef]
- Zhan, L.H.; Lin, J.G.; Dean, T.A. A review of the development of creep age forming: Experimentation, modeling and applications. Int. J. Mach. Tool. Manuf. 2011, 51, 1–17. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, H.B.; Wan, M. Prediction of fracture in press bend forming of aluminum alloy. Comput. Mater. Sci. 2011, 50, 2232–2244. [Google Scholar]
- Psyk, V.; Risch, D.; Kinsey, B.L.; Tekkaya, A.E.; Kleiner, M. Electromagnetic forming—A review. J. Mater. Proc. Technol. 2011, 211, 787–829. [Google Scholar] [CrossRef]
- Daehn, G.S. High velocity metal forming. In ASM Handbook Volume 14B: Metalworking: Sheet Forming; ASM International: Columbus, OH, USA, 2006; pp. 405–418. [Google Scholar]
- Woodward, S.; Weddeling, C.; Daehn, G.; Psyk, V.; Carson, B.; Tekkaya, A.E. Agile production of sheet metal aviation components using disposable electromagnetic actuators. In Proceedings of the 4th International Conference on High Speed Forming—ICHSF 2010, Columbus, OH, USA, 9–10 March 2010. [Google Scholar]
- Eguia, I.; Mangas, A.; Iturbe, R.; Gutiérrez, M.A. Electromagnetic forming of longitudinal strengthening ribs in roll formed automotive profiles. In Proceedings of the 4th International Conference on High Speed Forming—ICHSF 2010, Columbus, OH, USA, 9–10 March 2010. [Google Scholar]
- Psyk, V.; Kurka, P.; Kimme, S.; Werner, M.; Landgrebe, D.; Ebert, A.; Schwarzendahl, M. Structuring by electromagnetic forming and by forming with an elastomer punch as a tool for component optimisation regarding mechanical stiffness and acoustic performance. Manuf. Rev. 2015, 2, 23. [Google Scholar] [CrossRef]
- El-Azab, A.; Garnich, M.; Kapoor, A. Modeling of the electromagnetic forming of sheet metals: State-of-the-art and future needs. J. Mater. Proc. Technol. 2003, 142, 744–754. [Google Scholar] [CrossRef]
- Oliveira, D.A.; Worswick, M.J.; Finn, M.; Newman, D. Electromagnetic forming of aluminum alloy sheet: Free-form and cavity fill experiments and model. J. Mater. Proc. Technol. 2005, 170, 350–362. [Google Scholar] [CrossRef]
- Imbert, J.; Worswick, M. Reduction of a pre-formed radius in aluminum sheet using electromagnetic and conventional forming. J. Mater. Proc. Technol. 2012, 212, 1963–1972. [Google Scholar] [CrossRef]
- Lai, Z.P.; Cao, Q.L.; Han, X.T.; Liu, N.; Li, X.X.; Huang, Y.J.; Chen, M.; Cai, H.; Wang, G.D.; Liu, L.Y.; et al. A comprehensive electromagnetic forming approach for large sheet metal forming. In Proceedings of the International Conference on the Technology of Plasticity (ICTP 2017), Cambridge, UK, 17–22 September 2017. [Google Scholar]
- Okoye, C.N.; Jiang, J.H.; Hu, Z.D. Application of electromagnetic-assisted stamping (EMAS) technology in incremental forming. Int. J. Mach. Tools Manuf. 2006, 46, 1248–1252. [Google Scholar] [CrossRef]
- Shang, J.H.; Daehn, G.S. Electromagnetically assisted sheet metal stamping. J. Mater. Proc. Technol. 2011, 211, 868–874. [Google Scholar] [CrossRef]
- Jeswiet, J.; Geiger, M.; Engel, U.; Kleiner, M.; Schikorra, M.; Duflou, J.; Neugebauer, R.; Bariani, P.; Bruschi, S. Metal forming progress since 2000. CIRP J. Manuf. Sci. Technol. 2008, 1, 2–17. [Google Scholar] [CrossRef]
- Cui, X.H.; Mo, J.H.; Li, J.J.; Zhao, J.; Xiao, S.J. Produce a large aluminum alloy sheet metal using electromagnetic-incremental (EM-IF) forming method: Experiment and Numerical simulation. In Proceedings of the 5th International Conference on High Speed Forming, Dortmund, Germany, 24–26 April 2012; pp. 59–70. [Google Scholar]
- Cui, X.H.; Mo, J.H.; Li, J.J.; Zhao, J.; Zhu, Y.; Huang, L.; Li, Z.W.; Zhong, K. Electromagnetic incremental forming (EMIF): A novel aluminum alloy sheet and tube forming technology. J. Mater. Proc. Technol. 2014, 214, 409–427. [Google Scholar] [CrossRef]
- Cui, X.H.; Mo, J.H.; Li, J.J.; Xiao, X.T.; Zhou, B.; Fang, J.X. Large-scale sheet deformation process by electromagnetic incremental forming combined with stretch forming. J. Mater. Proc. Technol. 2016, 237, 139–154. [Google Scholar] [CrossRef]
- Oliveira, D.A.; Worswick, M.J. Electromagnetic forming of aluminum alloy sheet. J. Phys. IV France 2003, 110, 293–298. [Google Scholar] [CrossRef]
- Yu, H.P.; Li, C.F.; Deng, J.H. Sequential coupling simulation for electromagnetic mechanical tube compression by finite element analysis. J. Mater. Proc. Technol. 2009, 209, 707–713. [Google Scholar]
- Fenton, G.K.; Daehn, G.S. Modeling of electromagnetically formed sheet metal. J. Mater. Proc. Technol. 1998, 75, 6–16. [Google Scholar] [CrossRef]
- Unger, J.; Stiemer, M.; Svendsen, B.; Blum, H. Multifield modeling of electromagnetic metal forming processes. J. Mater. Proc. Technol. 2006, 177, 270–273. [Google Scholar] [CrossRef]
- Cui, X.H.; Li, J.J.; Mo, J.H.; Fang, J.X.; Zhu, Y.T.; Zhong, K. Investigation of large sheet deformation process in electromagnetic incremental forming. Mater. Des. 2015, 76, 86–96. [Google Scholar] [CrossRef]
- Tan, J.Q.; Zhan, M.; Liu, S. Guideline for forming stiffened panels by using the electromagnetic forces. Metals 2016, 6, 267. [Google Scholar] [CrossRef]
- Cao, Q.L.; Han, X.T.; Lai, Z.P.; Xiong, Q.; Zhang, X.; Chen, Q.; Xiao, H.X.; Li, L. Analysis and reduction of coil temperature rise in electromagnetic forming. J. Mater. Proc. Technol. 2015, 225, 185–194. [Google Scholar] [CrossRef]
- Rodríguez, A.A.; Valli, A. Eddy Current Approximation of Maxwell Equations: Theory, Algorithms and Applications; Springer: Milan, UK, 2010. [Google Scholar]
- Biro, O.; Preis, K. On the Use of the Magnetic Vector Potential in the Finite Element Analysis of Three-Dimensional Eddy Currents. IEEE Trans. Magn. 1989, 25, 3145–3159. [Google Scholar] [CrossRef]
- Hallquist, J.O. LS-DYNA Theoretical Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 1998. [Google Scholar]
- Pao, Y.H. Electromagnetic force in deformable continua. In Mechanics Today; Nemat-Nasser, S., Ed.; Pergamon Press: Oxford, UK, 1978. [Google Scholar]
- International Organization for Standardization. ISO 209: Aluminium and Aluminum Alloy—Chemical Composition; International Organization for Standardization (ISO): Geneva, Switzerland, 2007. [Google Scholar]
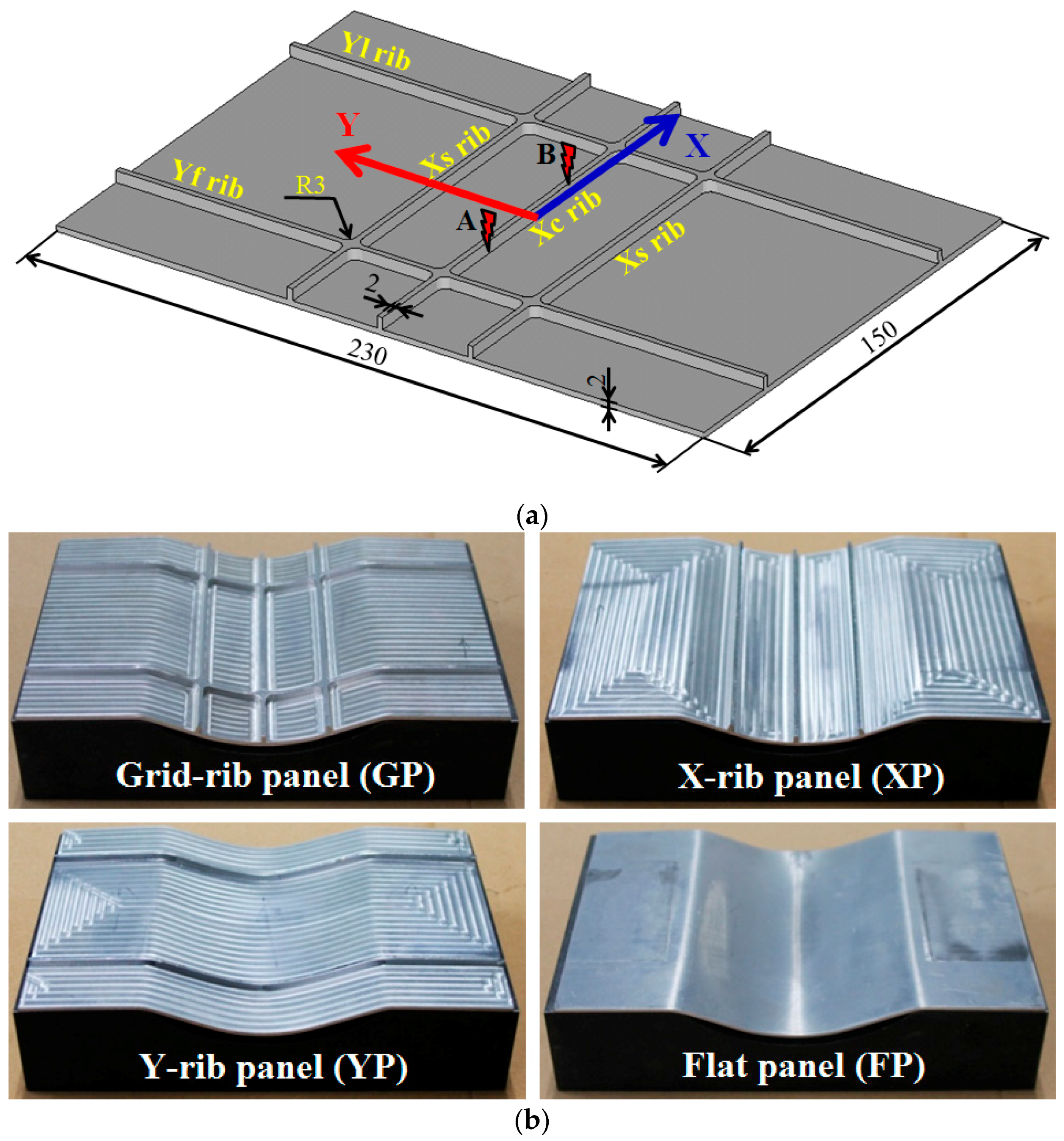
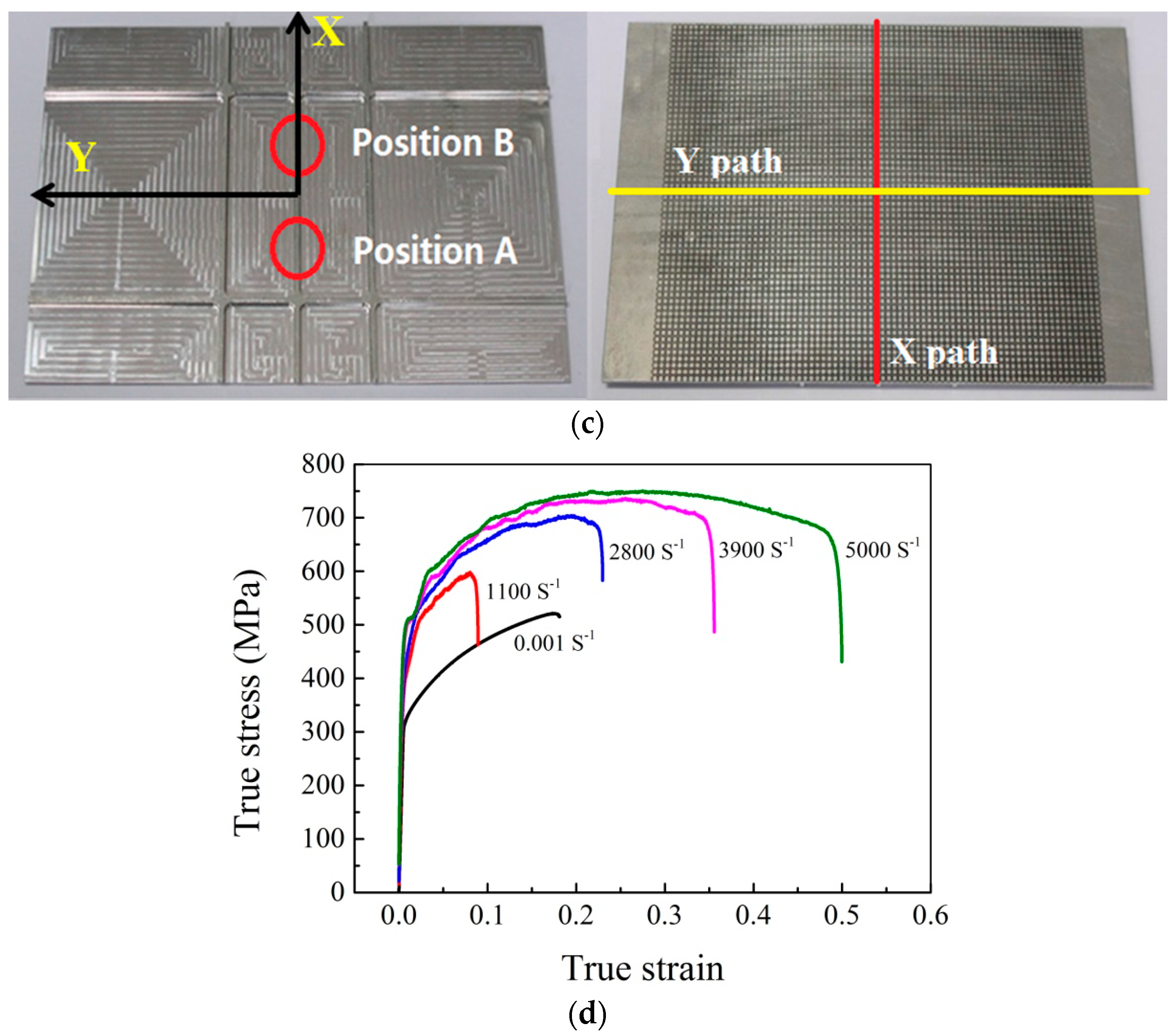
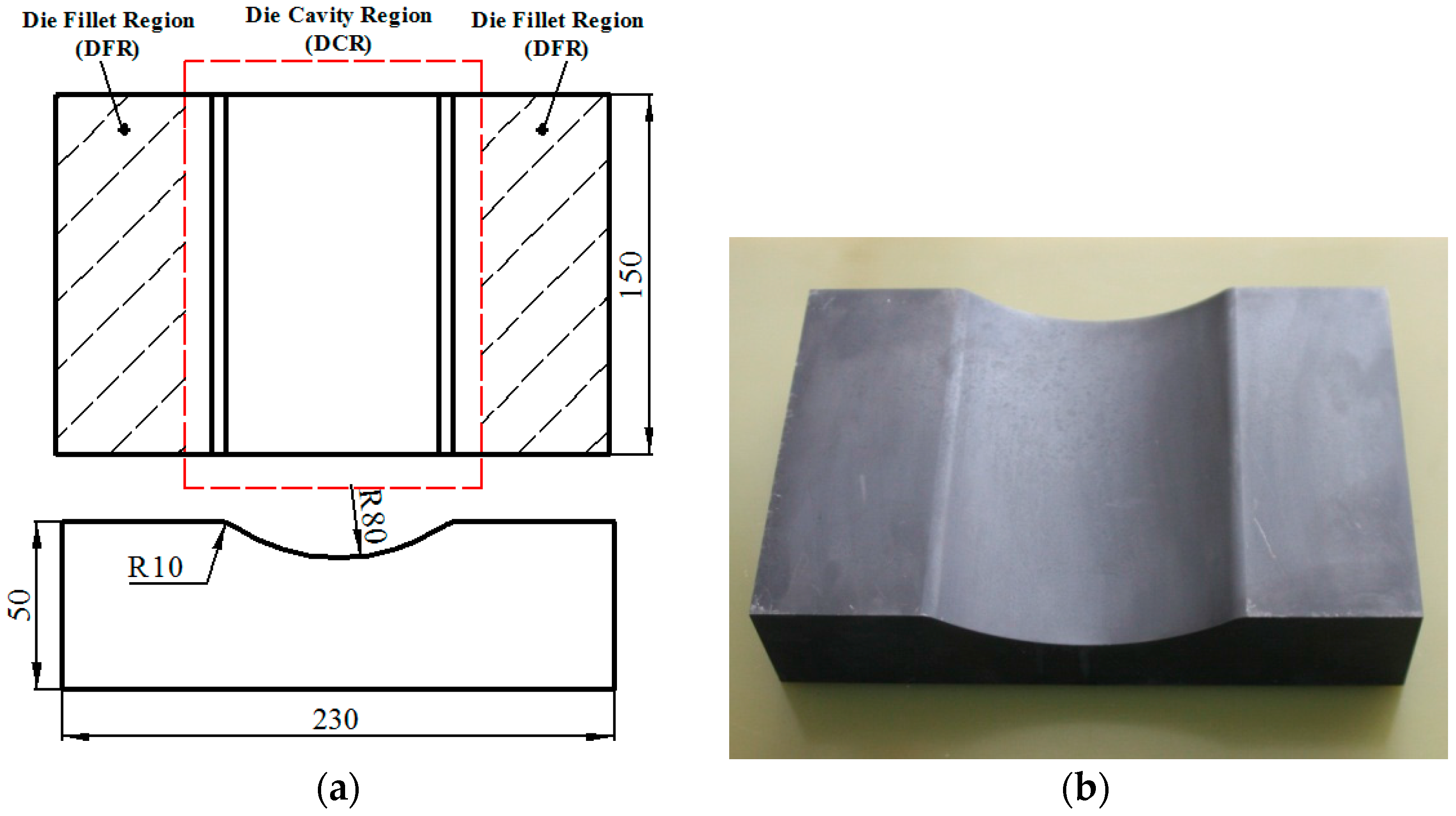

| Blank Form | Rib Height (mm) | Rib Width (mm) | Web Thickness (mm) |
|---|---|---|---|
| Flat panel (FP) | 0 | 0 | 2 |
| X-rib panel (XP) | 4 | 2 | 2 |
| Y-rib panel (YP) | 4 | 2 | 2 |
| Grid-rib panel (GP) | 4 | 2 | 2 |
| Discharge Capacity (μF) | X Coordinate at the 1st Pass (mm) | Voltage at the 1st Pass (kV) | X Coordinate at the 2nd Pass (mm) | Voltage at the 2nd Pass (kV) | X Coordinate at the 3rd Pass (mm) | Voltage at the 3rd Pass (kV) |
|---|---|---|---|---|---|---|
| 80 | −20 | 9.9 | −20 | 12 | +20 | 12 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, J.; Zhan, M.; Gao, P.; Li, H. Electromagnetic Forming Rules of a Stiffened Panel with Grid Ribs. Metals 2017, 7, 559. https://doi.org/10.3390/met7120559
Tan J, Zhan M, Gao P, Li H. Electromagnetic Forming Rules of a Stiffened Panel with Grid Ribs. Metals. 2017; 7(12):559. https://doi.org/10.3390/met7120559
Chicago/Turabian StyleTan, Jinqiang, Mei Zhan, Pengfei Gao, and Hongwei Li. 2017. "Electromagnetic Forming Rules of a Stiffened Panel with Grid Ribs" Metals 7, no. 12: 559. https://doi.org/10.3390/met7120559
APA StyleTan, J., Zhan, M., Gao, P., & Li, H. (2017). Electromagnetic Forming Rules of a Stiffened Panel with Grid Ribs. Metals, 7(12), 559. https://doi.org/10.3390/met7120559




