Evaluation of Methods for Estimation of Cyclic Stress-Strain Parameters from Monotonic Properties of Steels
Abstract
:1. Introduction
2. Overview of Existing Methods for Estimation of Cyclic Stress-Strain Parameters
2.1. Methods for Estimation of Cyclic Yield Stress Re′
2.2. Methods for Estimation of Cyclic Parameters K′and n′
2.3. Conclusions
3. Methods and Data
3.1. Methods for Statistical Analysis
3.2. Data to Be Analyzed
4. Analysis and Results
4.1. Results of One-Way ANOVA and Tukey’s Multiple Comparison Test
4.2. Evaluation of Methods for Estimation of Cyclic Yield Stress Re′ and Ramberg-Osgood Parameters K′ and n′ of Steels
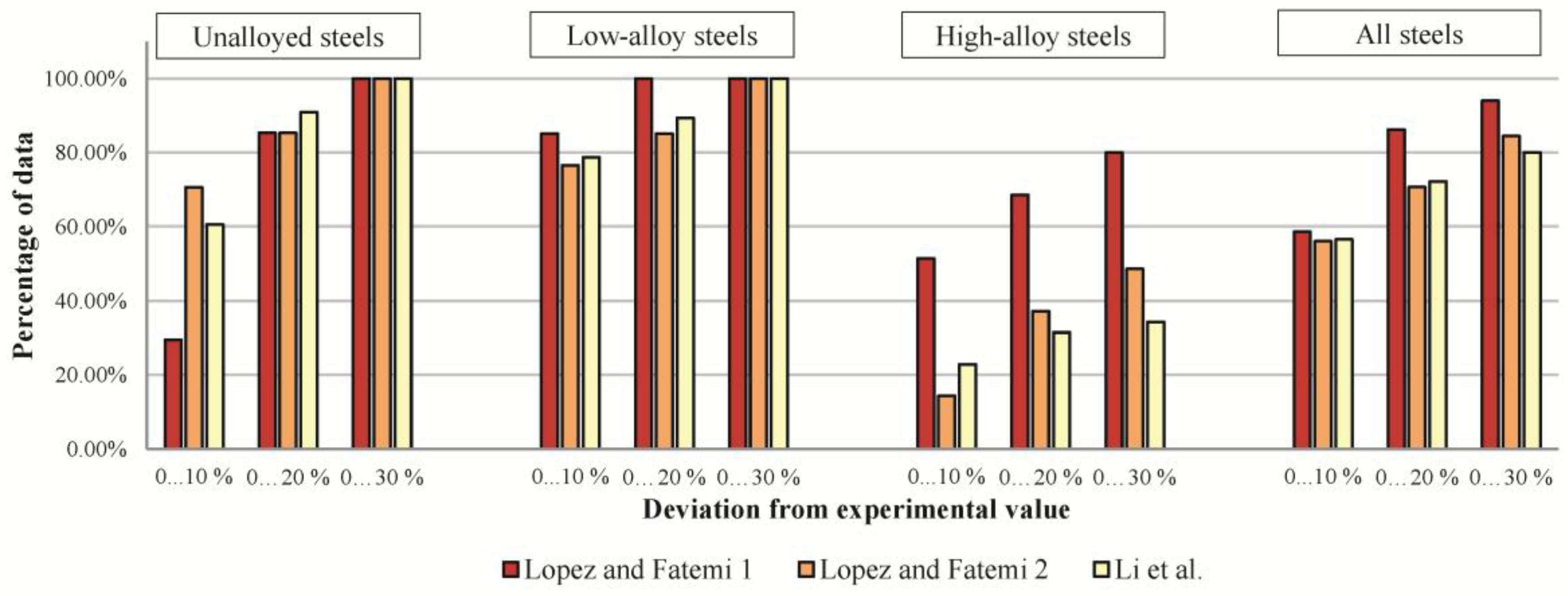
4.2.1. Evaluation of Methods for Estimation of Cyclic Yield Stress Re′
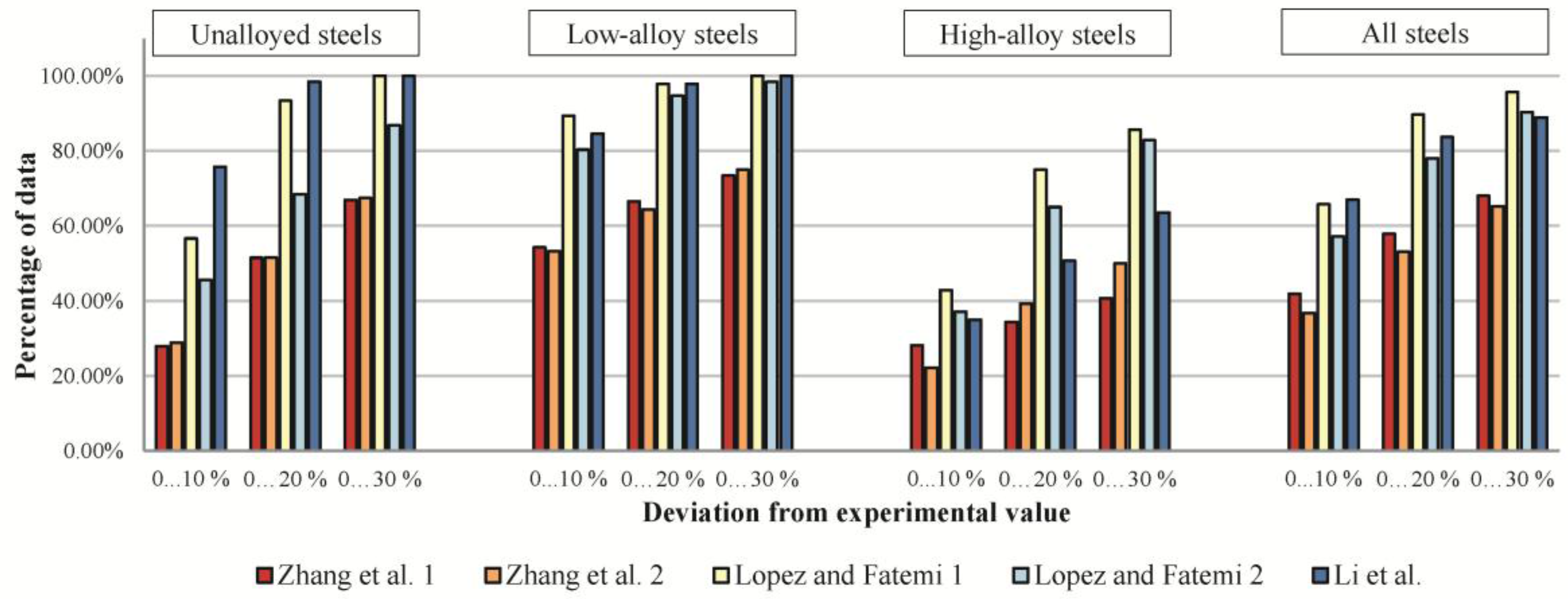
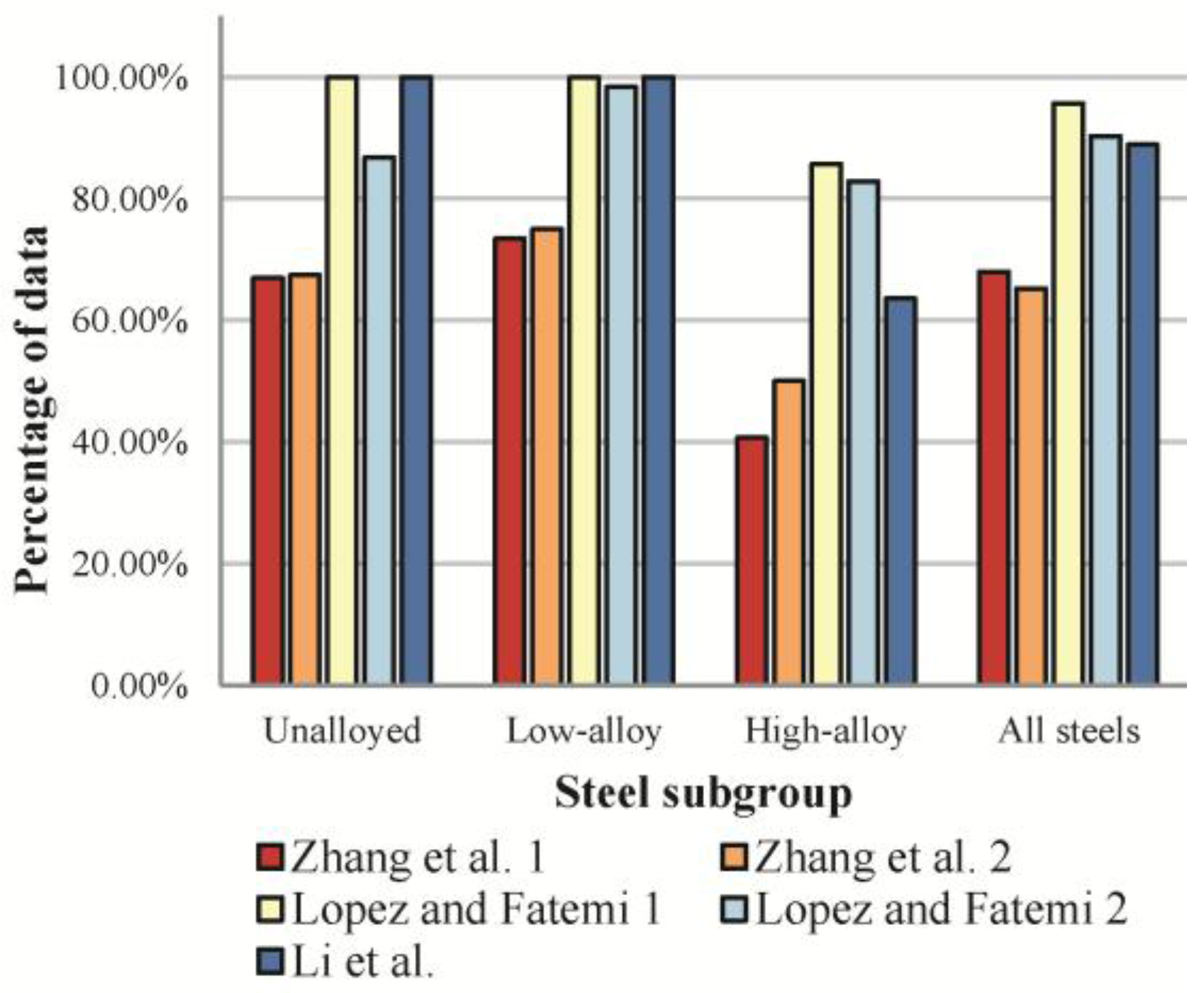
4.2.2. Evaluation of Methods for Estimation of Ramberg-Osgood Parameters K′ and n′ of Steels
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Material Designation | Monotonic Properties | Cyclic Parameters | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DIN or SAE/other | E (MPa) | Re or Rp0.2 (MPa) | Rm (MPa) | Rm/Re (-) | RA (%) | K (MPa) | n (-) | σf (MPa) | εf (-) | Re′ (MPa) | K′ (MPa) | n′ (-) |
| 1038 (SAE) | 207,000 | 347 | 610 | 1.758 | 55.5 | 511 | 0.071 | 956 | 0.590 | 332 | 1207 | 0.208 |
| Armco (other) | 210,000 | 207 | 359 | 1.734 | 64 | 675 | 0.285 | 653 | 1.030 | 280 | 858 | 0.18 |
| C 20 | 190,000 | 224 | 414 | 1.848 | 70 | 330 | 0.061 | 953 | 1.190 | 239 | 1050 | 0.238 |
| C 10 | 217,510 | 435 | 566 | 1.301 | 68 | 659 | 0.073 | 1205 | 1.130 | 463 | 1381 | 0.176 |
| Ck 15 | 196,793 | 263 | 392 | 1.490 | 55 | 711 | 0.224 | 746 | 0.806 | 249 | 824 | 0.193 |
| Ck 15 | 204,500 | 320 | 434 | 1.356 | 67.5 | 394 | 0.067 | 848.7 | 1.126 | 269 | 813 | 0.178 |
| Ck 15 | 202,000 | 431.3 | 615.2 | 1.426 | 54 | 598 | 0.045 | 1011.7 | 0.776 | 492 | 1296 | 0.156 |
| Ck 15 | 203,000 | 660 | 828 | 1.255 | 2.6 | 863 | 0.042 | 850.5 | 0.026 | 687 | 1165 | 0.085 |
| Ck 25 | 210,000 | 346 | 507 | 1.465 | 63 | 926 | 0.264 | 1027 | 0.994 | 280 | 1345 | 0.252 |
| Ck 25 | 210,000 | 307 | 464 | 1.511 | 65 | 924 | 0.276 | 982 | 1.050 | 278 | 1111 | 0.223 |
| Ck 25 | 210,000 | 366 | 527 | 1.440 | 60 | 1033 | 0.264 | 997 | 0.916 | 303 | 1217 | 0.224 |
| Ck 35 | 210,000 | 414 | 617 | 1.490 | 58 | 1216 | 0.258 | 1150 | 0.868 | 328 | 1355 | 0.229 |
| Ck 35 | 210,000 | 394 | 593 | 1.505 | 62 | 1168 | 0.257 | 1169 | 0.968 | 333 | 1460 | 0.238 |
| Ck 35 | 210,000 | 396 | 565 | 1.427 | 63 | 1134 | 0.264 | 1134 | 0.994 | 316 | 1534 | 0.254 |
| Ck 35 | 210,000 | 587 | 780 | 1.329 | 67 | 1356 | 0.186 | 1514 | 1.109 | 463 | 1106 | 0.14 |
| Ck 35 | 210,000 | 480 | 656 | 1.367 | 74 | 1196 | 0.207 | 1468 | 1.347 | 393 | 1033 | 0.156 |
| Ck 35 | 210,000 | 596 | 733 | 1.230 | 71 | 1170 | 0.152 | 1541 | 1.238 | 447 | 1027 | 0.134 |
| Ck 35 | 210,000 | 542 | 730 | 1.347 | 68 | 1311 | 0.2 | 1473 | 1.139 | 430 | 1087 | 0.149 |
| Ck 35 | 210,000 | 513 | 669 | 1.304 | 70 | 1121 | 0.18 | 1417 | 1.204 | 387 | 1081 | 0.165 |
| Ck 45 | 206,000 | 540 | 790 | 1.463 | 60 | 730 | 0.047 | 1400 | 0.916 | 481 | 980 | 0.115 |
| Ck 45 | 210,500 | 531 | 790 | 1.488 | 60 | 1219 | 0.0151 | 1271 | 0.777 | 462 | 1078 | 0.133 |
| Ck 45 | 199,700 | 622 | 915 | 1.471 | 59 | 1606 | 0.18 | 1784 | 0.900 | 591 | 2407 | 0.226 |
| Ck 45 | 199,700 | 622 | 915 | 1.471 | 59 | 1606 | 0.18 | 1784 | 0.900 | 538 | 1762 | 0.191 |
| Ck 45 | 201,500 | 380 | 684 | 1.800 | 36.8 | 735 | 0.092 | 987 | 0.460 | 336 | 1414 | 0.231 |
| Ck 45 | 205,000 | 760 | 1018 | 1.339 | 0 | 1141 | 0.059 | 1018 | 0.000 | 722 | 2075 | 0.17 |
| Ck 45 | 199,000 | 466 | 737 | 1.582 | 54 | 1469 | 0.248 | 1296 | 0.777 | 368 | 1486 | 0.225 |
| Ck 45 | 207,000 | 462 | 672 | 1.455 | 61 | 1288 | 0.235 | 1298 | 0.942 | 354 | 1391 | 0.22 |
| Ck 45 | 208,000 | 588 | 730 | 1.241 | 70 | 1154 | 0.148 | 1540 | 1.204 | 420 | 1194 | 0.168 |
| Ck 45 | 207,000 | 551 | 774 | 1.405 | 68 | 1297 | 0.166 | 1559 | 1.139 | 464 | 1235 | 0.158 |
| Ck 45 | 206,000 | 728 | 844 | 1.159 | 64 | 1208 | 0.108 | 1582 | 1.022 | 516 | 1217 | 0.138 |
| Ck 45 | 210,000 | 652 | 787 | 1.207 | 68 | 1200 | 0.129 | 1568 | 1.139 | 472 | 1285 | 0.161 |
| Ck 45 | 204,000 | 702 | 863 | 1.229 | 66 | 1268 | 0.118 | 1651 | 1.079 | 526 | 1243 | 0.138 |
| St 37 | 210,000 | 295 | 435 | 1.475 | 64 | 829 | 0.275 | 835 | 1.020 | 273 | 988 | 0.207 |
| St 52-3 | 210,000 | 400 | 597 | 1.493 | 63 | 1061 | 0.225 | 1083 | 0.980 | 389 | 1228 | 0.185 |
| Material Designation | Monotonic Properties | Cyclic Parameters | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DIN | E (MPa) | Re or Rp0.2 (MPa) | Rm (MPa) | Rm/Re (-) | RA (%) | K (MPa) | n (-) | σf (MPa) | εf (-) | Re′ (MPa) | K′ (MPa) | n′ (-) |
| 100 Cr 6 | 207,000 | 1927 | 2016 | 1.046 | 12 | 2281 | 0.031 | 2230 | 0.120 | 1341 | 3328 | 0.146 |
| 11 NiMnCrMo 55 | 210,000 | 745 | 852 | 1.144 | 57 | 1277 | 0.124 | 1327 | 0.834 | 663 | 1145 | 0.088 |
| 14 Mn 5 | 206,000 | 580 | 697 | 1.202 | 68 | 858 | 0.067 | 1222 | 1.150 | 537 | 1436 | 0.158 |
| 16 NiCrMo 3 2 | 209,000 | 891 | 939 | 1.054 | 63 | 963 | 0.011 | 1491 | 0.994 | 617 | 1080 | 0.09 |
| 17 MnCrMo 33 | 214,000 | 833 | 929 | 1.115 | 58 | 1285 | 0.099 | 1446 | 0.867 | 663 | 1252 | 0.102 |
| 20 Mn 3 | 206,000 | 910 | 960 | 1.055 | 43 | 1190 | 0.06 | 1090 | 0.561 | 675 | 1313 | 0.107 |
| 22 MnCrNi 3 | 198,000 | 1200 | 1510 | 1.258 | 42 | 2447 | 0.114 | 2034 | 0.549 | 1046 | 2149 | 0.112 |
| 22 MnCrNi 3 | 195,000 | 1200 | 1586 | 1.322 | 3 | 2586 | 0.115 | 1669 | 0.026 | 1193 | 2759 | 0.135 |
| 23 Mn 4 | 207,000 | 1008 | 1091 | 1.082 | 61 | 1185 | 0.026 | 1616 | 0.950 | 656 | 1616 | 0.145 |
| 23 NiCr 4 | 208,531 | 725 | 808 | 1.114 | 66 | 762 | 0.007 | 1215 | 1.080 | 541 | 1221 | 0.131 |
| 25 Mn 3 | 200,000 | 351 | 540 | 1.538 | 67 | 992 | 0.236 | 1173 | 1.100 | 322 | 1219 | 0.214 |
| 25 Mn 5 | 207,000 | 904 | 1008 | 1.115 | 49 | 1138 | 0.033 | 1284 | 0.680 | 608 | 1900 | 0.183 |
| 28 MnCu 6 | 204,000 | 330 | 580 | 1.758 | 64 | 938 | 0.19 | 950 | 1.030 | 347 | 1151 | 0.193 |
| 30 CrMo 2 | 221,000 | 780 | 898 | 1.151 | 67 | 1117 | 0.063 | 1692 | 1.120 | 579 | 1366 | 0.138 |
| 30 CrMo 2 | 200,250 | 1360 | 1429 | 1.051 | 55 | 1661 | 0.033 | 2085 | 0.790 | 814 | 1758 | 0.124 |
| 30 CrMoNiV 5 11 | 212,000 | 605 | 773 | 1.278 | 62 | 717 | 0.027 | 1332 | 0.968 | 497 | 894 | 0.094 |
| 30 CrNiMo 8 | 206,000 | 700 | 910 | 1.300 | 66 | 1128 | 0.079 | 1168 | 0.708 | 573 | 972 | 0.085 |
| 30 CrNiMo 8 | 206,000 | 700 | 910 | 1.300 | 66 | 1128 | 0.079 | 1168 | 0.708 | 522 | 995 | 0.095 |
| 30 MnCr 5 | 206,000 | 820 | 950 | 1.159 | 64 | 1250 | 0.097 | 1445 | 1.068 | 576 | 1618 | 0.166 |
| 34 CrMo 4 | 193,000 | 1017 | 1088 | 1.070 | 65 | 1344 | 0.056 | 1903 | 1.050 | 692 | 1310 | 0.103 |
| 34 CrMo 4 | 188,000 | 847 | 939 | 1.109 | 69 | 1215 | 0.074 | 1795 | 1.171 | 624 | 1008 | 0.077 |
| 34 CrMo 4 | 190,000 | 893 | 978 | 1.095 | 67 | 1338 | 0.089 | 1787 | 1.109 | 650 | 987 | 0.067 |
| 34 CrMo 4 | 197,000 | 980 | 1078 | 1.100 | 61 | 1382 | 0.07 | 1818 | 0.942 | 711 | 1373 | 0.106 |
| 34 CrMo 4 | 194,000 | 780 | 881 | 1.129 | 71 | 1299 | 0.116 | 1740 | 1.238 | 556 | 1198 | 0.124 |
| 4 NiCrMn 4 | 206,000 | 454 | 623 | 1.372 | 76 | 753 | 0.081 | 1229 | 1.450 | 505 | 1111 | 0.127 |
| 40 CrMo 4 | 208,780 | 840 | 940 | 1.119 | 64 | 1300 | 0.094 | 1440 | 1.035 | 583 | 1307 | 0.13 |
| 40 NiCrMo 6 | 201,000 | 1084 | 1146 | 1.057 | 59 | 1549 | 0.083 | 1857 | 0.890 | 758 | 1550 | 0.115 |
| 40 NiCrMo 6 | 190,000 | 910 | 1015 | 1.115 | 62 | 1372 | 0.089 | 1808 | 0.970 | 660 | 1392 | 0.12 |
| 40 NiCrMo 6 | 202,000 | 953 | 1029 | 1.080 | 62 | 1448 | 0.1 | 1724 | 0.970 | 659 | 1628 | 0.145 |
| 40 NiCrMo 6 | 193,000 | 998 | 1067 | 1.069 | 62 | 1474 | 0.092 | 1761 | 0.970 | 716 | 1292 | 0.095 |
| 40 NiCrMo 6 | 205,000 | 810 | 884 | 1.091 | 67 | 1378 | 0.142 | 1680 | 1.110 | 586 | 1303 | 0.129 |
| 40 NiCrMo 7 | 193,500 | 1374 | 1471 | 1.071 | 38 | 1796 | 0.04 | 1920 | 0.480 | 905 | 1890 | 0.118 |
| 40 NiCrMo 7 | 193,500 | 635 | 829 | 1.306 | 43 | 1175 | 0.098 | 1201 | 0.570 | 474 | 1332 | 0.167 |
| 41 MnCr 3 4 | 207,280 | 800 | 930 | 1.163 | 62 | 1350 | 0.112 | 1390 | 0.960 | 551 | 1340 | 0.143 |
| 42 Cr 4 | 195,000 | 903 | 1006 | 1.114 | 62 | 1293 | 0.068 | 1716 | 0.968 | 679 | 1153 | 0.085 |
| 42 Cr 4 | 194,000 | 813 | 921 | 1.133 | 65 | 1249 | 0.086 | 1674 | 1.050 | 613 | 1147 | 0.101 |
| 42 Cr 4 | 194,000 | 845 | 952 | 1.127 | 62 | 1288 | 0.086 | 1689 | 0.968 | 619 | 1207 | 0.107 |
| 42 Cr 4 | 192,000 | 833 | 943 | 1.132 | 65 | 1289 | 0.09 | 1690 | 1.050 | 621 | 1192 | 0.105 |
| 42 Cr 4 | 193,000 | 717 | 840 | 1.172 | 69 | 1240 | 0.118 | 1617 | 1.171 | 543 | 1161 | 0.122 |
| 42 CrMo 4 | 211,400 | 998 | 1111 | 1.113 | 60 | 1469 | 0.069 | 1525 | 0.496 | 716 | 1367 | 0.104 |
| 49 MnVS 3 | 210,200 | 566 | 840 | 1.484 | 19 | 1428 | 0.194 | 1152 | 0.380 | 520 | 1396 | 0.159 |
| 50 CrMo 4 | 205,000 | 970 | 1086 | 1.120 | 48.6 | 1132 | 0.026 | 1609 | 0.665 | 700 | 1568 | 0.13 |
| 50 CrMo 4 | 205,000 | 947 | 983 | 1.038 | 14.6 | 1042 | 0.018 | 926 | 0.157 | 774 | 1754 | 0.132 |
| 8 Mn 6 | 198,000 | 862 | 965 | 1.119 | 57 | 1227 | 0.054 | 1579 | 0.850 | 580 | 1256 | 0.125 |
| 8 Mn 6 | 198,000 | 821 | 869 | 1.058 | 53 | 1085 | 0.046 | 1434 | 0.750 | 674 | 1258 | 0.101 |
| 80 Mn 4 | 187,500 | 502 | 931 | 1.855 | 16 | 1100 | 0.127 | 1060 | 0.174 | 459 | 1859 | 0.225 |
| WStE 460 | 210,000 | 560 | 667 | 1.191 | 61 | 1096 | 0.153 | 1171 | 0.932 | 514 | 1194 | 0.128 |
| Material Designation | Monotonic Properties | Cyclic Parameters | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DIN | E (MPa) | Re or Rp0.2 (MPa) | Rm (MPa) | Rm/Re (-) | RA (%]) | K (MPa) | n (-) | σf (MPa) | εf (-) | Re′ (MPa) | K′ (MPa) | n′ (-) |
| X 10 CrNi 18 8 | 204,000 | 245 | 635 | 2.592 | 79 | 1416 | 0.362 | 1908 | 1.563 | 307 | 2397 | 0.331 |
| X 10 CrNiNb 18 9 | 210,000 | 237 | 615 | 2.595 | 72 | 1398 | 1.273 | 271 | 1967 | 0.319 | ||
| X 10 CrNiNb 18 9 | 210,000 | 237 | 615 | 2.595 | 72 | 1398 | 1.273 | 276 | 1667 | 0.289 | ||
| X 10 CrNiTi 18 9 | 210,000 | 211 | 677 | 3.209 | 67 | 1428 | 1.109 | 455 | 8384 | 0.469 | ||
| X 10 CrNiTi 18 9 | 210,000 | 182 | 668 | 3.670 | 68 | 1429 | 1.139 | 414 | 6179 | 0.435 | ||
| X 10 CrNiTi 18 9 | 210,000 | 211 | 677 | 3.209 | 69 | 1470 | 1.171 | 496 | 3647 | 0.321 | ||
| X 10 CrNiTi 18 9 | 210,000 | 177 | 516 | 2.915 | 74 | 1211 | 1.347 | 220 | 2264 | 0.375 | ||
| X 10 CrNiTi 18 9 | 210,000 | 177 | 516 | 2.915 | 74 | 1211 | 1.347 | 250 | 1535 | 0.292 | ||
| X 10 CrNiTi 18 9 | 210,000 | 214 | 529 | 2.472 | 74 | 1242 | 1.347 | 228 | 2086 | 0.357 | ||
| X 10 CrNiTi 18 9 | 210,000 | 214 | 529 | 2.472 | 74 | 1242 | 1.347 | 251 | 1682 | 0.306 | ||
| X 10 CrNiTi 18 9 | 210,000 | 177 | 535 | 3.023 | 77 | 1321 | 1.470 | 220 | 3080 | 0.424 | ||
| X 10 CrNiTi 18 9 | 210,000 | 177 | 535 | 3.023 | 77 | 1321 | 1.470 | 241 | 2097 | 0.348 | ||
| X 15 Cr 13 | 210,000 | 598 | 736 | 1.231 | 70 | 1622 | 1.204 | 475 | 1056 | 0.128 | ||
| X 15 Cr 13 | 210,000 | 598 | 736 | 1.231 | 70 | 1622 | 1.204 | 497 | 987 | 0.11 | ||
| X 15 CrNiSi 25 20 | 210,000 | 271 | 630 | 2.325 | 69 | 1368 | 1.171 | 289 | 2302 | 0.334 | ||
| X 15 CrNiSi 25 20 | 210,000 | 271 | 630 | 2.325 | 69 | 1368 | 1.171 | 284 | 2242 | 0.332 | ||
| X 2 CrNi 18 9 | 192,000 | 280 | 601 | 2.146 | 46 | 455 | 0.097 | 971 | 0.616 | 207 | 2807 | 0.419 |
| X 20 CrMo 12 1 | 210,000 | 795 | 1013 | 1.274 | 47 | 1656 | 0.635 | 716 | 1325 | 0.099 | ||
| X 20 CrMo 12 1 | 210,000 | 795 | 1013 | 1.274 | 47 | 1656 | 0.635 | 730 | 1301 | 0.093 | ||
| X 25 CrNiMn 25 20 | 193,340 | 220 | 642 | 2.918 | 63 | 754 | 0.228 | 1360 | 1.010 | 421 | 2267 | 0.271 |
| X 3 CrNi 19 9 | 172,625 | 746 | 953 | 1.277 | 69 | 1114 | 0.063 | 2037 | 1.160 | 882 | 2313 | 0.155 |
| X 3 CrNi 19 9 | 186,435 | 255 | 746 | 2.925 | 74 | 548 | 0.136 | 1920 | 1.370 | 678 | 4634 | 0.309 |
| X 5 CrNi 18 9 | 210,000 | 207 | 611 | 2.952 | 75 | 1458 | 1.386 | 197 | 3331 | 0.455 | ||
| X 5 CrNi 18 9 | 210,000 | 207 | 611 | 2.952 | 83 | 1694 | 1.772 | 203 | 3001 | 0.434 | ||
| X 5 CrNiMo 18 10 | 210,000 | 230 | 587 | 2.552 | 78 | 1476 | 1.514 | 256 | 1644 | 0.299 | ||
| X 5 CrNiMo 18 10 | 210,000 | 231 | 587 | 2.541 | 78 | 1476 | 1.514 | 247 | 2755 | 0.388 | ||
| X 5 CrNiMo 18 10 | 210,000 | 257 | 606 | 2.358 | 79 | 1830 | 1.561 | 313 | 2000 | 0.298 | ||
| X 5 CrNiMo 18 10 | 210,000 | 228 | 665 | 2.917 | 81 | 1769 | 1.661 | 259 | 2081 | 0.336 | ||
| X 5 CrNiMo 18 10 | 210,000 | 228 | 665 | 2.917 | 81 | 1769 | 1.661 | 259 | 2674 | 0.376 | ||
| X 5 NiCrTi 26 15 | 210,000 | 777 | 1158 | 1.490 | 52 | 2008 | 0.734 | 713 | 1617 | 0.132 | ||
| X 5 NiCrTi 26 15 | 210,000 | 777 | 1158 | 1.490 | 52 | 2008 | 0.734 | 711 | 1543 | 0.125 | ||
| X 6 CrNi 19 11 | 183,000 | 325 | 650 | 2.000 | 80 | 1210 | 0.193 | 1400 | 1.610 | 267 | 1628 | 0.291 |
| X 8 CrNiTi 18 10 | 204,000 | 222 | 569 | 2.563 | 76 | 349 | 0.062 | 1381 | 1.427 | 383 | 5234 | 0.421 |
| X2 CrNiMo 18 10 | 210,000 | 373 | 700 | 1.877 | 75 | 1670 | 1.386 | 295 | 1232 | 0.23 | ||
| X5 CrNi 18 9 | 198,000 | 242 | 666 | 2.752 | 82 | 484 | 0.113 | 2407 | 1.715 | 275 | 2872 | 0.378 |
References
- Williams, C.R.; Lee, Y.-L.; Rilly, J.T. A practical method for statistical analysis of strain-life fatigue data. Int. J. Fatigue 2003, 25, 427–436. [Google Scholar] [CrossRef]
- Blackmore, P.A. A critical review of Baumel-Seeger method for estimating strain-life fatigue properties of metallic materials. Eng. Integr. 2009, 27, 6–11. [Google Scholar]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; Technical Note No. 902; National Advisory Committee for Aeronautics (NACA): Washington, DC, USA, 1943.
- Manson, S.S.; Halford, G.R. Fatigue and Durability of Structural Materials, 1st ed.; ASM International: Materials Park, OH, USA, 2005. [Google Scholar]
- Manson, S.S. Fatigue: A complex subject—Some simple approximations. Exp. Mech. SESA 1965, 5, 193–226. [Google Scholar] [CrossRef]
- Bäumel, A., Jr.; Seeger, T. Materials Data for Cyclic Loading—Supplement 1, 1st ed.; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Roessle, M.L.; Fatemi, A. Strain-controlled fatigue properties of steels and some simple approximations. Int. J. Fatigue 2000, 22, 495–511. [Google Scholar] [CrossRef]
- Hatscher, A.; Seeger, T.; Zenner, H. Abschätzung von zyklischen Werkstoffkennwerten—Erweiterung und Vergleich bisheriger Ansätze. Materialprufung 2007, 49, 2–14. [Google Scholar]
- Park, J.H.; Song, J.H. Detailed evaluation of methods for estimation of fatigue properties. Int. J. Fatigue 1995, 17, 365–373. [Google Scholar] [CrossRef]
- Zhang, Z.; Qiao, Y.; Sun, Q.; Li, C.; Li, J. Theoretical estimation to the cyclic strength coefficient and the cyclic strain-hardening exponent for metallic materials: Preliminary study. J. Mater. Eng. Perform. 2009, 18, 245–254. [Google Scholar] [CrossRef]
- Li, J.; Sun, Q.; Zhang, Z.; Li, C.; Qiao, Y. Theoretical estimation to the cyclic yield strength and fatigue limit for alloy steels. Mech. Res. Commun. 2009, 36, 316–321. [Google Scholar] [CrossRef]
- Lopez, Z.; Fatemi, A. A method of predicting cyclic stress-strain curve from tensile properties for steels. Mater. Sci. Eng. A Struct. 2012, 556, 540–550. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Z.; Li, C. An improved method for estimation of Ramberg-Osgood curves of steels from monotonic tensile properties. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 412–426. [Google Scholar] [CrossRef]
- Marohnić, T.; Basan, R. Study of Monotonic Properties’ Relevance for Estimation of Cyclic Yield Stress and Ramberg–Osgood Parameters of Steels. J. Mater. Eng. Perform. 2016, 25, 4812–4823. [Google Scholar] [CrossRef]
- Basan, R.; Franulović, M.; Prebil, I.; Črnjarić-Žic, N. Analysis of strain-life fatigue parameters and behavior of different groups of metallic materials. Int. J. Fatigue 2011, 33, 484–491. [Google Scholar] [CrossRef]
- Basan, R.; Marohnić, T.; Prebil, I.; Franulović, M. Preliminary investigation of the existence of correlation between cyclic Ramberg-Osgood parameters and monotonic properties of low-alloy steels. In Proceedings of the 3rd International Conference Mechanical Technologies and Structural Materials MTSM 2013, Split, Croatia, 26–27 September 2013; Živković, D., Ed.; Croatian society for mechanical technologies: Split, Croatia, 2013. [Google Scholar]
- Marohnić, T.; Basan, R.; Franulović, M. Evaluation of the Possibility of Estimating Cyclic Stress-strain Parameters and Curves from Monotonic Properties of Steels. Procedia Eng. 2015, 101, 277–284. [Google Scholar] [CrossRef]
- Smith, R.W.; Hirschberg, M.H.; Manson, S.S. Fatigue Behavior of Materials under Strain Cycling in Low and Intermediate Life Range; Technical Note D-1574; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1963.
- Zhang, Z.; Wu, W.; Chen, D.; Sun, Q.; Zhao, W. New Formula Relating the Yield Stress-Strain with the Strength Coefficient and the Strain-Hardening Exponent. J. Mater. Eng. Perform. 2004, 13, 509–512. [Google Scholar]
- Landgraf, R.W.; Morrow, J.; Endo, T. Determination of cyclic stress-strain curve. J. Mater. 1969, 4, 176–188. [Google Scholar]
- Devore, J. Probability and Statistics for Engineering and the Sciences; Brooks/Cole Cengage Learning: Boston, MA, USA, 2011. [Google Scholar]
- Minitab 17 Statistical Software, Product version 17.3.1; Computer Software; Minitab, Inc.: State College, PA, USA, 2010.
- Boller, C.; Seeger, T. Materials Data for Cyclic Loading, Part A–D, 1st ed.; Elsevier: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Basan, R. MATDAT Materials Properties Database, Version 1.1. 2011. Available online: http://www.matdat.com/ (accessed on 15 January 2016).
| Evaluated Value | Method | Estimated Parameters | Originally Proposed for | Equation Number |
|---|---|---|---|---|
| Re′ | Lopez and Fatemi 1 [12] | Re′ | steels divided by Rm/Re | (4a,b) |
| Lopez and Fatemi 2 [12] | Re′ | all steels | (5) | |
| Li et al. [13] | Re′ | all steels | (6) | |
| Δσ/2 | Zhang et al. 1 [10] (K and n available) | K′ | steels, Al and Ti alloys | (10) |
| n′ | steels, Al and Ti alloys divided by α | (11a,b,c) | ||
| Zhang et al. 2 [10] (K and n not available) | K′ | steels, Al and Ti alloys divided by α | (12a,b) | |
| n′ | steels, Al and Ti alloys divided by α | (13a,b,c) | ||
| Lopez and Fatemi 1 [12] | K′ | steels divided by Rm/Re | (14a,b) | |
| n′ | steels divided by Rm/Re | (15a,b) | ||
| Lopez and Fatemi 2 [12] | K′ | steels divided by Rm/Re | (14a,b) | |
| n′ | all steels | (16) | ||
| Li et al. [13] | K′ | steels divided by Rm/Re | (19a,b,c) | |
| n′ | steels divided by Rm/Re | (18) |
| Steel Subgroup | Estimation of Re′ | Estimation of Δσ/2 (K′, n′) |
|---|---|---|
| Unalloyed steels | Li et al. | 1. Li et al. |
| Lopez and Fatemi 2 | 2. Lopez and Fatemi 1 | |
| Low-alloy steels | 1. Lopez and Fatemi 1 | Lopez and Fatemi 1 |
| 2. Li et al. | Lopez and Fatemi 2 | |
| 3. Lopez and Fatemi 2 | Li et al. | |
| High-alloy steels | Lopez and Fatemi 1 | Lopez and Fatemi 1 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marohnić, T.; Basan, R.; Franulović, M. Evaluation of Methods for Estimation of Cyclic Stress-Strain Parameters from Monotonic Properties of Steels. Metals 2017, 7, 17. https://doi.org/10.3390/met7010017
Marohnić T, Basan R, Franulović M. Evaluation of Methods for Estimation of Cyclic Stress-Strain Parameters from Monotonic Properties of Steels. Metals. 2017; 7(1):17. https://doi.org/10.3390/met7010017
Chicago/Turabian StyleMarohnić, Tea, Robert Basan, and Marina Franulović. 2017. "Evaluation of Methods for Estimation of Cyclic Stress-Strain Parameters from Monotonic Properties of Steels" Metals 7, no. 1: 17. https://doi.org/10.3390/met7010017
APA StyleMarohnić, T., Basan, R., & Franulović, M. (2017). Evaluation of Methods for Estimation of Cyclic Stress-Strain Parameters from Monotonic Properties of Steels. Metals, 7(1), 17. https://doi.org/10.3390/met7010017







