The Unified Creep-Fatigue Equation for Stainless Steel 316
Abstract
:1. Introduction
2. Existing Approaches
2.1. The Linear Damage Rule
2.2. The Linear Damage Rule
2.3. Recent Developments towards a Unified Creep-Fatigue Equation
3. Methods
3.1. Research Question
3.2. Approach
4. Results: Theory and Calculation
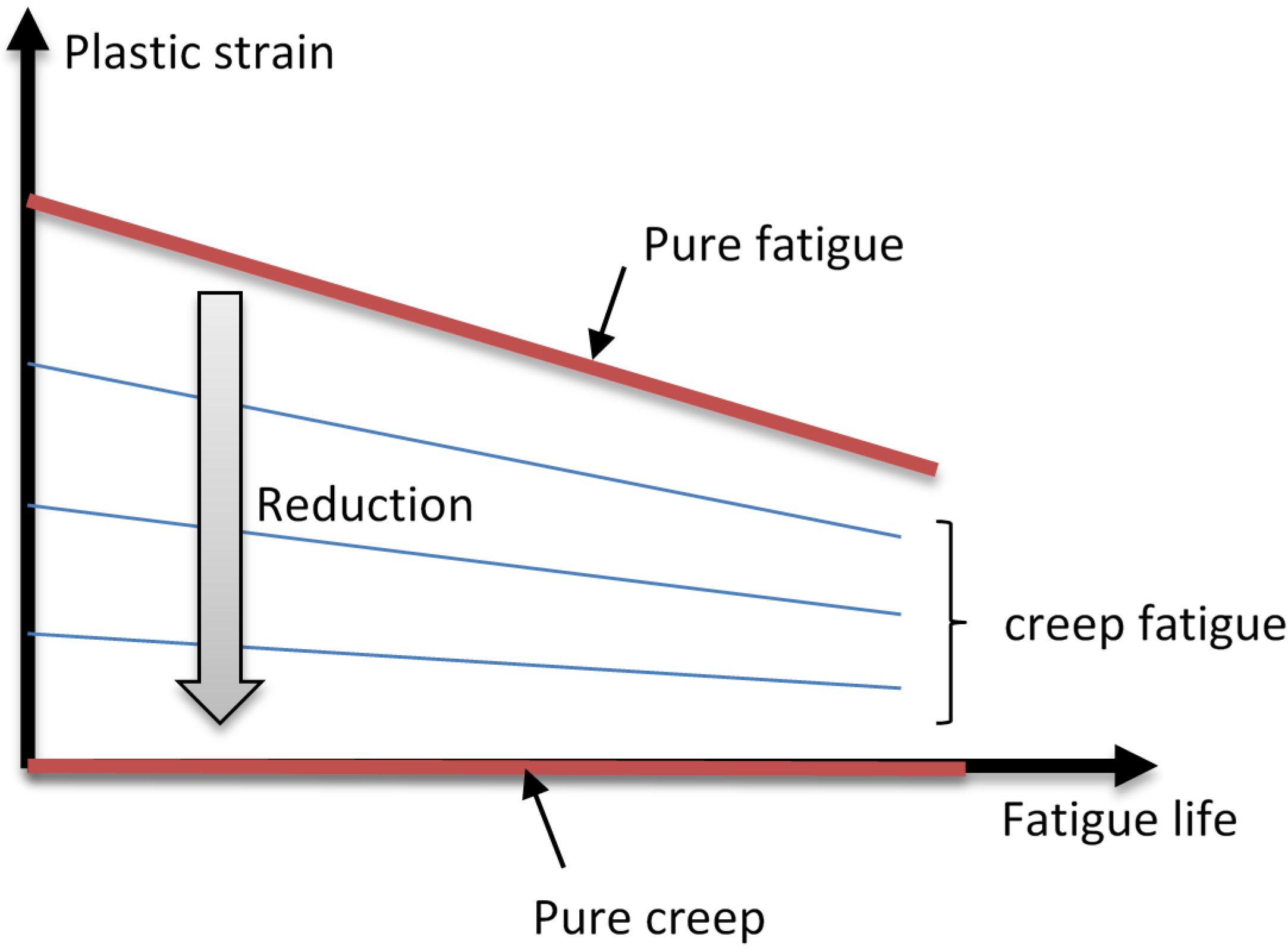
4.1. Introduction to the Unified Creep-Fatigue Equation
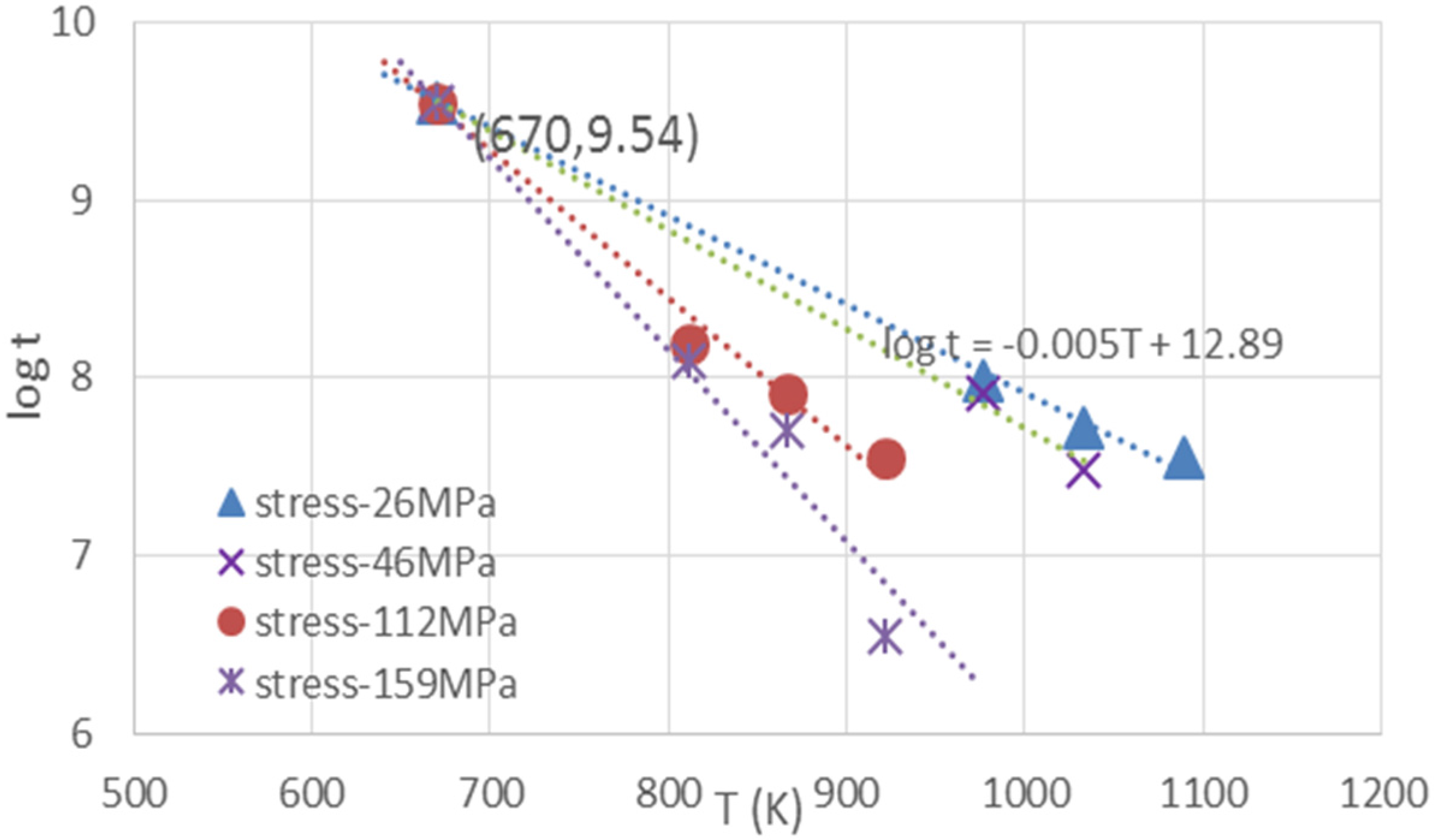
4.2. Extracting the Creep-Rupture Properties of Stainless Steel 316
4.3. Evaluation of the Coefficients of the Strain-Form Unified Creep-Fatigue Equation for the Stainless Steel 316 and Validation
4.3.1. Evaluation of Creep-Fatigue Coefficients
4.3.2. Validations
4.3.3. Application
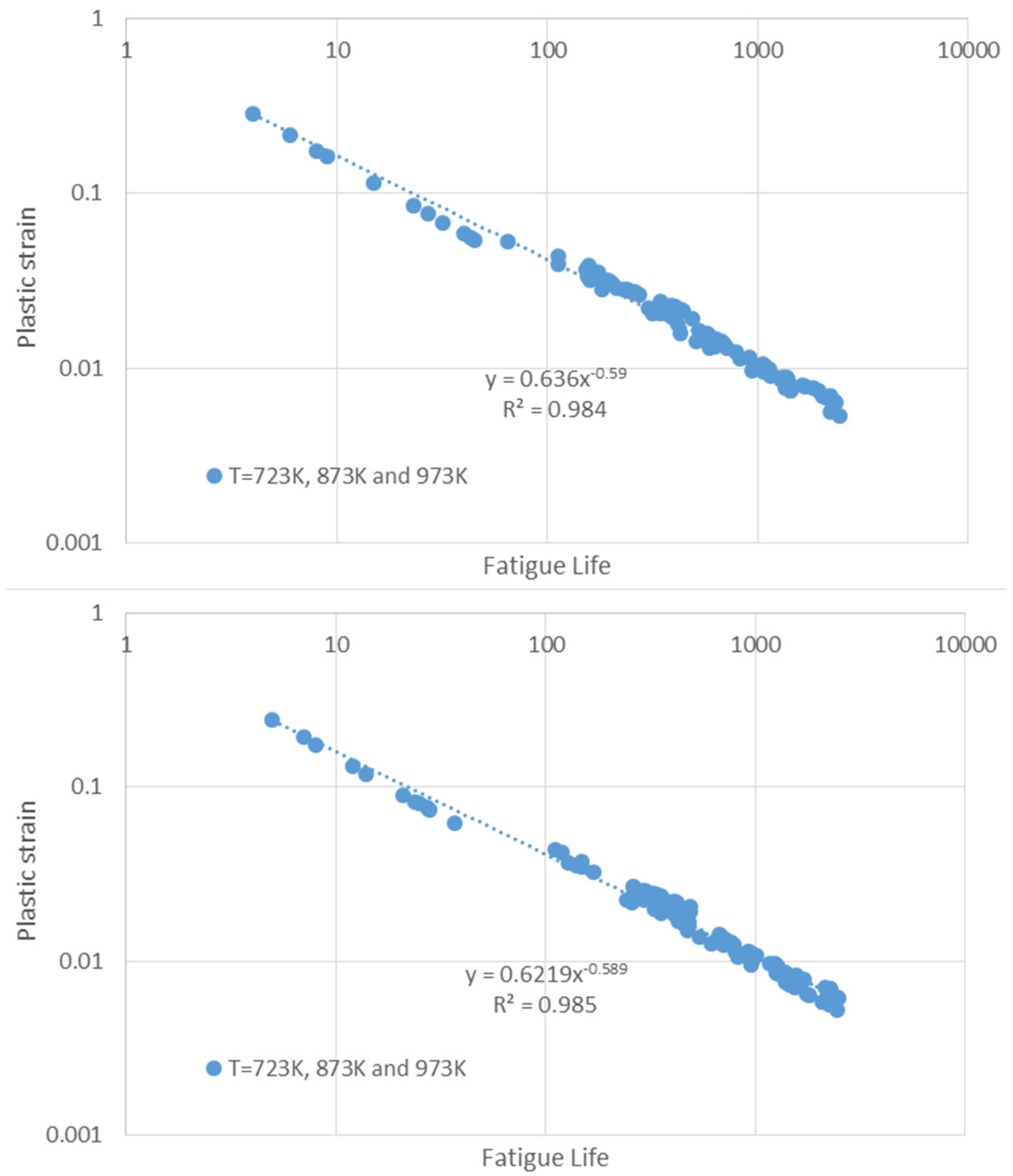
4.4. Evaluation of the Coefficients of the Power-Law Unified Creep-Fatigue Equation for the Stainless Steel 316 and Validation
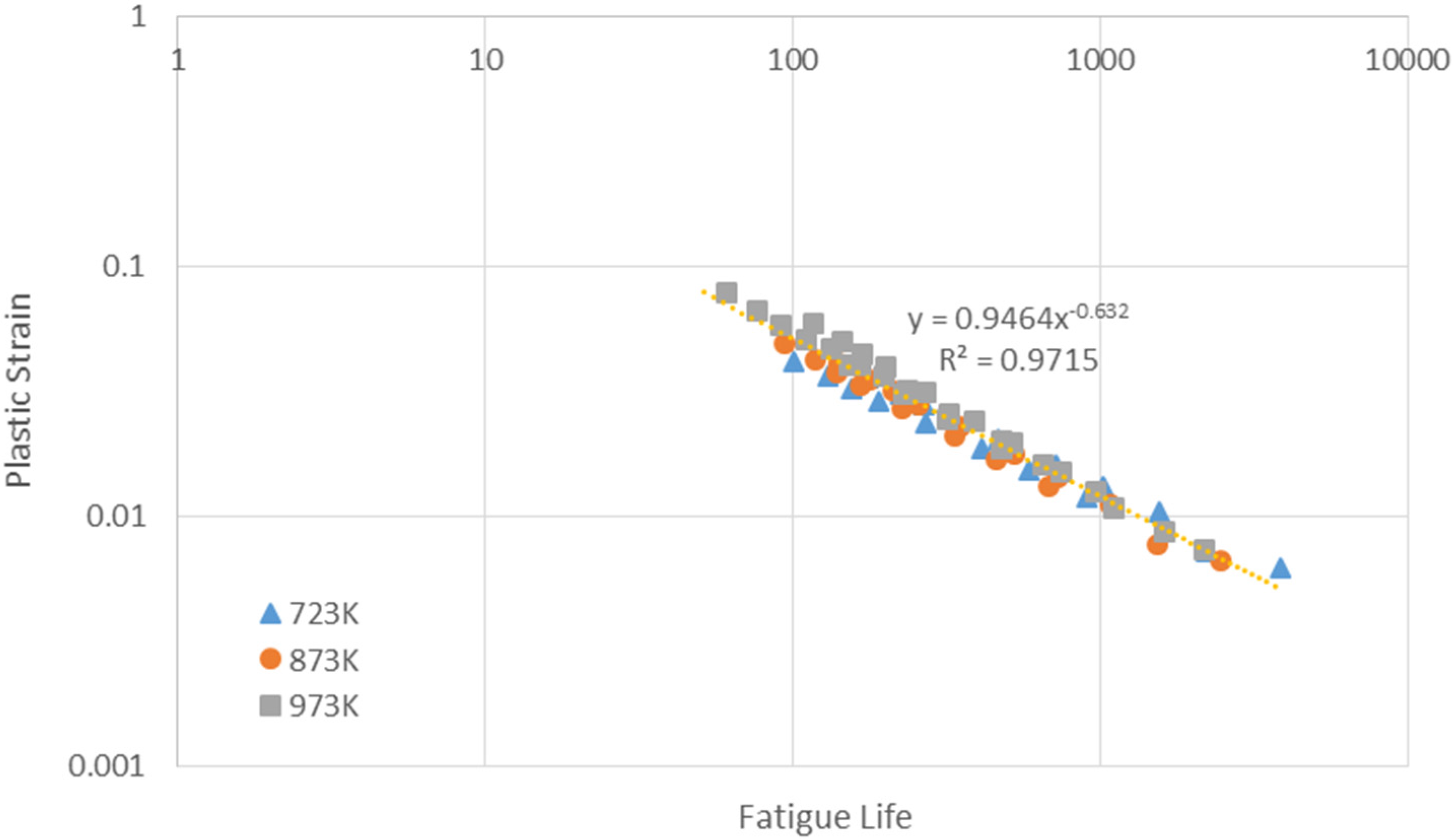
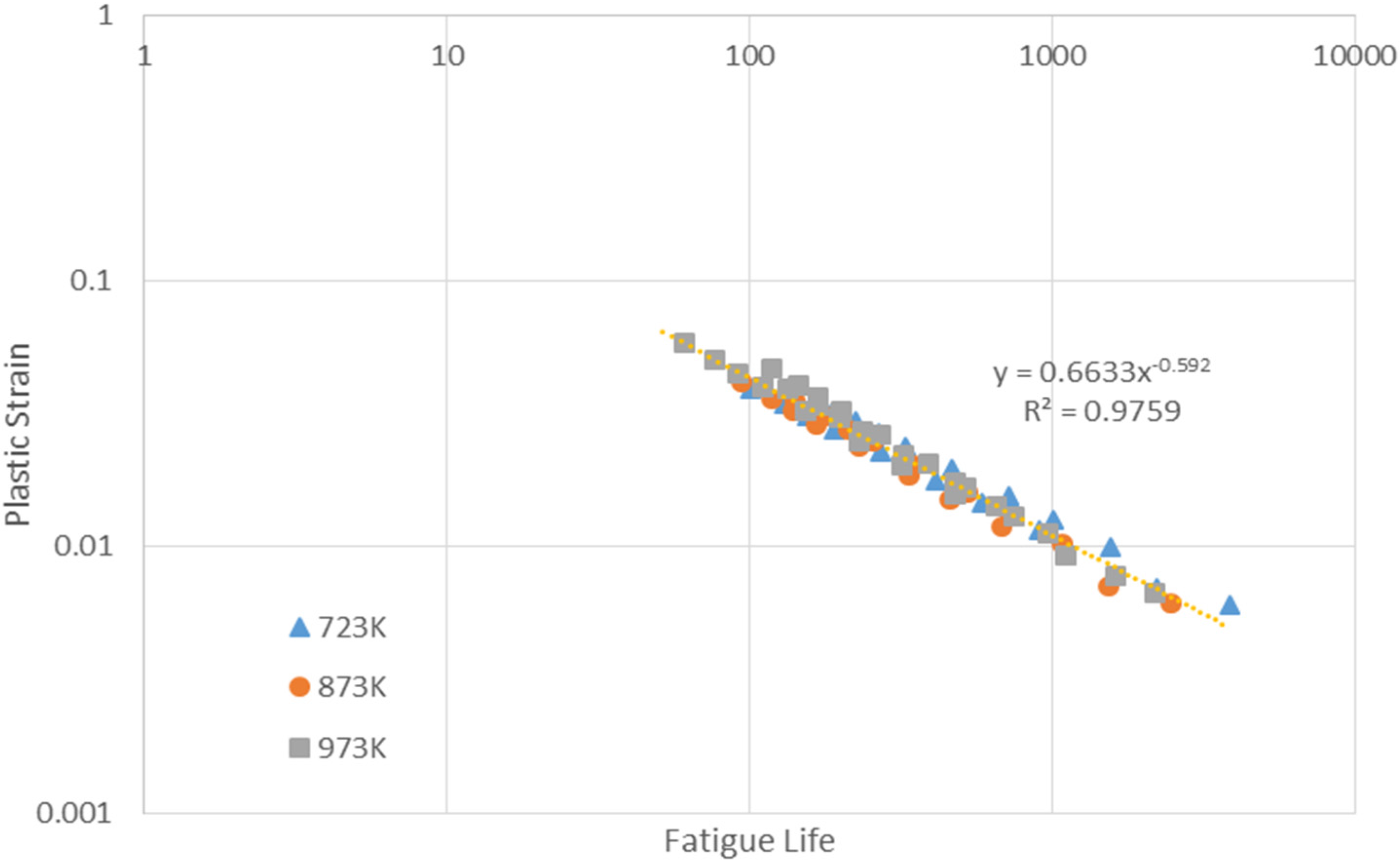
4.4.1. Evaluation of Creep-Fatigue Coefficients and Validation below 873 K
4.4.1.1. Evaluation of Creep-Fatigue Coefficients
4.4.1.2. Validations
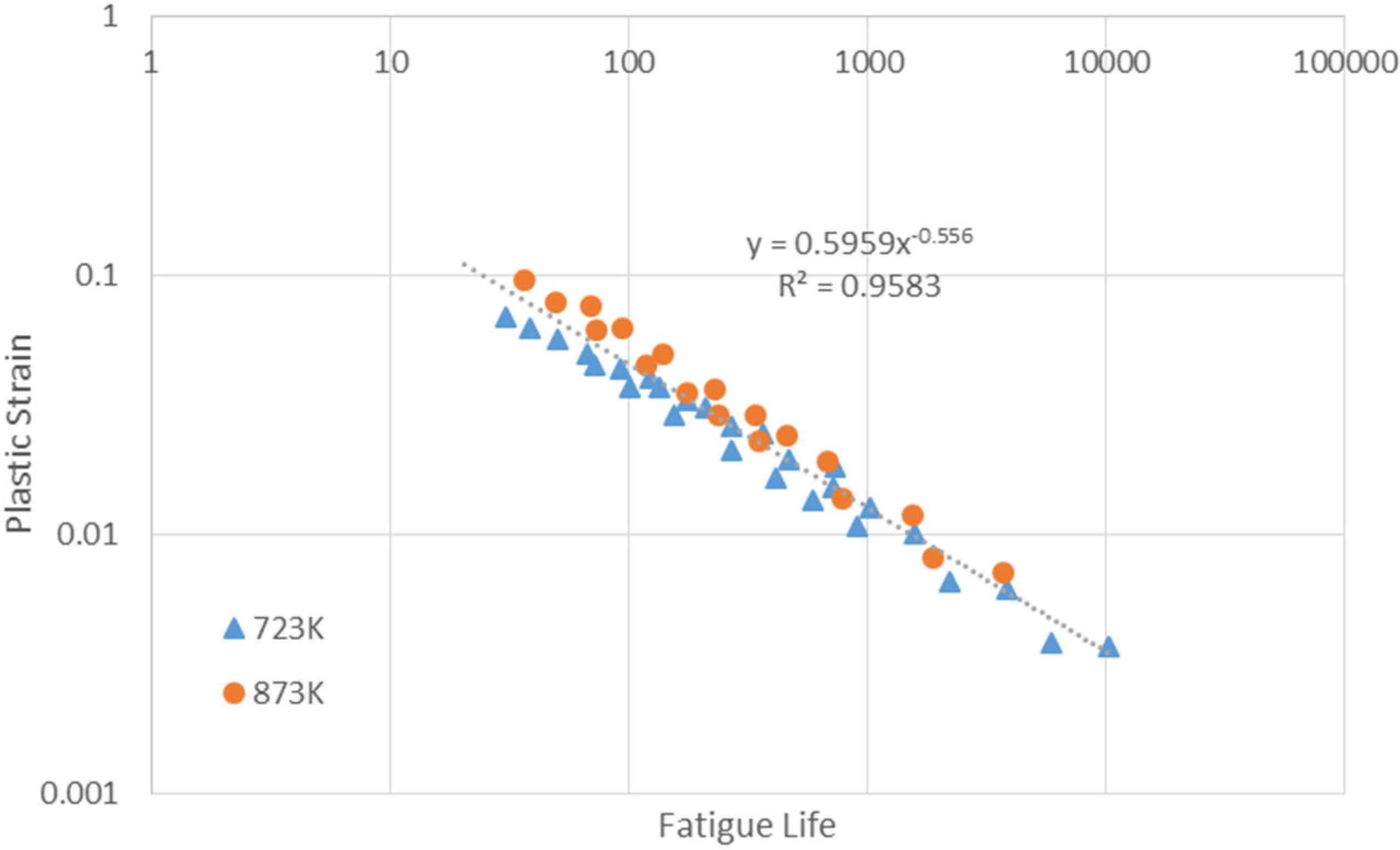
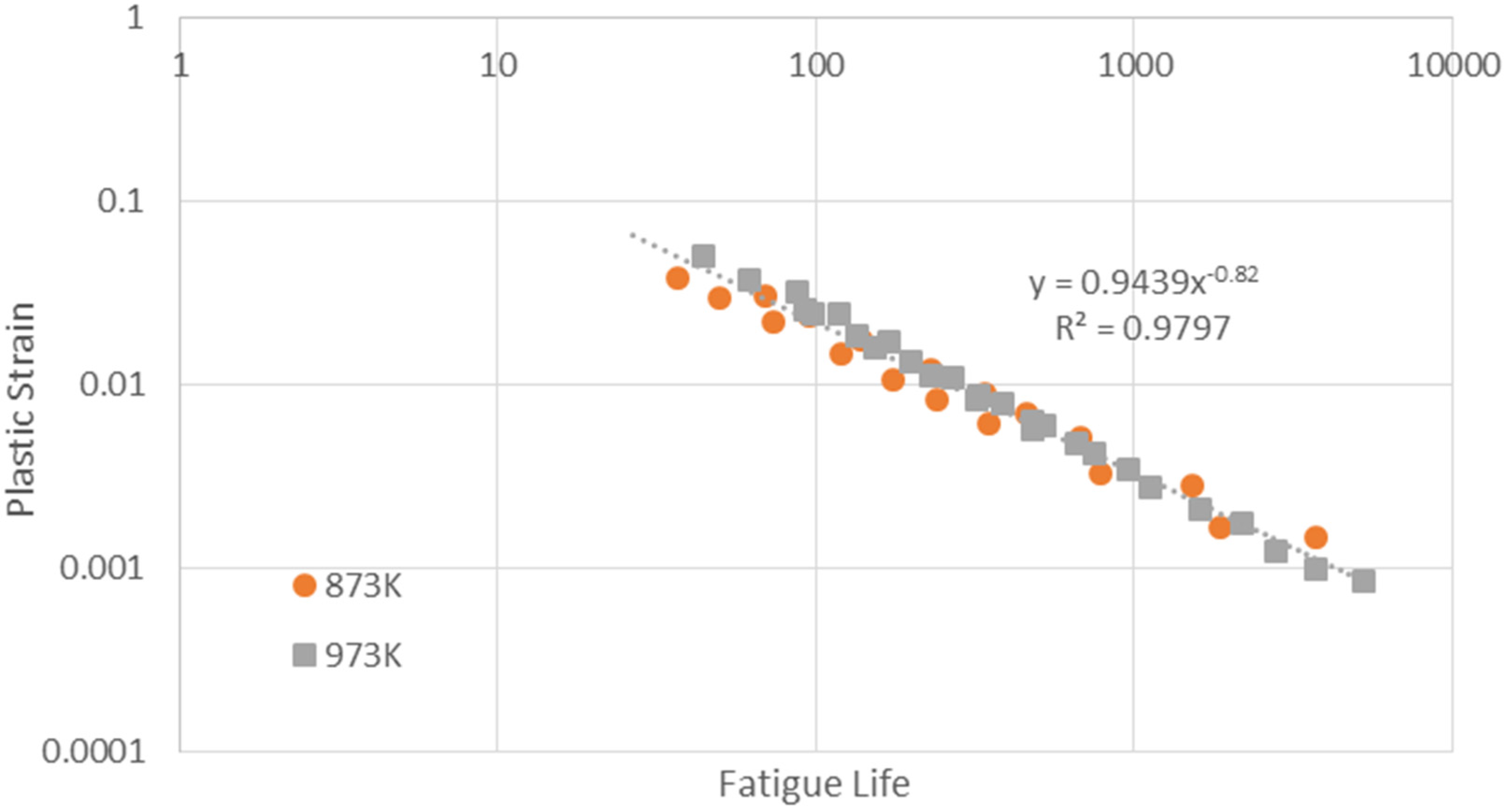
4.4.2. Evaluation of Creep-Fatigue Coefficients and Validation above 873 K
4.4.2.1. Evaluation of Creep-Fatigue Coefficients
4.4.2.2. Validations
4.4.3. Application
5. Discussion
5.1. The Moderating Factor
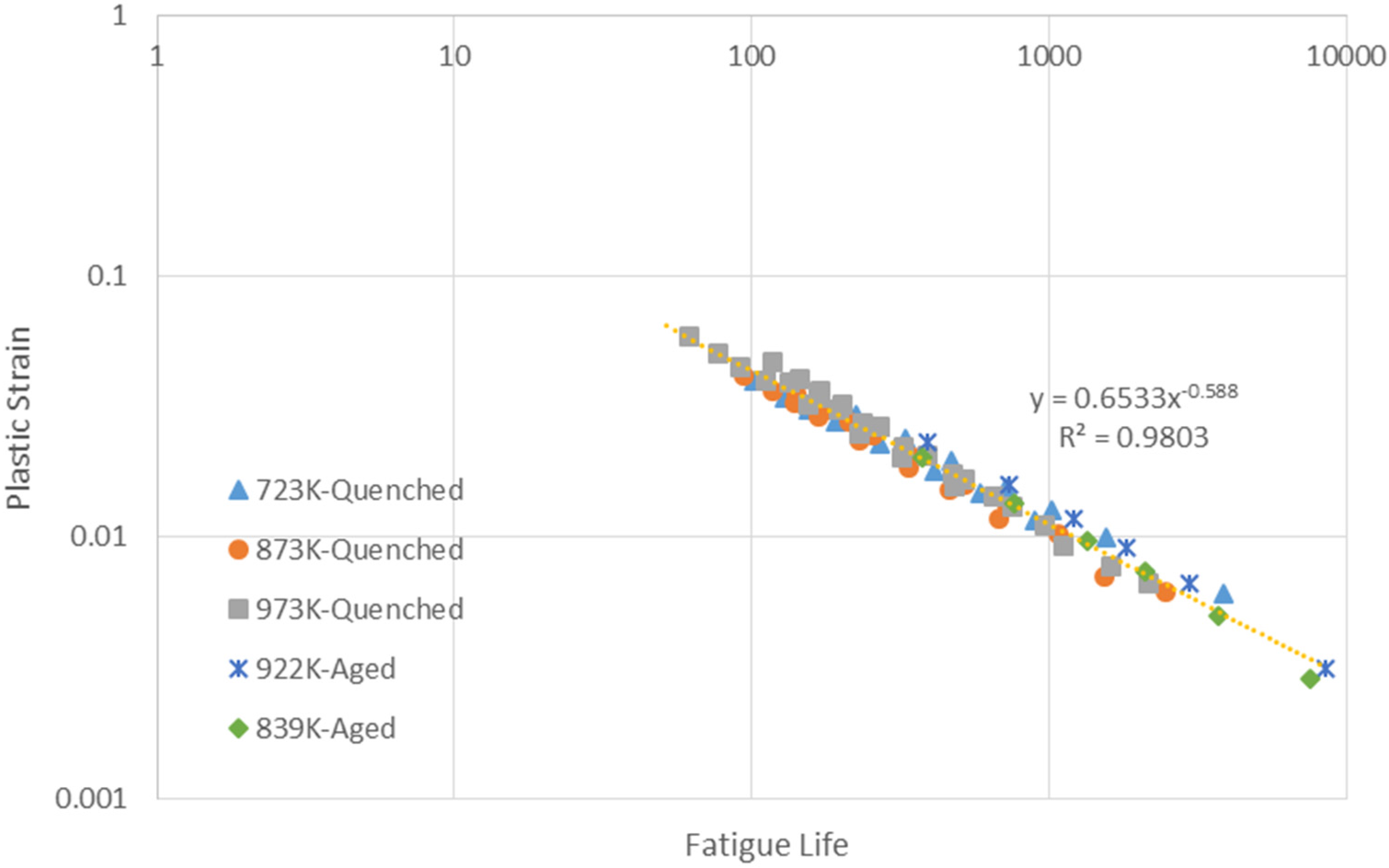
5.2. The Heat Treatment
5.3. Reliability
5.4. The Initial Proposal of Creep-Fatigue-Equation-Based Temperature Modified Coffin-Manson Equation
5.5. Application and Future Research
6. Conclusions
Author Contributions
Conflicts of Interest
Appendix A
A1. The Coefficients in the Strain-Form Unified Creep-Fatigue Equation
A2. The Coefficients in the Power-Law Unified Creep-Fatigue Equation
References
- Holmström, S.; Pohja, R.; Nurmela, A.; Moilanen, P.; Auerkari, P. Creep and creep-fatigue behaviour of 316 stainless steel. Procedia Eng. 2013, 55, 160–164. [Google Scholar] [CrossRef] [Green Version]
- Basquin, O. The Exponential Law of Endurance Tests. Am. Soc. Test. Mater. Proc. 1910, 10, 625–630. [Google Scholar]
- Coffin, L.F., Jr. A Study of the Effects of Cyclic Thermal Stresses on a Ductile Metal; Knolls Atomic Power Lab.: Niskayuna, NY, USA, 1953. [Google Scholar]
- Manson, S.S. Behavior of Materials under Conditions of Thermal Stress; National Advisory Committee for Aeronautics: Cleveland, OH, USA, 1954.
- Feltner, C.E.; Morrow, J.D. Microplastic strain hysteresis energy as a criterion for fatigue fracture. J. Basic Eng. 1961, 83, 15–22. [Google Scholar] [CrossRef]
- Morrow, J. Cyclic plastic strain energy and fatigue of metals. In Internal Friction, Damping, and Cyclic Plasticity; ASTM International: West Conshohocken, PA, USA, 1965. [Google Scholar]
- Dowling, N.E. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture, and Fatigue; Prentice Hall: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; National Advisory Committee for Aeronautics: Cleveland, OH, USA, 1943.
- Palmgren, A. Die lebensdauer von kugellagern. ZVDI 1924, 68, 339–341. [Google Scholar]
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. 1945, 12, 159–164. [Google Scholar]
- Chopra, O.K. Environmental Effects on Fatigue Crack Initiation in Piping and Pressure Vessel Steels; Argonne National Lab.: Argonne, IL, USA, 2000.
- Gosselin, S.R.; Deardorff, A.F.; Peltola, D.W. Fatigue assessments in operating nuclear power plants. In Changing Priorities of Codes and Standards: Failure, Fatigue, and Creep. Pvp-vol. 286; American Society of Mechanical Engineers: New York, NY, USA, 1994. [Google Scholar]
- Rodabaugh, E. Comparisons of Asme-Code Fatigue-Evaluation Methods for Nuclear Class 1 Piping with Class 2 or 3 Piping; Rodabaugh (EC) and Associates: Hilliard, OH, USA, 1983. [Google Scholar]
- Rudolph, J.; Heinz, B.; Jouan, B.; Bergholz, S. Areva Fatigue Concept—A Three Stage Approach to the Fatigue Assessment of Power Plant Components; INTECH Open Access Publisher: Rijeka, Croatia, 2012. [Google Scholar]
- Zhu, Y.; Li, X.; Wang, C.; Gao, R. A new creep-fatigue life model of lead-free solder joint. Microelectron. Reliab. 2015, 55, 1097–1100. [Google Scholar] [CrossRef]
- Richart, F.; Newmark, N. An Hypothesis for the Determination of Cumulative Damage in Fatigue; Selected Papers By Nathan M. Newmark@ sCivil Engineering Classics; ASCE: Reston, VA, USA, 1948; pp. 279–312. [Google Scholar]
- Manson, S. Interfaces between fatigue, creep, and fracture. Int. J. Fract. Mech. 1966, 2, 327–363. [Google Scholar] [CrossRef]
- Gosselin, S. Fatigue Crack Flaw Tolerance in Nuclear Power Plant Piping: A Basis for Improvements to ASME Code Section XI Appendix L; US Nuclear Regulatory Commission, Office of Nuclear Regulatory Research, Division of Fuel, Engineering and Radiological Research: Washington, DC, USA, 2007.
- Rudolph, J.; Bergholz, S.; Willuweit, A.; Vormwald, M.; Bauerbach, K. Methods of detailed thermal fatigue evaluation of nuclear power plant components. Mater. Werkst. 2011, 42, 1082–1092. [Google Scholar] [CrossRef]
- Ainsworth, R.; Ruggles, M.; Takahashi, Y. Flaw assessment procedure for high-temperature reactor components. J. Press. Vessel Technol. 1992, 114, 166–170. [Google Scholar] [CrossRef]
- Paris, P.; Erdogan, F. A critical analysis of crack propagation laws. J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Wong, E.; Mai, Y.-W. A unified equation for creep-fatigue. Int. J. Fatigue 2014, 68, 186–194. [Google Scholar] [CrossRef]
- Shi, X.; Pang, H.; Zhou, W.; Wang, Z. Low cycle fatigue analysis of temperature and frequency effects in eutectic solder alloy. Int. J. Fatigue 2000, 22, 217–228. [Google Scholar] [CrossRef]
- Wong, E.H.; Liu, D. The unified equations for creep-fatigue—Deriving creep function from creep-rupture parameters. Int. J. Fatigue submitted for publication. 2016. [Google Scholar]
- Kanazawa, K.; Yoshida, S. Effect of Temperature and Strain Rate on the High Temperature Low-Cycle Fatigue Behavior of Austenitic Stainless Steels. In Proceedings of the International Conference on Creep and Fatigue in Elevated Temperature Applications, Philadelphia, PA, USA, 23–27 September 1973; Institution of Mechanical Engineers: London, UK, 1975; Volume 1. [Google Scholar]
- High Temperature Characteristics of Stainless Steels. Available online: https://www.nickelinstitute.org/~/Media/Files/TechnicalLiterature/High_TemperatureCharacteristicsofStainlessSteel_9004_.pdf (accessed on 8 September 2016).
- Orr, R.L.; Sherby, O.D.; Dorn, J.E. Correlations of Rupture Data for Metals at Elevated Temperatures; DTIC Document: Fort Belvoir, VA, USA, 1953. [Google Scholar]
- Larson, F.R.; Miller, J. A Time-Temperature Relationship for Rupture and Creep Stresses; Trans ASME: New York, NY, USA, 1952; pp. 765–771. [Google Scholar]
- Manson, S.; Haferd, A. A Linear Time-Temperature Relation for Extrapolation of Creep and Stress Rupture Data; NaCA TN 2890; Lewis Flight Propulsion Laboratory Cleveland: Cleveland, OH, USA, 1953.
- Penny, R.K.; Mariott, D.L. Design for Creep; Chapman & Hall: London, UK, 1995. [Google Scholar]
- Engineering Virtual Organization for CyberDesign. 316 Stainless Steel. Available online: https://icme.hpc.msstate.edu/mediawiki/index.php/316_Stainless_Steel (accessed on 6 September 2016).
- Halford, G. Cyclic creep-rupture behavior of three high-temperature alloys. Metall. Trans. 1972, 3, 2247–2256. [Google Scholar] [CrossRef]
- Jaske, C.; Mindlin, H.; Perrin, J. Development of Elevated Temperature Fatigue Design Information for Type 316 Stainless Steel; Battelle Columbus Labs.: Columbus, OH, USA, 1975. [Google Scholar]
- Coffin, L., Jr. Predictive Parameters and Their Application to High Temperature, Low Cycle Fatigue; ICF2: Brighton, UK, 1969. [Google Scholar]
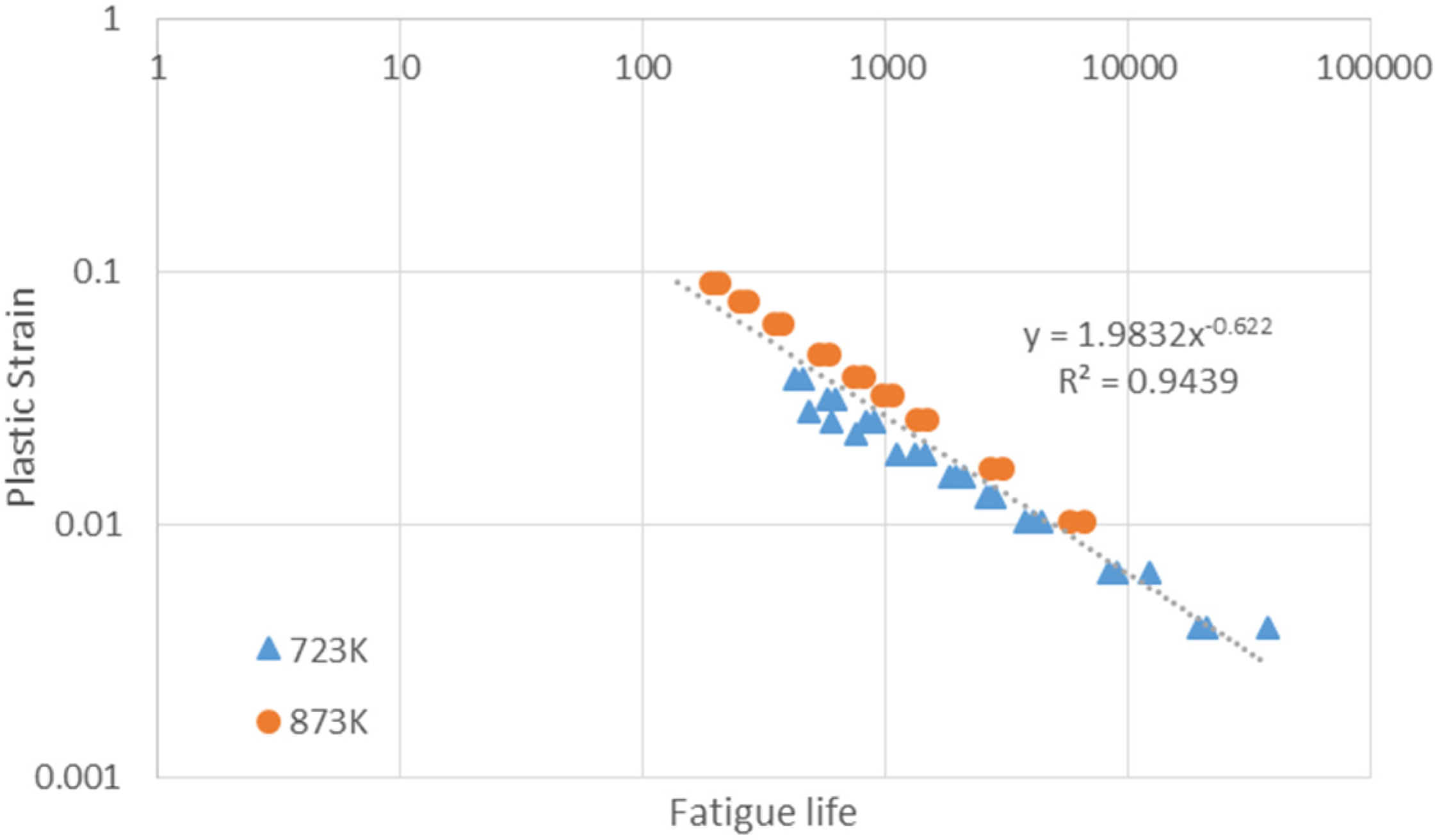
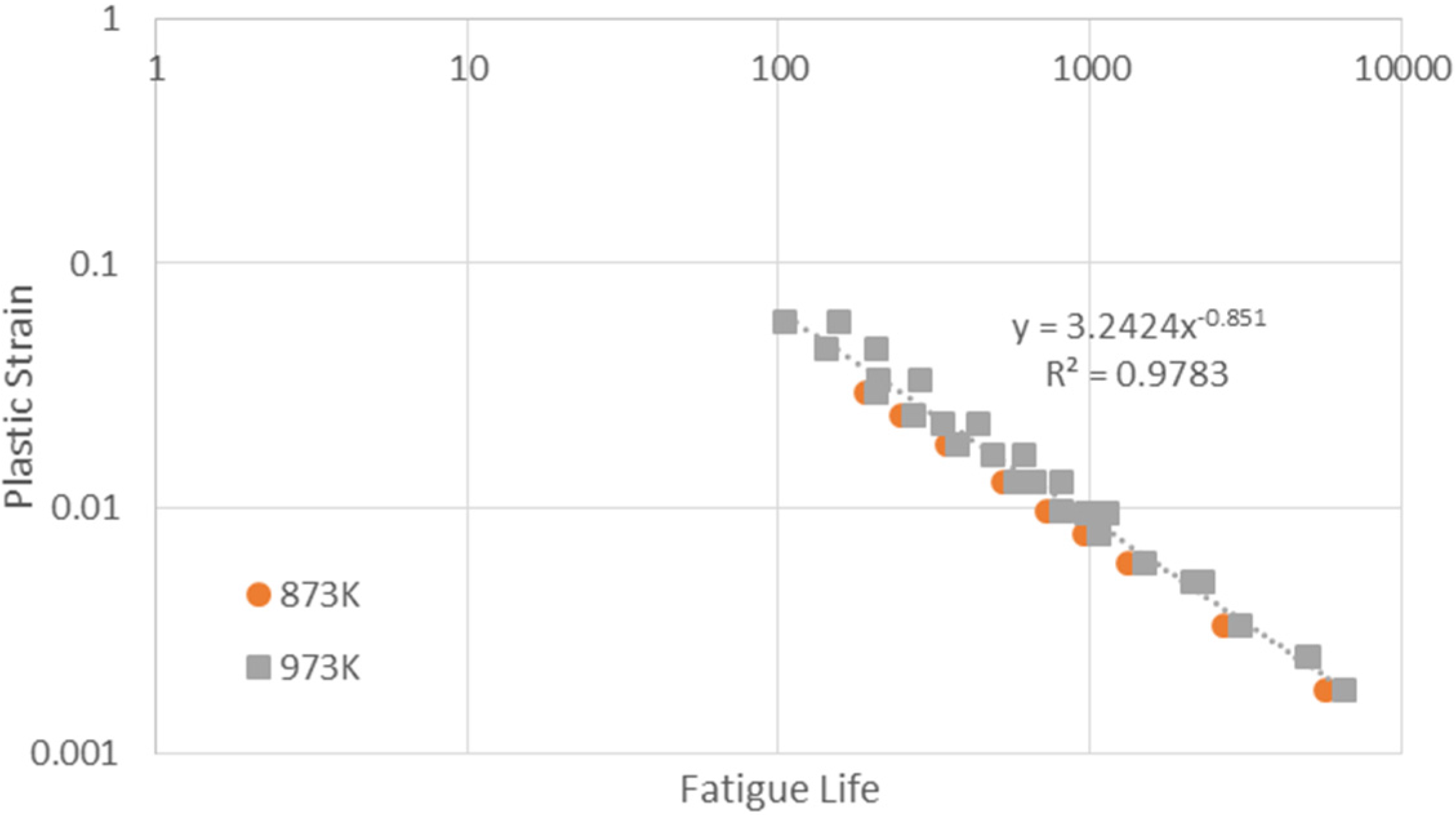
| Temperature Regimes | k | ||||
|---|---|---|---|---|---|
| 723 K–873 K | 1.997 | 0.002955 | 0.62375 | −0.000309 | 723 K: 0.728 873 K: 0.758 |
| 873 K–973 K | 2.452 | 0.002668 | 0.80713 | 0.00088 | 873 K: 0.758 973 K: 0.873 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Pons, D.J.; Wong, E.-h. The Unified Creep-Fatigue Equation for Stainless Steel 316. Metals 2016, 6, 219. https://doi.org/10.3390/met6090219
Liu D, Pons DJ, Wong E-h. The Unified Creep-Fatigue Equation for Stainless Steel 316. Metals. 2016; 6(9):219. https://doi.org/10.3390/met6090219
Chicago/Turabian StyleLiu, Dan, Dirk John Pons, and Ee-hua Wong. 2016. "The Unified Creep-Fatigue Equation for Stainless Steel 316" Metals 6, no. 9: 219. https://doi.org/10.3390/met6090219
APA StyleLiu, D., Pons, D. J., & Wong, E.-h. (2016). The Unified Creep-Fatigue Equation for Stainless Steel 316. Metals, 6(9), 219. https://doi.org/10.3390/met6090219







