Predicted Fracture Behavior of Shaft Steels with Improved Corrosion Resistance
Abstract
:1. Introduction
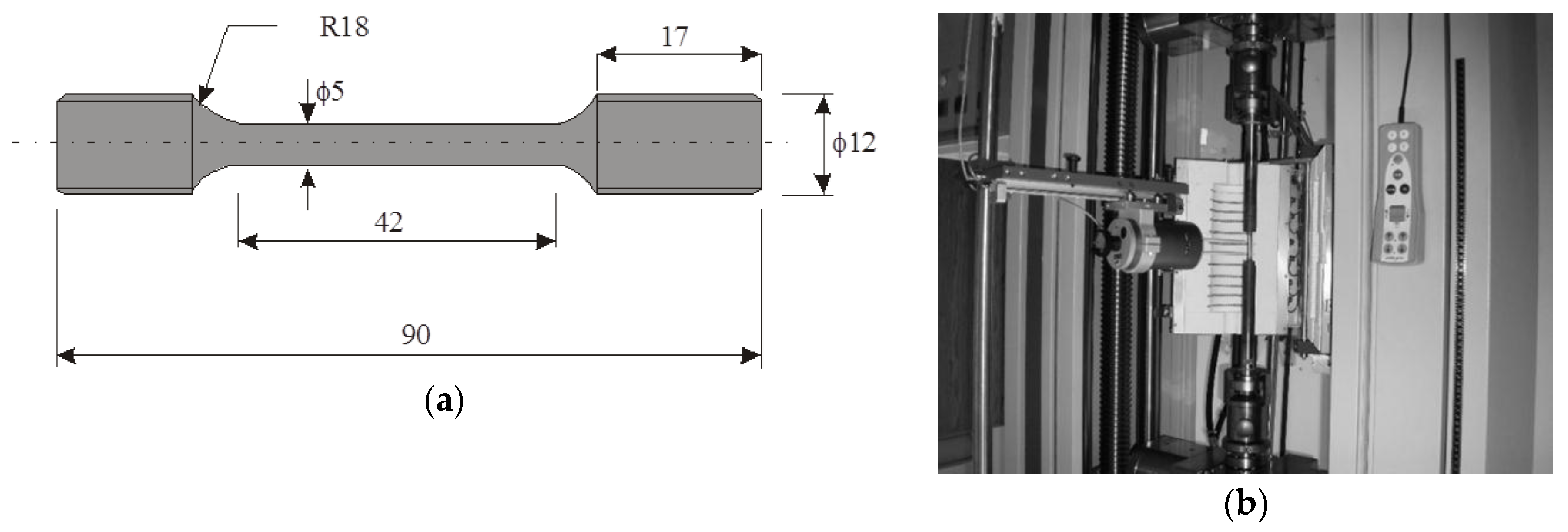
2. Materials and Methods
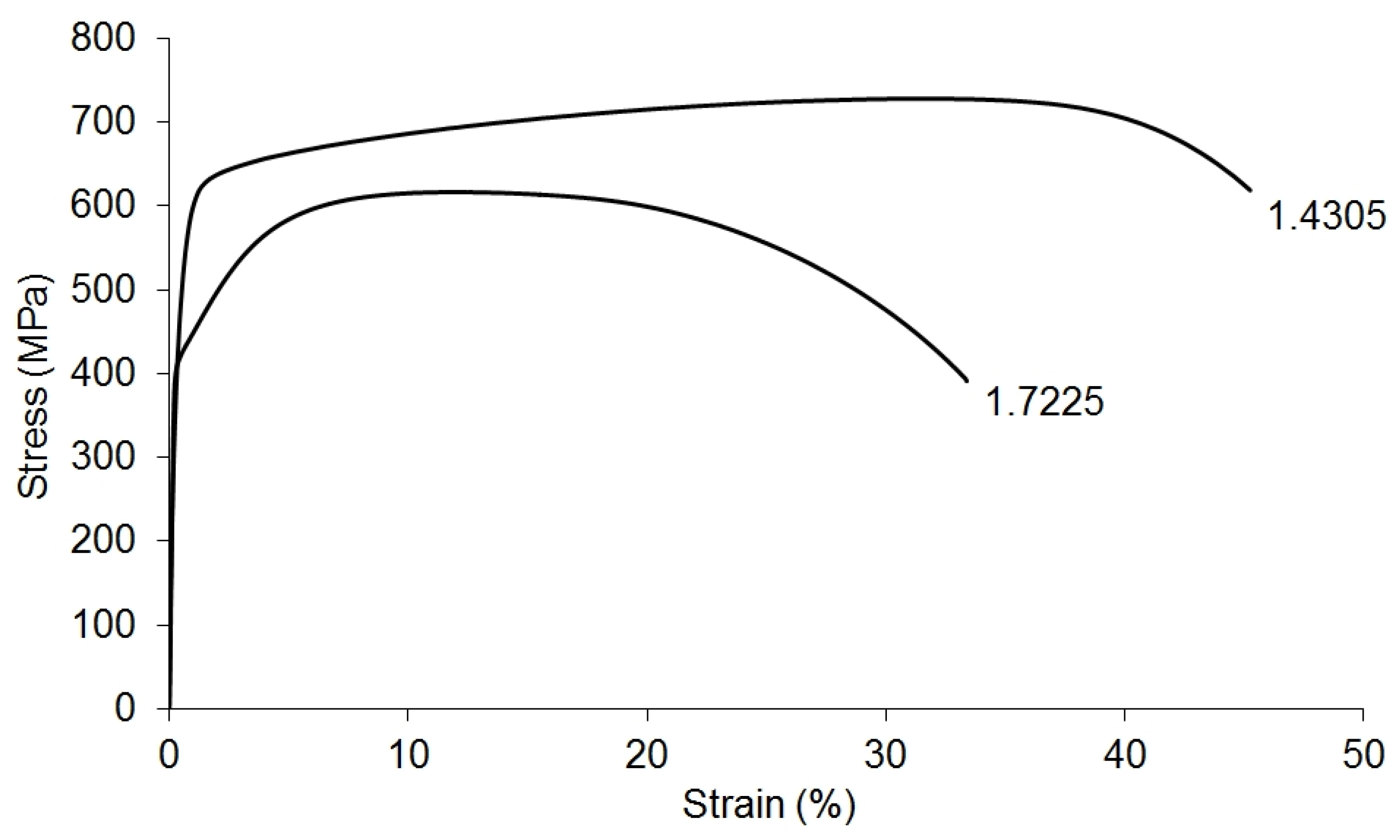
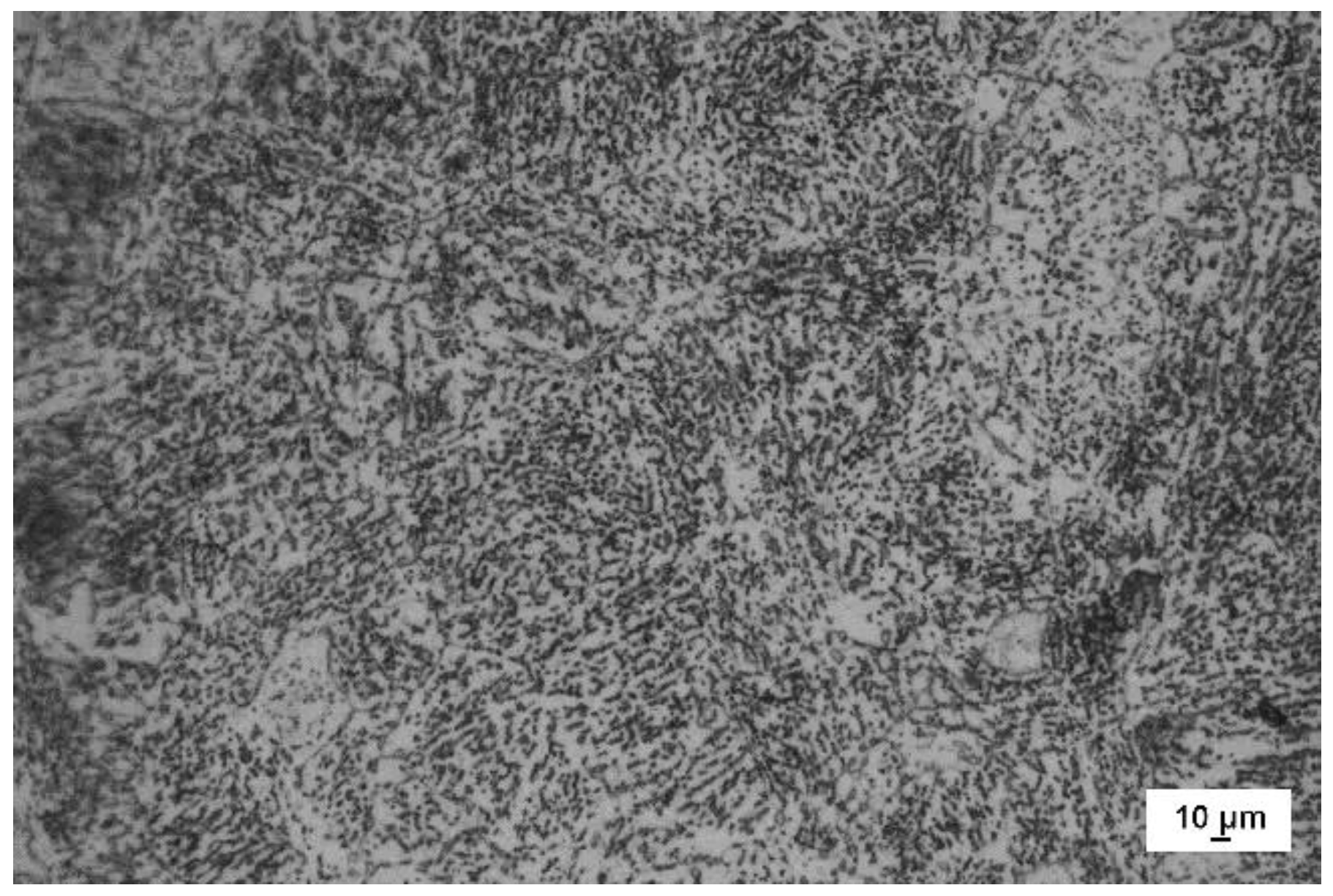
2.1. Considered Materials
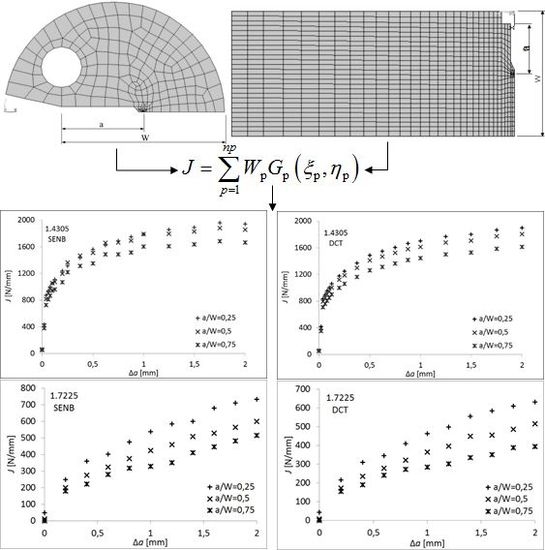
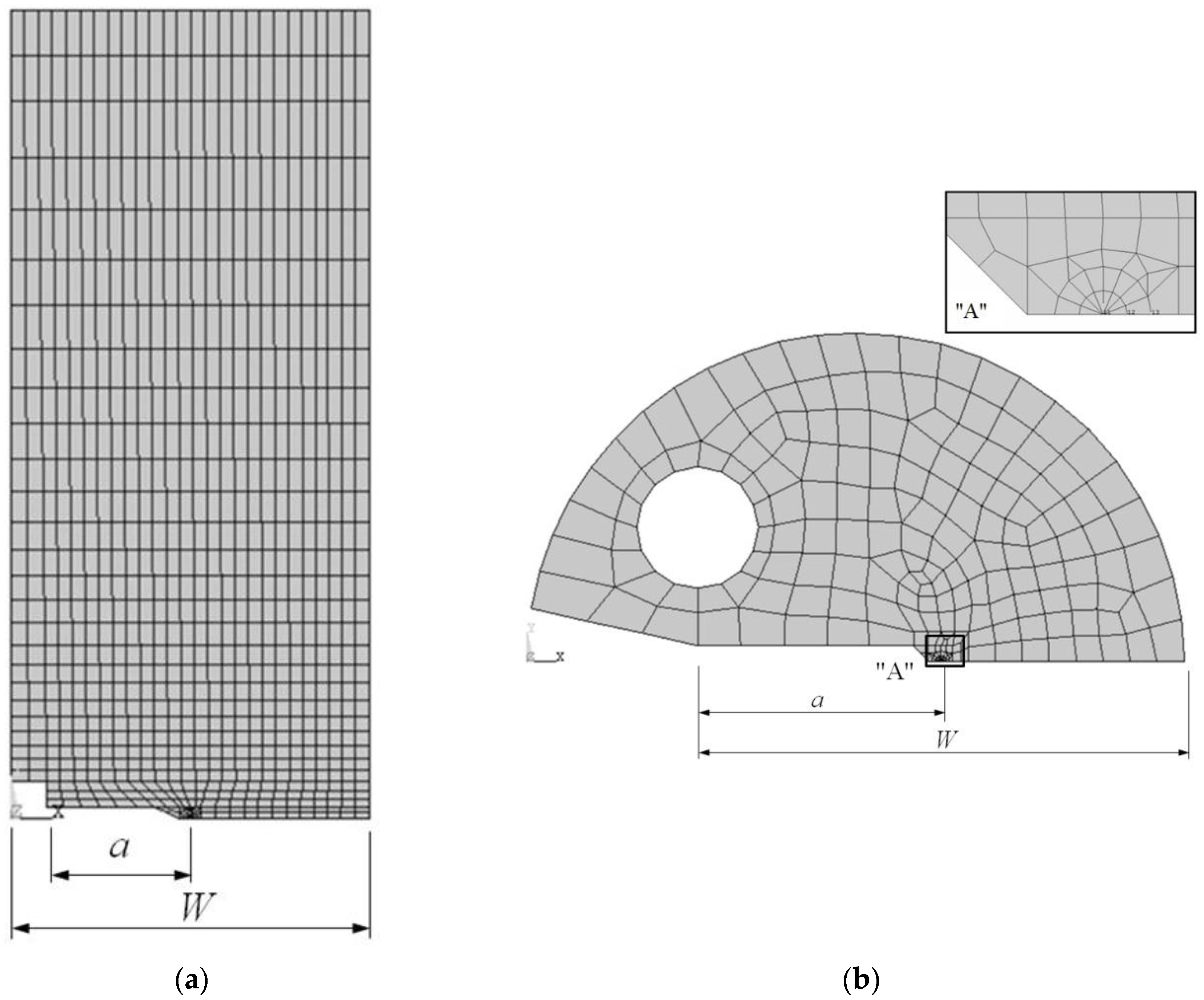
2.2. Predicted Fracture Behavior of Considered Materials
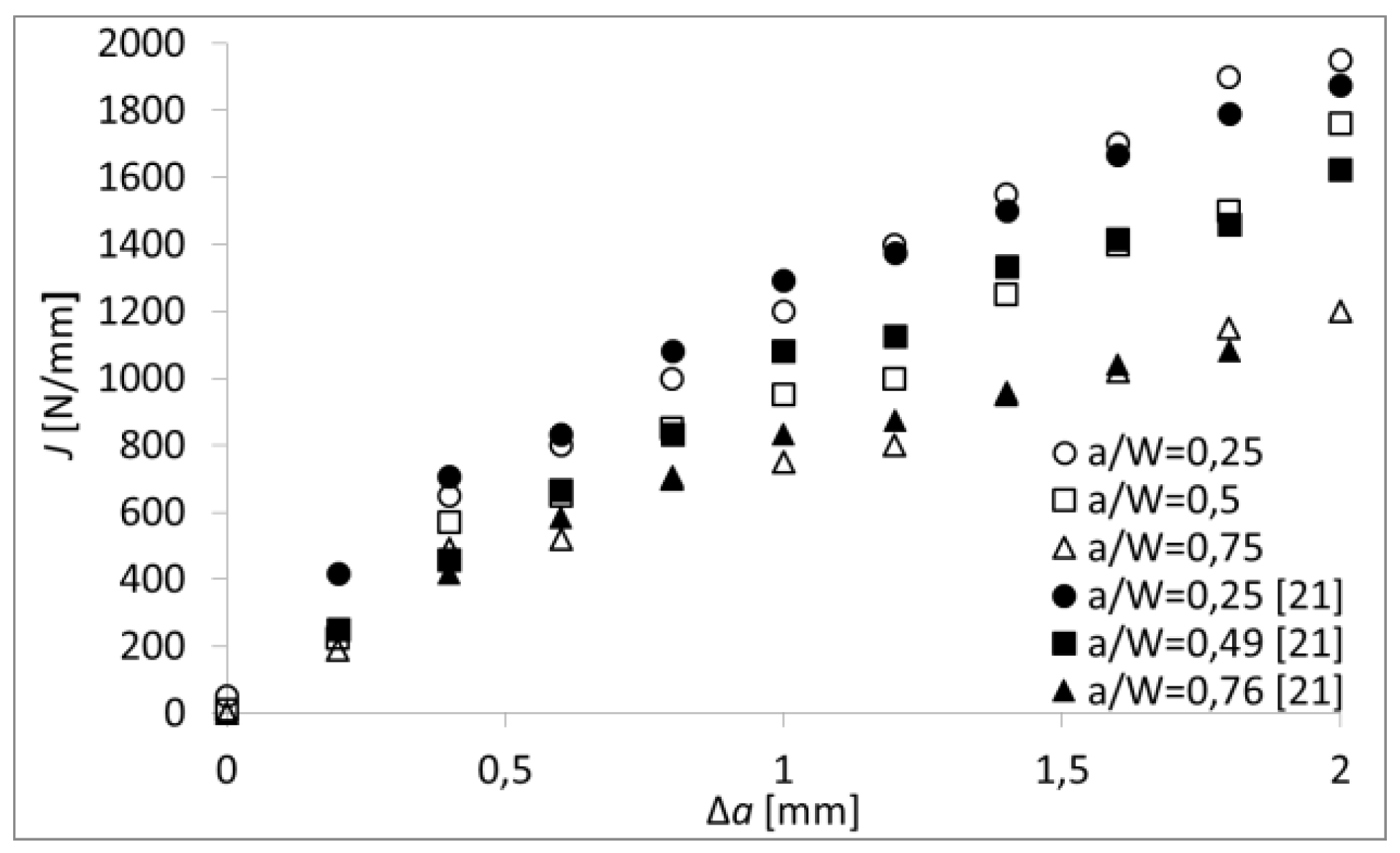
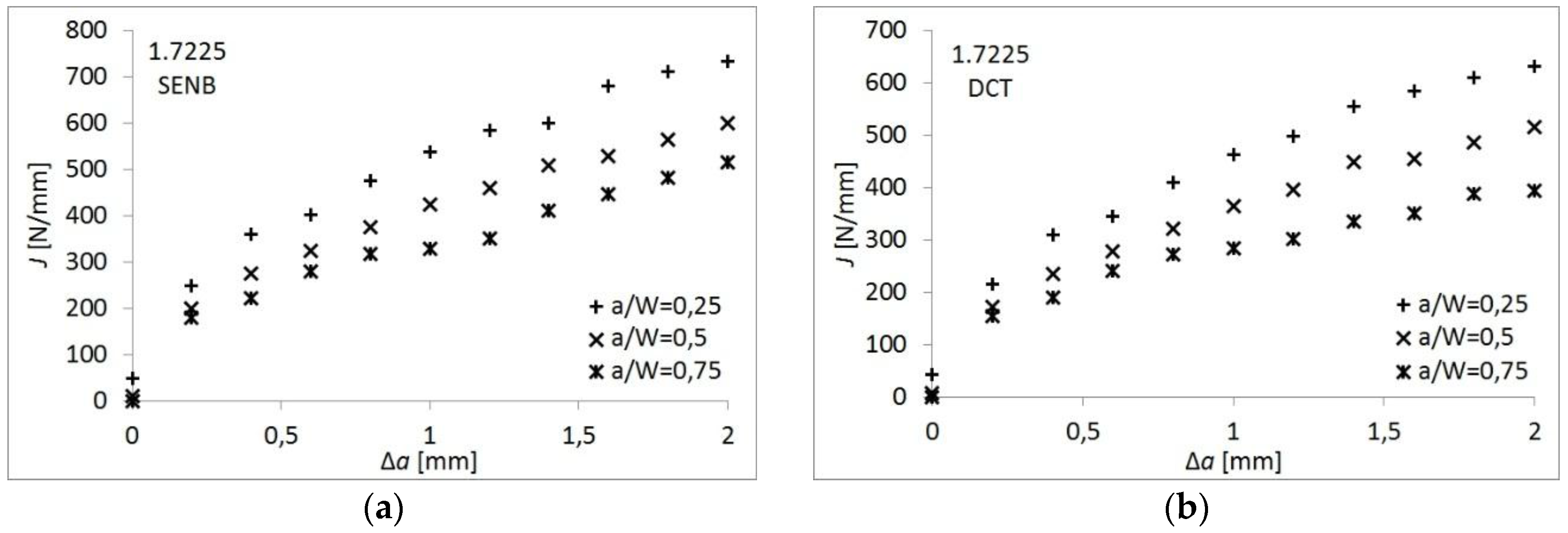
3. Results
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| FE | Finite Element |
| DCT | Disc Compact Tension |
| SENB | Single Edge Notched Bend |
| CVN | Charpy V-notch |
References
- Fonte, M.; de Freitas, M. Marine main engine crankshaft failure analysis: A case study. Eng. Fail. Anal. 2009, 16, 1940–1947. [Google Scholar] [CrossRef]
- Zangeneh, Sh.; Ketabchi, M.; Kalaki, A. Fracture failure analysis of AISI 304L stainless steel shaft. Eng. Fail. Anal. 2014, 36, 155–165. [Google Scholar] [CrossRef]
- Moolwan, C.; Netpu, S. Failure analysis of a two high gearbox shaft. Procedia Soc. Behav. Sci. 2013, 88, 154–163. [Google Scholar] [CrossRef]
- Das, S.; Mukhopadhyay, G.; Bhattacharyya, S. Failure analysis of axle shaft of a fork lift. Case Stud. Eng. Fail. Anal. 2015, 3, 46–51. [Google Scholar] [CrossRef]
- Kossakowski, P.G. Simulation of ductile fracture of S235JR steel using computational cells with microstructurally-based length scales. J. Theor. Appl. Mech. 2012, 50, 589–607. [Google Scholar]
- Dai, Q.; Zhou, C.; Peng, J.; He, X. Experiment, finite element analysis and EPRI solution for J-integral of commercially pure titanium. Rare Metal. Mat. Eng. 2014, 42, 257–263. [Google Scholar]
- Huang, Y.; Zhou, W. J-CTOD relationship for clamped SE(T) specimens based on three-dimensional finite element analyses. Eng. Fract. Mech. 2014, 131, 643–655. [Google Scholar] [CrossRef]
- Koshima, T.; Okada, H. Three-dimensional J-integral evaluation for finite strain elastic-plastic solid using the quadratic tetrahedral finite element and automatic meshing methodology. Eng. Fract. Mech. 2015, 135, 34–63. [Google Scholar] [CrossRef]
- Saputra, A.A.; Birk, C.; Song, C. Computation of three-dimensional fracture parameters at interface cracks and notches by the scaled boundary finite element method. Eng. Fract. Mech. 2015, 148, 213–242. [Google Scholar] [CrossRef]
- Zambrano, O.A.; Coronado, J.J.; Rodríguez, S.A. Failure analysis of a bridge crane shaft. Case Stud. Eng. Fail. Anal. 2014, 2, 25–32. [Google Scholar] [CrossRef]
- Fonte, M.; Duarte, P.; Anes, V.; Freitas, M.; Reis, L. On the assessment of fatigue life of marine diesel engine crankshafts. Eng. Fail. Anal. 2015, 56, 51–57. [Google Scholar] [CrossRef]
- Tawancy, H.M.; Al-Hadhrami, L.M. Failure of a rear axle shaft of an automobile due to improper heat treatment. J. Fail. Anal. Prev. 2013, 13, 353–358. [Google Scholar] [CrossRef]
- Bai, S.Z.; Hu, Y.P.; Zhang, H.L.; Zhou, S.W.; Jia, Y.J.; Li, G.X. Failure analysis of commercial vehicle crankshaft: A case study. Appl. Mech. Mater. 2012, 192, 78–82. [Google Scholar] [CrossRef]
- Fuller, R.W.; Ehrgott, J.Q., Jr.; Heard, W.F.; Robert, S.D.; Stinson, R.D.; Solanki, K.; Horstemeyer, M.F. Failure analysis of AISI 304 stainless steel shaft. Eng. Fail. Anal. 2008, 15, 835–846. [Google Scholar] [CrossRef]
- American Society for Testing and Materials (ASTM International). Metals Test Methods and Analytical Procedures; Annual BOOK of ASTM Standards; ASTM International: Baltimore, Maryland, MD, USA, 2005; Volume 03.01. [Google Scholar]
- Brnic, J.; Turkalj, G.; Canadija, M.; Lanc, D.; Krscanski, S. Responses of austenitic stainless steel American iron and steel institute (AISI) 303 (1.4305) subjected to different environmental conditions. J. Test. Eval. 2012, 40, 319–328. [Google Scholar] [CrossRef]
- Brnic, J.; Turkalj, G.; Canadija, M.; Lanc, D.; Brcic, M. Study of the effects of high temperatures on the engineering properties of steel 42CrMo4. High Temp. Mater. Proc. 2015, 34, 27–34. [Google Scholar] [CrossRef]
- Roberts, R.; Newton, C. Interpretive Report on Small Scale Test Correlations with KIc Data; Welding Research Council Bulletin: New York, NY, USA, 1981; pp. 1–16. [Google Scholar]
- Rice, J.R. A path independent integral and the approximate analysis of strain concentration by notches and cracks. J. Appl. Mech. 1968, 35, 379–386. [Google Scholar] [CrossRef]
- Cherepanov, G.P. The propagation of cracks in a continuous medium. J. Appl. Math. Mech. 1967, 31, 503–512. [Google Scholar] [CrossRef]
- Mohammadi, S. Extended finite element method; Blackwell Publishing: Singapore, 2008; pp. 56–58. [Google Scholar]
- Vukelic, G.; Brnic, J. Prediction of fracture behavior of 20MnCr5 and S275JR steel based on numerical crack driving force assessment. J. Mater. Civ. Eng. 2015, 27, 14132–14132(6). [Google Scholar] [CrossRef]
- Narasaiah, N.; Tarafder, S.; Sivaprasad, S. Effect of crack depth on fracture toughness of 20MnMoNi55 pressure vessel steel. Mater. Sci. Eng. A 2010, 527, 2408–2411. [Google Scholar] [CrossRef]

| Material | C | Cr | Mn | Si | Mo | S | P |
|---|---|---|---|---|---|---|---|
| 1.4305 | 0.047 | 17.4 | 2.0 | 0.584 | − | 0.252 | 0.0323 |
| 1.7225 | 0.45 | 1.06 | 0.74 | 0.32 | 0.17 | 0.018 | 0.014 |
| Material | Ni | Al | V | Nb | W | Cu | Rest |
| 1.4305 | 7.95 | − | − | − | − | − | 71.734 |
| 1.7225 | 0.04 | 0.02 | 0.01 | 0.02 | 0.02 | 0.04 | 97.078 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vukelic, G.; Brnic, J. Predicted Fracture Behavior of Shaft Steels with Improved Corrosion Resistance. Metals 2016, 6, 40. https://doi.org/10.3390/met6020040
Vukelic G, Brnic J. Predicted Fracture Behavior of Shaft Steels with Improved Corrosion Resistance. Metals. 2016; 6(2):40. https://doi.org/10.3390/met6020040
Chicago/Turabian StyleVukelic, Goran, and Josip Brnic. 2016. "Predicted Fracture Behavior of Shaft Steels with Improved Corrosion Resistance" Metals 6, no. 2: 40. https://doi.org/10.3390/met6020040
APA StyleVukelic, G., & Brnic, J. (2016). Predicted Fracture Behavior of Shaft Steels with Improved Corrosion Resistance. Metals, 6(2), 40. https://doi.org/10.3390/met6020040





.JPG)