Abstract
Using the advanced acoustic emission (AE) technique, we address the problem of early identification of crack initiation and growth in ductile structural steels under cyclic loading. The notched 9MnSi5 steel specimens with weld joints were fatigue tested at room and lower temperatures with concurrent AE measurements. Detection of AE in ductile materials where fatigue crack initiation and propagation is mediated by local dislocation behavior ahead of the notch or crack tip is challenging because of an extremely low amplitude of the AE signal. With account of this issue, two new practically oriented criteria for recognition of different stages of fatigue are proposed on the basis of AE data: (1) a power spectrum-based criterion and (2) a pattern recognition-based criterion utilizing modern clustering algorithms. The applicability of both criteria is verified using obtained AE data. A good correspondence between AE outcomes and experimental observations of the fatigue behavior was obtained and is discussed.
1. Introduction
The critical state of a cyclically loaded material is often associated with accumulated cracks. Although integrity remains, the catastrophic growth of a main crack is expected with further loading. This state characterizes the material that has accumulated a large number of microcracks tending to merge with high probability, thus forming a main crack. Being a root cause of catastrophic failure, the main crack has a critical length and critical stress intensity ahead of its tip. According to fracture mechanics, such a crack is unstable and can grow spontaneously to final failure. This scenario of gradual damage accumulation followed by a rapid main crack propagation to fracture is common for many structural steels and industrial facilities such as pressure vessels, pipelines, and tanks operating under cyclic load, vibration, or both.
Crack nucleation and growth generate elastic stress waves are commonly referred to as acoustic emission (AE). The amplitude of AE transients depends primarily and explicitly on the crack growth rate and the crack orientation relative to the AE transducer, and more implicitly on the stress intensity ahead of the crack tip during loading and the microstructure that controls the local plasticity of the material around the crack [1,2,3]. The AE technique has therefore emerged as a powerful means for the early non-destructive detecting and monitoring of crack initiation and growth under cyclic loading [1,2]. This technique is unique in that it has an excellent temporal and spatial resolution of dynamically evolving defects in solids in real time. For that reason, AE has found many applications in industrial non-destructive testing (NDT) in the past several decades. Practical applications of the AE technique are subject to regulations and standards [4,5,6]. Weldable ductile low alloy steels are the most common structural materials, used in a wealth of industrial equipment. However, the AE sources caused by crack growth in ductile steels are associated with plastic processes ahead of the crack tip and are featured by their particularly low amplitude AE response [7]. In fact, the AE peak amplitude is often comparable or lower than the background noise level. This substantially complicates the use of standard criteria, which have been developed for the threshold AE hit detection schemes [4]. The latter apparently do not work when the AE amplitude is low. Therefore, in such cases the conventional AE approaches towards AE source discrimination during industrial equipment testing and monitoring fail to detect early stages of fracture in ductile steels. This fact has prompted many researchers to development of advanced data mining methodologies such as unsupervised pattern recognition and signal clustering for the classification of AE data. The present work is aimed at extending efforts in this direction and developing robust AE criteria specifically suitable for the effective identification of the transition of ductile structural steels to the critical condition corresponding to approaching failure under fatigue loading.
2. Materials and Methods
The most widely used application of AE non-destructive testing nowadays might be to find the active defects in the pressure vessel equipment [4,5,6,8], which is biaxially loaded by cyclically changing internal operating pressure. A ductile low-alloy ferritic-martensitic steel grade 9MnSi5 is among the most widely used structural steels in the pressure vessel design. As virtually all industrial facilities are assembled by welding, the heat-affected zone (HAZ) of welded joints represent the weakest link in such structures. Therefore, the weld joints made in the steel grade 9MnSi5 are the focus of the present study. Flat I-shaped specimens where machined from the strips with double-sided through weld joints extended in the transverse direction edge-to-edge according to the standard arc welding procedures [9]. This type of weld joint is admittedly the most common in shell structures used for vessel equipment in the chemical, petrochemical, and refining industries.
Fatigue tests were carried out using the servo hydraulic machine Instron 8802™ (Instron®, High Wycombe, UK) under uniaxial tension-tension loading in accordance with guidance provided in [10]. Sine-wave signal was used to control the tensile load at constant frequency of 10 Hz in the range of 1800–18,000 N. The cyclic load tests were carried out at room (296 K) and low (233 K) temperature. Loading at lower temperature was carried out in a thermal chamber cooled by liquid nitrogen vapor. The temperature during preparation and testing was kept constant using the feedback from a thermocouple sensor mounted directly on the sample.
The V-shaped notches were introduced near the HAZ to promote crack nucleation in the area of interest. The notches with a tip radius of 0.16 mm were cut by an electro-erosion wire cutter AG400L™ (Sodick®, Yokohama, Japan), ensuring a high positioning accuracy and reproducibility. The total length of the specimen was 200 mm with a gauge length of 40 mm. The most stressed area at the section between the stress concentrators, Figure 1a, was set at 6 × 8 mm2.

Figure 1.
A view of the specimen. (a) A magnified image showing the weld joint and the notch shape. (b) Specimens mounted in the grips of the testing machine at 296 K (left) and 233 K inside the thermal chamber (right).
AE was recorded at a sampling rate of 2 MSPS in two modes simultaneously: (1) via conventional threshold amplitude hit detection and (2) with a continuous streaming signal in the threshold-less mode of operation by the PCI-2™ acquisition board (Physical Acoustics Corporation, Princeton, NJ, USA). A wideband piezoelectric transducer MSAE-1300WBTM (Microsensors AE®, Sarov, Russia) was clamped to the specimen surface as shown in Figure 1. Total gain was set at +60 dB using a low noise amplifier MSAE-FA010™ (Microsensors AE®, Sarov, Russia) with a programmable bandpass analog filter 150–1000 kHz. Further processing of the AE data was performed using original algorithms implemented in a Python programming environment.
3. Results
As expected, all specimens fractured in the specified sections narrowed by stress concentrators at the HAZ of the welding joint (Figure 2).

Figure 2.
Specimens after failure (a); optical micrographs showing the fracture morphology of specimens at HAZ at temperature 296 K (b) and 233 K (c).
Fracture surface morphology of the samples after fatigue testing at room and lower temperature is shown in Figure 2b,c, respectively. For both temperatures, the fracture surfaces appear to be ductile with a well-developed relief and typical dimple structure. The photographs clearly show that cracks nucleated at the stress concentrators and propagated into the sample until rapture, which started in the middle part of the specimen under action of normal stresses. The fracture topology of the samples tested at 233 K is less developed than that obtained at room temperature, reflecting less ductility and more brittle fracture with temperature reduction. However, the fracture surface shows no cleavage-like signs of an abrupt brittle growth of fatigue cracks. This attests to the predominance of the ductile fracture mechanism assuming the nucleation, growth, and coalescence of micro-voids or cracks in the plastically deformed zone ahead of the crack, both at room and at low temperatures. These findings agree with the low brittle-to-ductile transition temperature for this steel, which is known to be below 223 K as determined from the V-notch Charpy testing [11]. This means that, even at 233 K, the 9MnSi5 steel is on the upper shelf of toughness. For this reason, the trend in the AE behavior, which is represented in Figure 3 and Figure 4, is commonly seen during fatigue tests at either 296 K or 233 K. For clarity, the figures show the randomly chosen AE frames recorded within two successive cycles at different times during the long-term testing at room temperature. Although in what follows the results will be illustrated and discussed for the tests performed at 296 K, they extend to lower temperatures without any restrictions or corrections. Analysis of the bulk of experimental data revealed the following features:
- (1)
- The crack nucleates within the first 15 ± 10 loading cycles at stress concentrators. The average number of cycles to failure was 20,900 at 296 K and 26,900 at 233 K, i.e., as desired, the tests correspond to low-cycle fatigue conditions whereby by the fatigue life is controlled by material’s tolerance to fatigue crack propagation [12]. The increase in fatigue life (by a factor of 1.3) at low temperature agrees with results reported in [12,13] and supports our suggestion that fatigue fracture is ductile in all cases investigated and is mediated by plastic deformation, which is impeded to some extent by low temperature.
- (2)
- AE does not reveal any periodicity in appearance of transient signals associated with brittle fracture due to fatigue crack advance. The latter occurs typically at the maximum cyclic load [1,2]. The AE stream is formed by continuous-like signals, thus making it impossible to use any traditional hit detection approach based on an amplitude threshold. For example, Figure 3 shows what would be recorded if the amplitude threshold was set as indicated by a red line. Obviously, the result of such a detection would not represent the real picture of damage development in terms of either the number of hits detected or their amplitude distribution. Therefore, the high ambiguity of the AE output obtained with the threshold-based detection prevents conclusive decisions regarding the fracture process and the damage state of the material.
- (3)
- The AE behavior changes synchronously with the loading cycle. It was systematically observed in all tests that the shape of the AE peak changes with the number of cycles as the critical state approaches. Specifically, a wide AE peak, which is commonly observed at on the early stages of cyclic deformation cycle, splits up into two sharper peaks with fatigue crack advance. This pattern becomes increasingly clearly visible as final rupture approaches, differentiating AE signals corresponding to early and late stages of fatigue crack propagation. Compared with signal classification methods based on single features detected via threshold-based acquisition, pattern recognition techniques are computationally intense. However, they are significantly more adequate for processes investigated and, fortunately, can now be implemented in a variety of efficient and elegant mathematical ways [14].
- (4)
- The most important finding, which was observed in all tests at both temperatures, is that, as final rupture approached, the AE energy per cycle increased, while the spectral density function progressively shifted to the low-frequency domain, as reflected in the median frequency reduction. The similar behavior in the AE power spectral density has been reported earlier in [15,16] for cyclically and monotonically tested metals when strain localization occurred prior to fracture. Thus, the drop in AE median frequency, which reflects the increasing memory of the past and increasing correlation in the ensemble of emitting AE sources, appears to be a stable indicator and a reliable harbinger of the approaching critical state and failure of a material under load.
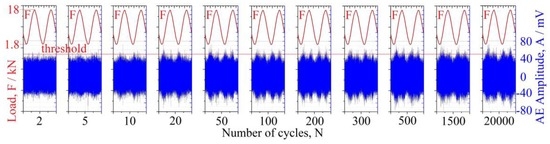
Figure 3.
Trend in the AE behavior during fatigue tests at room temperature. Duration of each loading cyclic equals to 0.1 s.
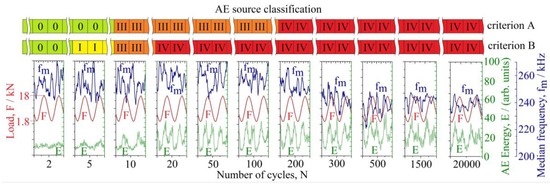
Figure 4.
A diagram showing typical changes in the AE spectral parameters—energy and median frequency fm—with increasing number of cycles (these are typical for either room or lower temperature); the color-coded bars above the AE diagrams illustrate the procedures assigning the estimated rank of danger based on AE criteria proposed.
Low amplitude AE indicates a very small crack length increment during the single loading cycle. Nevertheless, the results are promising, showing a possibility to detect developing cracks long before catastrophic failure. On the one hand, this confirms the general applicability of the AE method for damage monitoring in materials under cyclic loading. On the other, it shows that the traditional approaches cease to generate reliable results, and a new methodology for ductile crack monitoring has yet to be developed. In what follows, we endeavor to propose a variant of such methodology.
4. AE Data Analysis
Two AE-based criteria for evaluating material damages and assessing the state of the welded structural steel under cyclic load were developed based on experimental data: a “frequency-energy” criterion and an “energy-cluster” criterion, as discussed in the following sub-sections. Both criteria rely on integral AE parameters measured per each load cycle. These parameters include the total energy of the AE signal, the median frequency of the power spectral density function, and the experimental time function of AE energy.
The RAW streaming signal was used to calculate the AE parameters. The continuously streamed data were sectioned into consecutive individual realizations (termed “frames”) of 4096 samples without overlapping. A Fourier power spectral density (PSD) function G(f) was calculated from these data using a Welch procedure. The average AE power (which is also often loosely termed “Energy”) per each frame was calculated from the corresponding PSD, Equation (1), and the median frequency fm of the PSD function was introduced in terms of the implicit equation, Equation (2):
The sequence of Pi constitutes the time series representing the temporal behavior of the AE power P(t) which exhibits a strong correlation with load cycles. To estimate the total AE energy per cycle, the resulting curve P(t) was synchronized with loading data. Denoting the time when each cycle starts and ends as t1 and t2, respectively, the total energy AE for each loading cycle can be calculated as the area under the P(t) curve in the interval between t1 and t2:
The shape of the P(t) curve exhibits notable variations when cyclic deformation proceeds as one can see with the naked eye in Figure 4. Therefore, it is essential to assesses whether a significant difference exists between P(t) curves at different stages of fatigue. We employed a cluster analysis as a mathematical tool designed for statistical categorization of similar and dissimilar objects. Each P(t) curve was normalized to the total energy per cycle EC as
Apparently, the normalized Ẽ(t) dimensionless function obeys the condition and is thus independent of the energy value. These functions are used as input for the recently proposed adaptive sequential k-means clustering (ASK) algorithm [14]. In the standard k-means procedure, each cluster is represented by a set of variables with the middle point of the cluster-centroid. The inter-cluster distance between the centroids is a measure of the difference between the clusters. The k-means clustering algorithm aims at partitioning the dataset S into k disjoint clusters so as to minimize a sum of intra-cluster distances D (in the standard procedure, they are taken in the Euclidian form) between the data point xi and the centroid of the cluster cj [17].
where Sj is the input data matrix (xiєSj), j = 1,2,3, …, k; i = 1,2,3, …, N; D = ‖•‖2 is the measure of the distance between data xiєSj and centroid cj.
As has been suggested in [14] and then probed in several studies on different materials [18,19,20], satisfactory results of clustering are obtained if the if the Kullback–Leibler divergence (KL) in its symmetric version is used as the distance measure ‖•‖2 as
The ASK algorithm applied to a set of Ẽ(t) functions obtained during fatigue test of the welded steel specimens under investigation classifies them into three major groups according to statistically measurable differences in shapes of Ẽ(t). It should be noted that, in the ASK procedure, the number of clusters to be derived is not fixed a priori but rather is data driven. This makes the present analysis advantageous, for instance, in comparison with popular conventional k-means or c-means schemes. When the minimization of Equation (5) is achieved, each Ẽ(t) is assigned to a certain cluster so that all Ẽ(t) belonging to the same cluster are supposed to be similar and vice versa—all Ẽ(t) belonging to the different clusters are supposed to be statistically dissimilar, reflecting different states of the underlying source mechanisms. Based on observations of different stages of fatigue, the three obtained clusters are identified as follows.
Cluster c1 corresponds to the regular AE pattern when the material is deformed cyclically without cracks on the initial stage. The AE energy curve is characterized by a single wide peak within each loading cycle.
Cluster c2 corresponds to the loading stage when the fatigue crack has nucleated but has not reached the critical size yet. The AE energy curves exhibit the second low-level peak during this stage.
Cluster c3 corresponds to the stage when the fatigue crack is close to the critical state and the material is close to failure. The AE energy curve shows the second peak with the level comparable to the level of the first peak.
The obtained AE energy data and spectral density functions serve as input parameters for estimation algorithms, which identify the AE sources and assign them a certain hazard class label based on pre-determined acceptance criteria. According to existing common NDT practice, the proposed evaluation criteria divide AE sources into four classes depending on the “activity” of the source [4,21]:
- -
- I class [4] (A and B [21]) corresponds to a passive AE source. This kind of source does not assume immediate danger, but its behavior should be monitored for possible increases in activity.
- -
- II class (C) corresponds to an active AE source. This is a source that should be monitored continuously and inspected by alternative NDT methods.
- -
- III class (D) corresponds to a critical AE source. This kind of source is placed under continuous surveillance with the use of an arsenal of NDT methods available.
- -
- IV class (E) corresponds to a catastrophically active AE source. An operator is directed to stop operating the equipment immediately and exercise safety measures after detecting this kind of source.
The most obvious limitations of these criteria is that the definition of “activity” is loose and is merely subjective since it is based on limited information provided by a single feature (or few extractable features) of the AE hit detected, i.e., this approach does consider an actual AE pattern. With these limitations, these criteria cannot be translated without caveats to the detection of ductile fatigue cracks considered above. In an attempt to get rid of these obvious limitations, we propose two new criteria as described in the following section.
4.1. Criterion A: Frequency-Energy
Criterion A is based on the experimental observations showing the trend to increase the total AE energy per cycle in parallel with decreasing median frequency when the material under load approached fracture, i.e., when it was in a critical state.
Two parameters kE and kf are introduced as
which reflect the relative difference of the energy (7) and median frequency (8), respectively, between the first N cycles (En0 and fm0) and N pre-defined cycles followed the fatigue cycle number n (En and fmn). It is tacitly assumed that the material does not contain the propagating defects at the beginning of loading. Depending on the trends in the behavior of the energy and median frequency in the cyclic history, several combinations of kE and kf can be distinguished, and the hazard class can be assigned to the source accordingly:
- (a)
- (kE = 1, kf = 1). This combination indicates that no changes occur in the behavior of E and fm, i.e., both parameters remain at their initial levels corresponding to the incubation fatigue stage preceding crack initiation. Thus, the hazard class I is not assigned, and the source class is labeled as “0”;
- (b)
- (kE = 1, kf > 1). This combination indicates the increase in the median frequency while the energy remains unchanged, which is observed at the stage of crack nucleation. This behavior is associated with the active AE source II;
- (c)
- (kE = 1, kf < 1). This combination represents the steady energy behavior, but the decreasing median frequency, which is commonly observed during the ductile fatigue crack growth stage featured by low values of energy increments. It can be associated with the critical active AE source IV;
- (d)
- (kE > 1, kf = 1). This combination arises when the AE energy increases while the median frequency remains constant. This pattern was also observed during the crack growth stage; therefore, it was labeled as the critically active AE source III;
- (e)
- (kE > 1, kf > 1). This combination represents the case when both the energy and median frequency increase. It is observed during the initial crack growth stage; therefore, the AE source belongs the class of critically active sources III;
- (f)
- (kE > 1, kf < 1).This combination reflects the increasing AE energy and concurrently falling median frequency. It is observed before rupture; therefore, it is classified as the catastrophically active AE source IV;
- (g)
- The combinations (kE < 1, kf < 1), (kE < 1, kf > 1), and (kE < 1, kf = 1) have not been observed experimentally during fatigue crack growth in the tested specimens. Therefore, they represent a hypothetical passive source labeled by “0”.
The final classification of AE sources by the Frequency-Energy criterion is given in Table 1.

Table 1.
Classification of AE sources according to Frequency and Energy of AE.
4.2. Criterion B: Cluster-Energy
The Cluster-Energy criterion is based on a comparative analysis of AE energy curves in terms of the energy value and the shape of the energy curve per cycle. The applicability of this criterion as justified by the following experimental observations:
- (i)
- the AE changes synchronously with the load during each cycle with good reproducibility;
- (ii)
- AE energy features systematically change with fatigue crack advance, i.e., the AE energy curve per cycle shows a single wide peak in the beginning of loading, which then splits into two sharper peaks as the crack grows up and the critical stage approaches;
- (iii)
- the AE energy increments progressively when the crack propagates on the late stage of fatigue before failure.
Thus, the experiments highlight two most prominent features in the AE behavior at the critical stage of fatigue of a ductile steel: (i) the increment of AE energy per loading cycle and (ii) the characteristic change in the shape of the AE energy curve. Fatigue damage accumulation is a gradual process, which may take a long time, so the increment of the AE energy per cycle is quite small compared to the total AE energy in the same cycle. To increase the sensitivity of the energy-based indicator, we use the difference between the relation of the energy measured during the analyzing period, ECi, to the average energy during the initial period of cycling, ĒC0, and the relation of the energy of obtained during the previous cycle, ECi−1, to the energy ECi.
Thus, Δe indicates the AE energy increment. The analysis of experimental data shows that, for the “crack free” material experiencing initial loading, ECi−1 ≈ ĒC0 ≈ ECi; thus, Δe < z, where the factor z is experimentally determined (z = 0.25 in our case). At the crack nucleation stage when microscopic flaws of subcritical size cracks are present, the difference between the energies in subsequent cycles become more significant such that ECi > ECi−1 > ĒC0 and in this case ECi/ĒC0 > 1, ECi−1/ECi < 1 and z < Δe < 1. When the crack growth approaches the critical length, the AE energy per cycle is large, but the AE difference in the subsequent cycles is small (at least smaller than at the nucleation stage); thus, ECi ≈ ECi−1 >> ĒC0, ECi/ĒC0 >> 1, ECi−1/ECi ≈ 1, and, finally, Δe > 1.
Although the indicator Δe is rather crude and cannot be used alone, it has a clear correlation with the damage mechanism. The other independent characteristic of the same mechanism is the shape of the AE energy curve per cycle, which can be quantitatively classified into three groups as has been discussed above depending on the features of Ẽ(t) curves. These three groups represent the following major stages of fatigue evolution: group (cluster) c1 corresponds to the “crack free” material on the initial cyclic hardening stage before crack initiation, group c2 is specific to the crack nucleation stage, and group c3 represents the actively growing defects. Thus, based on these premises, the AE signals classification for the Cluster-Energy AE criterion is as presented in Table 2.

Table 2.
Classification of AE sources according to Cluster-Energy AE criterion.
4.3. Verification of the Criteria
The efficiency of proposed criteria A and B was tested using AE data obtained during the fatigue testing of notched weld joints. The results of the hazard assessment according to criteria A and B were compared with experimental observations of the fatigue crack behavior and fatigue life. A high sensitivity of both criteria to fatigue stages was observed. Figure 4 illustrates the criteria indicators signaling the level of hazard on different stages of fatigue crack evolution from nucleation to stable growth and finally to rupture. Criterion A showed less sensitivity to crack nucleation. According to this criterion, crack nucleation occurred from 37 to 123 cycles, which is actually a bit late compared to actual observations of crack nucleation. Criterion B is apparently more sensitive. It identifies the nucleation stage quite correctly. However, criterion A shows a good correlation with the stable crack growth behavior, indicating qualitative changes in the crack propagation activity associated with the reduction in the median frequency. Criterion A is much less demanding on computational resources than criterion B. However, criterion B is more flexible and can be adapted (tuned) to fatigue mechanisms more precisely. For this purpose, it is sufficient to reassign the values of cluster centroids (c1, c2, c3) depending on the experience and experimental observations.
The potential industrial applications of these criteria would strongly benefit from their low sensitivity to their high-amplitude burst signals and random mechanical noise due to the integral nature of the parameters and approaches used. The choice of the criterion depends on the complexity of the monitored object and the purpose, e.g., the detection of crack initiation, the identification of the fatigue stage, or the evaluation of structural damage.
5. Conclusions
Using the modern AE technique, we addressed the problem of early identification of crack initiation and growth in ductile structural steels under cyclic loading. The notched 9MnSi5 steel specimens with weld joints were fatigue tested at room and lower temperatures with concurrent AE measurements, which were performed in a threshold-less acquisition mode. Detection of AE in ductile materials, where fatigue crack initiation and propagation is mediated by local dislocation behavior ahead of the notch or crack tip, is challenging because of the extremely low amplitude of the noise-like continuous AE signal. On account of this issue, two new practically oriented criteria for recognition of different stages of fatigue are proposed on the basis of AE data: (1) a power spectrum-based criterion considers the trends in the energy and median frequency of the AE power spectral density with cycling; (2) the second criterion exploits a power of the pattern recognition approach to AE signal processing in a form of modern clustering algorithms applied to a set of curves representing the normalized energy as a function of time per cycle. The applicability of both criteria is verified using obtained AE data; a good correspondence between AE outcomes and experimental observations of the fatigue behavior was observed.
As opposed to the existing commercial software, including that appealing to a variety of statistical and pattern recognition techniques, the proposed criteria are based on the integral AE parameters defined within the threshold-less mode of recording and analysis of AE data. This allows for the inclusion of low amplitude AE signals close to the noise level into explicit consideration, ensuring thereby early defect detection with high reliability.
Acknowledgments
Financial support from the Russian Ministry of Education and Science through the contract No. RFMEFI57714X0145 is gratefully appreciated.
Author Contributions
I.R., D.M., and A.D. conceived and designed the experiments; M.A. prepared the specimens and performed the fatigue experiments; I.R., A.D., and A.V. analyzed AE data; F.B. and all co-authors discussed the results; I.R. and A.V. wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dunegan, H.L.; Harris, D.O.; Tetelman, A.S. Detection of Fatigue Crack Growth by Acoustic Emission Techniques. Mater. Eval. 1970, 28, 221–227. [Google Scholar] [CrossRef]
- Bassim, M.N.; Houssny-Emam, M. Acoustic emission during the low cycle fatigue of AISI 4340 steel. Mater. Sci. Eng. 1984, 68, 79–83. [Google Scholar] [CrossRef]
- Scruby, C.B.; Wadley, H.N.G.; Hill, J.J. Dynamic elastic displacements at the surface of an elastic half-space due to defect sources. J. Phys. D Appl. Phys. 1983, 16, 1069–1083. [Google Scholar] [CrossRef]
- PB 03-593-03. Rules of Organizing and Conducting Acoustic Emission Testing of Vessels, Apparatuses, Boilers, and Technological Pipelines; Promyshlennaya Bezopasnost: Moscow, Russia, 2004. [Google Scholar]
- American Society of Mechanical Engineers (AMSE). Section V-Nondestructive Examination, Boiler and Pressure Vessel Code (BPVC); ASME: New York, NY, USA, 2007. [Google Scholar]
- E1419-00. Standard Test Method for Examination of Seamless, Gas-Filled, Pressure Vessels Using Acoustic Emission; ASTM: New York, NY, USA, 2000. [Google Scholar]
- Takeda, R.; Kaneko, Y.; Merson, D.; Vinogradov, A. Cluster Analysis of Acoustic Emissions Measured during Deformation of Duplex Stainless Steels. Mater. Trans. 2013, 54, 532–539. [Google Scholar] [CrossRef]
- Palmer, I.G. Acoustic emission measurements on reactor pressure vessel steel. Mater. Sci. Eng. 1973, 11, 227–236. [Google Scholar] [CrossRef]
- GOST (State Standard) 5264-80. Manual Arc Welding. Welding Joints. Main Types, Design Elements and Dimensions; Standartinform: Moscow, Russia, 2010. [Google Scholar]
- E647-00. Standard Test Method for Measurement of Fatigue Crack Growth Rates; ASTM: New York, NY, USA, 2000. [Google Scholar]
- Botvina, L.R.; Tetyueva, T.V.; Geikhman, T.D.; Kagan, L.S.; Artamoshkin, S.A. Features of the fracture of specimens of low-carbon steels under impact and static loading conditions. Met. Sci. Heat Treat. 1992, 34, 614–621. [Google Scholar] [CrossRef]
- Suresh, S. Fatigue of Materials, 2nd ed.; Cambridge University Press: London, UK, 1998; pp. 1–679. [Google Scholar]
- Dowling, N. Mechanical Behavior of Materials; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2012; pp. 1–960. [Google Scholar]
- Pomponi, E.; Vinogradov, A. A real-time approach to acoustic emission clustering. Mech. Syst. Signal Process. 2013, 40, 791–804. [Google Scholar] [CrossRef]
- Vinogradov, A.; Patlan, V.; Hashimoto, S. Spectral analysis of acoustic emission during cyclic deformation of copper single crystals. Philos. Mag. A 2001, 81, 1427–1446. [Google Scholar] [CrossRef]
- Vinogradov, A.; Yasnikov, I.; Estrin, Y. Stochastic dislocation kinetics and fractal structures in deforming metals probed by acoustic emission and surface topography measurements. J. Appl. Phys. 2014, 115, 233506. [Google Scholar] [CrossRef]
- Everitt, B.; Landau, S.; Leese, M.; Stahl, D. Cluster Analysis, 5th ed.; Wiley-Blackwell: Oxford, UK, 2011; pp. 1–346. [Google Scholar]
- Linderov, M.; Segel, C.; Weidner, A.; Biermann, H.; Vinogradov, A. Deformation mechanisms in austenitic TRIP/TWIP steels at room and elevated temperature investigated by acoustic emission and scanning electron microscopy. Mater. Sci. Eng. A 2014, 597, 183–193. [Google Scholar] [CrossRef]
- Vinogradov, A.; Lazarev, A.; Linderov, M.; Weidner, A.; Biermann, H. Kinetics of deformation processes in high-alloyed cast transformation-induced plasticity/twinning-induced plasticity steels determined by acoustic emission and scanning electron microscopy: Influence of austenite stability on deformation mechanisms. Acta Mater. 2013, 61, 2434–2449. [Google Scholar] [CrossRef]
- Vinogradov, A.; Orlov, D.; Danyuk, A.; Estrin, Y. Effect of grain size on the mechanisms of plastic deformation in wrought Mg–Zn–Zr alloy revealed by acoustic emission measurements. Acta Mater. 2013, 61, 2044–2056. [Google Scholar] [CrossRef]
- Fowler, T.J.; Blessing, J.A.; Conlisk, P.J.; Swanson, T.L. The MONPAC System. J. Acoust. Emiss. 1989, 8, 1–8. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).