A New Continuous Bending and Straightening Curve Based on the High-Temperature Creep Property of a Low-Alloy Steel Continuous Casting Slab
Abstract
1. Introduction
2. Methodology
2.1. Parameters of the R9300 Continuous Casting Machine
2.2. Realization of Creep Bending and Straightening
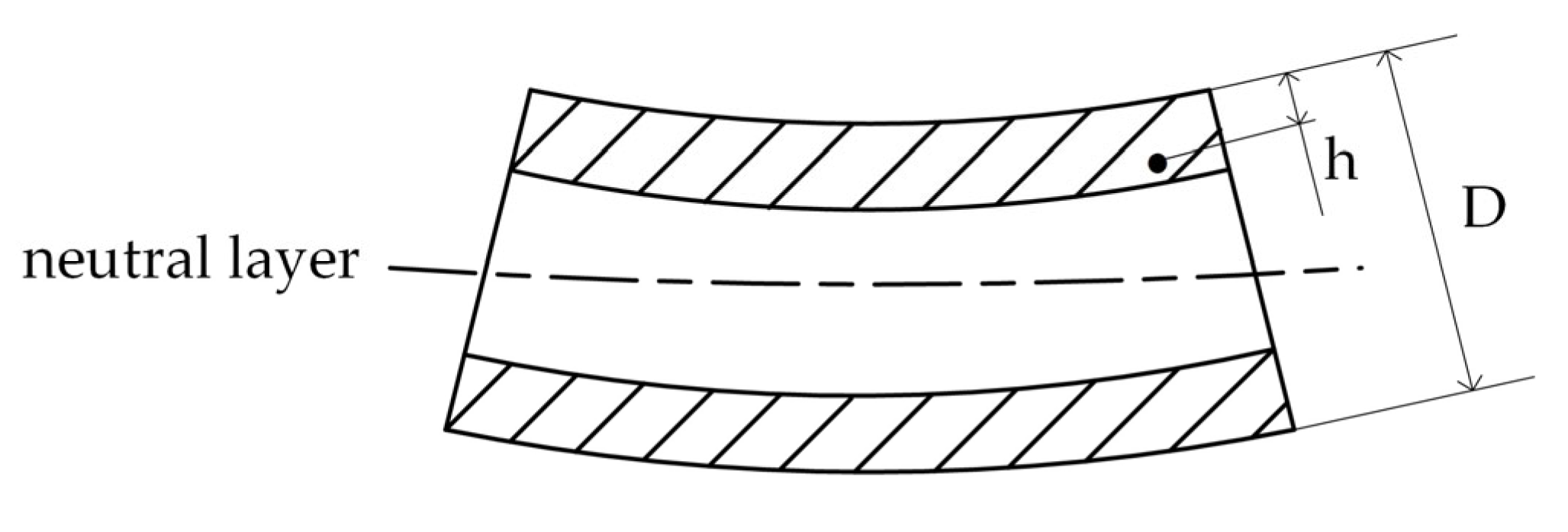
- (1)
- The end of the straightening curve is tangent to the horizontal segment of the continuous caster, and the slope and curvature at the tangent point are zero.
- (2)
- If the initiation point of the straightening curve is connected to the basic arc segment of the continuous caster, the curvature radius at the connection point should be equal to the basic arc radius, and there should be a common tangent at the connection point.
- (3)
- If the basic arc segment is cancelled and the beginning of the straightening curve is directly connected to the end of the bending segment, then there should be an equal curvature radius and a common tangent at the connection point.
2.3. The Design of the New Curve
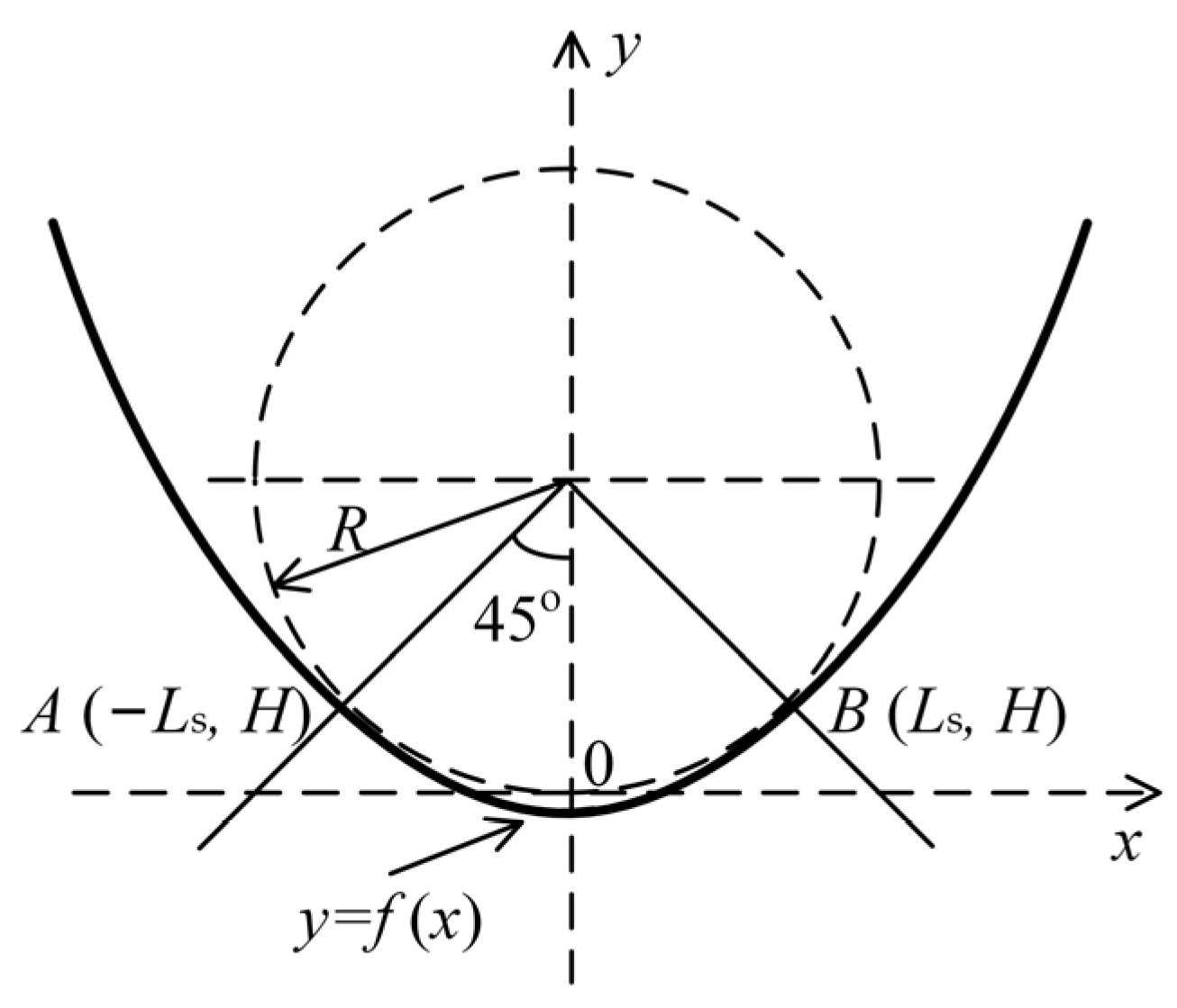
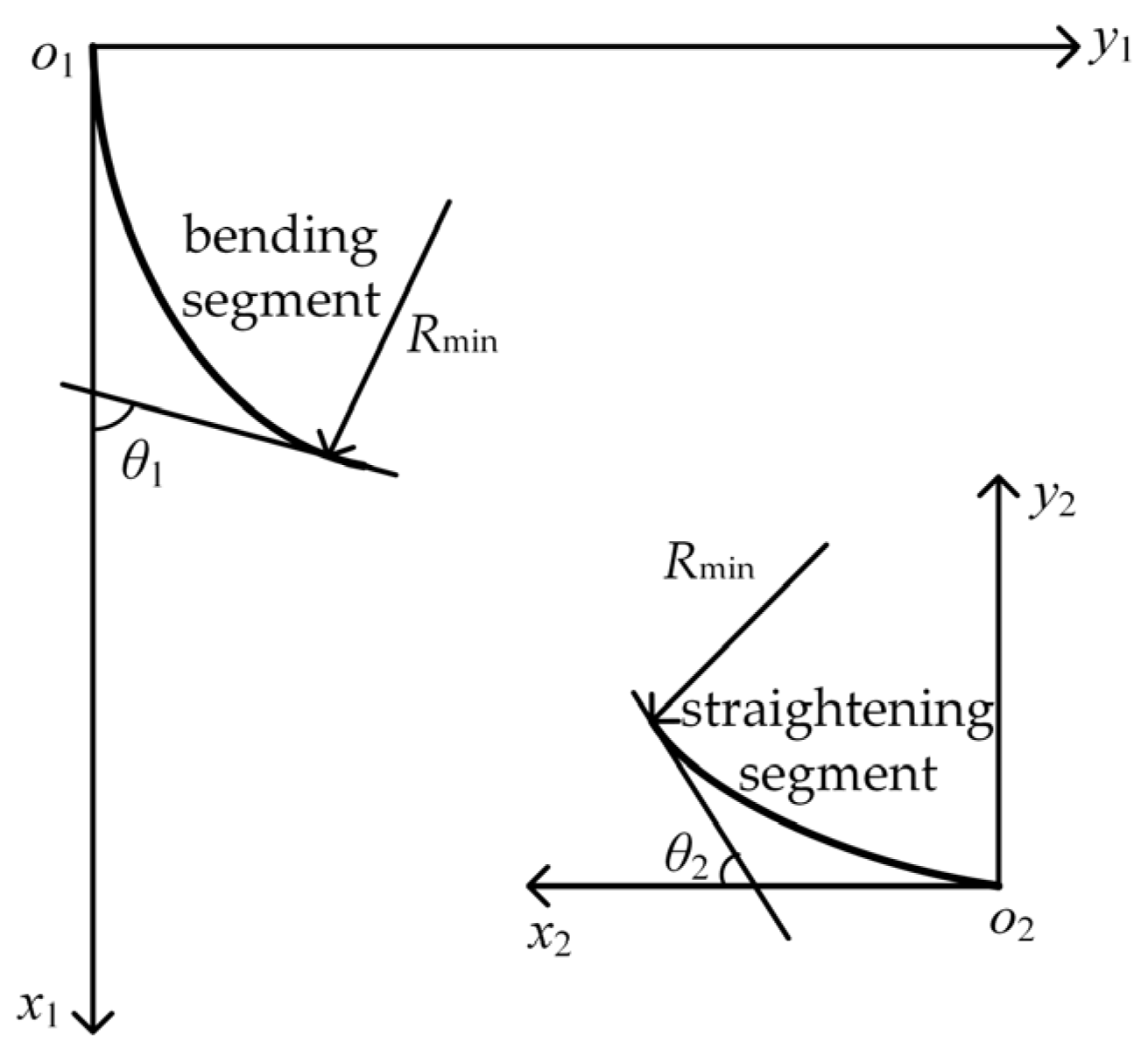
2.3.1. Quartic Even Polynomial Curve (Straightening Segment)
2.3.2. Sinusoidally Varying Curvature Curve (Bending Segment)
2.3.3. Combination of Bending and Straightening Segments
3. Results
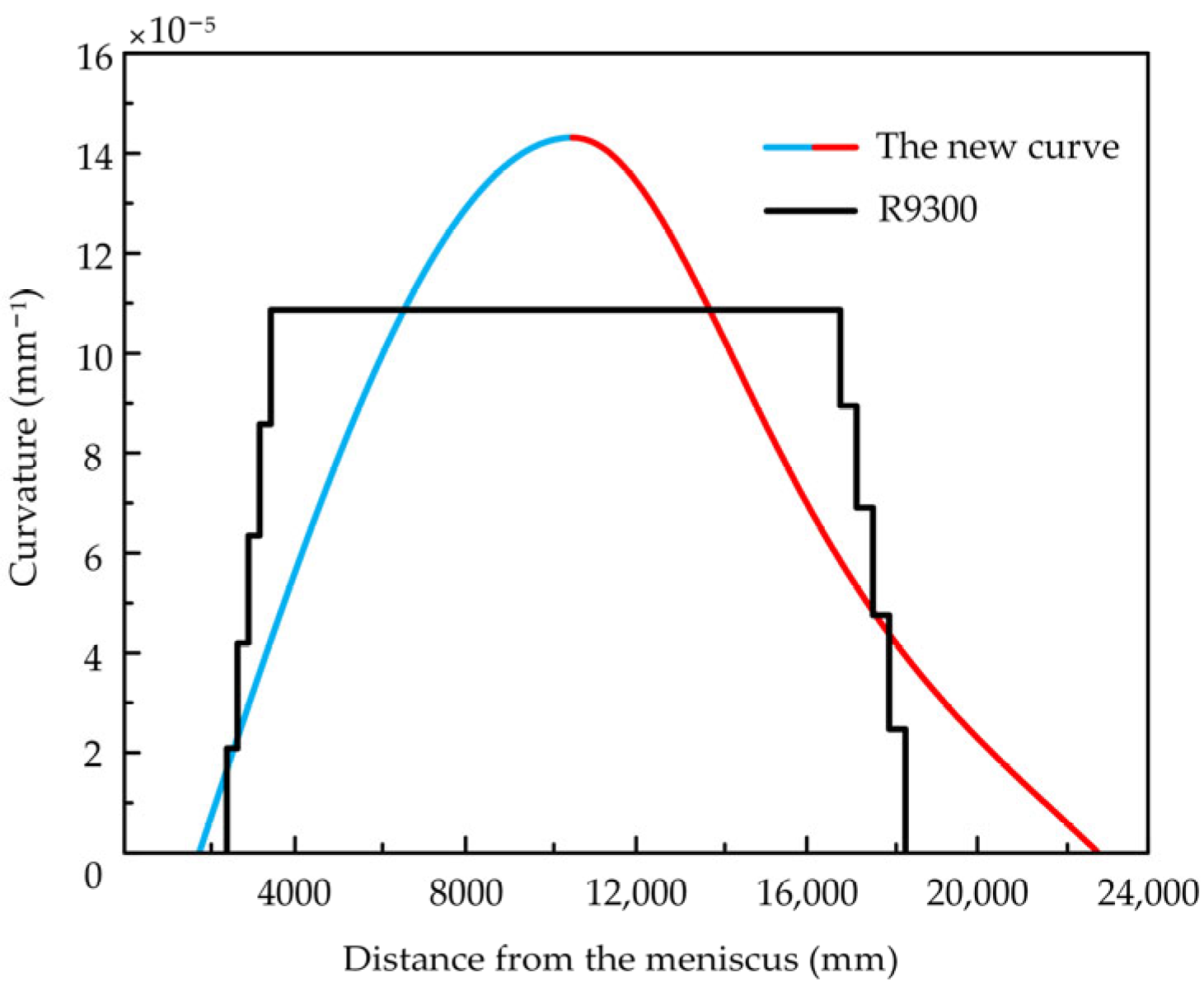
3.1. The Expression of the Continuous Bending and Straightening Curve
3.2. Roller Arrangement of the New Curve
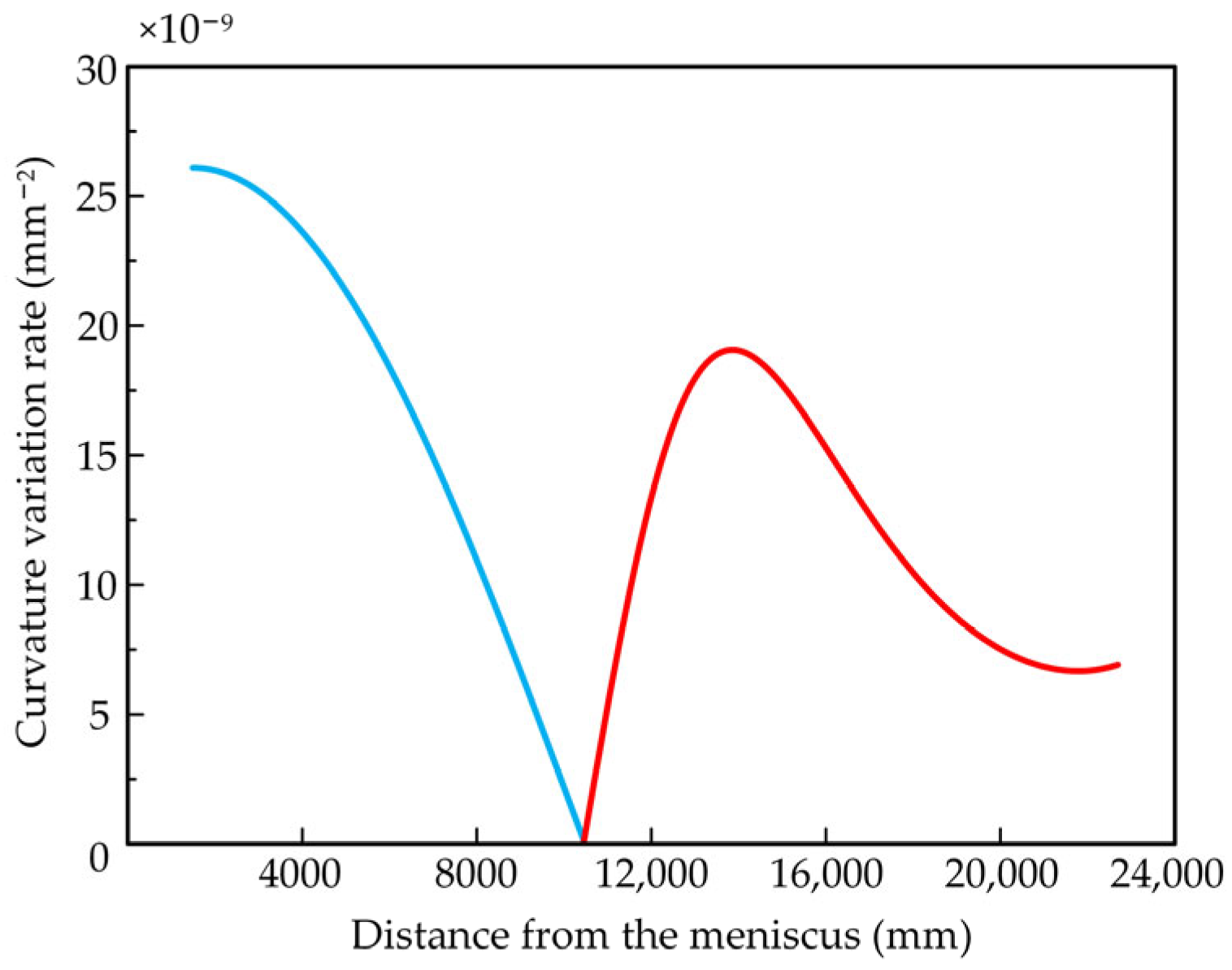
3.3. The Curvature and Curvature Variation Rate of the New Curve
4. Discussion
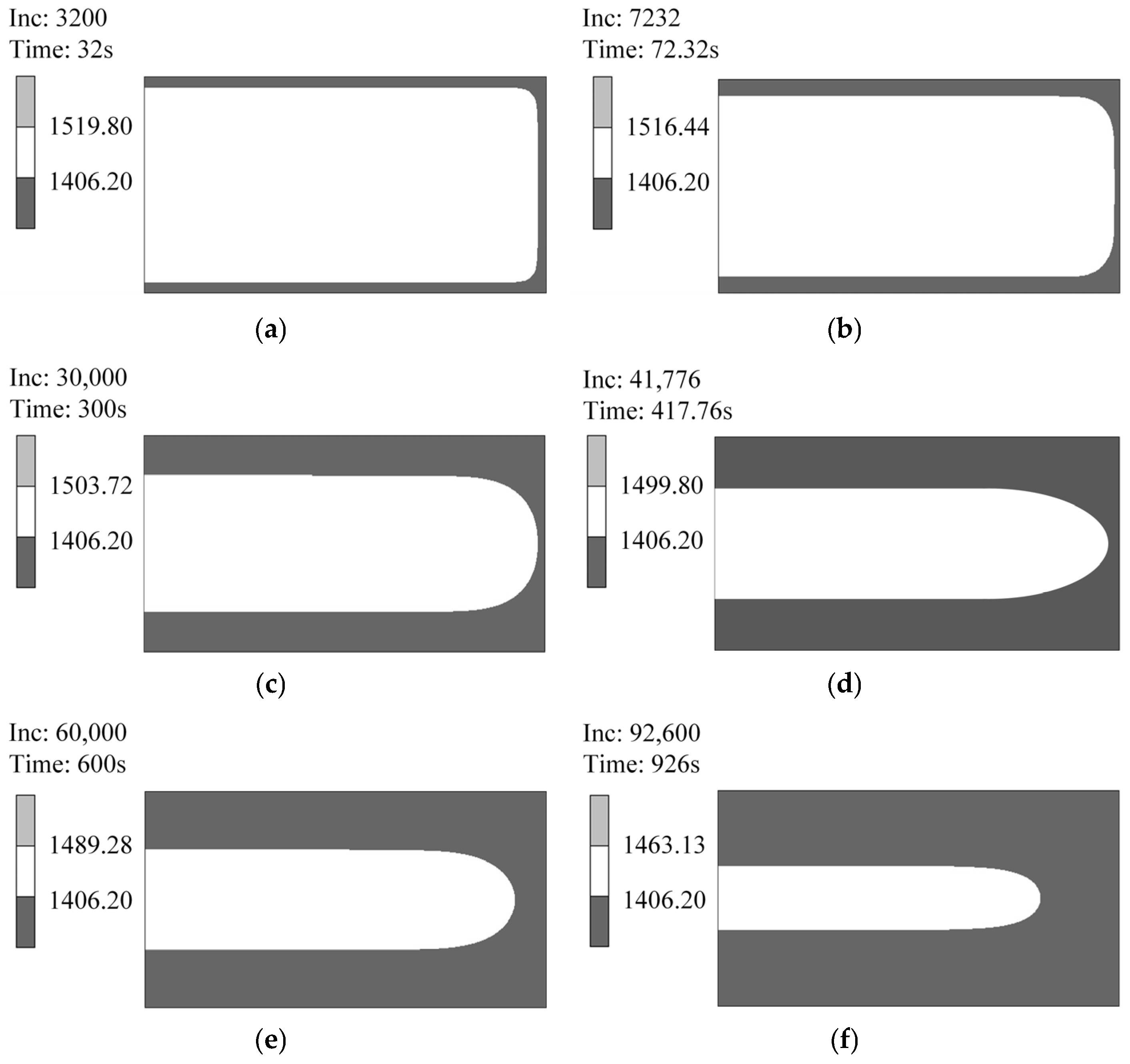
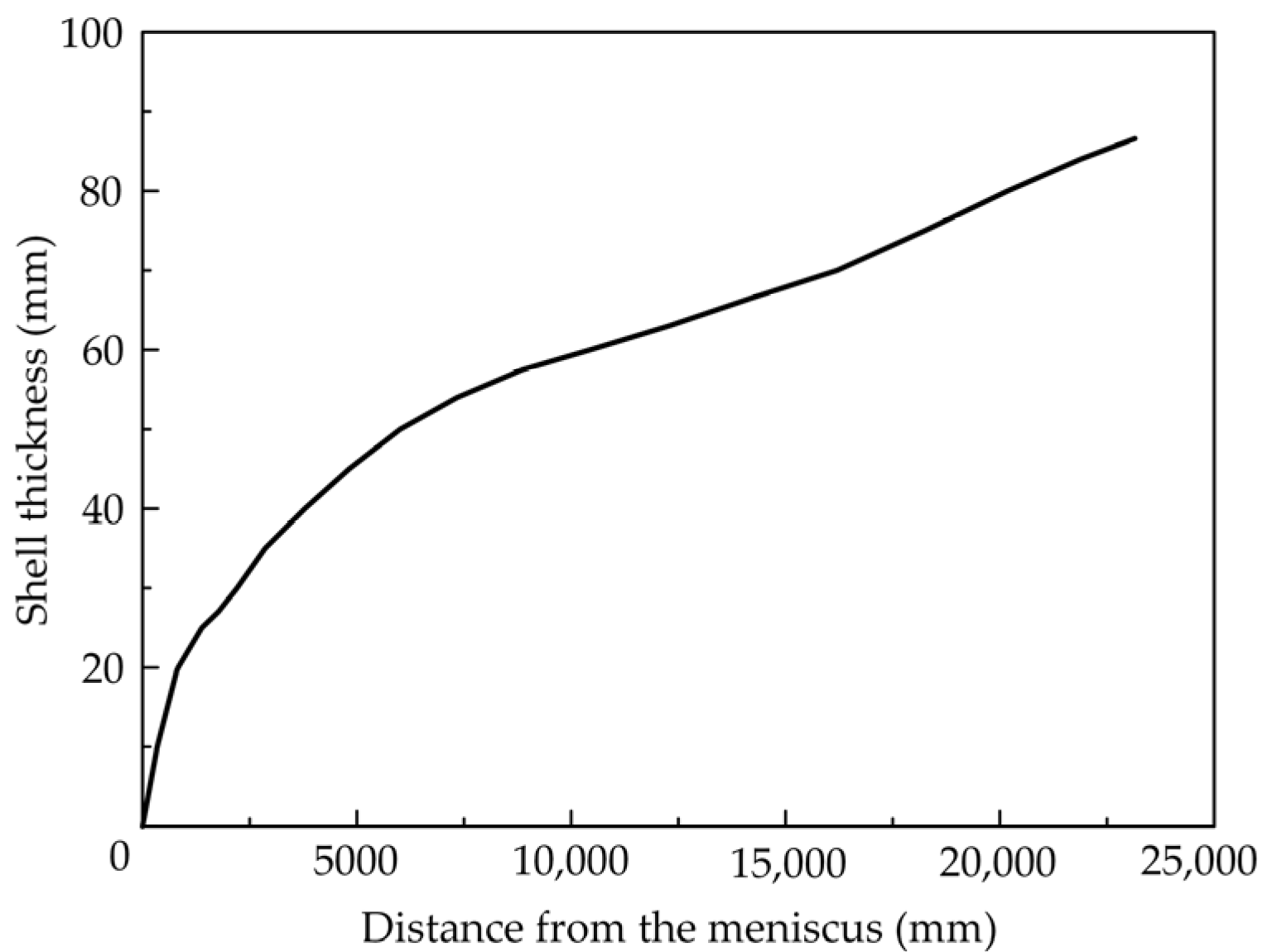
4.1. Temperature Field Simulation of a Continuous Casting Slab Based on the New Curve
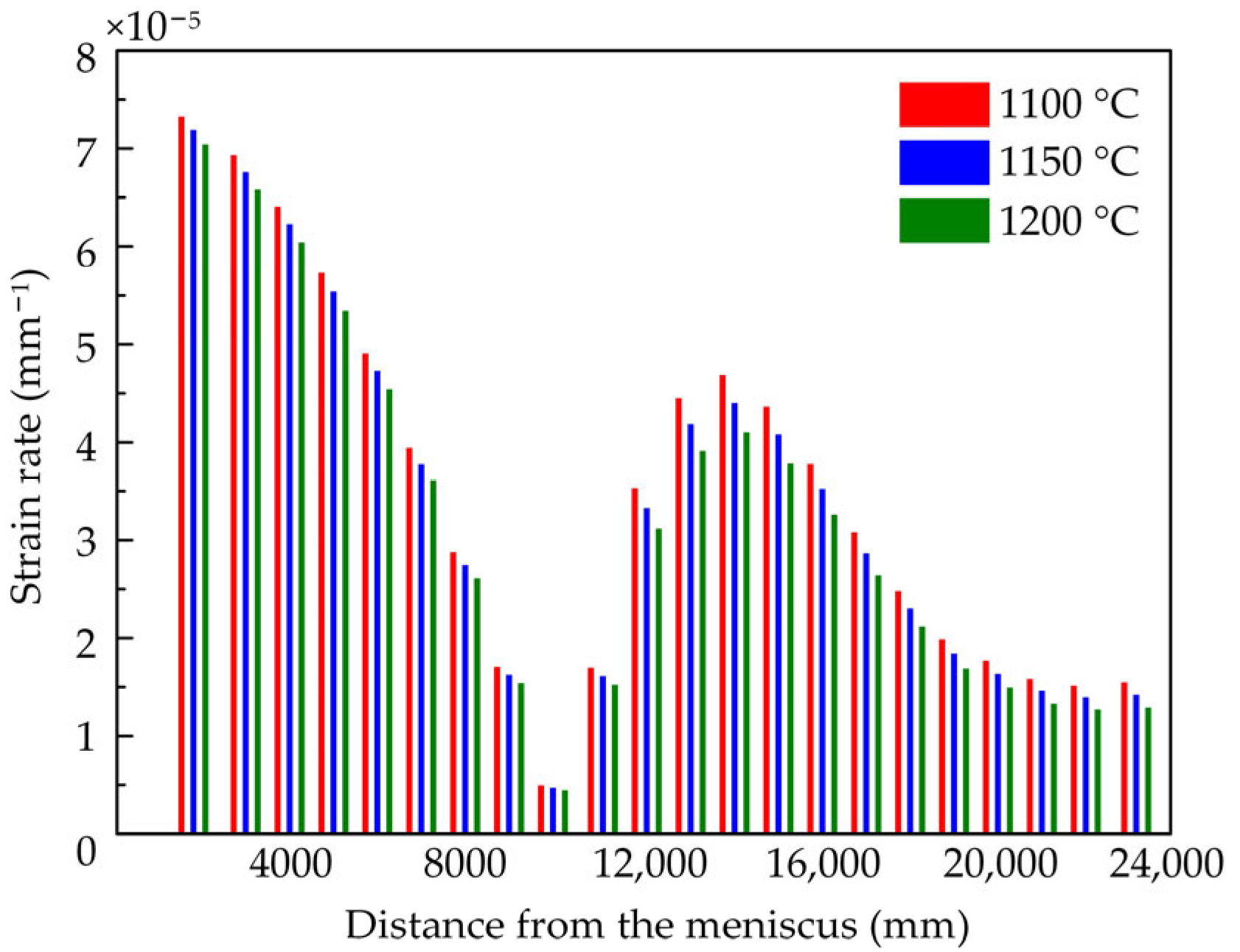
4.2. Calculation of the Strain Rate of the Continuous Casting Slab
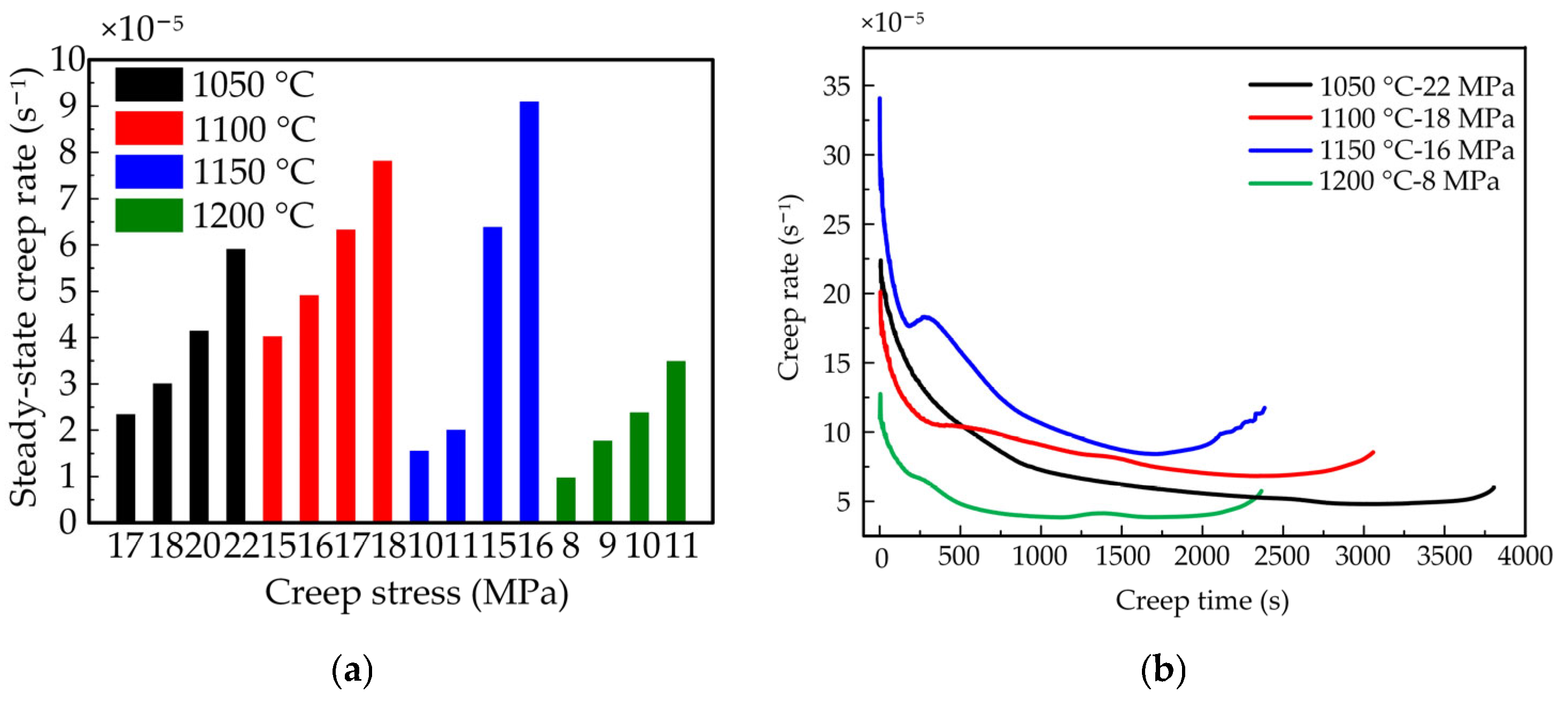
4.3. Verification of Creep Continuous Bending and Straightening
5. Conclusions
- The establishment condition of utilizing the high-temperature creep property of the continuous casting slab to achieve its bending and straightening deformation was derived, namely, that a position within the solidified shell could undergo bending and straightening deformation through creep deformation when the local strain rate at that position is less than the local steady-state creep rate.
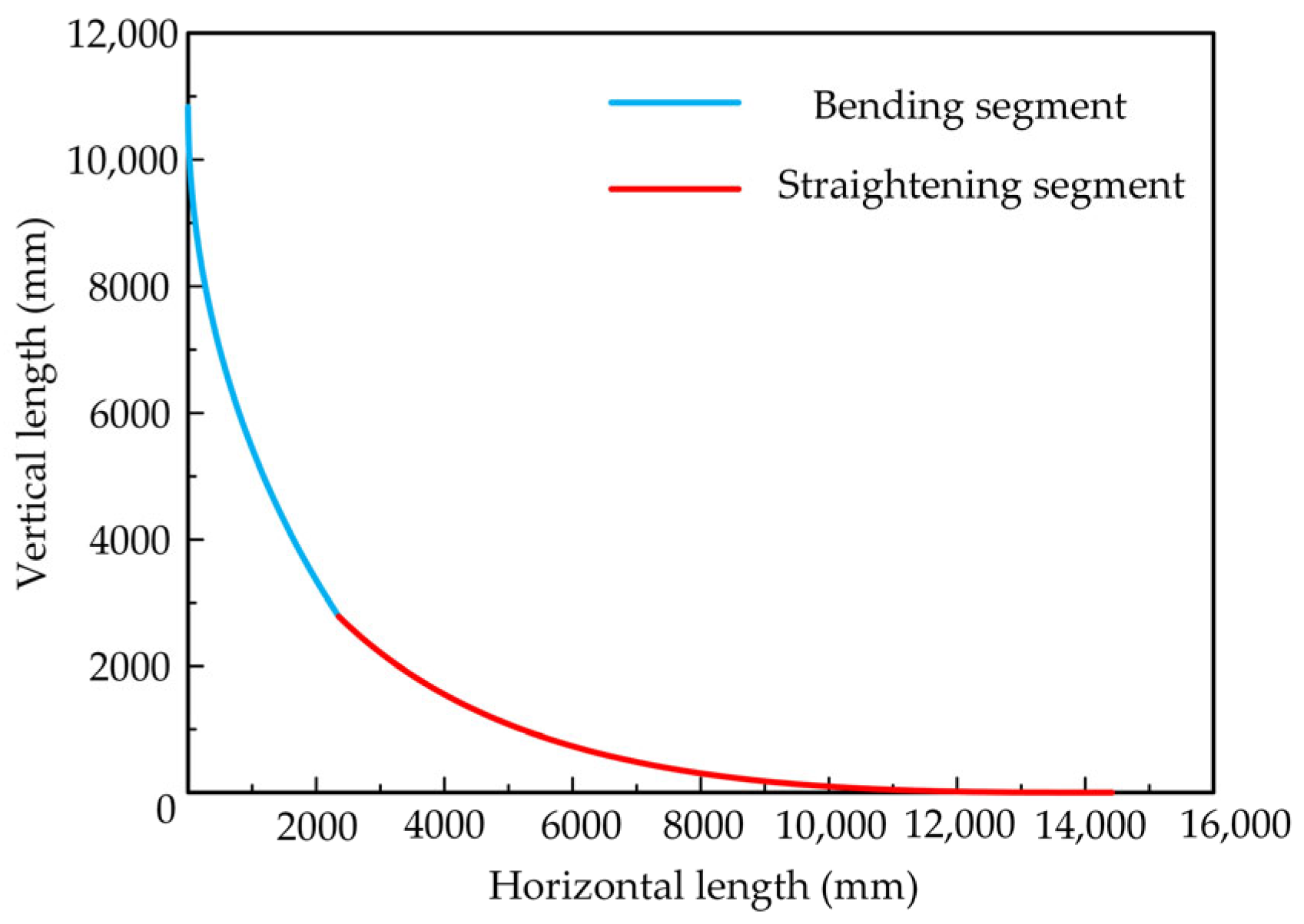
- Based on the existing R9300 vertical-arc continuous caster, the newly designed caster layout curve integrated a bending segment curve, whose curvature varied sinusoidally, and a straightening segment curve, which varied according to a quartic even polynomial. These segments were smoothly connected to form a continuous bending and straightening caster layout curve, whose curvature and curvature variation rate are continuous. Although the new caster layout curve increased the overall height by 159.45 mm, it significantly extended the bending segment by 7606 mm and the straightening segment by 11,186 mm. The newly designed curve not only substantially prolonged the effective duration for bending and straightening deformation, thereby reducing associated strain rates, but also extended the time available for creep deformation. Consequently, the role of creep deformation could be more effectively exploited.
- From the simulated temperature field results, the locations within the continuous casting slab corresponding to the temperature range of 1100 °C to 1200 °C were identified. A comparison of the calculated strain rates with the steady-state creep rates obtained from high-temperature tensile creep tests revealed that within the temperature range exhibiting favorable hot ductility, the bending and straightening deformation of the slab could be accomplished entirely through creep deformation. However, at some locations of 1200 °C, where hot ductility is relatively poor, bending and straightening deformation could be partially achieved by creep deformation. This partial contribution of creep deformation also aided in reducing the magnitude of the bending and straightening forces, thus reducing the probability of crack formation and thereby enhancing the quality of the final casting product.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luo, X.; Xie, Q.; Wang, Y.; Yang, C. Estimation of heat transfer coefficients in continuous casting under large disturbance by Gaussian kernel particle swarm optimization method. Int. J. Heat Mass Tran. 2017, 11, 1087–1097. [Google Scholar] [CrossRef]
- Qiu, D.; Zhang, Z.; Li, X.; Lv, M.; Mi, X.; Xi, X. Numerical simulation of the flow field in an ultrahigh-speed continuous casting billet mold. Metals 2023, 13, 964. [Google Scholar] [CrossRef]
- Pang, X.; Li, H.; Wang, J.; Zhu, L.; Sun, L. Optimization of billet tube mold designs for high-speed continuous casting. Processes 2023, 11, 3367. [Google Scholar] [CrossRef]
- Sun, L.; Li, H.; Song, Z.; Guo, G.; Wang, C.; Matsveichuk, N.M.; Sotskov, Y.N. A review of dynamic flexible regulation strategies for multi-energy coupled steelmaking-continuous casting production. Eng. Appl. Artif. Intel. 2025, 160, 111799. [Google Scholar] [CrossRef]
- Ai, S.; Long, M.; Yang, X.; Chen, D.; Xu, P.; Duan, H. Prediction model for crack sensitive temperature region and phase fractions of slab under continuous casting cooling rates based on finite element number of experiments. J. Mater. Res. Technol. 2023, 22, 1103–1117. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, F.; Li, J.; Liu, W.; Wang, T.; Yuan, H.; Cang, D. Bending and straightening of a medium carbon steel continuous casting slab with low temperature end plastic groove. Materials 2022, 15, 2609. [Google Scholar] [CrossRef]
- Zhou, Q.; Yin, Y.; Liu, Z.; Zhang, J.; Zhang, J. Research mechanism of formation on transverse corner cracks in the continuous casting slab of peritectic steel. Steel Res. Int. 2022, 93, 2200336. [Google Scholar] [CrossRef]
- Zhang, Z.; Ji, C.; Ju, J.; Li, K.; Zhu, M. Micromechanical behavior and microcrack evolution in continuous casting slab: Experimental characterization, multiscale simulation and industrial validation. J. Mater. Process Tech. 2025, 340, 118866. [Google Scholar] [CrossRef]
- Luo, Z. Steelmaking Machinery, 2nd ed.; Metallurgical Industry Press: Beijing, China, 1989; p. 220. [Google Scholar]
- Cheng, N.; Wang, H. Investigation and practice on single-point straightening caster with liquid core straightening. Continuous casting. Cont. Cast. 2005, 2, 29–31. [Google Scholar]
- Sun, L.; Liu, Y.; Ren, Y.; Liu, Z.; Zhu, L. Research on solidification behavior and process optimization in single point straightening rectangular billet continuous casting for 65Mn steel. Iron Steel Vanadium Titan. 2015, 36, 120–125. [Google Scholar]
- Xing, G.; Zhu, M.; Lin, Q.; Liu, X. Finite element simulation of stress and strain of concasting slab during straightening. Spec. Steel 2006, 27, 10–12. [Google Scholar]
- Zhou, L. Design & calculation of multipoint straightening. CFHI Technol. 2009, 6, 10–12. [Google Scholar]
- Deisinger, M.; Tacke, K.H. Unbending of continuously cast slabs with liquid core. Ironmak. Steelmak. 1997, 24, 321–328. [Google Scholar]
- Wu, J.; Du, S. Application of VAI high-efficiency billet caster technology in Maanshan steel. Cont. Cast. 2004, 6, 23–24. [Google Scholar]
- Wang, M.; Hu, L.; Yan, Z.; Tian, X.; Su, Q. Production practice of steel continuous casting machine introduced by VAI. Iron Steel 2004, 39 (Suppl. S1), 173–175. [Google Scholar]
- Li, X.; Shi, C. Improvement of Concast continuous straightening curve. Chin. J. Mech. Eng. 1996, 32, 106–110. [Google Scholar]
- Li, X. Low-head continuous casting machine with two smooth continuous straightening areas. Iron Steel 1996, 31, 31–35. [Google Scholar]
- Jing, F.; Li, X.; Yang, L.; Sun, H.; Wang, T.; Chen, Z. Optimization of continuous bending and straightening curve of vertical-arc slab caster. Iron Steel 2009, 44, 23–27. [Google Scholar]
- Jing, F.; Li, X.; Wang, T.; Chen, Z.; Sun, H. Research and application of strand’s new-ideal continuous straightening curve. China Mech. Eng. 2009, 20, 1240–1244. [Google Scholar]
- Jing, F.; Zhang, X.; Meng, J.; Guo, W. Analysis of the numerical solution to the ideal straightening curve equation of continuous casting slab. Heavy Mach. 2004, 3, 49–52. [Google Scholar]
- Wang, T.; Chen, Z.; Li, X.; Man, Y. Application of continuous straightening on slab casting. Cont. Cast. 2007, 5, 9–11. [Google Scholar]
- Liu, C.; Gadelmeier, C.; Lu, S.; Yeh, J.; Yen, H.; Gorsse, S.; Glatzel, U.; Yeh, A. Tensile creep behavior of HfNbTaTiZr refractory high entropy alloy at elevated temperatures. Acta Mater. 2022, 237, 118188. [Google Scholar] [CrossRef]
- Dong, S.; Gong, Z.; Chen, Z.; Qu, Y.; Chen, R.; Liu, S.; Li, G. High temperature tensile creep behavior and microstructure evolution of Ti60 alloy rolled sheet. Mater. Today Commun. 2024, 41, 110805. [Google Scholar] [CrossRef]
- Wang, T.; Kai, X.; Huang, L.; Peng, Q.; Sun, K.; Zhao, Y. High temperature creep behavior and creep mechanism of in situ (ZrB2+Al2O3)np/7055 Al nanocomposites. J. Alloys Compd. 2024, 981, 173662. [Google Scholar] [CrossRef]
- Pan, X.; Jia, C.; Qiu, C. On the high-temperature creep and fatigue behaviours of an advanced hot-extruded nickel-based alloy. Mater. Des. 2025, 257, 114514. [Google Scholar] [CrossRef]
- Gai, Y.; Zhang, R.; Cui, C.; Zhou, Z.; Tao, X.; Tan, Y.; Zhou, Y. Creep behavior and microstructure evolution of a novel Ni-Co-based superalloy with long-life designed for high temperature application. Mat. Sci. Eng. A 2025, 935, 148396. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, L. Creep straightening technology of continuous casting slab based on high-temperature creep property. ISIJ Int. 2017, 57, 76–83. [Google Scholar] [CrossRef]
- Sui, Y.; Zhang, H.; Zhang, X. Study on the creep behavior and microstructure evolution of a low alloy steel in continuous casting processing. Mat. Sci. Eng. A 2022, 838, 142828. [Google Scholar] [CrossRef]
- Han, Z.; Feng, K.; Qu, T.; Cao, J.; Ren, B.; Mao, J. The discussion about the determination of basic radius for extra-thick slab caster. Ind. Heat. 2013, 42, 19–21. [Google Scholar]
- Chen, C.; Zhang, J. Determination of reasonable basic arc radius for bloom casters. Heavy Mach. 2010, S1, 119–124. [Google Scholar]
- Savage, J.; Pritchard, W. The problem of rupture of the billet in the continuous casting of steel. J. Iron Steel Inst. 1954, 178, 269–277. [Google Scholar]
- Sun, J. Heat Transfer Analysis in the Continuous Casting and Rolling Process; Metallurgical Industry Press: Beijing, China, 2010; pp. 93–94. [Google Scholar]


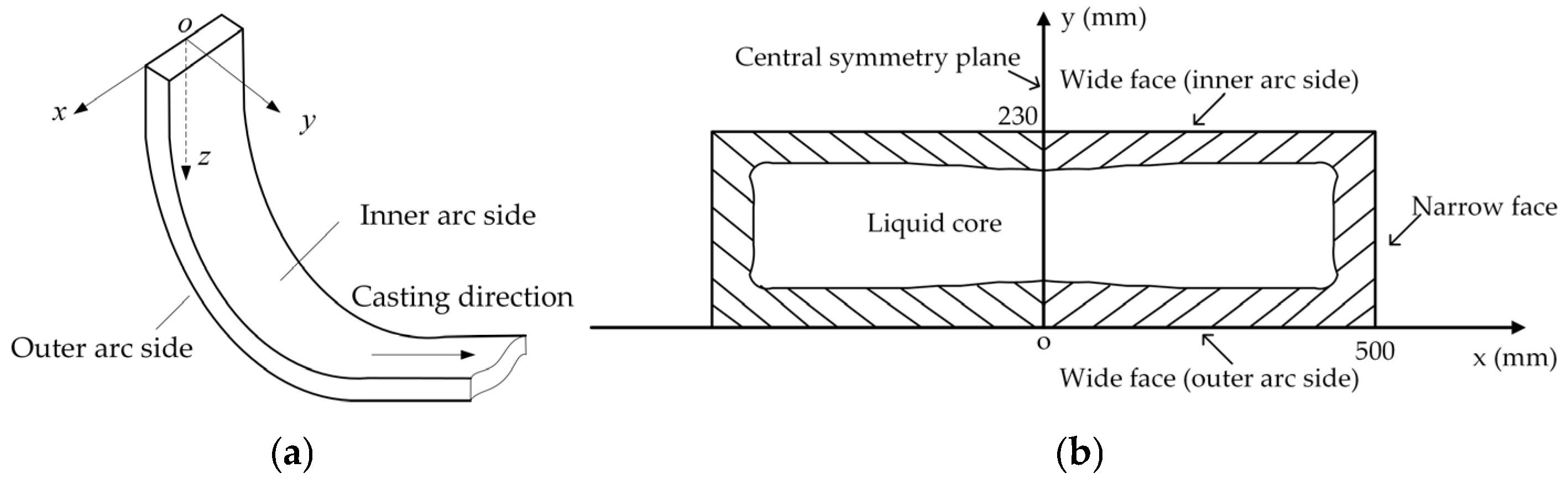

| Parameters | Value (mm) |
|---|---|
| Vertical segment | 1465 |
| Bending segment | 1030 |
| Basic arc length | 13,300 |
| Straightening segment | 1520 |
| Basic arc radius | 9300 |
| Thickness of slab | 230 |
| Metallurgical length | 35,862 |
| Continuous casting machine height | 12,305.55 |
| Curvature radius of roller No. 7 in bending segment | 49,420.83 |
| Curvature radius of roller No. 8 in bending segment | 24,328.14 |
| Curvature radius of roller No. 9 in bending segment | 15,971.29 |
| Curvature radius of roller No. 10 in bending segment | 11,797.72 |
| Curvature radius of roller No. 51 in straightening segment | 11,312.89 |
| Curvature radius of roller No. 52 in straightening segment | 14,671.99 |
| Curvature radius of roller No. 53 in straightening segment | 21,396.38 |
| Curvature radius of roller No. 54 in straightening segment | 41,581.55 |
| Parameters | Value |
|---|---|
| Cross-sectional size of the slab (mm × mm) | 1000 × 230 |
| Casting speed (mm/s) | 25 |
| Casting temperature (°C) | 1520 |
| Casting machine height (mm) | 12,465 |
| Valid length of the mold (mm) | 800 |
| Length of the secondary cooling zone (mm) | 22,350 |
| Cooling Loop | Cooling Zone | Cooling Location | Cooling Water Volume (L/min) |
|---|---|---|---|
| 1 | Foot roller after mold (F1) | Wide side: in and out | 126 |
| 2 | Narrow side: left and right | 17.5 | |
| 3 | No.1-No.7 roller pair segment | Wide side: in and out | 554.4 |
| 4 | Narrow side: left and right | 108.5 | |
| 5 | No.8-No.13 roller pair segment | Wide side: in and out | 184.8 |
| 6 | Narrow side: left and right | 3.83 | |
| 7 | No.14-No.19 roller pair segment | Wide side: in and out | 109.2 |
| 8 | Narrow side: left and right | 3.83 | |
| 9 | No.20-No.31 roller pair segment | Wide side: in and out | 112 |
| 10 | Narrow side: left and right | 3.83 | |
| 11 | No.32-No.44 roller pair segment | Wide side: in and out | 84 |
| 12 | Narrow side: left and right | 3.83 | |
| 13 | No.45-No.58 roller pair segment | Wide side: in and out | 92.4 |
| 14 | Narrow side: left and right | 3.83 | |
| 15 | No.58-No.68 roller pair segment | Wide side: inner arc | 91.8 |
| 16 | Wide side: outer arc | 91.8 |
| Distance from the Meniscus (mm) | Distance from the Upper Surface in the Inner Arc of the Slab (mm) | ||
|---|---|---|---|
| 1100 °C | 1150 °C | 1200 °C | |
| 1808 | 2.22 | 4.31 | 6.60 |
| 3000 | 5.56 | 8.29 | 11.09 |
| 4000 | 7.73 | 10.70 | 13.84 |
| 5000 | 9.00 | 12.58 | 16.23 |
| 6000 | 9.93 | 13.73 | 17.73 |
| 7000 | 10.57 | 14.96 | 19.43 |
| 8000 | 10.65 | 15.39 | 20.28 |
| 9000 | 11.45 | 16.38 | 21.52 |
| 10,000 | 12.58 | 17.62 | 22.91 |
| 11,000 | 12.82 | 18.18 | 23.60 |
| 12,000 | 13.41 | 19.22 | 25.27 |
| 13,000 | 14.11 | 20.11 | 26.32 |
| 14,000 | 15.13 | 21.21 | 27.61 |
| 15,000 | 15.89 | 22.32 | 29.02 |
| 16,000 | 16.64 | 23.27 | 30.12 |
| 17,000 | 17.63 | 24.38 | 31.48 |
| 18,000 | 18.62 | 25.49 | 32.73 |
| 19,000 | 19.64 | 26.64 | 33.98 |
| 20,000 | 20.80 | 27.97 | 35.40 |
| 21,000 | 21.92 | 29.17 | 36.78 |
| 22,000 | 22.70 | 29.84 | 37.50 |
| 23,150 | 23.95 | 31.37 | 39.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sui, Y.; Lu, H.; Zhang, X. A New Continuous Bending and Straightening Curve Based on the High-Temperature Creep Property of a Low-Alloy Steel Continuous Casting Slab. Metals 2025, 15, 1059. https://doi.org/10.3390/met15091059
Sui Y, Lu H, Zhang X. A New Continuous Bending and Straightening Curve Based on the High-Temperature Creep Property of a Low-Alloy Steel Continuous Casting Slab. Metals. 2025; 15(9):1059. https://doi.org/10.3390/met15091059
Chicago/Turabian StyleSui, Yunhuan, Haiqing Lu, and Xingzhong Zhang. 2025. "A New Continuous Bending and Straightening Curve Based on the High-Temperature Creep Property of a Low-Alloy Steel Continuous Casting Slab" Metals 15, no. 9: 1059. https://doi.org/10.3390/met15091059
APA StyleSui, Y., Lu, H., & Zhang, X. (2025). A New Continuous Bending and Straightening Curve Based on the High-Temperature Creep Property of a Low-Alloy Steel Continuous Casting Slab. Metals, 15(9), 1059. https://doi.org/10.3390/met15091059





