Optimization of Different Metal Casting Processes Using Three Simple and Efficient Advanced Algorithms
Abstract
1. Introduction
- To extend the application of the very recently developed BWR and BMR algorithms to the single- and multi-objective optimization of different metal casting processes.
- To introduce a new simple, metaphor-independent, and parameter-free algorithm, the best–mean–worst–random (BMWR) algorithm, along with its multi-objective variant and to apply the same to the single- and multi-objective optimization of different metal casting processes.
- To evaluate the convergence behavior, robustness, and solution quality of the proposed algorithms in solving the optimization problems.
- To apply a simple decision-making method as a post-optimization decision-making tool for selecting the most balanced compromise solution from the Pareto front in multi-objective contexts of metal casting processes.
2. Materials and Methods: Proposed Algorithms
2.1. Proposed Algorithms for Single-Objective Constrained Optimization Problems
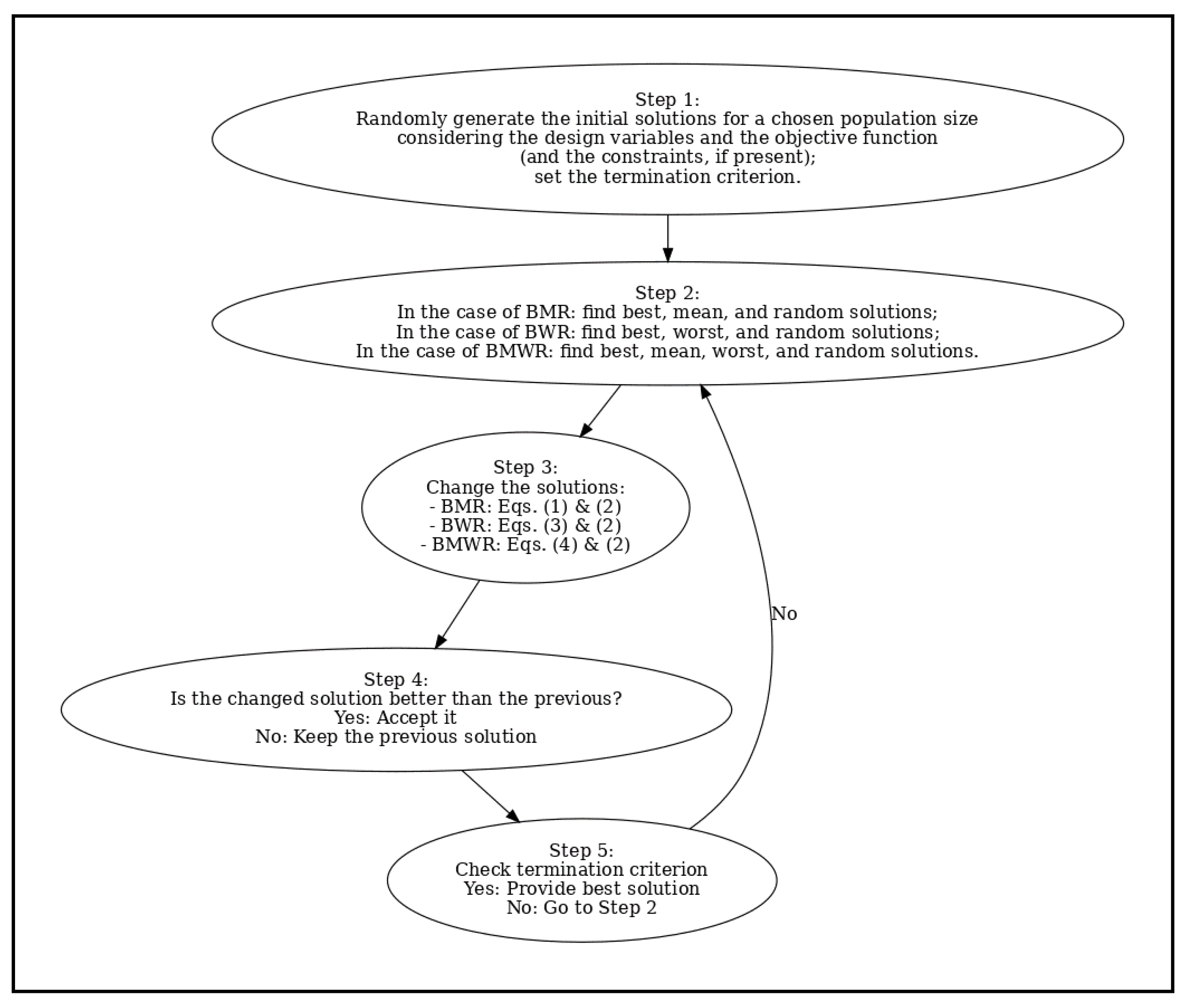
2.1.1. BWR Algorithm
2.1.2. BMR Algorithm
2.1.3. Best–Mean–Worst–Random (BMWR) Algorithm
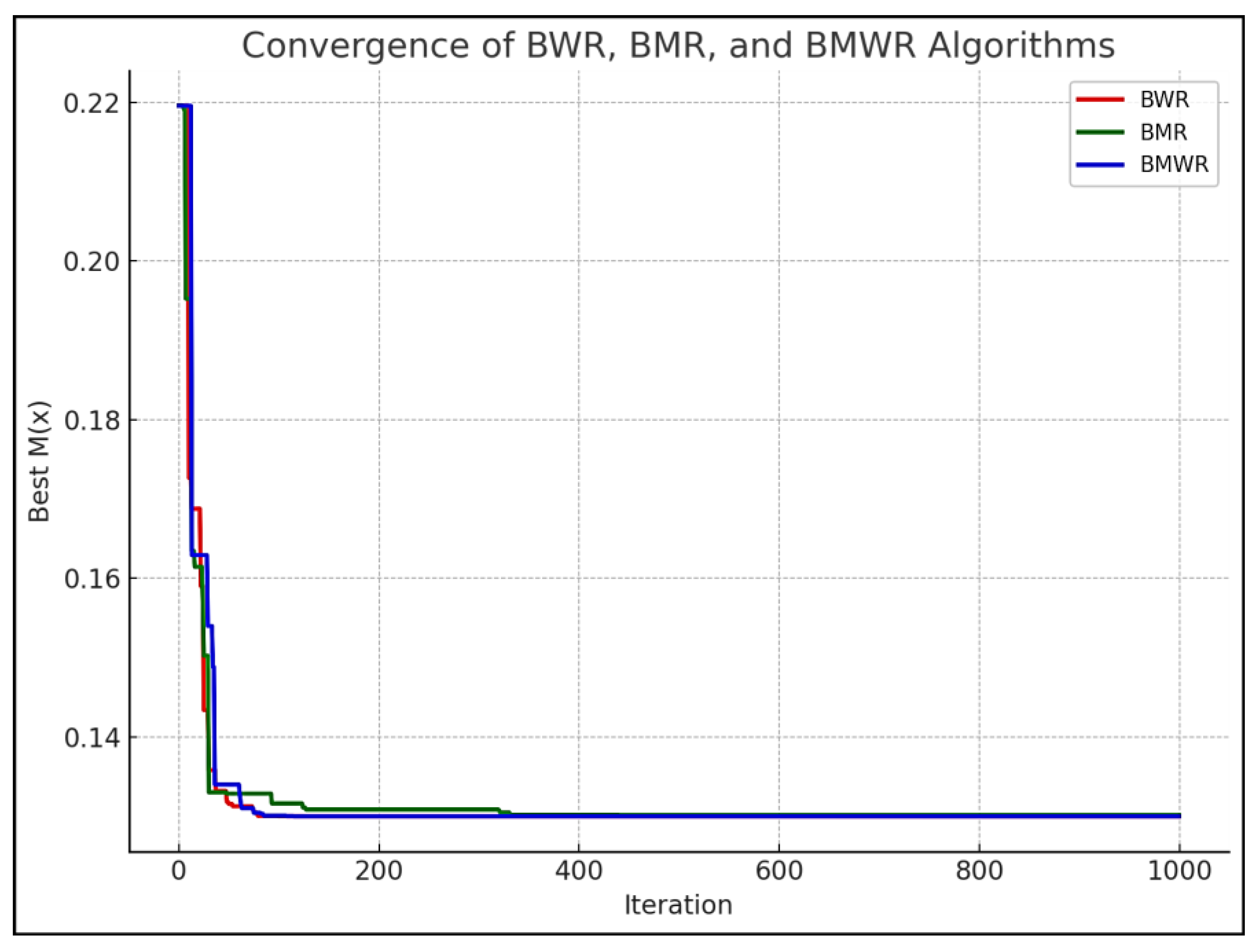
2.1.4. Demonstration of the BWR, BMR, and BMWR Algorithms on a Constrained Benchmark Problem
Demonstration of the BWR Algorithm
Demonstration of BMR Algorithm
Demonstration of BMWR Algorithm
2.2. Proposed Algorithms for Multi-Objective Constrained Optimization Problems
2.2.1. Multi-Objective Optimization with the BWR, BMR, and BMWR Algorithms
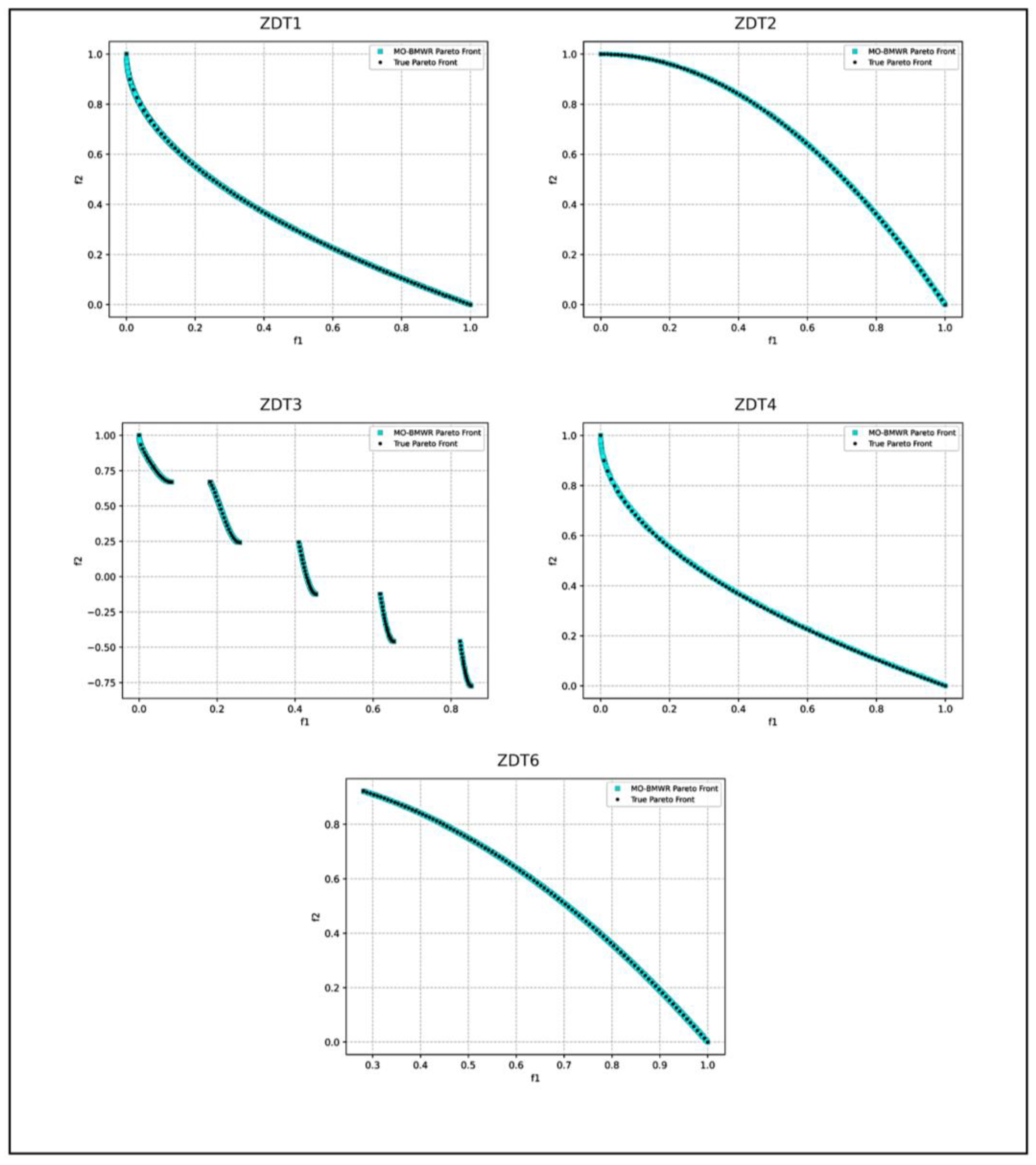
2.2.2. Validation of the MO-BWR, MO-BMR, MO-BMWR Algorithms for ZDT Functions
3. Results and Discussion on the Application of the Proposed Algorithms for Optimizing Various Metal Casting Processes
3.1. Single-Objective Optimization of Metal Casting Processes
3.1.1. Optimization of the Lost Foam Casting Process for Manufacturing a Fifth Wheel Coupling Shell from EN-GJS-400-18 Ductile Iron
3.1.2. Optimization of Process Parameters of Die Casting of A360 Al-Alloy
3.1.3. Optimization of Wear Rate of an AA7178 Alloy Reinforced with Nano-SiC Particles Produced Using a Stir-Casting Process
3.2. Multi-Objective Optimization of Metal Casting Processes
- Minimizing porosity;
- Minimizing shrinkage defects;
- Minimizing solidification time;
- Maximizing mechanical properties (e.g., hardness, tensile strength);
- Reducing production costs.
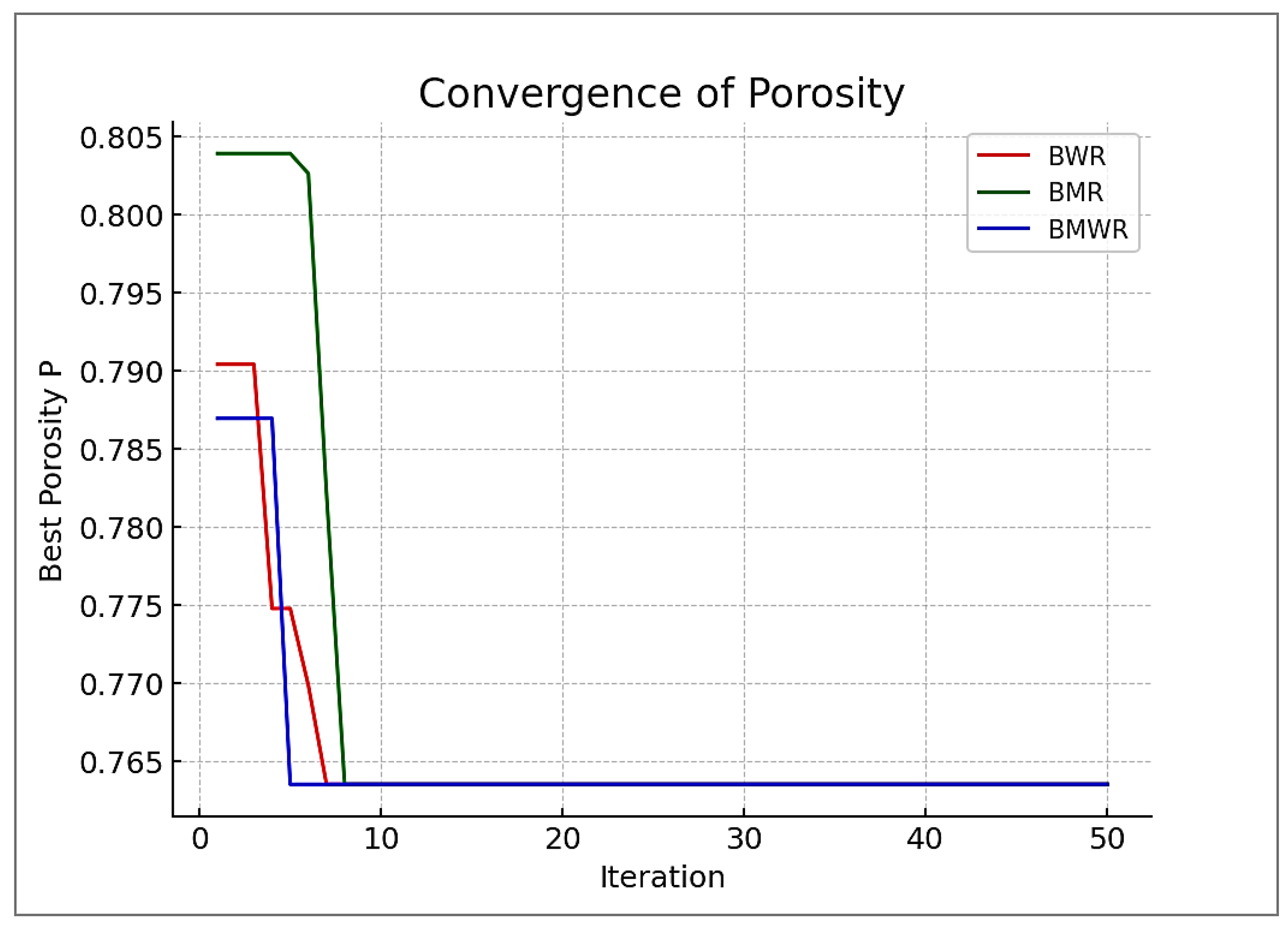
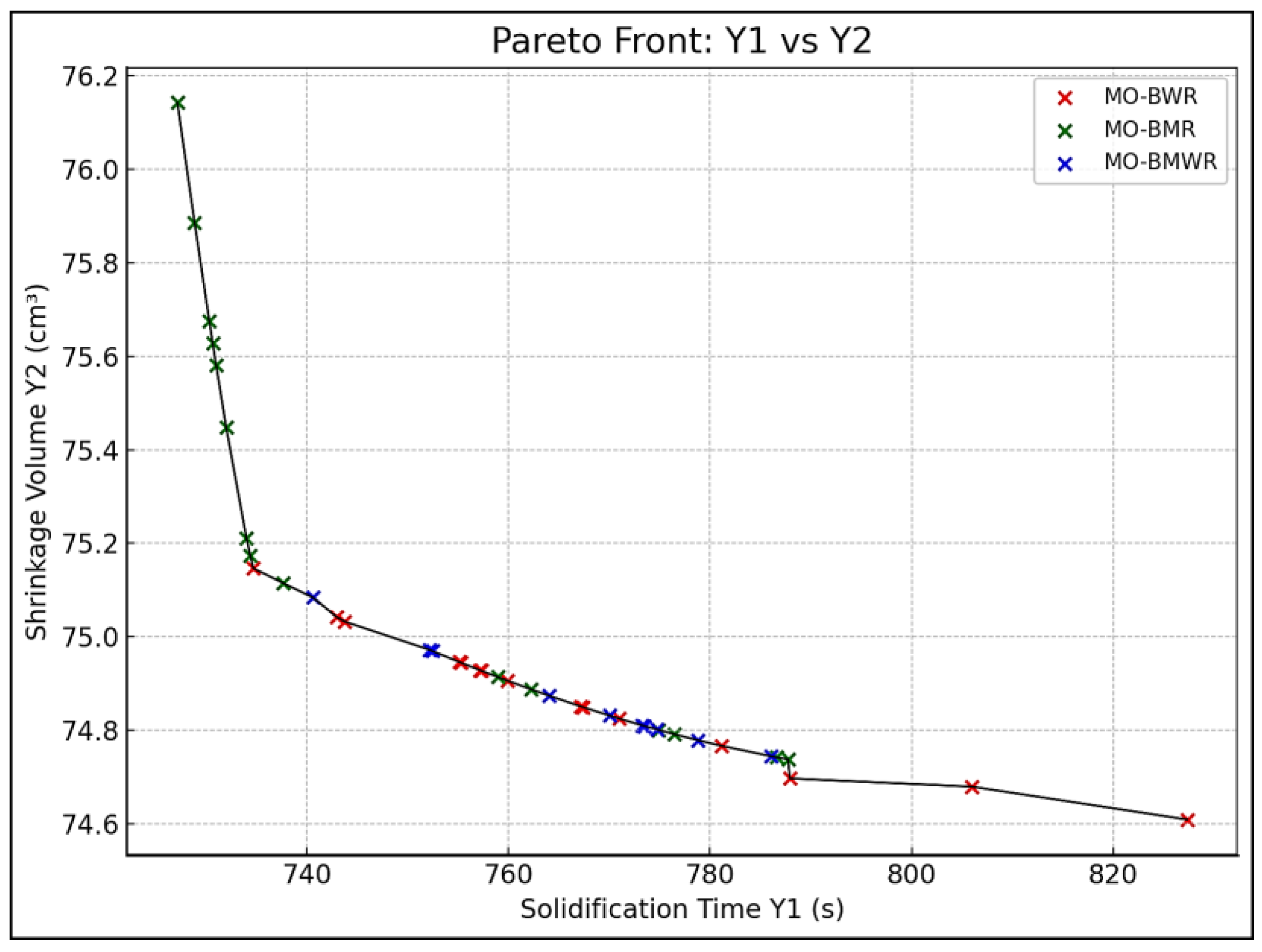
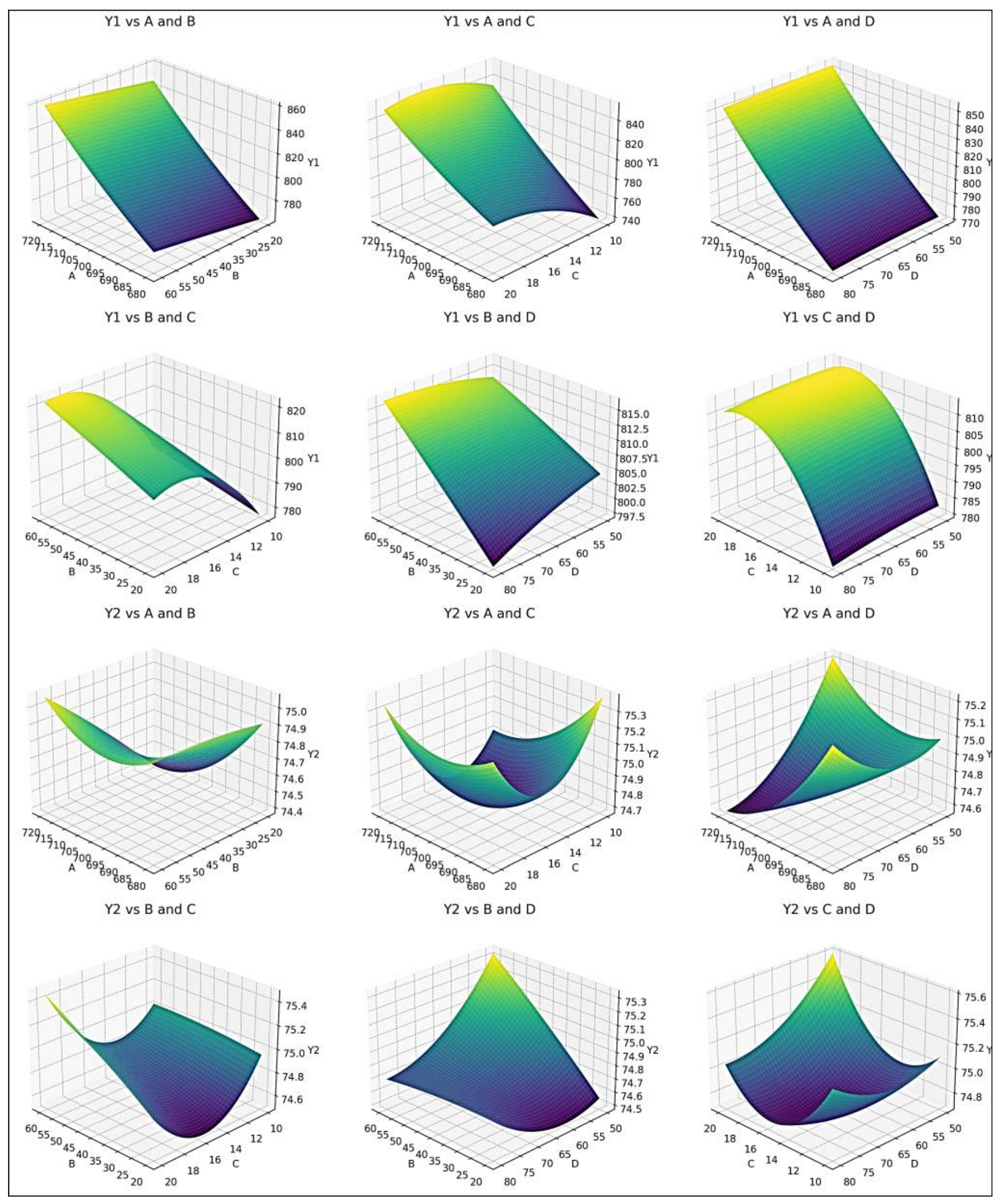
3.2.1. Multi-Objective Optimization of a Low-Pressure Casting Process Using a Sand Mold for Producing A356 Engine Block
+ 0.300926 ∗ D − 0.001438 ∗ A ∗ B − 0.07175 ∗ A ∗ C − 0.0005 ∗ A ∗ D + 0.0235 ∗ B ∗ C + 0.00825 ∗ B ∗ D + 0.004667 ∗ C ∗ D + 0.009823 ∗ A2 − 0.00049 ∗ B2 − 0.474333 ∗ C2 − 0.003259 ∗ D2
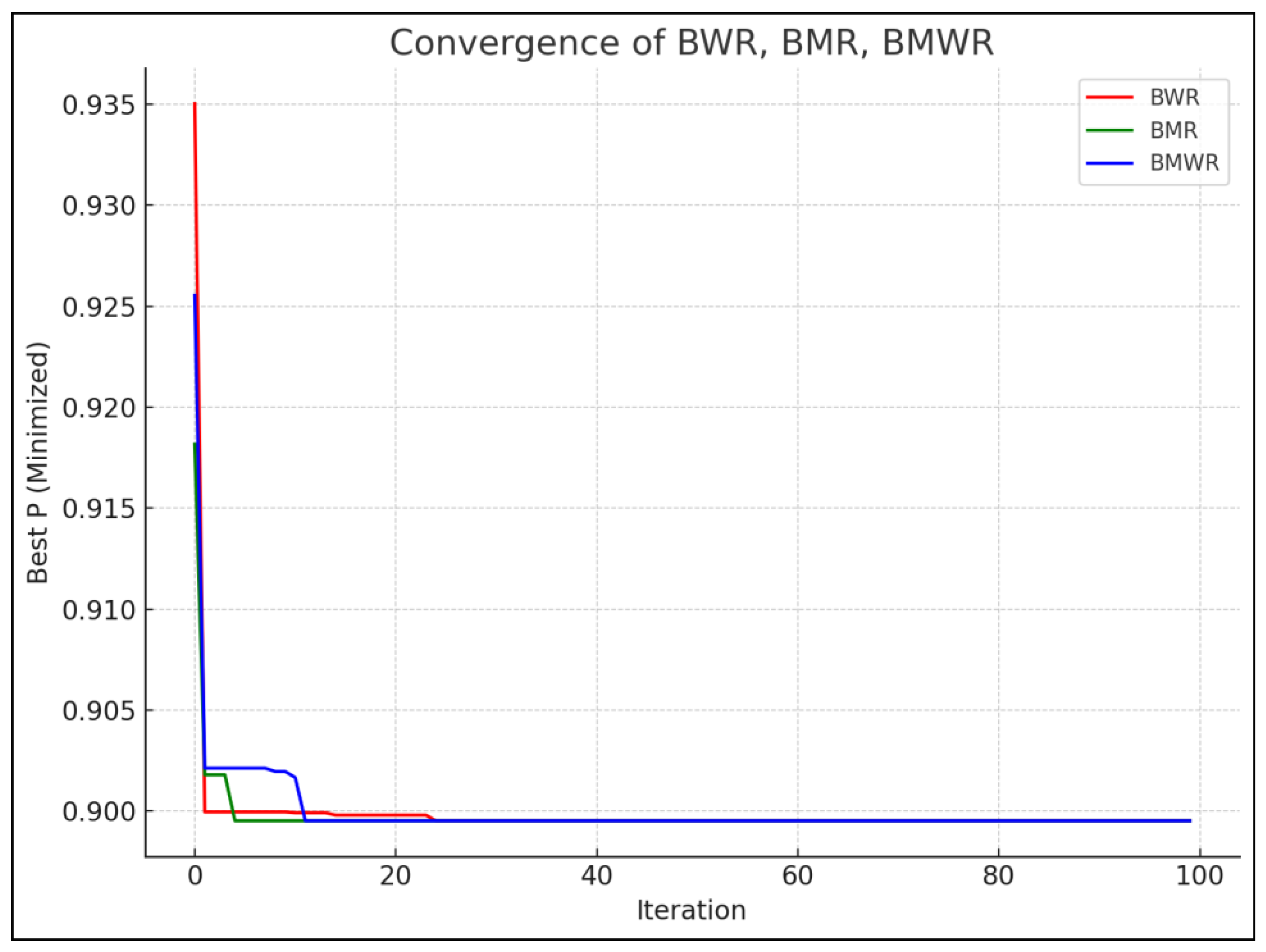
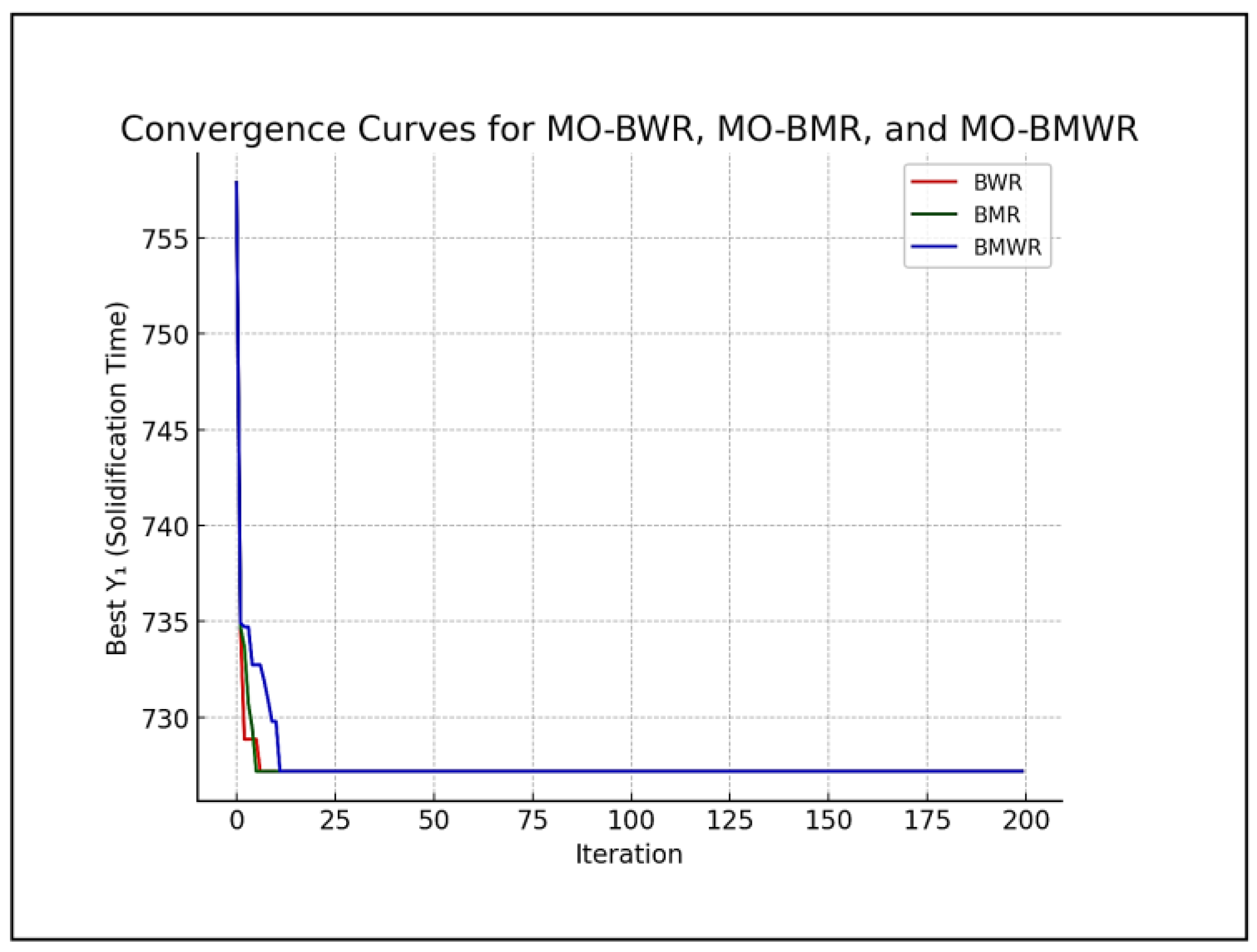
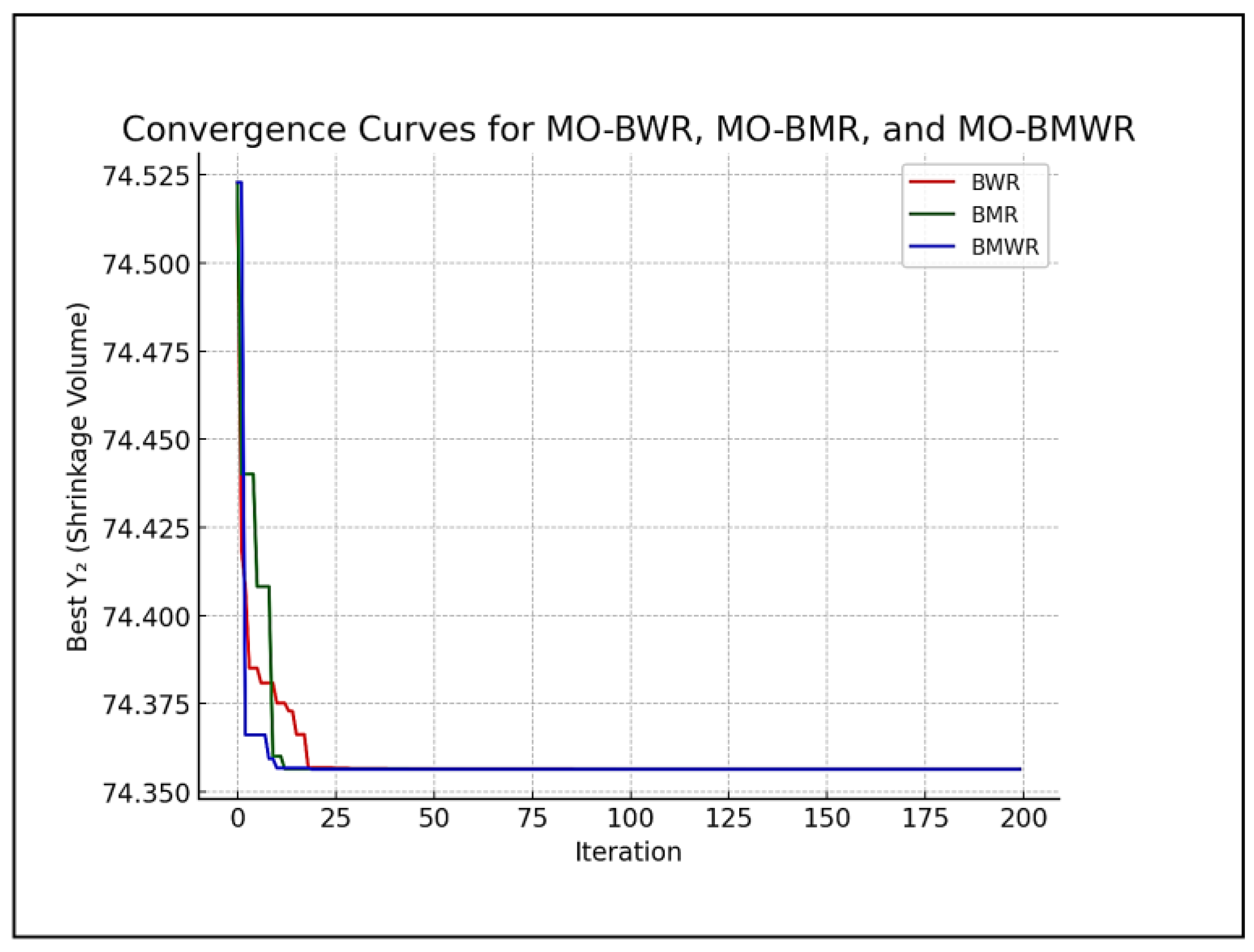
- All three algorithms have given the best minimum value of Y1 as 727.18127 s, corresponding to A = 680 °C, B = 20 °C, C = 10 s, and D = 80 kPa. The convergence graphs are shown in Figure 10.
- Similarly, all three algorithms have given the best minimum value of Y2 as 74.3563 cm3, corresponding to A = 720 °C, B = 20 °C, C = 15.01 s, and D = 71.057 kPa. The convergence graphs are shown in Figure 11.
3.2.2. Multi-Objective Optimization of a Squeeze Casting Process for LM20 Material
- Case 1: Assigning equal weightages to all the objectives Ra, YS, UTS, and H, (i.e., WRa = WYS = WUTS = WH = 0.25).
- Case 2: Assigning 70% weightage to Ra and assigning 10% weightage each to YS, UTS, and H (i.e., WRa = 0.7, WYS = WUTS = WH = 0.10).
- Case 3: Assigning 70% weightage to YS and assigning 10% weightage each to Ra, UTS, and H (i.e., WYS = 0.7, WRa = WUTS = WH = 0.10).
- Case 4: Assigning 70% weightage to UTS and assigning 10% weightage each to Ra, YS, and H (i.e., WUTS = 0.7, WRa = WYS = WH = 0.10).
- Case 5: Assigning 70% weightage to H and assigning 10% weightage each to Ra, YS, and UTS (i.e., WH = 0.7, WRa = WYS = WUTS = 0.10).
4. Conclusions
- Applications to single-objective metal casting process: The BWR, BMR, and BMWR algorithms are applied to the real case studies of (i) optimization of a lost foam casting process for producing a fifth wheel coupling shell from EN-GJS-400-18 ductile iron, (ii) optimization of process parameters of die casting of A360 Al-alloy, and (iii) optimization of wear rate of an AA7178 alloy reinforced with nano-SiC particles produced using a stir-casting process. Comparisons of results are made with RSM and ProCAST 2021 simulations in case study (i), RSM and CAE simulation software in case study (ii), and the metaheuristics such as ABC, Rao-1, and PSO algorithms in case study (iii). The three algorithms achieve better results compared to the simulation software and the metaheuristics. The proposed algorithms showed faster convergence and superior solution quality with fewer function evaluations, highlighting their computational efficiency. For single-objective optimization, BWR, BMR, and BMWR provided the same results for the case studies considered. In general, these three algorithms provide almost the same results with minor variations in the case of single-objective optimization problems. But it is not so in the case of multi-objective optimization problems. Their performances may give different Pareto fronts (and some Pareto front solutions may match), and hence a composite front concept that takes into account all non-duplicated and unique non-dominated solutions is suggested in this paper for the multi-objective optimization of metal casting processes.
- Applications to multi-objective metal casting processes: The multi-objective variants (MO-BWR, MO-BMR, and MO-BMWR) are tested on (iv) two-objectives optimization of a low-pressure casting process using a sand mold for producing A356 engine block and (v) four-objective optimization of a squeeze casting process for LM20 material. These are compared with established methods such as NSGA-II and FEA simulation in case study (iv), and the a priori approach of GA in case study (v). The results show that competitive performance is achievable without added complexity, making the proposed algorithms transparent, interpretable, robust, and versatile for optimizing metal casting processes.
- Decision-making integration: This study employs the BHARAT method—a structured MADM approach—to select the most suitable compromise solutions from Pareto-optimal sets, especially when visual interpretation is impractical in multi-objective problems. This leads to better decision-making for choosing the optimal process parameters in the case of multi-objective optimization problems.
- Broader applicability: The findings suggest that these algorithms are well suited for a wide range of real-world manufacturing challenges across high-dimensional settings and constrained/unconstrained problems alike. Applications include additive manufacturing process optimization, toolpath planning, welding parameter tuning, multi-axis machining, and thermal processing, with further potential through coupling with ML, DL, and ANN models for data-driven workflows. The versatility, scalability, and robustness of the BWR, BMR, and BMWR algorithms make them promising tools for the future of intelligent manufacturing optimization.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Problem | NSGA-II [24] | MOIPSO [24] | MOAGDE [24] | MOGBO [24] | MORCOA [24] | MO-BWR | MO-BMR | MO-BMWR | NSGA-III |
|---|---|---|---|---|---|---|---|---|---|
| ZDT1 | 1.8507 × 10−2 | 1.3665 × 10−2 | 7.9902 × 10−3 | 1.6956 × 10−2 | 2.2389 × 10−2 | 0.0005928 (2.4024 × 10−5) | 0.000633 (1.9272 × 10−5) | 6.0783 × 10−04 [7.9093 × 10−5] | 0.010218 (4.3086 × 10−4) |
| ZDT2 | 1.5718 × 10−2 | 1.3397 × 10−2 | 9.5609 × 10−3 | 1.6123 × 10−2 | 8.6954 × 10−3 | 0.000821 (5.6432 × 10−4) | 0.001060 (7.2644 × 10−4) | 1.5277 × 10−3 [8.5514 × 10−5] | 0.004172 (2.9634 × 10−5) |
| ZDT3 | 1.8403 × 10−2 | 1.5737 × 10−2 | 3.2391 × 10−2 | 1.7805 × 10−2 | 2.3700 × 10−2 | 0.0012825 (3.4899 × 10−4) | 0.0008835 (3.3653 × 10−4) | 9.8901 × 10−4 [3.4633 × 10−4] | 0.007505 (1.7482 × 10−4) |
| ZDT4 | 1.8022 × 10−2 | 2.1423 × 10−2 | 8.0906 × 10−3 | 3.5745 × 10−2 | 1.8508 × 10−2 | 0.001852 (8.3442 × 10−5) | 0.001803 (1.1073 × 10−4) | 1.8412 × 10−3 [8.8294 × 10−5] | 0.010484 (4.8832 × 10−4) |
| ZDT6 | 1.3490 × 10−2 | 1.7261 × 10−1 | 7.0428 × 10−3 | 6.9157 × 10−2 | 4.3206 × 10−3 | 0.054858 (7.5815 × 10−2) | 0.068319 (7.3691 × 10−2) | 3.1609 × 10−2 [6.8207 × 10−2] | 0.002476 (1.0359 × 10−4) |
| Problem | NSGA-II [24] | MOIPSO [24] | MOAGDE [24] | MOGBO [24] | MORCOA [24] | MO-BWR | MO-BMR | MO-BMWR | NSGA-III |
|---|---|---|---|---|---|---|---|---|---|
| ZDT1 | 7.1001 × 10−1 | 7.1584 × 10−1 | 7.1508 × 10−1 | 7.1202 × 10−1 | 7.1367 × 10−1 | 0.875832 (2.7768 × 10−4) | 0.876091 (1.7750 × 10−5) | 8.7585 × 10−1 [2.5627 × 10−4] | 0.871460 (5.9923 × 10−5) |
| ZDT2 | 4.3822 × 10−1 | 4.4061 × 10−1 | 4.3711 × 10−1 | 4.3831 × 10−1 | 4.4099 × 10−1 | 0.527392 (7.5723 × 10−3) | 0.539351 (1.6764 × 10−3) | 5.4111 × 10−1 [1.0968 × 10−3] | 0.538386 (2.4044 × 10−5) |
| ZDT3 | 5.9737 × 10−1 | 5.9804 × 10−1 | 6.1872 × 10−1 | 5.9761 × 10−1 | 5.9735 × 10−1 | 0.72128 (6.9315 × 10−3) | 0.72463 (5.4288 × 10−3) | 7.2442 × 10−1 [5.3662 × 10−3] | 0.724230 (7.6240 × 10−5) |
| ZDT4 | 7.1339 × 10−1 | 0.0000e+0 | 7.0461 × 10−1 | 1.4846 × 10−1 | 7.1533 × 10−1 | 0.872858 (2.9916 × 10−4) | 0.872257 (6.4334 × 10−4) | 8.7258 × 10−1 [6.0676 × 10−4] | 0.867990 (5.2656 × 10−3) |
| ZDT6 | 3.8417 × 10−1 | 3.8400 × 10−1 | 3.8198 × 10−1 | 3.8406 × 10−1 | 3.8595 × 10−1 | 0.615821 (1.7178 × 10−5) | 0.615820 (1.8577 × 10−5) | 6.1574 × 10−1 [1.6094 × 10−5] | 0.607590 (3.2857 × 10−4) |
| Problem | NSGA-II [24] | MOIPSO [24] | MOAGDE [24] | MOGBO [24] | MORCOA [24] | MO-BWR | MO-BMR | MO-BMWR | NSGA-III |
|---|---|---|---|---|---|---|---|---|---|
| ZDT1 | 7.2045 × 10−4 | 5.5523 × 10−5 | 2.3922 × 10−4 | 1.6882 × 10−4 | 7.0812 × 10−6 | 0.005128 (1.1805 × 10−4) | 0.005051 (7.3743 × 10−5) | 5.1523 × 10−3 [2.2083 × 10−4] | 0.003548 (5.0038 × 10−5) |
| ZDT2 | 4.9576 × 10−4 | 5.9375 × 10−6 | 8.3658 × 10−4 | 2.2611 × 10−4 | 6.4197 × 10−6 | 0.004021 (5.1599 × 10−4) | 0.004121 (6.2991 × 10−4) | 4.1159 × 10−3 [3.0825 × 10−4] | 0.003609 (1.5771 × 10−5) |
| ZDT3 | 1.6936 × 10−4 | 5.1251 × 10−5 | 9.2672 × 10−4 | 8.6095 × 10−5 | 7.6050 × 10−5 | 0.003869 (3.2657 × 10−4) | 0.003633 (2.5603 × 10−4) | 3.6800 × 10−3 [3.6984 × 10−4] | 0.002818 (5.8555 × 10−5) |
| ZDT4 | 1.1637 × 10−4 | 6.4948 × 10−1 | 1.4447 × 10−3 | 2.0847 × 10−1 | 7.3824 × 10−5 | 0.005478 (1.5433 × 10−4) | 0.005676 (2.9654 × 10−4) | 5.6024 × 10−3 [2.6104 × 10−4] | 0.004254 (6.5069 × 10−4) |
| ZDT6 | 1.3663 × 10−5 | 1.1629 × 10−1 | 7.2840 × 10−4 | 9.0456 × 10−3 | 4.9198 × 10−6 | 0.006370 (4.1160 × 10−3) | 0.007295 (4.1911 × 10−3) | 4.8786 × 10−3 [2.3941 × 10−3] | 0.004303 (1.4614 × 10−4) |
| Problem | NSGA-II [24] | MOIPSO [24] | MOAGDE [24] | MOGBO [24] | MORCOA [24] | MO-BWR | MO-BMR | MO-BMWR | NSGA-III |
|---|---|---|---|---|---|---|---|---|---|
| ZDT1 | 1.2703 × 10−2 | 8.2757 × 10−3 | 7.8680 × 10−3 | 1.0942 × 10−2 | 9.8560 × 10−3 | 0.000549 (1.6931 × 10−4) | 0.000435 (3.2228 × 10−5) | 5.3919 × 10−4 [1.6076 × 10−4], | 0.003543 (6.8238 × 10−5) |
| ZDT2 | 1.0230 × 10−2 | 8.4165 × 10−3 | 8.9290 × 10−3 | 9.8612 × 10−3 | 7.6915 × 10−3 | 0.018096 (9.1079 × 10−2) | 0.002203 (8.3148 × 10−3) | 1.3404 × 10−3 [4.2971 × 10−4] | 0.003438 (1.6013 × 10−5) |
| ZDT3 | 1.0944 × 10−2 | 9.9319 × 10−3 | 2.8845 × 10−2 | 1.1069 × 10−2 | 1.2028 × 10−2 | 0.003187 (2.8226 × 10−3) | 0.001671 (2.2589 × 10−3) | 1.7209 × 10−3 [2.1574 × 10−3] | 0.003709 (1.0524 × 10−4) |
| ZDT4 | 9.8920 × 10−3 | 4.1352e+0 | 1.3027 × 10−2 | 1.1744e+0 | 7.8954 × 10−3 | 0.002180 (1.5306 × 10−4) | 0.002498 (3.6697 × 10−4) | 2.3071 × 10−3 [3.4921 × 10−4] | 0.005634 (1.3859 × 10−3) |
| ZDT6 | 7.7923 × 10−3 | 7.9355 × 10−3 | 7.7894 × 10−3 | 7.9693 × 10−3 | 6.0637 × 10−3 | 0.000418 (2.8515 × 10−5) | 0.000424 (2.8036 × 10−5) | 4.6332 × 10−4 [3.2756 × 10−5] | 0.004245 (1.3982 × 10−4) |
| Problem | NSGA-II [24] | MOIPSO [24] | MOAGDE [24] | MOGBO [24] | MORCOA [24] | MO-BWR | MO-BMR | MO-BMWR | NSGA-III |
|---|---|---|---|---|---|---|---|---|---|
| ZDT1 | 4.3487 × 10−1 | 3.1745 × 10−1 | 2.5930 × 10−1 | 4.9742 × 10−1 | 2.9873 × 10−1 | 3.1361 × 10−1 [1.1120 × 10−2] | 3.2806 × 10−1 [1.0249 × 10−2] | 3.2199 × 10−1 [3.8097 × 10−2] | 1.0218 × 10−2 [4.3086 × 10−4] |
| ZDT2 | 4.4451 × 10−1 | 3.2170 × 10−1 | 1.6461 × 10−1 | 4.5021 × 10−1 | 1.4780 × 10−1 | 4.0886 × 10−1 [1.9311 × 10−1] | 3.7987 × 10−1 [2.2124 × 10−1] | 3.1730 × 10−1 [1.6494 × 10−2] | 4.1718 × 10−3 [2.9634 × 10−5] |
| ZDT3 | 4.3451 × 10−1 | 3.4276 × 10−1 | 5.8171 × 10−1 | 4.0807 × 10−1 | 5.9475 × 10−1 | 1.1641 × 10−1 [9.8612 × 10−2] | 1.0645 × 10−1 [1.2725 × 10−1] | 1.0169 × 10−1 [1.0970 × 10−1] | 7.5058 × 10−3 [1.7482 × 10−4] |
| ZDT4 | 6.0984 × 10−1 | 8.1658 × 10−1 | 2.5680 × 10−1 | 8.1966 × 10−1 | 2.9792 × 10−1 | 2.8269 × 10−1 [1.3513 × 10−2] | 2.7832 × 10−1 [1.4771 × 10−2] | 2.7892 × 10−1 [1.3435 × 10−2] | 1.0484 × 10−2 [4.8832 × 10−4] |
| ZDT6 | 5.3100 × 10−1 | 1.1330 × 100 | 1.5160 × 10−1 | 7.1663 × 10−1 | 1.0774 × 10−1 | 7.4914 × 10−1 [4.6623 × 10−1] | 8.7928 × 10−1 [4.7150 × 10−1] | 5.5934 × 10−1 [3.8586 × 10−1] | 2.4764 × 10−3 [1.0359 × 10−4] |
References
- Xu, Z.; Chen, T.; Li, B.; Wang, C.; Yang, S.; Chen, Y.; Guo, Z.; Zhang, W.; Guan, R. Optimization of process parameters and microstructure prediction of A360 Al-alloy during die casting. Int. J. Metalcast. 2025, 1–13. [Google Scholar] [CrossRef]
- Li, J.; Wang, D.; Xu, Q. Research on the squeeze casting process of large wheel hub based on FEM and RSM. Int. J. Adv. Manuf. Technol. 2023, 127, 1445–1458. [Google Scholar] [CrossRef]
- Triller, J.; Lopez, M.L.; Nossek, M.; Frenzel, M.A. Multidisciplinary optimization of automotive mega-castings using RSM enhanced by machine learning. Sci. Rep. 2023, 13, 4532. [Google Scholar] [CrossRef]
- Deng, W.; Song, Z.; Lei, J.; Luo, K.; Zhang, Y.; Yu, M. Multi-objective optimization of A356 engine block casting process parameters based on response surface method and NSGA II genetic algorithm. Int. J. Metalcast. 2025, 1–19. [Google Scholar] [CrossRef]
- Bharat, N.; Akhil, G.; Bose, P.S.C. Metaheuristic approach to enhance wear characteristics of novel AA7178/nSiC metal matrix composites. J. Mater. Eng. Perform. 2024, 33, 12638–12655. [Google Scholar] [CrossRef]
- He, B.; Lei, Y.; Jiang, M.; Wang, F. Optimal design of the gating and riser system for complex casting using an evolutionary algorithm. Materials 2022, 15, 7490. [Google Scholar] [CrossRef]
- Deshmukh, S.; Ingle, A.; Thakur, D. Optimization of stir casting process parameters in the fabrication of aluminium based metal matrix composites. Mater. Today Proc. 2023, 82, 485–490. [Google Scholar] [CrossRef]
- Kavitha, M.; Raja, V. Optimization of Insert Roughness and Pouring Conditions to Maximize Bond Strength of (Cp)Al-SS304 Bimetallic Castings Using RSM-GA Coupled Technique. Mater. Today Commun. 2024, 39, 108754. [Google Scholar] [CrossRef]
- Patel, D.S.; Nayak, R.K. Design and Development of Copper Slag Mold for A-356 Alloy Casting. Trans. Indian Inst. Met. 2025, 78, 48. [Google Scholar] [CrossRef]
- Panicker, P.G.; Kuriakose, S. Parameter Optimisation of Squeeze Casting Process Using LM 20 Alloy: Numeral Analysis by Neural Network and Modified Coefficient-Based Deer Hunting Optimization. Aust. J. Mech. Eng. 2020, 21, 351–367. [Google Scholar] [CrossRef]
- Patel, G.C.M.; Krishna, P.; Parappagoudar, M.B. Modelling and Multi-Objective Optimisation of Squeeze Casting Process Using Regression Analysis and Genetic Algorithm. Aust. J. Mech. Eng. 2015, 14, 182–198. [Google Scholar] [CrossRef]
- Li, H.; Ji, H.; Chen, B.; Huang, X.; Xing, M.; Cui, G.; Qiu, C. Optimization of Defects in the Lost Foam Casting Process for Fifth Wheel Coupling Shell. Int. J. Met. 2025, 1–17. [Google Scholar] [CrossRef]
- Simon, D. Evolutionary Optimization Algorithms: Biologically-Inspired and Population-Based Approaches to Computer Intelligence; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Salgotra, R.; Sharma, P.; Raju, S.; Gandomi, A.H. A contemporary systematic review on meta-heuristic optimization algorithms with their MATLAB and Python code reference. Arch. Comput. Methods Eng. 2024, 31, 1749–1822, Erratum in Arch. Comput. Methods Eng. 2024, 31, 1749–1822. [Google Scholar] [CrossRef]
- Rajwar, K.; Deep, K.; Das, S. An exhaustive review of the metaheuristic algorithms for search and optimization: Taxonomy, applications, and open challenges. Artif. Intell. Rev. 2023, 56, 13187–13257. [Google Scholar] [CrossRef]
- Benaissa, B.; Kobayashi, M.; Ali, M.A.; Khatir, T.; Elmeliani, M.E.A.E. Metaheuristic optimization algorithms: An overview. HCMCOUJS-Adv. Comput. Struct. 2024, 14, 34–62. [Google Scholar] [CrossRef]
- Rao, R.V. Rao algorithms: Three metaphor-less simple algorithms for solving optimization problems. Int. J. Ind. Eng. Comput. 2020, 11, 107–130. [Google Scholar]
- Sörensen, K. Metaheuristics—The metaphor exposed. Int. Trans. Oper. Res. 2015, 22, 3–18. [Google Scholar] [CrossRef]
- Aranha, C.L.C.; Villalón, F.; Dorigo, M.; Ruiz, R.; Sevaux, M.; Sörensen, K.; Stützle, T. Metaphor-based metaheuristics, a call for action: The elephant in the room. Swarm Intell. 2021, 16, 1–6. [Google Scholar] [CrossRef]
- Velasco, L.; Guerrero, H.; Hospitaler, A. A literature review and critical analysis of metaheuristics recently developed. Arch. Comput. Methods Eng. 2023, 31, 125–146. [Google Scholar] [CrossRef]
- Sarhani, M.; Voß, S.; Jovanovic, R. Initialization of metaheuristics: Comprehensive review, critical analysis, and research directions. Int. Trans. Oper. Res. 2022, 30, 3361–3397. [Google Scholar] [CrossRef]
- Rao, R.V.; Davim, J.P. Single, multi-, and many-objective optimization of manufacturing processes using two novel and efficient algorithms with integrated decision-making. J. Manuf. Mater. Process. 2025, 9, 249. [Google Scholar] [CrossRef]
- Rao, R.V. BHARAT: A simple and effective multi-criteria decision-making method that does not need fuzzy logic, Part-1: Multi-attribute decision-making applications in the industrial environment. Int. J. Ind. Eng. Comput. 2024, 15, 13–40. [Google Scholar] [CrossRef]
- Ravichandran, S.; Manoharan, P.; Sinha, D.K.; Jangir, P.; Abualigah, L.; Alghamdi, T.A.H. Multi-objective resistance–capacitance optimization algorithm: An effective multi-objective algorithm for engineering design problems. Heliyon 2024, 10, e35921. [Google Scholar] [CrossRef] [PubMed]


| Solution | x1 | x2 | f(x) | c1(x) | p1 | c2(x) | p2 | c3(x) | p3 | M(x) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.37454 | 0.950714 | 1.044138 | 0.325254 | 0.10579 | −0.17454 | 0 | −0.65071 | 0 | 1.149928 (worst) |
| 2 | 0.731994 | 0.598658 | 0.894207 | 0.330652 | 0.109331 | −0.53199 | 0 | −0.29866 | 0 | 1.003538 |
| 3 | 0.156019 | 0.155995 | 0.048676 | −0.68799 | 0 | 0.043981 | 0.001934 | 0.144005 | 0.020738 | 0.071348 (best) |
| 4 | 0.058084 | 0.866176 | 0.753635 | −0.07574 | 0 | 0.141916 | 0.02014 | −0.56618 | 0 | 0.773775 |
| 5 | 0.601115 | 0.708073 | 0.862706 | 0.309188 | 0.095597 | −0.40112 | 0 | −0.40807 | 0 | 0.958303 |
| Solution | x1 | x2 | f(x) | c1(x) | p1 | c2(x) | p2 | c3(x) | p3 | M(x) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.267545 | 0.774863 | 0.671992 | 0.042407 | 0.001798 | −0.067545 | 0 | −0.47486 | 0 | 0.673791 |
| 2 | 0.733605 | 0.391178 | 0.691196 | 0.124783 | 0.015571 | −0.533605 | 0 | −0.091178 | 0 | 0.706767 |
| 3 | 0.183806 | 0 | 0.033788 | −0.816194 | 0 | 0.016194 | 0.000262 | 0.3 | 0.09 | 0.124047 |
| 4 | 0 | 0.548288 | 0.30062 | −0.451712 | 0 | 0.2 | 0.04 | −0.248288 | 0 | 0.34062 |
| 5 | 0.557411 | 0.549129 | 0.61225 | 0.10654 | 0.011351 | −0.357411 | 0 | −0.249129 | 0 | 0.6236 |
| Solution | x1 | x2 | f(x) | c1(x) | p1 | c2(x) | p2 | c3(x) | p3 | M(x) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.267545 | 0.774863 | 0.671992 | 0.042407 | 0.001798 | −0.067545 | 0 | −0.47486 | 0 | 0.673791 |
| 2 | 0.733605 | 0.391178 | 0.691196 | 0.124783 | 0.015571 | −0.533605 | 0 | −0.091178 | 0 | 0.706767 (worst) |
| 3 | 0.156019 | 0.155995 | 0.048676 | −0.68799 | 0 | 0.043981 | 0.001934 | 0.144005 | 0.020738 | 0.071348 (best) |
| 4 | 0 | 0.548288 | 0.30062 | −0.451712 | 0 | 0.2 | 0.04 | −0.248288 | 0 | 0.34062 |
| 5 | 0.557411 | 0.549129 | 0.61225 | 0.10654 | 0.011351 | −0.357411 | 0 | −0.249129 | 0 | 0.6236 |
| Solution | x1 | x2 | f(x) | c1(x) | p1 | c2(x) | p2 | c3(x) | p3 | M(x) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.2 | 0.3 | 0.13 | −0.5 | 0 | 0 | 0 | 0 | 0 | 0.13 |
| 2 | 0.2 | 0.3 | 0.13 | −0.5 | 0 | 0 | 0 | 0 | 0 | 0.13 |
| 3 | 0.2 | 0.3 | 0.13 | −0.5 | 0 | 0 | 0 | 0 | 0 | 0.13 |
| 4 | 0.2 | 0.3 | 0.13 | −0.5 | 0 | 0 | 0 | 0 | 0 | 0.13 |
| 5 | 0.2 | 0.3 | 0.13 | −0.5 | 0 | 0 | 0 | 0 | 0 | 0.13 |
| Solution | x1 | x2 | f(x) | c1(x) | p1 | c2(x) | p2 | c3(x) | p3 | M(x) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.368048 | 0.566656 | 0.456558 | −0.065296 | 0 | −0.168048 | 0 | −0.266656 | 0 | 0.456558 |
| 2 | 0.508289 | 0.277833 | 0.335549 | −0.213877 | 0 | −0.308289 | 0 | 0.22167 | 0.000491 | 0.336041 |
| 3 | 0 | 0 | 0 | −1 | 0 | 0.2 | 0.04 | 0.3 | 0.09 | 0.13 |
| 4 | 0.012418 | 0.766191 | 0.587202 | −0.221392 | 0 | 0.187582 | 0.035187 | −0.466191 | 0 | 0.622389 |
| 5 | 0.46804 | 0.2902 | 0.303278 | −0.24176 | 0 | −0.26804 | 0 | 0.0098 | 0.000096 | 0.303374 |
| Solution | x1 | x2 | f(x) | c1(x) | p1 | c2(x) | p2 | c3(x) | p3 | M(x) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.368048 | 0.566656 | 0.456558 | −0.065296 | 0 | −0.168048 | 0 | −0.266656 | 0 | 0.456558 |
| 2 | 0.508289 | 0.277833 | 0.335549 | −0.213877 | 0 | −0.308289 | 0 | 0.22167 | 0.000491 | 0.336041 |
| 3 | 0.156019 | 0.155995 | 0.048676 | −0.68799 | 0 | 0.043981 | 0.001934 | 0.144005 | 0.020738 | 0.071348 |
| 4 | 0.012418 | 0.766191 | 0.587202 | −0.221392 | 0 | 0.187582 | 0.035187 | −0.466191 | 0 | 0.622389 |
| 5 | 0.46804 | 0.2902 | 0.303278 | −0.24176 | 0 | −0.26804 | 0 | 0.0098 | 0.000096 | 0.303374 |
| Solution | x1 | x2 | f(x) | c1(x) | p1 | c2(x) | p2 | c3(x) | p3 | M(x) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.202291 | 0.816913 | 0.708269 | 0.019205 | 0.000369 | −0.002291 | 0 | −0.516913 | 0 | 0.708638 |
| 2 | 0.776958 | 0.401608 | 0.764953 | 0.178566 | 0.031886 | −0.576958 | 0 | −0.101608 | 0 | 0.796838 |
| 3 | 0.253334 | 0 | 0.064178 | −0.746666 | 0 | −0.053334 | 0 | 0.3 | 0.09 | 0.154178 |
| 4 | 0 | 0.448303 | 0.200976 | −0.551697 | 0 | 0.2 | 0.04 | −0.148303 | 0 | 0.240976 |
| 5 | 0.555449 | 0608088 | 0.678294 | 0.163536 | 0.026744 | −0.355449 | 0 | −0.308088 | 0 | 0.705038 |
| Solution | x1 | x2 | f(x) | c1(x) | p1 | c2(x) | p2 | c3(x) | p3 | M(x) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.202291 | 0.816913 | 0.708269 | 0.019205 | 0.000369 | −0.002291 | 0 | −0.516913 | 0 | 0.708638 |
| 2 | 0.776958 | 0.401608 | 0.764953 | 0.178566 | 0.031886 | −0.576958 | 0 | −0.101608 | 0 | 0.796838 |
| 3 | 0.156019 | 0.155995 | 0.048676 | −0.68799 | 0 | 0.043981 | 0.001934 | 0.144005 | 0.020738 | 0.071348 |
| 4 | 0 | 0.448303 | 0.200976 | −0.551697 | 0 | 0.2 | 0.04 | −0.148303 | 0 | 0.240976 |
| 5 | 0.555449 | 0608088 | 0.678294 | 0.163536 | 0.026744 | −0.355449 | 0 | −0.308088 | 0 | 0.705038 |
| Feature | BWR | BMR | BMWR |
|---|---|---|---|
| Search mechanism type | Hybrid arithmetic with best–worst–random guidance | Hybrid arithmetic with best–mean–random guidance | Hybrid arithmetic combining best–mean–worst–random |
| Novel equation logic | Combines (best–F × random) and (worst–random) differences; fallback to uniform sampling | Combines (best–F × mean) and (best–random); fallback to uniform sampling | Combines (best–F × mean) and (worst–random); fallback to uniform sampling |
| Handling of random influence | Direct—random solution explicitly part of update | Same as BWR | Same as BWR and BMR |
| Fallback sampling | Yes: if r4 ≤ 0.5, fallback to uniform random within bounds | Same as BWR | Same as BWR |
| Diversity mechanism | Very strong, due to combination of best, worst, and random solutions | Strong, but more conservative due to mean guidance | Very strong, integrates best, mean, worst, and random |
| Exploration–exploitation balance | Highly exploratory, still exploits best | More exploitative, smoother convergence via mean-based pull | Balanced—exploration from worst/random, exploitation from best/mean |
| Design simplicity | Slightly complex (two difference terms + fallback), but parameter-free and metaphor-free | Similarly to BWR and still parameter-free | Slightly more complex (all four references), but parameter-free |
| Robustness to local optima | Strong—fallback randomness + worst guidance help escape | Good, but conservative due to mean-based bias | Strongest—mixed forces reduce trapping in local optima |
| Risk of premature convergence | Low (due to worst + random) | Low–moderate (mean pulls population together) | Low (conflicting forces maintain diversity) |
| Parameter dependence | None beyond population size and iterations | None beyond population size and iterations | None beyond population size and iterations |
| Convergence speed | Slower—broad exploration before exploitation | Faster—mean accelerates convergence | Intermediate—not as fast as BMR, but more diverse |
| Constraint handling compatibility | Works well with penalty methods, strong exploration helps recover feasibility | May converge prematurely in tight feasible spaces | More robust than both, balances feasibility search and convergence |
| Multi-objective performance | Produces well-spread Pareto sets due to strong diversity | Generates smoother but sometimes narrower Pareto sets | Best compromise—well-distributed and convergent Pareto fronts |
| Scalability with dimensionality | May lose efficiency in very high dimensions (overexplores) | Stable, but risks local trapping as dimensions grow | Better scalability—multiple guiding forces adapt well |
| Computational cost per iteration | Light—simple difference calculations | Same as BWR | Slightly higher (two guiding forces), but still lighter than GA/PSO/DE |
| Step No. | Step Title | Description |
|---|---|---|
| 1 | Start | Initiate the algorithm. |
| 2 | Initialize population | Generate the initial set of solutions within defined variable bounds. |
| 3 | Elite seeding | Introduce high-quality or historically good solutions into the initial population. |
| 4 | Fast non-dominated sorting | Rank solutions based on Pareto dominance and compute crowding distance. |
| 5 | Constraint repair | Try to rectify any constraint violations in the solutions as the primary strategy. |
| 6 | Penalty application | Impose penalties on the objective functions if constraint violations persist (fallback strategy). |
| 7 | Objective function evaluation | Assess all objective functions for every solution in the population. |
| 8 | Edge boosting | Promote exploration in regions close to the extreme ends of the Pareto front. |
| 9 | Local exploration | Improve elite or high-potential solutions by conducting a search in their local neighborhood. |
| 10 | Population update (BWR/BMR/BMWR) | Create new candidate solutions using the specific update mechanism of BWR, BMR, or BMWR. |
| 11 | Check termination criterion | Check if the stopping condition (e.g., maximum iterations or evaluations) has been reached. |
| 12 | If not terminated, repeat (go to step 5) | If termination condition is not met, return to Step 5 and continue the process. |
| 13 | If terminated, output solutions | Terminate the algorithm and present the final set of non-dominated Pareto-optimal solutions. |
| Method | Optimal Porosity (%) | Process Input Parameters | ||
|---|---|---|---|---|
| Pouring Temperature A (°C) | Pouring Speed B (kg/s) | Ferro-Static Head Pressure C (Pa) | ||
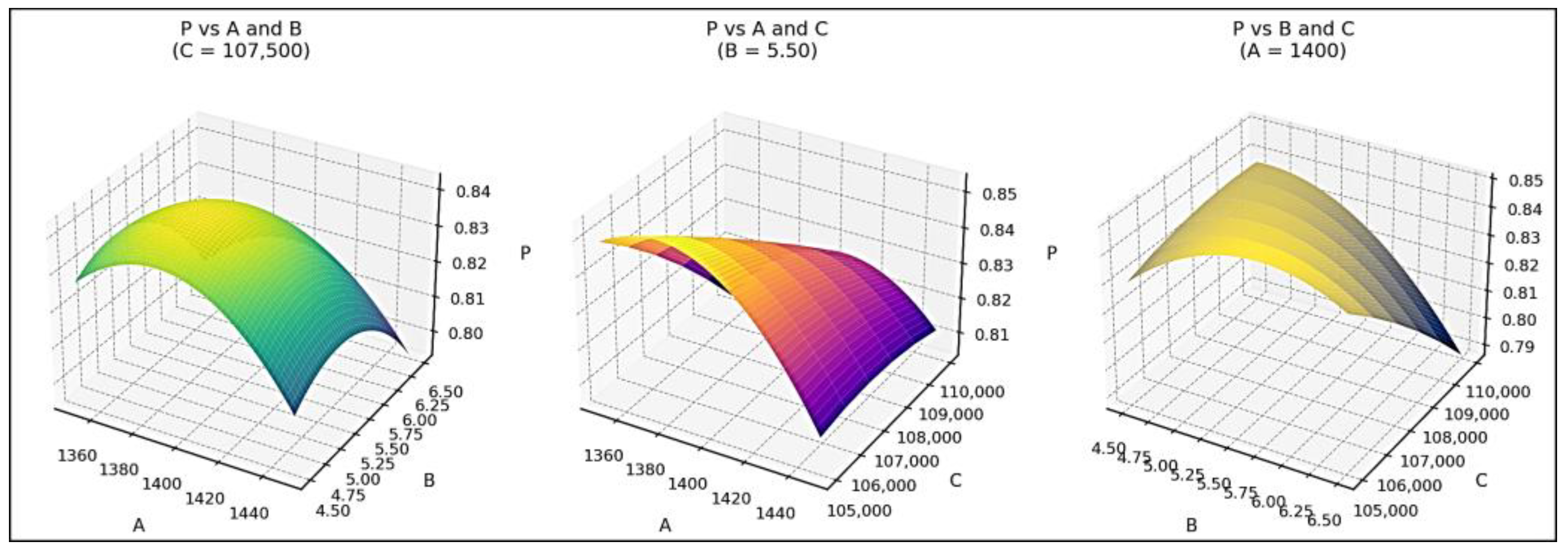
| Simulation by RSM and ProCAST 2021 [12] | 0.7920 | 1386 | 6.42 | 109751 |
| BWR | 0.7635 | 1350 | 6.5 | 110000 |
| BMR | 0.7635 | 1350 | 6.5 | 110000 |
| BMWR | 0.7635 | 1350 | 6.5 | 110000 |
| Method | Optimal Volumetric Porosity (cm3) | Process Input Parameters | ||
|---|---|---|---|---|
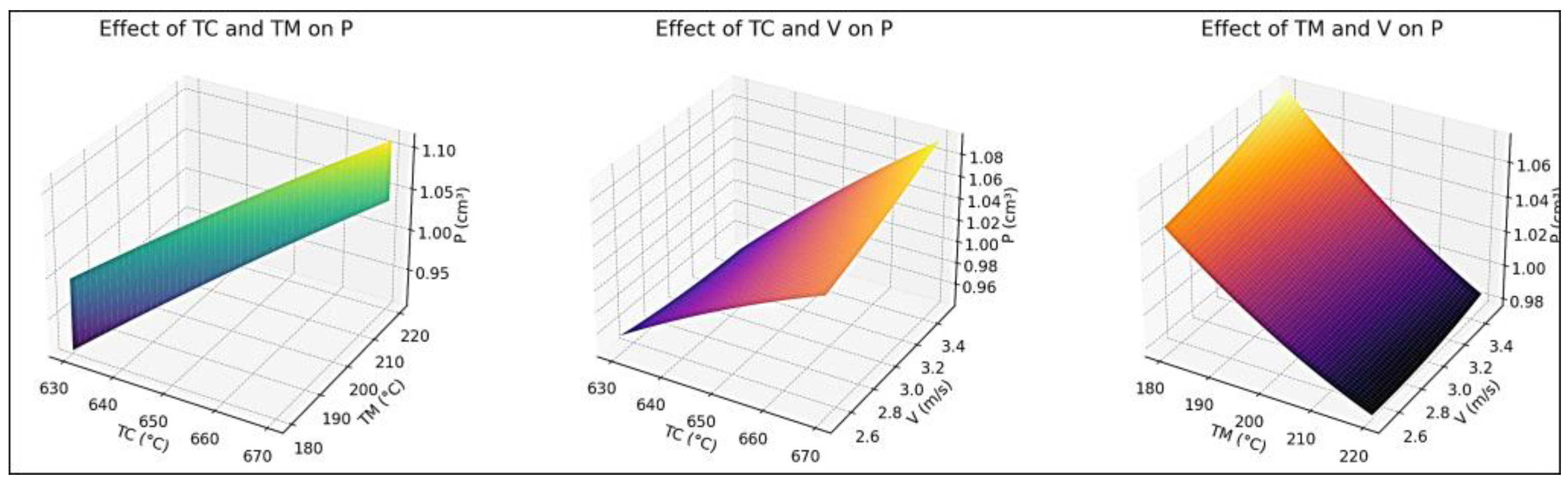
| Casting Temperature TC (°C) | Mold Preheating Temperature TM (°C) | Fast Injection Speed V (m/s) | ||
| Simulation by RSM and CAE software [1] | 0.9203 (corrected value) | 630 | 220 | 2.5 |
| BWR | 0.8995 | 630 | 220 | 3.5 |
| BMR | 0.8995 | 630 | 220 | 3.5 |
| BMWR | 0.8995 | 630 | 220 | 3.5 |
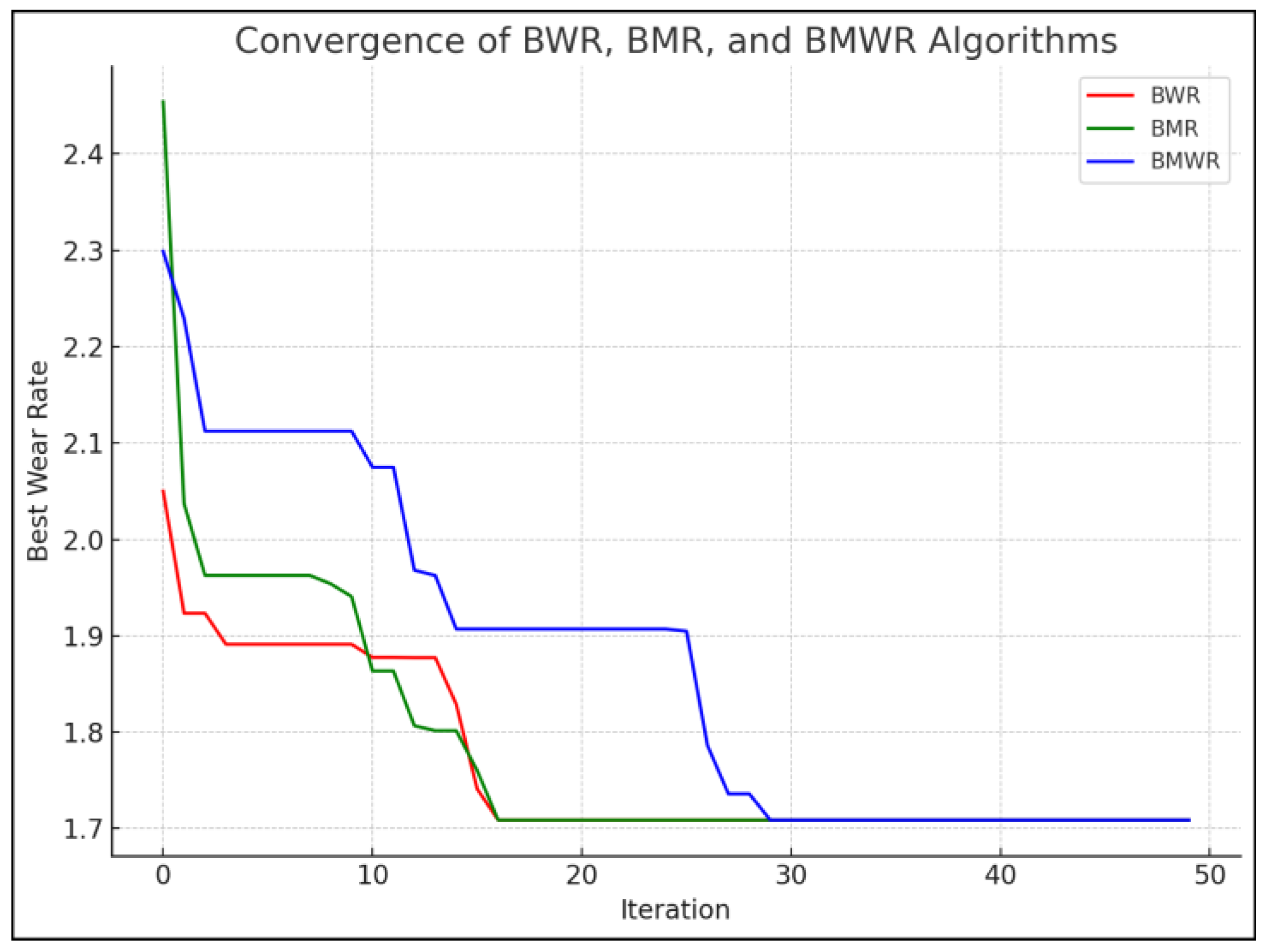
| Algorithm | Optimal Wear Rate ((mm3/m) ∗ 10−3) | Optimum Values of Input Variables | |||
|---|---|---|---|---|---|
| A (m/s) | B (m) | C (N) | D (%) | ||
| ABC [5] | 1.7093 | Not given | Not given | Not given | Not given |
| Rao-1 [5] | 1.7088 | 4 | 500 | 9.81 | 3 |
| PSO [5] | 2.1809 | Not given | Not given | Not given | Not given |
| BWR | 1.7088 | 4 | 500 | 9.81 | 3 |
| BMR | 1.7088 | 4 | 500 | 9.81 | 3 |
| BMWR | 1.7088 | 4 | 500 | 9.81 | 3 |
| Algorithm | GD | IGD | Spacing | Spread | Hypervolume |
|---|---|---|---|---|---|
| MO-BWR | 0 | 0.162757 | 0.267771 | 0.836069 | 0.516014 |
| MO-BMR | 0 | 0.065284 | 0.021535 | 0.845045 | 0.623620 |
| MO-BMWR | 0 | 0.032764 | 0.045740 | 0.506841 | 0.731088 |
| Composite | 0 | 0 | 0.042701 | 0.811891 | 0.762125 |
| S.No. | A (°C) | B (°C) | C (s) | D (kPa) | Y1 (s) | Y2 (cm3) | Algorithm | Normalized Y1 | Normalized Y2 | Score |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 680 | 20 | 10 | 50 | 734.7135 | 75.14654 | MO-BWR | 0.989748 | 0.992843 | 0.991296 |
| 2 | 685.4846 | 25.48459 | 11.37115 | 54.11345 | 757.3426 | 74.92711 | MO-BWR | 0.960175 | 0.995751 | 0.977963 |
| 3 | 708.8844 | 36.02023 | 15.90399 | 71.66332 | 827.3466 | 74.60873 | MO-BWR | 0.878932 | 1 | 0.939466 |
| 4 | 684.9727 | 24.97272 | 11.24318 | 53.72954 | 755.3044 | 74.94447 | MO-BWR | 0.962766 | 0.99552 | 0.979143 |
| 5 | 685.4491 | 25.44909 | 11.36227 | 54.08682 | 757.2017 | 74.9283 | MO-BWR | 0.960353 | 0.995735 | 0.978044 |
| 6 | 686.138 | 26.13801 | 11.5345 | 54.60351 | 759.9224 | 74.9059 | MO-BWR | 0.956915 | 0.996033 | 0.976474 |
| 7 | 682.0422 | 20 | 10.51054 | 51.53162 | 742.955 | 75.04257 | MO-BWR | 0.978769 | 0.994219 | 0.986494 |
| 8 | 688.066 | 28.06604 | 12.01651 | 56.04953 | 767.3905 | 74.84942 | MO-BWR | 0.947603 | 0.996784 | 0.972193 |
| 9 | 688.0047 | 28.00472 | 12.00118 | 56.00354 | 767.1563 | 74.85108 | MO-BWR | 0.947892 | 0.996762 | 0.972327 |
| 10 | 694.0565 | 29.85468 | 13.51413 | 60.54238 | 787.9312 | 74.69669 | MO-BWR | 0.922899 | 0.998822 | 0.960861 |
| 11 | 682.2537 | 20 | 10.56343 | 51.69028 | 743.7901 | 75.03229 | MO-BWR | 0.97767 | 0.994355 | 0.986012 |
| 12 | 691.7727 | 31.77268 | 12.94317 | 58.82951 | 781.1432 | 74.76651 | MO-BWR | 0.930919 | 0.99789 | 0.964405 |
| 13 | 699.3755 | 36.86892 | 14.84387 | 64.53161 | 805.9659 | 74.67923 | MO-BWR | 0.902248 | 0.999056 | 0.950652 |
| 14 | 684.9284 | 24.92842 | 11.2321 | 53.69631 | 755.1272 | 74.946 | MO-BWR | 0.962992 | 0.9955 | 0.979246 |
| 15 | 689.0101 | 29.01013 | 12.25253 | 56.75759 | 770.9689 | 74.8251 | MO-BWR | 0.943204 | 0.997108 | 0.970156 |
| 16 | 693.636 | 33.63601 | 13.409 | 60.22701 | 787.756 | 74.73758 | MO-BMR | 0.923105 | 0.998276 | 0.96069 |
| 17 | 690.4862 | 30.48621 | 12.62155 | 57.86466 | 776.4602 | 74.79146 | MO-BMR | 0.936534 | 0.997557 | 0.967045 |
| 18 | 680 | 20 | 10 | 80 | 727.1813 | 76.14287 | MO-BMR | 1 | 0.979852 | 0.989926 |
| 19 | 680 | 20 | 10 | 69.99374 | 730.3456 | 75.67571 | MO-BMR | 0.995667 | 0.985901 | 0.990784 |
| 20 | 693.3065 | 33.3065 | 13.32663 | 59.97988 | 786.6013 | 74.74207 | MO-BMR | 0.92446 | 0.998216 | 0.961338 |
| 21 | 680.6979 | 20.69788 | 10.17447 | 50.52341 | 737.6896 | 75.11451 | MO-BMR | 0.985755 | 0.993267 | 0.989511 |
| 22 | 680 | 20 | 10 | 63.60292 | 732.0251 | 75.44797 | MO-BMR | 0.993383 | 0.988877 | 0.99113 |
| 23 | 686.7382 | 26.73821 | 11.68455 | 55.05365 | 762.2703 | 74.88734 | MO-BMR | 0.953968 | 0.99628 | 0.975124 |
| 24 | 680 | 20 | 10 | 67.52154 | 731.0268 | 75.58108 | MO-BMR | 0.994739 | 0.987135 | 0.990937 |
| 25 | 685.892 | 25.89203 | 11.47301 | 54.41903 | 758.9542 | 74.91376 | MO-BMR | 0.958136 | 0.995928 | 0.977032 |
| 26 | 680 | 20 | 10 | 51.89557 | 734.4112 | 75.17359 | MO-BMR | 0.990156 | 0.992486 | 0.991321 |
| 27 | 680 | 20 | 10 | 68.7771 | 730.6858 | 75.62811 | MO-BMR | 0.995204 | 0.986521 | 0.990862 |
| 28 | 680 | 20 | 10 | 54.11347 | 734.0277 | 75.21138 | MO-BMR | 0.990673 | 0.991987 | 0.99133 |
| 29 | 690.0543 | 30.0543 | 12.51358 | 57.54073 | 774.8665 | 74.80075 | MO-BMR | 0.93846 | 0.997433 | 0.967947 |
| 30 | 680 | 20 | 10 | 74.86169 | 728.8877 | 75.88612 | MO-BMR | 0.997659 | 0.983167 | 0.990413 |
| 31 | 689.6883 | 29.68833 | 12.42208 | 57.26624 | 773.5076 | 74.80898 | MO-BMWR | 0.940109 | 0.997323 | 0.968716 |
| 32 | 684.2734 | 24.27337 | 11.06834 | 53.20503 | 752.4951 | 74.96921 | MO-BMWR | 0.96636 | 0.995192 | 0.980776 |
| 33 | 691.1338 | 31.13376 | 12.78344 | 58.35032 | 778.8293 | 74.77839 | MO-BMWR | 0.933685 | 0.997731 | 0.965708 |
| 34 | 688.7624 | 28.76243 | 12.19061 | 56.57182 | 770.035 | 74.83127 | MO-BMWR | 0.944348 | 0.997026 | 0.970687 |
| 35 | 684.201 | 24.20103 | 11.05026 | 53.15078 | 752.2029 | 74.97184 | MO-BMWR | 0.966736 | 0.995157 | 0.980946 |
| 36 | 690.0159 | 30.03474 | 12.50854 | 57.52065 | 774.7549 | 74.80144 | MO-BMWR | 0.938595 | 0.997424 | 0.96801 |
| 37 | 693.1592 | 33.15919 | 13.2898 | 59.86939 | 786.083 | 74.74417 | MO-BMWR | 0.925069 | 0.998188 | 0.961629 |
| 38 | 689.6283 | 29.58275 | 12.40043 | 57.2085 | 773.2337 | 74.81047 | MO-BMWR | 0.940442 | 0.997303 | 0.968873 |
| 39 | 687.2027 | 27.20275 | 11.80069 | 55.40206 | 764.0732 | 74.87358 | MO-BMWR | 0.951717 | 0.996463 | 0.97409 |
| 40 | 681.3968 | 21.39681 | 10.3492 | 51.04761 | 740.642 | 75.08364 | MO-BMWR | 0.981826 | 0.993675 | 0.98775 |
| Optimization Method | Optimum Pouring Temperature A (°C) | Optimum Mold Preheating Temperature B (°C) | Optimum Filling Time C (s) | Optimum Holding Pressure D (kPa) | Optimum Solidification Time Y1 (s) | Optimum Shrinkage Volume Y2 (cm3) |
|---|---|---|---|---|---|---|
| NSGA-II [4] | 680 | 20 | 12 | 50 | 750.17 | 74.89 |
| Finite Element Simulation [4] | Not given | Not given | Not given | Not given | 745 | 74.25 |
| Composite front of the present work | 680 | 20 | 10 | 54.11 | 734.02 | 75.21 (MO-BMR) |
| 680 | 20 | 10 | 51.89 | 734.41 | 75.17 (MO-BMR) | |
| 680 | 20 | 10 | 50 | 734.71 | 75.14 (MO-BWR) | |
| 680 | 20 | 10 | 63.60 | 732.02 | 75.44 (MO-BMR) | |
| 680 | 20 | 10 | 67.52 | 731.02 | 75.58 (MO-BMR) |
| Algorithm | Process Parameters | Objectives (i.e., Process Responses) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Td (s) | Dp (s) | Sp (MPa) | Pt (°C) | Dt (°C) | Ra (µm) | YS (MPa) | UTS (MPa) | H (BHN) | |
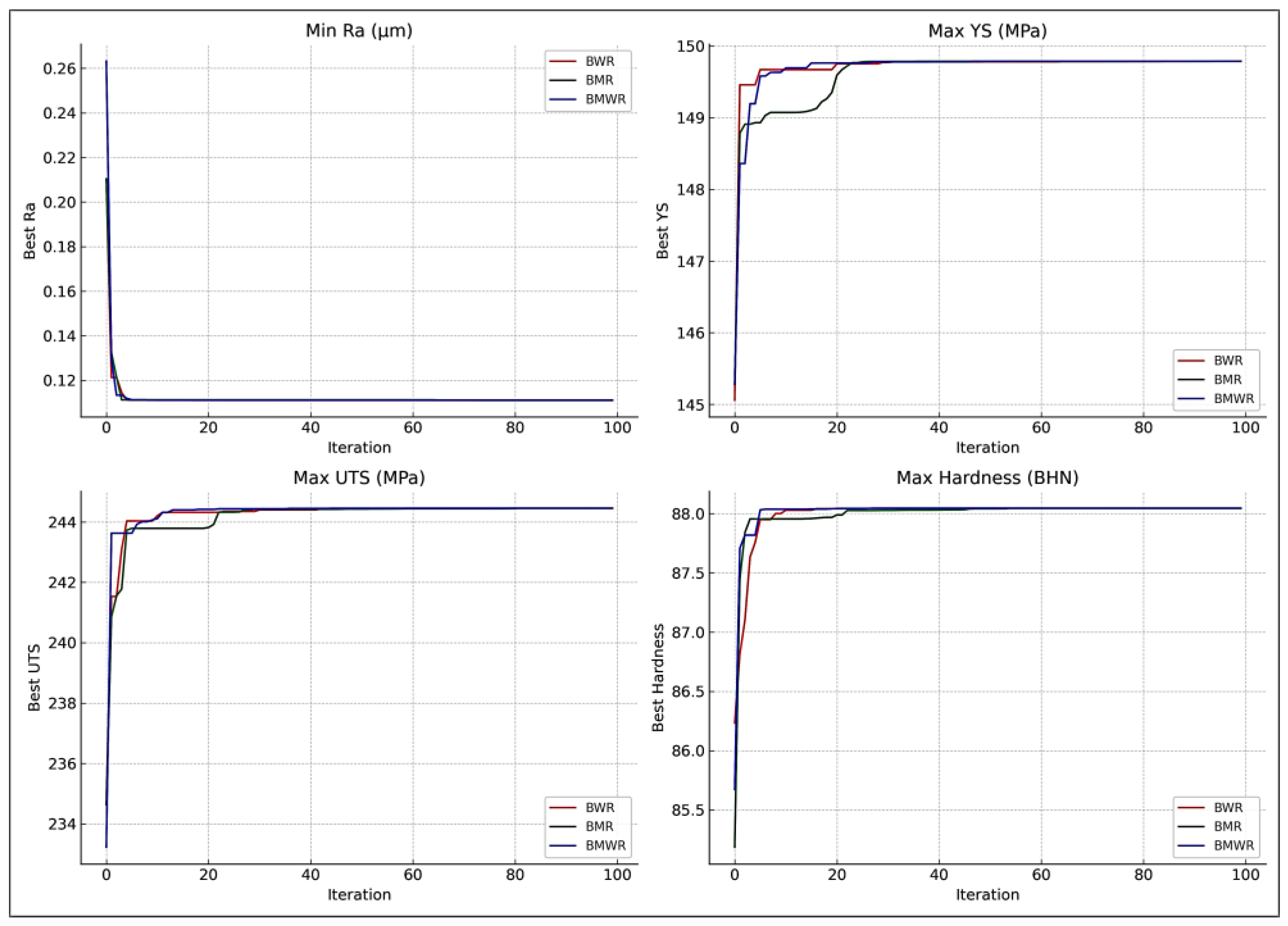
| BWR | 4.261923 | 50 | 182.6434 | 750 | 300 | 0.111111 | |||
| BMR | 4.261923 | 50 | 182.6434 | 750 | 300 | 0.111111 | |||
| BMWR | 4.261923 | 50 | 182.6434 | 750 | 300 | 0.111111 | |||
| BWR | 3 | 42.41497 | 154.1347 | 708.4726 | 230.3095 | 149.7879 | |||
| BMR | 3 | 42.41497 | 154.1347 | 708.4726 | 230.3095 | 149.7879 | |||
| BMWR | 3 | 42.41497 | 154.1347 | 708.4726 | 230.3095 | 149.7879 | |||
| BWR | 3 | 43.12943 | 167.647 | 708.146 | 240.6784 | 244.4533 | |||
| BMR | 3 | 43.12943 | 167.647 | 708.146 | 240.6784 | 244.4533 | |||
| BMWR | 3 | 43.12943 | 167.647 | 708.146 | 240.6784 | 244.4533 | |||
| BWR | 3 | 50 | 164.1633 | 723.1391 | 273.3112 | 88.0455 | |||
| BMR | 3 | 50 | 164.1633 | 723.1391 | 273.3112 | 88.0455 | |||
| BMWR | 3 | 50 | 164.1633 | 723.1391 | 273.3112 | 88.0455 | |||
| Solution | Squeeze Casting Process Parameters | Process Responses (i.e., Objectives) | Algorithm | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Td (s) | Dp (s) | Sp (MPa) | Pt (°C) | Dt (°C) | Ra (µm) | YS (MPa) | UTS (MPa) | H (BHN) | Algorithm | |
| 1 | 3 | 44.18163 | 161.653 | 711.2367 | 240.5869 | 0.293334 | 149.4999 | 244.3224 | 87.34117 | MO-BMWR |
| 2 | 3 | 44.54666 | 160.6631 | 711.2168 | 243.4631 | 0.289372 | 149.4262 | 244.2634 | 87.42063 | MO-BWR |
| 3 | 3 | 44.67159 | 159.4151 | 714.4595 | 239.9935 | 0.283978 | 149.5085 | 244.1367 | 87.37318 | MO-BMR |
| 4 | 3 | 44.83501 | 163.0088 | 712.1447 | 246.8998 | 0.27798 | 149.1982 | 244.2393 | 87.53026 | MO-BWR |
| 5 | 3 | 45.15195 | 166.6539 | 713.2368 | 242.3581 | 0.272064 | 149.1896 | 244.3084 | 87.45358 | MO-BMWR |
| 6 | 3 | 44.14191 | 157.9521 | 708.5658 | 234.6453 | 0.313732 | 149.7124 | 244.1432 | 87.10444 | MO-BMWR |
| 7 | 3 | 45.26108 | 161.1808 | 716.6505 | 241.7855 | 0.269015 | 149.3383 | 244.0703 | 87.47581 | MO-BWR |
| 8 | 3 | 45.10441 | 163.5533 | 714.0757 | 246.921 | 0.269522 | 149.1363 | 244.1793 | 87.56658 | MO-BMR |
| 9 | 3 | 44.17161 | 155.1055 | 708.3735 | 237.4219 | 0.316343 | 149.6931 | 244.0364 | 87.14081 | MO-BWR |
| 10 | 3 | 45.04359 | 163.7003 | 714.3668 | 249.1897 | 0.266989 | 149.0196 | 244.1136 | 87.61104 | MO-BWR |
| 11 | 3 | 44.09115 | 152.9356 | 711.4833 | 238.185 | 0.310642 | 149.6621 | 243.8713 | 87.16622 | MO-BWR |
| 12 | 3 | 47.68317 | 159.557 | 714.556 | 236.1015 | 0.26574 | 149.4178 | 243.8217 | 87.38652 | MO-BMR |
| 13 | 3 | 45.52768 | 158.0346 | 719.1317 | 245.1684 | 0.262198 | 149.1917 | 243.7526 | 87.5529 | MO-BWR |
| 14 | 3 | 44.99959 | 165.8949 | 715.562 | 251.3382 | 0.259457 | 148.7867 | 244.0225 | 87.65617 | MO-BMWR |
| 15 | 3 | 46.57805 | 159.0652 | 719.7985 | 246.6745 | 0.249873 | 149.0289 | 243.6312 | 87.63913 | MO-BMR |
| 16 | 3 | 44.73873 | 152.6987 | 714.4641 | 232.0572 | 0.30372 | 149.6756 | 243.6198 | 87.04827 | MO-BMR |
| 17 | 3 | 47.40826 | 166.9209 | 714.6235 | 251.2354 | 0.243811 | 148.6293 | 243.8452 | 87.73349 | MO-BMWR |
| 18 | 3 | 46.42214 | 159.6335 | 714.8783 | 253.8669 | 0.257495 | 148.7964 | 243.6796 | 87.73055 | MO-BWR |
| 19 | 3 | 47.67281 | 158.9126 | 719.9781 | 246.2668 | 0.242383 | 148.9663 | 243.4879 | 87.6682 | MO-BMR |
| 20 | 3 | 45.96921 | 160.8699 | 723.0505 | 236.6517 | 0.252846 | 149.1796 | 243.5409 | 87.39452 | MO-BMWR |
| 21 | 3 | 46.35167 | 161.9085 | 723.0113 | 237.7331 | 0.247604 | 149.1107 | 243.5543 | 87.44449 | MO-BWR |
| 22 | 3 | 49.3623 | 159.9883 | 720.2755 | 242.8822 | 0.23172 | 148.91 | 243.2814 | 87.65448 | MO-BWR |
| 23 | 3 | 45.59133 | 167.3896 | 719.3487 | 254.638 | 0.240582 | 148.3674 | 243.6343 | 87.75124 | MO-BMWR |
| 24 | 3 | 45.89205 | 162.5846 | 722.1216 | 253.2663 | 0.238232 | 148.5263 | 243.4117 | 87.75852 | MO-BWR |
| 25 | 3 | 47.35981 | 167.9442 | 721.7841 | 250.5326 | 0.224544 | 148.3718 | 243.4575 | 87.75625 | MO-BMR |
| 26 | 3 | 48.11982 | 158.2283 | 716.7499 | 257.6829 | 0.239842 | 148.3936 | 243.1094 | 87.84279 | MO-BMR |
| 27 | 3 | 47.6624 | 162.7167 | 720.2609 | 256.8525 | 0.227484 | 148.2548 | 243.1699 | 87.86863 | MO-BMR |
| 28 | 3 | 47.4309 | 156.3822 | 722.9969 | 252.775 | 0.235388 | 148.545 | 242.9492 | 87.75364 | MO-BMR |
| 29 | 3 | 46.76511 | 161.2831 | 728.2398 | 244.7107 | 0.22718 | 148.581 | 242.943 | 87.61221 | MO-BMWR |
| 30 | 3 | 47.84515 | 168.0365 | 722.0871 | 255.4358 | 0.216485 | 148.0183 | 243.1438 | 87.84824 | MO-BMWR |
| 31 | 3 | 49.658 | 165.1301 | 715.4336 | 259.0886 | 0.222522 | 147.9725 | 243.0083 | 87.92303 | MO-BMR |
| 32 | 3 | 49.26079 | 176.1734 | 721.0641 | 244.8636 | 0.212542 | 147.9127 | 243.183 | 87.57998 | MO-BMWR |
| 33 | 3 | 48.20985 | 161.7354 | 730.0359 | 243.004 | 0.214461 | 148.3903 | 242.5638 | 87.61149 | MO-BMR |
| 34 | 3 | 49.43683 | 170.3026 | 717.9203 | 258.9769 | 0.211921 | 147.6521 | 242.9326 | 87.90114 | MO-BMR |
| 35 | 3 | 48.71912 | 161.6153 | 719.7256 | 262.7071 | 0.219162 | 147.7617 | 242.6019 | 87.9556 | MO-BMR |
| 36 | 3 | 47.04752 | 167.5148 | 729.3287 | 255.0058 | 0.206618 | 147.6918 | 242.5271 | 87.79658 | MO-BWR |
| 37 | 3 | 49.71336 | 177.3987 | 723.7574 | 247.6101 | 0.200155 | 147.5042 | 242.7592 | 87.62196 | MO-BMWR |
| 38 | 3 | 46.90786 | 160.7199 | 732.3403 | 252.8415 | 0.211979 | 147.8673 | 242.1331 | 87.73107 | MO-BWR |
| 39 | 3 | 49.18771 | 163.0856 | 732.9972 | 241.0105 | 0.202341 | 148.0762 | 242.0365 | 87.56661 | MO-BMR |
| 40 | 3 | 47.92386 | 169.7216 | 732.1216 | 249.4968 | 0.197437 | 147.6008 | 242.2661 | 87.69338 | MO-BWR |
| 41 | 3 | 47.12514 | 168.6922 | 725.2975 | 263.2747 | 0.207707 | 147.2544 | 242.404 | 87.90041 | MO-BWR |
| 42 | 3 | 50 | 168.4982 | 725.7775 | 258.6422 | 0.19083 | 147.3557 | 242.2272 | 87.94152 | MO-BMR |
| 43 | 3 | 48.93892 | 165.129 | 733.511 | 244.8578 | 0.196892 | 147.8439 | 242.0085 | 87.64298 | MO-BMR |
| 44 | 3 | 49.72561 | 161.2063 | 721.2148 | 265.0324 | 0.207904 | 147.4018 | 242.0963 | 88.00218 | MO-BMR |
| 45 | 3 | 49.50244 | 159.7381 | 728.6085 | 258.757 | 0.198868 | 147.5593 | 241.8547 | 87.91588 | MO-BMR |
| 46 | 3 | 48.41383 | 167.4577 | 722.2672 | 270.1418 | 0.203078 | 146.7202 | 241.8423 | 87.98825 | MO-BWR |
| 47 | 3 | 50 | 163.571 | 724.5179 | 268.0383 | 0.193123 | 146.8365 | 241.5285 | 88.03343 | MO-BMR |
| 48 | 3 | 49.10861 | 164.1719 | 737.4422 | 250.7196 | 0.185275 | 147.2155 | 241.1802 | 87.70436 | MO-BMR |
| 49 | 3 | 47.96363 | 174.5148 | 730.1604 | 262.1093 | 0.188 | 146.5517 | 241.7152 | 87.8109 | MO-BMWR |
| 50 | 3 | 49.52507 | 168.6063 | 737.6373 | 249.0467 | 0.178757 | 147.0242 | 241.1516 | 87.6636 | MO-BWR |
| 51 | 3 | 50 | 169.9449 | 736.4611 | 250.7107 | 0.174982 | 146.9246 | 241.1875 | 87.71212 | MO-BMR |
| 52 | 3 | 48.29039 | 176.5516 | 729.8205 | 262.4282 | 0.185274 | 146.348 | 241.6051 | 87.78321 | MO-BMWR |
| 53 | 3 | 49.40561 | 172.8693 | 731.537 | 262.6046 | 0.176421 | 146.3965 | 241.297 | 87.87337 | MO-BMR |
| 54 | 3 | 50 | 166.9879 | 735.5043 | 258.3186 | 0.173539 | 146.6959 | 240.967 | 87.86002 | MO-BMR |
| 55 | 3 | 48.75456 | 161.8118 | 729.9932 | 271.2853 | 0.189963 | 146.3178 | 240.7628 | 87.97771 | MO-BMR |
| 56 | 3 | 50 | 166.186 | 740.2653 | 253.1963 | 0.17093 | 146.5852 | 240.4182 | 87.71029 | MO-BMR |
| 57 | 3 | 50 | 170.2129 | 725.9818 | 274.6315 | 0.179098 | 145.6913 | 240.6593 | 88.00575 | MO-BMR |
| 58 | 3 | 49.12464 | 160.7683 | 730.1268 | 274.9778 | 0.186854 | 145.8805 | 240.2057 | 87.98186 | MO-BMR |
| 59 | 3 | 50 | 166.504 | 741.4914 | 256.4905 | 0.166364 | 146.2125 | 240.0125 | 87.72923 | MO-BMR |
| 60 | 3 | 48.84152 | 179.2203 | 737.3762 | 261.4312 | 0.167885 | 145.4522 | 240.3316 | 87.62692 | MO-BMR |
| 61 | 3 | 49.3342 | 170.4196 | 742.972 | 258.7064 | 0.163329 | 145.7197 | 239.6947 | 87.67342 | MO-BWR |
| 62 | 3 | 50 | 168.0049 | 744.2395 | 255.4344 | 0.162127 | 145.8695 | 239.5153 | 87.64115 | MO-BWR |
| 63 | 3 | 49.55151 | 163.2018 | 742.4222 | 263.659 | 0.167013 | 145.7215 | 239.3609 | 87.77374 | MO-BMR |
| 64 | 3 | 50 | 178.4454 | 741.7557 | 255.6128 | 0.158415 | 145.3632 | 239.7285 | 87.52599 | MO-BMR |
| 65 | 3 | 50 | 169.0259 | 742.0731 | 265.8839 | 0.156637 | 145.2329 | 239.1847 | 87.78616 | MO-BMR |
| 66 | 3 | 50 | 176.5496 | 726.7183 | 280.2386 | 0.170892 | 144.4518 | 239.6424 | 87.87592 | MO-BMR |
| 67 | 3 | 50 | 161.689 | 732.8145 | 280.1212 | 0.172362 | 144.8967 | 238.9955 | 87.96572 | MO-BMR |
| 68 | 3 | 48.58098 | 163.7929 | 739.8322 | 274.5845 | 0.169847 | 144.966 | 238.902 | 87.83897 | MO-BMR |
| 69 | 3 | 50 | 173.458 | 744.9693 | 265.3419 | 0.149999 | 144.6185 | 238.5558 | 87.65304 | MO-BWR |
| 70 | 3 | 49.04694 | 163.6946 | 737.7385 | 279.922 | 0.16754 | 144.4851 | 238.475 | 87.87562 | MO-BMR |
| 71 | 3 | 50 | 171.1127 | 747.9459 | 266.6533 | 0.147703 | 144.2615 | 237.8177 | 87.61229 | MO-BWR |
| 72 | 3 | 49.63502 | 163.8374 | 740.196 | 282.707 | 0.158752 | 143.7751 | 237.5047 | 87.82736 | MO-BMR |
| 73 | 3 | 50 | 173.3144 | 750 | 269.6785 | 0.142494 | 143.5003 | 236.9697 | 87.527 | MO-BWR |
| 74 | 3 | 50 | 164.5898 | 741.8089 | 284.6633 | 0.152533 | 143.2407 | 236.8215 | 87.78603 | MO-BMR |
| 75 | 3.818123 | 49.32544 | 168.2566 | 743.2671 | 256.8835 | 0.151013 | 144.9756 | 235.6326 | 86.62875 | MO-BMWR |
| 76 | 3.763176 | 49.29088 | 170.8912 | 743.7041 | 259.0603 | 0.147349 | 144.6746 | 235.6573 | 86.68662 | MO-BMWR |
| 77 | 3.528248 | 49.61432 | 167.588 | 743.1029 | 273.3304 | 0.143412 | 143.8518 | 235.5756 | 87.11926 | MO-BMR |
| 78 | 3 | 50 | 167.3271 | 741.5766 | 289.3435 | 0.148178 | 142.4335 | 236.0892 | 87.73309 | MO-BMR |
| 79 | 3 | 50 | 167.8223 | 750 | 280.6006 | 0.141617 | 142.5583 | 235.6593 | 87.57763 | MO-BMR |
| 80 | 3.780539 | 49.46084 | 171.2914 | 745.534 | 261.7692 | 0.141748 | 144.1539 | 234.9432 | 86.64287 | MO-BMWR |
| 81 | 3 | 50 | 183.1604 | 750 | 272.721 | 0.137881 | 142.2142 | 236.1184 | 87.27256 | MO-BMR |
| 82 | 3 | 50 | 180.9857 | 750 | 276.1779 | 0.136228 | 142.0528 | 235.8404 | 87.34246 | MO-BMR |
| 83 | 3.530566 | 50 | 168.8275 | 744.5875 | 276.5317 | 0.136316 | 143.1702 | 234.7665 | 87.07542 | MO-BMR |
| 84 | 3.884643 | 49.69957 | 172.2824 | 746.8306 | 263.5071 | 0.13596 | 143.594 | 233.9302 | 86.4788 | MO-BMWR |
| 85 | 3.944815 | 50 | 178.8443 | 741.1399 | 270.7461 | 0.132873 | 142.9231 | 233.8073 | 86.44568 | MO-BMR |
| 86 | 3.918808 | 50 | 173.1911 | 748.3075 | 265.0832 | 0.130687 | 143.0979 | 233.1985 | 86.39477 | MO-BMWR |
| 87 | 3 | 49.62956 | 175.2274 | 745.1802 | 295.2004 | 0.138476 | 140.5178 | 234.1645 | 87.44597 | MO-BMR |
| 88 | 3.598671 | 50 | 169.1933 | 747.9599 | 283.8465 | 0.128237 | 141.6381 | 232.6015 | 86.85274 | MO-BMR |
| 89 | 3.956939 | 49.36912 | 169.062 | 744.4129 | 282.4436 | 0.132944 | 141.9107 | 231.9596 | 86.48653 | MO-BMR |
| 90 | 3 | 50 | 176.2479 | 747.7101 | 298.4581 | 0.132308 | 139.4704 | 232.8056 | 87.30336 | MO-BMR |
| 91 | 3.617944 | 49.90341 | 170.8667 | 748.8612 | 287.9335 | 0.12487 | 140.7853 | 231.6107 | 86.74068 | MO-BMR |
| 92 | 3 | 49.81773 | 180.8679 | 750 | 299.8957 | 0.129845 | 138.4436 | 231.7404 | 87.07502 | MO-BWR |
| 93 | 3.974298 | 50 | 171.5308 | 748.3405 | 287.3691 | 0.120769 | 140.4134 | 230.0316 | 86.29786 | MO-BMR |
| 94 | 4.761999 | 50 | 186.6837 | 747.9199 | 300 | 0.116302 | 135.5975 | 223.0101 | 84.65361 | MO-BMWR |
| Solution | Normalized Ra | Normalized YS | Normalized UTS | Normalized H | Algorithm | Composite Scores of the Solutions for Different Weightages | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Equation Wts. (Case 1) | WRa = 0.7 (Case 2) | WYS = 0.7 (Case 3) | WUTS = 0.7 (Case 4) | WH= 0.7 (Case 5) | ||||||
| 1 | 0.396482 | 0.998581 | 1 | 0.992136 | MO-BMWR | 0.8468 | 0.576609 | 0.937869 | 0.93872 | 0.934002 |
| 2 | 0.40191 | 0.998089 | 0.999759 | 0.993039 | MO-BWR | 0.848199 | 0.580426 | 0.938133 | 0.939135 | 0.935103 |
| 3 | 0.409545 | 0.998638 | 0.99924 | 0.9925 | MO-BMR | 0.849981 | 0.585719 | 0.939175 | 0.939536 | 0.935492 |
| 4 | 0.418382 | 0.996565 | 0.99966 | 0.994284 | MO-BWR | 0.852223 | 0.591918 | 0.938828 | 0.940685 | 0.93746 |
| 5 | 0.427478 | 0.996509 | 0.999943 | 0.993413 | MO-BMWR | 0.854336 | 0.598221 | 0.939639 | 0.9417 | 0.937782 |
| 6 | 0.370704 | 1 | 0.999267 | 0.989447 | MO-BMWR | 0.839854 | 0.558364 | 0.935942 | 0.935502 | 0.92961 |
| 7 | 0.432324 | 0.997502 | 0.998968 | 0.993666 | MO-BWR | 0.855615 | 0.60164 | 0.940747 | 0.941627 | 0.938445 |
| 8 | 0.43151 | 0.996152 | 0.999414 | 0.994697 | MO-BMR | 0.855443 | 0.601084 | 0.939869 | 0.941826 | 0.938996 |
| 9 | 0.367644 | 0.999871 | 0.998829 | 0.98986 | MO-BWR | 0.839051 | 0.556207 | 0.935543 | 0.934918 | 0.929537 |
| 10 | 0.435605 | 0.995373 | 0.999145 | 0.995202 | MO-BWR | 0.856331 | 0.603895 | 0.939756 | 0.94202 | 0.939654 |
| 11 | 0.374392 | 0.999664 | 0.998154 | 0.990149 | MO-BWR | 0.84059 | 0.560871 | 0.936034 | 0.935128 | 0.930325 |
| 12 | 0.437652 | 0.998033 | 0.997951 | 0.992652 | MO-BMR | 0.856572 | 0.60522 | 0.941448 | 0.941399 | 0.93822 |
| 13 | 0.443565 | 0.996522 | 0.997668 | 0.994541 | MO-BWR | 0.858074 | 0.609368 | 0.941143 | 0.94183 | 0.939955 |
| 14 | 0.448251 | 0.993817 | 0.998773 | 0.995715 | MO-BMWR | 0.859139 | 0.612606 | 0.939946 | 0.942919 | 0.941084 |
| 15 | 0.465443 | 0.995435 | 0.997171 | 0.995521 | MO-BMR | 0.863392 | 0.624623 | 0.942618 | 0.943659 | 0.94267 |
| 16 | 0.382924 | 0.999755 | 0.997124 | 0.988809 | MO-BMR | 0.842153 | 0.566616 | 0.936714 | 0.935136 | 0.930147 |
| 17 | 0.477016 | 0.992766 | 0.998047 | 0.996593 | MO-BMWR | 0.866105 | 0.632652 | 0.942102 | 0.94527 | 0.944398 |
| 18 | 0.451666 | 0.993882 | 0.997369 | 0.99656 | MO-BWR | 0.859869 | 0.614948 | 0.940277 | 0.942369 | 0.941883 |
| 19 | 0.479826 | 0.995017 | 0.996585 | 0.995851 | MO-BMR | 0.86682 | 0.634623 | 0.943738 | 0.944679 | 0.944239 |
| 20 | 0.459971 | 0.996442 | 0.996801 | 0.992742 | MO-BMWR | 0.861489 | 0.620578 | 0.942461 | 0.942676 | 0.940241 |
| 21 | 0.469708 | 0.995981 | 0.996856 | 0.99331 | MO-BWR | 0.863964 | 0.627411 | 0.943174 | 0.943699 | 0.941572 |
| 22 | 0.501906 | 0.994641 | 0.995739 | 0.995695 | MO-BWR | 0.871995 | 0.649942 | 0.945583 | 0.946242 | 0.946215 |
| 23 | 0.483419 | 0.991016 | 0.997184 | 0.996794 | MO-BMWR | 0.867103 | 0.636892 | 0.941451 | 0.945152 | 0.944918 |
| 24 | 0.488186 | 0.992078 | 0.996273 | 0.996877 | MO-BWR | 0.868354 | 0.640253 | 0.942588 | 0.945105 | 0.945468 |
| 25 | 0.517946 | 0.991046 | 0.99646 | 0.996851 | MO-BMR | 0.875576 | 0.660998 | 0.944858 | 0.948106 | 0.948341 |
| 26 | 0.48491 | 0.991192 | 0.995035 | 0.997834 | MO-BMR | 0.867243 | 0.637843 | 0.941612 | 0.943918 | 0.945598 |
| 27 | 0.511251 | 0.990264 | 0.995283 | 0.998128 | MO-BMR | 0.873732 | 0.656243 | 0.943651 | 0.946662 | 0.948369 |
| 28 | 0.494084 | 0.992202 | 0.99438 | 0.996822 | MO-BMR | 0.869372 | 0.644199 | 0.94307 | 0.944377 | 0.945842 |
| 29 | 0.511936 | 0.992443 | 0.994354 | 0.995215 | MO-BMWR | 0.873487 | 0.656556 | 0.94486 | 0.946007 | 0.946524 |
| 30 | 0.537227 | 0.988685 | 0.995176 | 0.997896 | MO-BMWR | 0.879746 | 0.674235 | 0.945109 | 0.949004 | 0.950636 |
| 31 | 0.522651 | 0.988379 | 0.994621 | 0.998746 | MO-BMR | 0.876099 | 0.664031 | 0.943467 | 0.947213 | 0.949687 |
| 32 | 0.547194 | 0.987979 | 0.995337 | 0.994849 | MO-BMWR | 0.88134 | 0.680852 | 0.945323 | 0.949738 | 0.949445 |
| 33 | 0.542297 | 0.991169 | 0.992802 | 0.995207 | MO-BMR | 0.880369 | 0.677526 | 0.946849 | 0.947829 | 0.949272 |
| 34 | 0.548797 | 0.986239 | 0.994312 | 0.998497 | MO-BMR | 0.881961 | 0.682063 | 0.944528 | 0.949372 | 0.951883 |
| 35 | 0.530664 | 0.986971 | 0.992958 | 0.999116 | MO-BMR | 0.877427 | 0.66937 | 0.943153 | 0.946746 | 0.95044 |
| 36 | 0.562883 | 0.986503 | 0.992652 | 0.99731 | MO-BWR | 0.884837 | 0.691664 | 0.945837 | 0.949526 | 0.952321 |
| 37 | 0.581056 | 0.98525 | 0.993602 | 0.995326 | MO-BMWR | 0.888809 | 0.704157 | 0.946674 | 0.951685 | 0.952719 |
| 38 | 0.548647 | 0.987676 | 0.991039 | 0.996565 | MO-BWR | 0.880982 | 0.681581 | 0.944998 | 0.947016 | 0.950332 |
| 39 | 0.574782 | 0.989071 | 0.990644 | 0.994697 | MO-BMR | 0.887298 | 0.699788 | 0.948362 | 0.949306 | 0.951738 |
| 40 | 0.589057 | 0.985896 | 0.991584 | 0.996137 | MO-BWR | 0.890668 | 0.709702 | 0.947805 | 0.951218 | 0.95395 |
| 41 | 0.559931 | 0.983582 | 0.992148 | 0.998489 | MO-BWR | 0.883538 | 0.689374 | 0.943564 | 0.948704 | 0.952508 |
| 42 | 0.609453 | 0.984259 | 0.991424 | 0.998956 | MO-BMR | 0.896023 | 0.724081 | 0.948965 | 0.953264 | 0.957783 |
| 43 | 0.590688 | 0.98752 | 0.990529 | 0.995565 | MO-BMR | 0.891075 | 0.710843 | 0.948942 | 0.950748 | 0.953769 |
| 44 | 0.559401 | 0.984567 | 0.990888 | 0.999645 | MO-BMR | 0.883625 | 0.689091 | 0.94419 | 0.947983 | 0.953237 |
| 45 | 0.584819 | 0.985619 | 0.9899 | 0.998665 | MO-BMR | 0.889751 | 0.706792 | 0.947272 | 0.94984 | 0.955099 |
| 46 | 0.572695 | 0.980014 | 0.989849 | 0.999487 | MO-BWR | 0.885511 | 0.697821 | 0.942213 | 0.948114 | 0.953896 |
| 47 | 0.602215 | 0.980791 | 0.988565 | 1 | MO-BMR | 0.892892 | 0.718486 | 0.945631 | 0.950296 | 0.957157 |
| 48 | 0.627725 | 0.983322 | 0.987139 | 0.996262 | MO-BMR | 0.898612 | 0.73608 | 0.949438 | 0.951728 | 0.957202 |
| 49 | 0.618624 | 0.978889 | 0.989329 | 0.997472 | MO-BMWR | 0.896078 | 0.729606 | 0.945765 | 0.952029 | 0.956915 |
| 50 | 0.650612 | 0.982045 | 0.987022 | 0.995799 | MO-BWR | 0.903869 | 0.751915 | 0.950775 | 0.953761 | 0.959027 |
| 51 | 0.664651 | 0.981379 | 0.987169 | 0.99635 | MO-BMR | 0.907387 | 0.761745 | 0.951782 | 0.955256 | 0.960765 |
| 52 | 0.627729 | 0.977528 | 0.988878 | 0.997158 | MO-BMWR | 0.897823 | 0.735767 | 0.945646 | 0.952456 | 0.957424 |
| 53 | 0.659227 | 0.977852 | 0.987617 | 0.998182 | MO-BMR | 0.905719 | 0.757824 | 0.948999 | 0.954858 | 0.961197 |
| 54 | 0.670178 | 0.979852 | 0.986267 | 0.99803 | MO-BMR | 0.908581 | 0.765539 | 0.951344 | 0.955193 | 0.962251 |
| 55 | 0.612233 | 0.977326 | 0.985431 | 0.999367 | MO-BMR | 0.893589 | 0.724776 | 0.943831 | 0.948694 | 0.957056 |
| 56 | 0.680404 | 0.979112 | 0.98402 | 0.996329 | MO-BMR | 0.909966 | 0.772229 | 0.951454 | 0.954399 | 0.961784 |
| 57 | 0.649374 | 0.973141 | 0.985007 | 0.999686 | MO-BMR | 0.901802 | 0.750345 | 0.944605 | 0.951725 | 0.960532 |
| 58 | 0.622418 | 0.974405 | 0.983151 | 0.999414 | MO-BMR | 0.894847 | 0.73139 | 0.942582 | 0.947829 | 0.957587 |
| 59 | 0.699077 | 0.976622 | 0.98236 | 0.996545 | MO-BMR | 0.913651 | 0.784907 | 0.951434 | 0.954876 | 0.963387 |
| 60 | 0.692745 | 0.971544 | 0.983666 | 0.995382 | MO-BMR | 0.910834 | 0.77998 | 0.94726 | 0.954533 | 0.961563 |
| 61 | 0.712069 | 0.973331 | 0.981059 | 0.995911 | MO-BWR | 0.915593 | 0.793478 | 0.950236 | 0.954872 | 0.963783 |
| 62 | 0.71735 | 0.974332 | 0.980325 | 0.995544 | MO-BWR | 0.916888 | 0.797165 | 0.951354 | 0.95495 | 0.964081 |
| 63 | 0.696362 | 0.973343 | 0.979693 | 0.99705 | MO-BMR | 0.911612 | 0.782462 | 0.948651 | 0.95246 | 0.962875 |
| 64 | 0.734158 | 0.97095 | 0.981197 | 0.994236 | MO-BMR | 0.920135 | 0.808549 | 0.950624 | 0.956772 | 0.964596 |
| 65 | 0.742489 | 0.97008 | 0.978972 | 0.997191 | MO-BMR | 0.922183 | 0.814367 | 0.950921 | 0.956256 | 0.967188 |
| 66 | 0.680556 | 0.964862 | 0.980845 | 0.998211 | MO-BMR | 0.906119 | 0.770781 | 0.941365 | 0.950954 | 0.961374 |
| 67 | 0.674751 | 0.967834 | 0.978197 | 0.999231 | MO-BMR | 0.905003 | 0.766852 | 0.942702 | 0.94892 | 0.96154 |
| 68 | 0.684743 | 0.968297 | 0.977814 | 0.997791 | MO-BMR | 0.907161 | 0.77371 | 0.943843 | 0.949553 | 0.961539 |
| 69 | 0.775352 | 0.965975 | 0.976397 | 0.995679 | MO-BWR | 0.928351 | 0.836552 | 0.950926 | 0.957179 | 0.968748 |
| 70 | 0.694173 | 0.965084 | 0.976067 | 0.998207 | MO-BMR | 0.908383 | 0.779857 | 0.942404 | 0.948993 | 0.962278 |
| 71 | 0.7874 | 0.963591 | 0.973377 | 0.995216 | MO-BWR | 0.929896 | 0.844399 | 0.950113 | 0.955984 | 0.969088 |
| 72 | 0.732601 | 0.960342 | 0.972095 | 0.997659 | MO-BMR | 0.915674 | 0.80583 | 0.942475 | 0.949527 | 0.964865 |
| 73 | 0.816186 | 0.958507 | 0.969906 | 0.994247 | MO-BWR | 0.934711 | 0.863596 | 0.948989 | 0.955828 | 0.970433 |
| 74 | 0.76247 | 0.956773 | 0.969299 | 0.99719 | MO-BMR | 0.921433 | 0.826055 | 0.942637 | 0.950153 | 0.966887 |
| 75 | 0.770145 | 0.968361 | 0.964433 | 0.984044 | MO-BMWR | 0.921746 | 0.830785 | 0.949715 | 0.947358 | 0.959125 |
| 76 | 0.789294 | 0.96635 | 0.964534 | 0.984701 | MO-BMWR | 0.92622 | 0.844064 | 0.950298 | 0.949208 | 0.961309 |
| 77 | 0.810962 | 0.960855 | 0.9642 | 0.989616 | MO-BMR | 0.931408 | 0.85914 | 0.949076 | 0.951083 | 0.966333 |
| 78 | 0.784878 | 0.951381 | 0.966302 | 0.996588 | MO-BMR | 0.924787 | 0.840842 | 0.940744 | 0.949696 | 0.967868 |
| 79 | 0.821243 | 0.952215 | 0.964542 | 0.994822 | MO-BMR | 0.933205 | 0.866028 | 0.944611 | 0.952007 | 0.970176 |
| 80 | 0.820482 | 0.962872 | 0.961611 | 0.984204 | MO-BMWR | 0.932292 | 0.865206 | 0.95064 | 0.949884 | 0.963439 |
| 81 | 0.843492 | 0.949917 | 0.966421 | 0.991357 | MO-BMR | 0.937797 | 0.881214 | 0.945069 | 0.954972 | 0.969933 |
| 82 | 0.853726 | 0.948838 | 0.965284 | 0.992151 | MO-BMR | 0.94 | 0.888236 | 0.945303 | 0.95517 | 0.971291 |
| 83 | 0.853175 | 0.956302 | 0.960888 | 0.989118 | MO-BMR | 0.939871 | 0.887853 | 0.949729 | 0.952481 | 0.969419 |
| 84 | 0.855413 | 0.959133 | 0.957465 | 0.98234 | MO-BMWR | 0.938588 | 0.888683 | 0.950915 | 0.949914 | 0.964839 |
| 85 | 0.875287 | 0.954652 | 0.956962 | 0.981964 | MO-BMR | 0.942216 | 0.902059 | 0.949677 | 0.951064 | 0.966065 |
| 86 | 0.889924 | 0.955819 | 0.954471 | 0.981386 | MO-BMWR | 0.9454 | 0.912114 | 0.951651 | 0.950842 | 0.966991 |
| 87 | 0.839871 | 0.938585 | 0.958424 | 0.993327 | MO-BMR | 0.932552 | 0.876943 | 0.936172 | 0.948075 | 0.969017 |
| 88 | 0.906925 | 0.946068 | 0.952027 | 0.986588 | MO-BMR | 0.947902 | 0.923316 | 0.946802 | 0.950377 | 0.971114 |
| 89 | 0.874819 | 0.947889 | 0.9494 | 0.982428 | MO-BMR | 0.938634 | 0.900345 | 0.944187 | 0.945093 | 0.964911 |
| 90 | 0.879022 | 0.931589 | 0.952862 | 0.991707 | MO-BMR | 0.938795 | 0.902931 | 0.934472 | 0.947235 | 0.970542 |
| 91 | 0.931382 | 0.940372 | 0.947972 | 0.985315 | MO-BMR | 0.95126 | 0.939333 | 0.944727 | 0.949287 | 0.971693 |
| 92 | 0.895699 | 0.92473 | 0.948502 | 0.989113 | MO-BWR | 0.939511 | 0.913224 | 0.930643 | 0.944906 | 0.969272 |
| 93 | 0.96301 | 0.937888 | 0.941508 | 0.980285 | MO-BMR | 0.955673 | 0.960075 | 0.945002 | 0.947174 | 0.97044 |
| 94 | 1 | 0.90572 | 0.91277 | 0.961608 | MO-BMWR | 0.945024 | 0.97801 | 0.921442 | 0.925671 | 0.954974 |
| Case No. | Td (s) | Dp (s) | Sp (MPa) | Pt (°C) | Dt (°C) | Ra (µm) | YS (MPa) | UTS (MPa) | H (BHN) |
|---|---|---|---|---|---|---|---|---|---|
| Case 1: Equal weights (i.e., WRa = WYS = WUTS = WH = 0.25) | |||||||||
| GA [11] | 4.013 | 49.99 | 179.42 | 749.62 | 293.95 | 0.1142 | 138.79 | 228.44 | 85.98 |
| Present work | 3.974298 | 50 | 171.5308 | 748.3405 | 287.3691 | 0.120769 | 140.4134 | 230.0316 | 86.29786 |
| Case 2: WRa = 0.7, WYS = WUTS = WH = 0.10) | |||||||||
| GA [11] | 3.983 | 49.79 | 180.75 | 749.89 | 295.04 | 0.1139 | 138.03 | 227.27 | 85.76 |
| Present work | 4.761999 | 50 | 186.6837 | 747.9199 | 300 | 0.116302 | 135.5975 | 223.0101 | 84.65361 |
| Case 3: WYS = 0.7, WRa = WUTS = WH = 0.10 | |||||||||
| GA [11] | 3.102 | 49.87 | 177.15 | 748.52 | 279.96 | 0.1349 | 142.15 | 235.40 | 87.34 |
| Present work | 3 | 50 | 169.9449 | 736.4611 | 250.7107 | 0.174982 | 146.9246 | 241.1875 | 87.71212 |
| Case 4: WUTS = 0.7, WRa = WYS = WH = 0.10 | |||||||||
| GA [11] | 3.207 | 49.42 | 173.63 | 746.06 | 271.26 | 0.1437 | 143.69 | 236.76 | 87.33 |
| Present work | 3 | 50 | 173.458 | 744.9693 | 265.3419 | 0.149999 | 144.6185 | 238.5558 | 87.65304 |
| Case 5: WH = 0.7, WRa = WYS = WUTS = 0.10 | |||||||||
| GA [11] | 3.521 | 49.89 | 176.33 | 745.61 | 266.16 | 0.1365 | 143.64 | 235.63 | 86.95 |
| Present work | 3.617944 | 49.90341 | 170.8667 | 748.8612 | 287.9335 | 0.12487 | 140.7853 | 231.6107 | 86.74068 |
| Aspect | BWR, BMR, BMWR | Machine Learning/Deep Learning/ANNs |
|---|---|---|
| Principle | Population-based, stochastic, metaphor-free metaheuristics. | Data-driven models that learn patterns and decision boundaries from datasets. |
| Search strategy | Guided by best, mean, worst, and random solutions; exploration–exploitation balance. | Learns mappings x → f(x); optimization via gradient descent, reinforcement learning, or surrogate-assisted search. |
| Parameter dependence | Parameter-free (except population size and iterations). | High dependence on hyperparameters (layers, neurons, learning rate, batch size, epochs, etc.). |
| Computational cost | Moderate—requires multiple evaluations of objective function. | High training cost (especially for deep models); once trained, predictions are cheap. |
| Scalability | Performs well up to medium–high dimensions (50–100+ variables), but may degrade in very large-scale spaces. | Scales well if sufficient data is available; dimensionality handled via feature engineering and network depth. |
| Constraint handling | Penalty functions, feasibility rules, ε-constraints, etc. | Constraints are often embedded into model architecture or handled via constrained optimization layers. |
| Exploration vs. exploitation | Explicitly balanced (BWR → exploratory, BMR → exploitative, BMWR → hybrid). | Exploitation-oriented; exploration requires reinforcement learning or hybridization. |
| Robustness to local optima | Strong—random + worst interactions help escape local traps. | Vulnerable to local minima in gradient descent; mitigated by advanced training strategies (Adam, momentum, etc.). |
| Data requirements | No data required; works directly on objective evaluations. | Requires large, high-quality datasets; poor generalization if training data is limited. |
| Multi-objective optimization | Natural extension with Pareto archives, crowding distance, and ε-dominance. | Multi-objectives handled via multi-task learning or scalarization; less transparent in decision diversity. |
| Interpretability | Transparent update logic, easy to trace search behavior. | Often a black box; DL/ANNs lack interpretability. |
| Best use cases | Problems without prior data, black-box functions, and engineering design optimization. | Problems with abundant historical/simulation data; surrogate-assisted optimization for expensive evaluations. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rao, R.V.; Davim, J.P. Optimization of Different Metal Casting Processes Using Three Simple and Efficient Advanced Algorithms. Metals 2025, 15, 1057. https://doi.org/10.3390/met15091057
Rao RV, Davim JP. Optimization of Different Metal Casting Processes Using Three Simple and Efficient Advanced Algorithms. Metals. 2025; 15(9):1057. https://doi.org/10.3390/met15091057
Chicago/Turabian StyleRao, Ravipudi Venkata, and Joao Paulo Davim. 2025. "Optimization of Different Metal Casting Processes Using Three Simple and Efficient Advanced Algorithms" Metals 15, no. 9: 1057. https://doi.org/10.3390/met15091057
APA StyleRao, R. V., & Davim, J. P. (2025). Optimization of Different Metal Casting Processes Using Three Simple and Efficient Advanced Algorithms. Metals, 15(9), 1057. https://doi.org/10.3390/met15091057







