Investigation of Hot Deformation Behavior for 45CrNi Steel by Utilizing an Improved Cellular Automata Method
Abstract
1. Introduction
2. Experimental Procedure
2.1. Materials and Experimental Procedure
2.2. Microstructural Characterization
3. Results and Discussion
3.1. The Analysis of the True Stress–Strain Curve After Friction and Temperature Correction
3.2. Construction of Physical Model for 45CrNi Steel
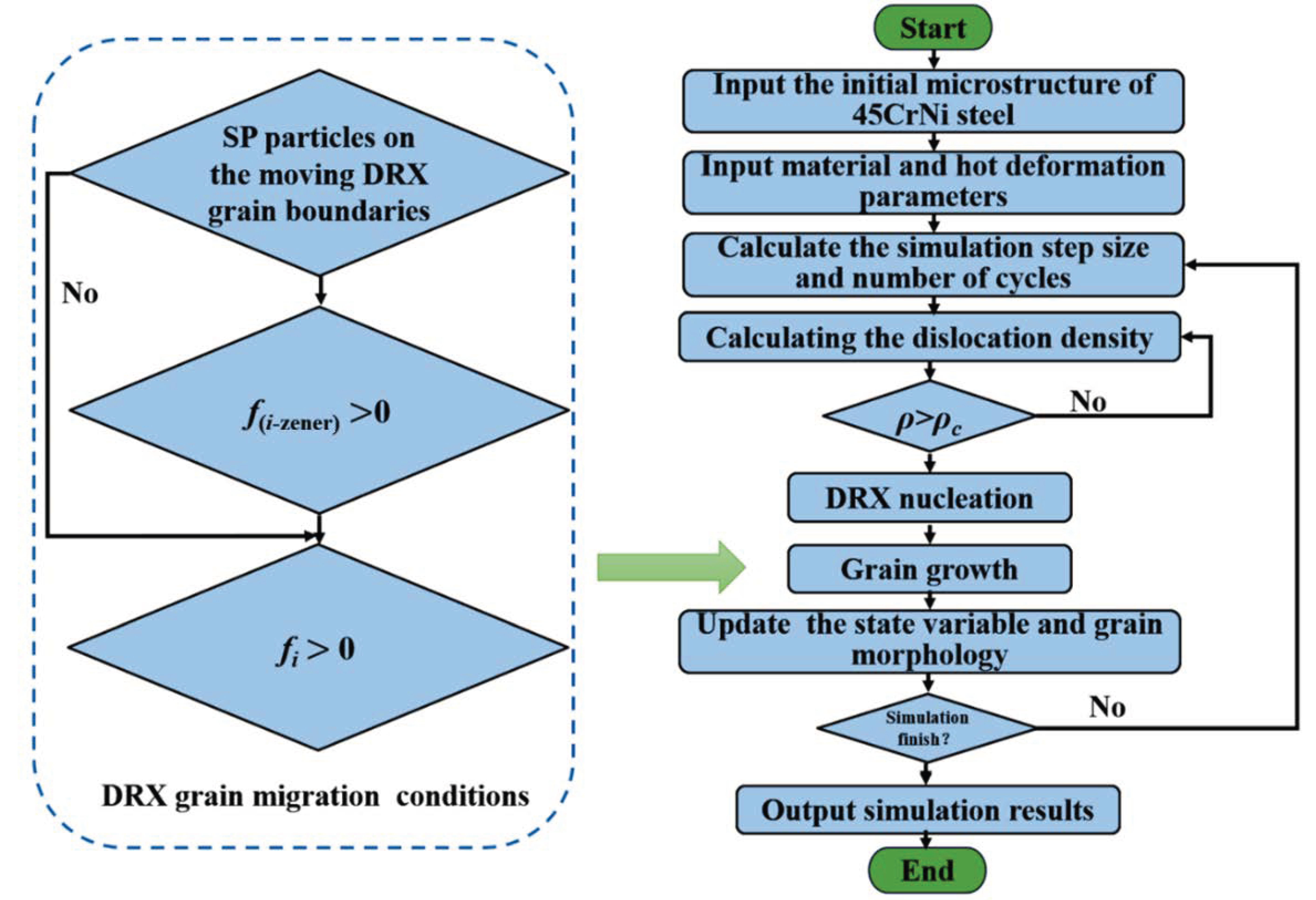
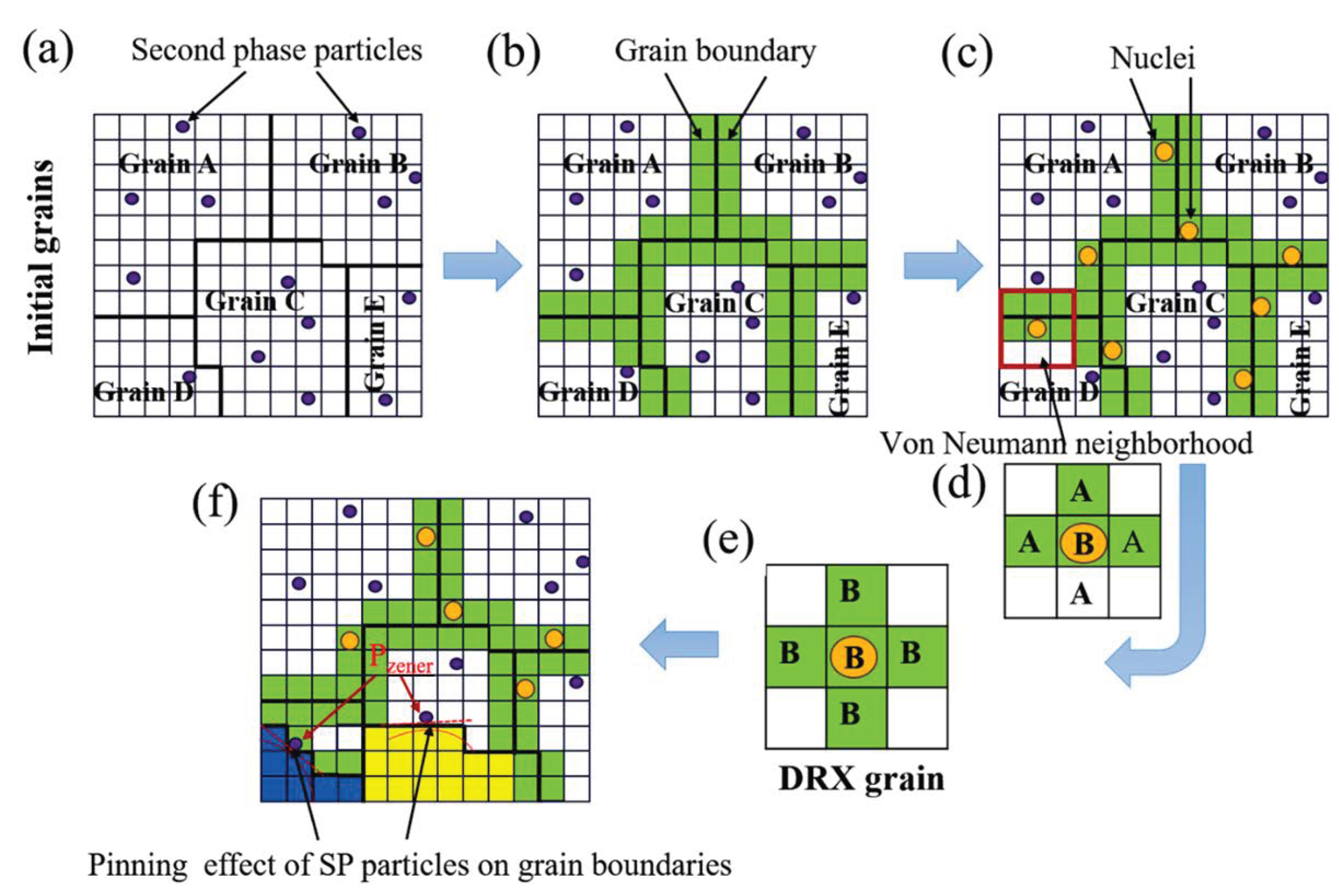
3.3. DRX Theoretical Model of CA
4. Experimental Results and Analysis
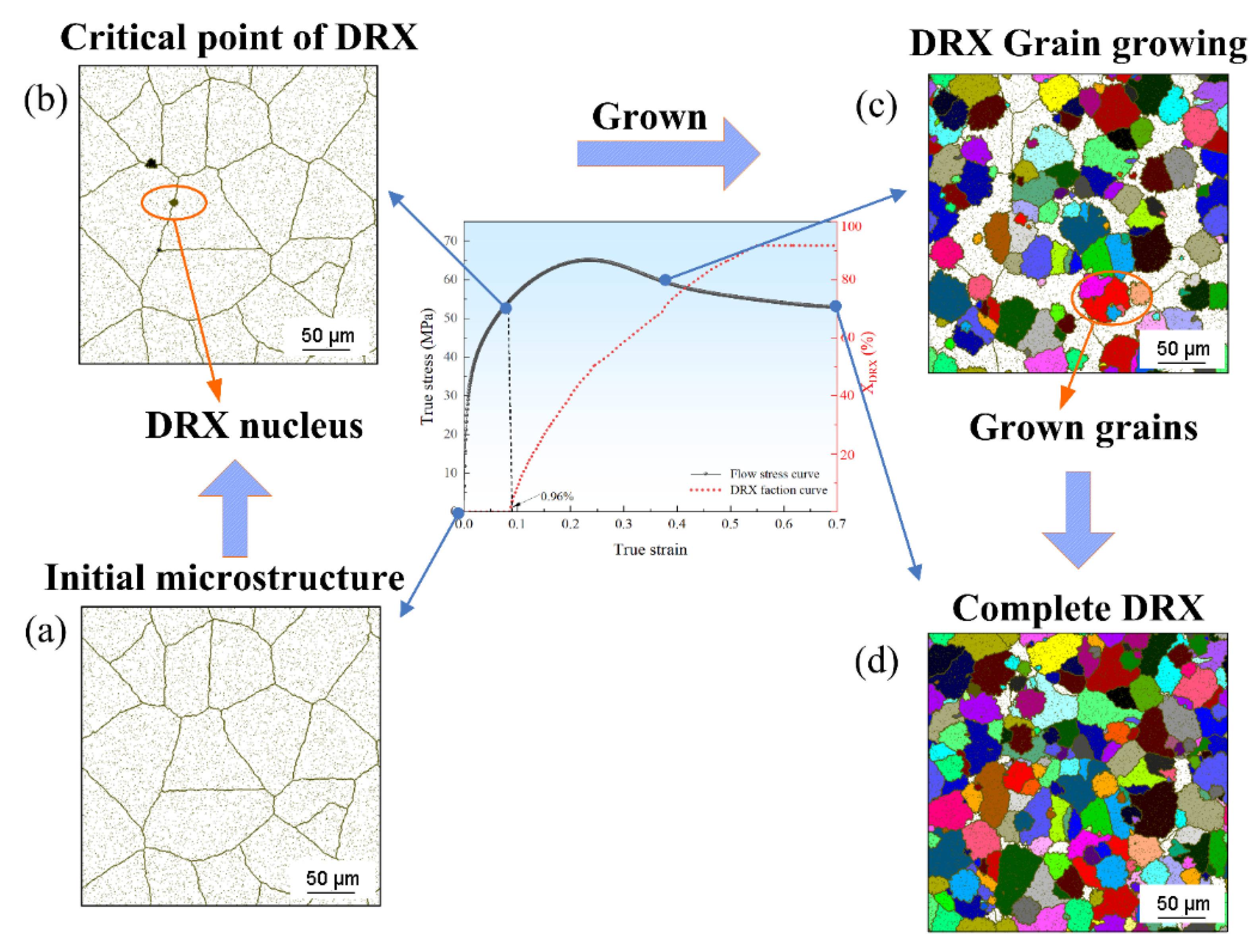
4.1. Simulation of DRX Behavior Utilizing SP-CA Method
4.2. Effect of Deformation Temperature on DRX
4.3. Effects of Strain Rate on DRX
5. Conclusions
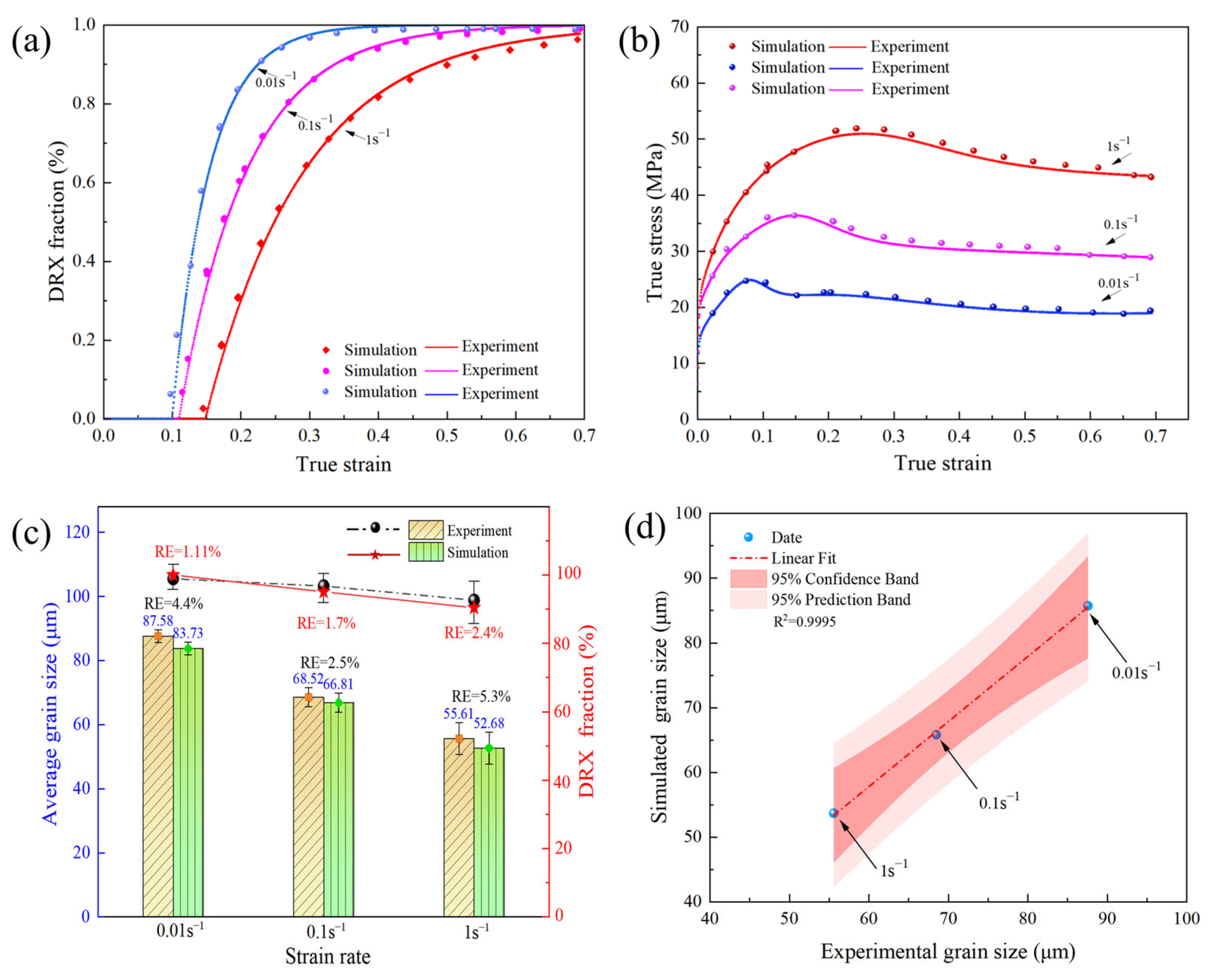
- (a)
- The DRX kinetic model of the studied 45CrNi steel is established as follows:
- (b)
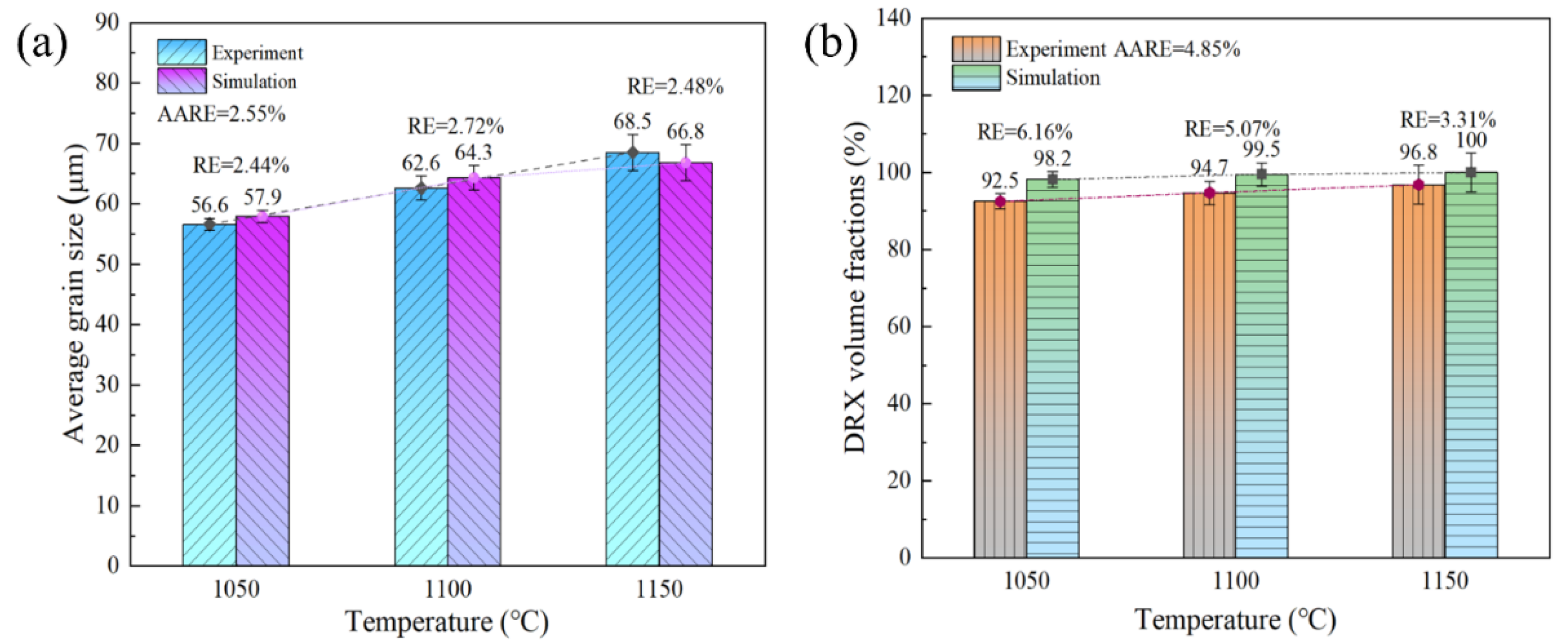
- The variation disciplines of average grain size and DRX volume fraction achieved through the experiment and SP-CA calculation in regard to the studied 45CrNi steel are consistent. Meanwhile, the average grain size and DRX volume fraction of the parent austenite increase gradually with rising deformation temperature and decreasing strain rate under constant strain.
- (c)
- The simulation results associated with the average grain size and DRX volume fraction achieved through the SP-CA model are in good agreement with the experimental results, with an AARE of less than 5%, indicating that the improved SP-CA model can accurately predict the DRX behavior of 45CrNi steel during hot deformation. According to the improved SP-CA model, the Zener pinning effect exerted by randomly dispersed SP particles on the initial austenite grain boundaries inhibits the DRX volume fraction in the 45CrNi steel from attaining 100%, even during the steady-state stress phase.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, J.; Jiang, Z.Y. Thermomechanical processing of advanced high strength steels. Prog. Mater. Sci. 2018, 94, 174–242. [Google Scholar] [CrossRef]
- Bodyakova, A.; Belyakov, A. Microstructure and mechanical properties of structural steels and alloys. Materials 2023, 16, 5188. [Google Scholar] [CrossRef]
- Li, D.Z.; Zhao, X.M.; Zhang, H.L.; Li, J. Flow stress-strain curves and dynamic recrystallization behavior of high carbon low alloy steels during hot deformation. J. Mater. Res. Technol. 2025, 35, 3144–3160. [Google Scholar] [CrossRef]
- Lee, C.; Jo, S.; Kim, Y.; Choi, Y.; Lee, K.; Jeon, J.B. Hot deformation behavior and dynamic recrystallization of Fe-24Mn steel: Influence on cryogenic hardness. J. Mater. Res. Technol. 2025, 36, 10547–10562. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, T.; Zhang, M.; Chen, Z.; Pan, H.; Yang, G.; Zhang, X. Hot deformation behavior, dynamic recrystallization mechanism and processing maps of Ti–V microalloyed high strength steel. J. Mater. Res. Technol. 2023, 25, 4201–4215. [Google Scholar] [CrossRef]
- Khodabakhshi, F.; Hasani, N.; Kalaie, M.R.; Hadadzadeh, A.; Wells, M.A.; Mohammadi, M. Dynamic recrystallization under hot deformation of additively manufactured 316 L stainless steel. Mater. Charact. 2023, 202, 113055. [Google Scholar] [CrossRef]
- Li, C.; Huang, L.; Zhao, M.; Zhang, X.; Li, J.; Li, P. Influence of hot deformation on dynamic recrystallization behavior of 300M steel: Rules and modeling. Mater. Sci. Eng. A 2020, 797, 139925. [Google Scholar] [CrossRef]
- Mozumder, Y.H.; Babu, K.A.; Saha, R.; Sarma, V.S.; Mandal, S. Dynamic microstructural evolution and recrystallization mechanism during hot deformation of intermetallic-hardened duplex lightweight steel. Mater. Sci. Eng. A 2020, 788, 139613. [Google Scholar] [CrossRef]
- Lee, J.; Kim, S.; Kim, B.; Kim, D. Physically-based constitutive model and dynamic recrystallization behavior of AISI 4330V mod. Alloy steel under hot working conditions. J. Mater. Res. Technol. 2025, 36, 8146–8159. [Google Scholar] [CrossRef]
- Guo, A.; Mao, F.; Shi, R.; Lin, Y.; Yin, L.; Yu, B.; Wei, S. Study on Dynamic Recrystallization Kinetics and Microstructural Refinement of High-Strength 36CrNi3MoV Steel during hot deformation. J. Mater. Res. Technol. 2025, 36, 8999–9012. [Google Scholar] [CrossRef]
- Mirzadeh, H.; Cabrera, J.M.; Najafizadeh, A. Constitutive relationships for hot deformation of austenite. Acta Mater. 2011, 59, 6441–6448. [Google Scholar] [CrossRef]
- Saadatkia, S.; Mirzadeh, H.; Cabrera, J.M. Hot deformation behavior, dynamic recrystallization, and physically-based constitutive modeling of plain carbon steels. Mater. Sci. Eng. A 2015, 636, 196–202. [Google Scholar] [CrossRef]
- Wang, F.; Liu, Z.F.; Hu, W.L.; Zhao, J.H.; He, W.W.; Hou, H. Understanding and exploring anisotropy mechanism of mechanical properties for ferrous alloy under different cooling paths. J. Mater. Res. Technol. 2024, 32, 261–272. [Google Scholar] [CrossRef]
- Singh, A.; Haase, C.; Barrales-Mora, L.A. Cellular Automaton Simulation Model for Predicting the Microstructure Evolution of an Additively Manufactured X30Mn21 Austenitic Advanced High-Strength Steel. Metals 2025, 15, 770. [Google Scholar] [CrossRef]
- Yu, K.; Wang, M.; Fan, H.; Zhan, Z.; Ren, Z.; Xu, L. Investigation on the Solidification Structure of Q355 in 475 Mm Extra-Thick Slabs Adopting Cellular Automaton-Finite Element Model. Metals 2024, 14, 1012. [Google Scholar] [CrossRef]
- Cheng, M.; Wu, X.; Zhang, Z. Study of the Dynamic Recrystallization Behavior of Mg-Gd-Y-Zn-Zr Alloy Based on Experiments and Cellular Automaton Simulation. Metals 2024, 14, 570. [Google Scholar] [CrossRef]
- He, Y.Y.; Lei, L.P.; Fang, G. Interactions between dynamic recrystallization and dynamic precipitation during hot forming of magnesium alloy: Multilevel cellular automaton modeling. J. Magnes. Alloys 2025, 13, 1953–1977. [Google Scholar] [CrossRef]
- Yang, X.; Tong, D.; Gong, M.; Guo, Z.; Li, C.; Gu, J. Developing and validating a fully coupled model of non-local crystal plasticity and probabilistic cellular automata for dynamic recrystallization simulation. Int. J. Plast. 2025, 190, 104375. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, L.; Xu, Q.; Xia, Y.; Shen, W. The kinetics and cellular automaton modeling of dynamic recrystallization behavior of a medium carbon Cr-Ni-Mo alloyed steel in hot working process. Mater. Sci. Eng. A 2016, 678, 33–43. [Google Scholar] [CrossRef]
- Liu, Y.X.; Lin, Y.C.; Li, H.B.; Wen, D.X.; Chen, X.M.; Chen, M.S. Study of dynamic recrystallization in a Ni-based superalloy by experiments and cellular automaton model. Mater. Sci. Eng. 2015, 626, 432–440. [Google Scholar] [CrossRef]
- Zhang, C.; Du, Y.; Zhang, L.; Jin, C.; Zhou, X.; Li, F. Hot deformation behavior of C276 superalloy in shifted strain rate compression: Experiments and cellular automaton modelling. J. Alloys Compd. 2022, 898, 162775. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, Z.; Zhou, G.; Jia, Z.; Li, D.; Wu, P. A polycrystal plasticity-cellular automaton integrated modeling method for continuous dynamic recrystallization and its application to AA2196 alloy. Int. J. Plast. 2024, 182, 104127. [Google Scholar] [CrossRef]
- Wu, G.C.; Lin, Y.C.; Chen, M.S.; Qiu, W.; Zeng, N.F.; Zhang, S.; Naseri, M. Continuous dynamic recrystallization behaviors in a single-phase deformed Ti-55511 alloy by cellular automata model. J. Alloys Compd. 2024, 1002, 175293. [Google Scholar] [CrossRef]
- Wang, L.; Qin, J.; Zhai, P.; Jia, H.; Li, M.; Zhu, Y.; Wang, Z. Microstructural Evolution of Dynamic Recrystallization in 30CrNiMoVW Steel During Hot Compression: Constitutive Modeling, Kinetic Model Optimization, and Multiscale FEM coupled CA Simulation. Def. Technol. 2025, in press. [Google Scholar] [CrossRef]
- Chen, S.; Li, L.; Peng, Z.; Huo, X.; Sun, H. On the correlation among continuous cooling transformations, interphase precipitation and strengthening mechanism in Ti-microalloyed steel. J. Mater. Res. Technol. 2021, 10, 580–593. [Google Scholar] [CrossRef]
- Xiong, Z.; Timokhina, I.; Pereloma, E. Clustering, nano-scale precipitation and strengthening of steels. Prog. Mater. Sci. 2021, 118, 100764. [Google Scholar] [CrossRef]
- Peng, Z.; Li, L.; Gao, J.; Huo, X. Precipitation strengthening of titanium microalloyed high-strength steel plates with isothermal treatment. Mater. Sci. Eng. A 2016, 657, 413–421. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, R.; Zhou, Z.; Zhang, P.; Yan, J.; Yuan, Y.; Sun, X. A novel under-aging design to improve the creep rupture life of a precipitation-strengthened Fe–Ni-based superalloy. Mater. Sci. Eng. A 2024, 899, 146459. [Google Scholar] [CrossRef]
- Churyumov, A.Y.; Khomutov, M.G.; Tsar’Kov, A.A.; Pozdnyakov, A.V.; Solonin, A.N.; Efimov, V.M.; Mukhanov, E.L. Study of the structure and mechanical properties of corrosion-resistant steel with a high concentration of boron at elevated temperatures. Phys. Met. Metallogr. 2014, 115, 809–813. [Google Scholar] [CrossRef]
- Wan, Z.; Hu, L.; Sun, Y.; Wang, T.; Li, Z. Hot deformation behavior and processing workability of a Ni-based alloy. J. Alloys Compd. 2018, 769, 367–375. [Google Scholar] [CrossRef]
- Evans, R.W.; Scharning, P.J. Axisymmetric compression test and hot working properties of alloys. Mater. Sci. Technol. 2001, 17, 995–1004. [Google Scholar] [CrossRef]
- Roebuck, B.; Lord, J.D.; Brooks, M.; Loveday, M.S.; Sellars, C.M.; Evans, R.W. Measurement of flow stress in hot axisymmetric compression tests. Mater. High Temp. 2006, 23, 59–83. [Google Scholar] [CrossRef]
- Ebrahimi, R.; Najafizadeh, A. A new method for evaluation of friction in bulk metal forming. J. Mater. Process. Technol. 2004, 152, 136–143. [Google Scholar] [CrossRef]
- Li, L.; Zhou, J.; Duszczyk, J. Determination of a constitutive relationship for AZ31B magnesium and validation through comparison between simulated and real extrusion. J. Mater. Process. Technol. 2006, 172, 372–380. [Google Scholar] [CrossRef]
- Dong, S.T.; Wang, J.; Pang, J.; Hu, W.L.; Zhao, J.H.; He, W.W.; Ma, Q.X. Investigation of dynamic recrystallization and grain size evolution behavior of 45CrNi steel treated by upsetting deformation by utilizing FE–CA method. J. Mater. Sci. 2025, 60, 15311–15338. [Google Scholar] [CrossRef]
- Dutta, B.; Valdes, E.; Sellars, C.M. Mechanism and kinetics of strain induced precipitation of Nb (C, N) in austenite. Acta Metall. Mater. 1992, 40, 653–662. [Google Scholar] [CrossRef]
- Vervynckt, S.; Verbeken, K.; Thibaux, P.; Houbaert, Y. Recrystallization–precipitation interaction during austenite hot deformation of a Nb microalloyed steel. Mater. Sci. Eng. A 2011, 528, 5519–5528. [Google Scholar] [CrossRef]
- Schwarze, C.; Kamachali, R.D.; Steinbach, I. Phase-field study of zener drag and pinning of cylindrical particles in polycrystalline materials. Acta Mater. 2016, 106, 59–65. [Google Scholar] [CrossRef]
- Hillert, M. On the estimation of the Zener drag on grain boundaries. Scr. Metall. 1984, 18, 1431–1432. [Google Scholar] [CrossRef]
- Raabe, D.; Hantcherli, L. 2D cellular automaton simulation of the recrystallization texture of an IF sheet steel under consideration of Zener pinning. Comput. Mater. Sci. 2005, 34, 299–313. [Google Scholar] [CrossRef]
- Gouné, M.; Drillet, J.; Maugis, P. Modelling of the interaction between phase transformation and precipitation: Coupled kinetics in microalloyed multiphase steels. Comput. Mater. Sci. 2012, 55, 127–135. [Google Scholar] [CrossRef]
- Niu, M.C.; Chen, C.J.; Li, W.; Yang, K.; Luan, J.H.; Wang, W.; Jiao, Z.B. Atomic-scale understanding of solute interaction effects on grain boundary segregation, precipitation, and fracture of ultrahigh-strength maraging steels. Acta Mater. 2023, 253, 118972. [Google Scholar] [CrossRef]
- Zhou, F.; Guo, J.; Zhao, Y.; Chu, X.H.; Lei, L.; Zhou, C.S.; Zhao, Z.Z. An improved cellular automaton model of dynamic recrystallization and the constitutive model coupled with dynamic recrystallization kinetics for microalloyed high strength steels. J. Mater. Res. Technol. 2024, 33, 10003–10021. [Google Scholar] [CrossRef]
- Lin, Y.C.; Liu, Y.X.; Chen, M.S.; Huang, M.H.; Ma, X.; Long, Z.L. Study of static recrystallization behavior in hot deformed Ni-based superalloy using cellular automaton model. Mater. Des. 2016, 99, 107–114. [Google Scholar] [CrossRef]
- Chen, M.S.; Yuan, W.Q.; Lin, Y.C.; Li, H.B.; Zou, Z.H. Modeling and simulation of dynamic recrystallization behavior for 42CrMo steel by an extended cellular automaton method. Vacuum 2017, 146, 142–151. [Google Scholar] [CrossRef]
- Guo, Y.N.; Li, Y.T.; Tian, W.Y.; Qi, H.P.; Yan, H.H. Confirmed. The references have been updated. Combined cellular automaton model for dynamic recrystallization evolution of 42CrMo cast steel. Chin. J. Mech. Eng. 2018, 31, 85. [Google Scholar] [CrossRef]
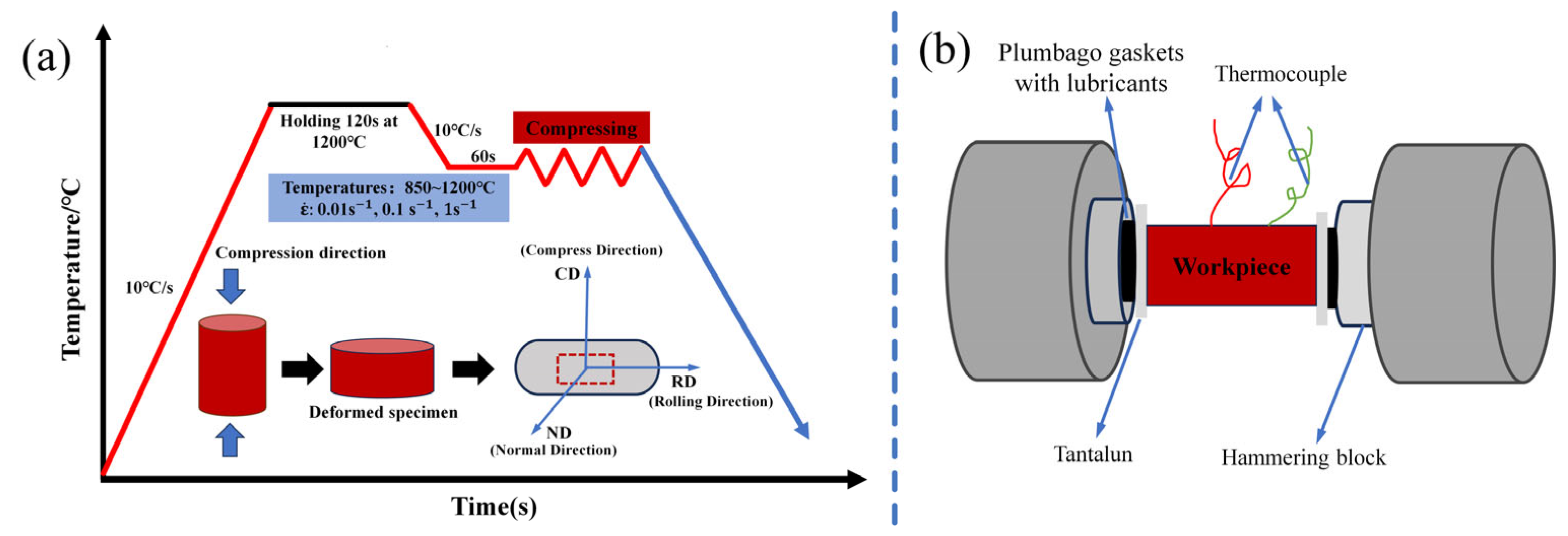
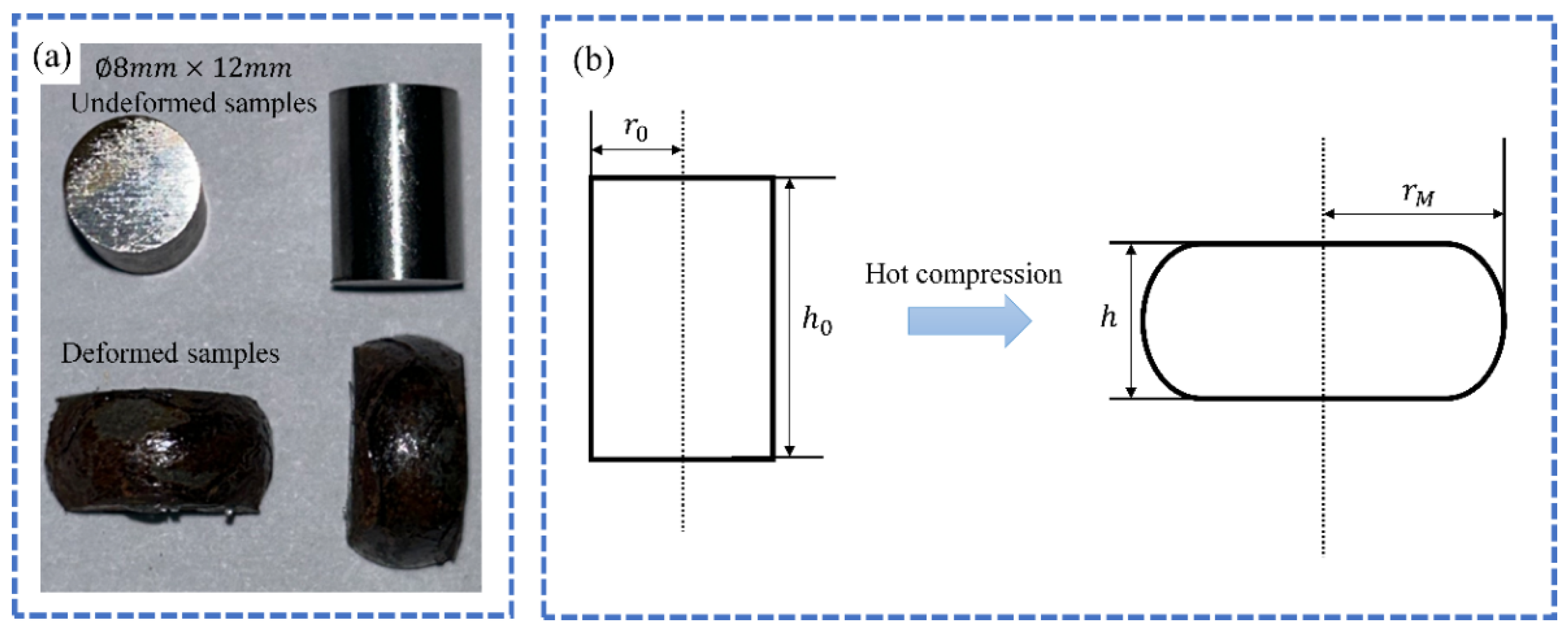
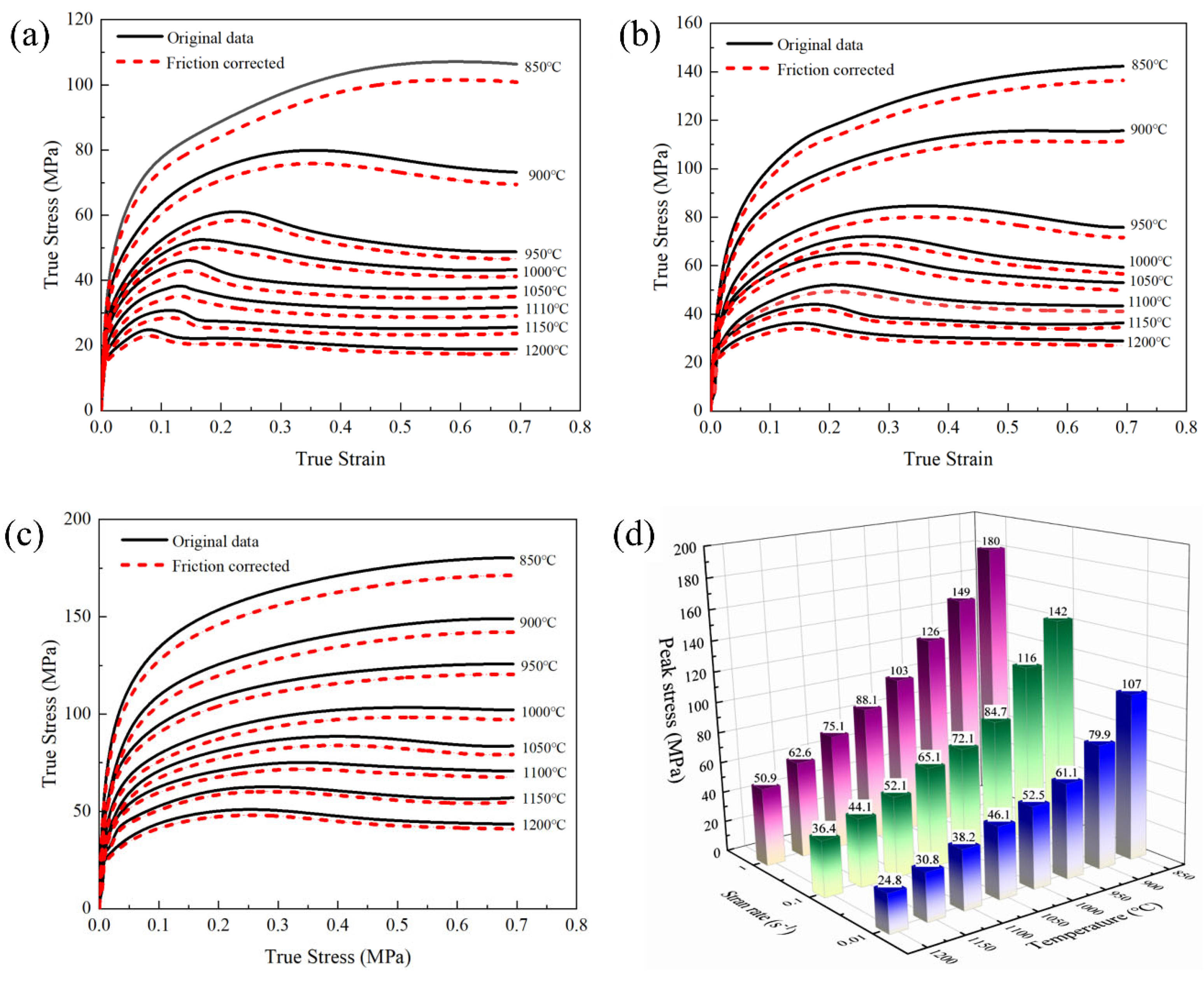
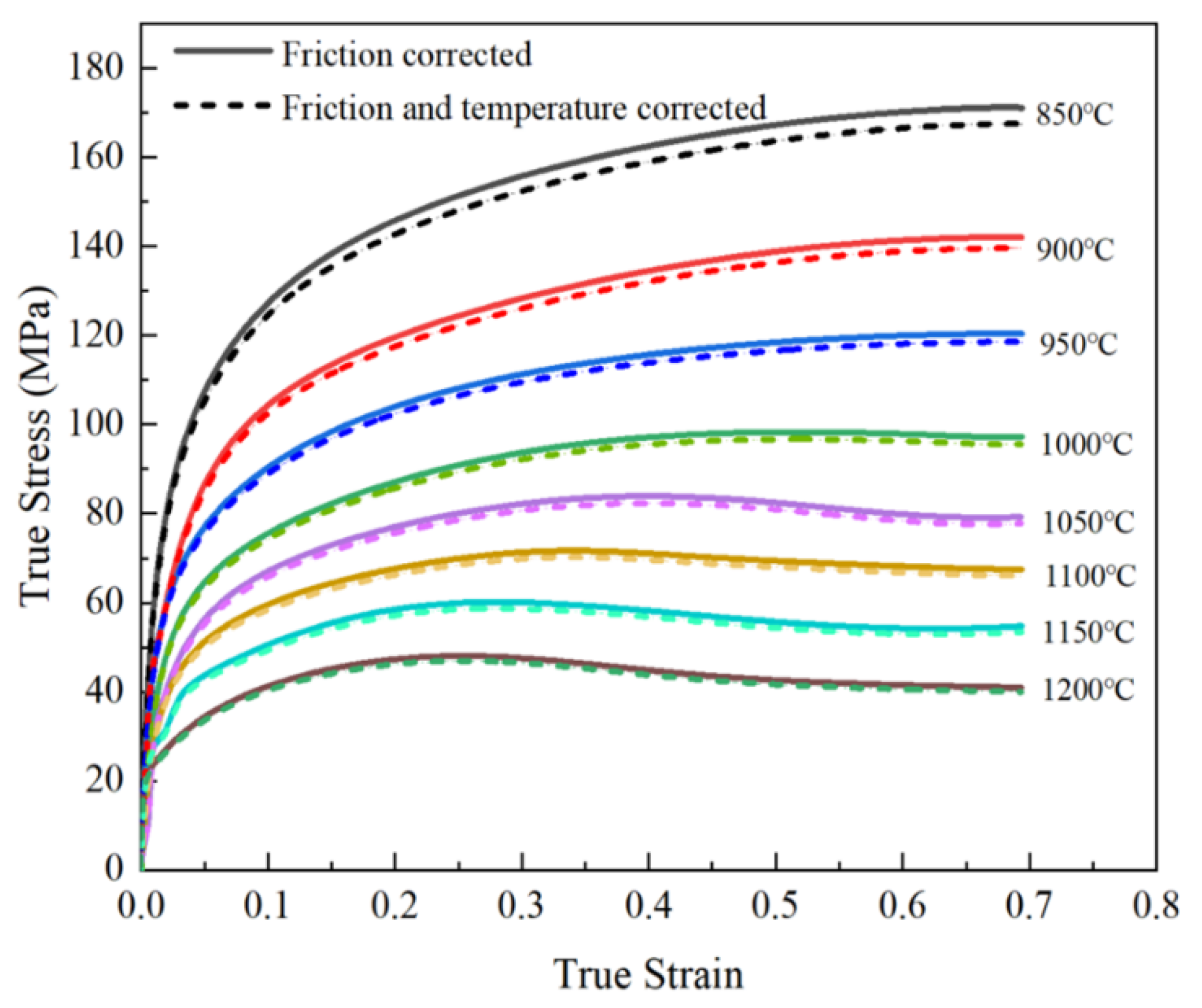




| Element | C | Si | Mn | Cr | Ni | P | S | Fe |
|---|---|---|---|---|---|---|---|---|
| Mass fraction | 0.45 | 0.27 | 0.7 | 0.6 | 1.2 | 0.03 | 0.035 | Bal. |
| Deformation Temperature (℃) | ) | ||
|---|---|---|---|
| 0.01 | 0.1 | 1 | |
| 850 | 1.237 | 1.112 | 1.134 |
| 900 | 1.082 | 1.105 | 1.119 |
| 950 | 1.133 | 1.106 | 1.128 |
| 1000 | 1.113 | 1.115 | 1.143 |
| 1050 | 1.122 | 1.124 | 1.114 |
| 1100 | 1.109 | 1.113 | 1.094 |
| 1150 | 1.101 | 1.112 | 1.088 |
| 1200 | 1.201 | 1.121 | 1.092 |
| Parameter | s−1) | b (m) | μ (Pa) | v | |||
|---|---|---|---|---|---|---|---|
| Value | 510−12 | 2.86 × 10−10 | 8.2 × 1010 | 15° | 0.35 | 361,246 | 215,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Dong, S.; Lv, H.; He, W. Investigation of Hot Deformation Behavior for 45CrNi Steel by Utilizing an Improved Cellular Automata Method. Metals 2025, 15, 1015. https://doi.org/10.3390/met15091015
Zhao J, Dong S, Lv H, He W. Investigation of Hot Deformation Behavior for 45CrNi Steel by Utilizing an Improved Cellular Automata Method. Metals. 2025; 15(9):1015. https://doi.org/10.3390/met15091015
Chicago/Turabian StyleZhao, Jinhua, Shitong Dong, Hongru Lv, and Wenwu He. 2025. "Investigation of Hot Deformation Behavior for 45CrNi Steel by Utilizing an Improved Cellular Automata Method" Metals 15, no. 9: 1015. https://doi.org/10.3390/met15091015
APA StyleZhao, J., Dong, S., Lv, H., & He, W. (2025). Investigation of Hot Deformation Behavior for 45CrNi Steel by Utilizing an Improved Cellular Automata Method. Metals, 15(9), 1015. https://doi.org/10.3390/met15091015






