Hot Extrusion Process Grain Size Prediction and Effects of Friction Models and Hydraulic Press Applications
Abstract
1. Introduction
2. Experimental Setup and Process Modeling
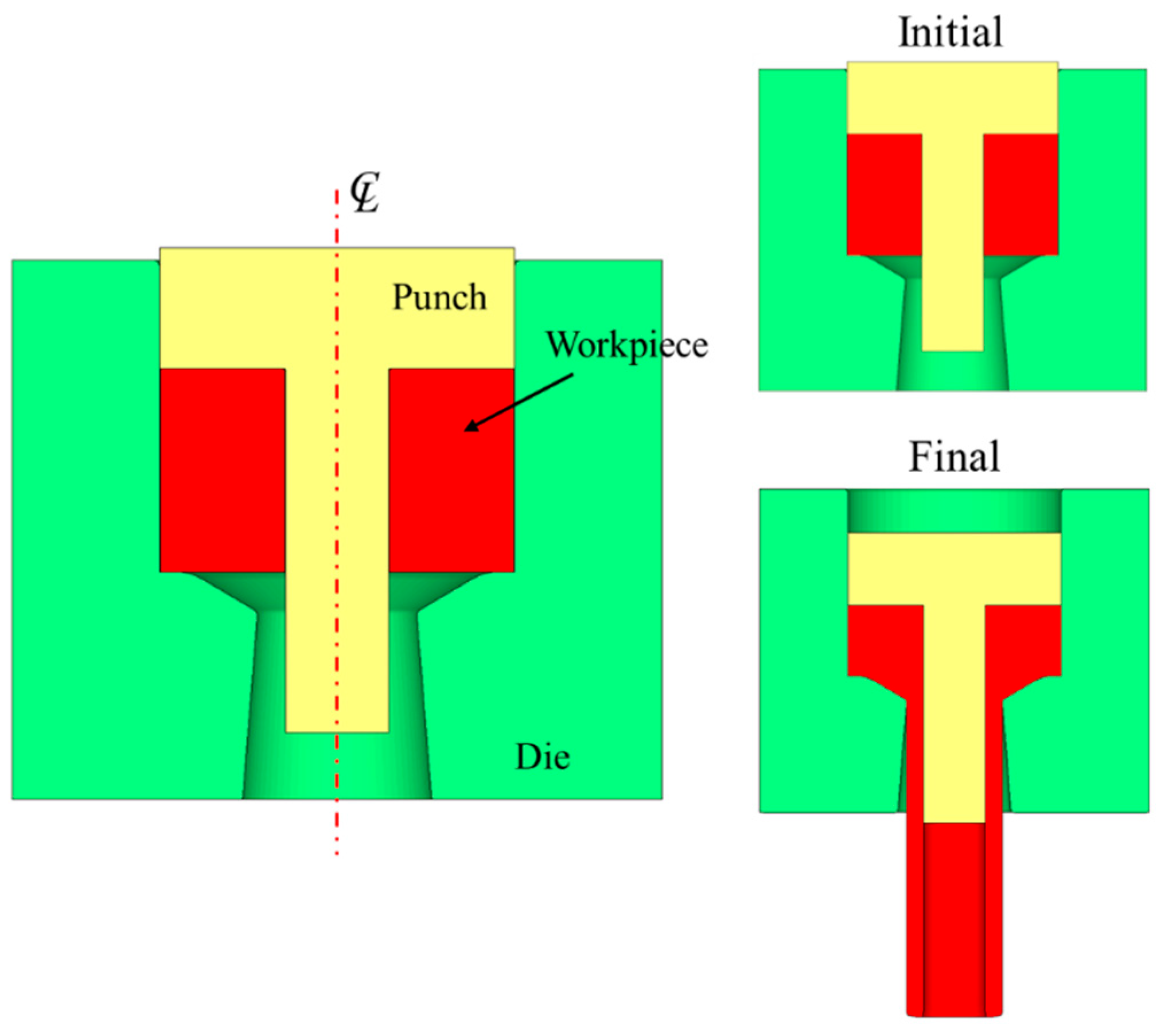
2.1. Experimental Setup and Process Conditions
2.2. Friction Modeling and Contact Interface Characterization
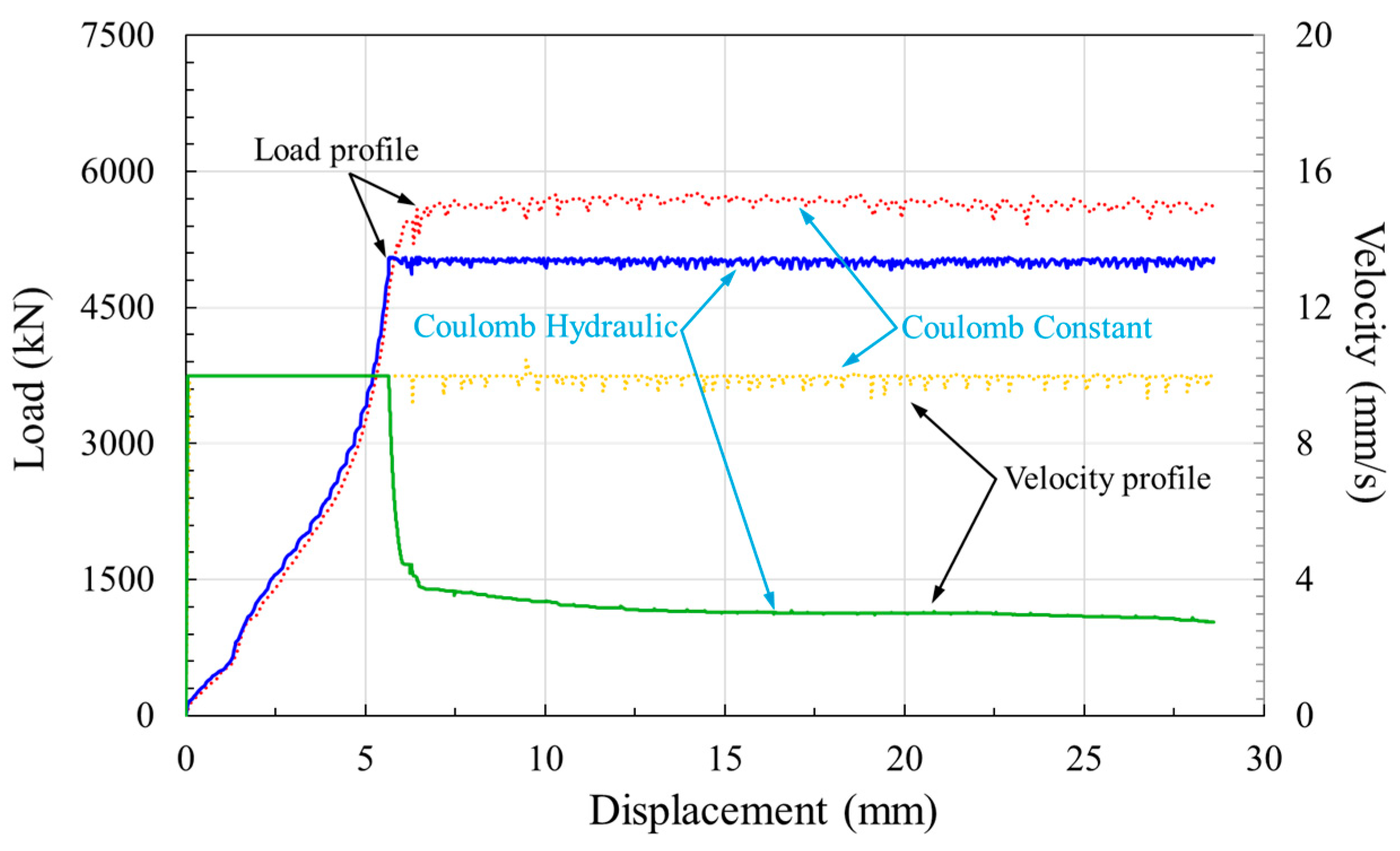
2.3. Punch Velocity Control and Load Constraint Conditions
- (a)
- Constant Velocity Mode: The punch initially travels at a fixed velocity of −10 mm/s. However, once the forming load exceeds the press capacity, the velocity is automatically reduced to accommodate the increasing resistance. In this mode, the load was observed to rise beyond 6000 kN, surpassing the actual machine limit of 5000 kN, resulting in an unrealistic representation of the industrial process.
- (b)
- Hydraulic Press Mode (Load-Constrained): This approach also starts with a −10 mm/s punch velocity, but with an active force limit of 5000 kN imposed. Once this threshold is reached, the punch speed is reduced dynamically to ensure the load remains within the allowable range, more accurately replicating real hydraulic press behavior.
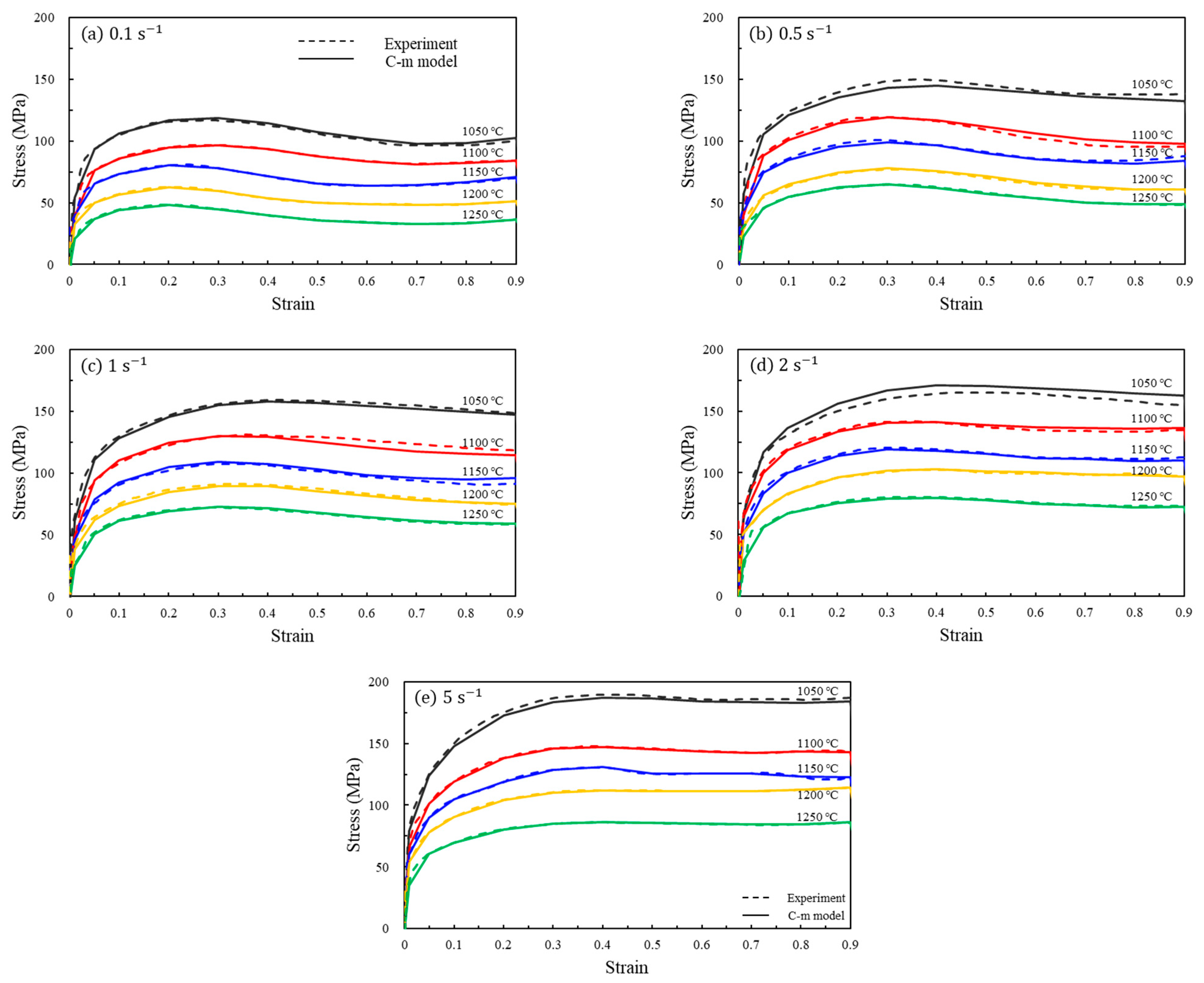
2.4. Flow Stress Calibration and Implementation
2.5. Grain Size Calibration and Implementation
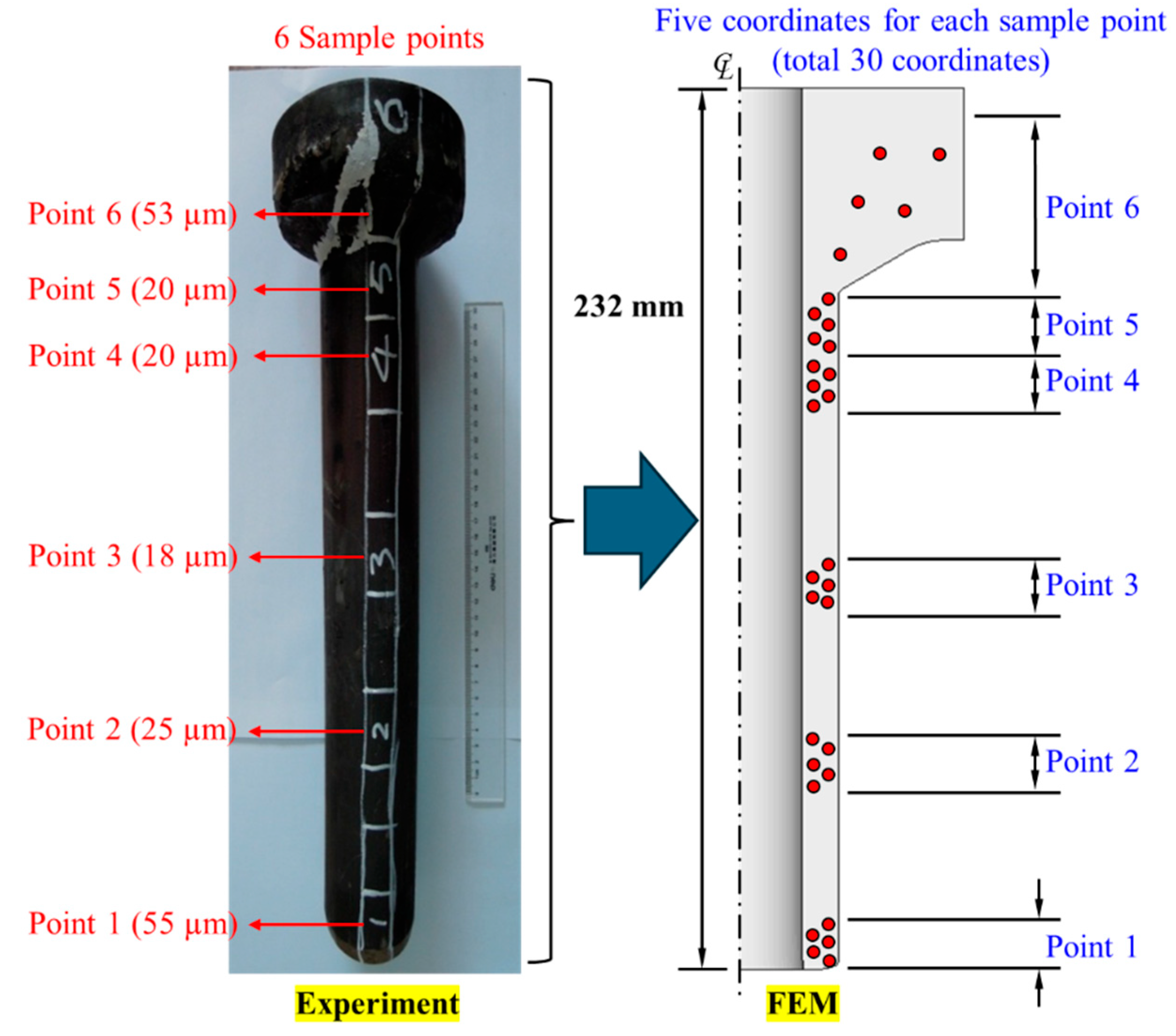
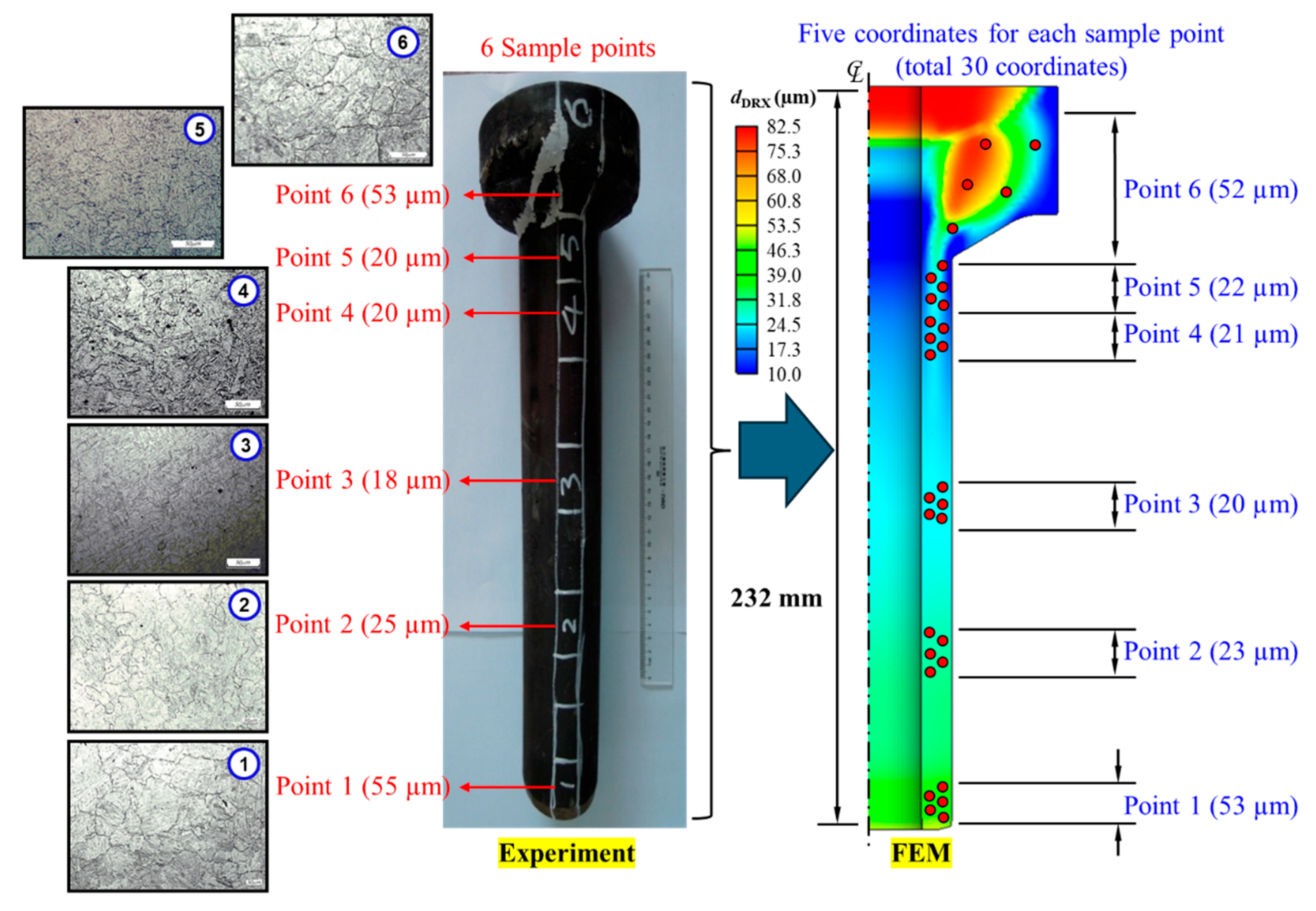
2.5.1. Experimental Grain Size Measurement in Extruded Billets
2.5.2. JMAK-Based Model
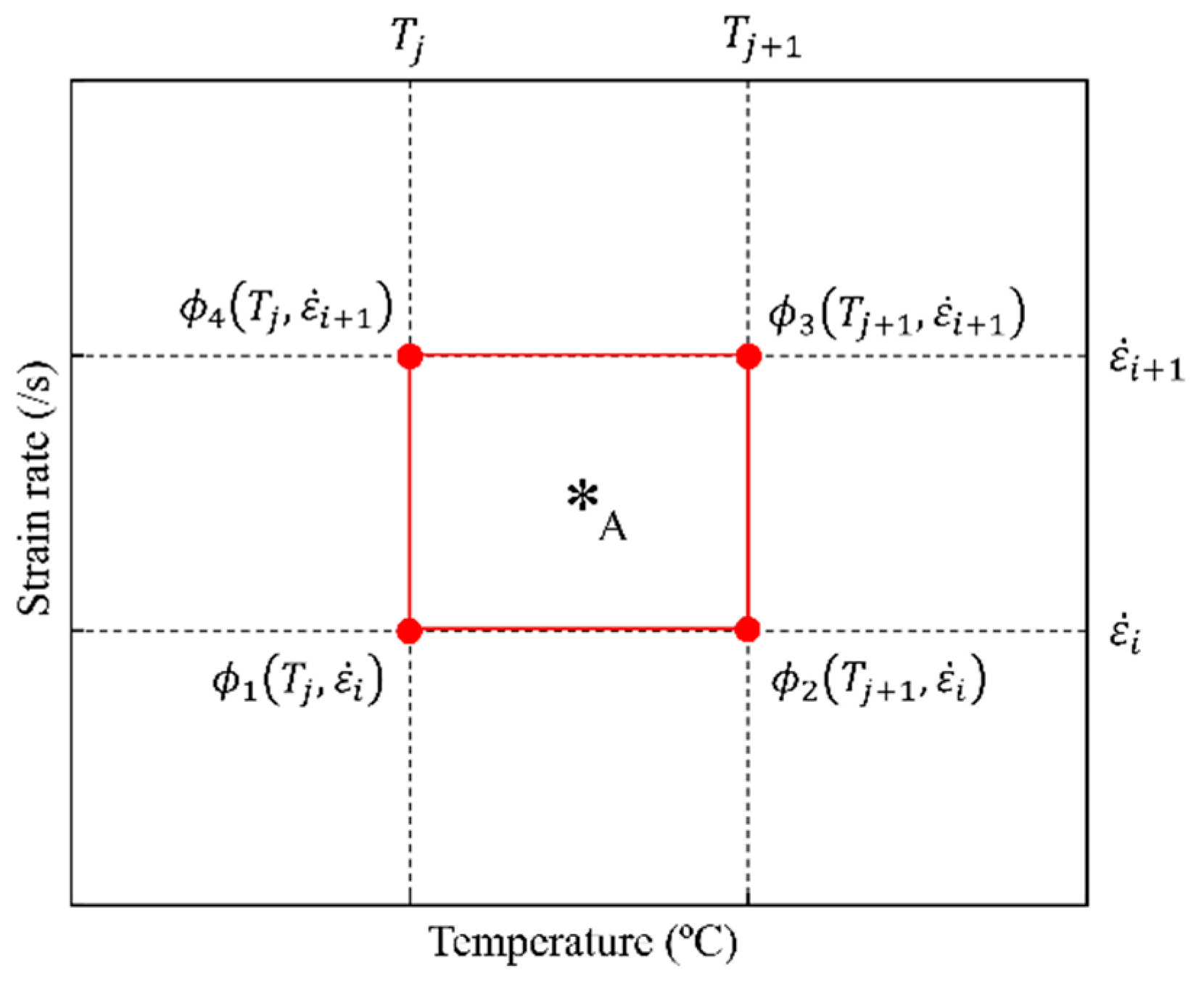
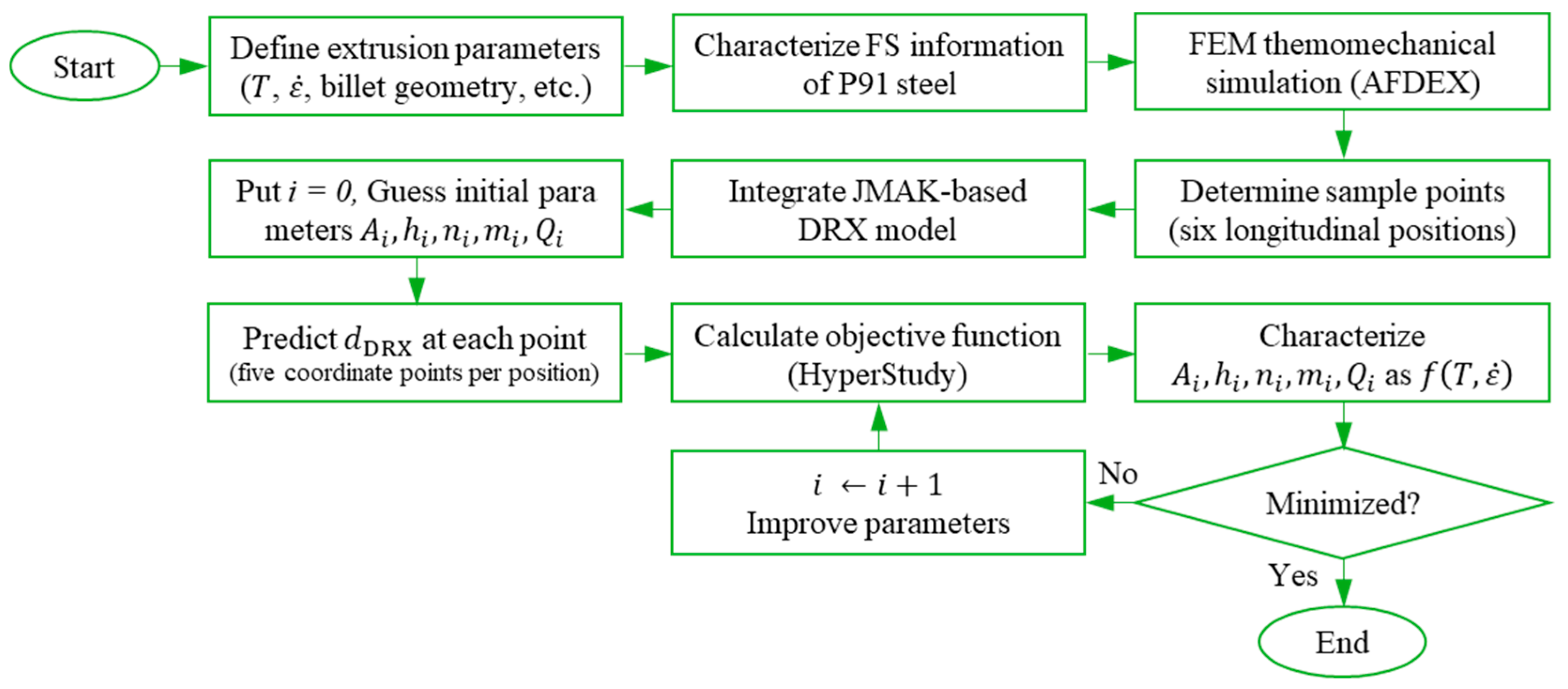
2.5.3. FEM-Coupled Optimization Technique
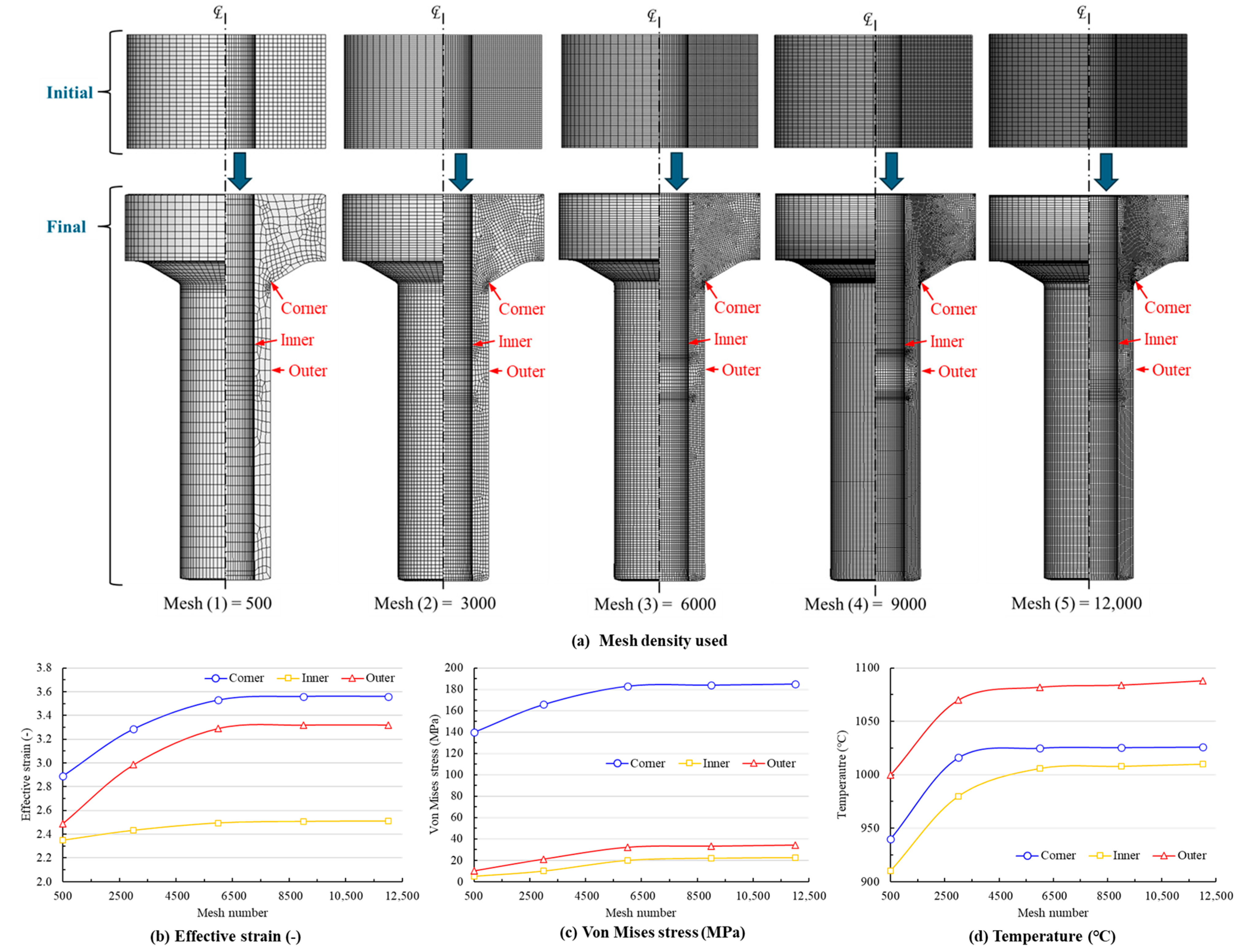
3. Model Calibration and Validation Framework
3.1. Optimization Outcomes for Microstructural Parameters
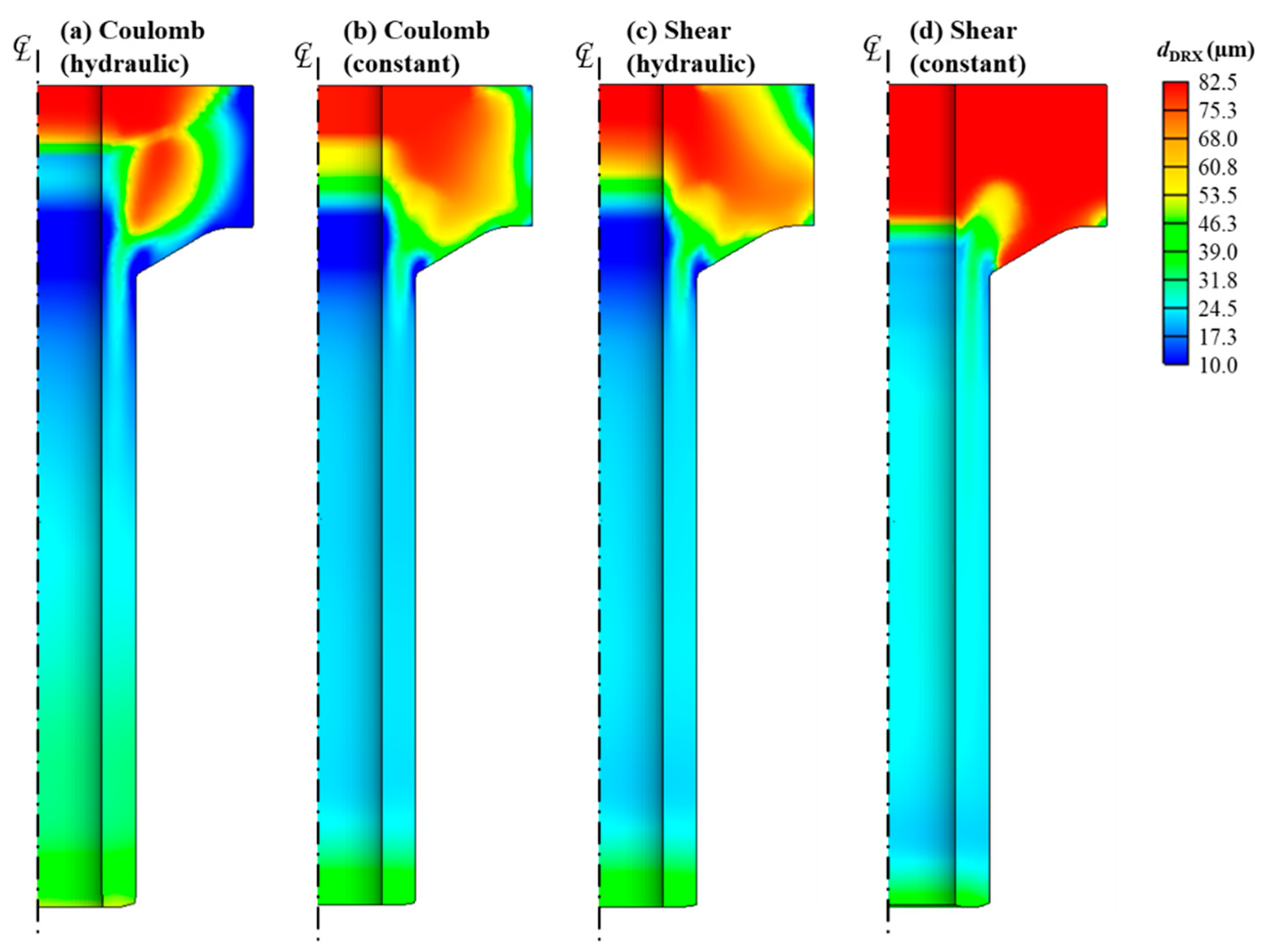
3.2. Influence of Friction Models and Punch Control Strategies on Hot Extrusion Microstructure Prediction
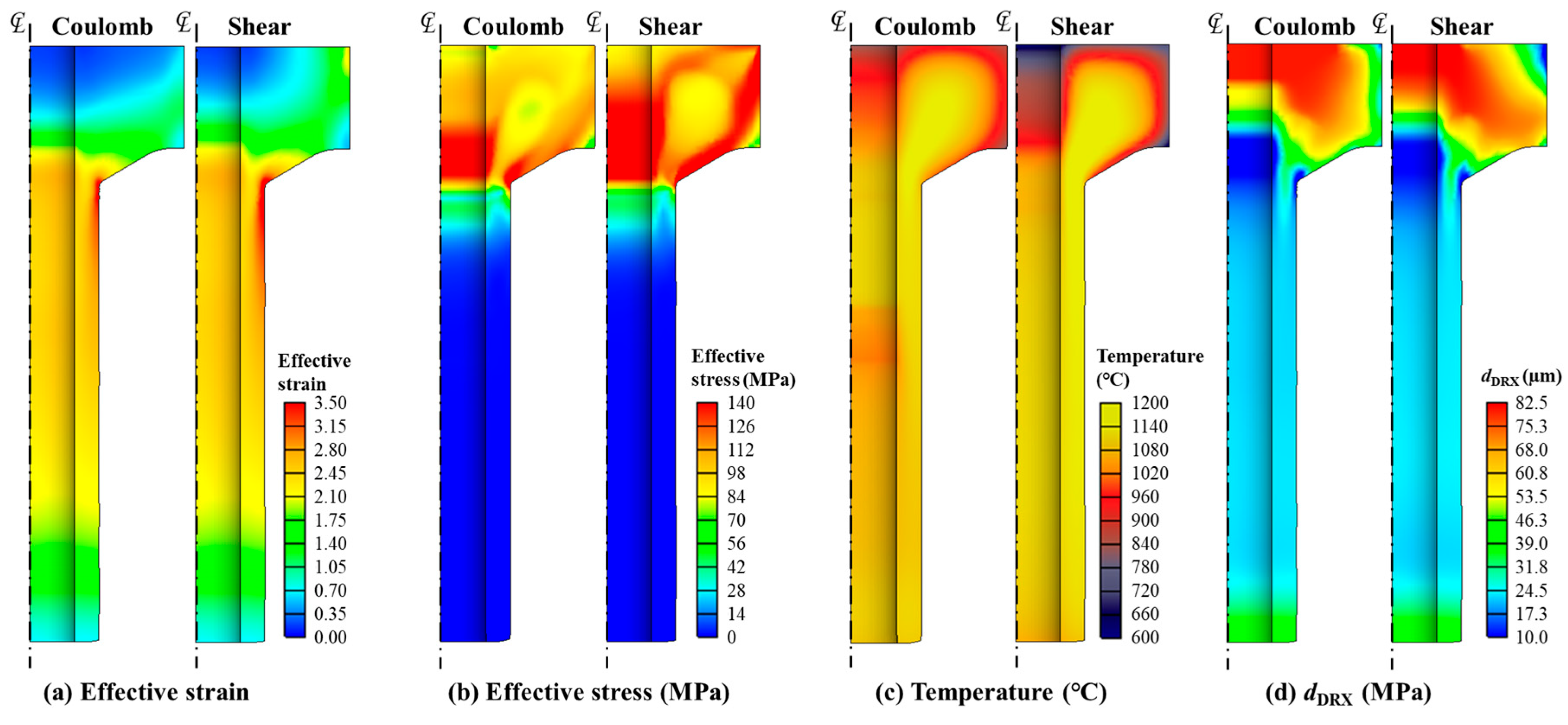
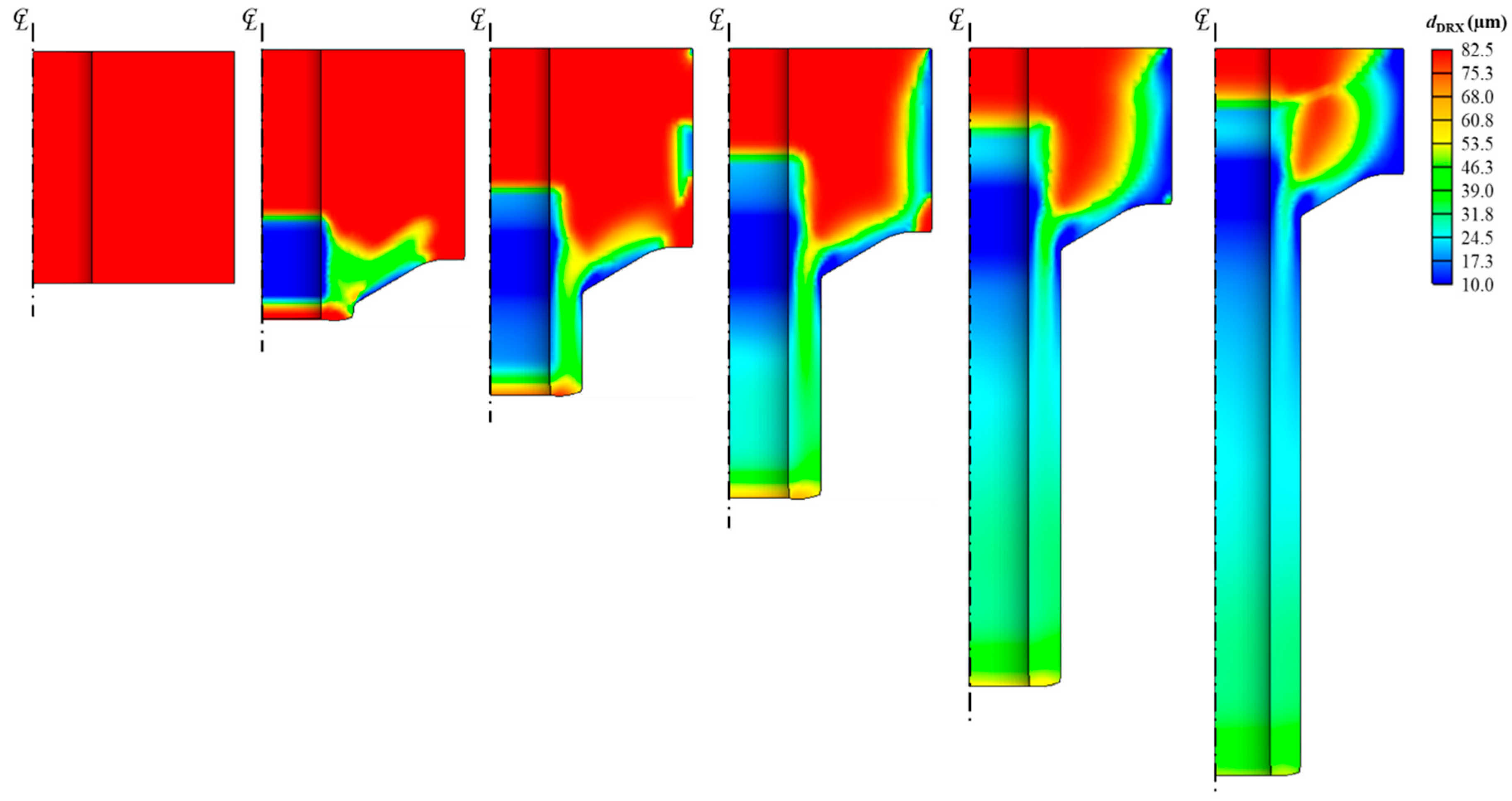
3.2.1. Strain, Stress and Temperature Distribution
3.2.2. Effect of Punch Control Mode
- (a)
- Constant velocity mode at −10 mm/s, which applies a fixed punch speed regardless of material resistance.
- (b)
- Hydraulic press mode, which adaptively reduces punch velocity to maintain a maximum allowable load of 5000 kN.
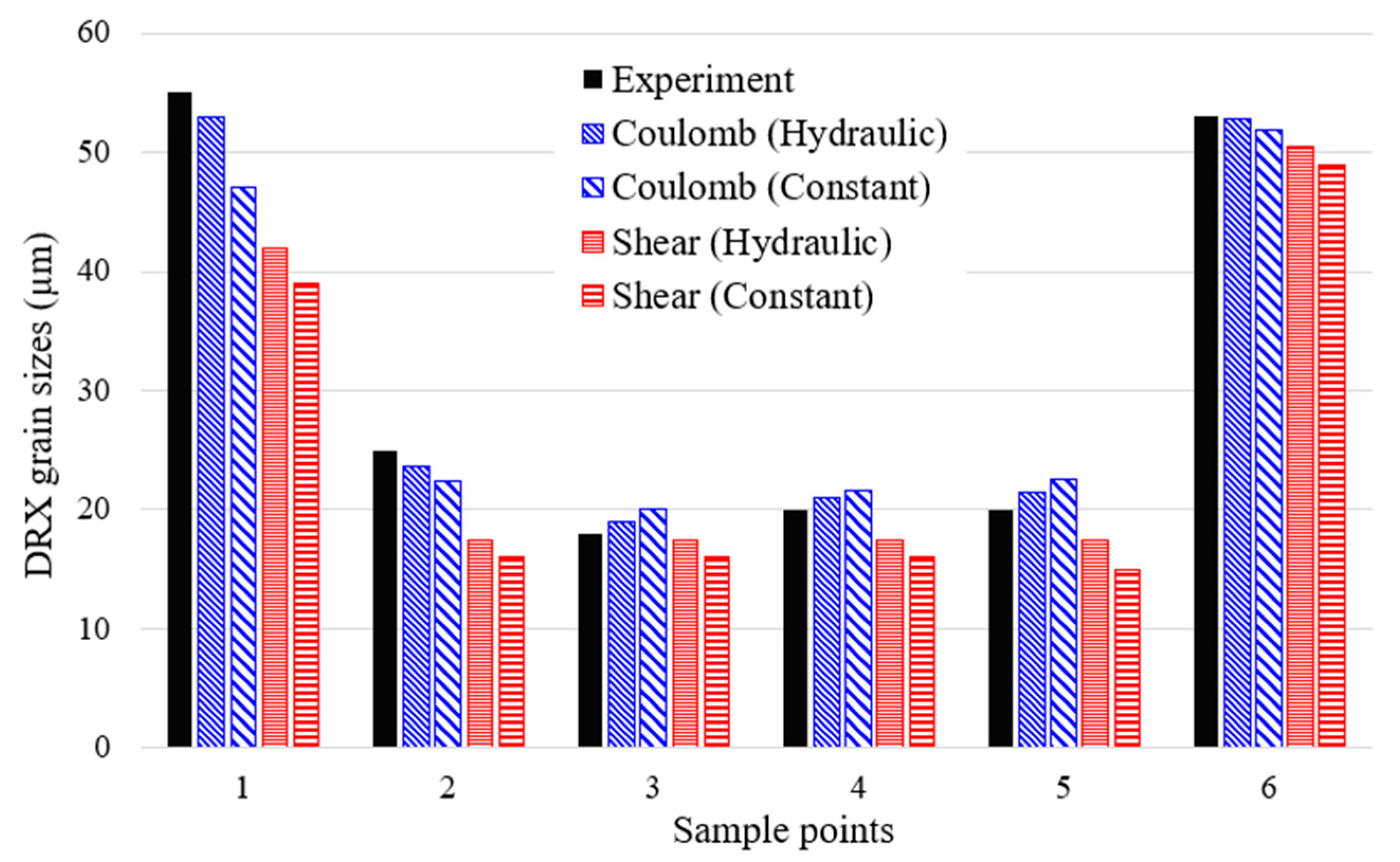
3.2.3. Summary of Insights
- Shear friction with constant velocity;
- Coulomb friction with constant velocity;
- Shear friction with hydraulic press control;
- Coulomb friction with hydraulic press control.
- Prediction accuracy: The Coulomb–hydraulic model provides the closest match to experiment, with errors consistently below 10%.
- Friction model sensitivity: Shear models overpredict deformation, leading to excessively fine grain sizes and poor agreement.
- Control strategy impact: Hydraulic press control smoothens strain input, moderates thermal gradients, and improves DRX prediction stability.
- Spatial resolution: The 30-coordinate comparison validates the simulation’s capability to reflect sub-regional variations in grain size, enhancing confidence in microstructural predictions.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Quantitative Comparison of Extruded Dimensions

Appendix B. Verification of the Computer-Aided Engineering Models
References
- Razali, M.K.; Chung, S.H.; Irani, M.; Choi, J.M.; Joun, M.S. Characterization of the dynamic recrystallization kinetics using directly flow stress model and Its application to 42CrMo steel. In International Conference on the Technology of Plasticity; Springer Nature: Cham, Switzerland, 2023; pp. 442–454. [Google Scholar] [CrossRef]
- Guo, P.; Deng, L.; Wang, X.; Li, J. Modelling of dynamic recrystallization kinetics of 300 M steel at high strain rates during hot deformation. Sci. China Technol. Sci. 2019, 62, 1534–1544. [Google Scholar] [CrossRef]
- Razali, M.K.; Heo, Y.; Irani, M.; Chung, S.H.; Joun, M.S. Grain size prediction in SCR420HB hot forging: Combining phenomenological and JMAK models with experimental and numerical analysis. Mater. Today Commun. 2024, 41, 110921. [Google Scholar] [CrossRef]
- Liu, Y.; Quan, G.; Yu, Y.; Wu, D. Loading path design for grain refinement in hot forming process of Ti-6Al-2Zr-1Mo-1V Alloy. J. Mater. Eng. Perform. 2024, 34, 1–17. [Google Scholar] [CrossRef]
- Du, H.Q.; Li, F.; Wang, Y.; Li, C.; Chen, Z.Y. Modification of grain refinement and texture based on pre-upsetting AZ31 Mg alloy in interactive alternating forward extrusion. Int. J. Adv. Manuf. Technol. 2022, 121, 4805–4815. [Google Scholar] [CrossRef]
- Foydl, A.; Segatori, A.; Khalifa, N.B.; Donati, L.; Brosius, A.; Tomesani, L.; Tekkaya, A.E. Grain size evolution simulation in aluminium alloys AA 6082 and AA 7020 during hot forward extrusion process. Mater. Sci. Technol. 2013, 29, 100–110. [Google Scholar] [CrossRef]
- Hou, H.; Zhang, L.; Wang, X.; Mei, M.; Zhao, Y. Numerical and experimental research of the effect of friction on cold extrusion internal thread process. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 515. [Google Scholar] [CrossRef]
- Breumier, S.; Adamski, F.; Badreddine, J.; Lévesque, M.; Kermouche, G. Microstructural and mechanical characterization of a shot peening induced rolled edge on direct aged Inconel 718 alloy. Mater. Sci. Eng. A 2021, 816, 141318. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, Z.; Wang, Q.; Yin, X.; Cui, J.; Qi, H. Dynamic recrystallization behavior of magnesium alloys with LPSO during hot deformation. J. Alloys Compd. 2017, 704, 382–389. [Google Scholar] [CrossRef]
- Mirzadeh, H. Grain refinement of magnesium alloys by dynamic recrystallization (DRX): A review. J. Mater. Res. Technol. 2023, 25, 7050–7077. [Google Scholar] [CrossRef]
- Chanda, T.; Zhou, J.; Kowalski, L.; Duszczyk, J. 3D FEM simulation of the thermal events during AA6061 aluminum extrusion. Scr. Mater. 1999, 41, 195–202. [Google Scholar] [CrossRef]
- Yeom, J.T.; Kim, J.H.; Hong, J.K.; Park, N.K.; Lee, C.S. Prediction of microstructure evolution in hot backward extrusion of Ti-6Al-4V Alloy. J. Metall. 2012, 1, 989834. [Google Scholar] [CrossRef]
- Kugler, G.; Turk, R. Modeling the dynamic recrystallization under multi-stage hot deformation. Acta Mater. 2004, 52, 4659–4668. [Google Scholar] [CrossRef]
- Sellars, C.M.; Tegart, W.M. Hot workability. Int. Metall. 1972, 17, 1–24. [Google Scholar] [CrossRef]
- Dourandish, S.; Champliaud, H.; Morin, J.B.; Jahazi, M. Numerical simulation and experimental validation of microstructure evolution during the upsetting process of a large size martensitic stainless steel forging. Int. J. Mater. Form. 2024, 17, 38. [Google Scholar] [CrossRef]
- Koizumi, T.; Kuroda, M. Grain size effects in aluminum processed by severe plastic deformation. Mater. Sci. Eng. A 2018, 710, 300–308. [Google Scholar] [CrossRef]
- Khajezade, A. Prediction of Grain Structure and Texture Evolution After High Temperature Extrusion of Aluminum Alloys. Doctoral Dissertation, University of British Columbia, Vancouver, BC, Canada, 2022. Available online: https://open.library.ubc.ca/soa/cIRcle/collections/ubctheses/24/items/1.0421260 (accessed on 11 October 2022).
- Diyoke, G.; Rath, L.; Chafle, R.; Ben Khalifa, N.; Klusemann, B. Numerical simulation of friction extrusion: Process characteristics and material deformation due to friction. Int. J. Mater. Form. 2024, 17, 26. [Google Scholar] [CrossRef]
- Bagherpour, E.; Mortezaei, S.; Ebrahimi, R.; Miyamoto, H.; Qods, F. On the production of severely deformed workpieces in large scales: A step towards industrialization. JOM 2019, 71, 4424–4435. [Google Scholar] [CrossRef]
- Mahmoodkhani, Y.; Wells, M.A.; Grajales, L.; Poole, W.J.; Parson, N.C. Material flow and grain deformation during extrusion. In Materials Science Forum; Trans Tech Publications Ltd.: Lincoln, NE, USA, 2014; Volume 794, pp. 664–669. [Google Scholar] [CrossRef]
- Lee, S.W.; Jo, J.W.; Joun, M.S.; Lee, J.M. Effect of friction conditions on material flow in FE analysis of Al piston forging process. Int. J. Precis. Eng. Manuf. 2019, 20, 1643–1652. [Google Scholar] [CrossRef]
- Lin, J.B.; Ma, L.F.; Chen, Y.X.; Wang, C.; Liang, Q.X.; Cui, X.C. Experimental and numerical investigation of the grain size evolvement of AZ31 Mg Alloy during high ratio extrusion. In Materials Science Forum; Trans Tech Publications Ltd.: Lincoln, NE, USA, 2013; Volume 747, pp. 211–216. [Google Scholar] [CrossRef]
- Zhang, D.W.; Xu, F.F.; Yu, Z.C.; Lu, K.Y.; Zheng, Z.B.; Zhao, S.D. Coulomb, Tresca and Coulomb-Tresca friction models used in analytical analysis for rolling process of external spline. J. Mater. Process. Technol. 2021, 292, 117059. [Google Scholar] [CrossRef]
- Joun, M.S.; Heo, Y.; Kim, N.H.; Kim, N.Y. On lubrication regime changes during forward extrusion, forging, and drawing. Lubricants 2024, 12, 352. [Google Scholar] [CrossRef]
- Abd Ghawi, A.A.; Razali, M.K.; Salleh, N.A.M.; Joun, M.S. Coupled elastoplastic FEM analysis of frictional boss forming. Next Res. 2025, 2, 100416. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. I General theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Ruckenstein, E.; Vavanellos, T. Kinetics of solid phase reactions. AIChE J. 1975, 21, 756–763. [Google Scholar] [CrossRef]
- Fanfoni, M.; Tomellini, M. The johnson-mehl-avrami-kohnogorov model: A brief review. Il Nuovo C. D 1998, 20, 1171–1182. [Google Scholar] [CrossRef]
- Jonas, J.J.; Quelennec, X.; Jiang, L.; Martin, É. The Avrami kinetics of dynamic recrystallization. Acta Mater. 2009, 57, 2748–2756. [Google Scholar] [CrossRef]
- Jiang, Y.; Wu, R.; Yuan, C.; Wang, W.; Jiao, W. Prediction and analysis of breakthrough extruding force based on a modified FE-model in large-scale extrusion process. Int. J. Adv. Manuf. Technol. 2019, 104, 3531–3544. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. II. transformation-time relations for random distribution of nuclei. J. Chem. Phys. 1940, 8, 212–224. [Google Scholar] [CrossRef]
- Shercliff, H.R.; Lovatt, A.M. Modelling of microstructure evolution in hot deformation. Philos. Trans. R. Soc. Lond. Ser. A 1999, 357, 1621–1643. [Google Scholar] [CrossRef]
- Zhou, W.; Lin, J.; Balint, D.S.; Dean, T.A. Clarification of the effect of temperature and strain rate on workpiece deformation behaviour in metal forming processes. Int. J. Mach. Tools. Manuf. 2021, 171, 103815. [Google Scholar] [CrossRef]
- Francy, K.A.; Rao, C.S.; Gopalakrishnaiah, P. Optimization of direct extrusion process parameter on 16MnCr5 and AISI1010 using DEFORM-3D. Procedia Manuf. 2019, 30, 498–505. [Google Scholar] [CrossRef]
- Lin, Y.C.; Nong, F.Q.; Chen, X.M.; Chen, D.D.; Chen, M.S. Microstructural evolution and constitutive models to predict hot deformation behaviors of a nickel-based superalloy. Vacuum 2017, 137, 104–114. [Google Scholar] [CrossRef]
- Karhausen, K.; Kopp, R. Model for integrated process and microstructure simulation in hot forming. Steel. Res. 1992, 63, 247–256. [Google Scholar] [CrossRef]
- Bakhtiani, T.; El-Mounayri, H.; Zhang, J. Numerical simulation of aluminum extrusion using coated die. Mater. Today Proc. 2014, 1, 94–106. [Google Scholar] [CrossRef]
- Mittelman, B.; Priel, E.; Navi, N.U. A finite element study of thermo-mechanical fields and their relation to friction conditions in Al1050 ring compression tests. J. Manuf. Mater. Process 2018, 2, 83. [Google Scholar] [CrossRef]
- Joun, M.S. Recent advances in metal forming simulation technology for automobile parts by AFDEX. IOP Conf. Ser. Mater. Sci. Eng. 2020, 834, 012016. [Google Scholar] [CrossRef]
- Petrik, J.; Ali, S.I.; Feistle, M.; Bambach, M. CrystalMind: A surrogate model for predicting 3D models with recrystallization in open-die hot forging including an optimization framework. Mech. Mater. 2024, 189, 104875. [Google Scholar] [CrossRef]
- Moon, H.K.; Lee, J.S.; Yoo, S.J.; Joun, M.S.; Lee, J.K. Hot deformation behavior of bearing steels. J. Eng. Mater. Technol. 2007, 129, 349–355. [Google Scholar] [CrossRef]
- Joun, M.S.; Razali, M.K.; Yoo, J.D.; Kim, M.C.; Choi, J.M. Novel extended Cm models of flow stress for accurate mechanical and metallurgical calculations and comparison with traditional flow models. J. Magnes. Alloys. 2022, 10, 2516–2533. [Google Scholar] [CrossRef]
- Menapace, C.; Sartori, N.; Pellizzari, M.; Straffelini, G. Hot deformation behavior of four steels: A comparative study. J. Eng. Mater. Technol. 2018, 140, 021006. [Google Scholar] [CrossRef]
- Bobrovskij, I.; Khaimovich, A.; Bobrovskij, N.; Travieso-Rodriguez, J.A.; Grechnikov, F. Derivation of the coefficients in the coulomb constant shear friction law from experimental data on the extrusion of a material into V-shaped channels with different convergence angles: New method and algorithm. Metals 2022, 12, 239. [Google Scholar] [CrossRef]
- Priel, E.; Mittelman, B.; Trabelsi, N.; Cohen, Y.; Koptiar, Y.; Padan, R. A computational investigation of equal channel angular pressing of molybdenum validated by experiments. J. Mater. Process. Technol. 2019, 264, 469–485. [Google Scholar] [CrossRef]



| Temperature (°C) | Thermal Conductivity [W/(mm °C)] | Heat Capacity [Ws/(mm3 °C)] |
|---|---|---|
| 20 | 0.0417 | 0.00283 |
| 100 | 0.0434 | 0.00305 |
| 200 | 0.0432 | 0.00328 |
| 400 | 0.0391 | 0.00376 |
| 600 | 0.0341 | 0.00479 |
| 1500 | 0.0341 | 0.00479 |
| 20 | 0.0134 | 0.00563 |
| 200 | 0.0134 | 0.00563 |
| 800 | 0.0138 | 0.00563 |
| 900 | 0.0146 | 0.00563 |
| 1000 | 0.0153 | 0.00571 |
| 1100 | 0.0161 | 0.00572 |
| 1200 | 0.0168 | 0.00585 |
| 1300 | 0.0175 | 0.00611 |
| Heat transfer coefficient to ambient from material and dies (W/ °C) | 2.95 × |
| Heat radiation coefficient to ambient from material and dies (W/ °C4) | 3.97 × |
| Heat transfer coefficient to material from die (W/ °C) | 0.01 |
| T (°C) | T (°C) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1050 | 0.01 | 48.39 | 13.01 | 0.093 | 0.026 | 1100 | 0.01 | 267.95 | −218.87 | 0.814 | 0.189 |
| 0.05 | 88.10 | 22.89 | 0.049 | −0.002 | 0.05 | 333.16 | −238.76 | 0.351 | 0.033 | ||
| 0.1 | 101.10 | 27.20 | 0.065 | 0.001 | 0.1 | 415.96 | −305.96 | 0.398 | 0.041 | ||
| 0.2 | 114.36 | 30.97 | 0.081 | 0.003 | 0.2 | 405.59 | −281.23 | 0.339 | 0.024 | ||
| 0.3 | 121.84 | 33.04 | 0.089 | −0.004 | 0.3 | 434.14 | −303.96 | 0.357 | 0.025 | ||
| 0.4 | 124.22 | 33.68 | 0.098 | −0.010 | 0.4 | 467.07 | −337.75 | 0.405 | 0.034 | ||
| 0.5 | 123.36 | 33.30 | 0.110 | −0.015 | 0.5 | 468.59 | −343.14 | 0.436 | 0.037 | ||
| 0.6 | 121.96 | 32.54 | 0.118 | −0.019 | 0.6 | 497.13 | −375.92 | 0.502 | 0.055 | ||
| 0.7 | 119.67 | 32.23 | 0.127 | −0.020 | 0.7 | 523.40 | −405.72 | 0.569 | 0.075 | ||
| 0.8 | 117.72 | 31.86 | 0.127 | −0.015 | 0.8 | 528.01 | −412.56 | 0.596 | 0.091 | ||
| 0.9 | 115.69 | 31.36 | 0.125 | −0.005 | 0.9 | 545.19 | −430.46 | 0.627 | 0.106 | ||
| 1150 | 0.01 | 36.24 | 9.91 | 0.102 | 0.025 | 1200 | 0.01 | 211.34 | −173.43 | 0.861 | 0.220 |
| 0.05 | 81.12 | −2.49 | 0.085 | 0.001 | 0.05 | 241.61 | −179.34 | 0.461 | 0.071 | ||
| 0.1 | 321.88 | −229.61 | 0.371 | 0.039 | 0.1 | 304.17 | −231.15 | 0.507 | 0.078 | ||
| 0.2 | 373.08 | −268.30 | 0.386 | 0.038 | 0.2 | 349.95 | −265.18 | 0.508 | 0.069 | ||
| 0.3 | 303.78 | −194.55 | 0.312 | 0.013 | 0.3 | 341.22 | −251.87 | 0.479 | 0.046 | ||
| 0.4 | 180.07 | −72.78 | 0.214 | −0.008 | 0.4 | 348.53 | −259.33 | 0.518 | 0.040 | ||
| 0.5 | 343.47 | −240.54 | 0.414 | 0.021 | 0.5 | 350.81 | −265.32 | 0.567 | 0.052 | ||
| 0.6 | 344.62 | −246.47 | 0.454 | 0.037 | 0.6 | 377.28 | −295.74 | 0.672 | 0.089 | ||
| 0.7 | 364.58 | −268.79 | 0.499 | 0.055 | 0.7 | 377.36 | −299.09 | 0.722 | 0.113 | ||
| 0.8 | 381.46 | −286.94 | 0.522 | 0.069 | 0.8 | 375.74 | −299.35 | 0.750 | 0.129 | ||
| 0.9 | 386.07 | −290.13 | 0.506 | 0.071 | 0.9 | 366.85 | −291.70 | 0.742 | 0.139 | ||
| 1250 | 0.01 | 19.69 | 5.35 | 0.132 | 0.032 | ||||||
| 0.05 | 171.08 | −120.20 | 0.385 | 0.033 | |||||||
| 0.1 | 237.16 | −176.00 | 0.443 | 0.044 | |||||||
| 0.2 | 217.50 | −148.11 | 0.355 | 0.017 | |||||||
| 0.3 | 126.02 | −53.42 | 0.219 | −0.022 | |||||||
| 0.4 | 191.28 | −119.81 | 0.352 | −0.013 | |||||||
| 0.5 | 230.09 | −161.93 | 0.464 | 0.006 | |||||||
| 0.6 | 216.07 | −151.79 | 0.482 | 0.014 | |||||||
| 0.7 | 240.58 | −179.36 | 0.575 | 0.043 | |||||||
| 0.8 | 237.18 | −177.62 | 0.586 | 0.056 | |||||||
| 0.9 | 253.02 | −193.95 | 0.627 | 0.085 |
| Constants | Optimized Value |
|---|---|
| 15,600 | |
| h | 0.0093 |
| 0.177 | |
| −0.072 | |
| Q (kJ/mol) | 69.466 |
| T (°C) | Constants | Initial Guess | Constrain | Optimized | |
|---|---|---|---|---|---|
| 1050 | 0.1 | a | 15,000 | 5000 < a < 25,000 | 11,533 |
| h | 0.0001 | −0.1 < h < 0.1 | 0.00001 | ||
| n | 0.177 | 0 < n < 1.0 | 0.216 | ||
| m | −0.072 | −0.5 < m < −0.001 | −0.086 | ||
| Q | 69.466 | 10.0 < Q < 100.0 | 62.262 | ||
| 1.0 | a | 15,200 | 5000 < a < 25,000 | 18,578 | |
| h | 0.0001 | −0.1 < h < 0.1 | 0.00001 | ||
| n | 0.177 | 0 < n < 1.0 | 0.215 | ||
| m | −0.072 | −0.5 < m < −0.001 | −0.058 | ||
| Q | 69.466 | 10.0 < Q < 100.0 | 87.082 | ||
| 5.0 | a | 15,400 | 5000 < a < 25,000 | 11,496 | |
| h | 0.0001 | −0.1 < h < 0.1 | 0.00001 | ||
| n | 0.177 | 0 < n < 1.0 | 0.217 | ||
| m | −0.072 | −0.5 < m < −0.001 | −0.08 | ||
| Q | 69.466 | 10.0 < Q < 100.0 | 88.577 | ||
| 1150 | 0.1 | a | 15,600 | 5000 < a < 25,000 | 16,699 |
| h | 0.0001 | −0.1 < h < 0.1 | 0.00001 | ||
| n | 0.177 | 0 < n < 1.0 | 0.222 | ||
| m | −0.072 | −0.5 < m < −0.001 | −0.081 | ||
| Q | 69.466 | 10.0 < Q < 100.0 | 48.689 | ||
| 1.0 | a | 15,800 | 5000 < a < 25,000 | 15,440 | |
| h | 0.0001 | −0.1 < h < 0.1 | 0.00001 | ||
| n | 0.177 | 0 < n < 1.0 | 0.159 | ||
| m | −0.072 | −0.5 < m < −0.001 | −0.083 | ||
| Q | 69.466 | 10.0 < Q < 100.0 | 69.426 | ||
| 5.0 | a | 16,000 | 5000 < a < 25,000 | 11,164 | |
| h | 0.0001 | −0.1 < h < 0.1 | 0.00001 | ||
| n | 0.177 | 0 < n < 1.0 | 0.156 | ||
| m | −0.072 | −0.5 < m < −0.001 | −0.06 | ||
| Q | 69.466 | 10.0 < Q < 100.0 | 49.217 | ||
| 1250 | 0.1 | a | 16,200 | 5000 < a < 25,000 | 13,322 |
| h | 0.0001 | −0.1 < h < 0.1 | 0.00001 | ||
| n | 0.177 | 0 < n < 1.0 | 0.214 | ||
| m | −0.072 | −0.5 < m < −0.001 | −0.078 | ||
| Q | 69.466 | 10.0 < Q < 100.0 | 51.575 | ||
| 1.0 | a | 16,600 | 5000 < a < 25,000 | 11,503 | |
| h | 0.0001 | −0.1 < h < 0.1 | 0.00001 | ||
| n | 0.177 | 0 < n < 1.0 | 0.199 | ||
| m | −0.072 | −0.5 < m < −0.001 | −0.083 | ||
| Q | 69.466 | 10.0 < Q < 100.0 | 49.784 | ||
| 5.0 | a | 16,930 | 5000 < a < 25,000 | 21,721 | |
| h | 0.0001 | −0.1 < h < 0.1 | 0.00001 | ||
| n | 0.177 | 0 < n < 1.0 | 0.209 | ||
| m | −0.072 | −0.5 < m < −0.001 | −0.086 | ||
| Q | 69.466 | 10.0 < Q < 100.0 | 69.411 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Razali, M.K.; Heo, Y.; Joun, M.S. Hot Extrusion Process Grain Size Prediction and Effects of Friction Models and Hydraulic Press Applications. Metals 2025, 15, 887. https://doi.org/10.3390/met15080887
Razali MK, Heo Y, Joun MS. Hot Extrusion Process Grain Size Prediction and Effects of Friction Models and Hydraulic Press Applications. Metals. 2025; 15(8):887. https://doi.org/10.3390/met15080887
Chicago/Turabian StyleRazali, Mohd Kaswandee, Yun Heo, and Man Soo Joun. 2025. "Hot Extrusion Process Grain Size Prediction and Effects of Friction Models and Hydraulic Press Applications" Metals 15, no. 8: 887. https://doi.org/10.3390/met15080887
APA StyleRazali, M. K., Heo, Y., & Joun, M. S. (2025). Hot Extrusion Process Grain Size Prediction and Effects of Friction Models and Hydraulic Press Applications. Metals, 15(8), 887. https://doi.org/10.3390/met15080887







