Effect of Pre-Hoop Expansion Deformation on High-Temperature Mechanical Properties of Zirconium Plate at 400 °C
Abstract
1. Introduction
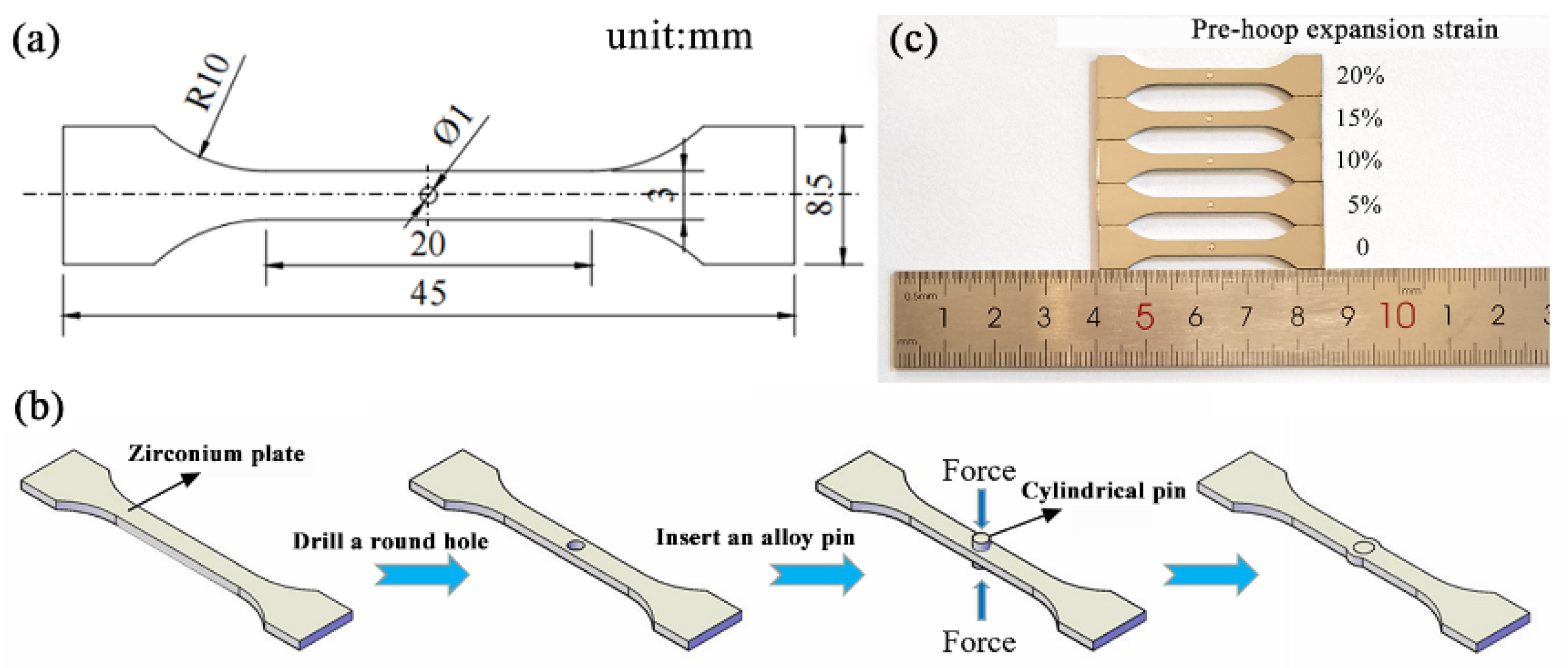
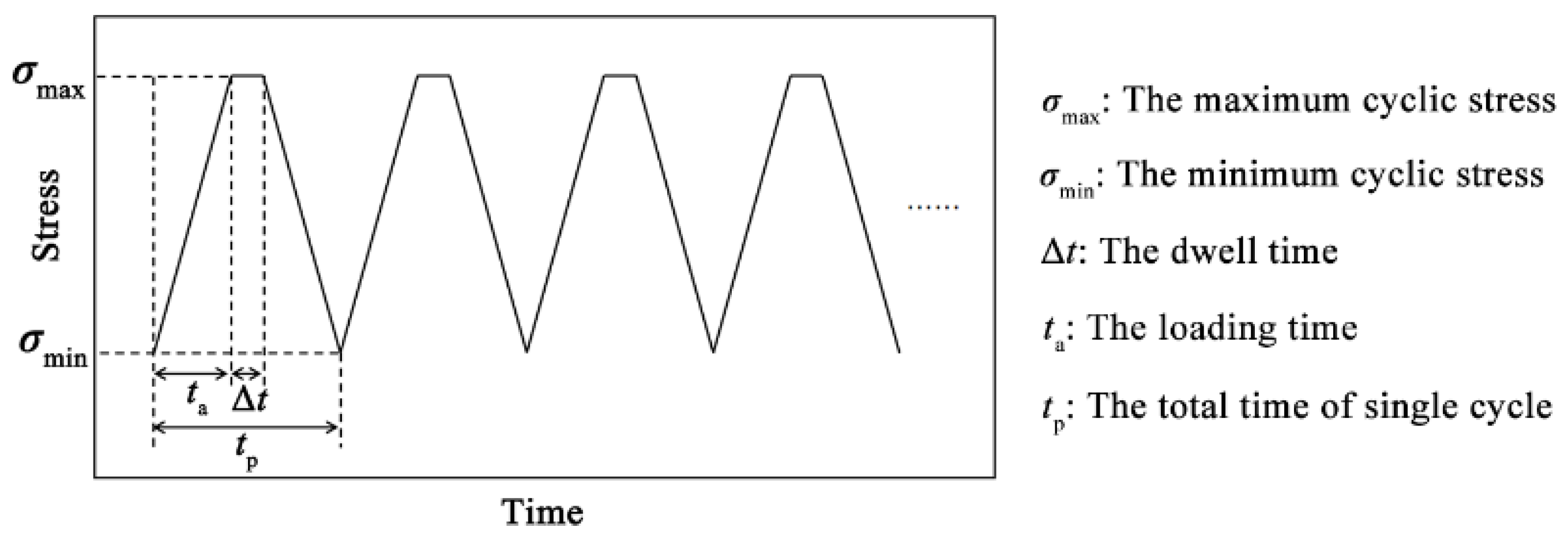
2. Materials and Methods
3. Results
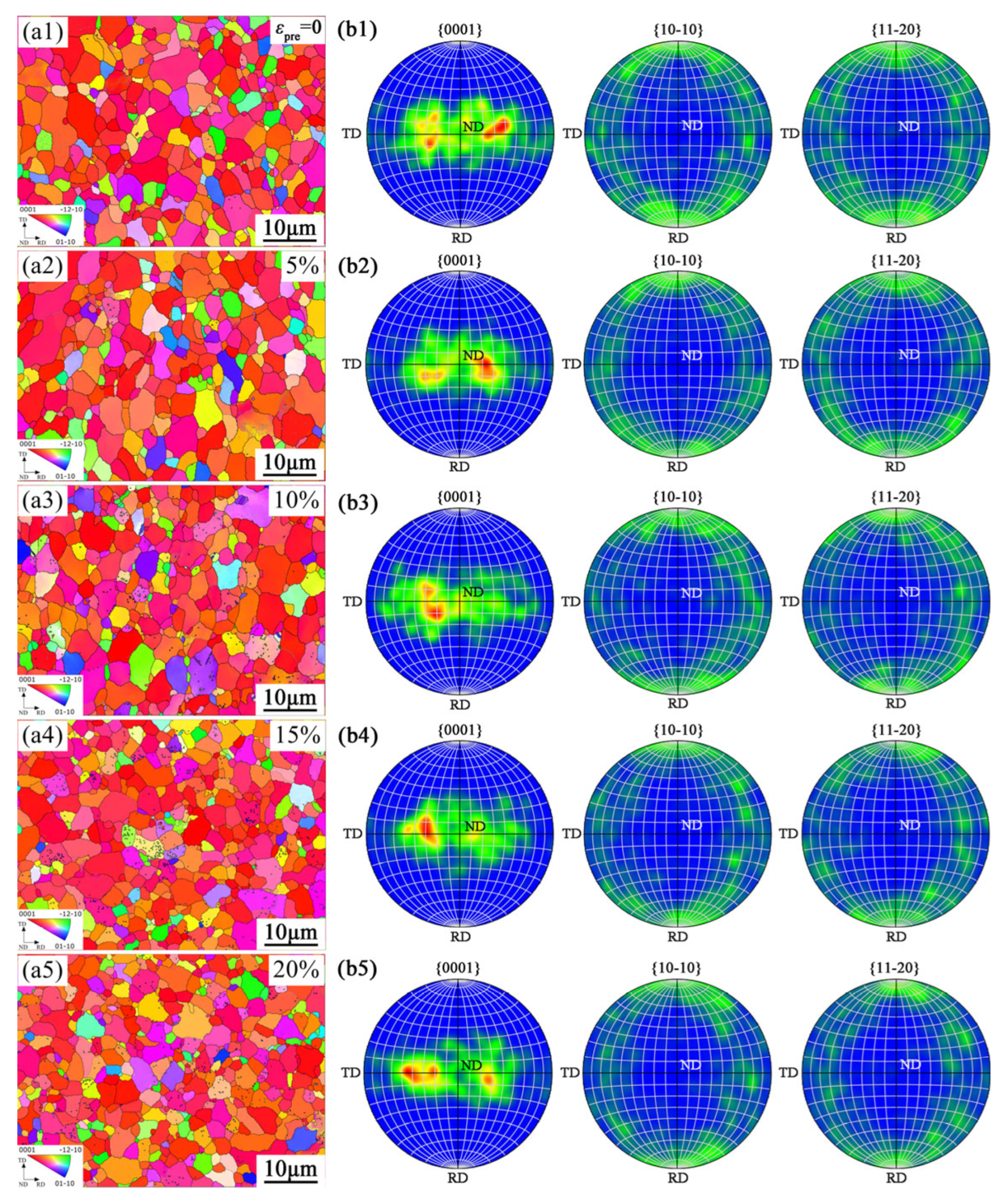
3.1. Microstructure After Different Pre-Hoop Expansion Deformations
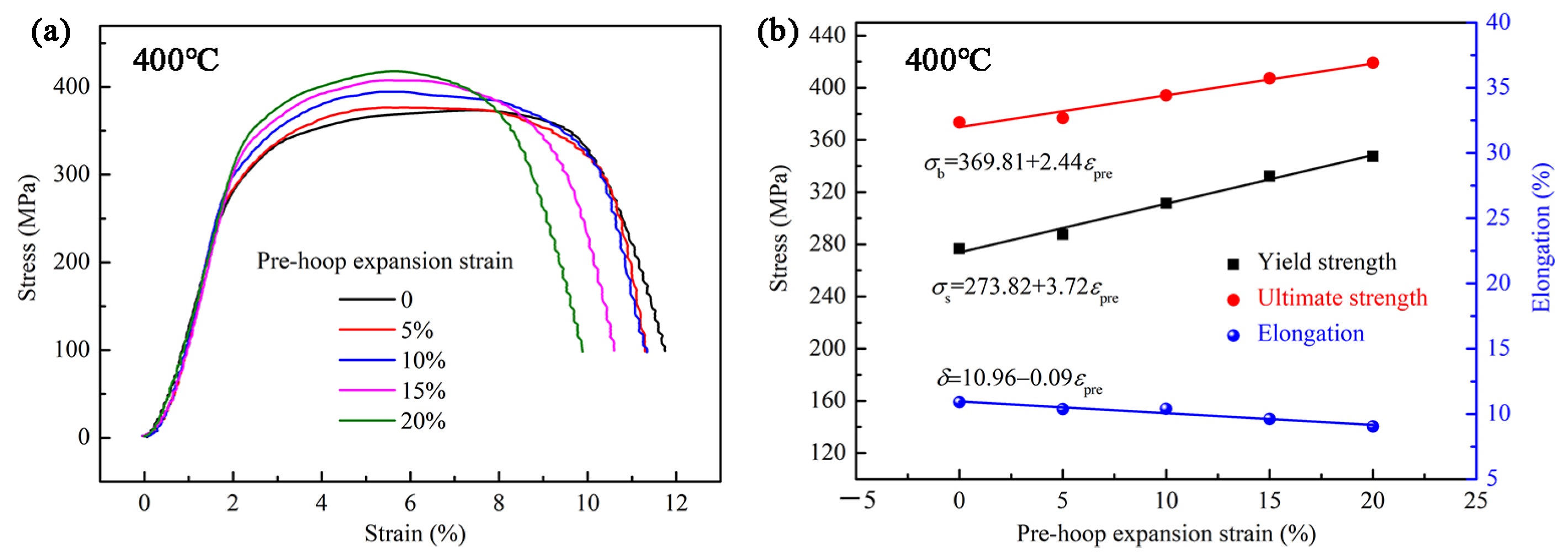
3.2. Tensile Properties Underwent Different Pre-Hoop Expansion Deformations
3.3. Creep Properties After Pre-Hoop Expansion Deformations
3.4. Fatigue–Creep Properties After Different Pre-Hoop Expansion Deformations
3.5. Fracture Surfaces Observation
3.6. The Stress Field Distributions Around the Center-Hole of Samples with Different Pre-Hoop Expansion Strains and Axial Stresses
4. Discussion
4.1. The Role of the Pre-Hoop Expansion Deformation on the Tensile Properties at 400 °C
4.2. The Role of the Pre-Hoop Expansion Deformation on the Creep Properties of Zirconium Plates at 400 °C
4.3. The Role of the Pre-Hoop Expansion Deformation on the Fatigue–Creep Properties at 400 °C
5. Conclusions
- The high-temperature tensile results indicated that with the hoop expansion strain increase, the yield strength and ultimate strength increased linearly, while the elongation decreased linearly.
- The creep results indicated that with the pre-hoop expansion strain increase, the creep life decreased, especially as the creep stress exceeded 276 MPa.
- The fatigue–creep results implied that as the stress ratio was less than 0.7, the fatigue–creep deformation process was dominated by fatigue, and with the pre-hoop expansion strain increase, the fatigue–creep life first increased, and then decreased as the pre-hoop expansion strain exceeded 10%. Meanwhile, as the stress ratio was higher than 0.7, the fatigue–creep deformation process was dominated by creep, and with the pre-hoop expansion strain increase, the fatigue–creep life decreased monotonically.
- The stress field simulation indicated that after the pre-hoop expansion deformation, there appeared a compressive stress zone at the root of the central hole, a tensile stress zone at the edges, and a stress transition zone in the middle. The compressive stress was beneficial for high-temperature mechanical properties, while the tensile stress was harmful for the high-temperature mechanical properties of zirconium plates.
- The fracture surface results showed that with the pre-hoop expansion deformation increase, the necking degree on the fracture surface gradually decreased. When the stress ratio was 0.1, the fatigue–creep fractures were similar to the tensile fractures, while when the stress ratio was 0.7, the fatigue–creep fractures were similar to the creep fractures.
- The variation equations of high-temperature tensile properties with the pre-hoop expansion strain were obtained. Some life prediction equations for creep deformation and fatigue–creep deformation were also obtained.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kozlovskiy, A.L.; Borgekov, D.B.; Zdorovets, M.V.; Kenzhina, I.E.; Shlimas, D.I. Study of radiation damage kinetics in dispersed nuclear fuel on zirconium dioxide doped with cerium dioxide. J. Compos. Sci. 2023, 7, 277. [Google Scholar] [CrossRef]
- Suman, S.; Khan, M.K.; Pathak, M.; Singh, R.N. Effects of hydrogen on thermal creep behaviour of Zircaloy fuel cladding. J. Nucl. Mater. 2018, 498, 20–32. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Li, J.; Liu, K.; Wang, J.; Jian, S.J.; Xu, C.; Wang, H.; Wang, L.X.; Zhu, X.L.; Okulov, A.; et al. Diffusion bonding, brazing and resistance welding of zirconium alloys: A review. J. Mater. Res. Technol. 2003, 26, 395–416. [Google Scholar] [CrossRef]
- Durdovic, M.; Turcanu, C.; Sala, R.; Geysmans, R.; López-Asensio, S.; Gonçalves, L. The outlooks of nuclear energy in society: Unraveling public attitudes in the context of climate and energy security challenges. Prog. Nucl. Energy 2024, 174, 105286. [Google Scholar] [CrossRef]
- Zhang, T.F.; Sun, Q.Z.; Xiao, W.; Luo, C.X.; Liu, X.J. A review on emerging mixed-spectrum nuclear reactors for safety and sustainability of nuclear energy systems. Renew. Sustain. Energy Rev. 2024, 202, 114666. [Google Scholar] [CrossRef]
- Rehm, T.E. Advanced nuclear energy: The safest and most renewable clean energy. Curr. Opin. Chen. Eng. 2023, 39, 100878. [Google Scholar] [CrossRef]
- Kurata, M.; Barrachin, M.; Haste, T.; Steinbrueck, M. Phenomenology of BWR fuel assembly degradation. J. Nucl. Mater. 2018, 500, 119–140. [Google Scholar] [CrossRef]
- Adamson, R.B.; Coleman, C.E.; Griffiths, M. Irradiation creep and growth of zirconium alloys: A critical review. J. Nucl. Mater. 2019, 521, 167–244. [Google Scholar] [CrossRef]
- Yoo, Y.; Kim, J.; Park, J.; Kim, H. Development of nuclear fuel assembly finite element model for mechanical integrity evaluation. Nucl. Eng. Des. 2023, 413, 112523. [Google Scholar] [CrossRef]
- Zeng, X.K.; Zhang, C.H.; Zhu, W.G.; Zhu, M.L.; Wang, Y.M.; Zhang, X. Quantitative characterization of short fatigue crack and grain boundary interaction behavior in zirconium. Int. J. Fatigue 2022, 161, 106894. [Google Scholar] [CrossRef]
- Jeong, D.H.; Kim, J.H. Fatigue characteristics of laser welded Zircaloy thin sheet. Int. J. Mod. Phys. Conf. Ser. 2012, 6, 367–372. [Google Scholar] [CrossRef]
- Gusev, M.; Danilov, V. Creep inverse problem of the power reactor fuel assembly elements contact interaction. Appl. Mech. Mater. 2015, 698, 643–648. [Google Scholar] [CrossRef]
- Patra, A.; Tomé, C.N. Finite element simulation of gap opening between cladding tube and spacer grid in a fuel rod assembly using crystallographic models of irradiation growth and creep. Nucl. Eng. Des. 2017, 315, 155–169. [Google Scholar] [CrossRef]
- Liu, H.D.; Chen, D.Q.; Hu, L.; Yuan, D.W.; Gao, H. Numerical investigations on flow-indeced vibration of fuel rods with spacer grids subjected to turbulent flow. Nucl. Eng. Des. 2017, 325, 68–77. [Google Scholar] [CrossRef]
- Liu, P.L.; Li, F.; Chen, B.S.; Zhang, S. Theoretical investigations on flow-induced vibration of fuel rods with spacer grids in axial flow. Ann. Nucl. Energy 2019, 133, 916–923. [Google Scholar] [CrossRef]
- Ihn, N. An investigation of structural strength of PWR fuel assembly spacer grid with fuel rod clad. Ann. Nucl. Energy 2024, 195, 110124. [Google Scholar] [CrossRef]
- Nagase, F. An experimental study related to axial constraint of fuel rod under LOCA conditions. Ann. Nucl. Energy 2022, 171, 109052. [Google Scholar] [CrossRef]
- Snowden, K.U.; Stathers, P.A. The fatigue behavior of α-zirconium and Zircaloy-2 in the temperature range 20 to 700 °C. J. Nucl. Mater. 1977, 67, 215–228. [Google Scholar] [CrossRef]
- Wang, X.; Cao, J.X.; Huang, X.; Wang, M.J.; Li, J. Effect of pre-deformation tensile property of zirconium alloy. Chin. J. Rare Met. 2013, 37, 857–862. Available online: https://kns.cnki.net/kcms2/article/abstract?v=5ykJdPmCibKlx7kyGvXLYVJlk1oivCK00vCUEW-OS4mEEYsDytUc-Gn3qZllsv3GAelQwhSKixBYfInWaQmeHAsjSb9LGXEnIsTGKT0F4Nw3Zo4qM2rbcuT0AfQ7QQzjUu_LC2l_RMvCmDme8aaoFoFOEbfI6DgJmrLjWgrd3QM1MHrkHjv5xQ==&uniplatform=NZKPT&language=CHS (accessed on 17 July 2025).
- Sklenicka, V.; Dvorak, J.; Kral, P.; Betekhtin, V.I.; Kadomtsev, A.G.; Narykova, M.V.; Dobatkin, S.V.; Kucharova, K.; Kvapilova, M. Influence of prior pressurization treatment on creep behaviour of an ultrafine-grained Zr-2.5% Nb alloy. Mater. Sci. Eng. A 2021, 820, 141570. [Google Scholar] [CrossRef]
- Zhao, Z.; Kunii, D.; Abe, T.; Yang, H.L.; Kano, S.; Matsukawa, Y.; Abe, H. Mechanical properties of Zircaloy-4 cladding tube by advanced expansion due to compression (A-EDC) test. Mater. Trans. 2017, 58, 46–51. [Google Scholar] [CrossRef]
- Zhao, Z.S.; Kunii, D.; Abe, T.; Yang, H.L.; Shen, J.J.; Shinohara, Y.; Kano, S.; Matsukawa, Y.; Satoh, Y.; Abe, H. A comparative study of hydride-induced embrittlement of Zircaloy-4 fuel cladding tubes in the longitudinal and hoop directions. J. Nucl. Sci. Technol. 2017, 54, 490–499. [Google Scholar] [CrossRef]
- Abe, H.; Abe, T.; Kishita, S.; Kano, S.; Li, Y.F.; Yang, H.L.; Tawara, K.; Matsukawa, Y.; Satoh, Y. Development of advanced expansion due to compression (A-EDC) test method for safety evaluation of degraded nuclear fuel cladding materials. J. Nucl. Sci. Technol. 2015, 52, 1232–1239. [Google Scholar] [CrossRef]
- Zhang, Y.; Qi, H.D.; Song, X.P. Expansion deformation behavior of zirconium alloy cladding with different hydrogen concentrations. J. Nucl. Mater. 2021, 554, 153082. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, D.W.; Yan, Y.R.L.; Liu, J.S.; Gao, B. Effect of pre-straining and subsequent annealing on microstructure and mechanical property of Zr-Sn-Nb-Fe zirconium alloy. Met. Mater. Int. 2022, 28, 603–617. [Google Scholar] [CrossRef]
- Yang, Z.N.; Xiao, Y.Y.; Zhang, F.C.; Yan, Z.G. Effect of cold rolling on microstructure and mechanical properties of pure Zr. Mater. Sci. Eng. A 2012, 556, 728–733. [Google Scholar] [CrossRef]
- Yu, L.; Song, X.P.; You, L.; Jiao, Z.H.; Yu, H.C. Effect of dwell time on creep-fatigue life of a high-Nb TiAl alloy at 750 °C. Scripta Mater. 2015, 109, 61–63. [Google Scholar] [CrossRef]
- Pilkey, W.D.; Pilkey, D.F. Peterson’s Stress Concentration Factors, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008; pp. 270–272. [Google Scholar] [CrossRef]
- Guo, J.; Fu, H.Y.; Pan, B.; Kang, R.K. Recent process of residual stress measurement methods: A review. Chin. J. Aeronaut. 2021, 34, 54–78. [Google Scholar] [CrossRef]
- Liu, M.; Zheng, Q.; Wang, X.; Xu, C.L. Characterization of distribution of residual stress in shot-peened layer of nickel-based single crystal superalloy DD6 by nanoindentation technique. Mech. Mater. 2022, 164, 104143. [Google Scholar] [CrossRef]
- Qi, H.D.; Song, X.P. Effect of pre-hoop expansion deformation on the tensile and fatigue properties of zirconium plate. J. Mater. Res. Technol. 2015, 35, 3073–3086. [Google Scholar] [CrossRef]
- Zhu, J.C.; Xie, J.J.; Wang, J.; Xia, X.L.; Lin, Z.D.; Qian, G.A.; Zhao, A.G. Low-cycle and dwell fatigue properties for a near alpha titanium alloy Ti-6Al-3Nb-2Zr-1Mo. J. Mater. Res. Technol. 2024, 29, 2204–2215. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Fan, J.K.; Fan, P.P.; Zhao, R.Z.; Li, B.B.; Jiang, P.; Xue, X.Y.; Liao, Z.Q.; Kou, H.C.; Li, J.S. Investigation of micro-mechanisms for facet formation during dwell fatigue in Ti6321 alloy with equiaxed microstructure. Int.J. Fatigue 2025, 190, 108587. [Google Scholar] [CrossRef]

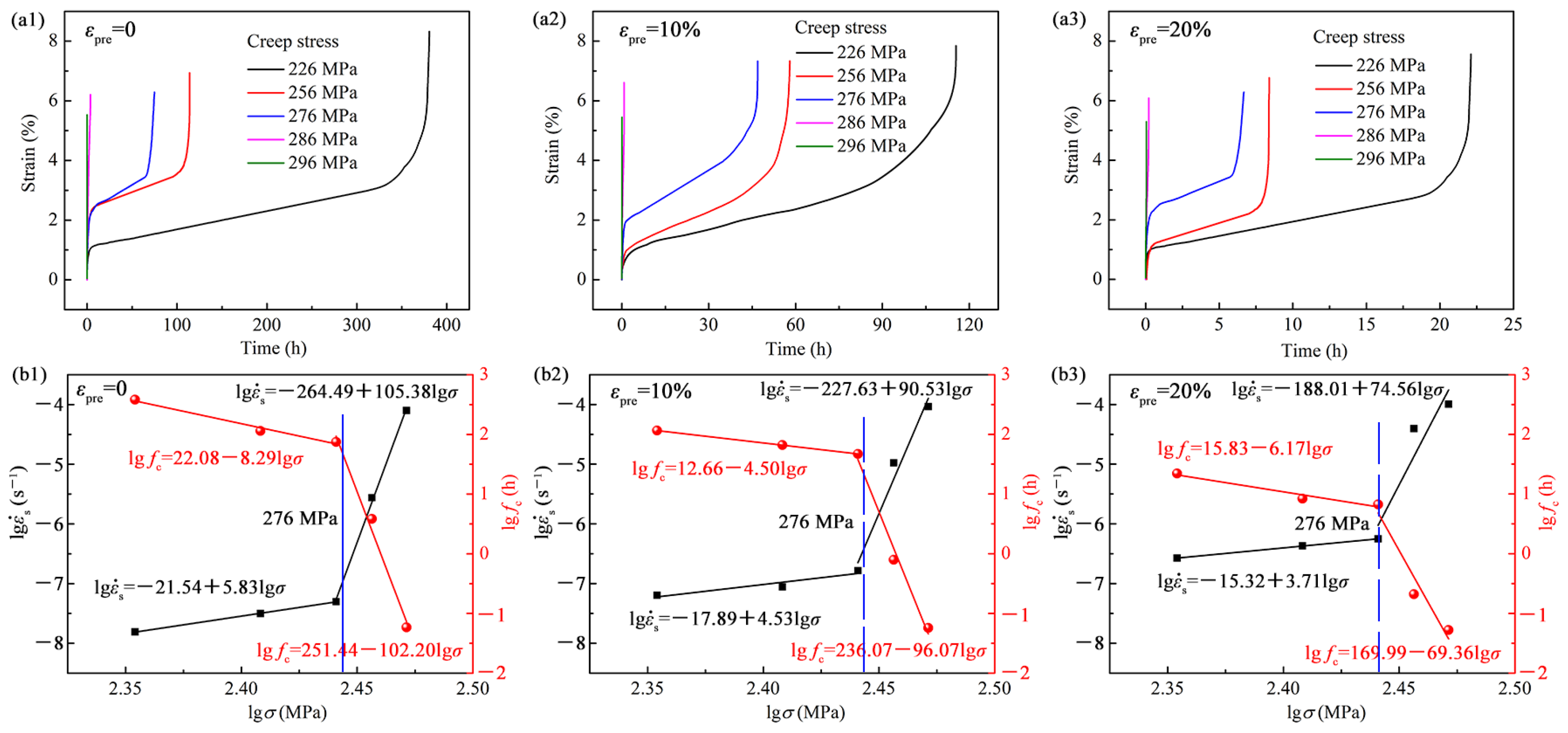
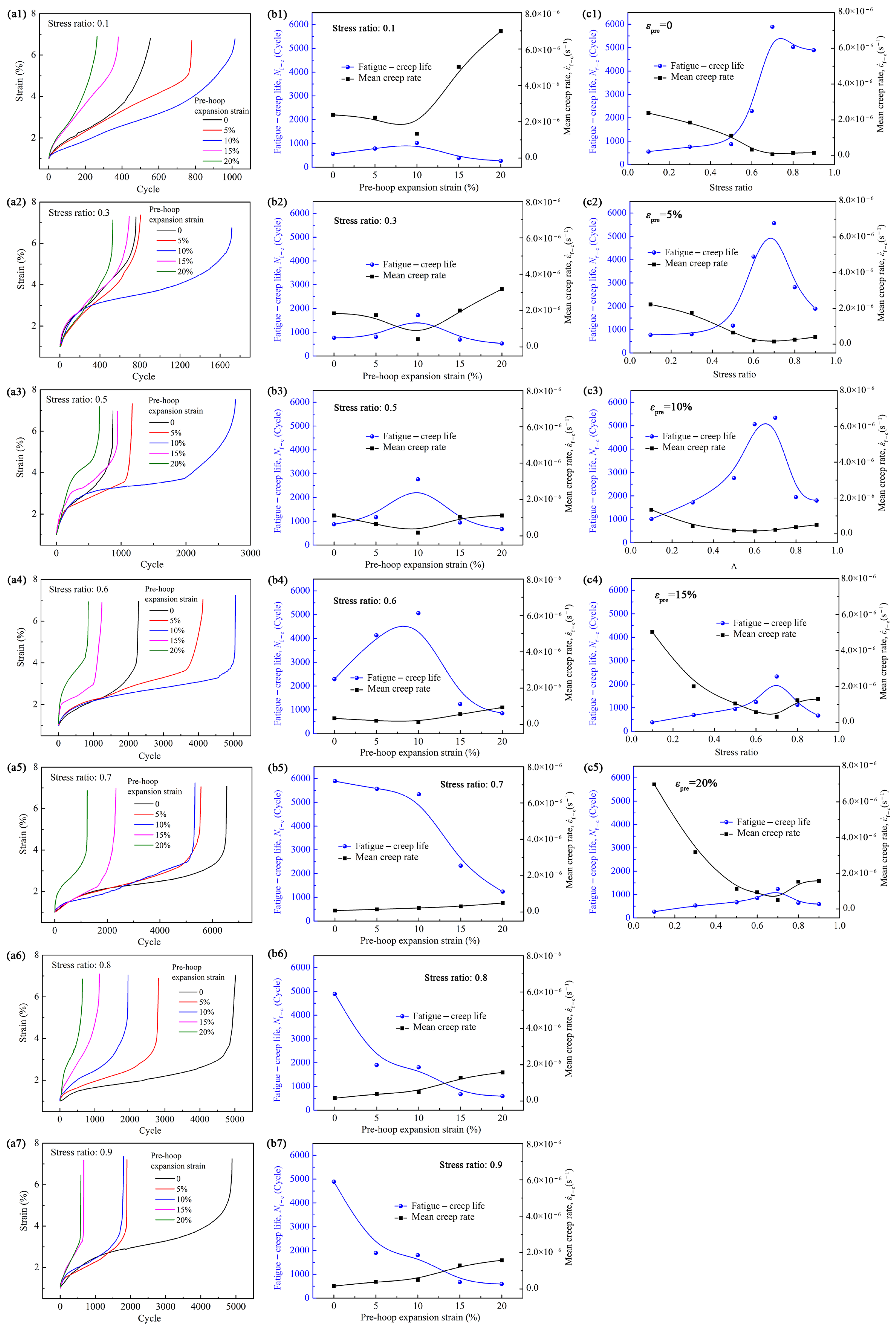
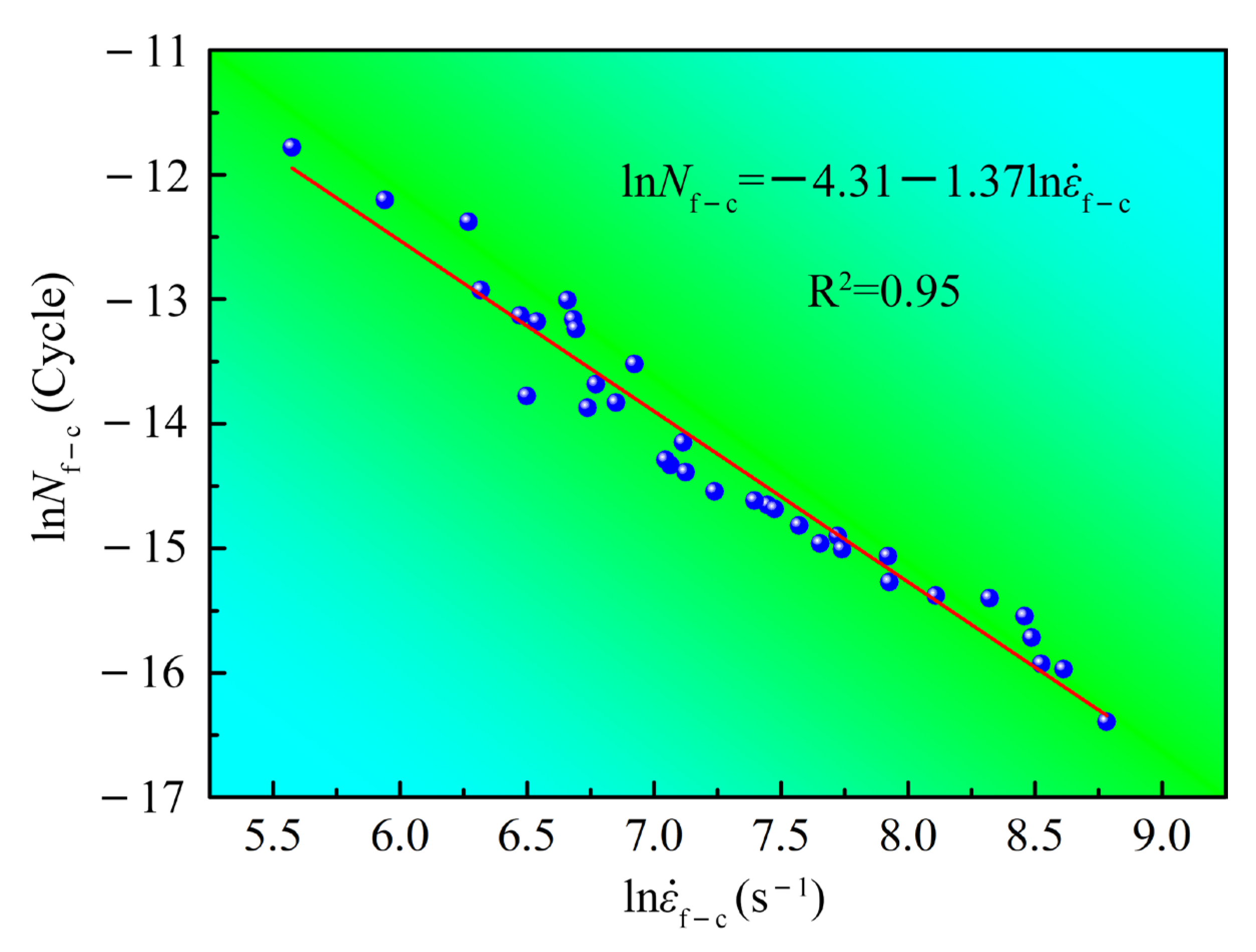
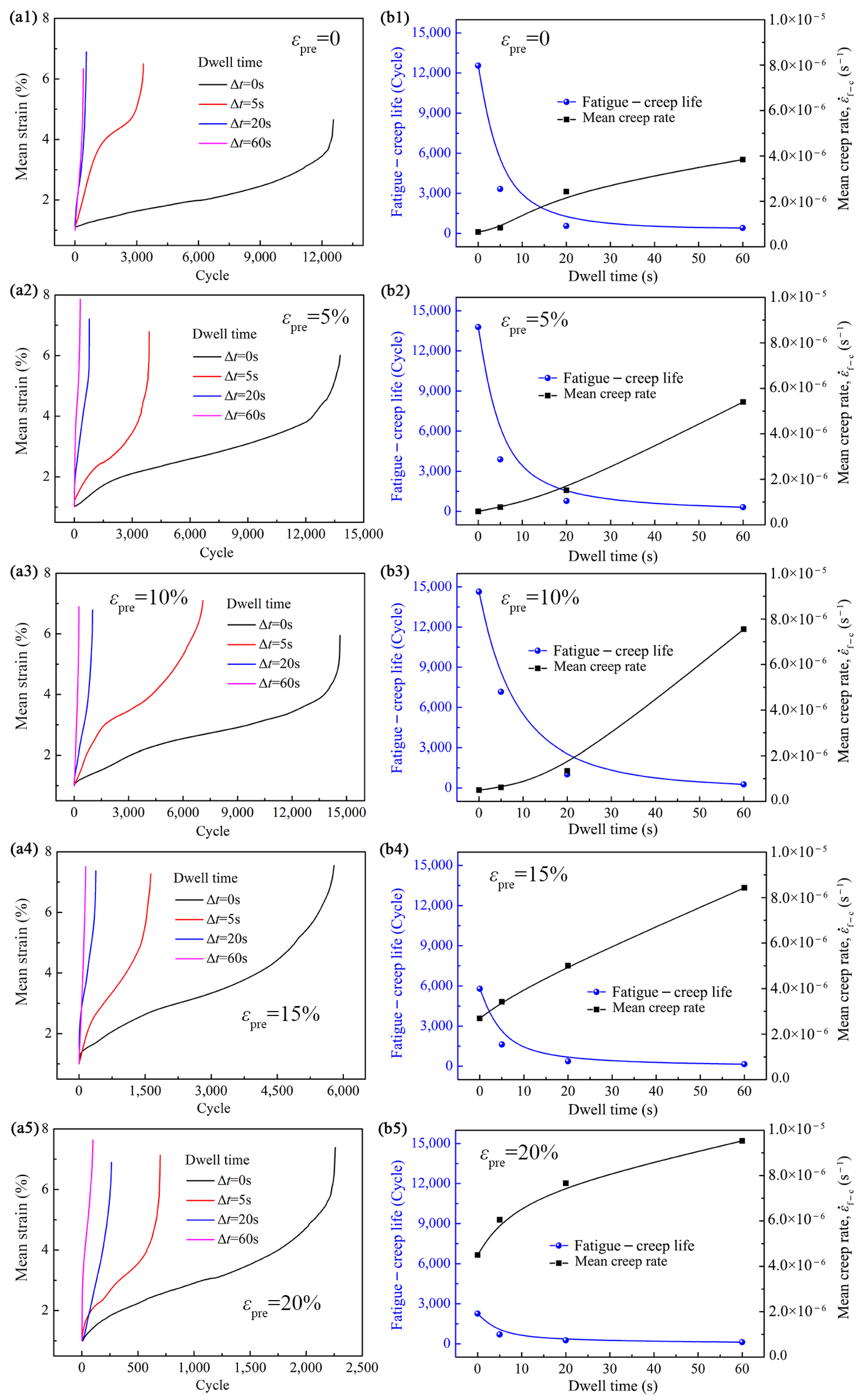




| Creep Stress (MPa) | Creep Properties | Pre-Hoop Expansion Strain | ||||
|---|---|---|---|---|---|---|
| 0 | 5% | 10% | 15% | 20% | ||
| 226 | Steady creep rate (s−1) | 1.55 × 10−8 | 3.15 × 10−8 | 7.76 × 10−8 | 1.33 × 10−7 | 2.66 × 10−7 |
| Creep life (h) | 380.69 | 186.61 | 115.42 | 56.06 | 22.09 | |
| 256 | Steady creep rate (s−1) | 3.14 × 10−8 | 8.83 × 10−8 | 8.82 × 10−8 | 2.23 × 10−7 | 4.28 × 10−7 |
| Creep life (h) | 113.96 | 66.04 | 66.06 | 30.73 | 8.38 | |
| 276 | Steady creep rate (s−1) | 4.97 × 10−8 | 1.40 × 10−7 | 1.65 × 10−7 | 3.00 × 10−7 | 5.56 × 10−7 |
| Creep life (h) | 74.86 | 55.42 | 46.89 | 25.71 | 6.68 | |
| 286 | Steady creep rate (s−1) | 2.75 × 10−6 | 5.37 × 10−6 | 1.05 × 10−5 | 2.01 × 10−5 | 3.95 × 10−5 |
| Creep life (h) | 3.84 | 1.93 | 0.792 | 0.51 | 0.21 | |
| 296 | Steady creep rate (s−1) | 7.77 × 10−5 | 8.78 × 10−5 | 9.09 × 10−5 | 9.35 × 10−5 | 1.04 × 10−4 |
| Creep life (h) | 0.06 | 0.06 | 0.06 | 0.06 | 0.05 | |
| Stress Ratio | Fatigue–Creep Properties | Pre-Hoop Expansion Strain | ||||
|---|---|---|---|---|---|---|
| 0 | 5% | 10% | 15% | 20% | ||
| 0.1 | Mean Creep rate (s−1) | 2.38 × 10−6 | 2.22 × 10−6 | 1.34 × 10−6 | 5.02 × 10−6 | 6.98 × 10−6 |
| Cycle life (Cycle) | 555 | 780 | 1016 | 380 | 264 | |
| 0.3 | Mean creep rate (s−1) | 1.85 × 10−6 | 1.75 × 10−6 | 4.25 × 10−7 | 2.00 × 10−6 | 3.18 × 10−6 |
| Cycle life (Cycle) | 760 | 806 | 1717 | 692 | 529 | |
| 0.5 | Mean creep rate (s−1) | 1.12 × 10−6 | 6.46 × 10−7 | 1.79 × 10−7 | 1.05 × 10−6 | 1.12 × 10−6 |
| Cycle life (Cycle) | 873 | 1170 | 2766 | 945 | 665 | |
| 0.6 | Mean creep rate (s−1) | 3.39 × 10−7 | 2.05 × 10−7 | 1.39 × 10−7 | 5.65 × 10−7 | 9.37 × 10−7 |
| Cycle life (Cycle) | 2290 | 4130 | 5062 | 1241 | 853 | |
| 0.7 | Mean creep rate (s−1) | 7.64 × 10−8 | 1.44 × 10−7 | 2.22 × 10−7 | 3.09 × 10−7 | 4.97 × 10−7 |
| Cycle life (Cycle) | 5890 | 5562 | 5334 | 2329 | 1238 | |
| 0.8 | Mean creep rate (s−1) | 1.53 × 10−7 | 2.46 × 10−7 | 3.74 × 10−7 | 1.23 × 10−6 | 1.53 × 10−6 |
| Cycle life (Cycle) | 5022 | 2818 | 1946 | 1130 | 642 | |
| 0.9 | Mean creep rate (s−1) | 1.60 × 10−7 | 3.95 × 10−7 | 5.02 × 10−7 | 1.29 × 10−6 | 1.58 × 10−6 |
| Cycle life (Cycle) | 4890 | 1898 | 1803 | 670 | 589 | |
| Dwell Time | Fatigue–Creep Properties | Pre-Hoop Expansion Strain | ||||
|---|---|---|---|---|---|---|
| 0 | 5% | 10% | 15% | 20% | ||
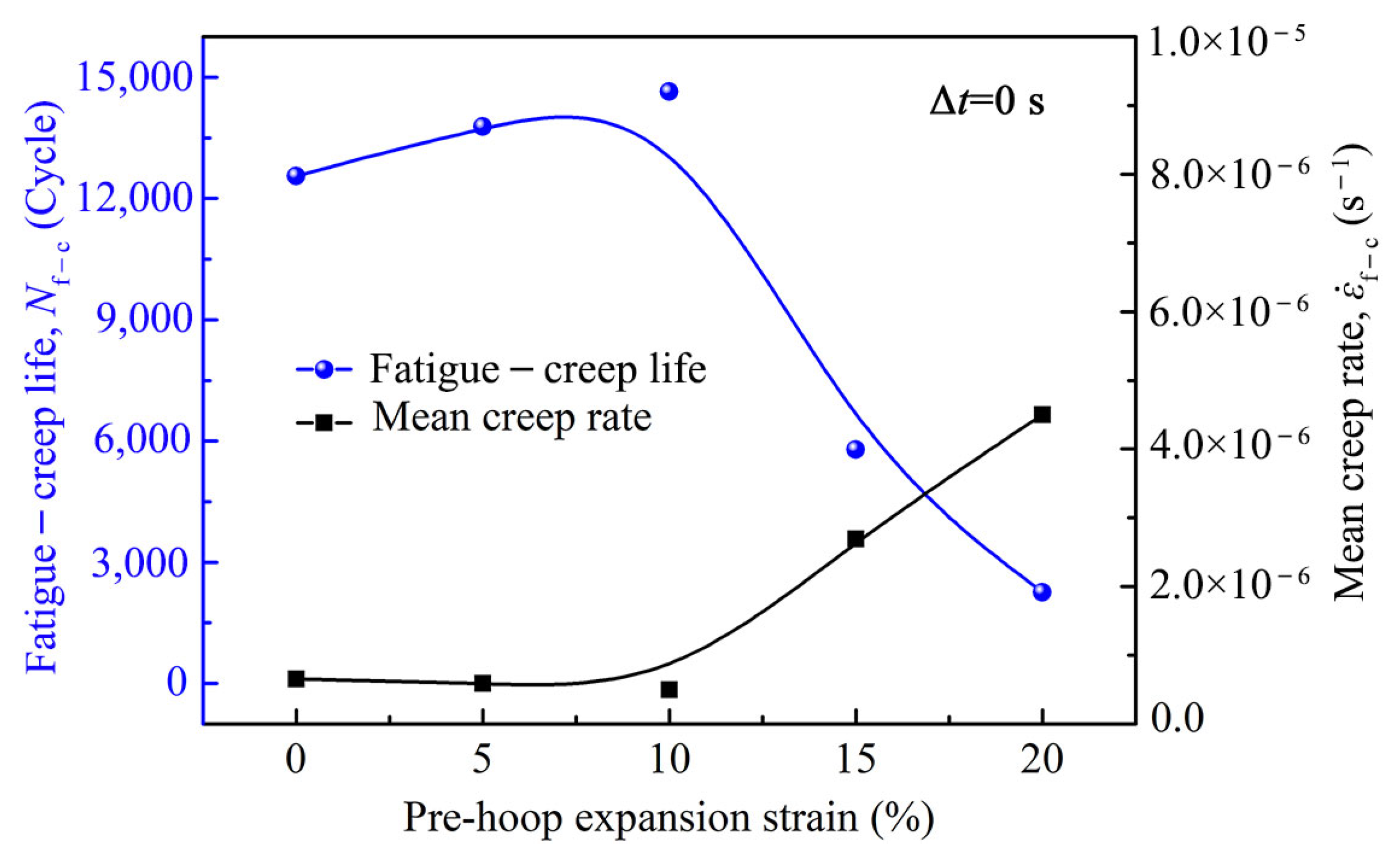
| 0 | Mean Creep rate (s−1) | 6.52 × 10−7 | 5.91 × 10−7 | 4.98 × 10−7 | 2.69 × 10−6 | 4.50 × 10−6 |
| Cycle life (Cycle) | 12560 | 13780 | 14640 | 5790 | 2260 | |
| 5 s | Mean creep rate (s−1) | 8.37 × 10−7 | 7.77 × 10−7 | 6.11 × 10−7 | 3.42 × 10−6 | 6.05 × 10−6 |
| Cycle life (Cycle) | 3325 | 3884 | 7158 | 1627 | 698 | |
| 20 s | Mean creep rate (s−1) | 2.43 × 10−6 | 1.52 × 10−6 | 1.34 × 10−6 | 5.01 × 10−6 | 7.66 × 10−6 |
| Cycle life (Cycle) | 555 | 780 | 1016 | 380 | 264 | |
| 60 s | Mean creep rate (s−1) | 3.84 × 10−6 | 5.40 × 10−6 | 7.55 × 10−6 | 8.43 × 10−6 | 9.53 × 10−6 |
| Cycle life (Cycle) | 406 | 312 | 264 | 156 | 117 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, H.; You, L.; Song, X. Effect of Pre-Hoop Expansion Deformation on High-Temperature Mechanical Properties of Zirconium Plate at 400 °C. Metals 2025, 15, 827. https://doi.org/10.3390/met15080827
Qi H, You L, Song X. Effect of Pre-Hoop Expansion Deformation on High-Temperature Mechanical Properties of Zirconium Plate at 400 °C. Metals. 2025; 15(8):827. https://doi.org/10.3390/met15080827
Chicago/Turabian StyleQi, Haidong, Li You, and Xiping Song. 2025. "Effect of Pre-Hoop Expansion Deformation on High-Temperature Mechanical Properties of Zirconium Plate at 400 °C" Metals 15, no. 8: 827. https://doi.org/10.3390/met15080827
APA StyleQi, H., You, L., & Song, X. (2025). Effect of Pre-Hoop Expansion Deformation on High-Temperature Mechanical Properties of Zirconium Plate at 400 °C. Metals, 15(8), 827. https://doi.org/10.3390/met15080827






