Modeling Mechanical Properties of Industrial C-Mn Cast Steels Using Artificial Neural Networks
Abstract
1. Introduction
2. Materials and Methods
2.1. The Material Data Preprocessing
Data Preprocessing
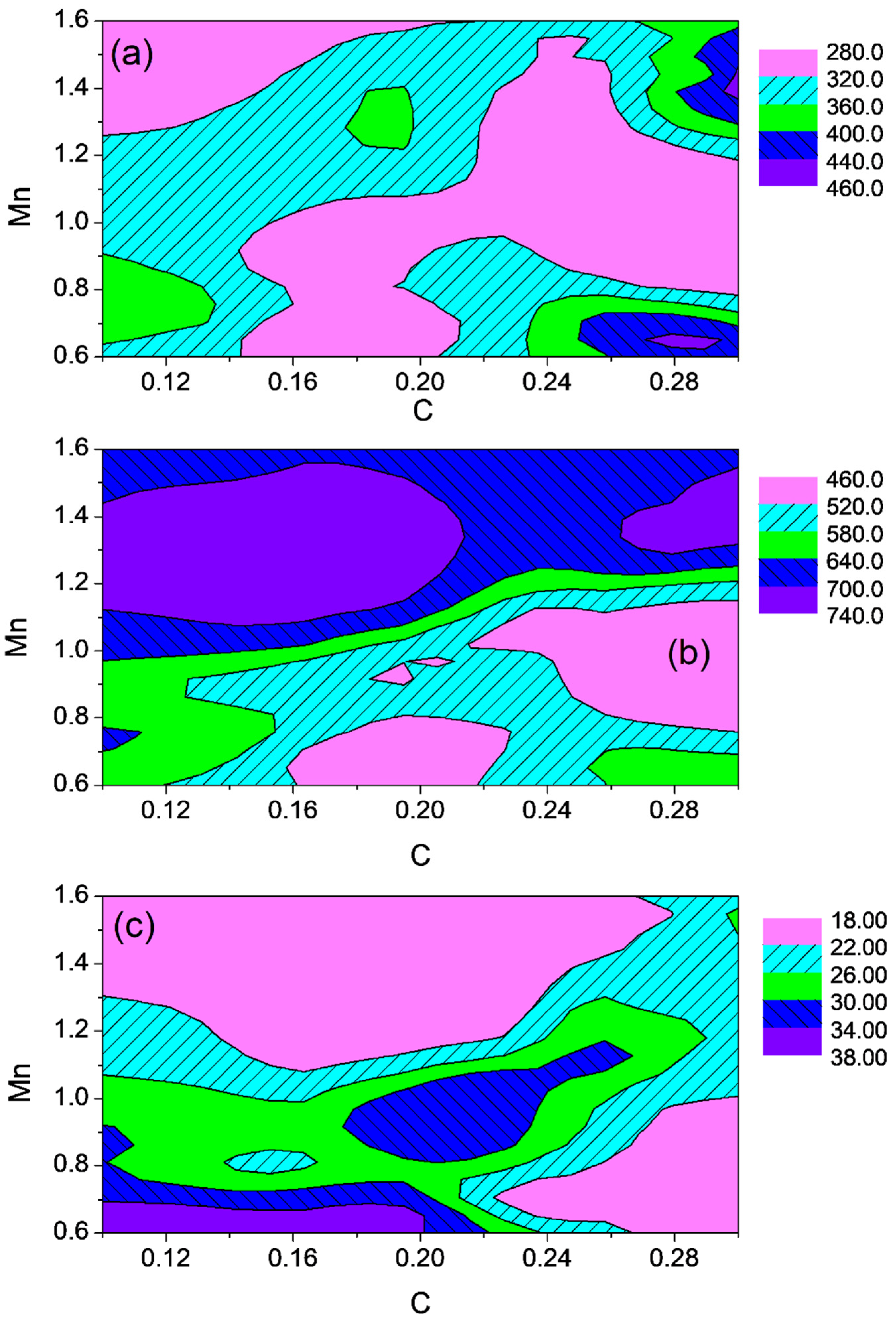
2.2. Visualizing the Relationship Between Composition, Heat Treatment, and Mechanical Properties
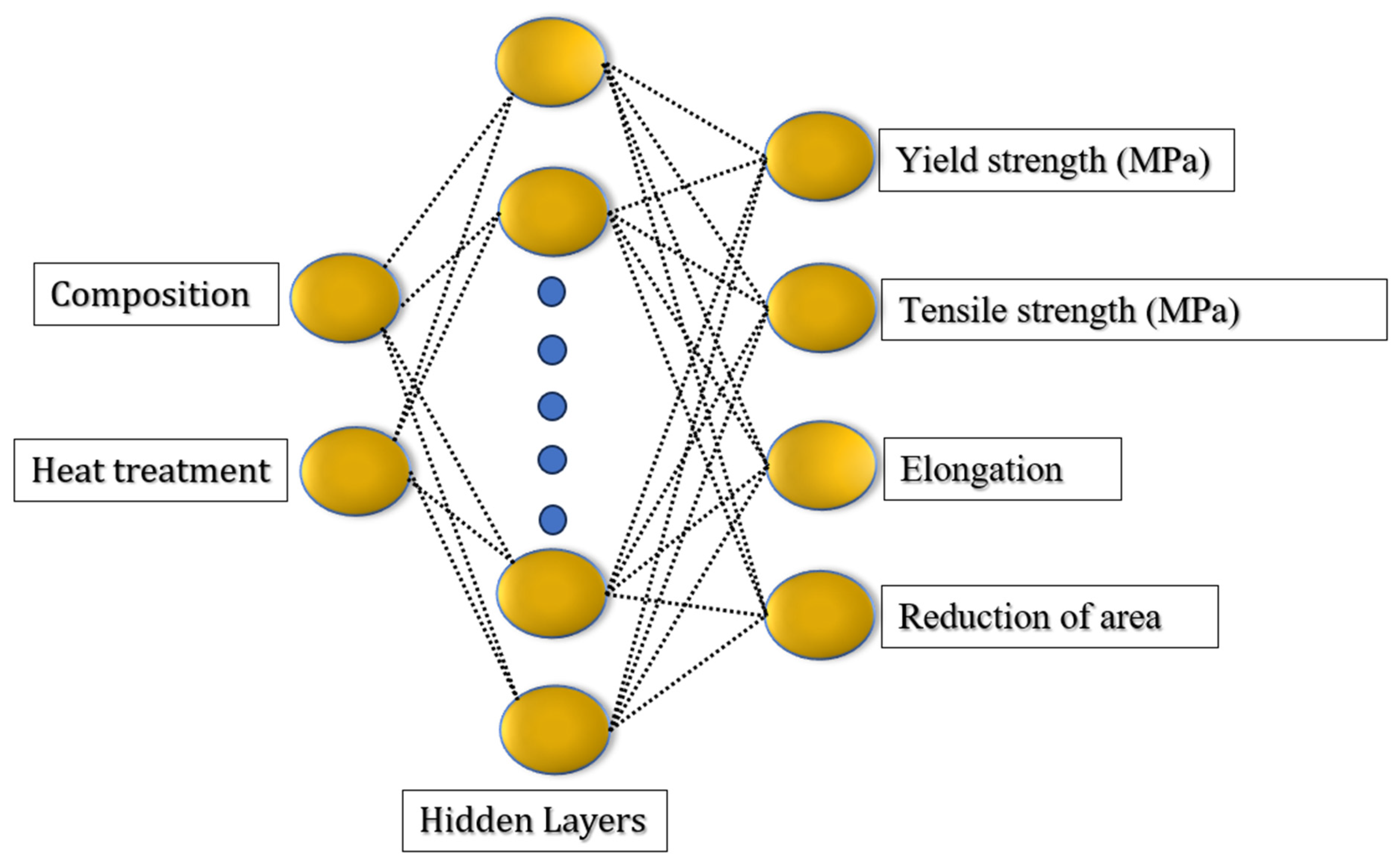
3. Developing ANN Model
4. Results and Discussion
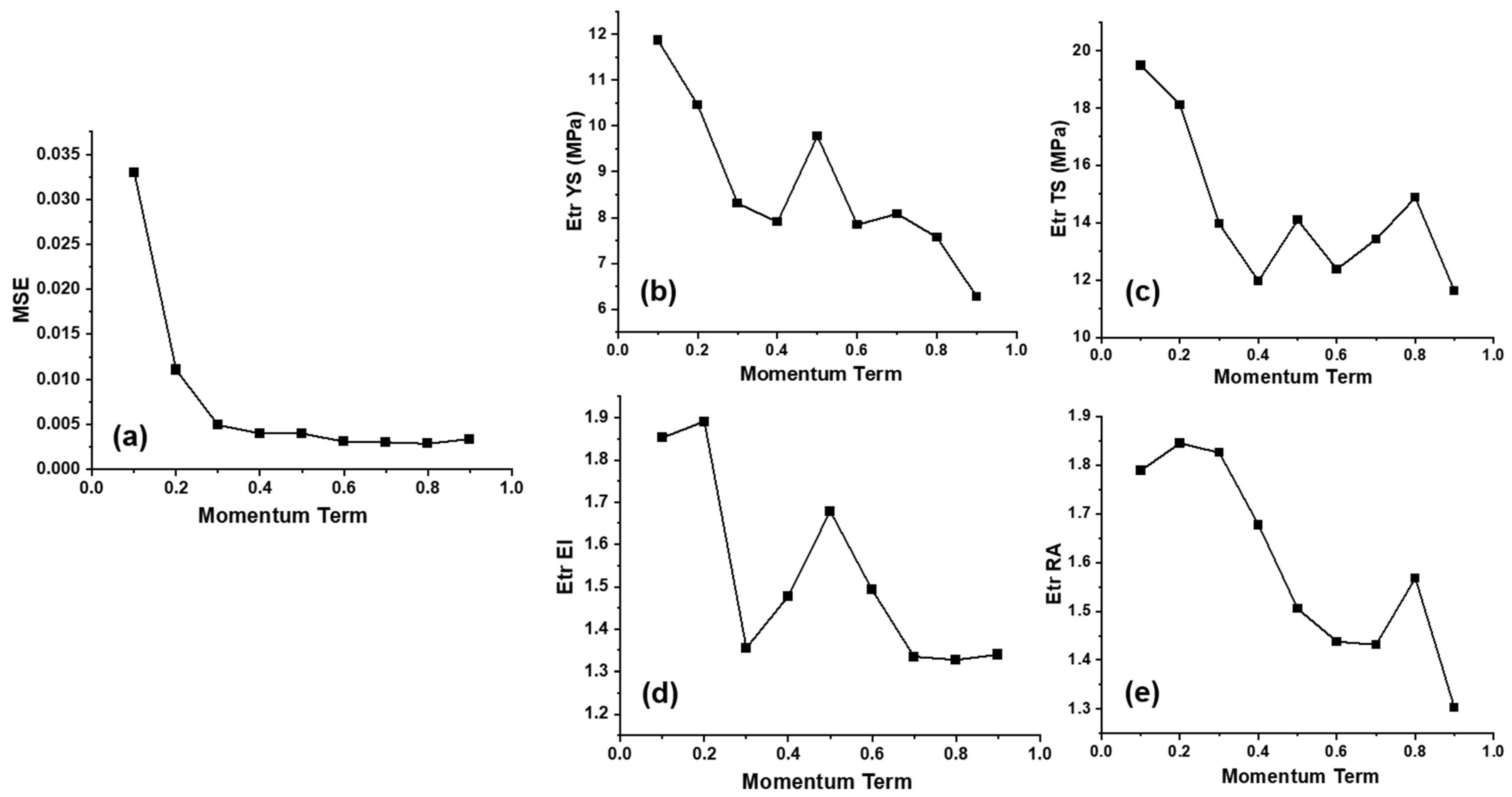
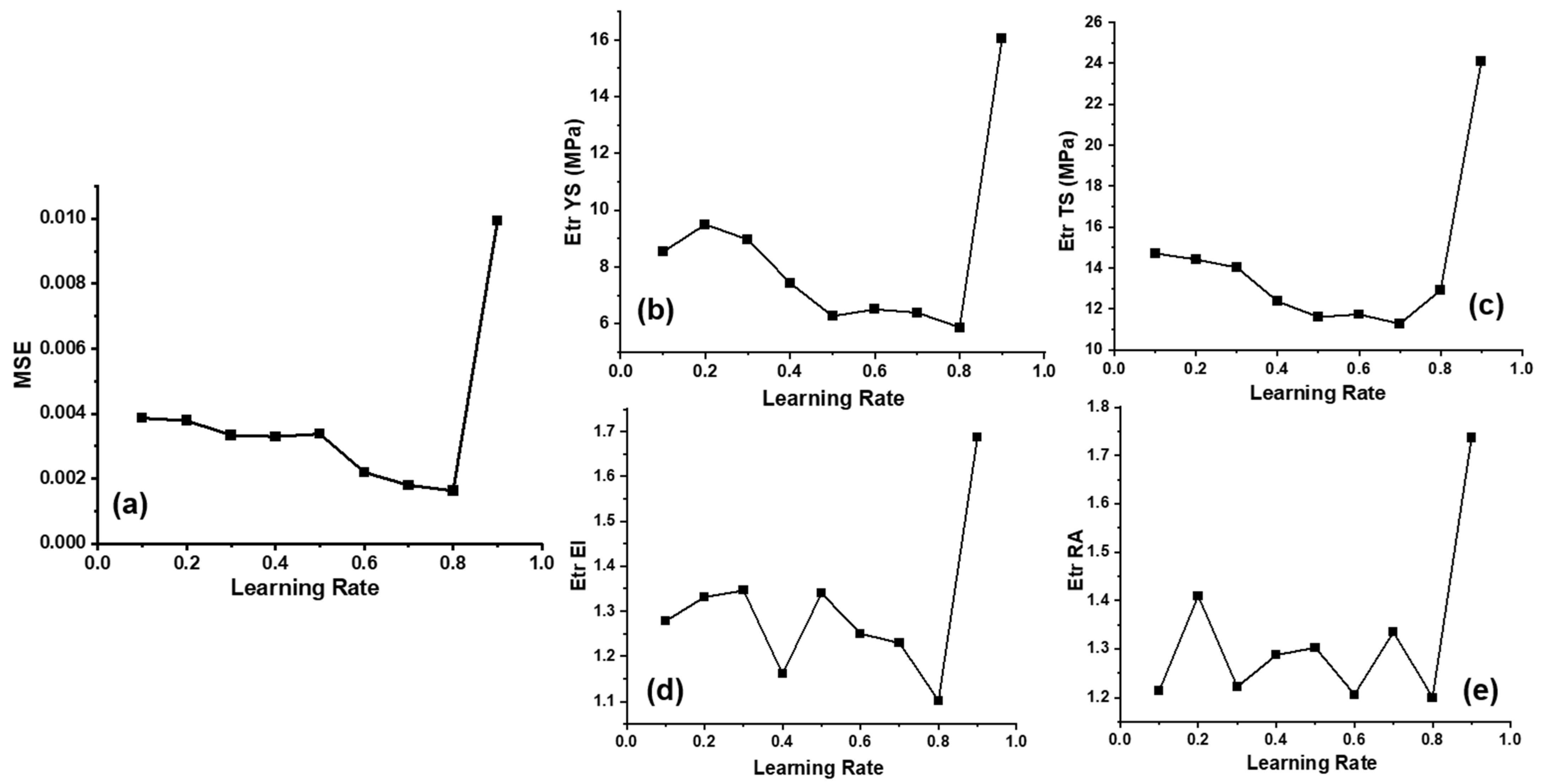
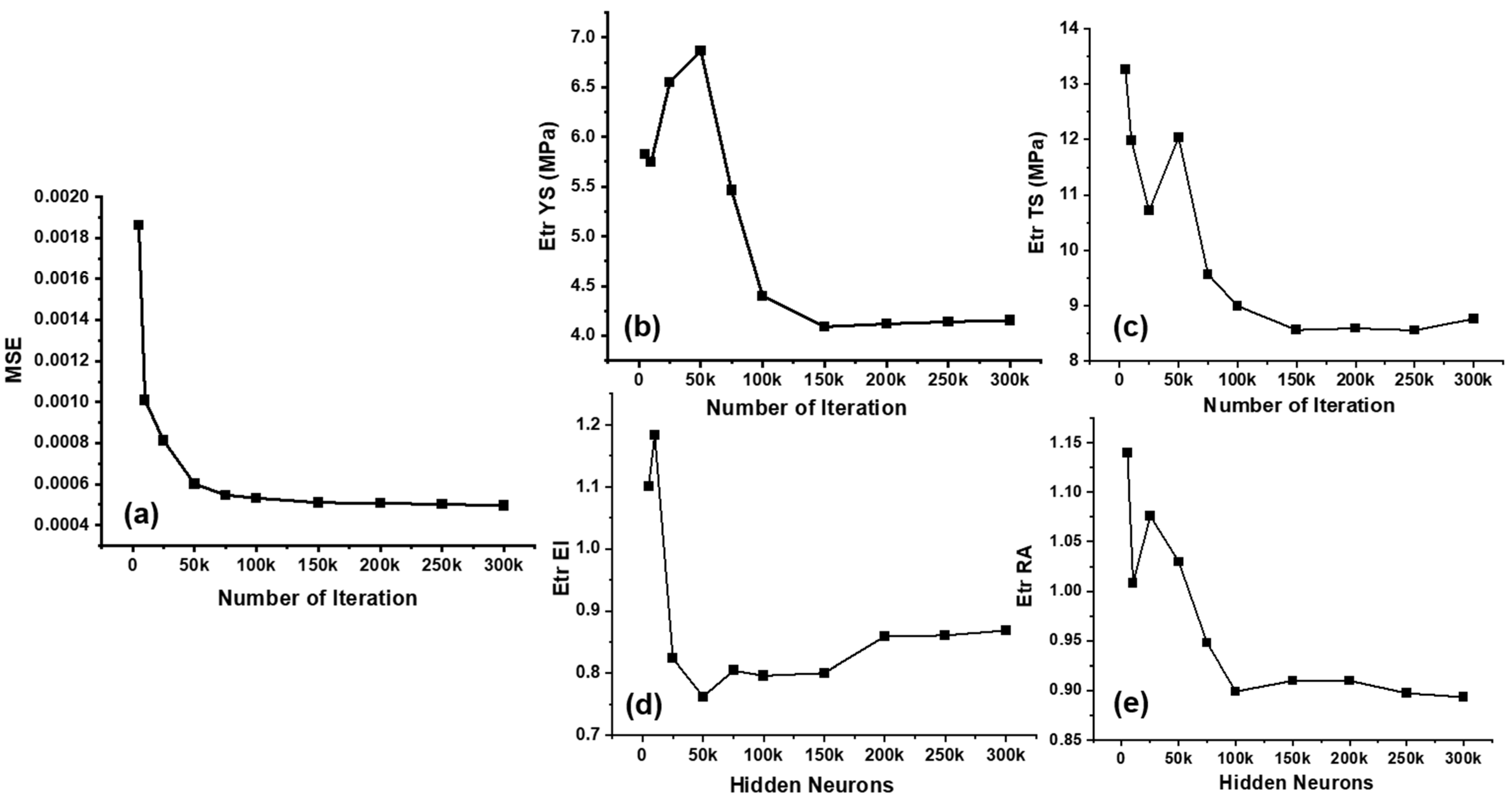
4.1. Performance of ANN Model
4.2. Creating a Graphical User Interface (GUI)
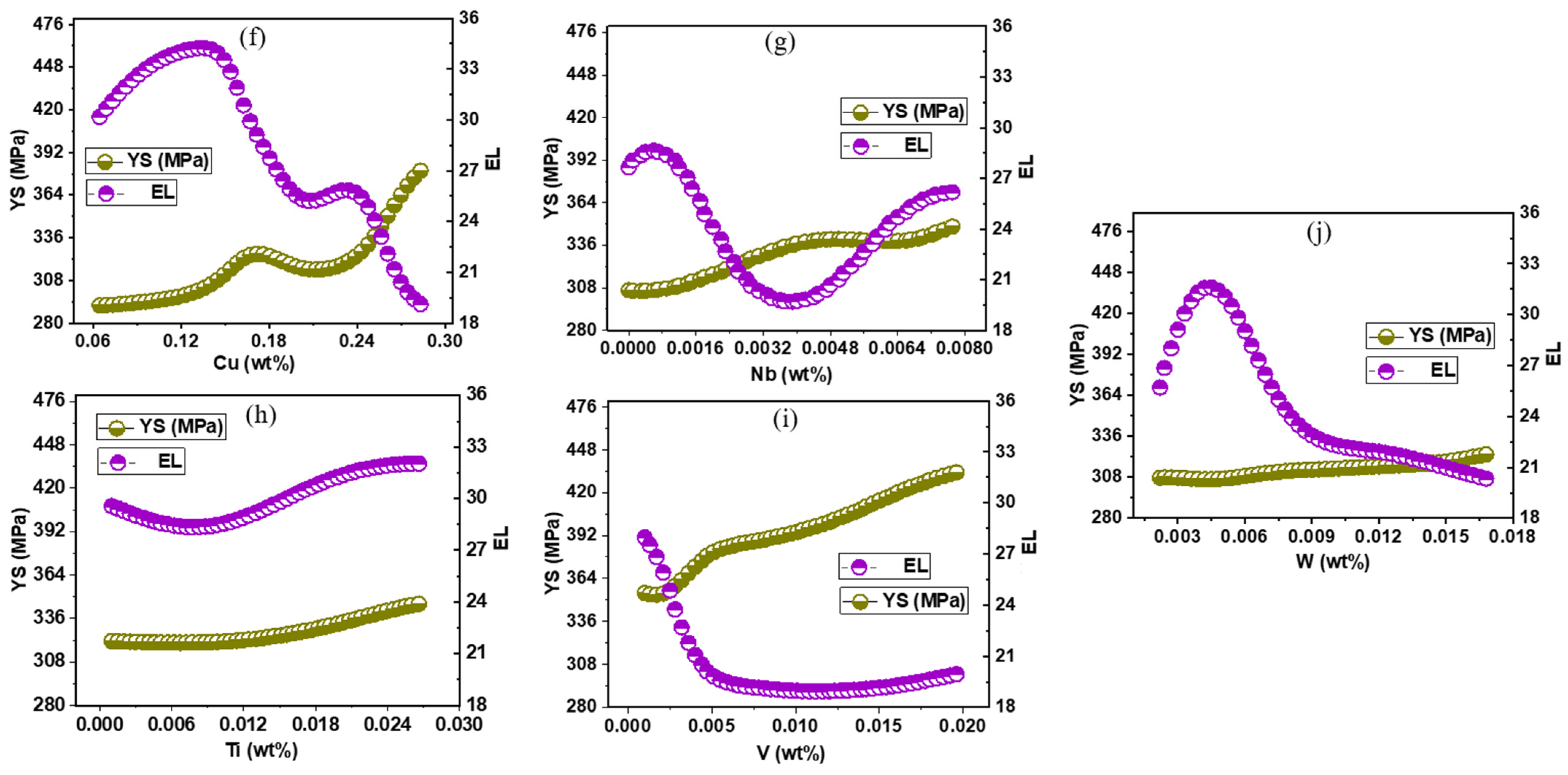
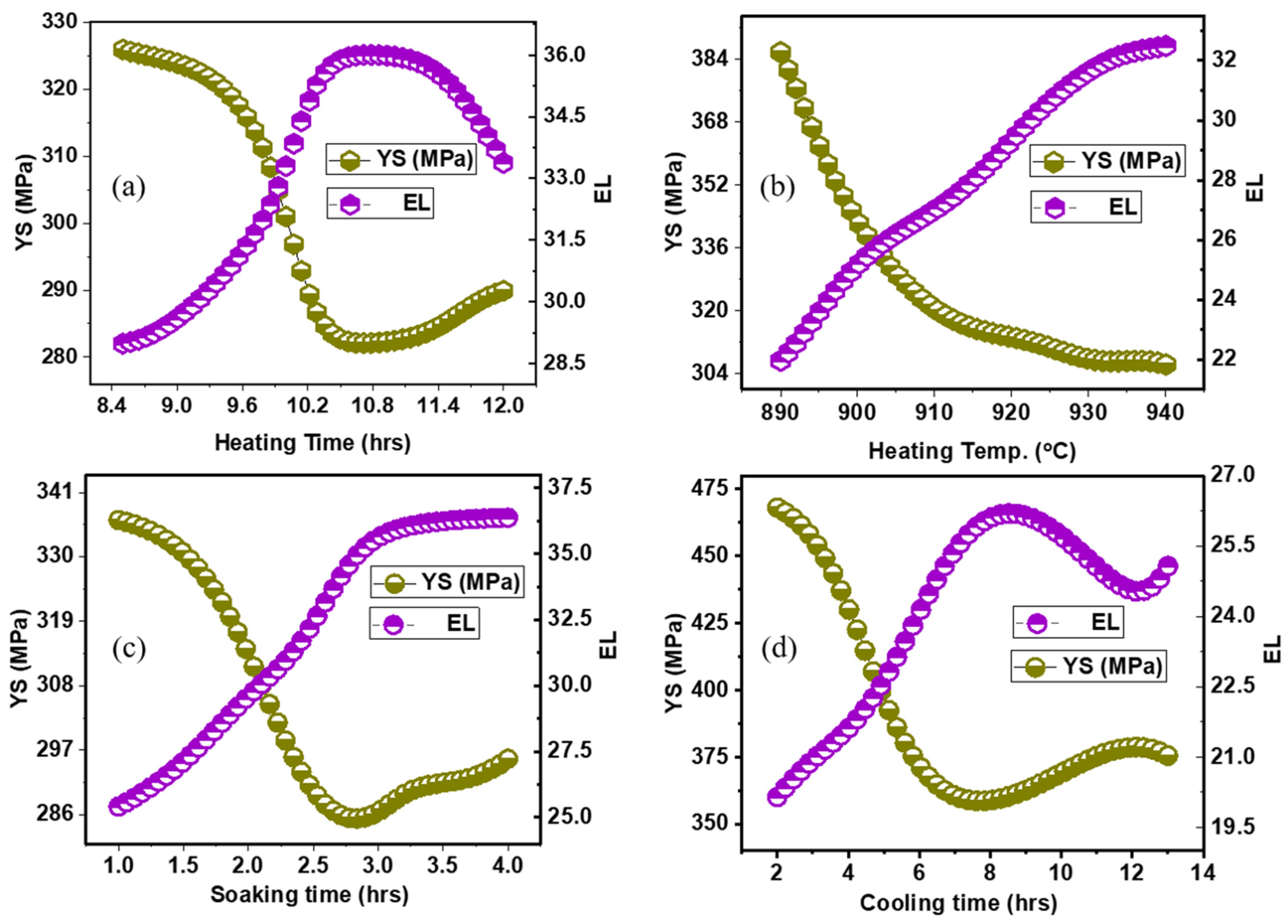
4.3. Creation of Hypothetical C-Mn Steels and Comprehensive Alloying Element Effects
Heat Treatment Parameters on Mechanical Properties
4.4. Literature Validation and Performance Comparison
5. Discussion and Future Perspectives
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Woolman, J.; Mottram, R.A. En 14—Carbon–Manganese Steel. In En 1 to En 20; Woolman, J., Mottram, R.A., Eds.; Pergamon: Oxford, UK, 1964; pp. 220–245. ISBN 978-0-08-010835-3. [Google Scholar]
- Lee, S.H.; Kim, K.H.; Van, D.; Nam, S. Effect of C-Mn Ratio on the Maximum Hardness and Toughness in TMCP Steels with an Identical Carbon Equivalent. J. Mater. Res. Technol. 2020, 9, 8916–8928. [Google Scholar] [CrossRef]
- Liu, R.; Wang, X.; Xu, X.; Cui, C.; Lv, D.; Sun, Q.-F.; Cao, Z.; He, L.; Teng, F.; Fan, W.; et al. Effect of Isothermal Treatment and Rolling on the Microstructure and Properties of Low Carbon Manganese Steel. J. Mater. Eng. Perform. 2025. print. [Google Scholar] [CrossRef]
- Gürol, U.; Can, K.S. Effect of Carbon and Manganese Content on the Microstructure and Mechanical Properties of High Manganese Austenitic Steel. J. Min. Metall. Sect. B 2020, 56, 171–182. [Google Scholar] [CrossRef]
- Timokhina, I.; Hodghson, P.; Pereloma, E.V. Effect of Alloying Elements on the Microstructure-property Relationship in Thermomechanically Processed C-Mn-Si TRIP Steels. Steel Res. 2002, 73, 274–279. [Google Scholar] [CrossRef]
- Ishtiaq, M.; Tiwari, S.; Nagamani, M.; Kang, S.-G.; Reddy, N.G. Data-Driven ANN-Based Predictive Modeling of Mechanical Properties of 5Cr-0.5Mo Steel: Impact of Composition and Service Temperature. Crystals 2025, 15, 213. [Google Scholar] [CrossRef]
- Zaitsev, A.; Koldaev, A.; Arutyunyan, N.; Dunaev, S.; D’yakonov, D. Effect of the Chemical Composition on the Structural State and Mechanical Properties of Complex Microalloyed Steels of the Ferritic Class. Processes 2020, 8, 646. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, A.; Zhao, Z.; Ye, J.; Tang, D.; Zhu, G. Microstructures and Mechanical Properties of C-Mn-Cr-Nb and C-Mn-Si-Nb Ultra-High Strength Dual-Phase Steels. Int. J. Miner. Metall. Mater. 2012, 19, 915–922. [Google Scholar] [CrossRef]
- Zhu, Y.Z.; Yin, Z.M.; Zeng, Y.; Huang, J.W.; Li, X.Q. Effects of Heat Treatment on Microstructure and Mechanical Properties of Fe-Co-Ni-Cr-Mo-C Alloy. J. Cent. South Univ. Technol. 2004, 11, 229–234. [Google Scholar] [CrossRef]
- Wendler, M.; Weiß, A.; Krüger, L.; Mola, J.; Franke, A.; Kovalev, A.; Wolf, S. Effect of Manganese on Microstructure and Mechanical Properties of Cast High Alloyed CrMnNi-N Steels. Adv. Eng. Mater. 2013, 15, 558–565. [Google Scholar] [CrossRef]
- Chernova, G.P.; Bogdashkina, N.L.; Porshneva, A.I.; Shvets, V.A.; Troshkin, G.N. Effect of C and Cr on the Structure, Phase Composition, and Mechanical Properties of Cast Fe−Cr Alloys. Met. Sci. Heat Treat. 1989, 31, 60–63. [Google Scholar] [CrossRef]
- Benedito, A.V.; Torres, C.A.B.; Silva, R.M.D.C.; Krahl, P.A.; Cardoso, D.C.T.; Silva, F.D.A.; Martins, C.H. Effects of Niobium Addition on the Mechanical Properties and Corrosion Resistance of Microalloyed Steels: A Review. Buildings 2024, 14, 1462. [Google Scholar] [CrossRef]
- Salvetr, P.; Gokhman, A.; Svoboda, M.; Donik, Č.; Podstranská, I.; Kotous, J.; Nový, Z. Effect of Cu Alloying on Mechanical Properties of Medium-C Steel after Long-Time Tempering at 500 °C. Materials 2023, 16, 2390. [Google Scholar] [CrossRef] [PubMed]
- Kumar, J.T.; Sudha, J.; Padmanabhan, K.; Frolova, A.; Stolyarov, V. Influence of Strain Rate and Strain at Temperature on TRIP Effect in a Metastable Austenitic Stainless Steel. Mater. Sci. Eng. Struct. Mater. Prop. Microstruct. Process 2020, 777, 139046. [Google Scholar] [CrossRef]
- Pantilimon, M.C.; Berbecaru, A.C.; Gherghescu, I.A.; Coman, G.; Ciucă, S.; Grecu, A.; Sohaciu, M.G.; Dumitrescu, R.E.; Predescu, C. Comparative Evaluation of the TRIP Effect in Steels with Different Contents of Mn and Al. Metals 2022, 12, 443. [Google Scholar] [CrossRef]
- Kučerová, L. The Effect of Two-Step Heat Treatment Parameters on Microstructure and Mechanical Properties of 42SiMn Steel. Metals 2017, 7, 537. [Google Scholar] [CrossRef]
- Zhou, Y.; Song, X.; Liang, J.; Shen, Y.; Misra, R. Innovative Processing of Obtaining Nanostructured Bainite with High Strength—High Ductility Combination in Low-Carbon-Medium-Mn Steel: Process-Structure-Property Relationship. Mater. Sci. Eng. Struct. Mater. Prop. Microstruct. Process 2018, 718, 267–276. [Google Scholar] [CrossRef]
- Caballero, F.; Bhadeshia, H.; Mawella, K.; Jones, D.; Brown, P. Design of Novel High Strength Bainitic Steels: Part 2. Mater. Sci. Technol. 2001, 17, 517–522. [Google Scholar] [CrossRef]
- Bhadeshia, H. Neural Networks in Materials Science: The Importance of Uncertainty; Tata McGraw–Hill Publishing Company Ltd.: Mumbai, India, 2006. [Google Scholar]
- Ishtiaq, M.; Tiwari, S.; Panigrahi, B.B.; Seol, J.B.; Reddy, N.S. Neural Network-Based Modeling of the Interplay between Composition, Service Temperature, and Thermal Conductivity in Steels for Engineering Applications. Int. J. Thermophys. 2024, 45, 137. [Google Scholar] [CrossRef]
- da Cunha Rocha, A.; Enrique Monforte Brandão Marques, P. The Use of Machine Learning to Predict Steel Properties—A Review on the Latest Works. In New Advances in Steel Engineering; da Cunha Rocha, A., Ed.; IntechOpen: Rijeka, Croatia, 2024; ISBN 978-1-83769-831-8. [Google Scholar]
- Bartsch, H.; Voelkel, J.; Feldmann, M. Developing Artificial Neural Networks to Estimate the Fatigue Strength of Structural Steel Details Using the New European Database. Steel Constr. 2025, 18, 1–13. [Google Scholar] [CrossRef]
- Hodroj, A.; Bouglia, R.; Ding, Y.; Zghal, M. Machine Learning for Density Prediction and Process Optimization of 316L Stainless Steel Fabricated by Selective Laser Melting. J. Intell. Manuf. 2025, 1–15. [Google Scholar] [CrossRef]
- Wang, S.; Wu, X. The Mechanical Performance Prediction of Steel Materials Based on Random Forest. Front. Comput. Intell. Syst. 2023, 6, 1–3. [Google Scholar] [CrossRef]
- Saarela, M.; Podgorelec, V. Recent Applications of Explainable AI (XAI): A Systematic Literature Review. Appl. Sci. 2024, 14, 8884. [Google Scholar] [CrossRef]
- Nikiforidis, K.; Kyrtsoglou, A.; Vafeiadis, T.; Kotsiopoulos, T.; Nizamis, A.; Ioannidis, D.; Votis, K.; Tzovaras, D.; Sarigiannidis, P. Enhancing Transparency and Trust in AI-Powered Manufacturing: A Survey of Explainable AI (XAI) Applications in Smart Manufacturing in the Era of Industry 4.0/5.0. ICT Express 2024, 11, 135–148. [Google Scholar] [CrossRef]
- Butler, K.T.; Oviedo, F.; Canepa, P. Machine Learning in Materials Science; ACS In focus; American Chemical Society: Washington, DC, USA, 2022; ISBN 978-0-8412-9946-7. [Google Scholar]
- Beyer, H.-G.; Tukey, J.W. Exploratory Data Analysis. Addison-Wesley Publishing Company Reading, Mass.—Menlo Park, Cal., London, Amsterdam, Don Mills, Ontario, Sydney 1977, XVI, 688 S. Biom. J. 1981, 23, 413–414. [Google Scholar] [CrossRef]
- Kotsiopoulos, T.; Papakostas, G.; Vafeiadis, T.; Dimitriadis, V.; Nizamis, A.; Bolzoni, A.; Bellinati, D.; Ioannidis, D.; Votis, K.; Tzovaras, D.; et al. Revolutionizing Defect Recognition in Hard Metal Industry through AI Explainability, Human-in-the-Loop Approaches and Cognitive Mechanisms. Expert Syst. Appl. 2024, 255, 124839. [Google Scholar] [CrossRef]
- Tiwari, S.; Narayana, P.L.; Ishtiaq, M.; Wang, X.-S.; Park, N.; Reddy, N.S. Artificial Neural Network-Based Prediction of Stacking Fault Energy in Fe-Cr-Mn-C-N Steels. Can. Metall. Q. 2025, 1–9. [Google Scholar] [CrossRef]
- BS EN 10293:2015; Steel Castings for General Engineering Uses. British Standards Institution: London, UK, 2015.
- BS EN 10340:2007; Steel Castings for Structural Uses. British Standards Institution: London, UK, 2007.
- BS EN 10213:2007+A1:2016; Steel Castings for Pressure Purposes. British Standards Institution: London, UK, 2016.
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4. [Google Scholar]
- Barnett, M.R.; Wang, H.; Guo, T. An Orowan Precipitate Strengthening Equation for Mechanical Twinning in Mg. Int. J. Plast. 2019, 112, 108–122. [Google Scholar] [CrossRef]
- Ahmadi, M.R.; Povoden-Karadeniz, E.; Öksüz, K.I.; Falahati, A.; Kozeschnik, E. A Model for Precipitation Strengthening in Multi-Particle Systems. Comput. Mater. Sci. 2014, 91, 173–186. [Google Scholar] [CrossRef]
- Gladman, T. The Physical Metallurgy of Microalloyed Steels; Taylor & Francis Group: London, UK, 2002; ISBN 978-1-902653-81-5. [Google Scholar]
- Bhadeshia, H.K.D.H. 21—Physical Metallurgy of Steels. In Physical Metallurgy, 5th ed.; Laughlin, D.E., Hono, K., Eds.; Elsevier: Oxford, UK, 2014; pp. 2157–2214. ISBN 978-0-444-53770-6. [Google Scholar]
- Baker, T.N. Microalloyed Steels. Ironmak. Steelmak. 2016, 43, 264–307. [Google Scholar] [CrossRef]
- Lugovy, M.; Slyunyayev, V.; Brodnikovskyy, M. Solid Solution Strengthening in Multicomponent Fcc and Bcc Alloys: Analytical Approach. Prog. Nat. Sci. Mater. Int. 2021, 31, 95–104. [Google Scholar] [CrossRef]
- Vervynckt, S.; Verbeken, K.; Thibaux, P.; Houbaert, Y. Characterization of the Precipitation State during Austenite Processing of a Microalloyed Steel. In Journées Annuelles de la SF2M 2010= SF2M Annual Meeting 2010; Société Française de Métallurgie et de Matériaux (SF2M): Paris, France, 2010; pp. 158–159. [Google Scholar]
- Fine, M.E.; Liu, J.Z.; Asta, M.D. An Unsolved Mystery: The Composition of Bcc Cu Alloy Precipitates in Bcc Fe and Steels. Mater. Sci. Eng. A 2007, 463, 271–274. [Google Scholar] [CrossRef]
- Cui, S.; Mamivand, M.; Morgan, D. Simulation of Cu Precipitation in Fe-Cu Dilute Alloys with Cluster Mobility. Mater. Des. 2020, 191, 108574. [Google Scholar] [CrossRef]
- Leslie, W.C. The Physical Metallurgy of Steels; Hempisphere Publishing Corporation: London, UK, 1981; ISBN 978-0-07-037780-6. [Google Scholar]
- Regenspurg, S.; Geigenmüller, I.; Milsch, H.; Kühn, M. Copper Precipitation as Consequence of Steel Corrosion in a Flow-through Experiment Mimicking a Geothermal Production Well. Geotherm. Energy 2017, 5, 11. [Google Scholar] [CrossRef]
- Majta, J.; Muszka, K. 9—Modelling Microstructure Evolution and Work Hardening in Conventional and Ultrafine-Grained Microalloyed Steels. In Microstructure Evolution in Metal Forming Processes; Lin, J., Balint, D., Pietrzyk, M., Eds.; Woodhead Publishing: New Delhi, India, 2012; pp. 237–264. ISBN 978-0-85709-074-4. [Google Scholar]
- Cai, F.; Zhou, M.; Tian, J.; Xu, G. Comparative Study of the Role of Niobium in Low-Carbon Ferritic and Bainitic Steels. Mater. Sci. Eng. A 2022, 851, 143579. [Google Scholar] [CrossRef]
- ASM Handbook Committee. Properties and Selection: Irons, Steels, and High-Performance Alloys; ASM International: Almere, The Netherlands, 1990; ISBN 978-1-62708-161-0. [Google Scholar]
- Burke, J.E.; Turnbull, D. Recrystallization and Grain Growth. Prog. Met. Phys. 1952, 3, 220–292. [Google Scholar] [CrossRef]
- Yue, C.; Zhang, L.; Liao, S.; Gao, H. Kinetic Analysis of the Austenite Grain Growth in GCr15 Steel. J. Mater. Eng. Perform. 2010, 19, 112–115. [Google Scholar] [CrossRef]
- Rajan, T.V.S.; Sharma, A.K.; Sharma, C.P. Heat Treatment: Principles and Techniques; PHI Learning: Delhi, India, 2011; ISBN 978-81-203-4095-4. [Google Scholar]
- Wang, Y.-X.; Wu, X.; Li, X.; Xie, Z.M.; Liu, R.; Liu, W.; Zhang, Y.; Xu, Y.; Liu, C. Prediction and Analysis of Tensile Properties of Austenitic Stainless Steel Using Artificial Neural Network. Metals 2020, 10, 234. [Google Scholar] [CrossRef]
- Xiong, J.; Zhang, T.; Shi, S.-Q. Machine Learning of Mechanical Properties of Steels. Sci. China-Technol. Sci. 2020, 63, 1247–1255. [Google Scholar] [CrossRef]
- Zippo, V.; Robotti, E.; Maestri, D.; Fossati, P.; Valenza, D.; Maggi, S.; Papallo, G.; Belay, M.; Cerruti, S.; Porcu, G.; et al. Development of a Self-Updating System for the Prediction of Steel Mechanical Properties in a Steel Company by Machine Learning Procedures. Technologies 2025, 13, 75. [Google Scholar] [CrossRef]
- Paupler, P. G. E. Dieter. Mechanical Metallurgy. 3rd ed., Mc Graw-Hill Book Co., New York 1986. XXIII + 751 p., DM 138.50, ISBN 0–07–016893–8. Cryst. Res. Technol. 1988, 23, 194. [Google Scholar] [CrossRef]
- Armstrong, R.W. The Influence of Polycrystal Grain Size on Several Mechanical Properties of Materials. Metall. Mater. Trans. B-Process Metall. Mater. Process Sci. 1970, 1, 1169–1176. [Google Scholar] [CrossRef]


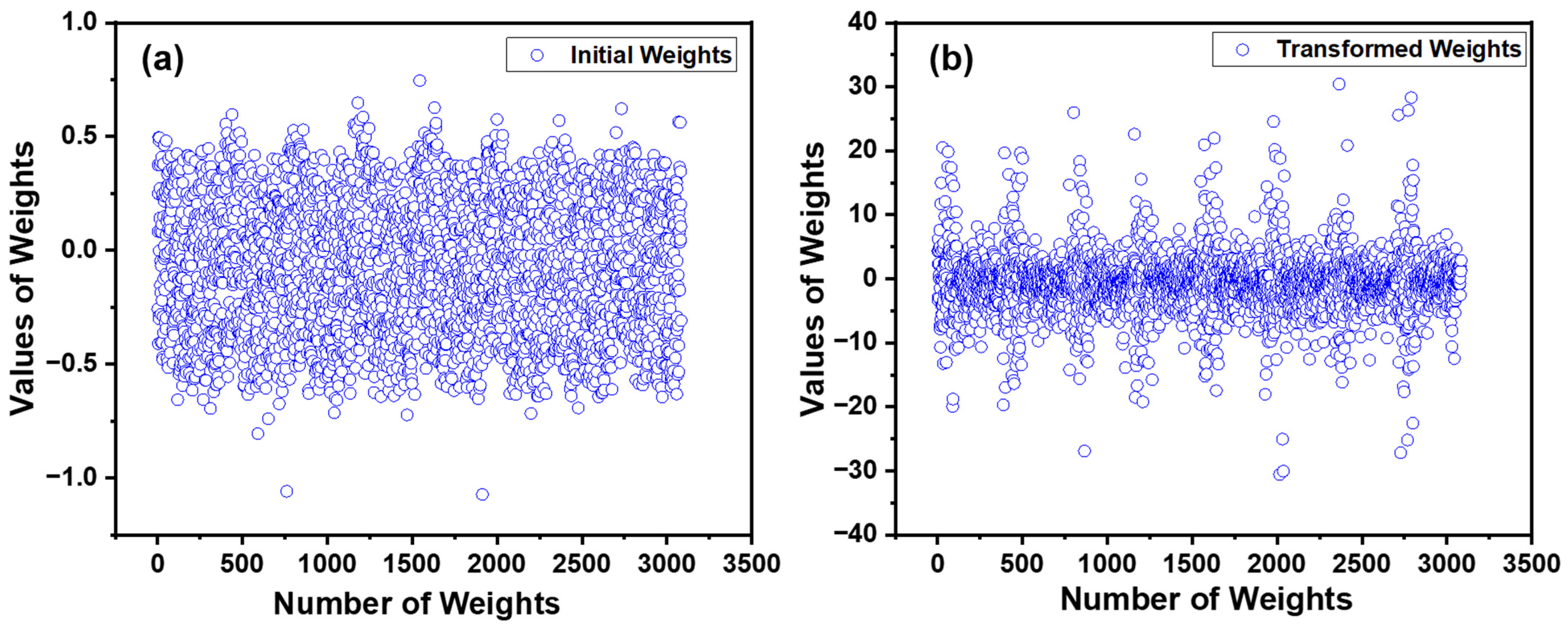
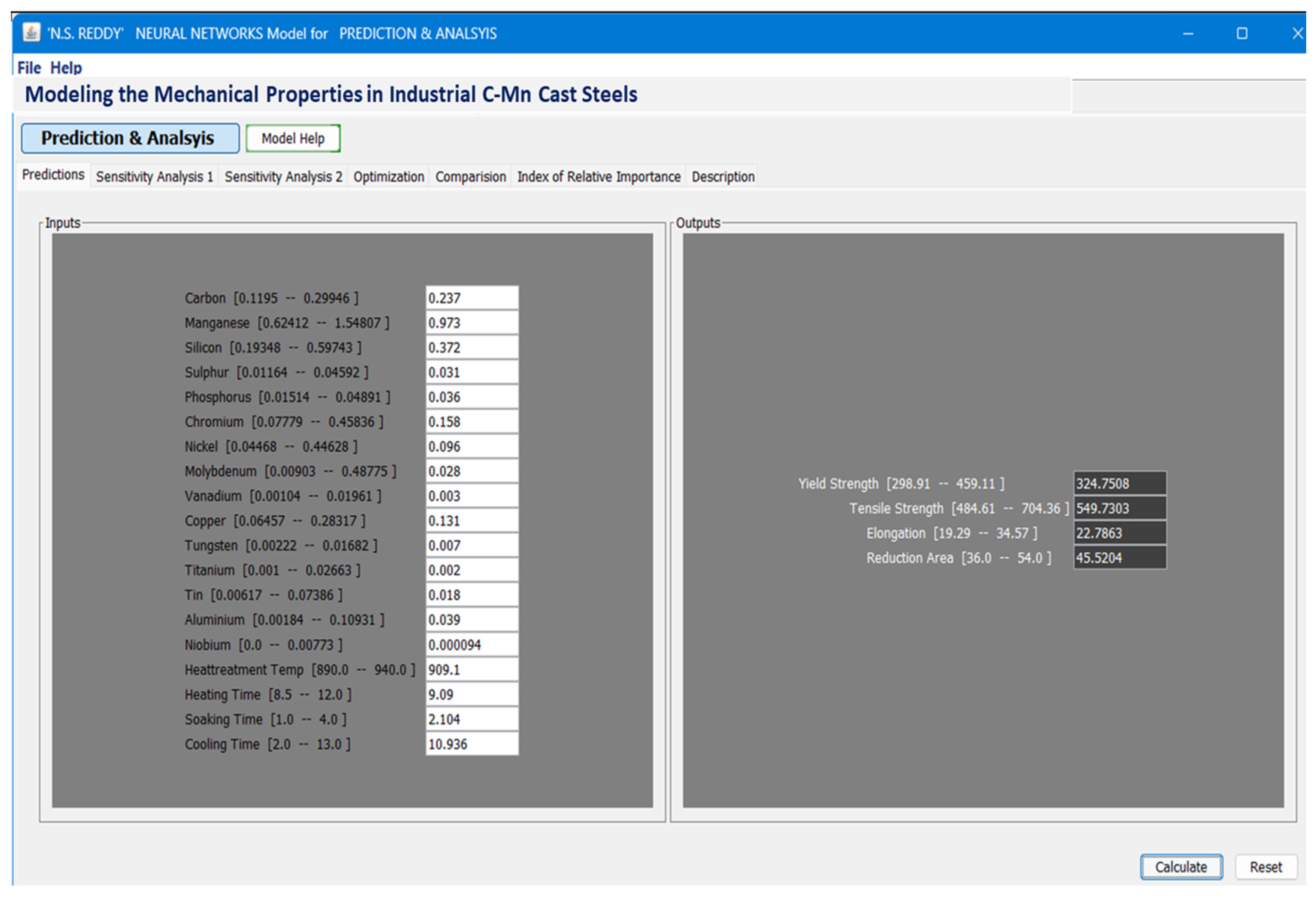
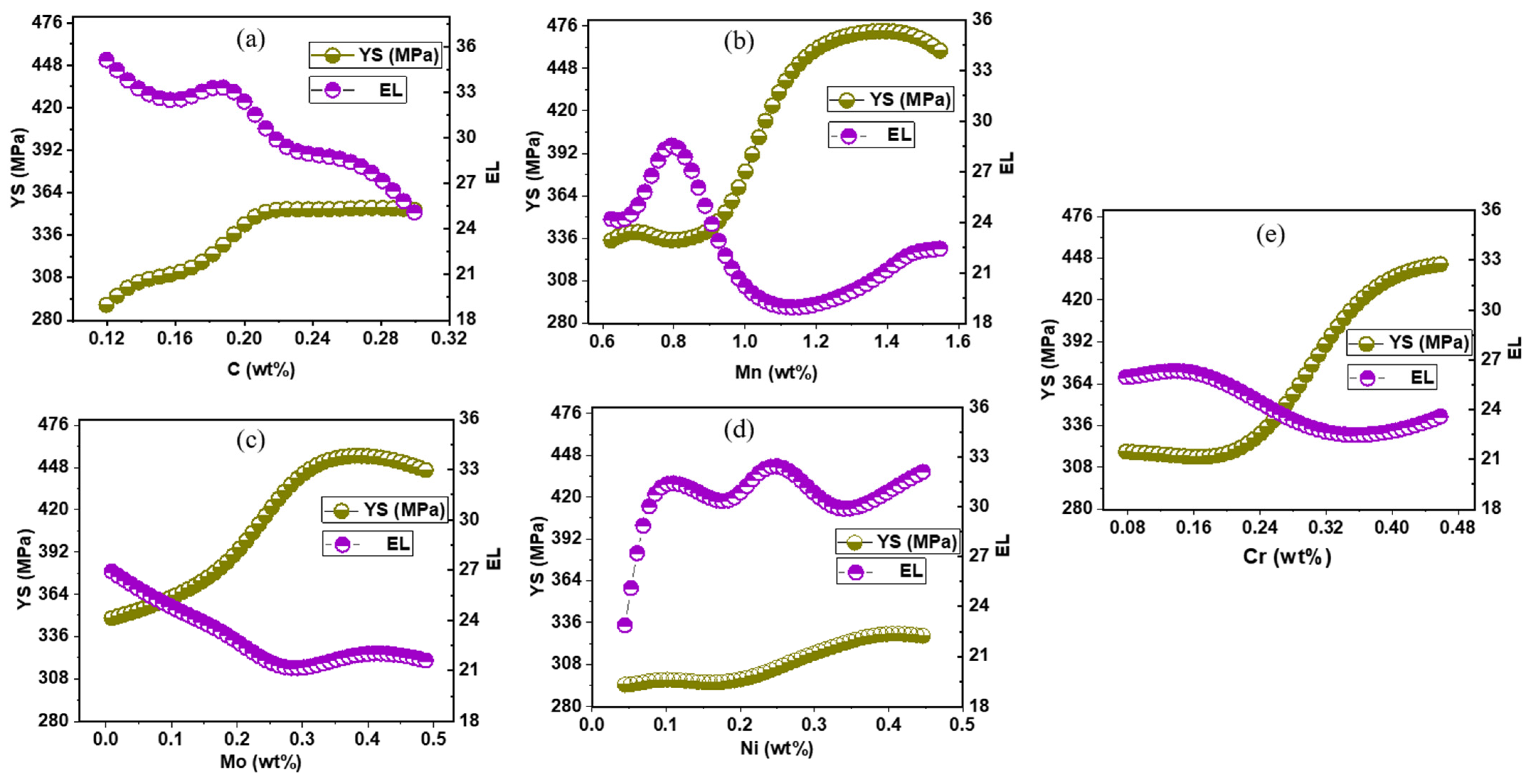
| Inputs/Outputs | Minimum | Maximum | Mean | Standard Deviation |
|---|---|---|---|---|
| Carbon (wt.%) | 0.119 | 0.299 | 0.237 | 0.022 |
| Manganese (wt.%) | 0.624 | 1.548 | 0.973 | 0.107 |
| Silicon (wt.%) | 0.193 | 0.597 | 0.372 | 0.072 |
| Sulfur (wt.%) | 0.011 | 0.046 | 0.031 | 0.005 |
| Phosphorous (wt.%) | 0.015 | 0.049 | 0.036 | 0.005 |
| Chromium (wt.%) | 0.077 | 0.458 | 0.158 | 0.055 |
| Nickel (wt.%) | 0.044 | 0.446 | 0.096 | 0.036 |
| Molybdenum (wt.%) | 0.009 | 0.488 | 0.028 | 0.032 |
| Vanadium (wt.%) | 0.001 | 0.019 | 0.003 | 0.001 |
| Copper (wt.%) | 0.064 | 0.283 | 0.131 | 0.03 |
| Tungsten (wt.%) | 0.002 | 0.017 | 0.007 | 0.002 |
| Titanium (wt.%) | 0.001 | 0.027 | 0.002 | 0.001 |
| Tin (wt.%) | 0.0062 | 0.074 | 0.018 | 0.006 |
| Aluminum (wt.%) | 0.002 | 0.109 | 0.039 | 0.022 |
| Niobium (wt.%) | 0.00000 | 0.008 | 0.000094 | 0.022 |
| Heating time (h) | 8.5 | 12 | 9.09 | 0.33 |
| Heating temp. °C | 890 | 940 | 909.1 | 9.65 |
| Soaking time (h) | 01 | 04 | 2.104 | 0.391 |
| Cooling time (h) | 02 | 13 | 10.936 | 2.234 |
| Yield strength (MPa) | 294 | 461 | 333.254 | 28.59 |
| Tensile strength (MPa) | 481 | 706 | 544.908 | 41.61 |
| Elongation | 19.29 | 34.57 | 26.072 | 2.95 |
| Reduction of area | 36.00 | 54.00 | 48.038 | 3.22 |
| C | Mn | Si | S | P | Cr | Ni | Mo | V | Cu |
|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 1.106 | 0.41 | 0.026 | 0.032 | 0.249 | 0.085 | 0.024 | 0.003 | 0.145 |
| W | Ti | Sn | Al | Nb | H. Temp. | H. Time | S. Time | C. Time | YS (MPa) |
| 0.009 | 0.001 | 0.019 | 0.050 | 0.001 | 900 | 9 | 2 | 11 | 324 |
| TS (MPa) | EL (%) | RA (%) | |||||||
| 540 | 23 | 48 | … | … |
| Study | Steel System | Method | Accuracy Metric | YS Prediction | TS Prediction | Notable Features |
|---|---|---|---|---|---|---|
| Present Study | C-Mn Cast Steel | ANN (20-44-44-4) | Mean Error | 3.45% | 4.2% | Industrial dataset (500 samples), 90% predictions within 5% |
| Liu et al. [52] | Austenitic Stainless | ANN | R2 | >0.93 | >0.93 | 200+ samples, tensile property focus |
| Xiong et al. [53] | C and Low-alloy | ML Ensemble | MAPE | 4.8% | 5.2% | 360 samples, multiple algorithms |
| Zippo et al. [54] | Industrial Steels | Self-updating ML | Real-time Error | <6% | <6% | Industrial scale, real-time prediction |
| Traditional Empirical [55] | General Steel | Regression | MAPE | 8–15% | 6–12% | Conventional approach |
| Hall-Petch Relations [56] | Various | Empirical | Typical Error | 10–20% | 8–15% | Grain size based |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tiwari, S.; Heo, S.; Park, N.; Reddy, N.G.S. Modeling Mechanical Properties of Industrial C-Mn Cast Steels Using Artificial Neural Networks. Metals 2025, 15, 790. https://doi.org/10.3390/met15070790
Tiwari S, Heo S, Park N, Reddy NGS. Modeling Mechanical Properties of Industrial C-Mn Cast Steels Using Artificial Neural Networks. Metals. 2025; 15(7):790. https://doi.org/10.3390/met15070790
Chicago/Turabian StyleTiwari, Saurabh, Seongjun Heo, Nokeun Park, and Nagireddy Gari S. Reddy. 2025. "Modeling Mechanical Properties of Industrial C-Mn Cast Steels Using Artificial Neural Networks" Metals 15, no. 7: 790. https://doi.org/10.3390/met15070790
APA StyleTiwari, S., Heo, S., Park, N., & Reddy, N. G. S. (2025). Modeling Mechanical Properties of Industrial C-Mn Cast Steels Using Artificial Neural Networks. Metals, 15(7), 790. https://doi.org/10.3390/met15070790









