Influence of Wear-Induced Turning on the Roll’s Fatigue Life

Abstract

Friction-induced wear during the rolling process needs periodic remachining of caliber roll grooves, which increases operational costs and reduces roll fatigue life. Stress analysis showed that a regular reduction in the initial diameter by up to 3.5% results in a 12.2% increase in maximum stress amplitude, reducing the estimated fatigue life by a factor of 1.5. Although fatigue life is reduced, the risk of failure under normal operating conditions remains low. Further analysis, considering mill design and roll hardness, demonstrated the feasibility of additional roll diameter reduction, thereby enabling increased production using the same rolls. The findings support further diameter reduction without compromising performance and underscore the importance of integrating such analysis into the roller design process to optimize fatigue life and roll utilization.

1. Introduction

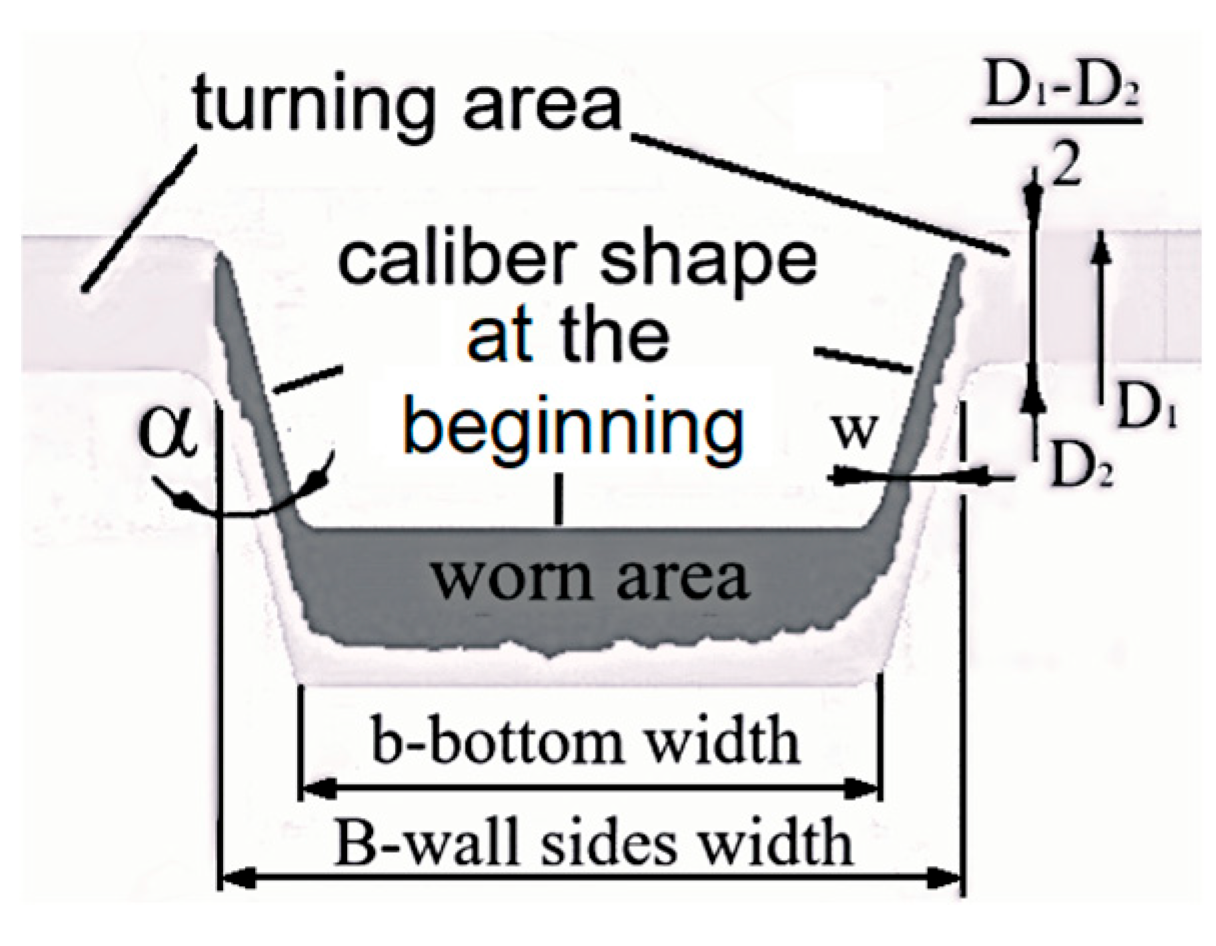
The rolling process, using grooved (caliber) rolls, is used to produce a wide range of profiles. The durability of these rolls is a crucial aspect of their performance, particularly because these rolls are subjected to significant mechanical and thermal stresses. Several factors influence their durability including groove design, material properties, operational conditions, wear, and turning. During the rolling process, friction between the rolls and the workpiece causes non-uniform wear of the caliber-shaped grooves, resulting in the loss of their required form, as shown in Figure 1.

$${\displaystyle \frac{D_1-D_2}{2}}={\displaystyle \frac{w}{tg\alpha }}$$

(1)

As shown in Figure 1, the points of extreme wear determine the total depth of subsequent turning. The required turning depth can be determined from Equation (1), as referenced in [1], where D₁—initial diameter; D_2—reduced diameter due to turning; $\propto$—caliber slope; and w—layer thickness. Wear-induced turning is an undesirable phenomenon, as it increases production costs and reduces the roll’s fatigue life.

Roll failure leads to production downtime and significantly increases overall operational costs. Consequently, research into the causes of roll failure has intensified, with particular focus on the influence of rolling parameters. Numerous researchers have investigated the wear mechanisms of rolling mill rolls [2,3,4,5].

The study in [6] presents a failure investigation and crack characterization of a spalled work roll in a hot strip mill. Backup roll failures, including cracking, are examined in [7]. The study in [8] presents a research methodology to gain better control of the process, allowing innovation in the production of profiles with more complex geometries and new materials. The study in [9] proposes a comprehensive approach to analyzing coupled wear and fatigue damage using a method based on the Manson–Coffin equation, a modified slope formula, and the Miner criterion.

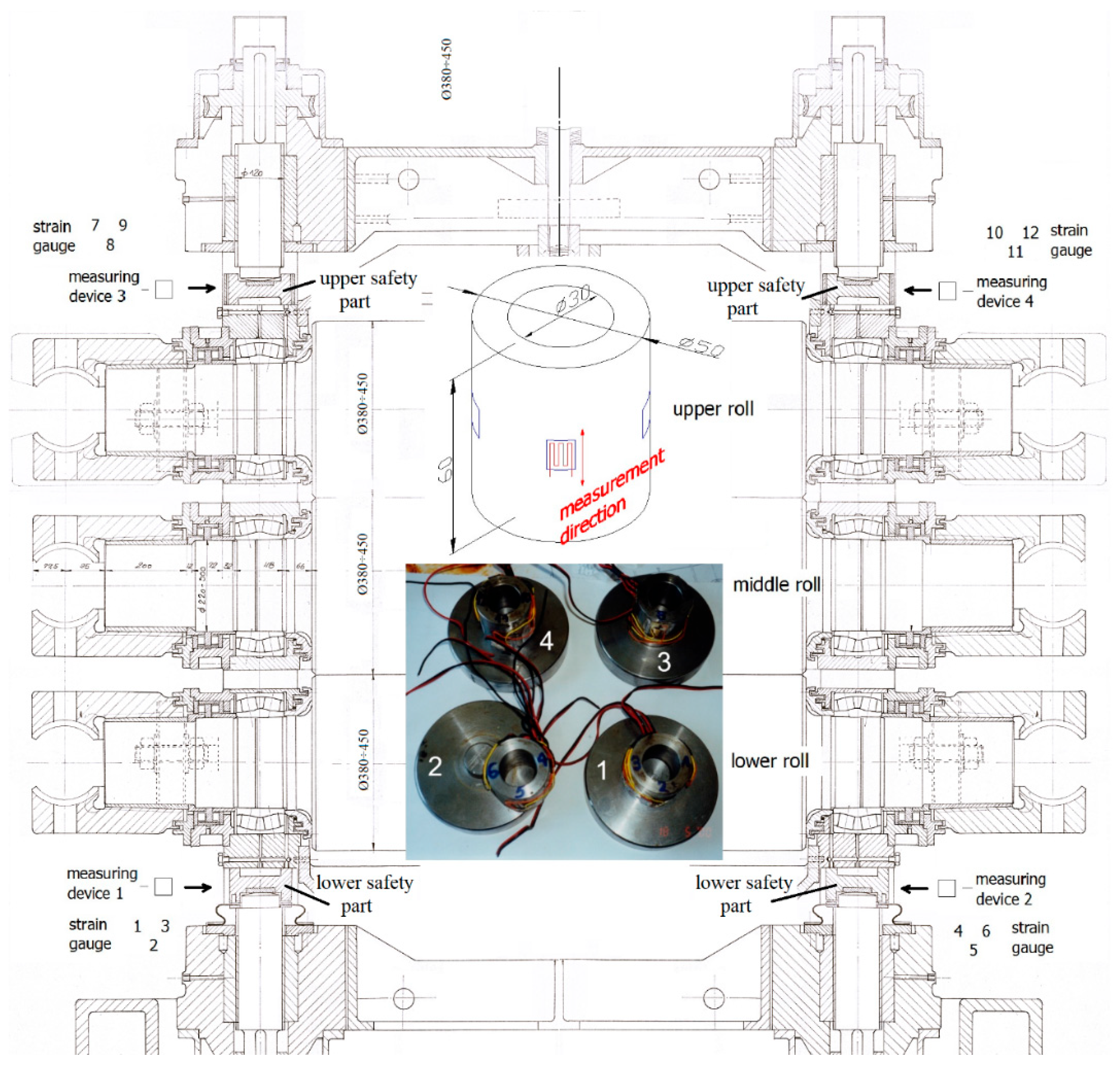
A three-high roughing mill stand is commonly used in hot-rolling processes to reduce the thickness of steel billets while extending their length. This configuration is particularly effective for handling billets with an initial cross-section of 100 mm square and an initial length of 3000 mm. In this case, three (3) rolls were used to reduce 100 mm square billets with a cross-sectional area of 9850 mm² to an oval shape measuring 58 × 20 mm, with a final cross-sectional area of 1075 mm², over eight passes, as shown in Figure 2 and

Table 1. Rolling passes [8].

Number of Pass	Caliber Shape	Pass Size [mm]	Cross-Section [mm2]	Width [mm]	Height Before Pass [mm]	Height After Pass [mm]	Absolute Draught [mm]	Absolute Reduction [mm2]	Stock Length [m]	Rolling Time [s]	Pause [s]
			9850	100					3
1	box	100 × 82	8015	104	100	82	18	1835	3.69	1.58	3
2	box	100 × 66	6474	108	82	66	16	1541	4.56	1.74	3
3	box	67 × 80	5398	71	108	80	28	1076	5.47	2.26	3
4	box	67 × 59	4032	76	80	59	21	1366	7.33	2.65	3
5	box	66 × 52	3280	65	76	52	24	752	9.01	3.53	3
6	oval	80 × 34	2286	82.5	52	34	18	994	12.93	4.65	3
7	square	40	1578	53.5	82.5	51	31.5	708	18.73	6.92	3
8	oval	58 × 20	1075	60.5	40	20.5	19.5	503	27.49	9.52	3

[10]. The roll speed was 120 rpm.

The dimensions of the new rolls were as follows: total length of 2300 mm, barrel length of 1400 mm, and barrel diameter of 450 mm. The upper roll had a diameter of 450 mm, the middle roll 445 mm, and the lower roll 440 mm. The minimum effective diameter of the rolls was 380 mm.

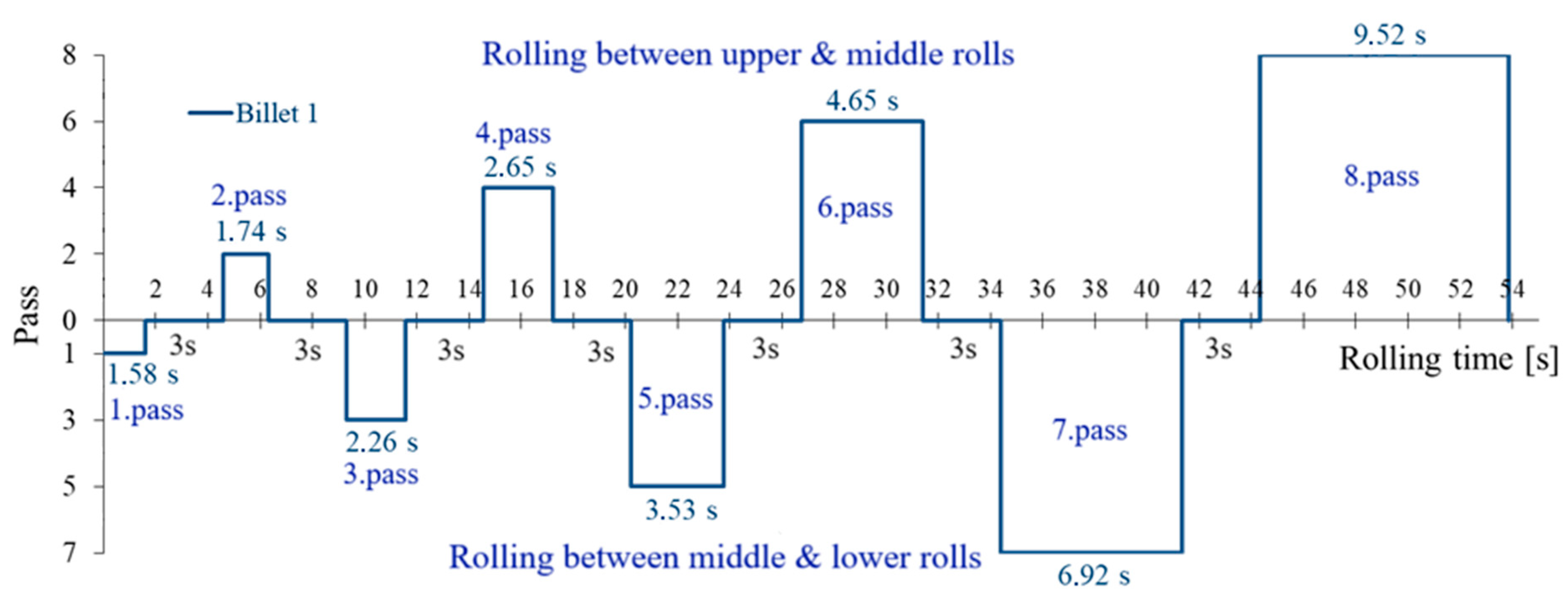
The rolling process begins with a single billet, as illustrated in the diagram shown in Figure 3.

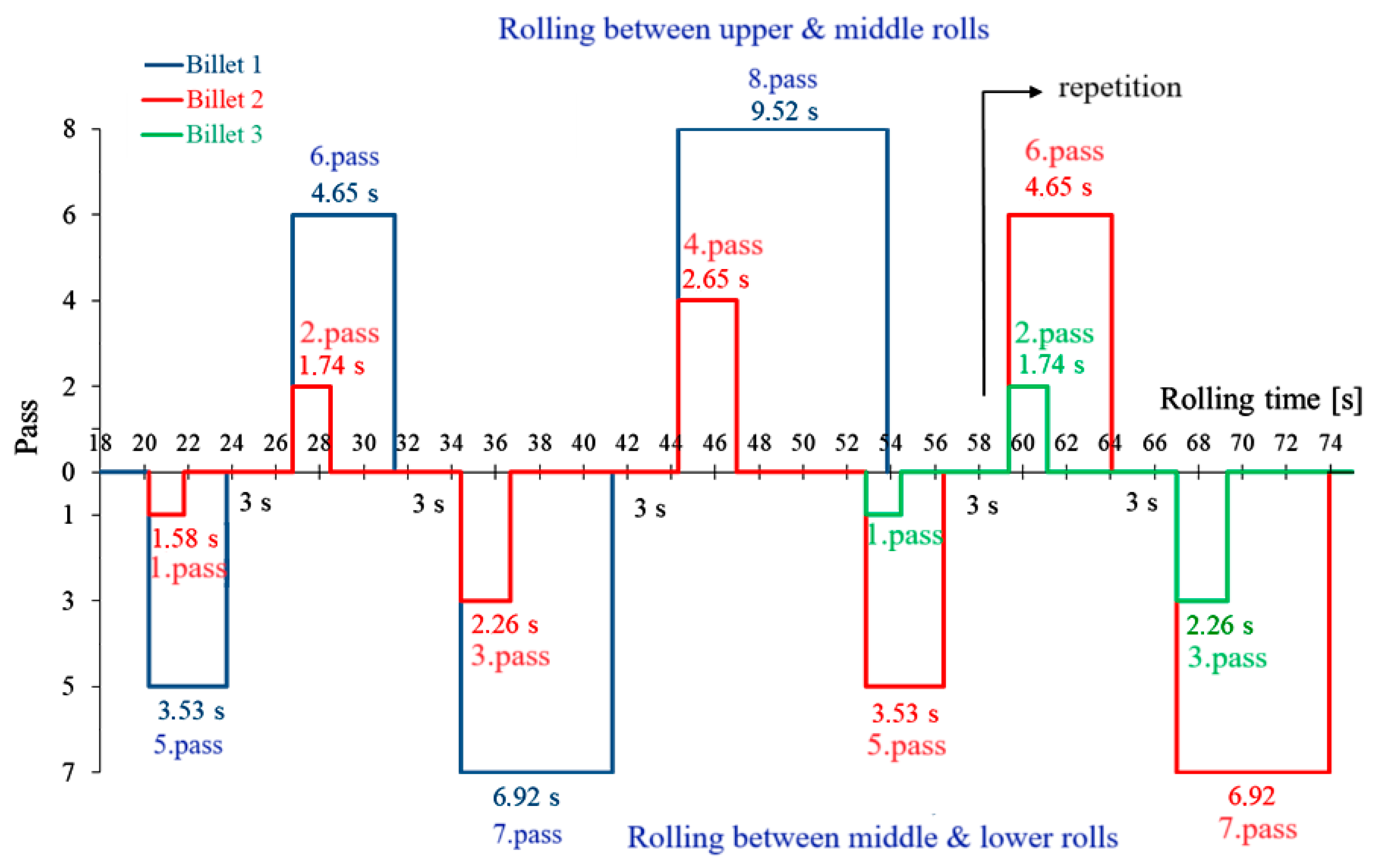
Usually, rolling was carried out with two billets and occasionally with three. The diagram in Figure 4 illustrates the rolling process with two and three billets. As shown, rolling with two billets began at 20.23 s.

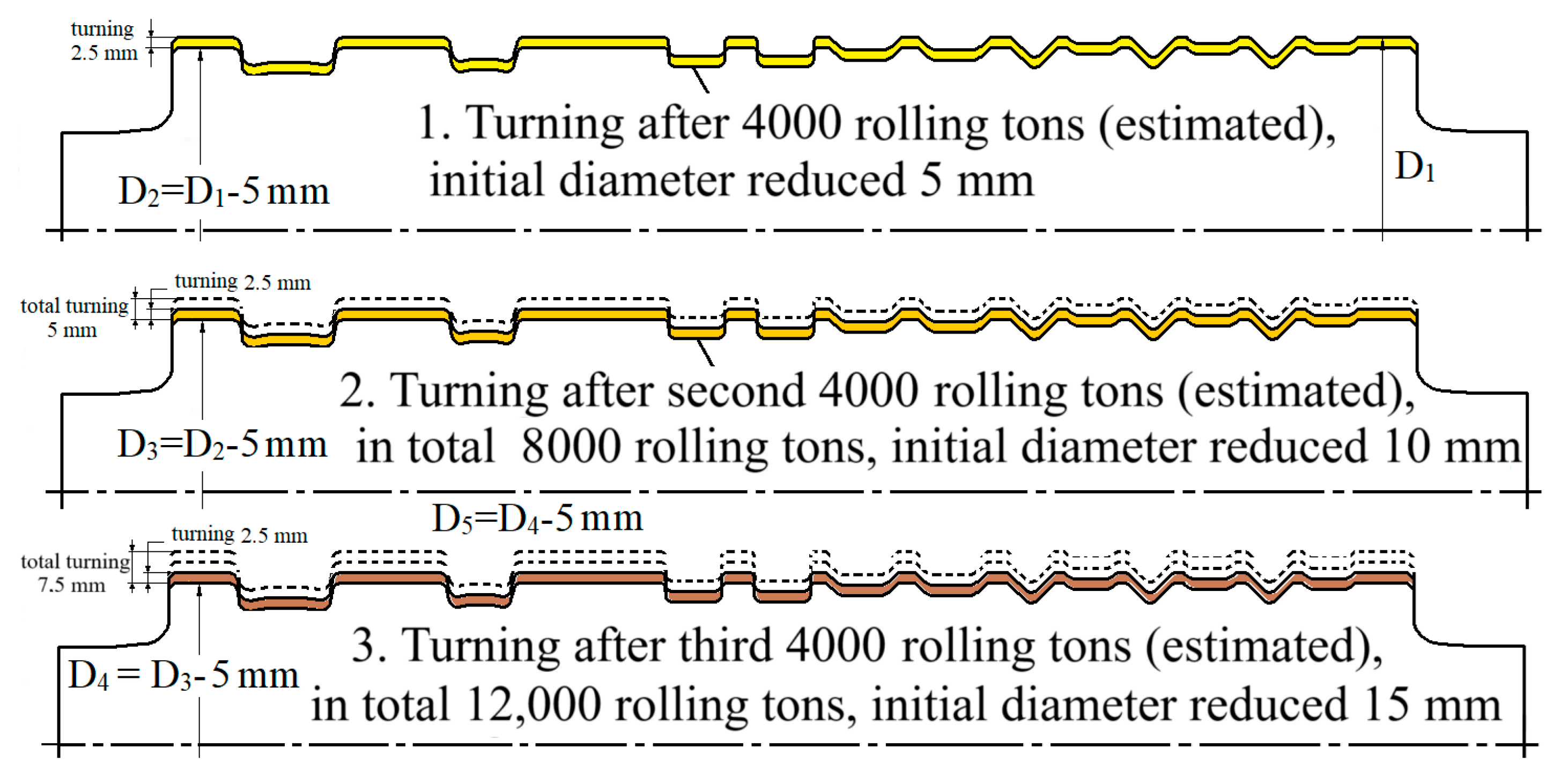
Caliber roll wear ‘life’ is measured in tons of hot-rolled steel per millimeter of machined roll diameter (t/mm) [1]. In this case, roll remachining due to wear was estimated after processing 4000 tons of hot-rolled steel. It was also estimated that the roll wear “life” would extend till 16.000 rolling tons of steel, which corresponds to a three-time reduction in roll diameter through turning. Typically, each turning operation reduced the roll diameter by 5 mm, depending on the extent of groove wear; see Figure 5.

Sometimes, thermal cracks may appear around the perimeter of a groove of a certain caliber (see Figure 6). The occurrence and distribution of these cracks vary depending on the caliber and the individual roll. During wear turning, thermal cracks are removed along with the worn material.

2. Service Load and Corresponding Stresses

Rolling forces cause bending stresses on the roll. The middle roll was selected for analysis because it is subjected to all eight rolling forces, as shown in Figure 7, while the upper and lower rolls are each loaded with four rolling forces.

There are several basic expressions for determining the force on the rolls in hot rolling, but they yield different results [1]. Many authors have studied the calculation of rolling forces [12,13,14,15]. The rolling forces listed in

Table 2. Measured forces on the rolls [13].

Caliber	No. 1	No. 2	No. 3	No. 4	No. 5	No. 6	No. 7	No. 8
Measured forces on the rolls [kN]	356.08	494.55	356.08	524.22	346.19	544.01	286.84	445.10

were determined through experimental testing for each of the eight (8) passes [16].

Four measuring devices, each equipped with three strain gauges, were designed based on rolling force calculations and installed in place of safety components to prevent roll breakage, as shown in the drawing in Figure 8. Measurements were taken over a two-hour production period.

Stresses in critical sections were determined through numerical analysis using the finite element method (ADINA software, version 8.4), as shown in Figure 9. The model is linear-elastic, using 3D solid elements, each with eight nodes. Each node has three degrees of freedom: translation in the X, Y, and Z directions. The model is fixed at both ends along the line and loaded with concentrated forces in the nodes. Material properties used in the model: Young’s modulus was 174 GPa and Poisson’s ratio was 0.275. The figure shows the concentrated forces caused by rolling in pass 2 and pass 6a.

As shown in Figure 3 and Figure 4, depending on the rolling order, the forces on the rollers act both individually and in combination, with varying durations. Thirty such cases of force application on the middle roll were used to determine the stress spectrum. The rolling forces listed in Table 2 were then applied to calculate the stresses in the critical sections. The analysis showed that maximum stresses on the middle roll occur at calibers 3–4 and 7a, and during rolling in calibers 2 and 6a. The stress on the roll neck was not considered, as it is not machined due to wear. Numerically obtained local stress values for pass grooves 3–4 and 7a are presented in

Table 3. Local stresses in the groove corners of pass groove 3–4 and pass groove 7a.

.	Local Stresses [MPa]			Local Stresses [Mpa]
Force	Pass Groove 3–4	Pass Groove 7a	Forces in Combination	Pass Groove 3–4	Pass Groove 7a
F1	25	12	F1 + F5a	64	46
F2	34	17	F1 + F5b	60	51
F3	43	23	F2 + F6a	83	85
F4	63	33	F2 + F6b	76	90
F5a	39.6	33	F3 + F7a	61.8	62
F5b	35	38.5	F3 + F7b	57.2	56
F6a	49	67.8	F3 + F7c	52.6	46
F6b	42	73	F4 + F8a	88.9	90
F7a	19	38.5	F4 + F8b	81.7	77
F7b	14	32	F4 + F8c	74.6	61
F7c	9.7	22	F1 + F5a + F8a	38	9.5
F8a	26	56	F1 + F5a + F8b	45	7.2
F8b	19	43	F1 + F5b + F8b	31	8.8
F8c	11	26	F1 + F5b + F8c	48	25

.

3. Roll Material Data and Stress Spectrum

The rolls were made of nodular graphite cast iron with a pearlitic matrix. The roll mark was KGR-380-P (Valji d.o.o., Štore, Slovenija), and the surface hardness was 380 HB; see Figure 10.

The S-N curve of the roll material in the pass groove was not initially available, so it was determined through experimental testing [16]. Specimens for testing were taken from a new roll with the mark KGR-460-P (Ø500 × 1500 mm) to obtain the same characteristics as roll mark KGR-380-P. From the new roll with dimensions Ø500 × 1500 mm, one ring was machined by turning, with final dimensions of Ø440 × Ø320 × 170 mm; see Figure 11.

Brinell hardness was measured at four points (A, B, C, and D) along the cross-section of the ring, as shown in Figure 11. As can be seen, the hardness drop from the surface of the real roll is less than predicted according to the catalog, which is better from a wear perspective. This hardness drop allows a greater reduction in roll diameter without losing wear resistance.

4. Fatigue Life Estimation

The fatigue life estimation was performed using the fatigue stress–life concept based on local stress. The estimated fatigue life was calculated using the elementary Miner’s rule. Figure 12 presents the S-N curve of the roll material [17], along with the stress spectra at the two locations subjected to the highest stress levels: pass grooves 3–4 and 7a. The cumulative stress spectra after 4000 tons of rolling at the two locations were obtained from Figure 3 and Figure 4, as well as Table 3.

A comparison of the presented spectra for 4000 tons of rolling reveals that the maximum stress in groove 7a is slightly higher than in groove 3–4. Additionally, the fatigue life at maximum stress in groove 3–4 is 35% higher than in groove 7a (4,199,290 cycles compared to 3,075,567). As a result, the stress spectrum of pass groove 7a was used to assess the influence of turning due to wear on fatigue life.

5. Impact of Wear-Induced Diameter Reduction on Roll Fatigue Life

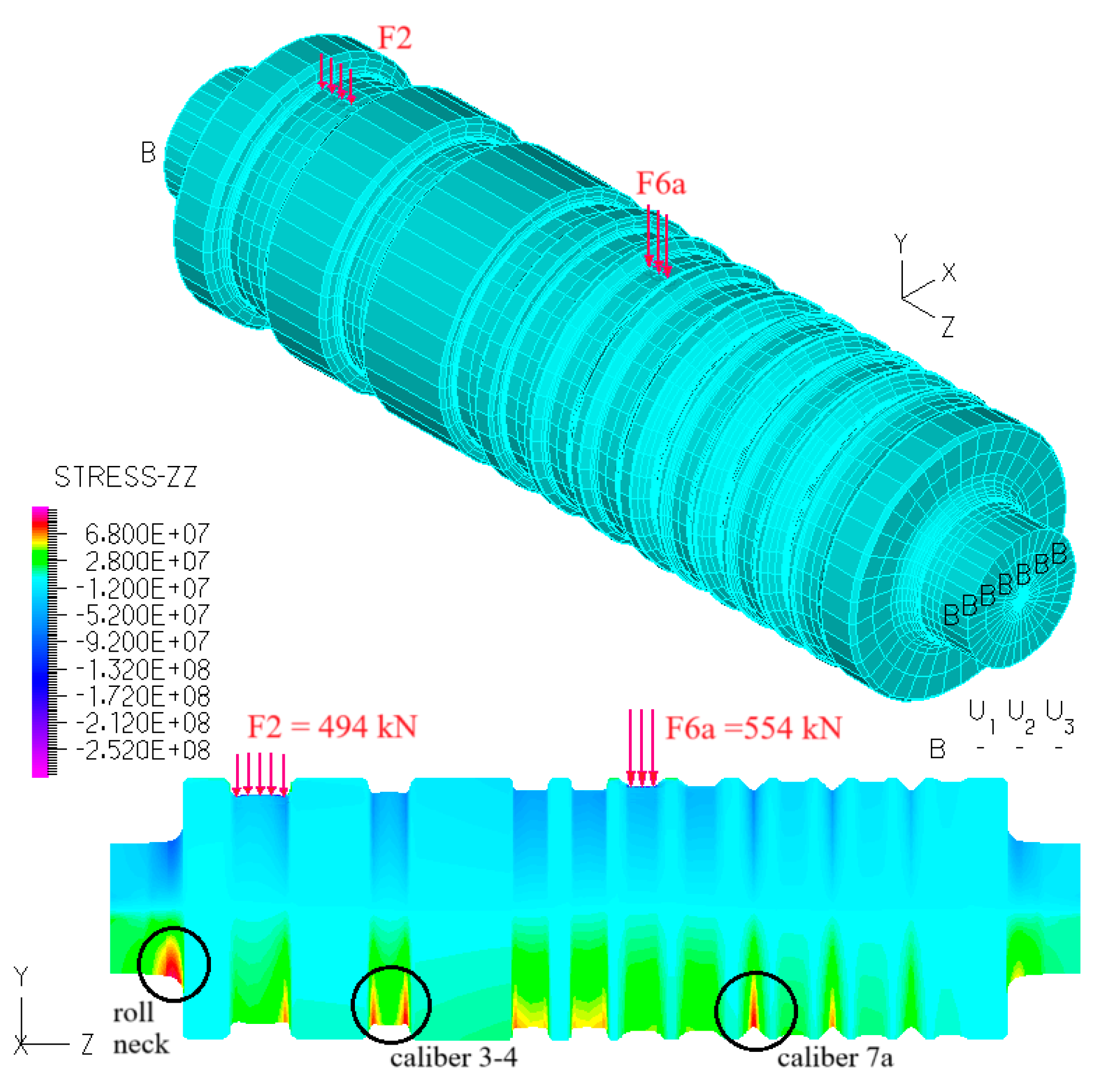
Due to wear, the diameter of the middle roll is reduced by 5 mm after each 4000 tons of rolling, decreasing from 445 mm to 430 mm. To evaluate the effect of this reduction, the same numerical model of the middle roll was used to determine local stresses for four-barrel diameters: 440 mm, 435 mm, and 430 mm. The corresponding stress spectra in pass groove 7a, calculated for 4000 tons of rolling, are presented in Figure 13.

The next facts are visible from the diagram in Figure 13:

After each turning of 2.5 mm due to wear, corresponding to a 5 mm reduction in roll diameter, the maximum stress amplitude increases by approximately 4%. For example, after the first turning—reducing the diameter from the initial 445 mm to 440 mm—the maximum stress amplitude increases from 90 MPa to 94 MPa.

After 16,000 rolled tons—the estimated practical working life—which corresponds to three turnings of 2.5 mm each due to wear and results in a total roll diameter reduction of 15 mm, the maximum stress amplitude increases by approximately 12.2%, from 90 MPa to 101 MPa.

The number of cycles at the maximum stress amplitude of 101 MPa is 53,300, which is approximately nine times fewer than the material’s fatigue life at the same stress level—465,000 cycles.

The calculation of fatigue life using the elementary Miner’s rule showed a reduction of approximately 1.5 times, from 3,075,567 to 2,042,000 cycles. Furthermore, when compared with the stress spectrum for 4000 rolled tons, the service life at a maximum stress amplitude of 101 MPa exceeds twice the maximum number of cycles in the stress spectrum (942,155).

It should also be noted that turning not only reduces the roll diameter but also removes any potential thermal cracks. After material removal, the roll—now with a reduced diameter—can be considered effectively new, with a different size and, consequently, a new fatigue life.

Ultimately, these findings indicate the potential for further diameter reduction.

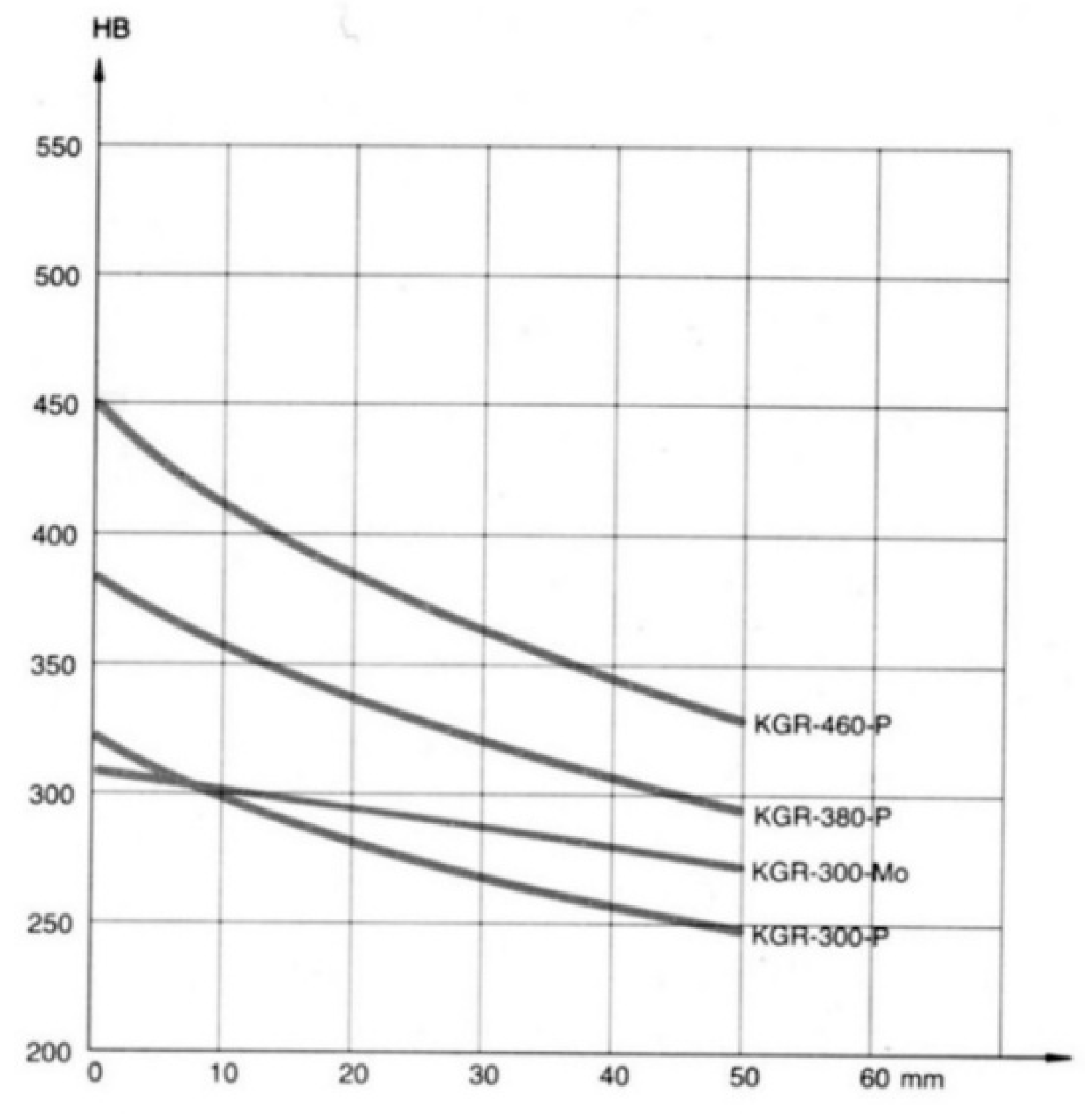
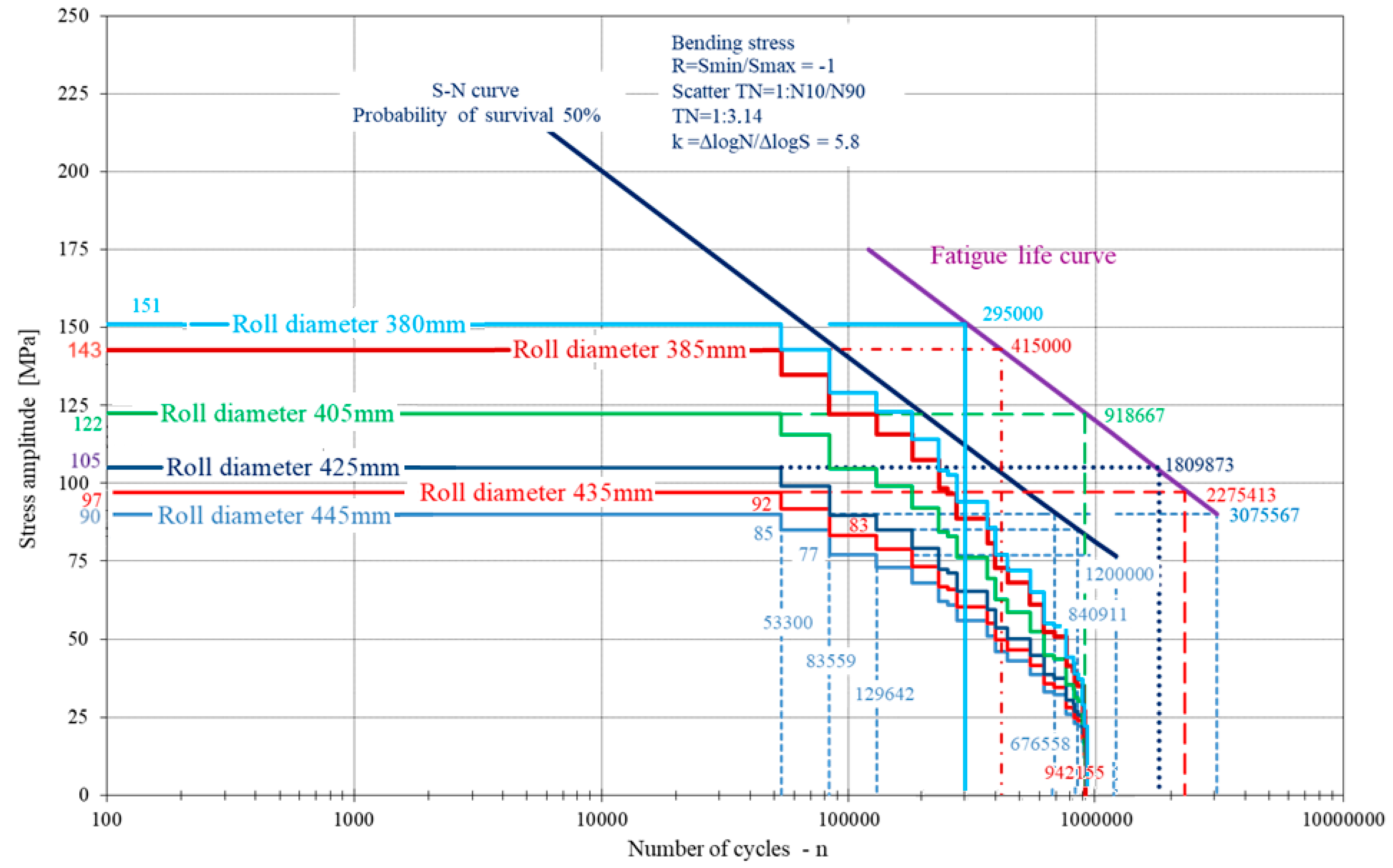
Further reduction in the roll diameter depends on the design of the rolling mill stand and the hardness of the rolls. According to the study in [7], the maximum reduction in roll diameter is from 450 mm to 380 mm (see Figure 7). Hardness measurements of the cut ring indicate that a similar reduction in roll diameter may be possible. To determine the maximum possible reduction in the roll diameter, the same numerical model of the middle roll was used to calculate local stresses for the following diameters: 405 mm, 385 mm, and 380 mm. The corresponding stress spectra in pass groove 7a for all six diameters are presented in Figure 14.

Figure 14 indicates that a further reduction in roll diameter by 20 mm—starting from a new initial diameter of 425 mm down to 420 mm, 415 mm, and 410 mm—is feasible, with 405 mm representing the limiting diameter for possible reduction. This would allow for an additional 16,000 tons of rolling to be produced using the same rolls.

6. Concluding Remarks

During rolling, friction causes wear in the grooves of the caliber rolls, necessitating turning to restore their shape—an undesirable process that increases operational costs and shortens the rolls’ fatigue life. In this case, roll remachining due to wear was required after 4000 tons of hot-rolled steel, with wear life extending up to 16,000 tons—equivalent to three turning operations, each reducing the roll diameter by 5 mm depending on groove wear, resulting in a total diameter reduction of 15 mm.

Stress analysis showed that a 15 mm reduction in roll diameter results in an approximate 12.2% increase in maximum stress amplitude, rising from 90 MPa to 101 MPa. At this elevated stress level, the number of cycles in the stress spectrum is 53,300—about seven times fewer than the material’s fatigue life of 465,000 cycles. Using Miner’s rule, the estimated fatigue life decreases by approximately 1.5 times, from 3,075,567 to 2,042,000 cycles. Although the fatigue life is significantly reduced, the analysis indicates that fatigue failure should still be avoided under normal operating conditions without overload. Furthermore, the results suggest that additional diameter reduction may still be feasible, as the predicted fatigue life at 101 MPa (2,042,000 cycles) exceeds twice the maximum number of cycles in the stress spectrum (942,155).

Based on the mill’s design, the roll diameter can be reduced from 450 mm to a minimum of 380 mm, in accordance with rolling process requirements. Hardness measurements of the actual roll indicate that such a reduction is feasible. Further analysis confirmed that an additional 20 mm diameter reduction is both feasible and reasonable, making 405 mm the limiting diameter for possible reduction in this case study. This would enable the production of an additional 16,000 tons of rolled steel using the same rolls.

Stress analysis was performed on the middle roll, as it carries twice the load of the upper and lower rolls. For the middle roll, the highest corresponding stresses in pass grooves 3–4 and 7a occur during rolling between the upper and middle rolls in pass grooves 4 and 8, as well as 2 and 6. Since the upper roll’s diameter is 5 mm larger than the middle roll’s, the corresponding stresses in pass groove 3–4 are assumed to be lower. For the same reason, there are no significant stresses in pass groove 7a of the lower roll during rolling in pass grooves 4 and 8, or 2 and 6.

To achieve optimal roll fatigue life and maximize utilization, this type of analysis should be integrated into the roller design process.