Deformation and Energy Absorption Characteristics of Metallic Thin-Walled Tube with Hierarchical Honeycomb Lattice Infills for Crashworthiness Application
Abstract
1. Introduction
2. Materials, Modelling and Methods
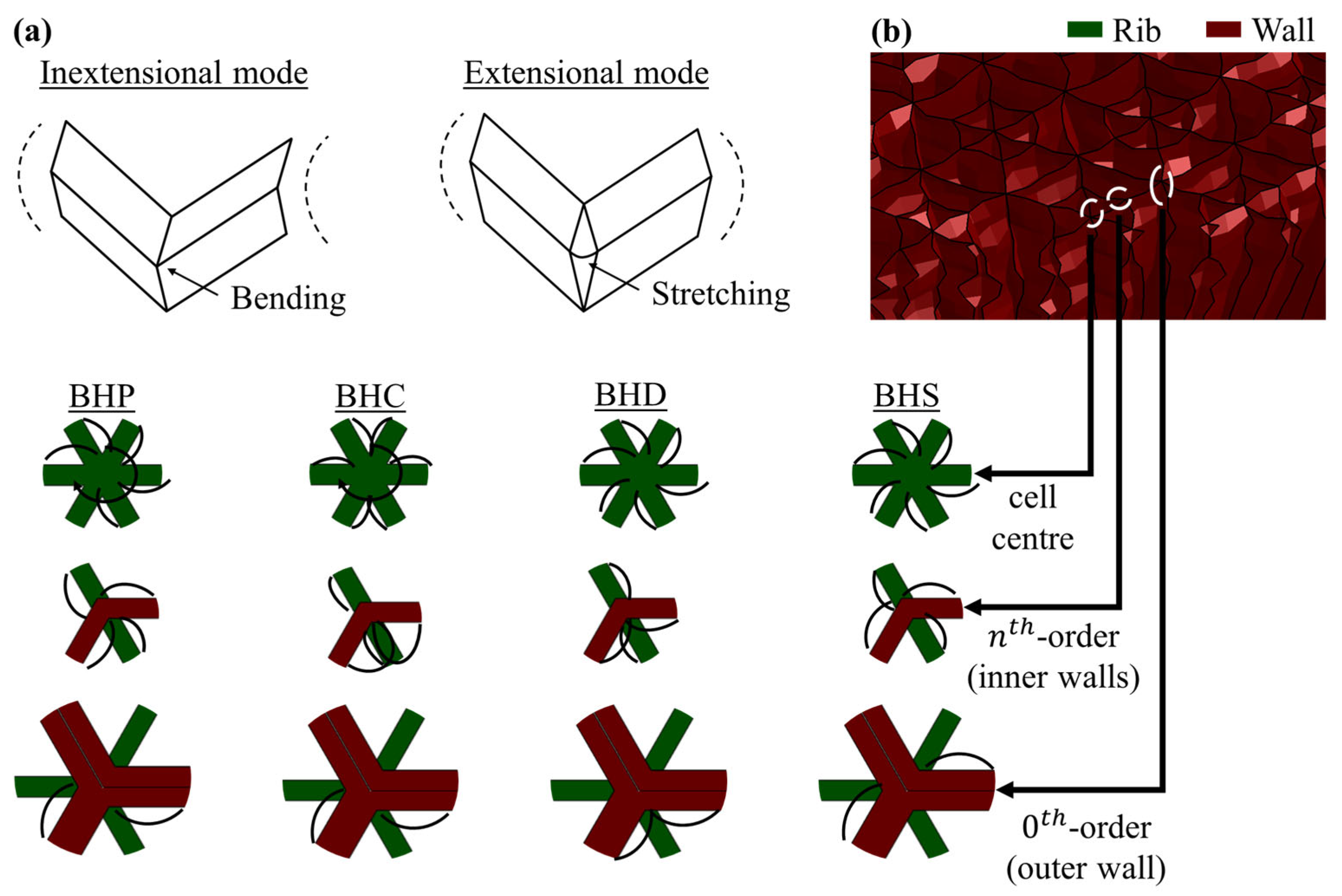
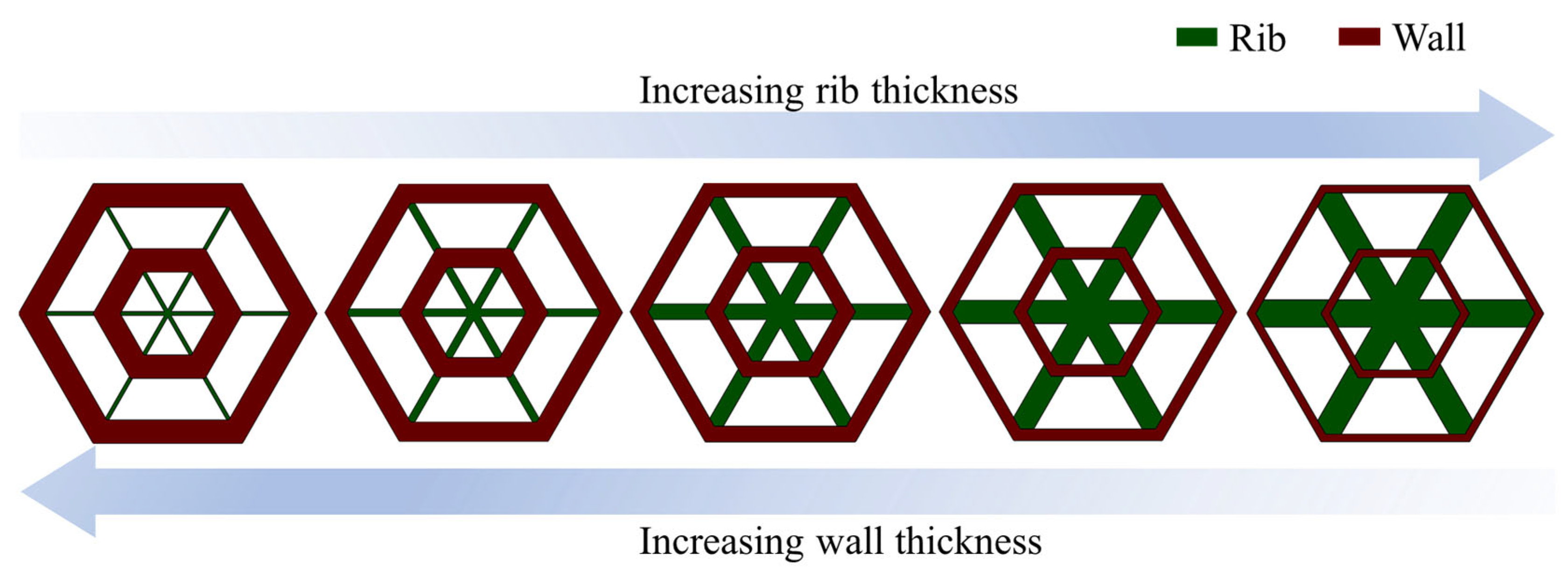
2.1. Design of Hierarchical Honeycomb-Filled Tubes
2.2. Crashworthiness Index
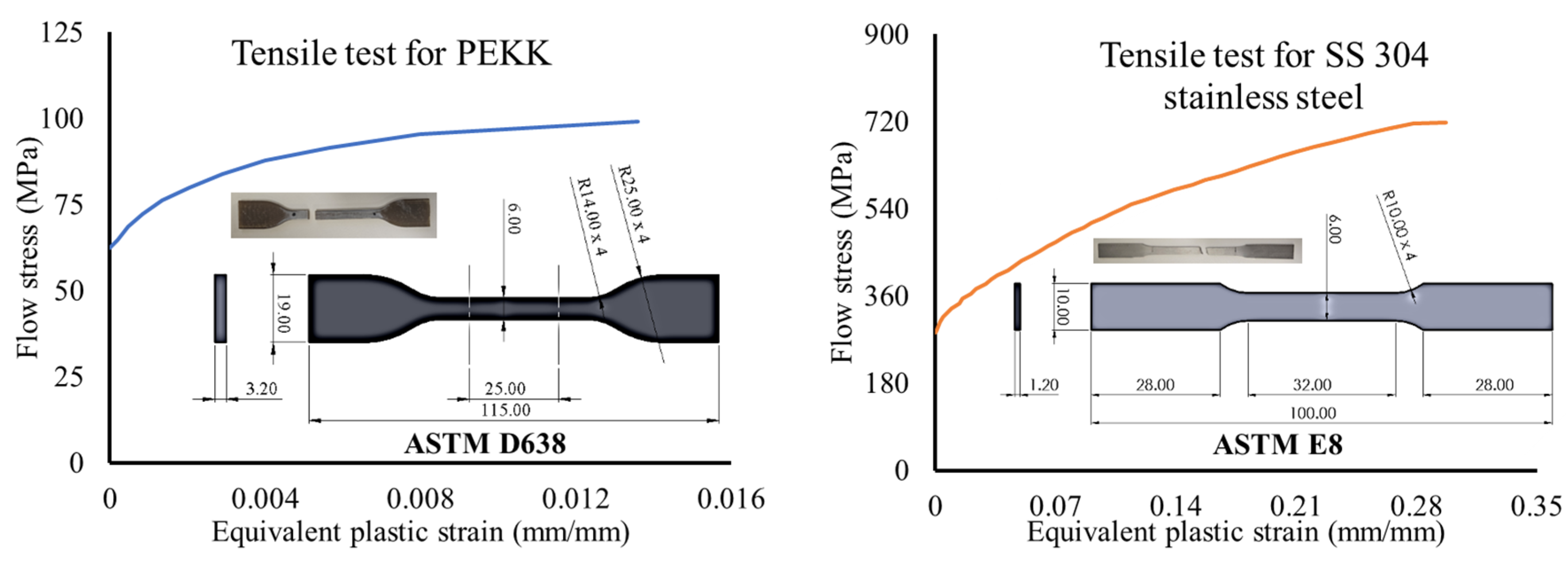
2.3. Materials and Specimens
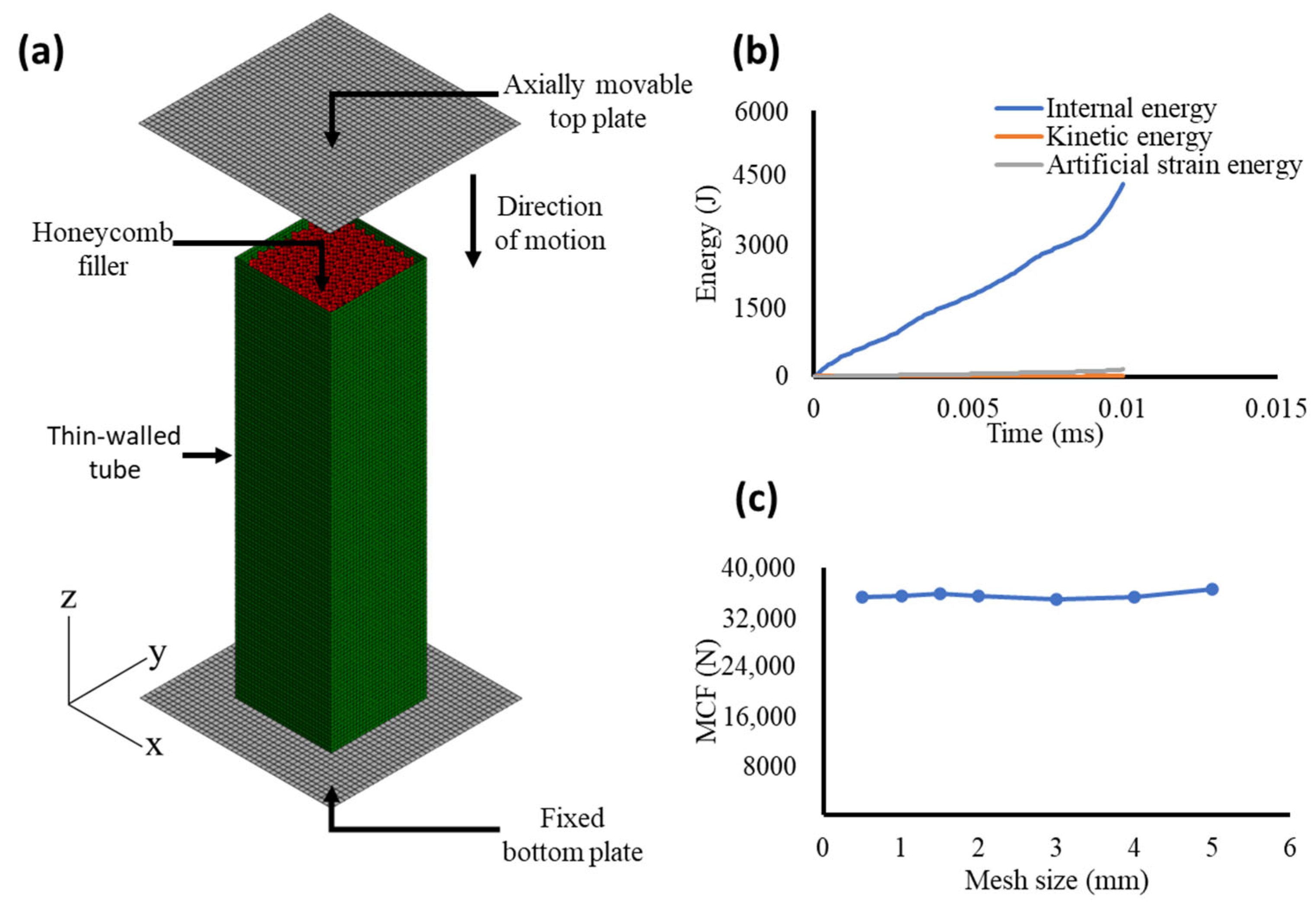
2.4. Numerical Modelling
3. Results and Discussion
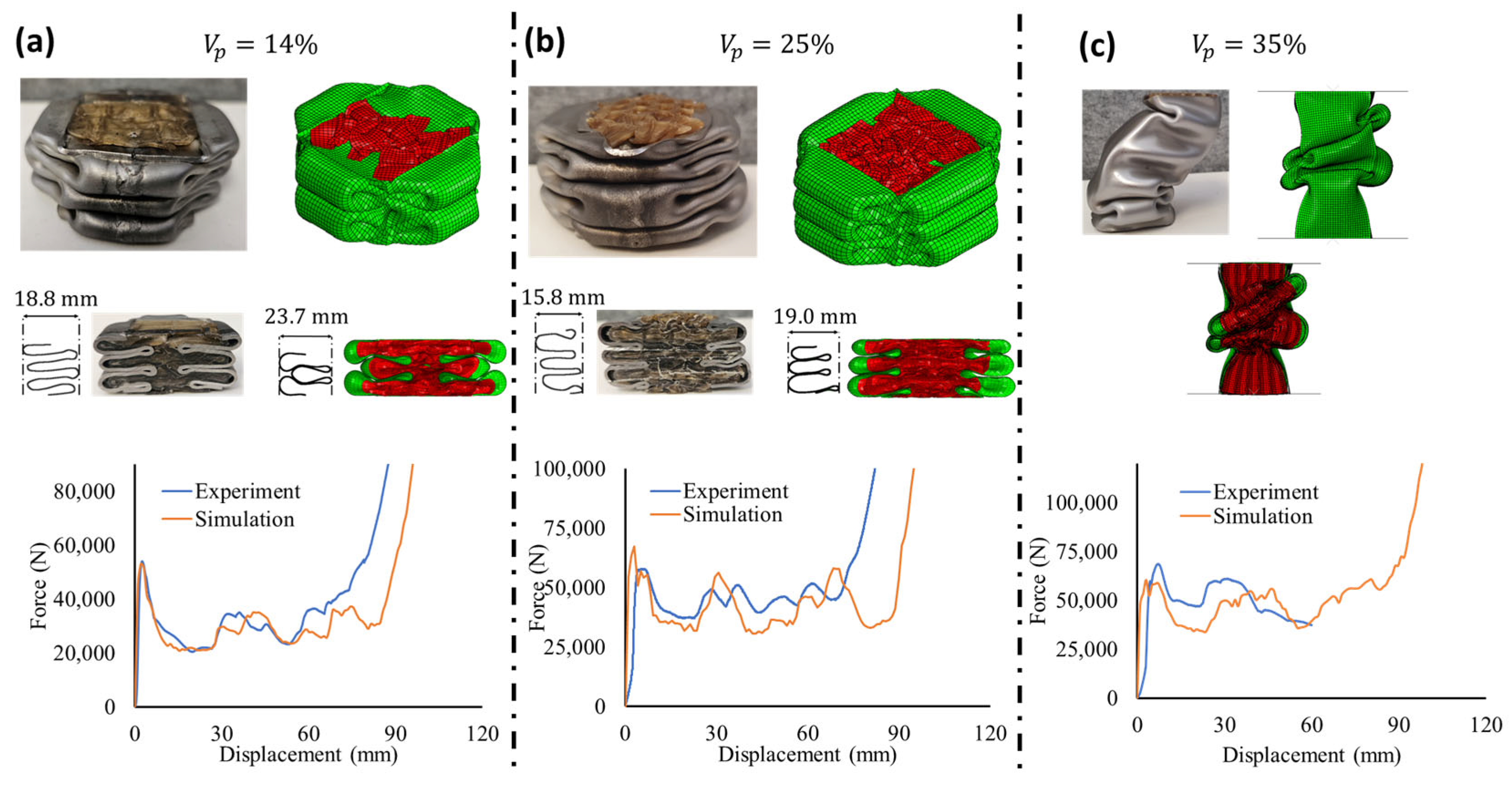
3.1. Crush Test and Numerical Validation
3.2. Deformation Analysis of Hierarchical Honeycomb-Filled Tubes
3.2.1. Deformation of TWT+BHS
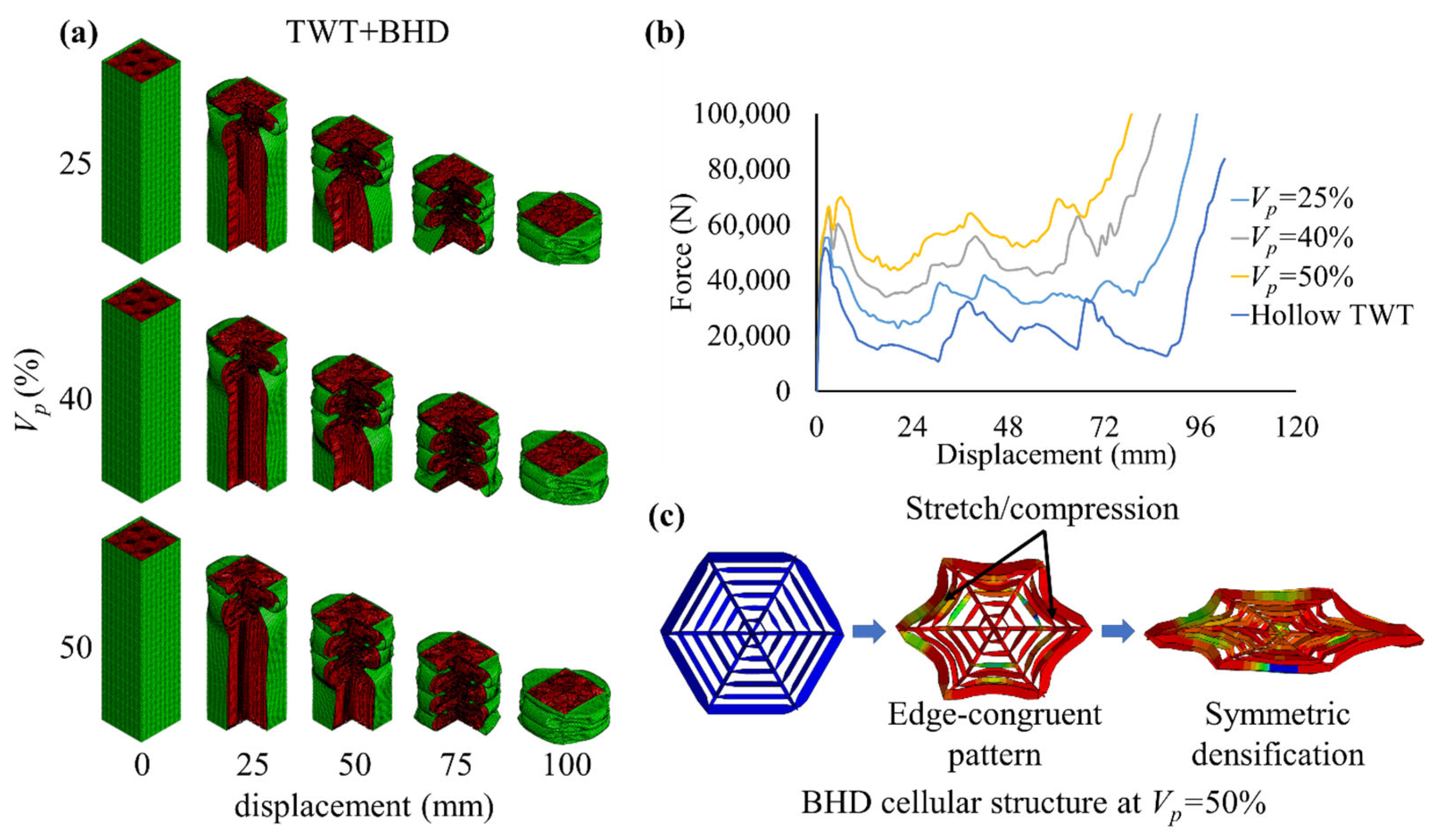
3.2.2. Deformation of TWT+BHD
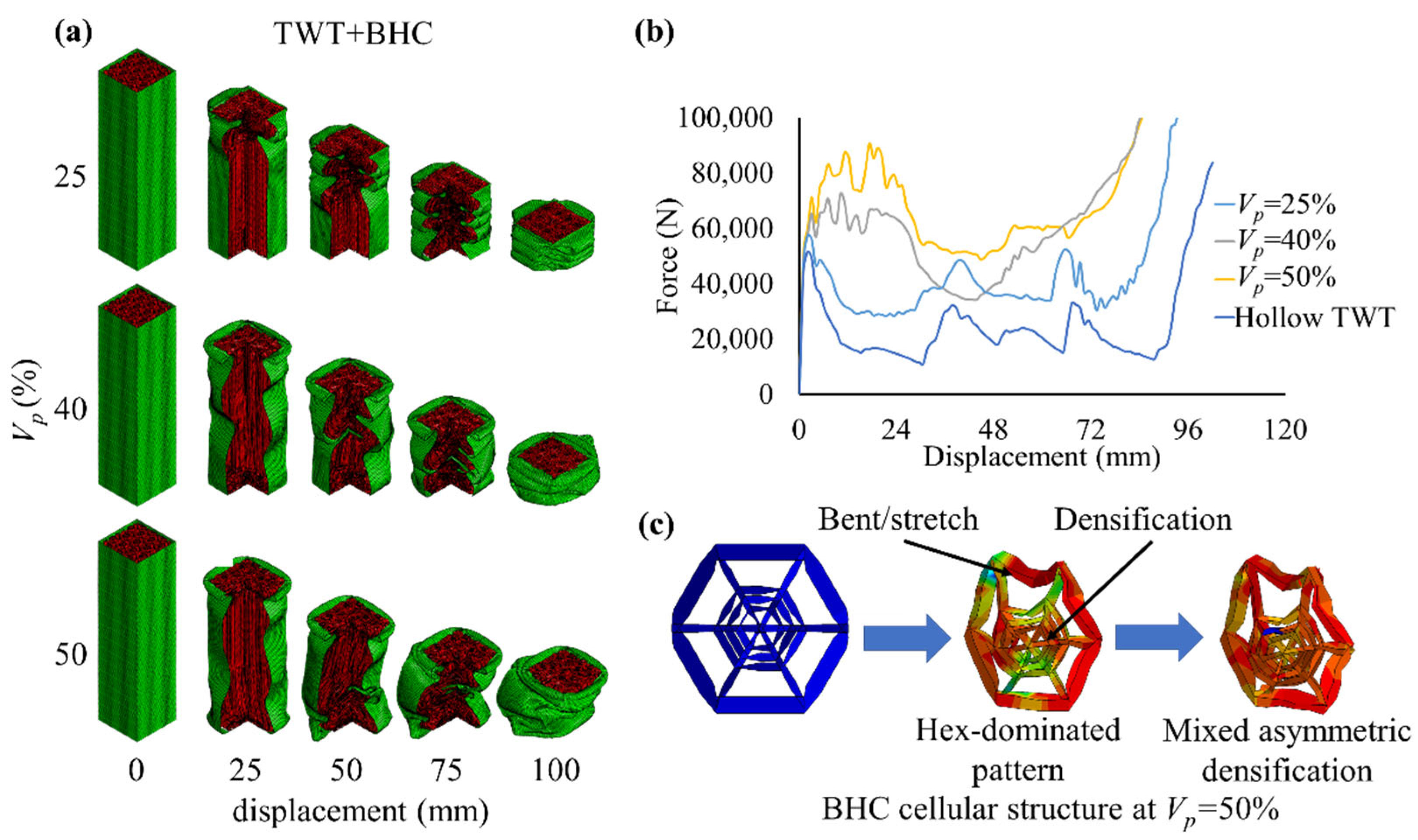
3.2.3. Deformation of TWT+BHC
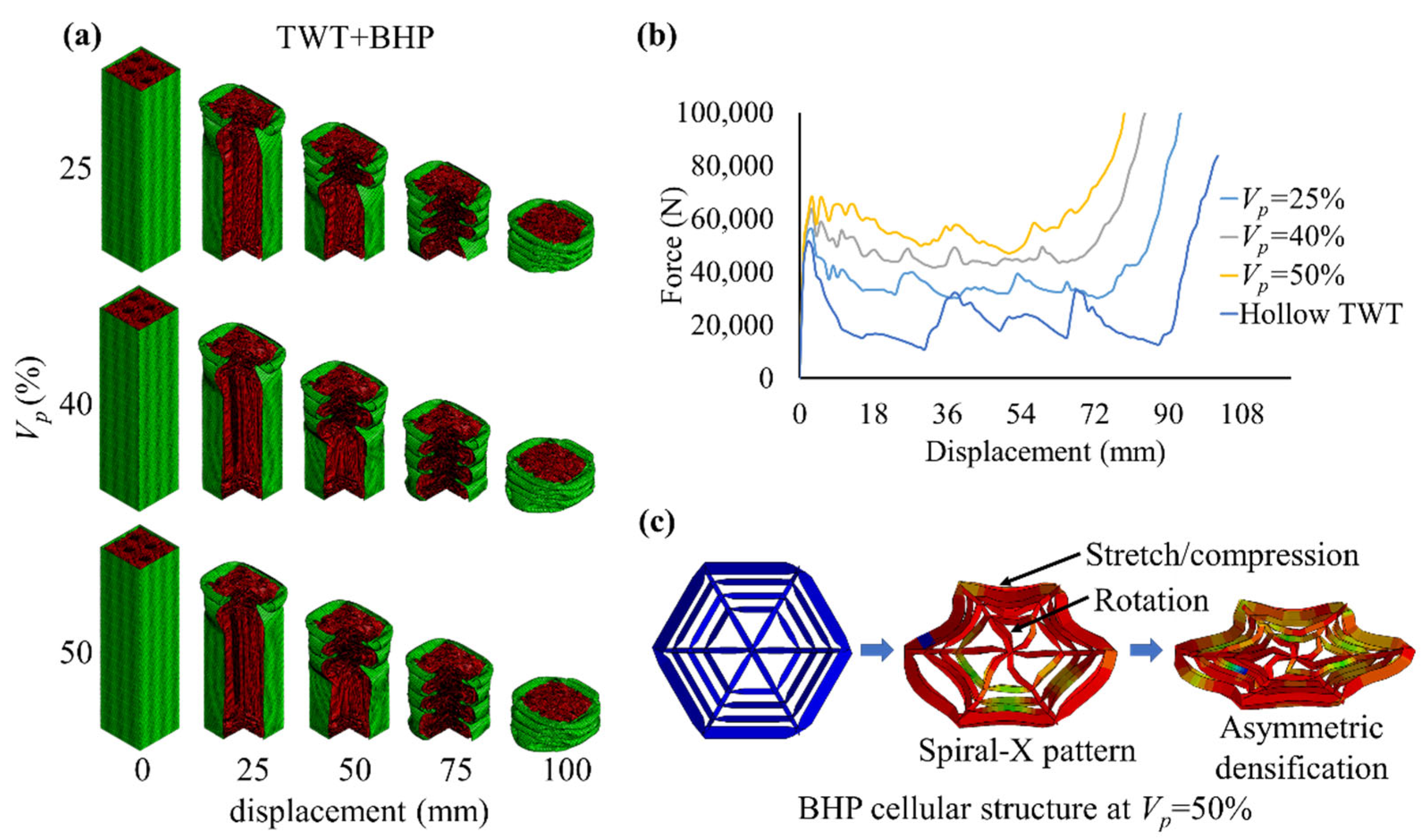
3.2.4. Deformation of TWT+BHP
3.2.5. Deformation Modes of Hierarchical Honeycomb Cells
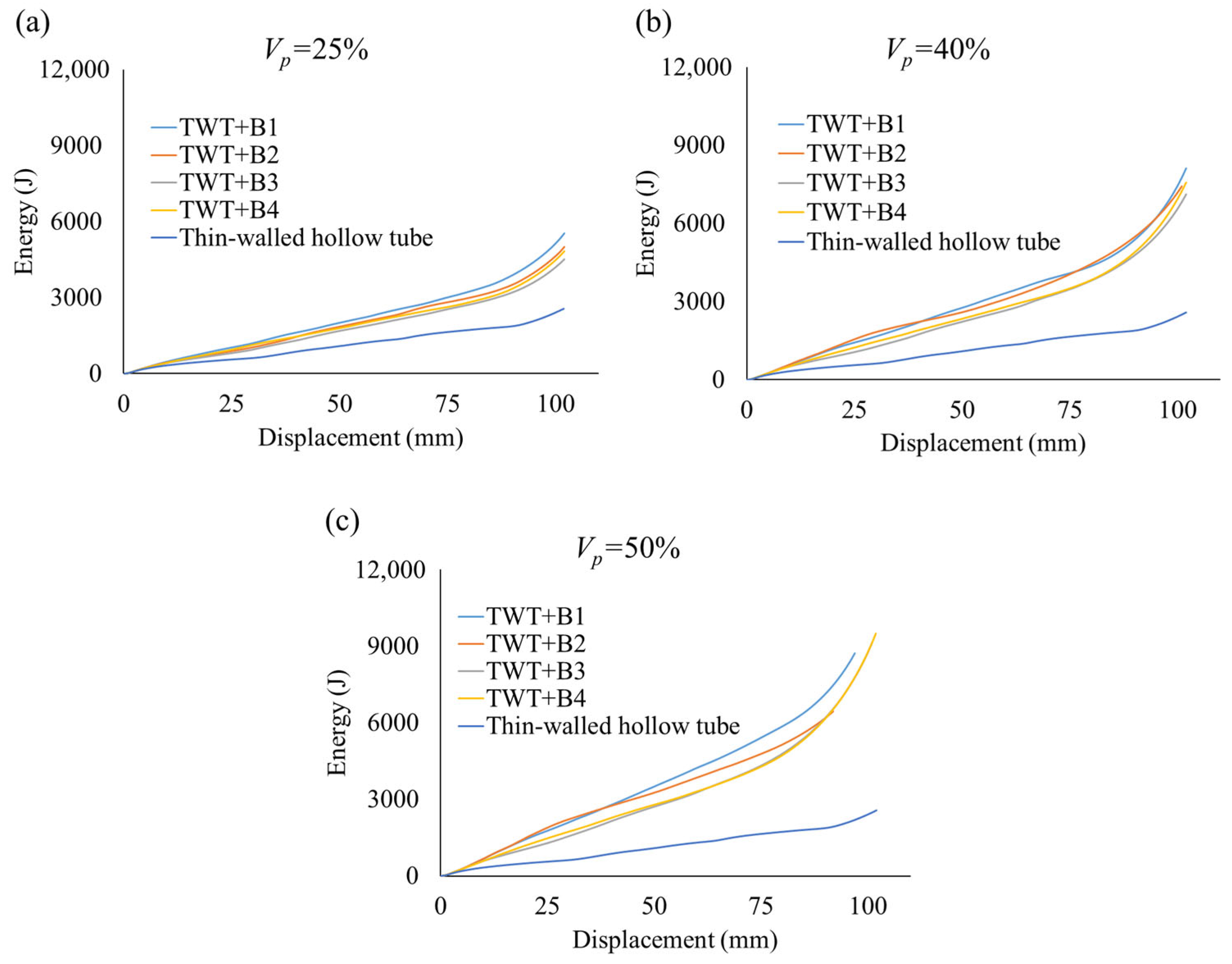
3.3. Crashworthiness Performance Analysis
3.4. Effect of Honeycomb’s Ribs on Crashworthiness of TWT+BHS
3.5. Structural Validation of Hierarchical Honeycomb-Filled Tube
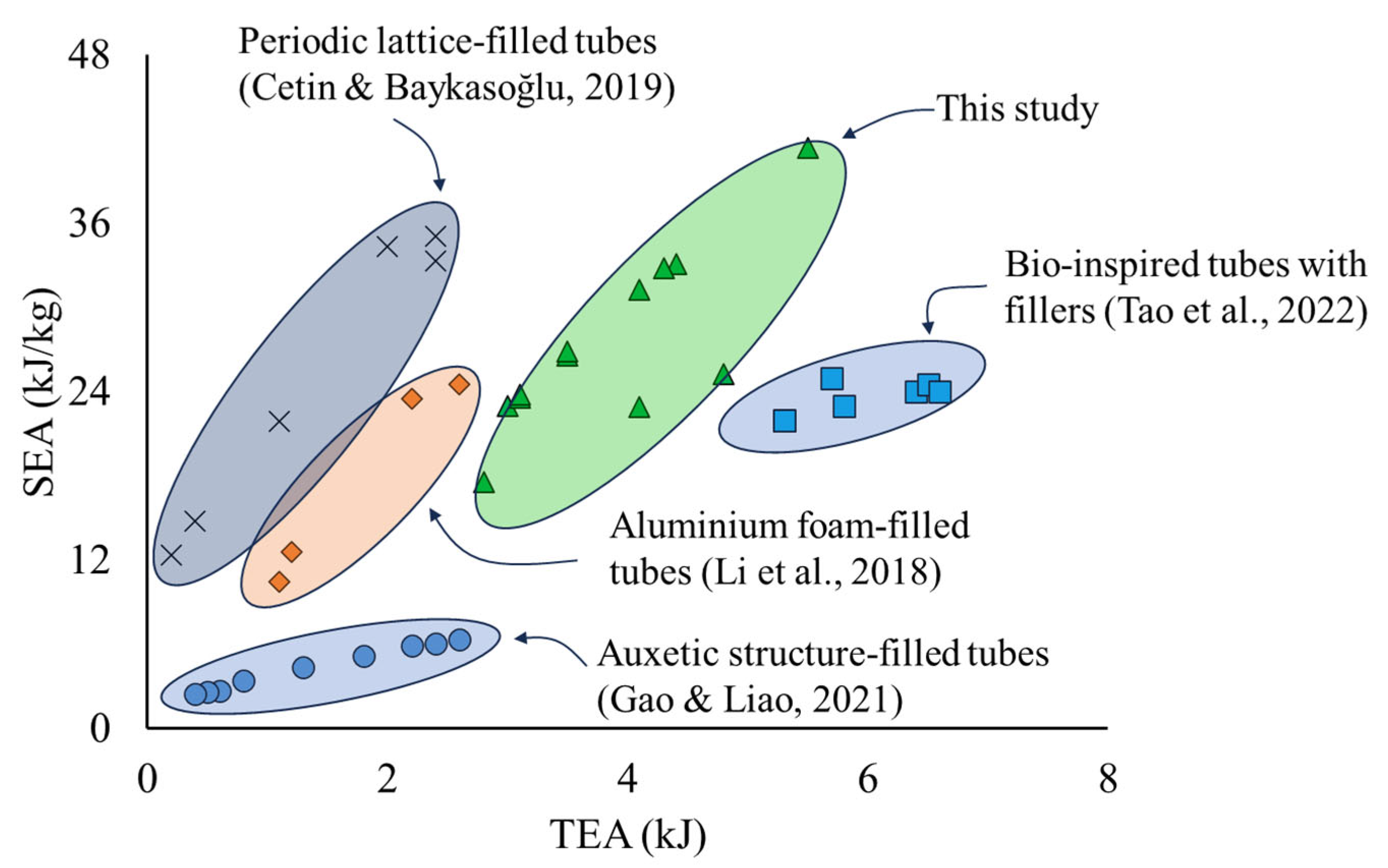
3.6. Crashworthiness Comparison with Existing Designs
4. Conclusions
- The TWT+BHS composite, characterised by the sparse hierarchical distribution of its cellular topology, reached an impressive level of SEA against the hollow TWT of over 202%. Furthermore, the hierarchical topology of this composite was superior to that of the regular honeycomb, as it maintained stable deformation at , while the latter failed at . As doubled from 25% to 50%, it deformed in a symmetric X-shaped pattern and improved its SEA by 80%. Conversely, this pattern corresponded to the low rigidity ratio (high stiffness) of its honeycomb cells, which simultaneously increased its IPF by 52%. It is reiterated that, while a high SEA is crucial for maximising energy absorption during impact, a low IPF is equally critical to minimise occupant injury. Therefore, the multi-criteria crashworthiness indicators require careful consideration during modelling such complex structures.
- Parametric analysis revealed that rib thickness and cell wall thickness affected the performance of the honeycomb-filled tubes. By increasing to and decreasing to , its IPF reduced by 3.7%, while SEA and CFE improved 2.1% and 6.0%, respectively. It can be inferred that fine tuning of these parameters can efficiently address the multi-criteria crashworthiness challenge.
- The TWT+BHC composite, characterised by the central distributed hierarchy of its cellular topology, collapsed in the global bending mode as the cells densified in a hex-dominated pattern. Simultaneously, its IPF inclined sharply, corresponding to low . The unfavourable matching between the honeycomb core and thin-walled tube suggests that the TWT+BHC composite should be avoided in design consideration.
- The TWT+BHD and TWT+BHP with respective dense and peripheral distributed cellular topologies collapsed in stable progressive modes, while their cells deformed in edge congruent and spiral X-pattern. As doubled from 25% to 50%, their SEA gradually elevated by approximately 40%. Their low cellular stiffness corresponding to a high limited the IPF increase to 12% at As a result, their CFE performance improved with . In particular, the ribs of BHP cells participated in energy absorption and hence, its structure was more efficient than the BHD cells.
- As compared to existing honeycomb-filled tubes, the proposed hierarchical honeycomb-filled metallic tubes present as better contenders for crashworthiness improvement. The high-performance PEKK composition of the fillers was extremely effective at enhancing the energy turnover per increase in mass (SEA) while simultaneously increasing the total energy absorption capacity (TEA). However, it should be noted that while the hierarchical honeycomb is an attractive design choice for its superior energy absorption capability and light weight, its cellular geometry directly influences the deformation behaviour when used as a filler for thin-walled tubes. Therefore, careful design consideration is required.
- While a scaled version of the hierarchical BHS honeycomb provides reasonable insight on the complex deformation pattern of the tube, the challenges associated with printing the original dimensions could be mitigated using more sophisticated manufacturing techniques such as Multi Jet Fusion (MJF) or Selective Laser Sintering (SLS). These technologies are tailored towards higher-dimensional accuracy, a better surface finish and improved mechanical performance. Similarly, the filler material can be replaced with metal alloys such as aluminium for low strength or titanium for high strength. These alternatives can be 3D printed with Electron Beam Melting or Laser Powder Bed Fusion which are optimised for producing sophisticated parts with exceptional quality and precision.
- It is important to note that the current study presented in this thesis was limited to the quasi-static crush rate. However, it cannot be considered as a substitute for a dynamic crush study, which is more prevalent during an actual crush scenario. Additional factors, such as the strain rate sensitivity of the material and inertial conditions, could drastically change the deformation kinematics of the filled tube. Our future interest is investigating the effect of PEKK fillers on the dynamic plastic buckling deformation mode of thin-walled tubes, which can trigger a different crush response altogether.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Abbreviations
| TWT | Thin-walled metal tubes |
| TWT+R | Thin-walled metal tube with regular honeycomb infill |
| SEA | Specific energy absorption |
| TEA | Total energy absorption |
| IPF | Initial peak force |
| CFE | Crush force efficiency |
| BHS | Bio-inspired hierarchical sparse honeycomb |
| BHC | Bio-inspired hierarchical central honeycomb |
| BHD | Bio-inspired hierarchical dense honeycomb |
| BHP | Bio-inspired hierarchical peripheral honeycomb |
| TWT+BHS/BHC/BHD/BHP | Thin-walled metal tube with bio-inspired honeycomb infills |
| PEKK | Polyetherketoneketone |
| PEEK | Polyetheretherketone |
| CF | Carbon fibre |
Appendix A

References
- Abramowicz, W.; Jones, N. Dynamic progressive buckling of circular and square tubes. Int. J. Impact Eng. 1986, 4, 243–270. [Google Scholar] [CrossRef]
- Abramowicz, W.; Jones, N. Transition from initial global bending to progressive buckling of tubes loaded statically and dynamically. Int. J. Impact Eng. 1997, 19, 415–437. [Google Scholar] [CrossRef]
- Jones, N. Recent Studies on the Dynamic Plastic Behavior of Structures. Appl. Mech. Rev. 1989, 42, 95–115. [Google Scholar] [CrossRef]
- Karagiozova, D.; Jones, N. Dynamic elastic–plastic buckling of circular cylindrical shells under axial Impact. Int. J. Solids Struct. 2000, 37, 2005–2034. [Google Scholar] [CrossRef]
- Karagiozova, D.; Jones, N. Dynamic buckling of elastic–plastic square tubes under axial impact—II: Structural response. Int. J. Impact Eng. 2004, 30, 167–192. [Google Scholar] [CrossRef]
- Wierzbicki, T.; Abramowicz, W. On the Crushing Mechanics of Thin-Walled Structures. J. Appl. Mech. 1983, 50, 727–734. [Google Scholar] [CrossRef]
- Hayduk, R.J.; Wierzbicki, T. Extensional collapse modes of structural members. Comput. Struct. 1984, 18, 447–458. [Google Scholar] [CrossRef]
- Abramowicz, W.; Jones, N. Dynamic axial crushing of square tubes. Int. J. Impact Eng. 1984, 2, 179–208. [Google Scholar] [CrossRef]
- Sun, G.; Pang, T.; Xu, C.; Zheng, G.; Song, J. Energy absorption mechanics for variable thickness thin-walled structures. Thin-Walled Struct. 2017, 118, 214–228. [Google Scholar] [CrossRef]
- Nia, A.A.; Parsapour, M. Comparative analysis of energy absorption capacity of simple and multi-cell thin-walled tubes with triangular, square, hexagonal and octagonal sections. Thin-Walled Struct. 2014, 74, 155–165. [Google Scholar] [CrossRef]
- Wu, S.; Zheng, G.; Sun, G.; Liu, Q.; Li, G.; Li, Q. On design of multi-cell thin-wall structures for crashworthiness. Int. J. Impact Eng. 2016, 88, 102–117. [Google Scholar] [CrossRef]
- Altin, M.; Kılınçkaya, Ü.; Acar, E.; Güler, M.A. Investigation of combined effects of cross section, taper angle and cell structure on crashworthiness of multi-cell thin-walled tubes. Int. J. Crashworthiness 2019, 24, 121–136. [Google Scholar] [CrossRef]
- Patel, V.; Tiwari, G.; Dumpala, R. Crashworthiness analysis of multi-configuration thin walled co-axial frusta tube structures under quasi-static loading. Thin-Walled Struct. 2020, 154, 106872. [Google Scholar] [CrossRef]
- Vinayagar, K.; Kumar, A.S. Crashworthiness analysis of double section bi-tubular thin-walled structures. Thin-Walled Struct. 2017, 112, 184–193. [Google Scholar] [CrossRef]
- Yang, X.; Ma, J.; Sun, Y.; Yang, J. An internally nested circular-elliptical tube system for energy absorption. Thin-Walled Struct. 2019, 139, 281–293. [Google Scholar] [CrossRef]
- Baroutaji, A.; Sajjia, M.; Olabi, A.-G. On the crashworthiness performance of thin-walled energy absorbers: Recent advances and future developments. Thin-Walled Struct. 2017, 118, 137–163. [Google Scholar] [CrossRef]
- Wang, Z. Recent advances in novel metallic honeycomb structure. Compos. Part B Eng. 2019, 166, 731–741. [Google Scholar] [CrossRef]
- Thomas, T.; Tiwari, G. Crushing behavior of honeycomb structure: A review. Int. J. Crashworthiness 2019, 24, 555–579. [Google Scholar] [CrossRef]
- Hussein, R.D.; Ruan, D.; Lu, G.; Guillow, S.; Yoon, J.W. Crushing response of square aluminium tubes filled with polyurethane foam and aluminium honeycomb. Thin-Walled Struct. 2017, 110, 140–154. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, S.; Lu, Z.; Hui, D.; Feo, L. Matching effect of honeycomb-filled thin-walled square tube—Experiment and simulation. Compos. Struct. 2016, 157, 494–505. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, X.; Lu, M.; Hu, Z.; Ge, P. Enhance crashworthiness of composite structures using gradient honeycomb material. Int. J. Crashworthiness 2018, 23, 569–580. [Google Scholar] [CrossRef]
- Zhu, G.; Li, S.; Sun, G.; Li, G.; Li, Q. On design of graded honeycomb filler and tubal wall thickness for multiple load cases. Thin-Walled Struct. 2016, 109, 377–389. [Google Scholar] [CrossRef]
- Tao, Y.; Wang, Y.; He, Q.; Xu, D.; Li, L. Comparative Study and Multi-Objective Crashworthiness Optimization Design of Foam and Honeycomb-Filled Novel Aluminum Thin-Walled Tubes. Metals 2022, 12, 2163. [Google Scholar] [CrossRef]
- Xie, S.; Wang, H.; Yang, C.; Zhou, H.; Feng, Z. Mechanical properties of combined structures of stacked multilayer Nomex® honeycombs. Thin-Walled Struct. 2020, 151, 106729. [Google Scholar] [CrossRef]
- Liu, Y.; Luo, D.; Wang, T. Hierarchical Structures of Bone and Bioinspired Bone Tissue Engineering. Small 2016, 12, 4611–4632. [Google Scholar] [CrossRef]
- Reznikov, N.; Bilton, M.; Lari, L.; Stevens, M.M.; Kröger, R. Fractal-like hierarchical organization of bone begins at the nanoscale. Science 2018, 360, eaao2189. [Google Scholar] [CrossRef]
- Tsang, H.H.; Raza, S. Impact energy absorption of bio-inspired tubular sections with structural hierarchy. Compos. Struct. 2018, 195, 199–210. [Google Scholar] [CrossRef]
- Wang, X.; Fang, J.; Zhu, W.; Zhong, C.; Ye, D.; Zhu, M.; Lu, X.; Zhao, Y.; Ren, F. Bioinspired Highly Anisotropic, Ultrastrong and Stiff, and Osteoconductive Mineralized Wood Hydrogel Composites for Bone Repair. Adv. Funct. Mater. 2021, 31, 2010068. [Google Scholar] [CrossRef]
- Ajdari, A.; Jahromi, B.H.; Papadopoulos, J.; Nayeb-Hashemi, H.; Vaziri, A. Hierarchical honeycombs with tailorable properties. Int. J. Solids Struct. 2012, 49, 1413–1419. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Z.; Shi, C.; Zhou, W. Theoretical and numerical analysis of the folding mechanism of vertex-based hierarchical honeycomb structure. Mech. Adv. Mater. Struct. 2020, 27, 789–799. [Google Scholar] [CrossRef]
- Yin, H.; Huang, X.; Scarpa, F.; Wen, G.; Chen, Y.; Zhang, C. In-plane crashworthiness of bio-inspired hierarchical honeycombs. Compos. Struct. 2018, 192, 516–527. [Google Scholar] [CrossRef]
- Zhan, C.; Li, M.; McCoy, R.; Zhao, L.; Lu, W. 3D printed hierarchical re-entrant honeycombs: Enhanced mechanical properties and the underlying deformation mechanisms. Compos. Struct. 2022, 290, 115550. [Google Scholar] [CrossRef]
- Gosline, J.M.; DeMont, M.E.; Denny, M.W. The structure and properties of spider silk. Endeavour 1986, 10, 37–43. [Google Scholar] [CrossRef]
- Ko, F.K.; Jovicic, J. Modeling of Mechanical Properties and Structural Design of Spider Web. Biomacromolecules 2004, 5, 780–785. [Google Scholar] [CrossRef] [PubMed]
- Mousanezhad, D.; Ebrahimi, H.; Haghpanah, B.; Ghosh, R.; Ajdari, A.; Hamouda, A.M.S.; Vaziri, A. Spiderweb honeycombs. Int. J. Solids Struct. 2015, 66, 218–227. [Google Scholar] [CrossRef]
- He, Q.; Feng, J.; Chen, Y.; Zhou, H. Mechanical properties of spider-web hierarchical honeycombs subjected to out-of-plane impact loading. J. Sandw. Struct. Mater. 2020, 22, 771–796. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J.; Li, Z.; Shi, C. On the crashworthiness of bio-inspired hexagonal prismatic tubes under axial compression. Int. J. Mech. Sci. 2020, 186, 105893. [Google Scholar] [CrossRef]
- Akman, A.; Sadhu, A. Recent Development of 3D-Printing Technology in Construction Engineering. Pract. Period. Struct. Des. Constr. 2024, 29, 03123005. [Google Scholar] [CrossRef]
- Ford, S.; Despeisse, M. Additive manufacturing and sustainability: An exploratory study of the advantages and challenges. J. Clean. Prod. 2016, 137, 1573–1587. [Google Scholar] [CrossRef]
- Nian, Y.; Wan, S.; Li, M.; Su, Q. Crashworthiness design of self-similar graded honeycomb-filled composite circular structures. Constr. Build. Mater. 2020, 233, 117344. [Google Scholar] [CrossRef]
- Zhang, X.G.; Jiang, W.; Zhang, Y.; Luo, C.; Zhang, X.Y.; Han, D.; Hao, J.; Teng, X.C.; Xie, Y.M.; Ren, X. Energy absorption properties of composite tubes with hexagonal and re-entrant honeycomb fillers. Constr. Build. Mater. 2022, 356, 129298. [Google Scholar] [CrossRef]
- Alkhatib, S.E.; Matar, M.S.; Tarlochan, F.; Laban, O.; Mohamed, A.S.; Alqwasmi, N. Deformation modes and crashworthiness energy absorption of sinusoidally corrugated tubes manufactured by direct metal laser sintering. Eng. Struct. 2019, 201, 109838. [Google Scholar] [CrossRef]
- Hussein, R.D.; Ruan, D.; Lu, G.; Sbarski, I. Axial crushing behaviour of honeycomb-filled square carbon fibre reinforced plastic (CFRP) tubes. Compos. Struct. 2016, 140, 166–179. [Google Scholar] [CrossRef]
- Sun, G.; Li, S.; Liu, Q.; Li, G.; Li, Q. Experimental study on crashworthiness of empty/aluminum foam/honeycomb-filled CFRP tubes. Compos. Struct. 2016, 152, 969–993. [Google Scholar] [CrossRef]
- Nassir, N.A.; Birch, R.S.; Cantwell, W.J.; Guan, Z.W. The response of glass fibre reinforced PEKK laminates subjected to single and multiple impact loading. Polym. Test. 2024, 131, 108323. [Google Scholar] [CrossRef]
- Derisi, B.; Hoa, S.V.; Xu, D.; Hojjati, M.; Fews, R. Mechanical Behavior of Carbon/PEKK Thermoplastic Composite Tube Under Bending Load. J. Thermoplast. Compos. Mater. 2011, 24, 29–49. [Google Scholar] [CrossRef]
- Wiese, M.; Thiede, S.; Herrmann, C. Rapid manufacturing of automotive polymer series parts: A systematic review of processes, materials and challenges. Addit. Manuf. 2020, 36, 101582. [Google Scholar] [CrossRef]
- Chattaraj, S.; Basu, S. Coarse-graining strategies for predicting properties of closely related polymer architectures: A case study of PEEK and PEKK. J. Mater. Res. 2022, 37, 1–12. [Google Scholar] [CrossRef]
- Nachtane, M.; Tarfaoui, M.; Ledoux, Y.; Khammassi, S.; Leneveu, E.; Pelleter, J. Experimental investigation on the dynamic behavior of 3D printed CF-PEKK composite under cyclic uniaxial compression. Compos. Struct. 2020, 247, 112474. [Google Scholar] [CrossRef]
- Andrew, J.J.; Alhashmi, H.; Schiffer, A.; Kumar, S.; Deshpande, V.S. Energy absorption and self-sensing performance of 3D printed CF/PEEK cellular composites. Mater. Des. 2021, 208, 109863. [Google Scholar] [CrossRef]
- He, P.; Wang, S.; Zhang, M.; Sang, L.; Tong, L.; Hou, W. Compression performance of 3D-printed thermoplastic auxetic structures. Thin-Walled Struct. 2024, 197, 111558. [Google Scholar] [CrossRef]
- ASTM D638-14; D20 Committee, Test Method for Tensile Properties of Plastics. ASTM: West Conshohocken, PA, USA, 2022. [CrossRef]
- ASTM E8/E8M-22; E28 Committee, Test Methods for Tension Testing of Metallic Materials. ASTM: West Conshohocken, PA, USA, 2022. [CrossRef]
- Lin, X.; Zhang, Y.X.; Pathak, P. Nonlinear Finite Element Analysis of Composite and Reinforced Concrete Beams; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar] [CrossRef]
- Yahiaoui, M.; Chabert, F.; Paris, J.-Y.; Nassiet, V.; Denape, J. Friction, acoustic emission, and wear mechanisms of a PEKK polymer. Tribol. Int. 2019, 132, 154–164. [Google Scholar] [CrossRef]
- Hu, Y.; Rong, B.; Zhang, R.; Zhang, Y.; Zhang, S. Study of buckling behavior for 7A04-T6 aluminum alloy rectangular hollow columns. Thin-Walled Struct. 2021, 169, 108410. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- Zhong, H.; Song, T.; Li, C.; Das, R.; Gu, J.; Qian, M. The Gibson-Ashby model for additively manufactured metal lattice materials: Its theoretical basis, limitations and new insights from remedies. Curr. Opin. Solid State Mater. Sci. 2023, 27, 101081. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, H.; Zhang, Q.; Ma, J.; Yang, X.; Yang, J. Energy absorption characteristics of a super hexagonal honeycomb under out-of-plane crushing. Thin-Walled Struct. 2023, 189, 110914. [Google Scholar] [CrossRef]
- Cetin, E.; Baykasoğlu, C. Energy absorption of thin-walled tubes enhanced by lattice structures. Int. J. Mech. Sci. 2019, 157–158, 471–484. [Google Scholar] [CrossRef]
- Gao, Q.; Liao, W.-H. Energy absorption of thin walled tube filled with gradient auxetic structures-theory and simulation. Int. J. Mech. Sci. 2021, 201, 106475. [Google Scholar] [CrossRef]
- Li, Z.; Chen, R.; Lu, F. Comparative analysis of crashworthiness of empty and foam-filled thin-walled tubes. Thin-Walled Struct. 2018, 124, 343–349. [Google Scholar] [CrossRef]
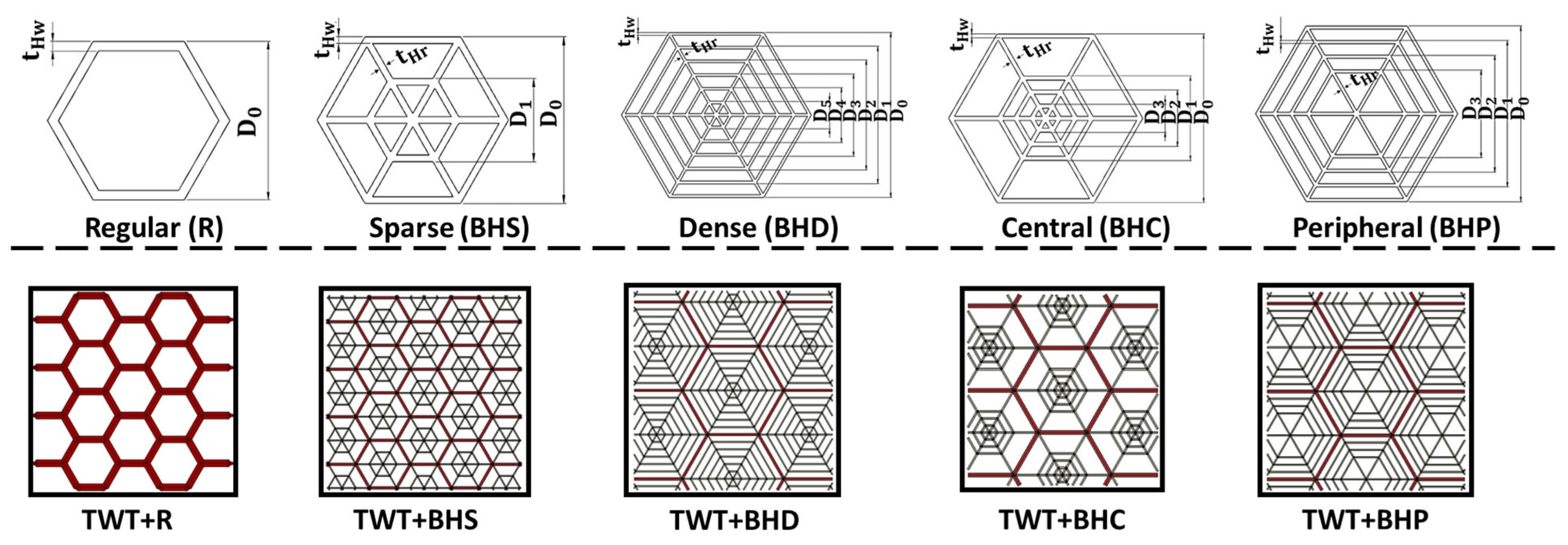
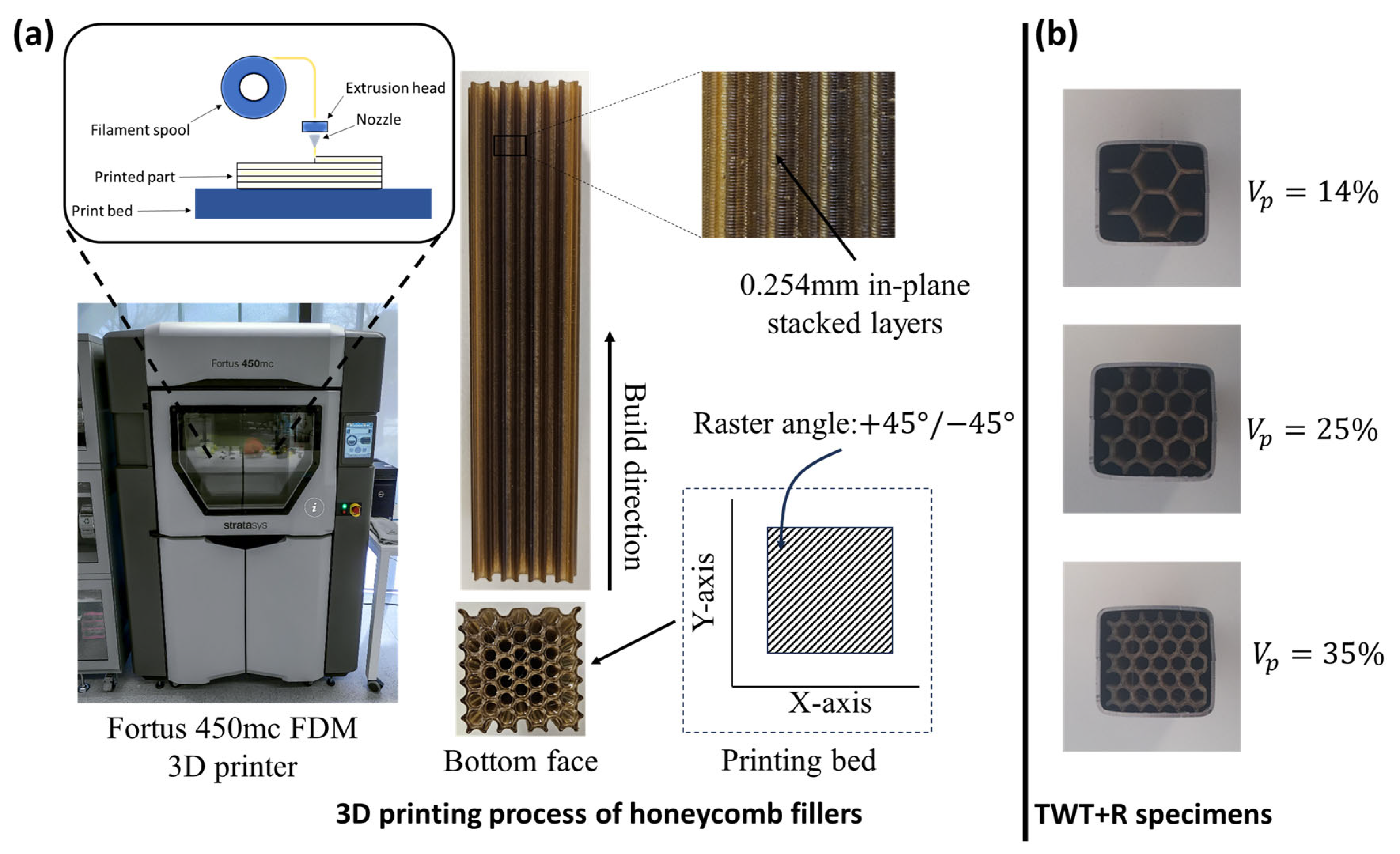



| Model | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (%) | |
|---|---|---|---|---|---|---|---|---|---|---|
| Regular (R) | 0.5 | - | 12 | - | - | - | - | - | 24 | 14 |
| Regular (R) | 0.5 | - | 6.6 | - | - | - | - | - | 13 | 25 |
| Regular (R) | 0.5 | - | 5 | - | - | - | - | - | 10 | 35 |
| Sparse (BHS) | 0.2 | 0.2 | 6.6 | 3.3 | - | - | - | - | 25 | 25 |
| Dense (BHD) | 0.2 | 0.2 | 12 | 10 | 8 | 6 | 4 | 2 | 35 | 25 |
| Central (BHC) | 0.2 | 0.2 | 8 | 4 | 3 | 2 | - | - | 21 | 25 |
| Peripheral (BHP) | 0.2 | 0.2 | 12 | 10 | 8 | 6 | - | - | 45 | 25 |
| Sparse (BHS) | 0.3 | 0.3 | 6.6 | 3.3 | - | - | - | - | 17 | 40 |
| Dense (BHD) | 0.3 | 0.3 | 12 | 10 | 8 | 6 | 4 | 2 | 23 | 40 |
| Central (BHC) | 0.3 | 0.3 | 8 | 4 | 3 | 2 | - | - | 14 | 40 |
| Peripheral (BHP) | 0.3 | 0.3 | 12 | 10 | 8 | 6 | - | - | 30 | 40 |
| Sparse (BHS) | 0.4 | 0.4 | 6.6 | 3.3 | - | - | - | - | 12 | 50 |
| Dense (BHD) | 0.4 | 0.4 | 12 | 10 | 8 | 6 | 4 | 2 | 18 | 50 |
| Central (BHC) | 0.4 | 0.4 | 8 | 4 | 3 | 2 | - | - | 11 | 50 |
| Peripheral (BHP) | 0.4 | 0.4 | 12 | 10 | 8 | 6 | - | - | 23 | 50 |
| Specimen | Young’s Modulus (GPa) | Yield Strength (MPa) | Ultimate Tensile Strength (MPa) |
|---|---|---|---|
| PEKK | 1.67 | 62.4 | 99 |
| SS 304 | 191 | 283 | 657 |
| Model | (%) | SEA (J/kg) | IPF (N) | CFE (%) | |
|---|---|---|---|---|---|
| Hollow TWT | - | - | 13,700 | 51,481 | 41 |
| TWT+BHS | 25 | 25 | 23,049 | 58,897 | 69 |
| 40 | 17 | 31,262 | 68,445 | 80 | |
| 50 | 12 | 41,436 | 89,696 | 81 | |
| TWT+BHD | 25 | 35 | 23,551 | 61,983 | 62 |
| 40 | 23 | 26,623 | 65,056 | 72 | |
| 50 | 18 | 33,114 | 69,780 | 83 | |
| TWT+BHC | 25 | 21 | 17,614 | 57,455 | 66 |
| 40 | 23 | 22,921 | 72,576 | 75 | |
| 50 | 11 | 25,313 | 90,593 | 71 | |
| TWT+BHP | 25 | 45 | 23,817 | 61,307 | 63 |
| 40 | 30 | 26,887 | 63,767 | 74 | |
| 50 | 23 | 32,783 | 68,369 | 84 |
| Model | (%) | (mm) | (mm) | SEA (kJ/kg) | IPF (kN) | CFE (%) |
|---|---|---|---|---|---|---|
| TWT+BHS | 50 | 0.10 | 0.60 | 22.6 | 75.8 | 75.5 |
| 50 | 0.20 | 0.50 | 25.2 | 82.9 | 76.9 | |
| 50 | 0.40 | 0.40 | 28.7 | 89.7 | 81.1 | |
| 50 | 0.60 | 0.30 | 29.3 | 86.4 | 86.0 | |
| 50 | 0.70 | 0.20 | 27.7 | 83.8 | 83.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alam, S.; Uddin, M.; Hall, C. Deformation and Energy Absorption Characteristics of Metallic Thin-Walled Tube with Hierarchical Honeycomb Lattice Infills for Crashworthiness Application. Metals 2025, 15, 629. https://doi.org/10.3390/met15060629
Alam S, Uddin M, Hall C. Deformation and Energy Absorption Characteristics of Metallic Thin-Walled Tube with Hierarchical Honeycomb Lattice Infills for Crashworthiness Application. Metals. 2025; 15(6):629. https://doi.org/10.3390/met15060629
Chicago/Turabian StyleAlam, Shahrukh, Mohammad Uddin, and Colin Hall. 2025. "Deformation and Energy Absorption Characteristics of Metallic Thin-Walled Tube with Hierarchical Honeycomb Lattice Infills for Crashworthiness Application" Metals 15, no. 6: 629. https://doi.org/10.3390/met15060629
APA StyleAlam, S., Uddin, M., & Hall, C. (2025). Deformation and Energy Absorption Characteristics of Metallic Thin-Walled Tube with Hierarchical Honeycomb Lattice Infills for Crashworthiness Application. Metals, 15(6), 629. https://doi.org/10.3390/met15060629







