Hot Isostatic Pressing Synthesis of Al-Ta Energetic Structural Material Based on Modified Drucker–Prager Cap Model
Abstract
1. Introduction
2. Model and Experiment
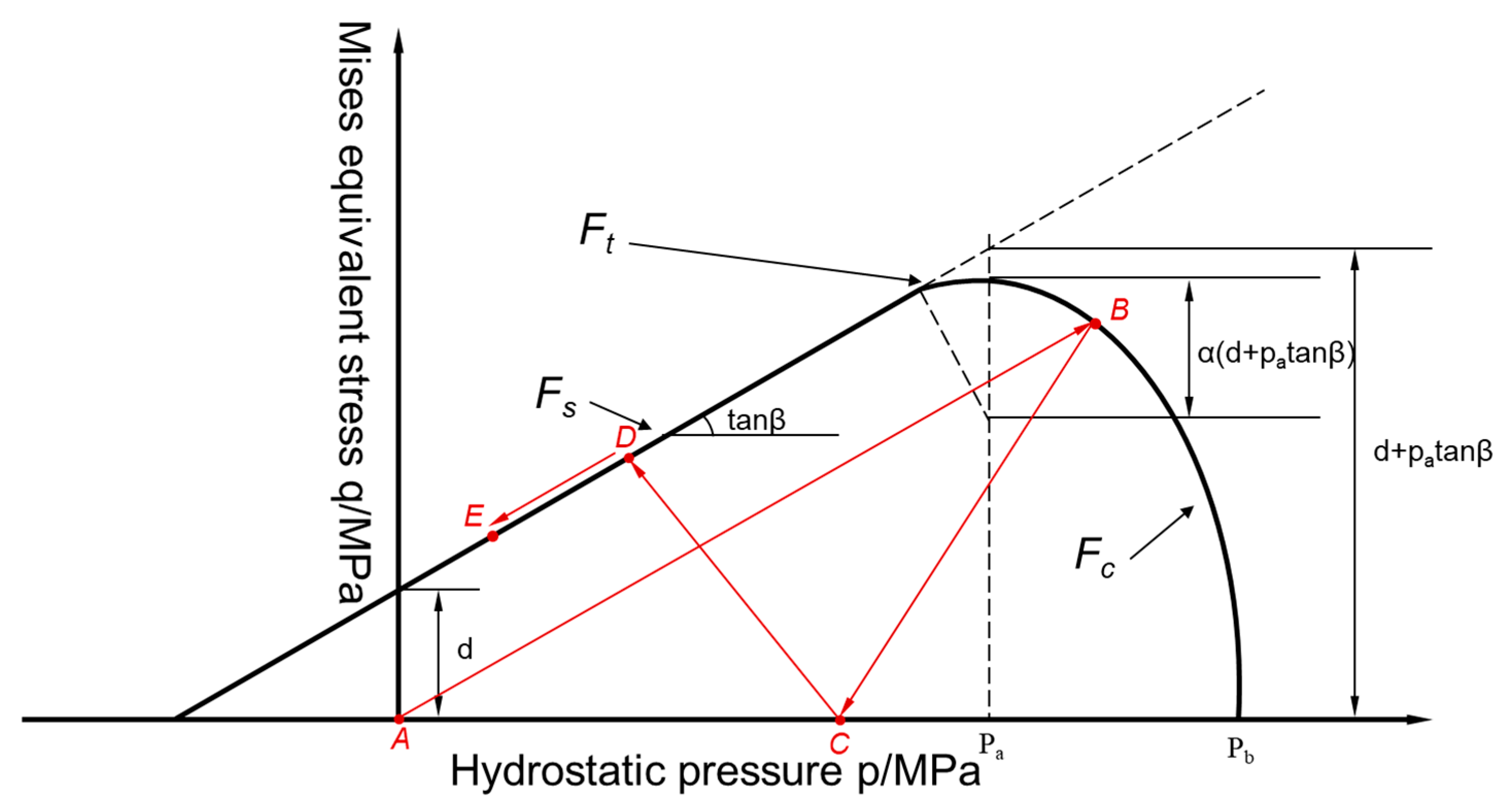
2.1. Modified DPC Model
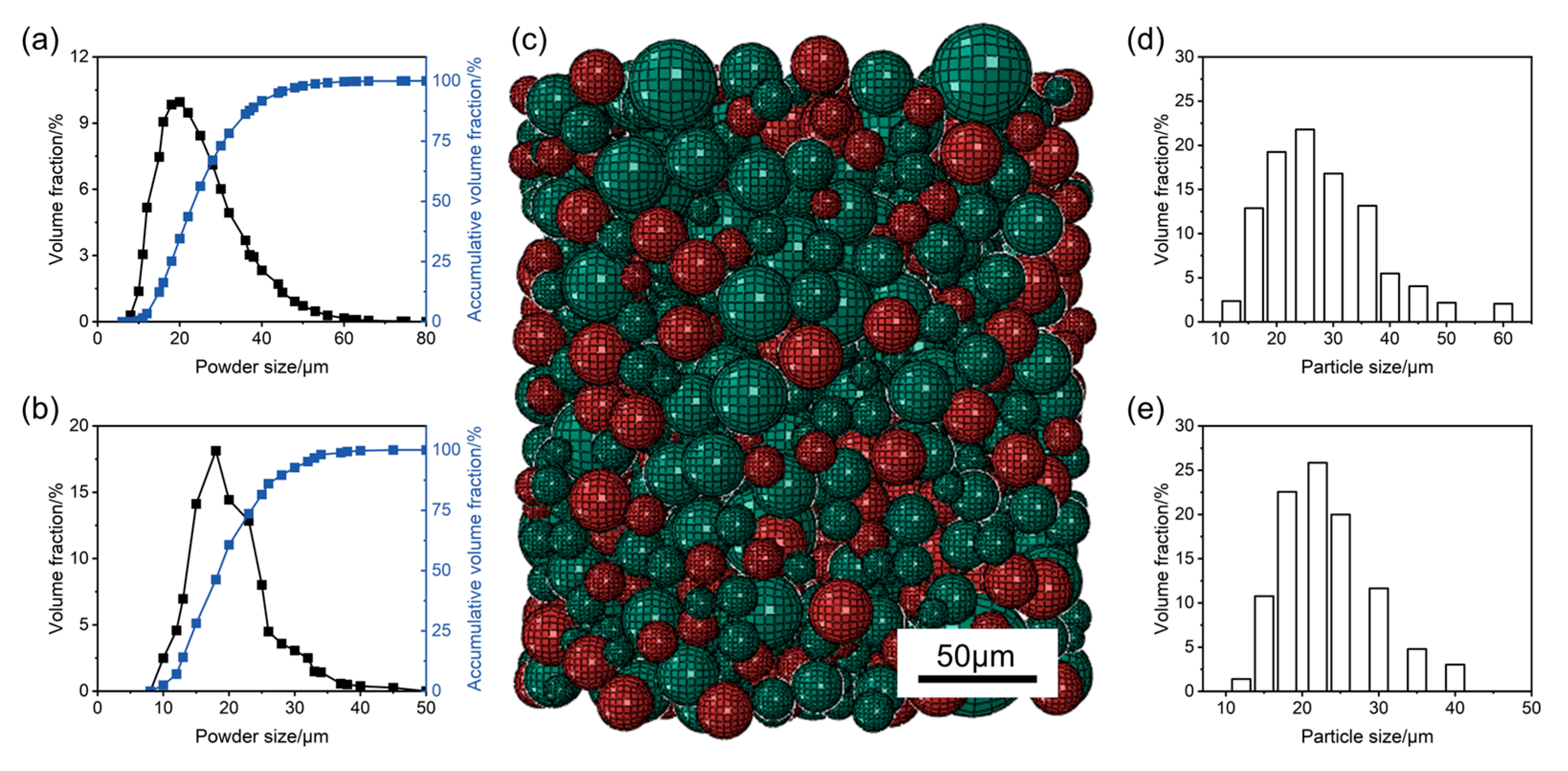
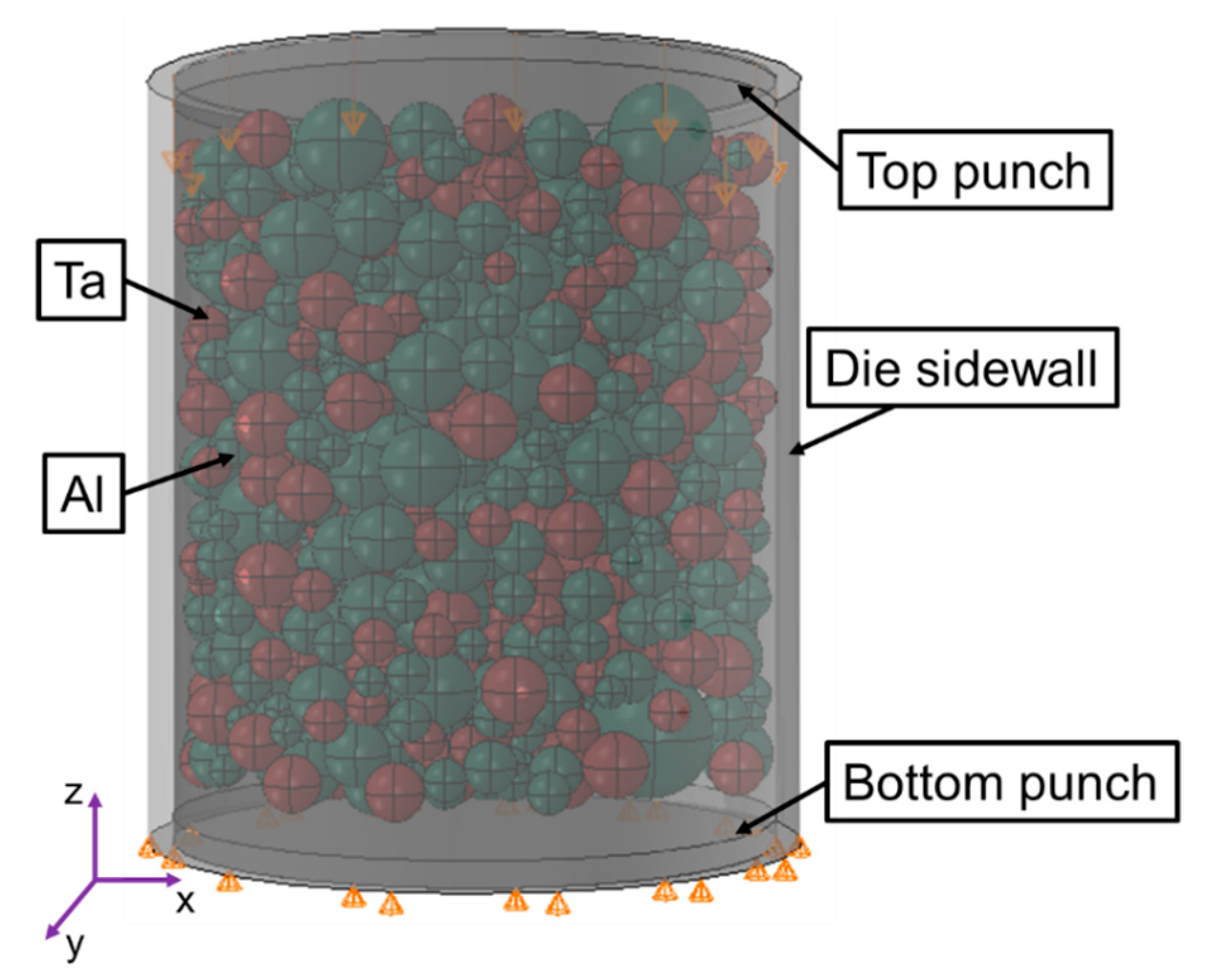
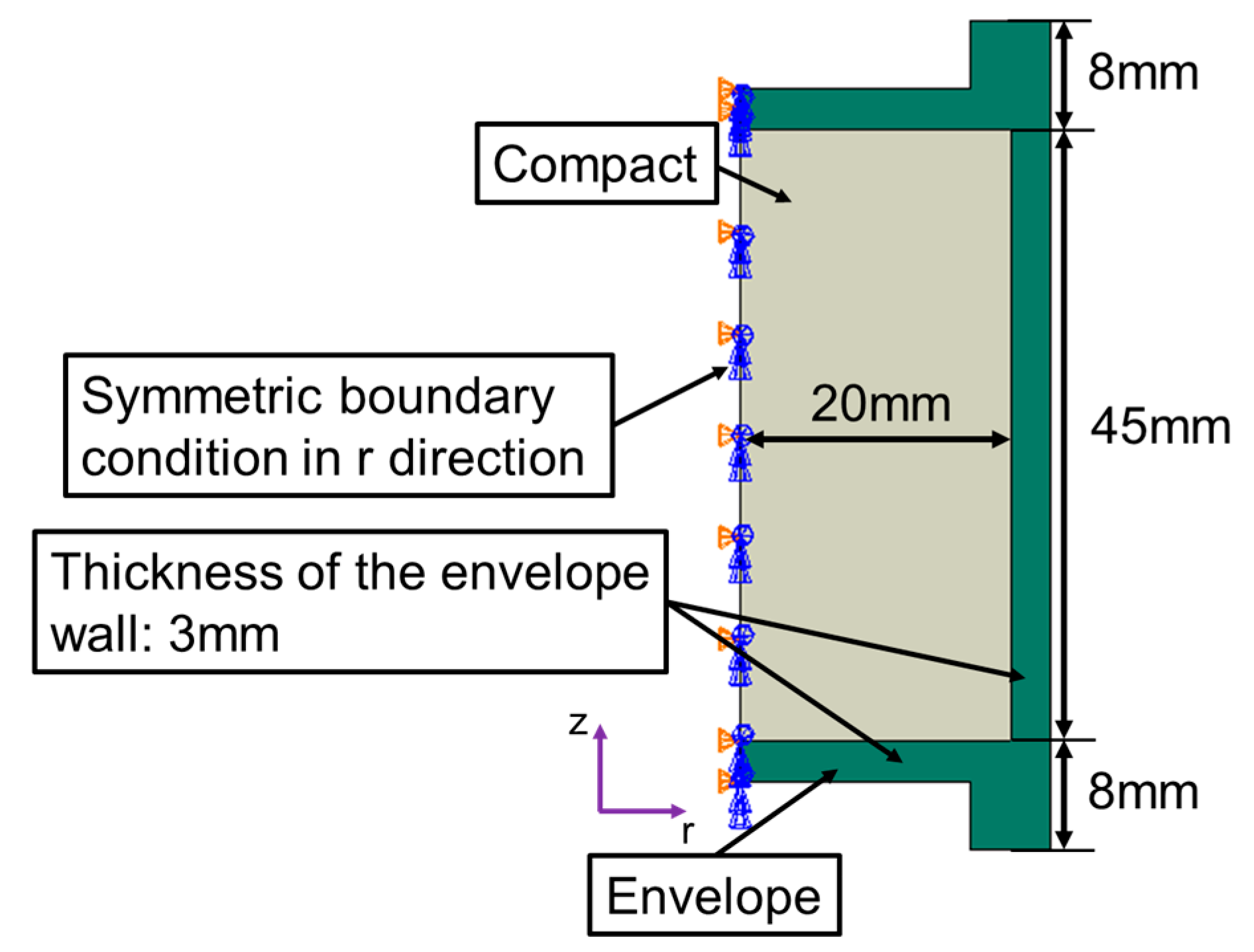
2.2. Multi-Particle Model to Identify Modified DPC Parameters
2.3. Modified DPC Parameter Verification
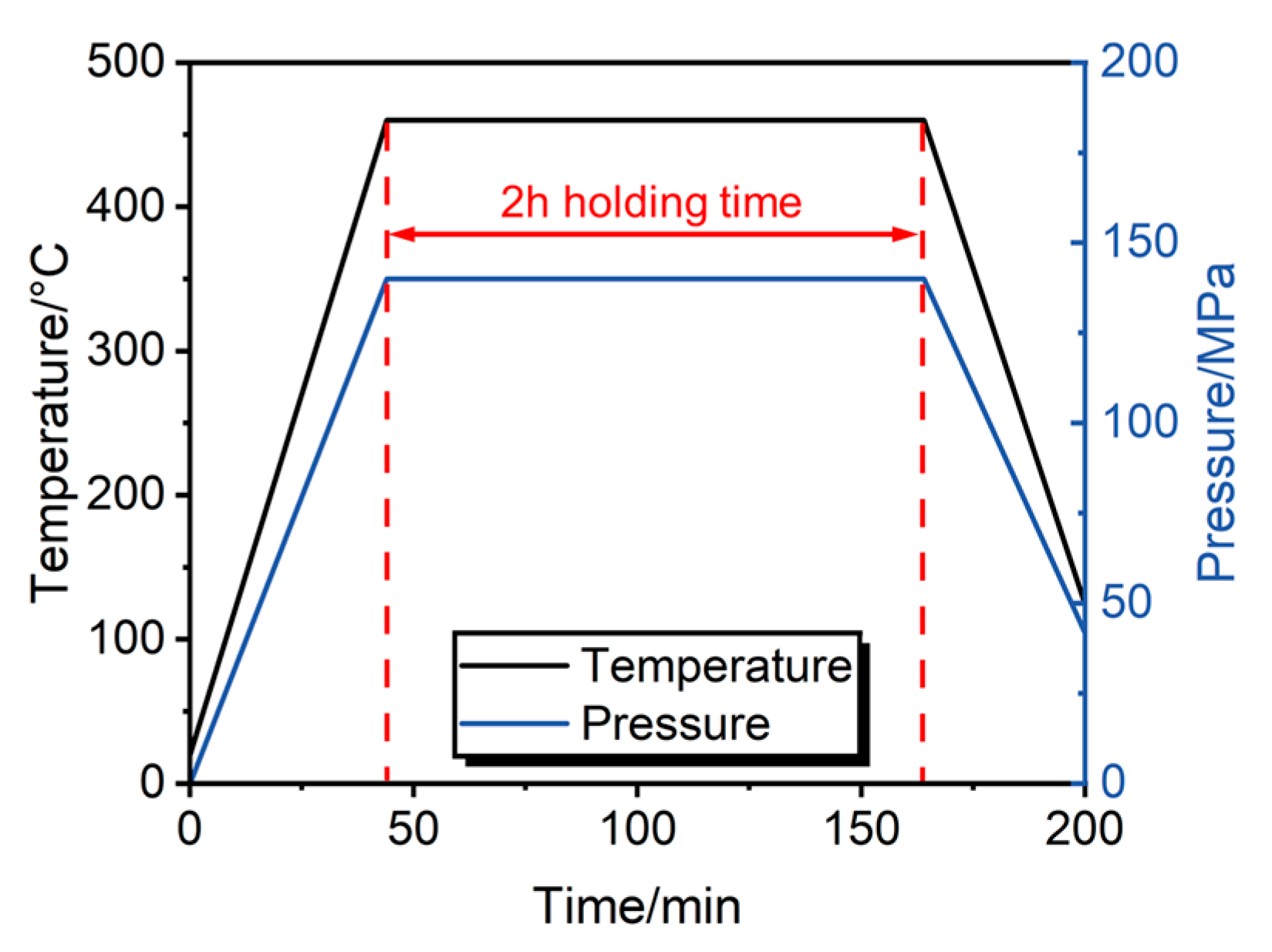
2.4. Microstructural Characterization and Property Evaluation
3. Results and Discussion
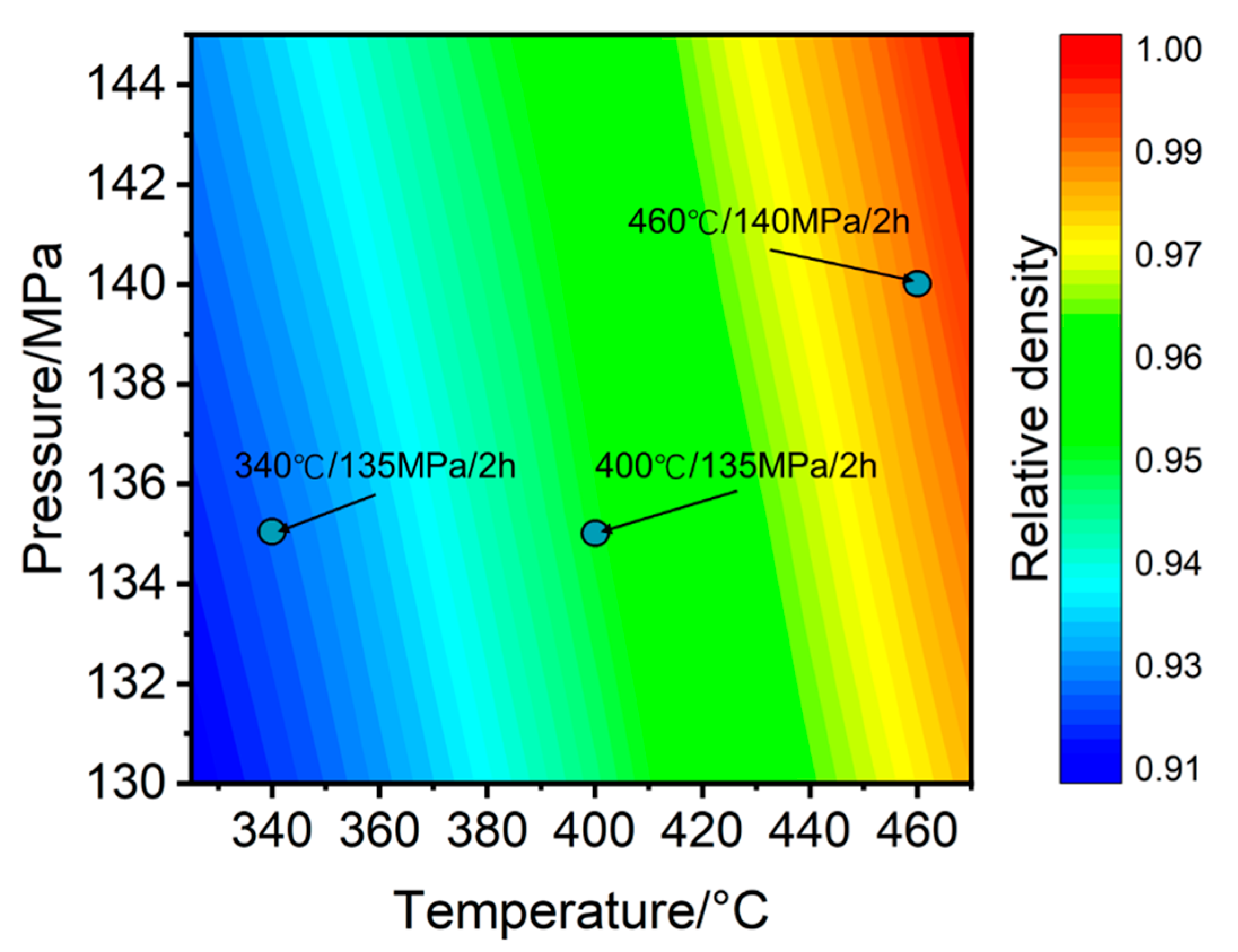
3.1. Modified DPC Parameters of Al/Ta Mixed Powder

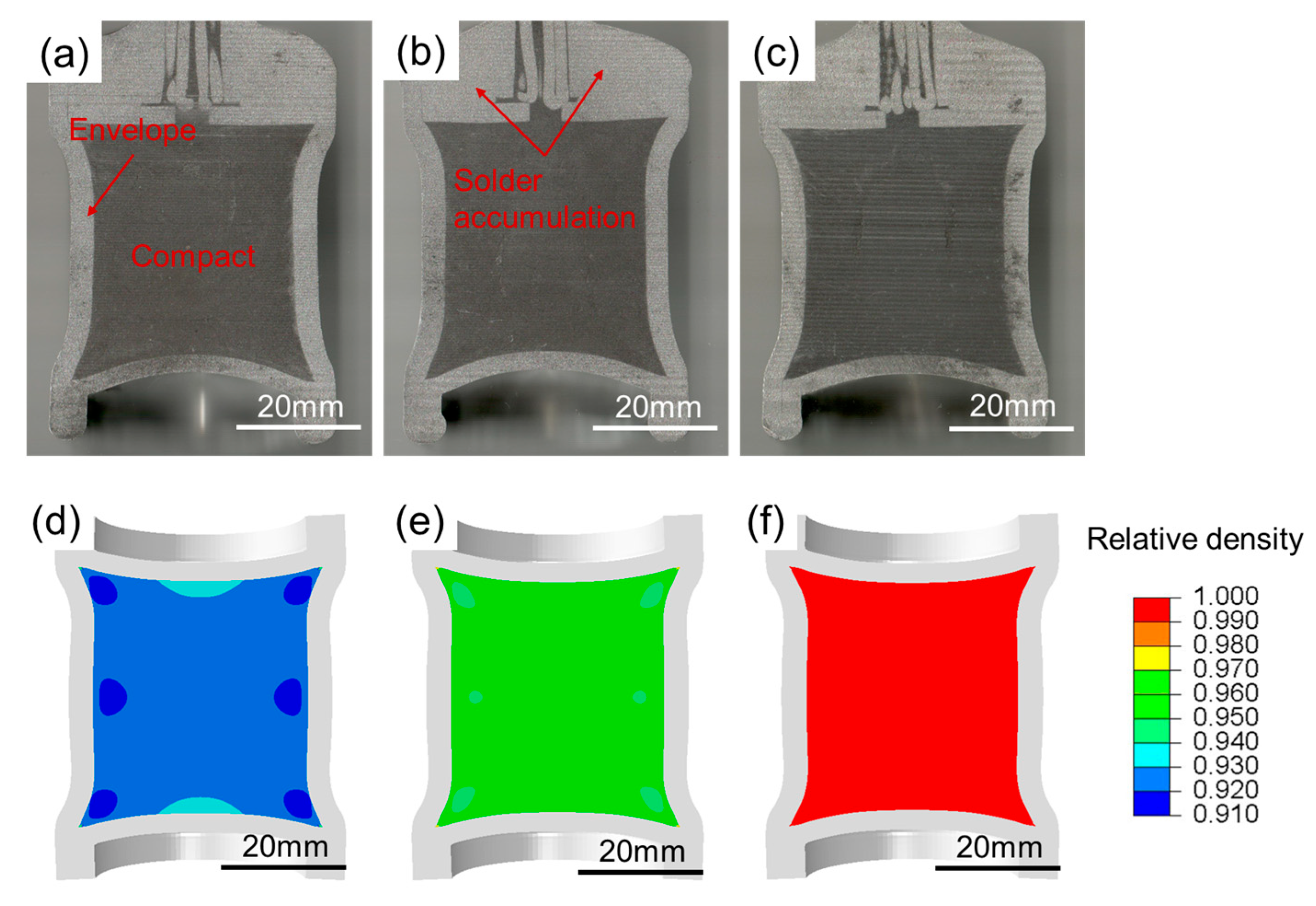
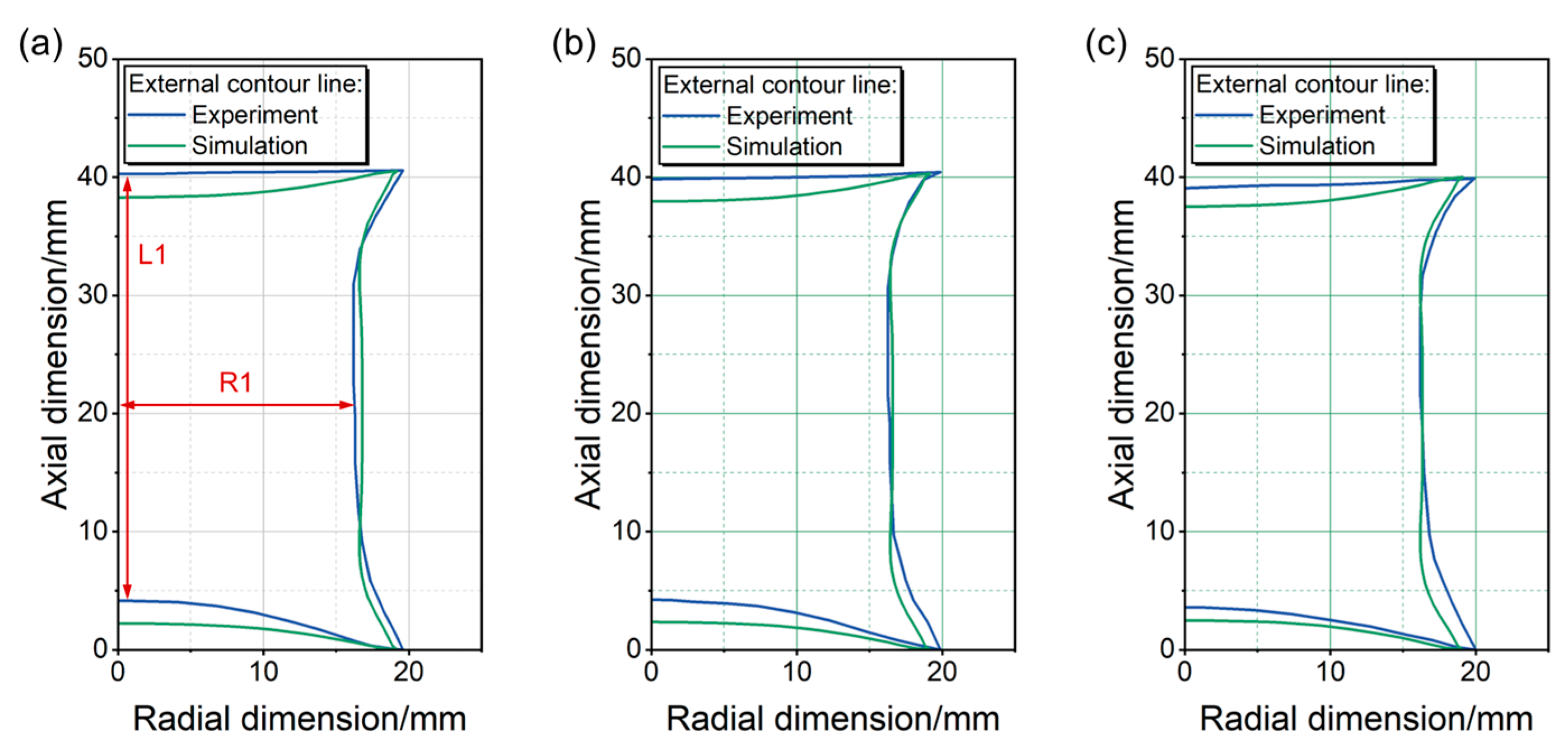
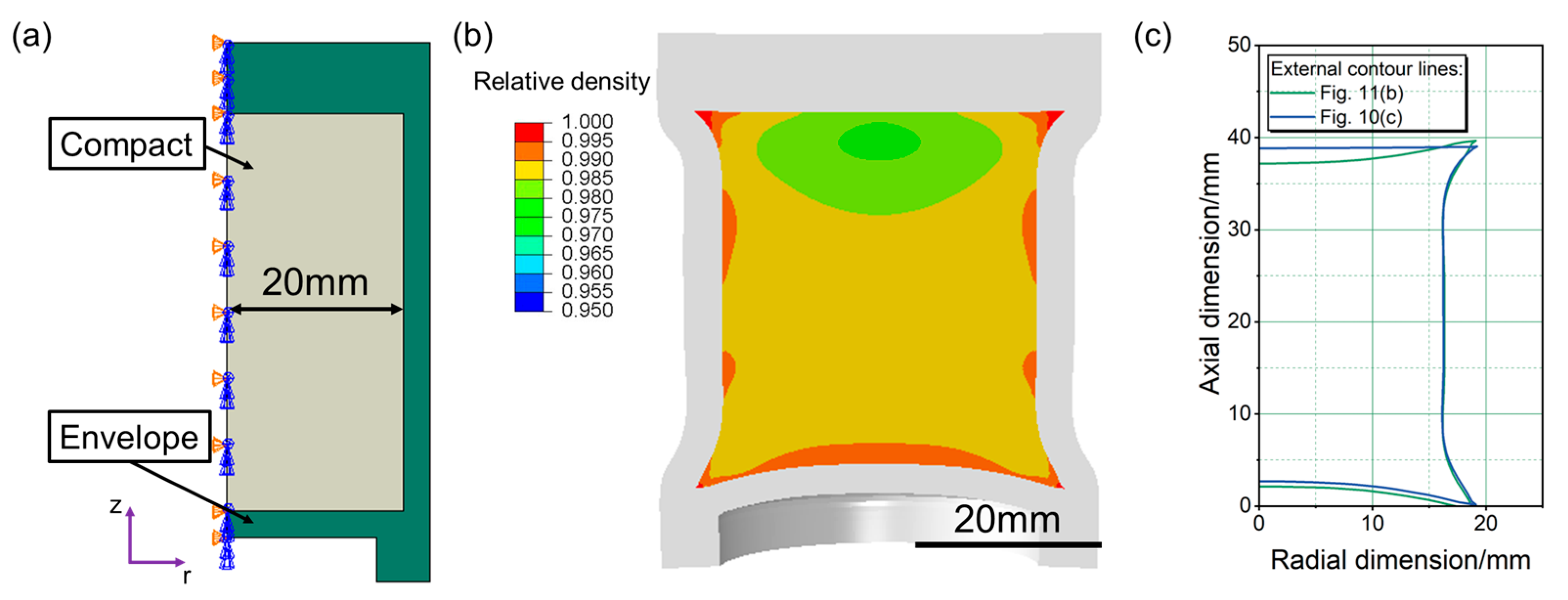
3.2. Verification of Modified DPC Parameters
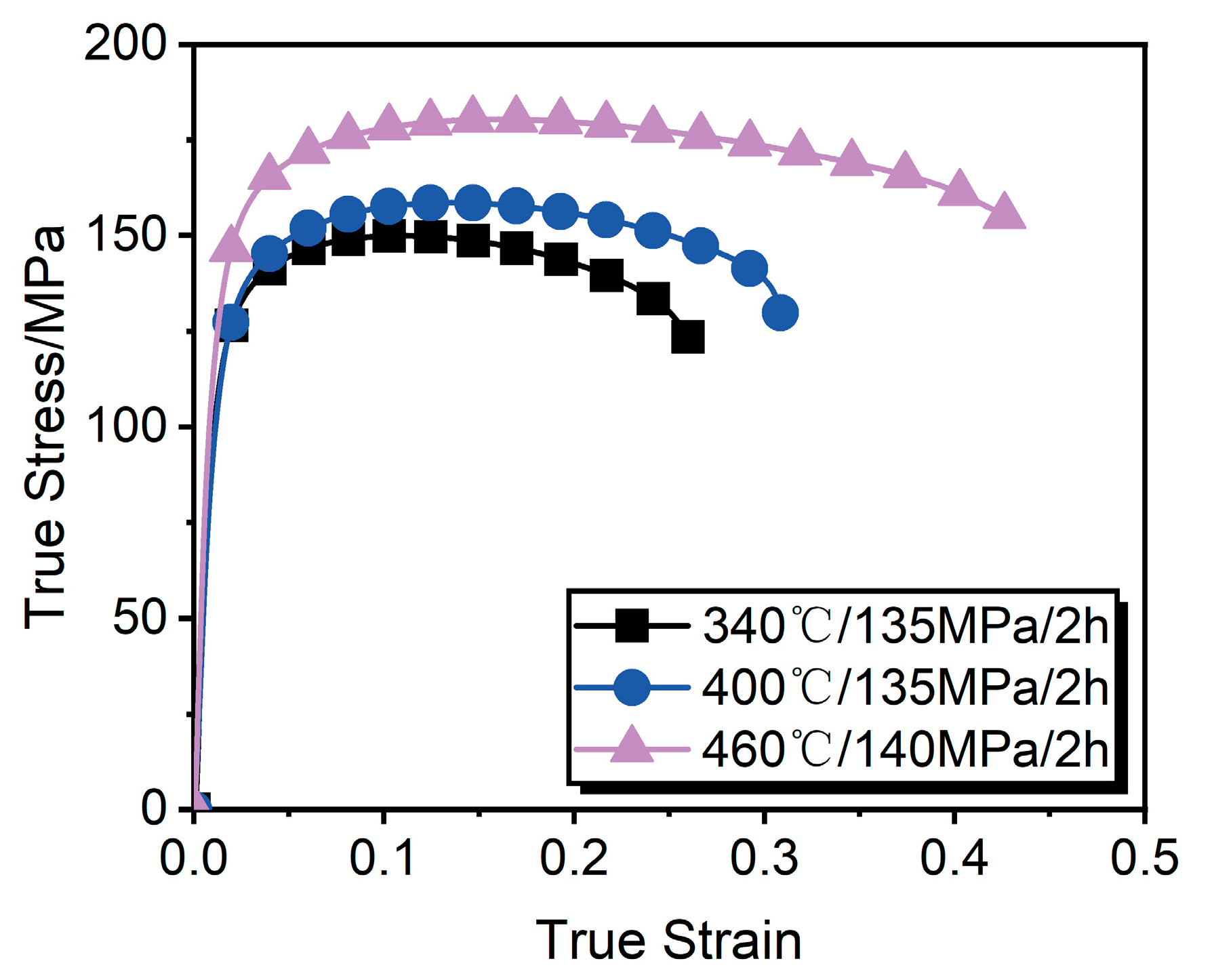
3.3. Microstructure and Mechanical Property Analysis
3.4. Impact-Induced Reaction Characteristics
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fischer, S.; Grubelich, M. A Survey of Combustible Metals, Thermites, and Intermetallics for Pyrotechnic Applications, United States; Defense Technical Information Center: Fort Belvoir, VA, USA, 1996. [Google Scholar]
- Wei, C.T.; Vitali, E.; Jiang, F.; Du, S.W.; Benson, D.J.; Vecchio, K.S.; Thadhani, N.N.; Meyers, M.A. Quasi-static and dynamic response of explosively consolidated metal–aluminum powder mixtures. Acta Mater. 2012, 60, 1418–1432. [Google Scholar] [CrossRef]
- Aydelotte, B.B.; Thadhani, N.N. Mechanistic aspects of impact initiated reactions in explosively consolidated metal+ aluminum powder mixtures. Mater. Sci. Eng. A 2013, 570, 164–171. [Google Scholar] [CrossRef]
- Ni, R.; Zhang, P.; Che, L.; Lv, Z.; Chen, S.; Zhang, L.; Li, X. Effect of Powder Production Methods on Microstructure and Mechanical Properties of Hot Isostatically Pressed TA15 Alloy. J. Phys. Conf. Ser. 2025, 2956, 012035. [Google Scholar] [CrossRef]
- Shi, Y.; Wei, Q.; Xue, P.; Song, B. Integrated Hot Isostatic Pressing Technology for Complex Metal Parts; Huangzhong University of Science and Technology Press: Wuhan, China, 2018. [Google Scholar]
- Abdelhafeez, A.M.; Essa, K.E.A. Influences of powder compaction constitutive models on the finite element simulation of hot isostatic pressing. Procedia CIRP 2016, 55, 188–193. [Google Scholar] [CrossRef]
- Shima, S.; Oyane, M. Plasticity theory for porous metals. Int. J. Mech. Sci. 1976, 18, 285–291. [Google Scholar] [CrossRef]
- Resende, L.; Martin, J.B. Formulation of Drucker-Prager cap model. J. Eng. Mech. 1985, 111, 855–881. [Google Scholar] [CrossRef]
- Drucker, D.C.; Gibson, R.E.; Henkel, D.J. Soil mechanics and work-hardening theories of plasticity. Trans. Am. Soc. Civ. Eng. 1957, 122, 338–346. [Google Scholar] [CrossRef]
- Khoei, A.R.; Molaeinia, Z.; Keshavarz, S. Modeling of hot isostatic pressing of metal powder with temperature–dependent cap plasticity model. Int. J. Mater. Form. 2013, 6, 363–376. [Google Scholar] [CrossRef]
- Diarra, H.; Mazel, V.; Busignies, V.; Tchoreloff, P. Sensitivity of elastic parameters during the numerical simulation of pharmaceutical die compaction process with Drucker-Prager/Cap model. Powder Technol. 2018, 332, 150–157. [Google Scholar] [CrossRef]
- Park, H.; Kim, K.T. Consolidation behavior of SiC powder under cold compaction. Mater. Sci. Eng. A 2001, 299, 116–124. [Google Scholar] [CrossRef]
- Rottmann, G.; Coube, O.; Riedel, H. Comparison between triaxial results and model predictions with special consideration of the anisotropy. Proc. Eur. Congr. Powder Metall. 2001, 3, 29–37. [Google Scholar]
- Zhou, M.; Huang, S.; Hu, J.; Lei, Y.; Xiao, Y.; Li, B.; Yan, S.; Zou, F. A density-dependent modified Drucker-Prager Cap model for die compaction of Ag57. 6-Cu22. 4-Sn10-In10 mixed metal powders. Powder Technol. 2017, 305, 183–196. [Google Scholar] [CrossRef]
- Zhang, B.; Jain, M.; Zhao, C.; Bruhis, M.; Lawcock, R.; Ly, K. Experimental calibration of density-dependent modified Drucker-Prager/Cap model using an instrumented cubic die for powder compact. Powder Technol. 2010, 204, 27–41. [Google Scholar] [CrossRef]
- Ogawa, R.; Yoshimura, T.; Yagi, N.; Mizuta, K.; Taniguchi, Y. Estimation of Yield Surface on Iron Powder Compaction for Finite Element Analysis using Drucker-Prager Cap Model. Mater. Sci. Eng. Conf. Ser. 2019, 501, 012021. [Google Scholar] [CrossRef]
- Bai, W.; Liu, W.; Wang, W.; Peng, C.; Wang, A.; He, Q.; Liu, G.; Huang, S. Drucker-Prager-Cap modelling of boron carbide powder for coupled electrical-thermal-mechanical finite element simulation of spark plasma sintering. Ceram. Int. 2021, 47, 21536–21545. [Google Scholar] [CrossRef]
- Hibbitt, Karlsson and Sorensen, Inc. ABAQUS Version 6.14 Documentation; Dassault Systemes Simulia Corp: Johnston, RI, USA, 2018. [Google Scholar]
- Li, W.; Kou, H.; Zhang, X.; Ma, J.; Li, Y.; Geng, P.; Wu, X.; Chen, L.; Fang, D. Temperature-dependent elastic modulus model for metallic bulk materials. Mech. Mater. 2019, 139, 103194. [Google Scholar] [CrossRef]
- Davoudi, K. Temperature dependence of the yield strength of aluminum thin films: Multiscale modeling approach. Scr. Mater. 2017, 131, 63–66. [Google Scholar] [CrossRef]
- Peyre, P.; Braham, C. FEM calculation of residual stresses induced by laser shock processing in stainless steels. Model. Simul. Mater. Sci. Eng. 2007, 15, 205. [Google Scholar] [CrossRef]
- Huang, S.-L.; Zhou, Z. Experimental study on the mechanical behavior of material at mid-strain-rate. Build. Tech. Dev. 2005, 32, 2. [Google Scholar]
- Škoro, G.P.; Bennett, J.R.J.; Edgecock, T.R.; Gray, S.A.; McFarland, A.J.; Booth, C.N.; Rodgers, K.J.; Back, J.J. Dynamic Young’s moduli of tungsten and tantalum at high temperature and stress. J. Nucl. Mater. 2011, 409, 40–46. [Google Scholar] [CrossRef]
- Lee, B.-J.; Vecchio, K.S.; Ahzi, S.; Schoenfeld, S. Modeling the mechanical behavior of tantalum. Metall. Mater. Trans. A 1997, 28, 113–122. [Google Scholar] [CrossRef]
- Aydin, İ.; Briscoe, B.J.; Şanlitürk, K.Y. The internal form of compacted ceramic components: A comparison of a finite element modelling with experiment. Powder Technol. 1996, 89, 239–254. [Google Scholar] [CrossRef]
- Han, L.H.; Elliott, J.A.; Bentham, A.C.; Mills, A.; Amidon, G.E.; Hancock, B.C. A modified Drucker-Prager Cap model for die compaction simulation of pharmaceutical powders. Int. J. Solids Struct. 2008, 45, 3088–3106. [Google Scholar] [CrossRef]
- Hust, J.G.; Lankford, A.B. Thermal Conductivity of Aluminum, Copper, Iron, and Tungsten for Temperatures from 1 K to the Melting Point; National Bureau of Standards: Boulder, CO, USA, 1984. [Google Scholar]
- Tanda, G.; Misale, M. Measurement of total hemispherical emittance and specific heat of aluminum and Inconel 718 by a calorimetric technique. J. Heat Transf. 2005, 128, 302–306. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, G.; Feng, Y.; Li, L. Study on constitutive parameters of 6061 aluminum alloy at high strain rate. Min. Metall. Eng. 2011, 31, 120–123. [Google Scholar]
- Savchenko, I.V.; Stankus, S.V. Thermal conductivity and thermal diffusivity of tantalum in the temperature range from 293 to 1800 K. Thermophys. Aeromech. 2008, 15, 679–682. [Google Scholar] [CrossRef]
- Arblaster, J.W. Thermodynamic Properties of Tantalum. J. Phase Equilibria Diffus. 2018, 39, 255–272. [Google Scholar] [CrossRef]
- Oladijo, P.; Awe, S.; Akinlabi, E.; Phiri, R.; Lebudi, C.; Phuti, R. High-Temperature Properties of Metal Matrix Composites. In Encyclopedia of Materials: Composites; Elsevier: Amsterdam, The Netherlands, 2021; pp. 360–374. [Google Scholar]
- Springer, G.; Tsai, S.W. Thermal Conductivities of Unidirectional Materials. J. Compos. Mater. 1967, 1, 166–173. [Google Scholar] [CrossRef]
- Hull, D.; Clyne, T.W. An Introduction to Composite Materials; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Chen, Z.; Wang, X.; Giuliani, F.; Atkinson, A. Microstructural characteristics and elastic modulus of porous solids. Acta Mater. 2015, 89, 268–277. [Google Scholar] [CrossRef]
- Wolff, C.; Mercier, S.; Couque, H.; Molinari, A.; Bernard, F.; Naimi, F. Thermal-electrical-mechanical simulation of the nickel densification by Spark Plasma Sintering. Comparison with experiments. Mech. Mater. 2016, 100, 126–147. [Google Scholar] [CrossRef]
- Chernikova, E.S.; Raichenko, A.I.; Olevskii, E.A. An analysis of electric heating of a cemented carbide taking into consideration the temperature relationship of its characteristics. Sov. Powder Metall. Met. Ceram. 1992, 31, 936–940. [Google Scholar] [CrossRef]
- Mahmoud, M.M.; Link, G.; Thumm, M. The role of the native oxide shell on the microwave sintering of copper metal powder compacts. J. Alloys Compd. 2015, 627, 231–237. [Google Scholar] [CrossRef]
- Kim, Y.W.; Griffith, W.M.; Froes, F.H. Surface oxides in P/M aluminum alloys. JOM 1985, 37, 27–33. [Google Scholar] [CrossRef]
- Martin, J.W.; Doherty, R.D.; Cantor, B. Stability of Microstructure in Metallic Systems; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Al-Maharma, A.Y.; Patil, S.P.; Markert, B. Effects of porosity on the mechanical properties of additively manufactured components: A critical review. Mater. Res. Express 2020, 7, 122001. [Google Scholar] [CrossRef]
- Chawla, N.; Shen, Y.-L. Mechanical behavior of particle reinforced metal matrix composites. Adv. Eng. Mater. 2001, 3, 357–370. [Google Scholar] [CrossRef]
- Peng, J.; Li, B.; Yuan, B.; Sun, X.; Yang, Q. Study on the behavioral characteristics of ladle covered active fragments penetrating double-layer aluminum targets. Chin. J. Explos. Propellants 2020, 43, 6. [Google Scholar]





| Properties | Mixing Law |
|---|---|
| Elastic modulus/GPa [32] | |
| Thermal conductivity/W·m−1·K−1 [33] | |
| Specific heat/J·kg−1·K−1 [34] |
| Properties | Properties as Density-Dependent |
|---|---|
| Elastic modulus/GPa [35] | |
| Thermal conductivity/W·m−1·K−1 [36] | |
| Specific heat/J·kg−1·K−1 [37] |
| HIP | 340 °C/135 MPa/2 h | 400 °C/135 MPa/2 h | 460 °C/140 MPa/2 h | |||
|---|---|---|---|---|---|---|
| L1/mm | R1/mm | L1/mm | R1/mm | L1/mm | R1/mm | |
| Experiment | 36.14 | 16.13 | 35.83 | 16.19 | 35.47 | 16.13 |
| Simulation | 35.60 | 16.78 | 35.59 | 16.66 | 35.13 | 16.40 |
| deviation/% | 1.5 | 4.0 | 0.7 | 2.9 | 0.9 | 1.7 |
| HIP | Yield Strength/MPa | Compressive Strength/MPa | Fracture Strain/% |
|---|---|---|---|
| 340 °C/135 MPa/2 h | 96.7 | 149.9 | 24.0 |
| 400 °C/135 MPa/2 h | 101.2 | 158.6 | 28.8 |
| 460 °C/140 MPa/2 h | 115.2 | 180.3 | 39.6 |
| Steel Target | Aluminum Target | |
|---|---|---|
| Hole area/mm2 | 184.17 | 965.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Zhang, P.; Yu, X.; Ning, X.; Tan, C. Hot Isostatic Pressing Synthesis of Al-Ta Energetic Structural Material Based on Modified Drucker–Prager Cap Model. Metals 2025, 15, 615. https://doi.org/10.3390/met15060615
Yang Z, Zhang P, Yu X, Ning X, Tan C. Hot Isostatic Pressing Synthesis of Al-Ta Energetic Structural Material Based on Modified Drucker–Prager Cap Model. Metals. 2025; 15(6):615. https://doi.org/10.3390/met15060615
Chicago/Turabian StyleYang, Zenglin, Pengjie Zhang, Xiaodong Yu, Xianjin Ning, and Chengwen Tan. 2025. "Hot Isostatic Pressing Synthesis of Al-Ta Energetic Structural Material Based on Modified Drucker–Prager Cap Model" Metals 15, no. 6: 615. https://doi.org/10.3390/met15060615
APA StyleYang, Z., Zhang, P., Yu, X., Ning, X., & Tan, C. (2025). Hot Isostatic Pressing Synthesis of Al-Ta Energetic Structural Material Based on Modified Drucker–Prager Cap Model. Metals, 15(6), 615. https://doi.org/10.3390/met15060615






