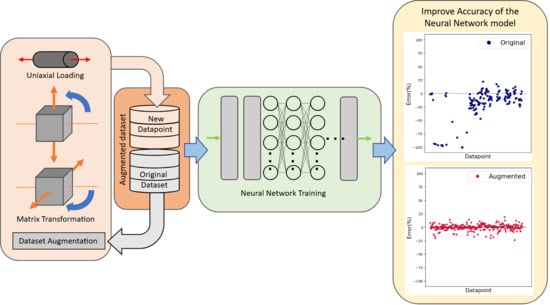
Augmenting Fatigue Datasets for Improved Multiaxial Fatigue Strength Prediction with Neural Networks
Abstract
1. Introduction
2. Materials and Methods
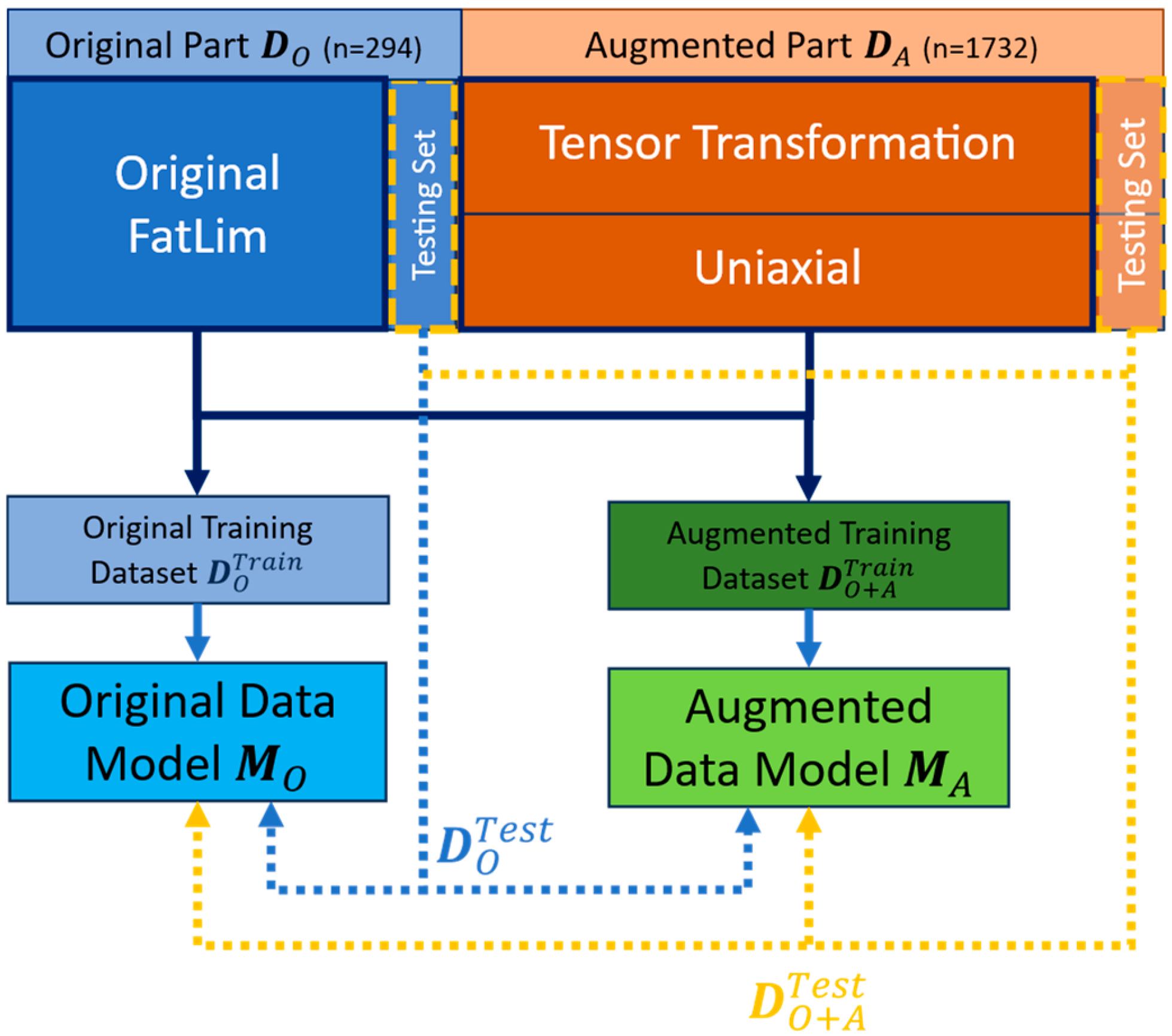
2.1. Dataset
- : Amplitude stress tensor in multiaxial loading. Represents the amplitude of normal and shear components of stress during cyclic multiaxial loading conditions.
- : Mean stress tensor in multiaxial loading. Represents the mean or average values of normal and shear components of stress during cyclic multiaxial loading conditions.
- : Tensile stress fatigue limit in repeated uniaxial loading (loading ratio R = 0). The fatigue limit is defined as the stress amplitude, where the stress cycles between zero and a maximum tensile value. In this case, the mean stress equals the amplitude, and the maximum stress is twice the fatigue limit amplitude [5].
- : Tensile stress fatigue limit in fully reversed uniaxial loading (loading ratio R = −1). The fatigue limit is defined as the stress amplitude, where the stress cycles symmetrically between equal magnitudes in tension and compression. The mean stress is zero, and the maximum and minimum stresses are equal in magnitude but opposite in sign [5].
- : Torsion stress fatigue limit in repeated uniaxial loading (loading ratio R = 0). The torsional fatigue limit is defined as the stress amplitude, where the shear stress cycles between zero and a maximum value in one direction. In this case, the mean shear stress equals the amplitude, and the maximum shear stress is twice the fatigue limit amplitude [5].
- : Torsion stress fatigue limit in fully reversed uniaxial loading (loading ratio R = −1). The torsional fatigue limit is defined as the stress amplitude, where the shear stress cycles symmetrically between equal magnitudes in positive and negative directions. The mean stress is zero, and the amplitude equals the maximum (absolute) shear stress [5].
- : Maximum (ultimate) strength. Refers to the maximum stress or force that a material can withstand before undergoing fracture or failure.
- : Yield strength. Denotes the stress or force at which a material begins to deform plastically without undergoing permanent deformation.
- : Shifted phase in stress loading refers to a different starting point of stress cycles due to a phase shift relative to the other loading components in multiaxial loading conditions.
2.2. Augmenting the Database
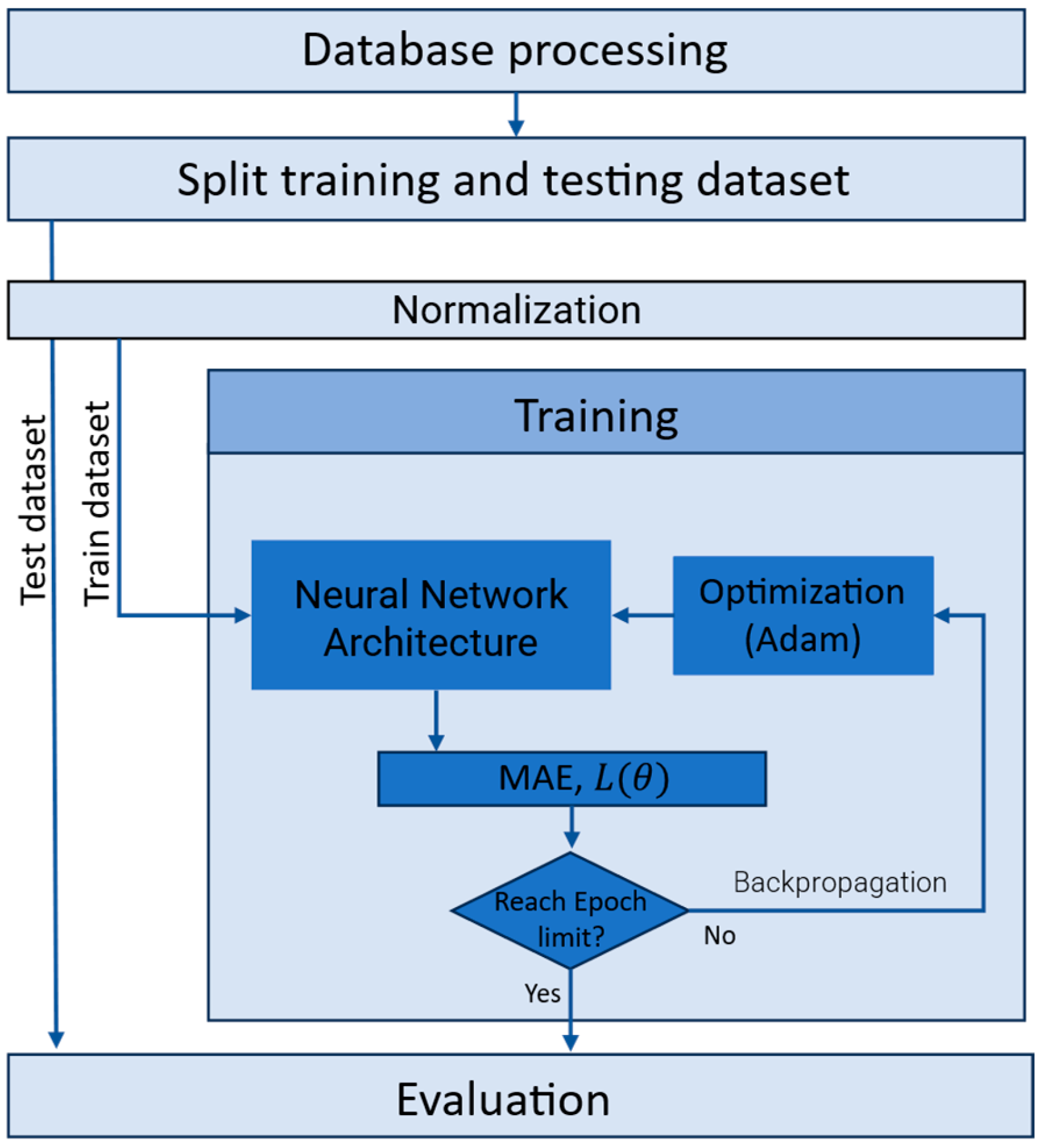
2.3. Model Training and Data Processing
2.4. Artificial Neural Network
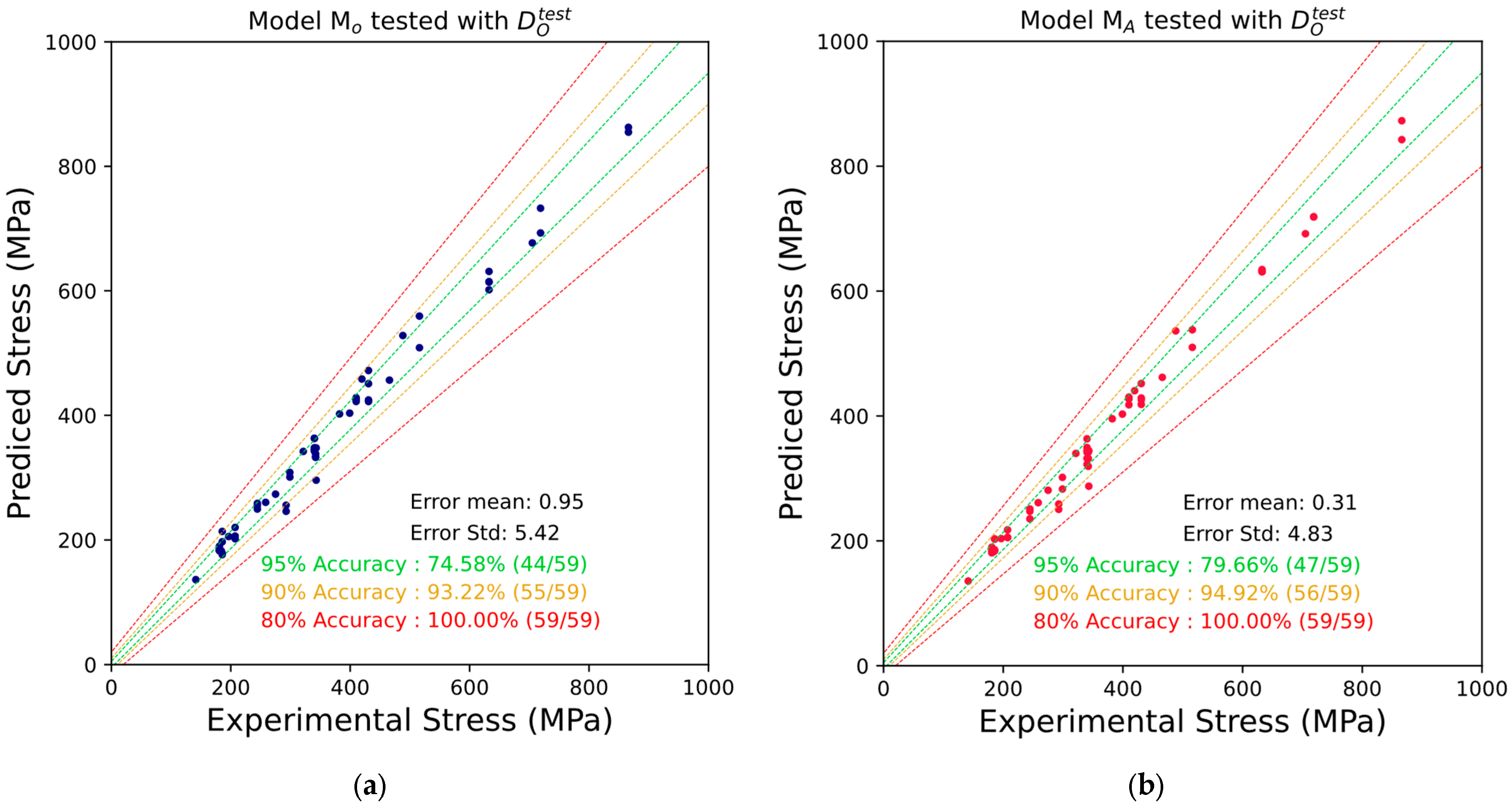
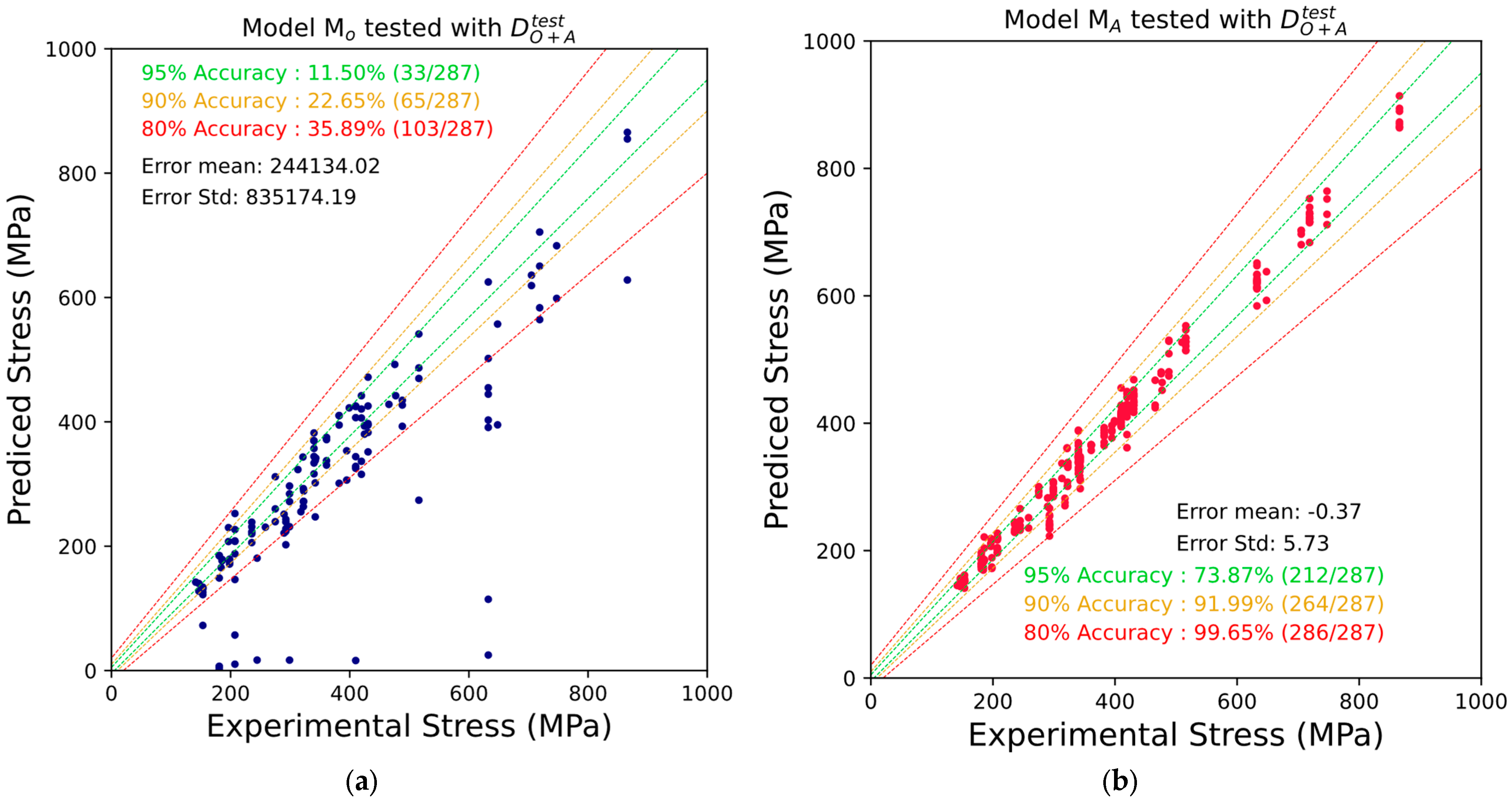
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Chen, J.; Liu, Y. Fatigue Modeling Using Neural Networks: A Comprehensive Review. Fatigue Fract. Eng. Mat. Struct. 2022, 45, 945–979. [Google Scholar] [CrossRef]
- Papuga, J.; Nesládek, M.; Hasse, A.; Cízová, E.; Suchý, L. Benchmarking Newer Multiaxial Fatigue Strength Criteria on Data Sets of Various Sizes. Metals 2022, 12, 289. [Google Scholar] [CrossRef]
- Papuga, J.; Kaľavský, A.; Lutovinov, M.; Vízková, I.; Parma, S.; Nesládek, M. Evaluation of Data Sets Usable for Validating Multiaxial Fatigue Strength Criteria. Int. J. Fatigue 2021, 145, 106093. [Google Scholar] [CrossRef]
- Nagode, M.; Papuga, J.; Oman, S. Application of Machine Learning Models for Estimating the Material Parameters for Multiaxial Fatigue Strength Calculation. Fatigue Fract. Eng. Mat. Struct. 2023, 46, 4142–4160. [Google Scholar] [CrossRef]
- DIN 50100:2022-12; Schwingfestigkeitsversuch—Durchführung und Auswertung von Zyklischen Versuchen mit Konstanter Lastamplitude für Metallische Werkstoffproben und Bauteile. DIN Media: Berlin, Germany, 2022. [CrossRef]
- Rennert, R.; Kullig, E.; Vormwald, M.; Esderts, A.; Luke, M.; Maschinenbau, F. (Eds.) Analytical Strength Assessment of Components: Made of Steel, Cast Iron and Aluminium Materials: FKM Guideline, 7th ed.; VDMA Verlag GmbH: Frankfurt, Germany, 2021; ISBN 978-3-8163-0745-7. [Google Scholar]
- Liu, J.; Zenner, H. Berechnung der Dauerschwingfestigkeit bei Mehrachsiger Beanspruchung—Teil 1. Mater. Werkst. 1993, 24, 240–249. [Google Scholar] [CrossRef]
- Ottosen, N.S.; Ristinmaa, M. The Mechanics of Constitutive Modeling; Elsevier: Amsterdam, The Netherlands, 2005; ISBN 978-0-08-044606-6. [Google Scholar]
- Kinsley, H.; Kukiela, D. Neural Networks from Scratch in Python, 1st ed. 2020. Available online: https://nnfs.io/ (accessed on 3 April 2024).
- Szandała, T. Review and Comparison of Commonly Used Activation Functions for Deep Neural Networks; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995; ISBN 978-0-19-853849-3. [Google Scholar]
- Brownlee, J. How to Choose Loss Functions When Training Deep Learning Neural Networks; Machine Learning Mastery: San Juan, Puerto Rico, 2020. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Papuga, J. A Survey on Evaluating the Fatigue Limit under Multiaxial Loading. Int. J. Fatigue 2011, 33, 153–165. [Google Scholar] [CrossRef]
| No. | Tensile Stress Amplitude (MPa) | Tensile Mean Stress (MPa) | Shear Stress Amplitude (MPa) | Shear Mean Stress (MPa) | Transformation Matrix | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| xx | yy | zz | xx | yy | zz | xy | xz | yz | xy | xz | yz | |||||
| 1 | 417 | 510 | 209 | 90 | Original datapoint | |||||||||||
| 2 | 417 | 510 | −209 | 90 | ||||||||||||
| 3 | 417 | 510 | 209 | 90 | ||||||||||||
| 4 | 417 | 510 | −209 | 90 | ||||||||||||
| No. | Tensile Stress Amplitude (MPa) | Tensile Mean Stress (MPa) | Shear Stress Amplitude (MPa) | Shear Mean Stress (MPa) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| xx | yy | zz | xx | yy | zz | xy | xz | yz | xy | xz | yz | |||||
| 1 [2] | 866 | 541 | 1060 | 822 | 417 | 510 | 209 | |||||||||
| 5 | 866 * | |||||||||||||||
| 6 | 866 † | |||||||||||||||
| 7 | 866 † | |||||||||||||||
| 8 | 541 * | |||||||||||||||
| 9 | 541 † | |||||||||||||||
| 10 | 541 † | |||||||||||||||
| 11 | 530 * | 530 * | ||||||||||||||
| 12 | 530 † | 530 † | ||||||||||||||
| 13 | 530 † | 530 † | ||||||||||||||
| 14 | 411 * | 411 * | ||||||||||||||
| 15 | 411 † | 411 † | ||||||||||||||
| 16 | 411 † | 411 † | ||||||||||||||
| Model | Fatigue Prediction Error (%) | |||
|---|---|---|---|---|
| Max | Min | Mean | Standard Deviation | |
| Original FatLim | 11.70 | −18.28 | −0.18 | 3.20 |
| Expanded FatLim | 22.77 | −26.91 | −0.15 | 4.59 |
| Model | Fatigue Prediction Error (%) | |||
|---|---|---|---|---|
| Max | Min | Mean | Standard Deviation | |
| Original FatLim | 15.09 | −15.94 | 0.95 | 5.41 |
| Expanded FatLim | 9.84 | −16.17 | 0.31 | 4.83 |
| Model | Fatigue Prediction Error (%) | |||
|---|---|---|---|---|
| Max | Min | Mean | Standard Deviation | |
| Original FatLim | 5.79 × 106 | −1.00 × 102 | 2.44 × 105 | 8.35 × 105 |
| Expanded FatLim | 19.21 | −23.81 | −0.37 | 5.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Opasanon, N.; Stahr, L.J.; Suchy, L.; Hasse, A. Augmenting Fatigue Datasets for Improved Multiaxial Fatigue Strength Prediction with Neural Networks. Metals 2025, 15, 528. https://doi.org/10.3390/met15050528
Opasanon N, Stahr LJ, Suchy L, Hasse A. Augmenting Fatigue Datasets for Improved Multiaxial Fatigue Strength Prediction with Neural Networks. Metals. 2025; 15(5):528. https://doi.org/10.3390/met15050528
Chicago/Turabian StyleOpasanon, Napon, Leon Josef Stahr, Lukas Suchy, and Alexander Hasse. 2025. "Augmenting Fatigue Datasets for Improved Multiaxial Fatigue Strength Prediction with Neural Networks" Metals 15, no. 5: 528. https://doi.org/10.3390/met15050528
APA StyleOpasanon, N., Stahr, L. J., Suchy, L., & Hasse, A. (2025). Augmenting Fatigue Datasets for Improved Multiaxial Fatigue Strength Prediction with Neural Networks. Metals, 15(5), 528. https://doi.org/10.3390/met15050528