The Effect of Reduced Co Content in CrMnFeCoNi Alloys: A First Principles Study
Abstract
1. Introduction
2. Methods
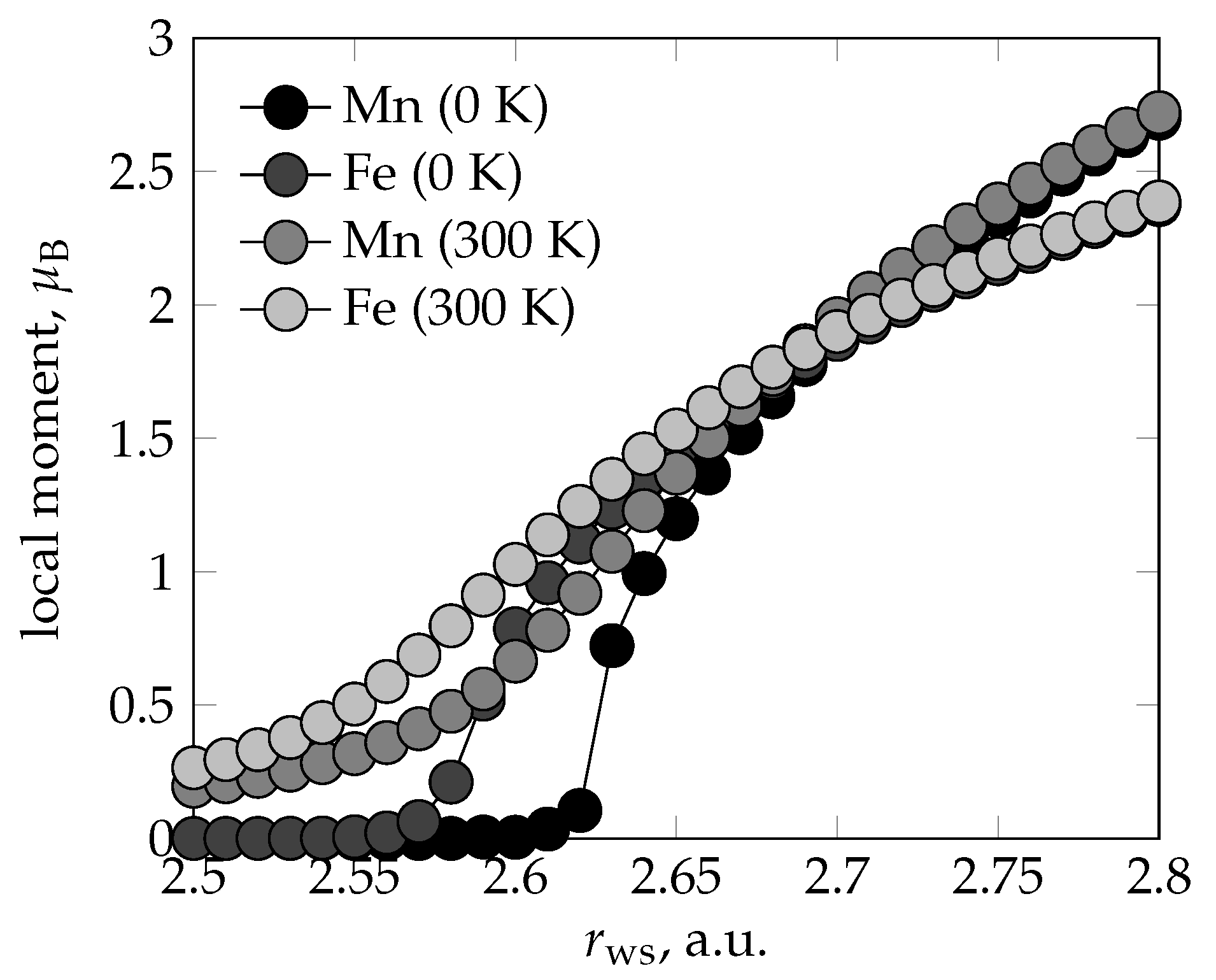
3. Results and Discussion
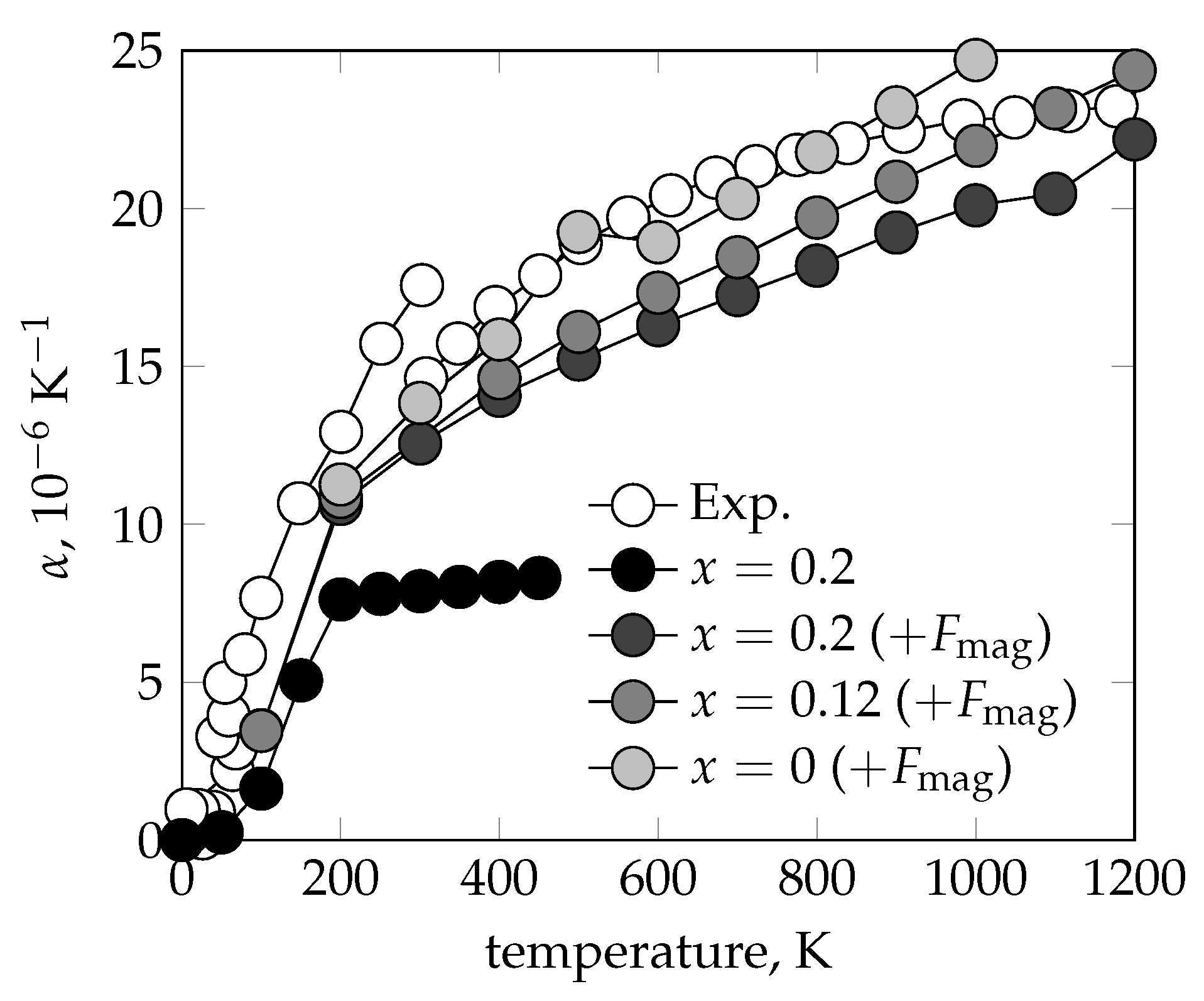
3.1. Equilibrium Lattice Parameter and Thermal Expansion Coefficient
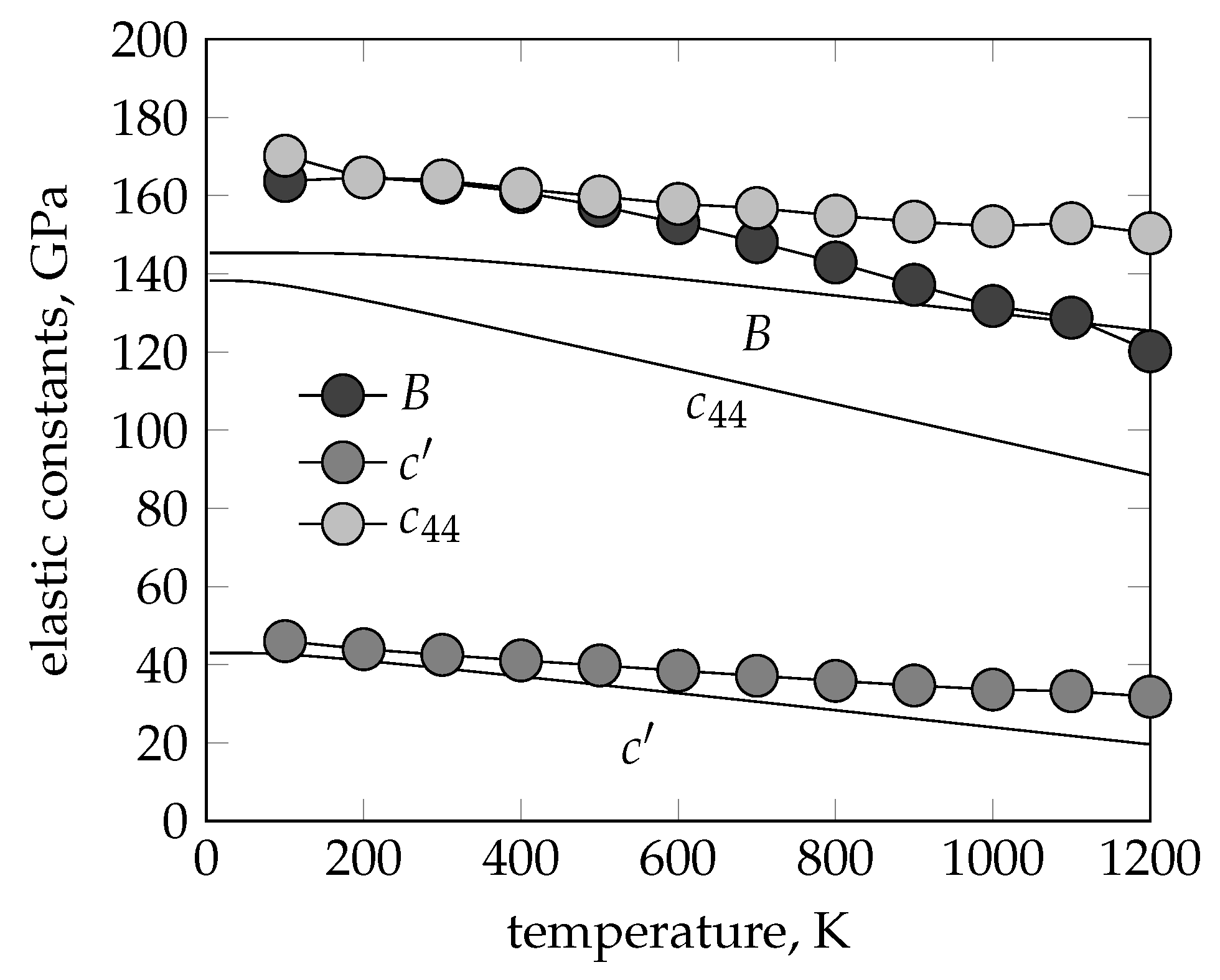
3.2. Elastic Constants
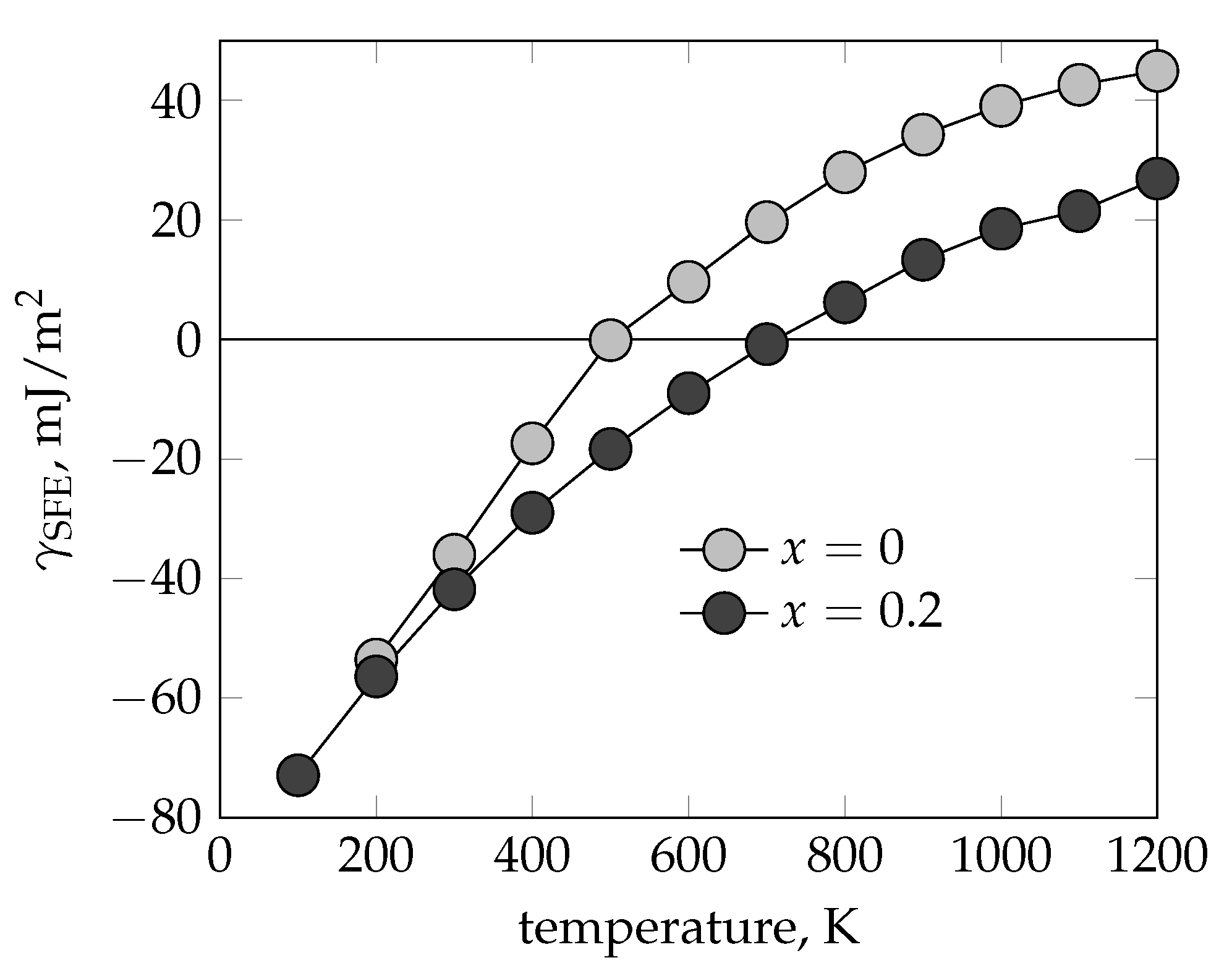
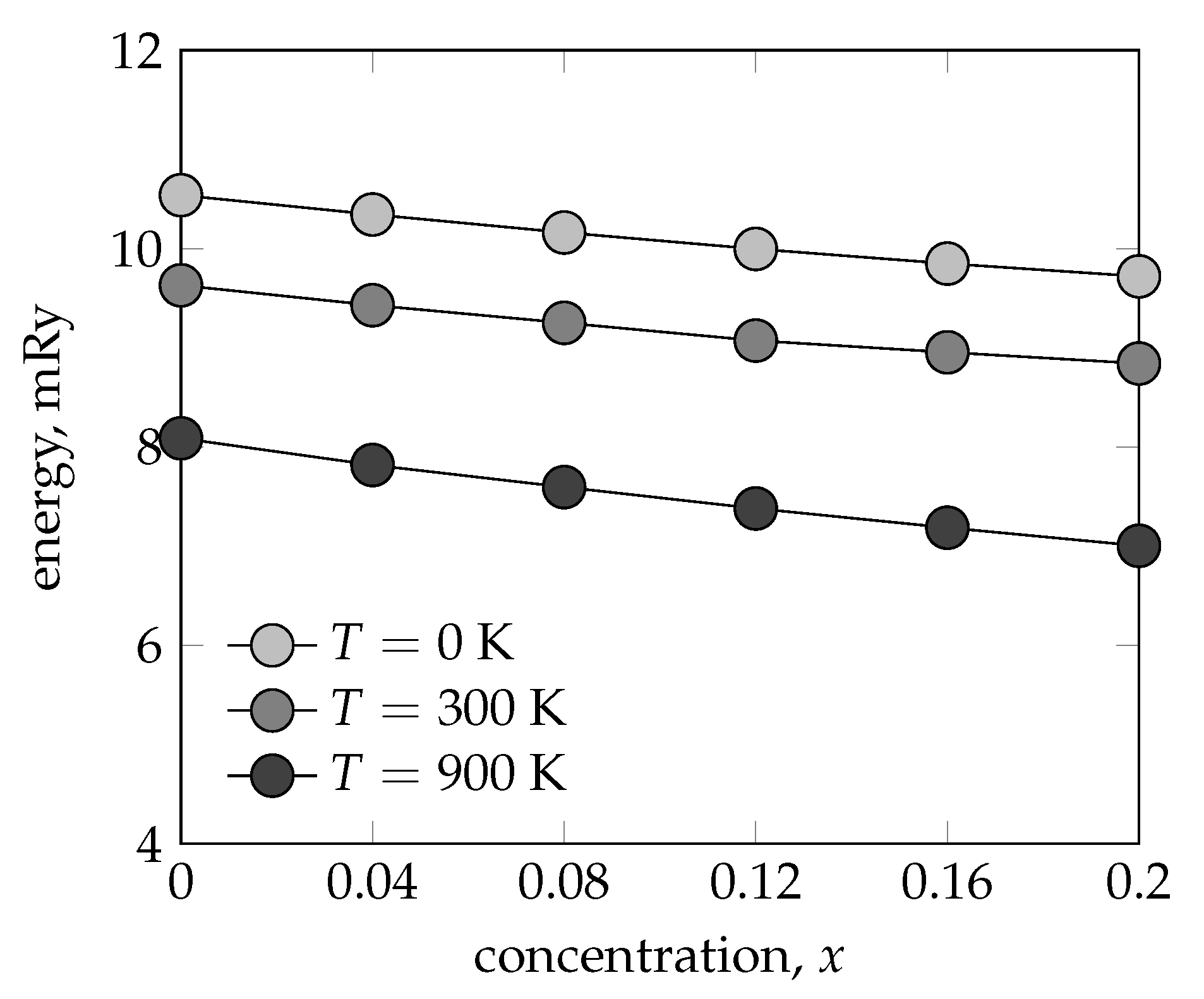
3.3. Stacking Fault and Mixing Energy
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, W.; Mu, W.; Wei, D.; Wu, H.; Yu, L.; Jonsson, T.; Larsson, H.; Mao, H. High corrosion resistance duplex fcc+hcp cobalt based entropic alloys: An experimental and theoretical investigation. Mater. Des. 2022, 223, 111166. [Google Scholar]
- Wang, X.F.; Zhang, Y.; Qiao, Y.; Chen, G.L. Novel microstructure and properties of multicomponent CoCrCuFeNiTix alloys. Intermetallics 2007, 15, 357–362. [Google Scholar]
- Hemphill, M.A.; Yuan, T.; Wang, G.Y.; Yeh, J.W.; Tsai, C.W.; Chuang, A.; Liaw, P.K. Fatigue behavior of Al0.5CoCrCuFeNi high entropy alloys. Acta Mater. 2012, 60, 5723–5734. [Google Scholar] [CrossRef]
- Chuang, M.-H.; Tsai, M.-H.; Wang, W.-R.; Lin, S.-J.; Yeh, J.-W. Microstructure and wear behavior of AlxCo1.5CrFeNi1.5Tiy high-entropy alloys. Acta Mater. 2011, 59, 6308–6317. [Google Scholar]
- Niu, C.; Zaddach, A.J.; Koch, C.C.; Irving, D.L. First principles exploration of near-equiatomic NiFeCrCo high entropy alloys. J. Alloys Compd. 2016, 672, 510–520. [Google Scholar] [CrossRef]
- Tian, F.; Varga, L.K.; Chen, N.; Delczeg, L.; Vitos, L. Ab initio investigation of high-entropy alloys of 3d elements. Phys. Rev. B 2013, 87, 075144. [Google Scholar]
- Tian, F.; Varga, L.K.; Shen, J.; Vitos, L. Calculating elastic constants in high-entropy alloys using the coherent potential approximation: Current issues and errors. Comput. Mater. Sci. 2016, 111, 350–358. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, K.; Xiao, H.; Chen, G.; Wang, Z.; Hu, T.; Fan, T.; Ma, L. Theoretical study of the mechanical properties of CrFeCoNiMox (0.1≤x≤0.3) alloys. RSC Adv. 2020, 10, 14080–14088. [Google Scholar] [CrossRef]
- Šebesta, J.; Carva, K.; Legut, D. Role of magnetism in the stability of the high-entropy alloy CoCrFeMnNi and its derivatives. Phys. Rev. Mater. 2019, 3, 124410. [Google Scholar]
- Cyrot, M. Phase transition in Hubbard model. Phys. Rev. Lett. 1970, 25, 871. [Google Scholar] [CrossRef]
- Gyorffy, B.L.; Pindor, A.J.; Staunton, J.; Stocks, G.M.; Winter, H. A first-principles theory of ferromagnetic phase transitions in metals. J. Phys. F Met. Phys. 1985, 15, 1337. [Google Scholar] [CrossRef]
- Moriya, T. Spin Fluctuations in Itinerant Electron Magnetism; Springer: Berlin/Heidelberg, Germany, 1985; Volume 56. [Google Scholar]
- Korzhavyi, P.A.; Sundman, B.; Selleby, M.; Johansson, B. Atomic, electronic, and magnetic structure of iron-based sigma-phases. MRS Online Proc. Lib. 2004, 842, 185–190. [Google Scholar]
- Kübler, J. Theory of Itinerant Electron Magnetism; Oxford Univeristy Press: New York, NY, USA, 2017; Volume 106. [Google Scholar]
- Ruban, A.V.; Khmelevskyi, S.; Mohn, P.; Johansson, B. Temperature-induced longitudinal spin fluctuations in Fe and Ni. Phys. Rev. B 2007, 75, 054402. [Google Scholar]
- Ruban, A.V.; Belonoshko, A.B.; Skorodumova, N.V. Impact of magnetism on Fe under Earth’s core conditions. Phys. Rev. B 2013, 87, 014405. [Google Scholar]
- Neding, B.; Gorbatov, O.I.; Tseng, J.-C.; Hedström, P. In Situ Bulk Observations and Ab Initio Calculations Revealing the Temperature Dependence of Stacking Fault Energy in Fe–Cr–Ni Alloys. Metall. Mater. Trans. A Phys. 2021, 52, 5357–5366. [Google Scholar]
- Cantor, B. Multicomponent high-entropy Cantor alloys. Prog. Mater. Sci. 2021, 120, 100754. [Google Scholar]
- Schneeweiss, O.; Friák, M.; Dudová, M.; Holec, D.; Šob, M.; Kriegner, D.; Holỳ, V.; Beran, P.; George, E.P.; Neugebauer, J.; et al. Magnetic properties of the CrMnFeCoNi high-entropy alloy. Phys. Rev. B 2017, 96, 014437. [Google Scholar]
- Zhang, Y.; Zuo, T.; Cheng, Y.; Liaw, P.K. High-entropy alloys with high saturation magnetization, electrical resistivity and malleability. Sci. Rep. 2013, 3, 1455. [Google Scholar] [CrossRef] [PubMed]
- Lucas, M.S.; Mauger, L.; Munoz, J.A.; Xiao, Y.; Sheets, A.O.; Semiatin, S.L.; Horwath, J.; Turgut, Z. Magnetic and vibrational properties of high-entropy alloys. J. Appl. Phys. 2011, 109, 07E307. [Google Scholar]
- Lucas, M.S.; Belyea, D.; Bauer, C.; Bryant, N.; Michel, E.; Turgut, Z.; Leontsev, S.O.; Horwath, J.; Semiatin, S.L.; McHenry, M.E.; et al. Thermomagnetic analysis of FeCoCrxNi alloys: Magnetic entropy of high-entropy alloys. J. Appl. Phys. 2013, 113, 17A923. [Google Scholar]
- Borkar, T.; Chaudhary, V.; Gwalani, B.; Choudhuri, D.; Mikler, C.V.; Soni, V.; Alam, T.; Ramanujan, R.; Banerjee, R. A combinatorial approach for assessing the magnetic properties of high entropy alloys: Role of Cr in AlCoxCr1-xFeNi. Adv. Eng. Mater. 2017, 19, 1700048. [Google Scholar]
- Mishra, R.K.; Kumari, P.; Gupta, A.K.; Shahi, R.R. Design and development of Co35Cr5Fe20-xNi20+xTi20 High Entropy Alloy with excellent magnetic softness. J. Alloys Compd. 2021, 889, 161773. [Google Scholar]
- Grilli, M.L.; Bellezze, T.; Gamsjäger, E.; Rinaldi, A.; Novak, P.; Balos, S.; Piticescu, R.R.; Ruello, M.L. Solutions for critical raw materials under extreme conditions: A review. Materials 2017, 10, 285. [Google Scholar] [CrossRef] [PubMed]
- Airhart, E. Alternatives to Cobalt, the Blood Diamond of Batteries. Wired Mag. 2018. Available online: https://www.wired.com/story/alternatives-to-cobalt-the-blood-diamond-of-batteries/ (accessed on 22 February 2025).
- Nemery, B.; Abraham, J.L. Hard metal lung disease: Still hard to understand. Am. J. Respir. Crit. Care Med. 2007, 176, 2–3. [Google Scholar] [PubMed]
- Wan, R.; Mo, Y.; Zhang, Z.; Jiang, Z.M.; Tang, S.; Zhang, Q. Cobalt nanoparticles induce lung injury, DNA damage and mutations in mice. Part. Fibre Toxicol. 2017, 14, 1–15. [Google Scholar]
- Linna, A.; Oksa, P.; Groundstroem, K.; Halkosaari, M.; Palmroos, P.; Huikko, S.; Uitti, J. Exposure to Cobalt in the production of Cobalt and Cobalt compounds and its effect on the heart. Occup. Environ. Med. 2004, 61, 877–885. [Google Scholar]
- Lee, J.; Kitchaev, D.A.; Kwon, D.-H.; Lee, C.-W.; Papp, J.K.; Liu, Y.-S.; Lun, Z.; Clement, R.J.; Shi, T.; McCloskey, B.D. Reversible Mn2+/Mn4+ double redox in lithium-excess cathode materials. Nature 2018, 556, 185–190. [Google Scholar]
- Kallmeier, F.; Kempe, R. Manganese complexes for (de)hydrogenation catalysis: A comparison to cobalt and iron catalysts. Angew. Chem. Int. Ed. 2018, 57, 46–60. [Google Scholar]
- Tien, J.K.; Howson, T.E.; Chen, G.L.; Xie, X.S. Cobalt availability and superalloys. J. Meteorol. 1980, 32, 12–20. [Google Scholar]
- Fernandes, C.M.; Senos, A.M.R. Cemented carbide phase diagrams: A review. Int. J. Refract. Hard Met. 2011, 29, 405–418. [Google Scholar]
- Ojo-Kupoluyi, O.J.; Tahir, S.M.; Baharudin, B.T.H.T.; Hanim, M.A.A.; Anuar, M.S. Mechanical properties of WC-based hardmetals bonded with iron alloys–A review. Mater. Sci. Technol. 2017, 33, 507–517. [Google Scholar]
- Holmström, E.; Lizarraga, R.; Linder, D.; Salmasi, A.; Wang, W.; Kaplan, B.; Mao, H.; Larsson, H.; Vitos, L. High entropy alloys: Substituting for Cobalt in cutting edge technology. Appl. Mater. Today 2018, 12, 322–329. [Google Scholar] [CrossRef]
- Moruzzi, V.L.; Janak, J.F.; Schwarz, K. Calculated thermal properties of metals. Phys. Rev. B 1988, 37, 790. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar]
- Vitos, L.; Skriver, H.L.; Johansson, B.; Kollár, J. Application of the exact muffin-tin orbitals theory: The spherical cell approximation. Comput. Mater. Sci. 2000, 18, 24–38. [Google Scholar]
- Vitos, L. Total-energy method based on the exact muffin-tin orbitals theory. Phys. Rev. B 2001, 64, 014107. [Google Scholar]
- Vitos, L.; Abrikosov, I.A.; Johansson, B. Anisotropic lattice distortions in random alloys from first-principles theory. Phys. Rev. Lett. 2001, 87, 156401. [Google Scholar]
- Gyorffy, B.L. Coherent-potential approximation for a nonoverlapping-muffin-tin-potential model of random substitutional alloys. Phys. Rev. B 1972, 5, 2382. [Google Scholar]
- Soven, P. Coherent-potential model of substitutional disordered alloys. Phys. Rev. 1967, 156, 809. [Google Scholar]
- Ruban, A.V.; Skriver, H.L. Screened Coulomb interactions in metallic alloys. I. Universal screening in the atomic-sphere approximation. Phys. Rev. B 2002, 66, 024201. [Google Scholar] [CrossRef]
- Ruban, A.V.; Simak, S.I.; Korzhavyi, P.A.; Skriver, H.L. Screened Coulomb interactions in metallic alloys. II. Screening beyond the single-site and atomic-sphere approximations. Phys. Rev. B 2002, 66, 024202. [Google Scholar] [CrossRef]
- Abrikosov, I.A.; Simak, S.I.; Johansson, B.; Ruban, A.V.; Skriver, H.L. Locally self-consistent Green’s function approach to the electronic structure problem. Phys. Rev. B 1997, 56, 9319. [Google Scholar] [CrossRef]
- Peil, O.E.; Ruban, A.V.; Johansson, B. Self-consistent supercell approach to alloys with local environment effects. Phys. Rev. B 2012, 85, 165140. [Google Scholar] [CrossRef]
- Ruban, A.V. On segregation in multicomponent alloys: Surface segregation in austenite and FeCrCoNiMn alloys. Comput. Mater. Sci. 2021, 187, 110080. [Google Scholar] [CrossRef]
- Ma, D.; Grabowski, B.; Körmann, F.; Neugebauer, J.; Raabe, D. Ab initio thermodynamics of the CoCrFeMnNi high entropy alloy: Importance of entropy contributions beyond the configurational one. Acta Mater. 2015, 100, 90–97. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Zhu, Z.G.; Ma, K.H.; Yang, X.; Shek, C.H. Annealing effect on the phase stability and mechanical properties of (FeNiCrMn)(100-x)Cox high entropy alloys. J. Alloys Compd. 2017, 695, 2945–2950. [Google Scholar] [CrossRef]
- Tracy, C.L.; Park, S.; Rittman, D.R.; Zinkle, S.J.; Bei, H.; Lang, M.; Ewing, R.C.; Mao, W.L. High pressure synthesis of a hexagonal close-packed phase of the high-entropy alloy CrMnFeCoNi. Nat. Commun. 2017, 8, 15634. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Wu, Y.; Lou, H.; Zeng, Z.; Prakapenka, V.B.; Greenberg, E.; Ren, Y.; Yan, J.; Okasinski, J.S.; Liu, X.; et al. Polymorphism in a high-entropy alloy. Nat. Commun. 2017, 8, 15687. [Google Scholar] [CrossRef]
- Vitos, L.; Nilsson, J.-O.; Johansson, B. Alloying effects on the stacking fault energy in austenitic stainless steels from first-principles theory. Acta Mater. 2006, 54, 3821–3826. [Google Scholar]
- Gorbatov, O.I.; Gornostyrev, Y.N.; Korzhavyi, P.A.; Ruban, A.V. Ab initio modeling of decomposition in iron based alloys. Phys. Met. Metallogr. 2016, 117, 1293–1327. [Google Scholar]
- Birch, F. The effect of pressure upon the elastic parameters of isotropic solids, according to Murnaghan’s theory of finite strain. J. Appl. Phys. 1938, 9, 279–288. [Google Scholar]
- Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 1947, 71, 809. [Google Scholar]
- Glensk, A.; Grabowski, B.; Hickel, T.; Neugebauer, J. Understanding anharmonicity in fcc materials: From its origin to ab initio strategies beyond the quasiharmonic approximation. Phys. Rev. Lett. 2015, 114, 195901. [Google Scholar] [CrossRef]
- Hafner, J. Atomic-scale computational materials science. Acta Mater. 2000, 48, 71–92. [Google Scholar]
- Wassermann, E.F.; Acet, M. Invar and anti-Invar: Magnetovolume effects in Fe-based alloys revisited. In Magnetism and Structure in Functional Materials; Springer: Berlin/Heidelberg, Germany, 2005; pp. 177–197. [Google Scholar]
- Ruban, A.V.; Abrikosov, I.A. Configurational thermodynamics of alloys from first principles: Effective cluster interactions. Rep. Prog. Phys. 2008, 71, 046501. [Google Scholar]
- He, S.; Scheiber, D.; Jechtl, T.; Moitzi, F.; Peil, O.; Romaner, L.; Zamberger, S.; Povoden-Karadeniz, E.; Razumovskiy, V.; Ruban, A.V. Solubility and segregation of B in paramagnetic fcc Fe. Phys. Rev. Mater. 2022, 6, 023604. [Google Scholar]
- Haas, P.; Tran, F.; Blaha, P. Calculation of the lattice constant of solids with semilocal functionals. Phys. Rev. B 2009, 79, 085104. [Google Scholar] [CrossRef]
- Laplanche, G.; Gadaud, P.; Horst, O.; Otto, F.; Eggeler, G.; George, E.P. Temperature dependencies of the elastic moduli and thermal expansion coefficient of an equiatomic, single-phase CoCrFeMnNi high-entropy alloy. J. Alloys Compd. 2015, 623, 348–353. [Google Scholar] [CrossRef]
- Reyes-Huamantinco, A.; Puschnig, P.; Ambrosch-Draxl, C.; Peil, O.E.; Ruban, A.V. Stacking-fault energy and anti-Invar effect in Fe-Mn alloy from first principles. Phys. Rev. B 2012, 86, 060201. [Google Scholar] [CrossRef]
- Razumovskiy, V.I.; Reyes-Huamantinco, A.; Puschnig, P.; Ruban, A.V. Effect of thermal lattice expansion on the stacking fault energies of fcc Fe and Fe75Mn25 alloy. Phys. Rev. B 2016, 93, 054111. [Google Scholar] [CrossRef]
- Acet, M. Inducing strong magnetism in Cr20Mn20Fe20Co20Ni20 high-entropy alloys by exploiting its anti-Invar property. AIP Adv. 2019, 9, 095037. [Google Scholar]
- Mehl, M.J.; Osburn, J.E.; Papaconstantopoulos, D.A.; Klein, B.M. Structural properties of ordered high-melting-temperature intermetallic alloys from first-principles total-energy calculations. Phys. Rev. B 1990, 41, 10311. [Google Scholar] [CrossRef]
- Mehl, M.J.; Klein, B.M.; Papaconstantopoulos, D.A. Intermetallic compounds: Principle and practice. Principles 1995, 1, 195–210. [Google Scholar]
- Teramoto, T.; Yamada, K.; Ito, R.; Tanaka, K. Monocrystalline elastic constants and their temperature dependences for equi-atomic Cr-Mn-Fe-Co-Ni high-entropy alloy with the face-centered cubic structure. J. Alloys Compd. 2019, 777, 1313–1318. [Google Scholar] [CrossRef]
- Vitos, L. Computational Quantum Mechanics for Materials Engineers: The EMTO Method and Applications; Springer: London, UK, 2007. [Google Scholar]
- Nguyen–Manh, D.; Mrovec, M.; Fitzgerald, S.P. Dislocation driven problems in atomistic modelling of materials. Mater. Trans. 2008, 49, 2497–2506. [Google Scholar] [CrossRef]
- Sun, X.; Lu, S.; Xie, R.; An, X.; Li, W.; Zhang, T.; Liang, C.; Ding, X.; Wang, Y.; Zhang, H.; et al. Can experiment determine the stacking fault energy of metastable alloys? Mater. Des. 2021, 199, 109396. [Google Scholar]
- Denteneer, P.J.H.; van Haeringen, W. Stacking-fault energies in semiconductors from first-principles calculations. J. Phys. C Solid State Phys. 1987, 20, L883. [Google Scholar]
- Razumovskiy, V.I.; Hahn, C.; Lukas, M.; Romaner, L. Ab initio study of elastic and mechanical properties in FeCrMn alloys. Materials 2019, 12, 1129. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]

| x | 0.00 | 0.04 | 0.08 | 0.12 | 0.16 | 0.20 |
|---|---|---|---|---|---|---|
| PM (0 K) | 2.6070 | 2.6066 | 2.6059 | 2.6051 | 2.6040 | 2.6027 |
| PM (300 K) | 2.6292 | 2.6276 | 2.6257 | 2.6249 | 2.6217 | 2.6198 |
| PM (900 K) | 2.6795 | 2.6757 | 2.6725 | 2.6690 | 2.6655 | 2.6619 |
| bcc-Cr | fcc-Mn | bcc-Fe | hcp-Co | fcc-Ni | |
|---|---|---|---|---|---|
| AFM | AFM | FM | FM | FM | |
| EMTO | 2.86 | 3.62 | 2.86 | 2.49/4.07 | 3.54 |
| VASP | 2.87 | 3.58 | 2.83 | 2.49/4.02 | 3.52 |
| Exp. [77] | 2.88 | - | 2.87 | 2.51/4.07 | 3.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Johansson, G.; Kuorak, J.-M.; Gorbatov, O.; Etz, C. The Effect of Reduced Co Content in CrMnFeCoNi Alloys: A First Principles Study. Metals 2025, 15, 362. https://doi.org/10.3390/met15040362
Johansson G, Kuorak J-M, Gorbatov O, Etz C. The Effect of Reduced Co Content in CrMnFeCoNi Alloys: A First Principles Study. Metals. 2025; 15(4):362. https://doi.org/10.3390/met15040362
Chicago/Turabian StyleJohansson, Gustav, Johan-Michael Kuorak, Oleg Gorbatov, and Corina Etz. 2025. "The Effect of Reduced Co Content in CrMnFeCoNi Alloys: A First Principles Study" Metals 15, no. 4: 362. https://doi.org/10.3390/met15040362
APA StyleJohansson, G., Kuorak, J.-M., Gorbatov, O., & Etz, C. (2025). The Effect of Reduced Co Content in CrMnFeCoNi Alloys: A First Principles Study. Metals, 15(4), 362. https://doi.org/10.3390/met15040362






