Ab Initio Investigation of the Stability, Electronic, Mechanical, and Transport Properties of New Double Half Heusler Alloys Ti2Pt2ZSb (Z = Al, Ga, In)
Abstract
1. Introduction
2. Computational Methods
3. Results
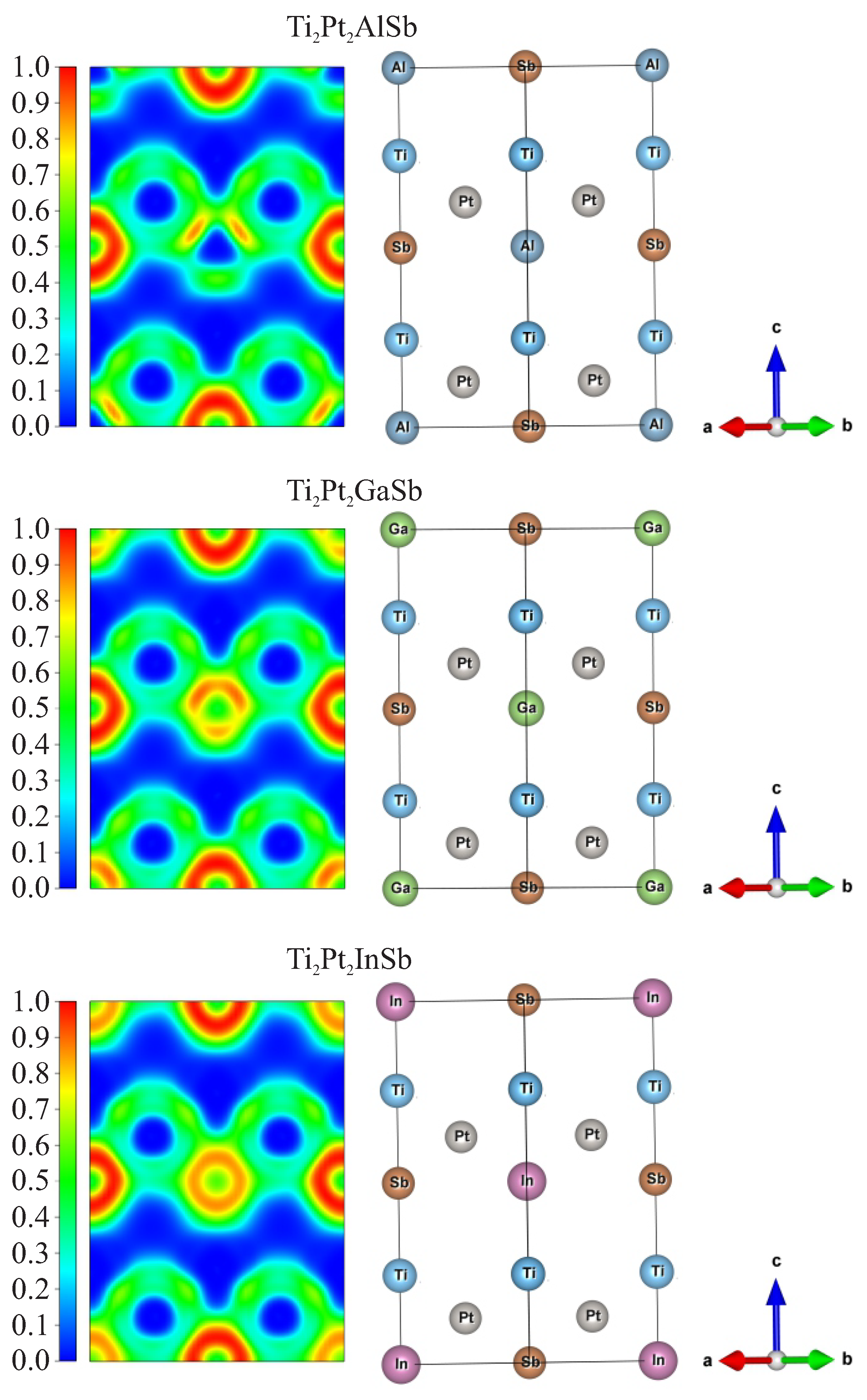
3.1. Structural Properties
3.2. Vibrational Properties
3.3. Elastic Properties
| Compounds | B | G | E | |||||
|---|---|---|---|---|---|---|---|---|
| Ti2Pt2AlSb | 139 | 58 | 152 | 0.318 | 5.3 | 2.5 | 0.01 | 2.26 |
| Ti2Pt2GaSb | 140 | 54 | 144 | 0.329 | 4.5 | 2.4 | 0.01 | 3.25 |
| Ti2Pt2InSb | 135 | 51 | 136 | 0.331 | 4.2 | 2.3 | 0.01 | 1.38 |
| TiPtSn | 146 | 57 | 150 | 0.329 | 4.7 | – | 0.00 | 1.72 |
3.4. Thermal Conductivity
3.5. Electronic Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Webster, P.J. Heusler alloys. Contemp. Phys. 1969, 10, 559–577. [Google Scholar] [CrossRef]
- Tavares, S.; Yang, K.; Meyers, M.A. Heusler alloys: Past, properties, new alloys, and prospects. Prog. Mater. Sci. 2023, 132, 101017. [Google Scholar] [CrossRef]
- Elphick, K.; Frost, W.; Samiepour, M.; Kubota, T.; Takanashi, K.; Sukegawa, H.; Mitani, S.; Hirohata, A. Heusler alloys for spintronic devices: Review on recent development and future perspectives. Sci. Technol. Adv. Mater. 2021, 22, 235–271. [Google Scholar] [CrossRef]
- Rogl, G.; Grytsiv, A.; Gürth, M.; Tavassoli, A.; Ebner, C.; Wünschek, A.; Puchegger, S.; Soprunyuk, V.; Schranz, W.; Bauer, E.; et al. Mechanical properties of half-Heusler alloys. Acta Mater. 2016, 107, 178–195. [Google Scholar] [CrossRef]
- Abuova, A.; Merali, N.; Abuova, F.; Khovaylo, V.; Sagatov, N.; Inerbaev, T. Electronic properties and chemical bonding in V2FeSi and Fe2VSi Heusler alloys. Crystals 2022, 12, 1546. [Google Scholar] [CrossRef]
- Abuova, F.; Inerbaev, T.; Abuova, A.; Merali, N.; Soltanbek, N.; Kaptagay, G.; Seredina, M.; Khovaylo, V. Structural, electronic, and magnetic properties of Mn2Co1−xVXZ (Z = Ga, Al) Heusler alloys: An insight from DFT study. Magnetochemistry 2021, 7, 159. [Google Scholar] [CrossRef]
- Casper, F.; Graf, T.; Chadov, S.; Balke, B.; Felser, C. Half-Heusler compounds: Novel materials for energy and spintronic applications. Semicond. Sci. Technol. 2012, 27, 063001. [Google Scholar] [CrossRef]
- Tangirbergen, A.; Amangeldi, N.; Revankar, S.T.; Yergaliuly, G. A review of irradiation-induced hardening in FeCrAl alloy systems for accident-tolerant fuel cladding. Nucl. Eng. Des. 2024, 429, 113659. [Google Scholar] [CrossRef]
- Anand, S.; Wood, M.; Xia, Y.; Wolverton, C.; Snyder, G.J. Double half-Heuslers. Joule 2019, 3, 1226–1238. [Google Scholar] [CrossRef]
- Zeier, W.G.; Schmitt, J.; Hautier, G.; Aydemir, U.; Gibbs, Z.M.; Felser, C.; Snyder, G.J. Engineering half-Heusler thermoelectric materials using Zintl chemistry. Nat. Rev. Mater. 2016, 1, 16032. [Google Scholar] [CrossRef]
- Rached, Y.; Caid, M.; Merabet, M.; Benalia, S.; Rached, H.; Djoudi, L.; Mokhtari, M.; Rached, D. A comprehensive computational investigations on the physical properties of TiXSb (X: Ru, Pt) half-Heusler alloys and Ti2RuPtSb2 double half-Heusler. Int. J. Quantum Chem. 2022, 122, e26875. [Google Scholar] [CrossRef]
- Bouhadjer, K.; Boudjelal, M.; Matougui, M.; Bentata, S.; Lantri, T.; Batouche, M.; Seddik, T.; Khenata, R.; Bouadjemi, B.; Bin Omran, S.; et al. Structural, optoelectronic, thermodynamic and thermoelectric properties of double half-Heusler (DHH) Ti2FeNiSb2 and Ti2Ni2InSb compounds: A TB-mBJ study. Chin. J. Phys. 2023, 85, 508–523. [Google Scholar] [CrossRef]
- Hasan, R.; Park, T.; Kim, S.; Kim, H.-S.; Jo, S.; Lee, K.H. Enhanced Thermoelectric Properties of Ti2FeNiSb2 Double Half-Heusler Compound by Sn Doping. Adv. Energy Sustain. Res. 2022, 3, 2100206. [Google Scholar] [CrossRef]
- Hassan, M.A.; El-Khouly, A.; Elsehly, E.M.; Almutib, E.N.; Elshamndy, S.K.; Serhiienko, I.; Argunov, E.V.; Sedegov, A.; Karpenkov, D.; Pashkova, D. Transport and thermoelectric properties of melt spinning synthesized M2FeNiSb2 (M = Ti, Hf) double half-Heusler alloys. Mater. Res. Bull. 2023, 164, 112246. [Google Scholar] [CrossRef]
- Charifi, Z.; Baaziz, H.; Uğur, Ş.; Uğur, G. Prediction of the electronic structure, optical and vibrational properties of ScXCo2Sb2 (X = V, Nb, Ta) double half-Heusler alloys: A theoretical study. Indian J. Phys. 2023, 97, 413–428. [Google Scholar] [CrossRef]
- Boudjelal, M.; Bouhadjer, K.; Matougui, M.; Bentata, S.; Srivastata, V.; Bin-Omran, S.; Khenata, R. Ab initio prediction of the structural, optoelectronic, and thermoelectric properties of double half-Heusler (DHH) ScXRh2Bi2 (X = Nb, Ta) alloys DFT study results. Indian J. Phys. 2024, 98, 3141–3154. [Google Scholar] [CrossRef]
- Mekhtiche, M.; Matougui, M.; Houari, M.; Bouadjemi, B.; Lantri, T.; Boudjelal, M.; Bentata, S. Predictive study of the new double half-Heusler compounds Hf2FeNiSb2, Nb2Co2GaSb, and ScNbCo2Sb2, promising candidates for thermoelectric applications. Indian J. Phys. 2024, 98, 3121–3129. [Google Scholar] [CrossRef]
- Diaf, M.; Righi, H.; Rached, H.; Rached, D.; Beddiaf, R. Ab initio study of the properties of Ti2PdFe (Ru) Sb2 double half-Heusler semiconducting alloys. J. Electron. Mater. 2023, 52, 6514–6529. [Google Scholar] [CrossRef]
- Ding, H.; Li, X.; Feng, Y.; Wu, B. Electronic structure, magnetism and disorder effect in double half-Heusler alloy Mn2FeCoSi2. J. Magn. Magn. Mater. 2022, 555, 169367. [Google Scholar] [CrossRef]
- Douinat, O.; Boucherdoud, A.; Seghier, A.; Houari, M.; Mesbah, S.; Lantri, T.; Bestani, B. Theoretical investigation of the physical, mechanical, and thermal properties of Zr2XBiNi2 (X: Al, Ga) double half-Heusler alloys. J. Mater. Res. 2023, 38, 4509–4521. [Google Scholar] [CrossRef]
- Berarma, K.; Essaoud, S.S.; Al Azar, S.; Al-Reyahi, A.Y.; Mousa, A.A.; Mufleh, A. Computational characterization of structural, optoelectronic, and thermoelectric properties of some double half-Heusler alloys X2FeY′Sb2 (X: Hf, Zr; Y′: Ni, Pd). Phase Transitions 2023, 96, 806–821. [Google Scholar] [CrossRef]
- Surucu, G.; Isik, M.; Candan, A.; Wang, X.; Gullu, H.H. Investigation of structural, electronic, magnetic, and lattice dynamical properties for XCoBi (X: Ti, Zr, Hf) half-Heusler compounds. Phys. B Condens. Matter 2020, 587, 412146. [Google Scholar] [CrossRef]
- Ma, H.; Yang, C.-L.; Wang, M.-S.; Ma, X.-G.; Yi, Y.-G. Effect of M elements (M = Ti, Zr, and Hf) on thermoelectric performance of the half-Heusler compounds MCoBi. J. Phys. D Appl. Phys. 2019, 52, 255501. [Google Scholar] [CrossRef]
- Zhu, H.; He, R.; Mao, J.; Zhu, Q.; Li, C.; Sun, J.; Ren, W.; Wang, Y.; Liu, Z.; Tang, Z.; et al. Discovery of ZrCoBi based half-Heuslers with high thermoelectric conversion efficiency. Nat. Commun. 2018, 9, 2497. [Google Scholar] [CrossRef]
- Radouan, D.; Besbes, A.; Bestani, B. Investigation on electronic and thermoelectric properties of (P, As, Sb) doped ZrCoBi. East Eur. J. Phys. 2021, 1, 27–33. [Google Scholar]
- Mekki, H.; Baaziz, H.; Charifi, Z.; Ghellab, T.; Genç, A.E.; Uğur, Ş.; Uğur, G. Properties of the double half-Heusler alloy ScNbNi2Sn2 with respect to structural, electronic, optical, and thermoelectric aspects. Solid State Commun. 2023, 363, 115103. [Google Scholar] [CrossRef]
- Saad Essaoud, S.; Bouhemadou, A.; Allali, D.; Ketfi, M.E.; Radjai, M.; Bin-Omran, S. An Ab Initio Investigation of the Structural Stability, Thermodynamic, Optoelectronic, and Thermoelectric Properties of LuXNi2Sn2 (X = V, Nb, Ta) Double Half Heusler Materials. J. Inorg. Organomet. Polym. 2024, 34, 885–902. [Google Scholar] [CrossRef]
- Diaf, M.; Righi, H.; Beddiaf, R.; Djaballah, Y.; Rached, H. Ab initio investigation of the structural, mechanical, electronic, thermodynamic, and optical properties of V2FeNiGe2 and Hf2FeNiSb2 double half-Heusler compounds. Can. J. Phys. 2024, 103, 288–301. [Google Scholar] [CrossRef]
- Liu, X.; Wang, S.; Dong, Z.; Chang, Y.; Zhang, J.; Zhang, X.; Luo, J. Discovery of (Sc, V) CoSb double half-Heusler alloys with low lattice thermal conductivity. J. Alloys Compd. 2025, 1010, 178078. [Google Scholar] [CrossRef]
- Imasato, K.; Sauerschnig, P.; Miyata, M.; Ishida, T.; Yamamoto, A.; Ohta, M. Effects of the Fe/Ni ratio in double half-Heusler composition HfFe1−xNixSb. J. Mater. Chem. C 2025, 13, 2154–2164. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Mastrikov, Y.A.; Chuklina, N.G.; Sokolov, M.N.; Popov, A.I.; Gryaznov, D.V.; Kotomin, E.A.; Maier, J. Small radius electron and hole polarons in PbX2 (X = F, Cl, Br) crystals: A computational study. J. Mater. Chem. C 2021, 9, 16536–16544. [Google Scholar] [CrossRef]
- Mastrikov, Y.A.; Gryaznov, D.; Sokolov, M.N.; Zvejnieks, G.; Popov, A.I.; Eglitis, R.I.; Kotomin, E.A.; Ananyev, M.V. Oxygen Vacancy Formation and Migration within the Antiphase Boundaries in Lanthanum Scandate-Based Oxides: Computational Study. Materials 2022, 15, 2695. [Google Scholar] [CrossRef]
- Kaptagay, G.A.; Satanova, B.M.; Abuova, A.U.; Konuhova, M.; Zakiyeva, Z.Y.; Tolegen, U.Z.; Koilyk, N.O.; Abuova, F.U. Effect of rhodium doping for photocatalytic activity of barium titanate. Opt. Mater. X 2025, 25, 100382. [Google Scholar] [CrossRef]
- Inerbaev, T.M.; Abuova, A.U.; Zakiyeva, Z.Y.; Abuova, F.U.; Mastrikov, Y.A.; Sokolov, M.; Gryaznov, D.; Kotomin, E.A. Effect of Rh doping on optical absorption and oxygen evolution reaction activity on BaTiO3 (001) surfaces. Molecules 2024, 29, 2707. [Google Scholar] [CrossRef]
- Inerbaev, T.M.; Graupner, D.R.; Abuova, A.U.; Abuova, F.U.; Kilin, D.S. Optical properties of BaTiO3 at room temperature: DFT modelling. RSC Adv. 2025, 15, 5405–5412. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Fan, T.; Oganov, A.R. AICON: A program for calculating thermal conductivity quickly and accurately. Comput. Phys. Commun. 2020, 251, 107074. [Google Scholar] [CrossRef]
- Anand, S.; Xia, K.; Hegde, V.I.; Aydemir, U.; Kocevski, V.; Zhu, T.; Wolverton, C.; Snyder, G.J. A valence balanced rule for discovery of 18-electron half-Heuslers with defects. Energy Environ. Sci. 2018, 11, 1480–1488. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.-X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
- Voigt, W. Lehrbuch der Kristallphysik (Textbook of Crystal Physics); BG Teubner: Leipzig, Germany; Berlin, Germany, 1928. [Google Scholar]
- Reuss, A.J.Z. Calculation of the flow limits of mixed crystals on the basis of the plasticity of monocrystals. Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Chen, H.; Yang, L.; Long, J. First-principles investigation of the elastic, Vickers hardness, and thermodynamic properties of Al–Cu intermetallic compounds. Superlattices Microstruct. 2015, 79, 156–165. [Google Scholar] [CrossRef]
- Frantsevich, I.N. Elastic constants and elastic moduli of metals and insulators. In Reference Book; Naukova Dumka: Kyiv, Ukraine, 1982. [Google Scholar]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Universal elastic anisotropy index. Phys. Rev. Lett. 2008, 101, 055504. [Google Scholar] [CrossRef]
- Chen, X.-Q.; Niu, H.; Li, D.; Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, B.; Zhao, Z. Microscopic theory of hardness and design of novel superhard crystals. Int. J. Refract. Met. Hard Mater. 2012, 33, 93–106. [Google Scholar] [CrossRef]
- Niu, H.; Niu, S.; Oganov, A.R. Simple and accurate model of fracture toughness of solids. J. Appl. Phys. 2019, 125, 6. [Google Scholar] [CrossRef]
- Thompson, R.P.; Clegg, W.J. Predicting whether a material is ductile or brittle. Curr. Opin. Solid State Mater. Sci. 2018, 22, 3–100. [Google Scholar] [CrossRef]
- Dasmahapatra, A.; Daga, L.E.; Karttunen, A.J.; Maschio, L.; Casassa, S. Key role of defects in thermoelectric performance of TiMSn (M = Ni, Pd, and Pt) half-Heusler alloys. J. Phys. Chem. C 2020, 124, 14997–15006. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhao, L.-D. Charge and phonon transport in PbTe-based thermoelectric materials. npj Quantum Mater. 2018, 3, 55. [Google Scholar] [CrossRef]
- Zhai, J.; Wang, T.; Wang, H.; Su, W.; Wang, X.; Chen, T.; Wang, C. Strategies for optimizing the thermoelectricity of PbTe alloys. Chin. Phys. B 2018, 27, 047306. [Google Scholar] [CrossRef]
- Xi, J.; Dong, Z.; Gao, M.; Luo, J.; Yang, J. Screening of half-Heuslers with temperature-induced band convergence and enhanced thermoelectric properties. arXiv 2024, arXiv:2407.00433. [Google Scholar]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Phys. Chem. C 2006, 125, 224106. [Google Scholar] [CrossRef]
- Gautier, R.; Zhang, X.; Hu, L.; Yu, L.; Lin, Y.; Sunde, T.O.L.; Chon, D.; Poeppelmeier, K.R.; Zunger, A. Prediction and accelerated laboratory discovery of previously unknown 18-electron ABX compounds. Nat. Chem. 2015, 7, 308–316. [Google Scholar] [CrossRef]
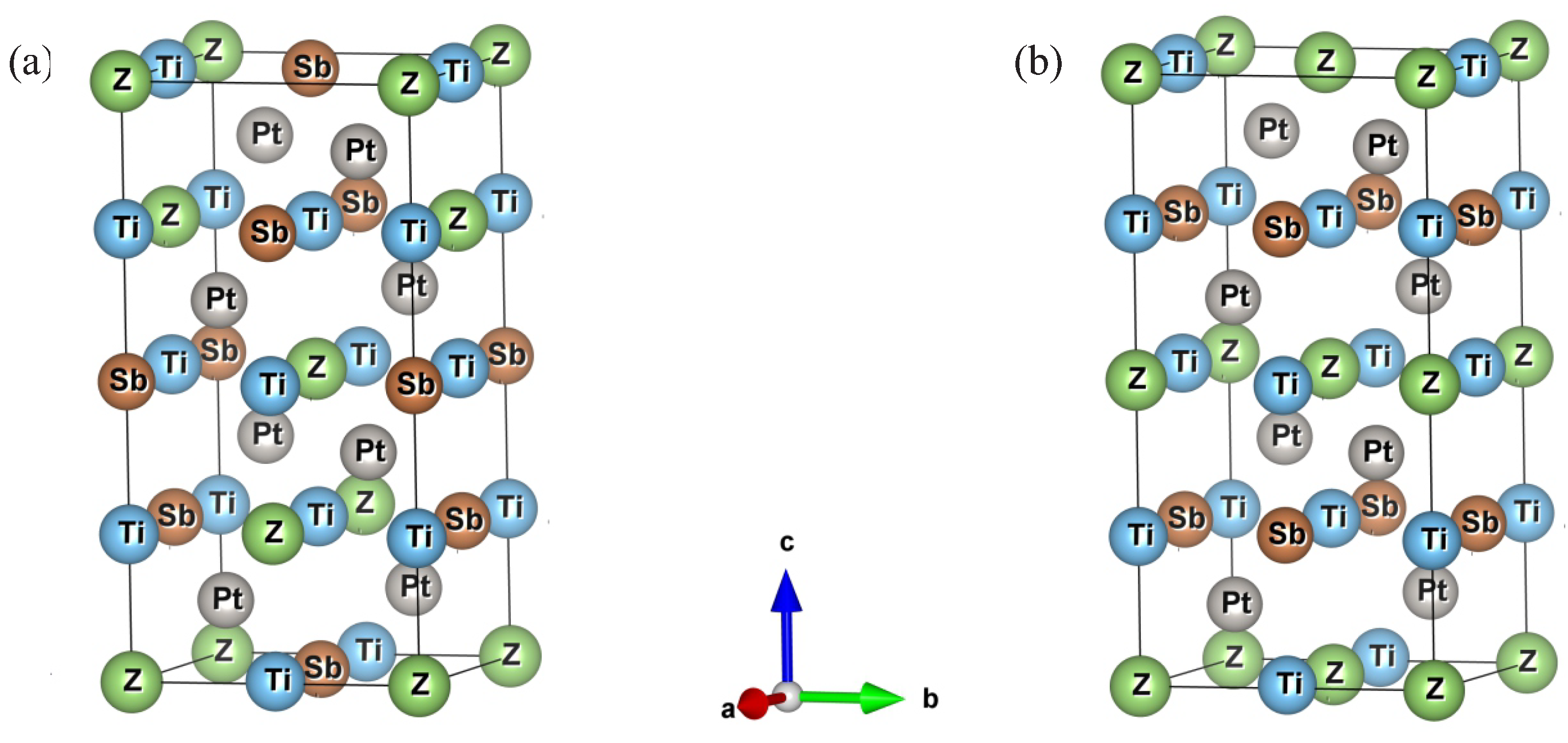
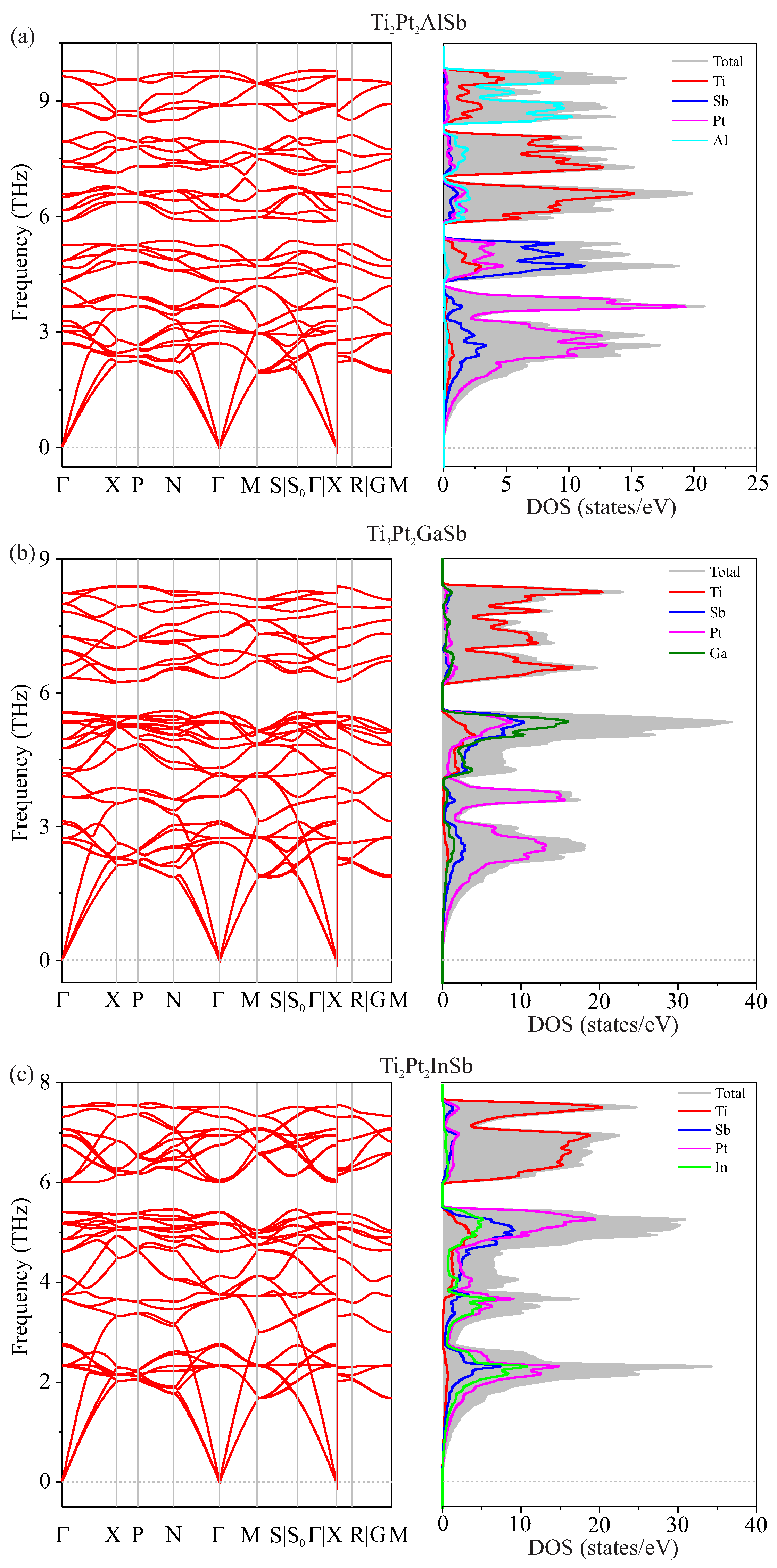
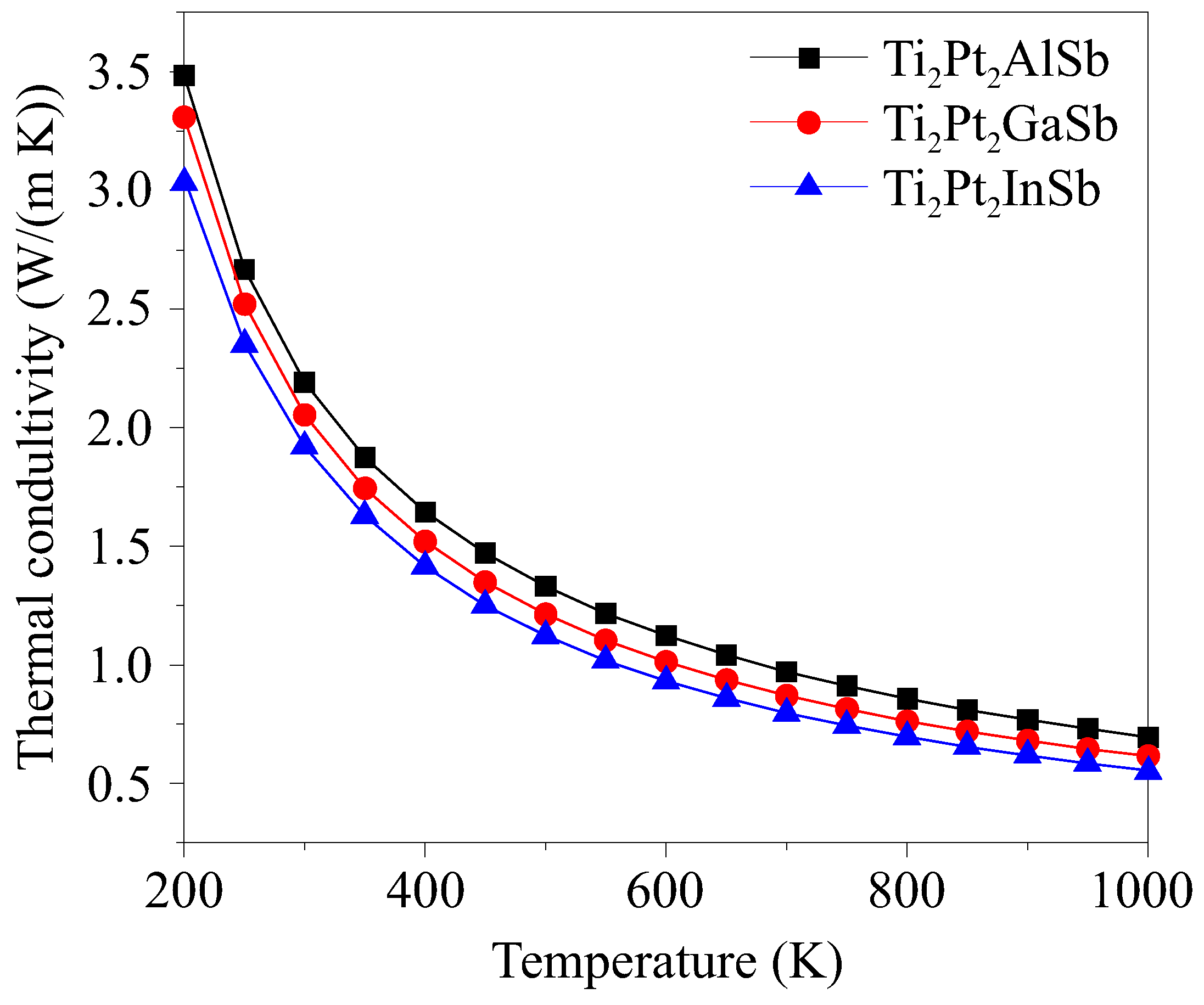
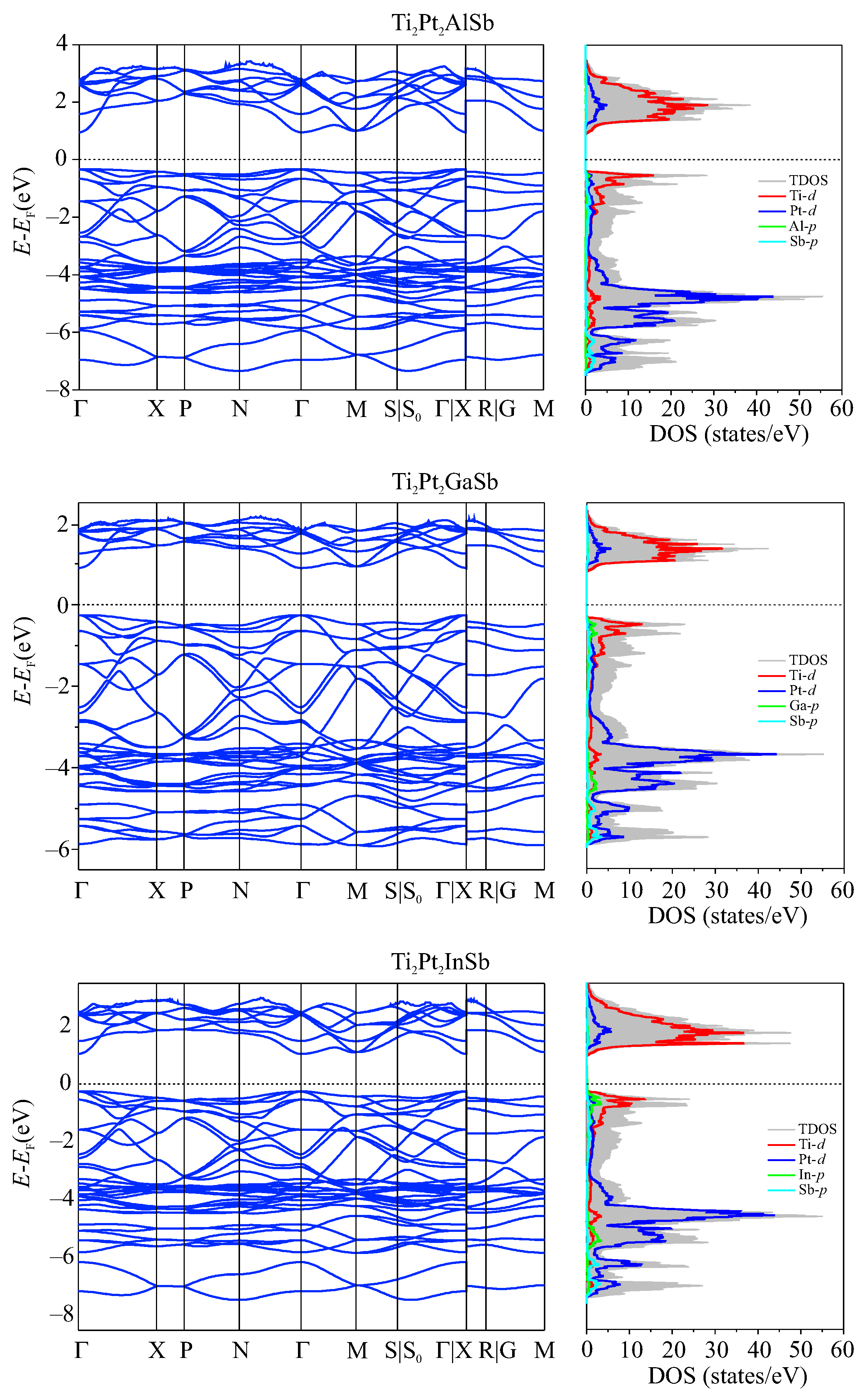
| Compounds | Ti2Pt2AlSb | Ti2Pt2GaSb | Ti2Pt2InSb | |
| Lattice | a = b | 6.120 | 6.121 | 5.905 |
| parameter | c | 12.228 | 12.216 | 11.826 |
| Coordinates | x | y | z | |
| Atoms | Ti | 0 | 0.5 | 0.495 |
| Pt | 0.75 | 0.25 | 0.625 | |
| Al/Ga/In | 0 | 0.5 | 0.25 | |
| Sb | 0 | 0 | 0.5 | |
| Mulliken | Activity | , THz | ||
|---|---|---|---|---|
| Symbol | Ti2Pt2AlSb | Ti2Pt2GaSb | Ti2Pt2InSb | |
| E | Raman, IR | 2.700 | 2.644 | 2.322 |
| E | Raman, IR | 3.023 | 2.750 | 2.322 |
| Raman | 3.158 | 3.049 | 2.768 | |
| Raman, IR | 3.287 | 3.116 | 2.732 | |
| Silent | 3.666 | 3.672 | 3.671 | |
| Raman | 3.678 | 3.674 | 3.658 | |
| Silent | 4.147 | 4.192 | 4.125 | |
| E | Raman, IR | 4.312 | 4.127 | 3.759 |
| Raman | 4.704 | 4.318 | 3.763 | |
| E | Raman, IR | 4.848 | 4.749 | 4.615 |
| Raman, IR | 5.251 | 5.358 | 5.163 | |
| E | Raman, IR | 5.874 | 4.949 | 4.862 |
| E | Raman, IR | 6.162 | 5.334 | 5.198 |
| Raman, IR | 6.512 | 5.544 | 5.411 | |
| Raman | 6.587 | 5.572 | 5.406 | |
| E | Raman, IR | 7.295 | 6.330 | 6.010 |
| Raman | 7.414 | 7.269 | 6.750 | |
| Silent | 7.433 | 7.265 | 6.756 | |
| E | Raman, IR | 7.952 | 6.953 | 6.946 |
| E | Raman, IR | 8.874 | 7.991 | 7.079 |
| Raman, IR | 8.914 | 6.625 | 6.059 | |
| E | Raman, IR | 9.634 | 8.231 | 7.323 |
| Raman | 9.783 | 7.824 | 7.523 | |
| Compounds | ||||||
|---|---|---|---|---|---|---|
| Ti2Pt2AlSb | 199.6 | 111.5 | 108.6 | 196.5 | 69.1 | 68 |
| Ti2Pt2GaSb | 194.2 | 115.2 | 113.5 | 191.7 | 66.9 | 66.9 |
| Ti2Pt2InSb | 191.3 | 106.6 | 106.9 | 188.8 | 58.6 | 59 |
| Compounds | Ref. | ||||
|---|---|---|---|---|---|
| Ti2Pt2AlSb | 2.67 | 4847 | 2505 | 2911 | this study |
| Ti2Pt2GaSb | 2.52 | 4653 | 2349 | 2732 | this study |
| Ti2Pt2InSb | 2.35 | 4523 | 2273 | 2661 | this study |
| TiPtSn | 9.2 | 4553 | 2569 | 2924 | [57] |
| Compounds | Ti | Pt | Z | Sb |
|---|---|---|---|---|
| Ti2Pt2AlSb | +1.99 | −3.59 | +3 | +0.20 |
| Ti2Pt2GaSb | +1.98 | −3.62 | +3 | +0.28 |
| Ti2Pt2InSb | +1.94 | −3.63 | +3 | +0.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soltanbek, N.S.; Merali, N.A.; Sagatov, N.E.; Abuova, F.U.; Elsts, E.; Abuova, A.U.; Khovaylo, V.V.; Inerbaev, T.M.; Konuhova, M.; Popov, A.I. Ab Initio Investigation of the Stability, Electronic, Mechanical, and Transport Properties of New Double Half Heusler Alloys Ti2Pt2ZSb (Z = Al, Ga, In). Metals 2025, 15, 329. https://doi.org/10.3390/met15030329
Soltanbek NS, Merali NA, Sagatov NE, Abuova FU, Elsts E, Abuova AU, Khovaylo VV, Inerbaev TM, Konuhova M, Popov AI. Ab Initio Investigation of the Stability, Electronic, Mechanical, and Transport Properties of New Double Half Heusler Alloys Ti2Pt2ZSb (Z = Al, Ga, In). Metals. 2025; 15(3):329. https://doi.org/10.3390/met15030329
Chicago/Turabian StyleSoltanbek, Nurgul S., Nurpeiis A. Merali, Nursultan E. Sagatov, Fatima U. Abuova, Edgars Elsts, Aisulu U. Abuova, Vladimir V. Khovaylo, Talgat M. Inerbaev, Marina Konuhova, and Anatoli I. Popov. 2025. "Ab Initio Investigation of the Stability, Electronic, Mechanical, and Transport Properties of New Double Half Heusler Alloys Ti2Pt2ZSb (Z = Al, Ga, In)" Metals 15, no. 3: 329. https://doi.org/10.3390/met15030329
APA StyleSoltanbek, N. S., Merali, N. A., Sagatov, N. E., Abuova, F. U., Elsts, E., Abuova, A. U., Khovaylo, V. V., Inerbaev, T. M., Konuhova, M., & Popov, A. I. (2025). Ab Initio Investigation of the Stability, Electronic, Mechanical, and Transport Properties of New Double Half Heusler Alloys Ti2Pt2ZSb (Z = Al, Ga, In). Metals, 15(3), 329. https://doi.org/10.3390/met15030329







