Study on Contact Characteristics of Cold Rolled Deformation Zone of Ultra-High-Strength Steel
Abstract
1. Introduction
2. Finite Element Modeling and Experimental Validation
2.1. Finite Element Modeling
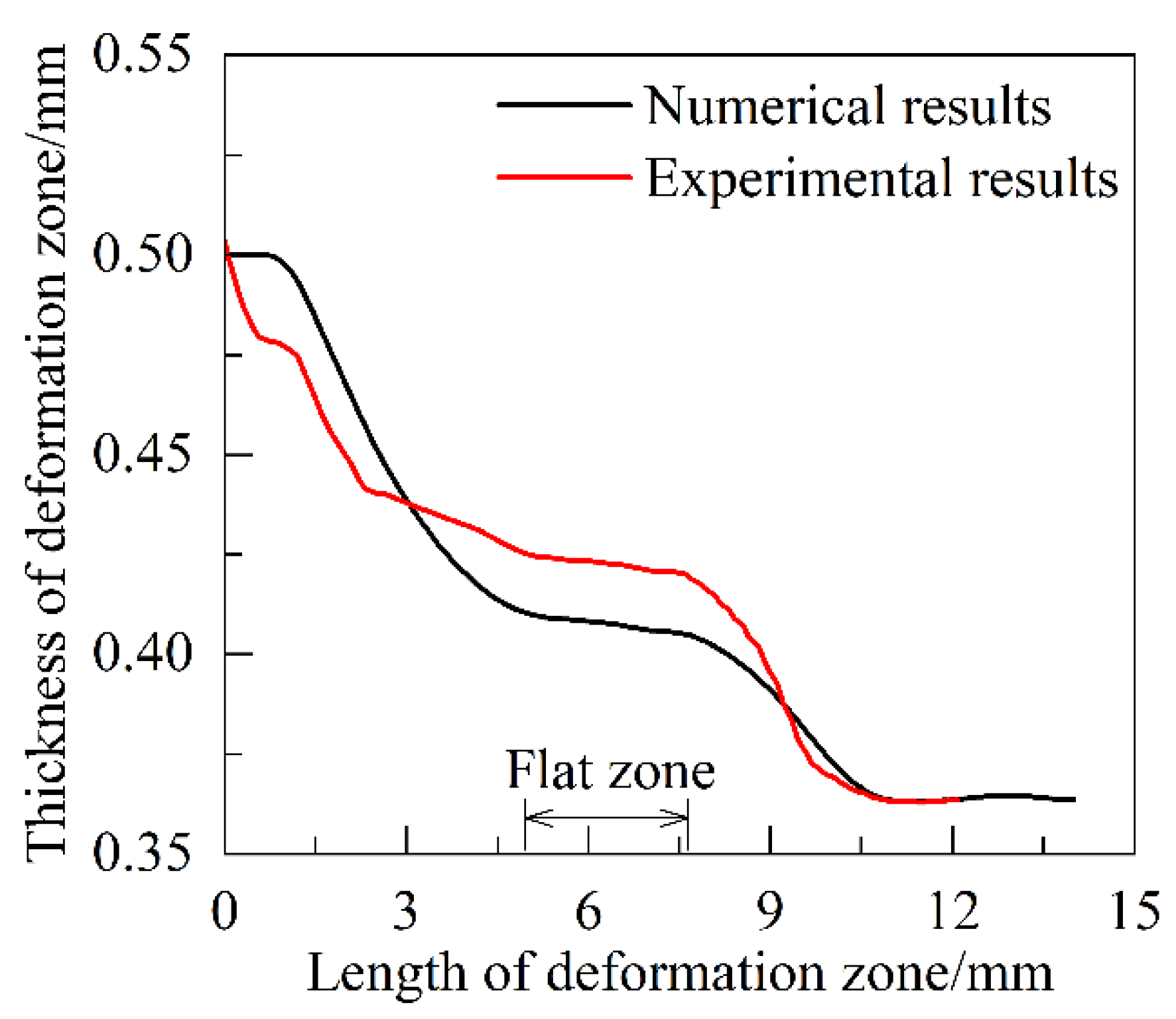
2.2. Experimental Validation
3. Results and Discussion
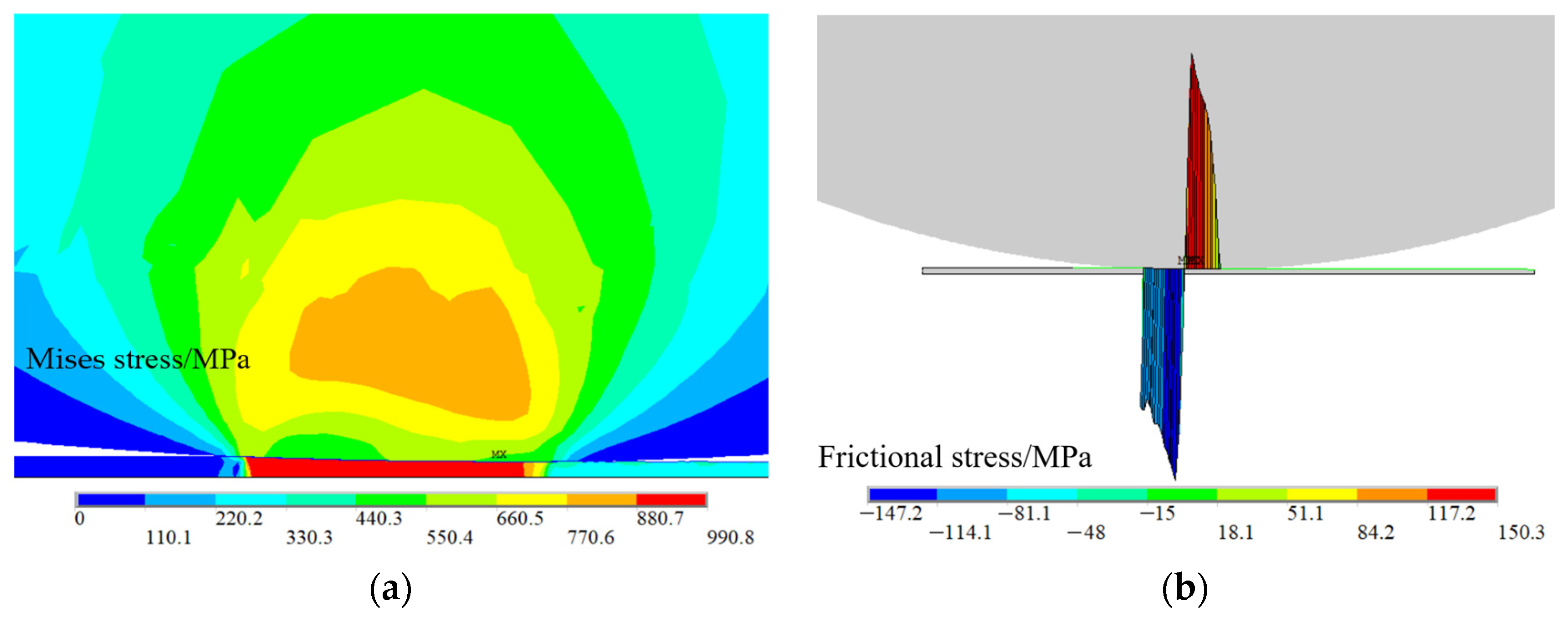
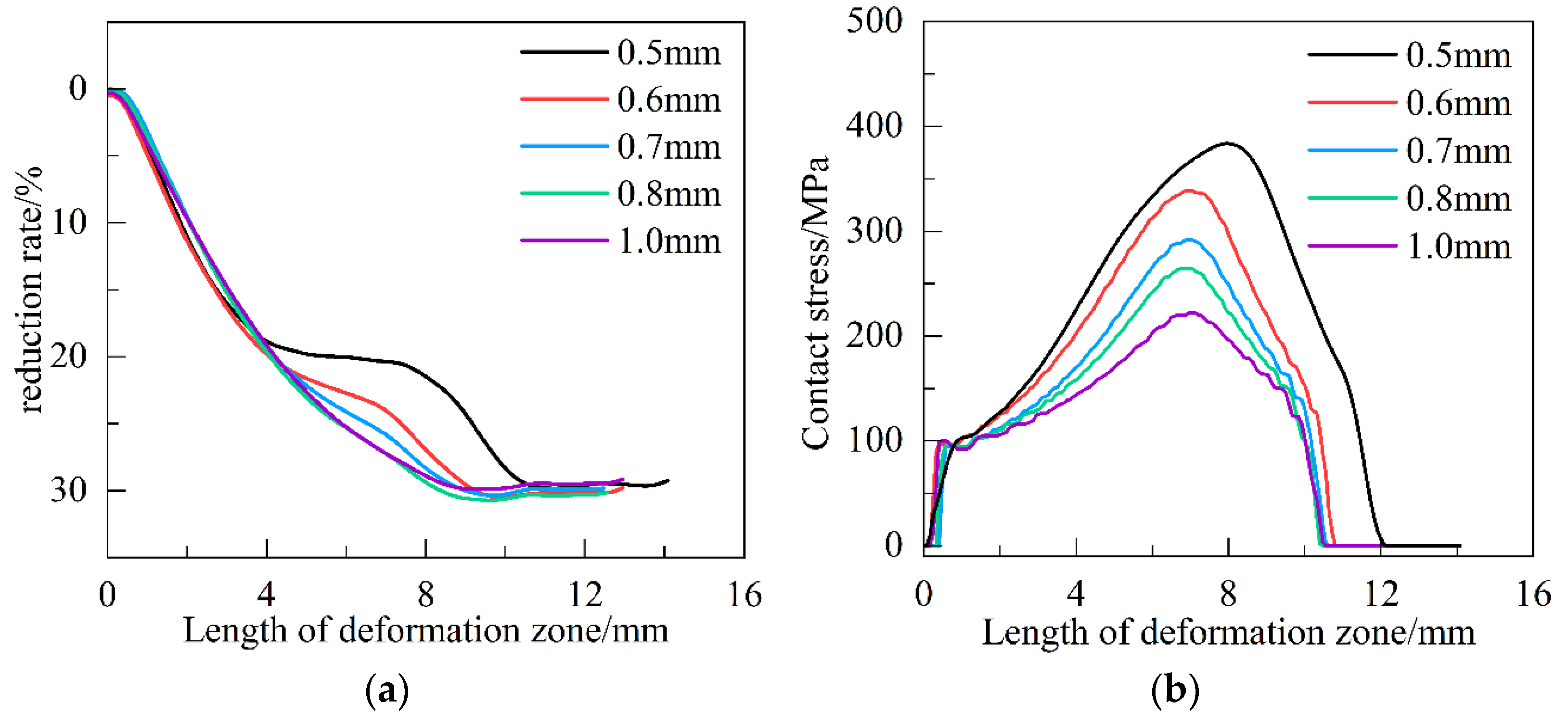
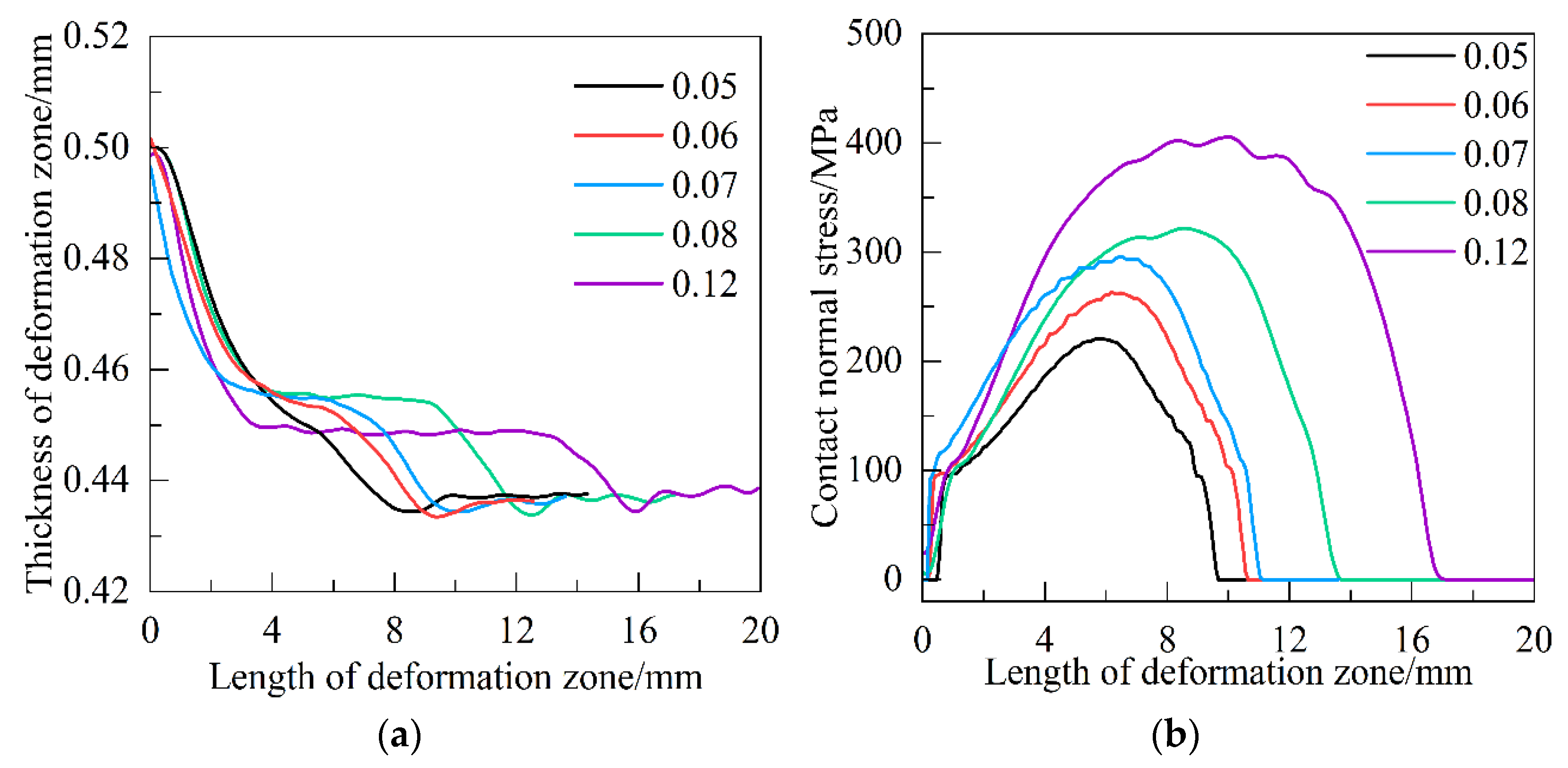
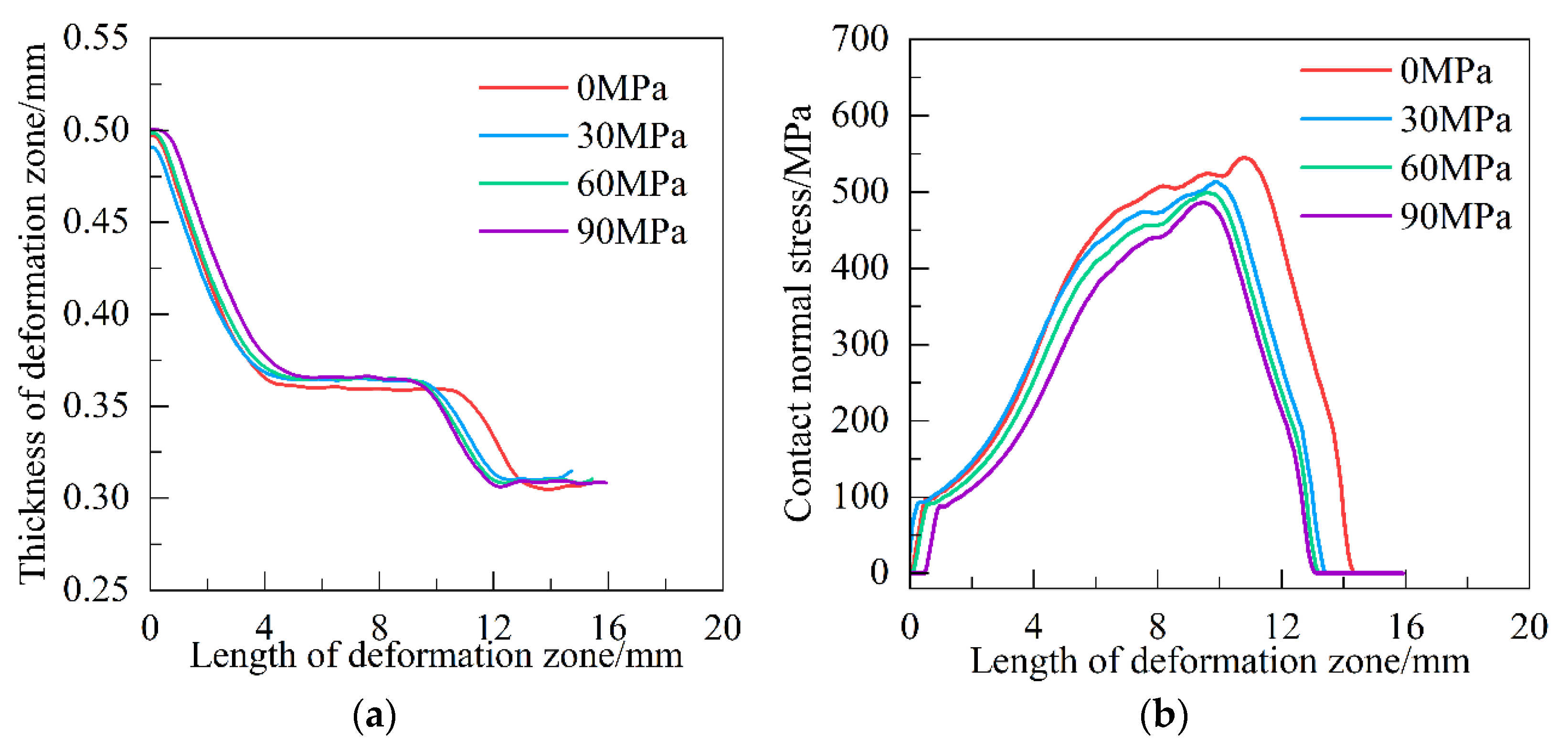
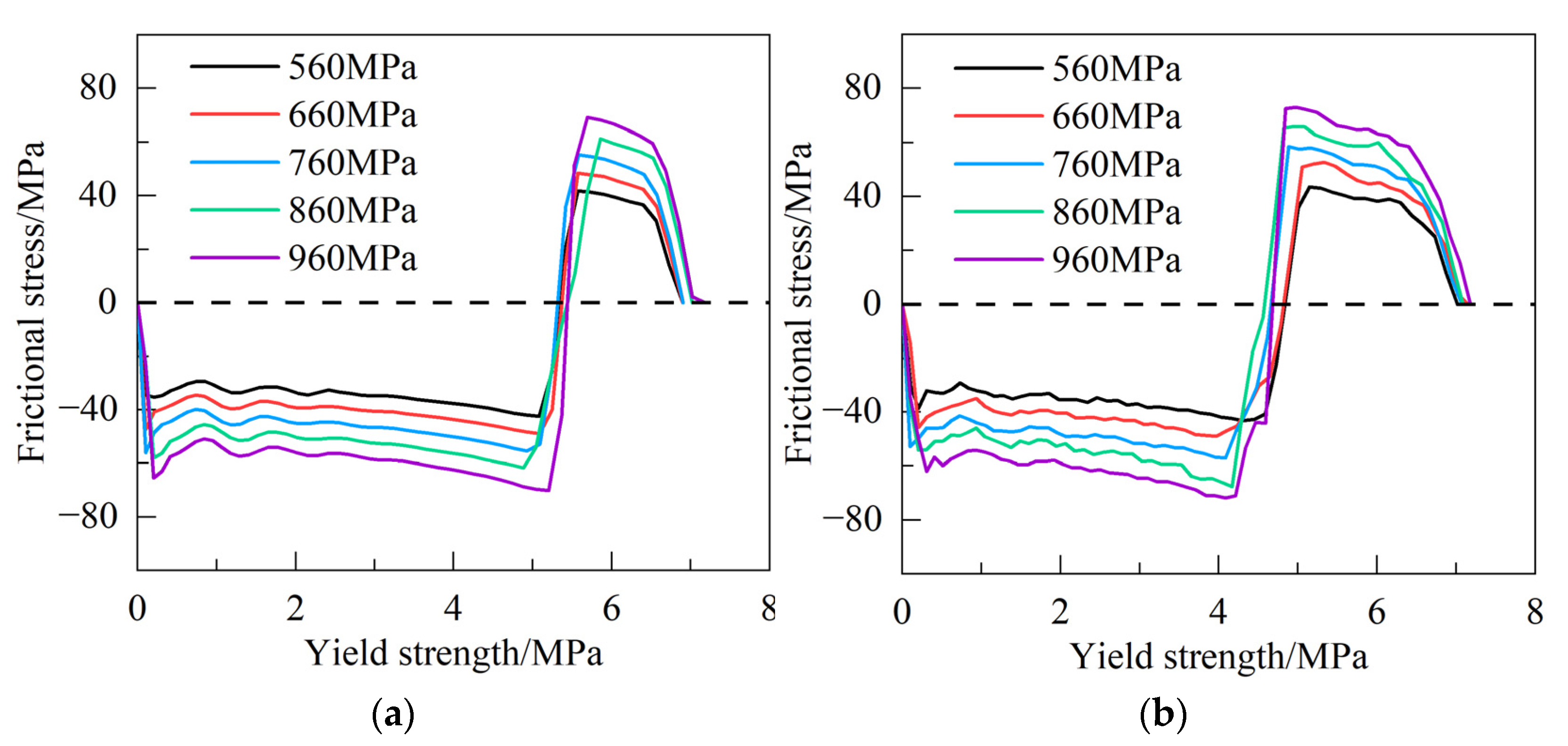
3.1. Analysis of Contact Arc Shape and Contact Stress in Deformation Zone
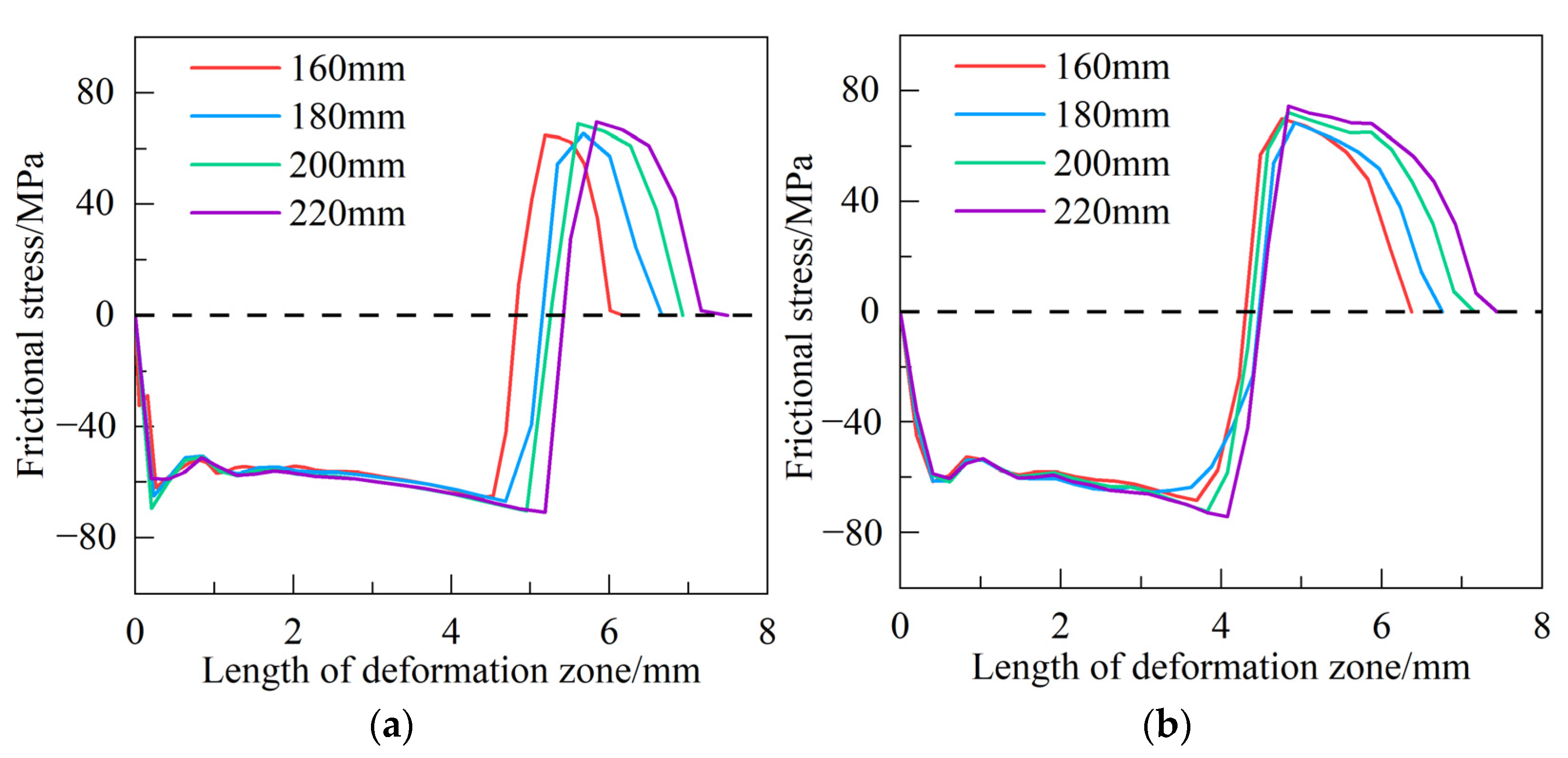
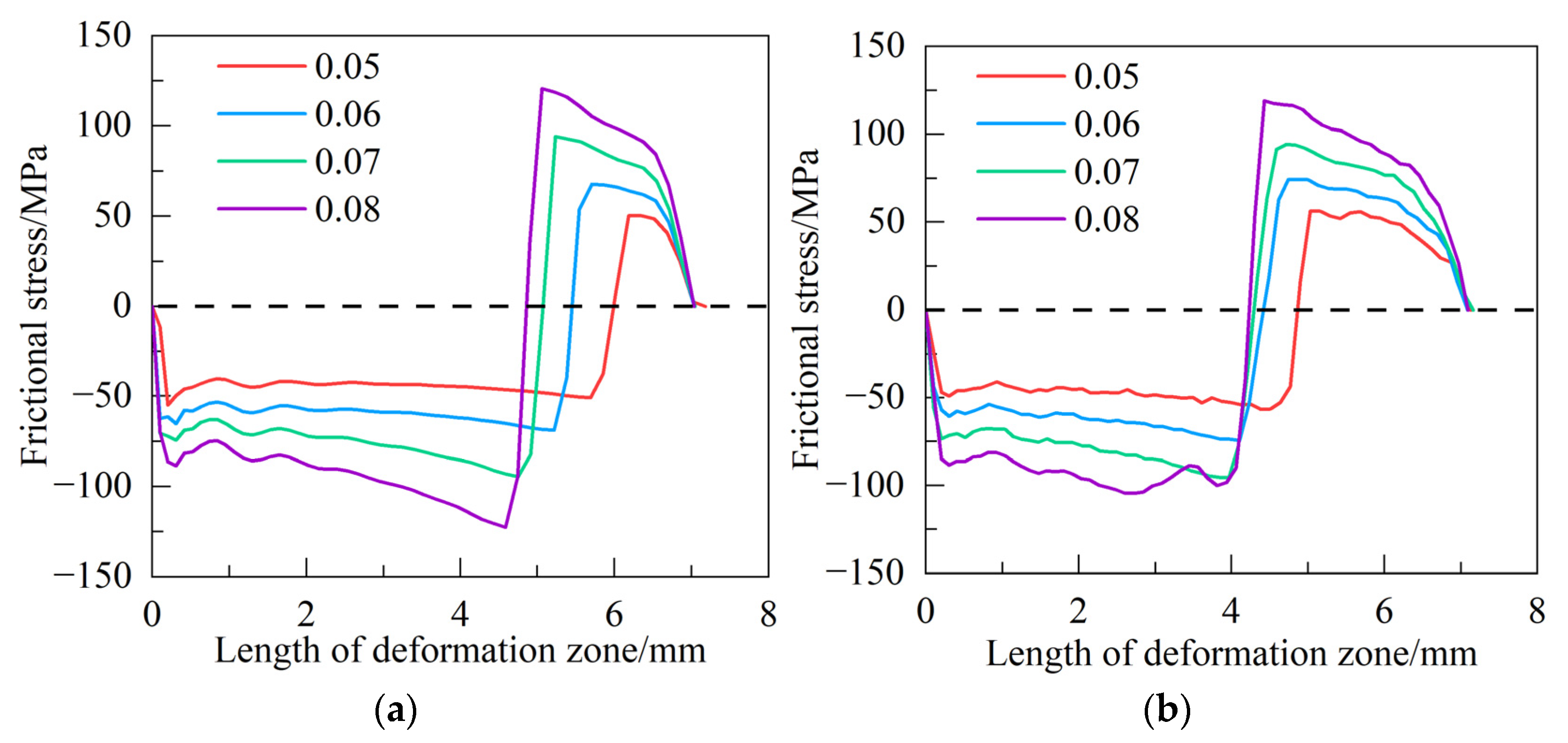
3.2. Calculation and Analysis of Forward Slip Within Deformation Zone
4. Conclusions
- The finite element simulation model of ultra-high-strength steel rolling was established and experimentally verified. By analyzing the reasons for the emergence of the “neutral zone”, it was found that the plastic deformation of the rolled parts is mainly concentrated in the entrance and exit zones and the magnitude of the rolled parts in the neutral zone is very small. The deformation zone is asymmetrically distributed about the centerline of the roll. The peak contact stress in the deformation zone is accompanied by the intensification of the degree of elastic compression of the rolls and it gradually expands to the exit of the rolling.
- With the increase in roll diameter, the deformation zone length increases, the neutral point gradually moves to the exit, and the movement of the neutral point is smaller than the increase in the deformation zone length. The increase in friction coefficient and yield strength has less influence on the length of rolling deformation zone, but the neutral point gradually moves to the entrance, so the forward slip becomes larger. For the yield strength of 960 MPa ultra-high-strength steel, the critical friction coefficient range of the neutral zone in the deformation zone of the rolling process is 0.05~0.08, and the critical yield strength of the neutral zone of the strip is 600~700 MPa.
- With the increase in reduction ratio, the roll diameter, friction coefficient, and yield strength of the rolled parts decrease, the value of the forward slip of the rolled deformation zone decreases. When the roll is converted from a rigid body to an elastic behavior body, the length of the deformation zone does not change significantly, the neutral point position moves relative to the entrance of the rolling, and the forward slip increases.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tang, W.J.; Jin, X.Y.; Hu, G.K. Internal oxidation of hot-rolled ultra-high strength steel and its effect on the surface quality of cold-rolled sheets. Baosteel Tech. Res. 2021, 15, 1–8. [Google Scholar]
- Yang, L.; Yin, F.; Wang, J. Local buckling resistances of cold-formed high-strength steel SHS and RHS with varying corner radius. Thin Walled Struct. 2022, 172, 108909. [Google Scholar] [CrossRef]
- Li, J.H.; Zhang, D.P.; Jiang, Z.H. Progress on improving strength-toughness of ultra-high strength martensitic steels for aerospace applications: A review. J. Mater. Res. Technol. 2023, 23, 172–190. [Google Scholar] [CrossRef]
- Zhao, Z.Z.; Chen, W.G.; Gao, P.F. Progress and perspective of advanced high strength automotive steel. J. Iron Steel Res. 2020, 32, 1059–1076. [Google Scholar]
- He, A.R.; Liu, C.; Shao, J. Research progress and application of new advanced and intelligent rolling technologies for hot rolled strip. J. Steel Roll. 2024, 41, 38–50. [Google Scholar]
- Li, G.Y.; Wang, L.; Ma, M.T. Development of 3rd generation advanced high strength steel for automotive. Steel Roll 2019, 36, 1–13. [Google Scholar]
- Cao, J.G.; Jiang, J.; Qiu, L. High precision integrated profile and flatness control for new-generation high-tech wide strip cold rolling mills. J. Cent. South Univ. Sci. Technol. 2019, 50, 1584–1591. [Google Scholar]
- Huang, Q.X. Research Progress on Key Equipment and Technology of High Quality Steel Plate and Strip Rolling. J. Mech. Eng. 2023, 59, 34–63. [Google Scholar]
- Zhang, K.; Liu, P.; Li, W. High Strength-Ductility Nb-microalloyed Low Martensitic Carbon Steel:Novel Process and Mechanism. Acta Metall. (Engl. Lett.) 2015, 28, 1264–1271. [Google Scholar] [CrossRef][Green Version]
- Kim, D.H.; Kang, J.; Gwon, H. Counter-balancing effects of Si on C partitioning and stacking fault energy of austenite in 10Mn quenching and partitioning steel. J. Mater. Sci. Technol. 2022, 98, 248–257. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, H.Z.; Tang, J.J. Integrated Modelling of Microstructure Evolution and Mechanical Properties Prediction for Q&P Hot Stamping Process of Ultra-High Strength Steel. Chin. J. Mech Eng. 2020, 33, 168–181. [Google Scholar]
- Jiang, J.; Wu, M.; Xu, T.T. Study on impact toughness of TMCP and quenched and tempered high strength steels. Case Stud. Constr. Mater. 2024, 20, e02795. [Google Scholar] [CrossRef]
- Ren, Z.K.; Wang, T.; Wang, Y.L. Analysis of contact contour and contact pressure in deformation zone of ultra-thin strip rolling. Iron Steel 2018, 53, 62–68. [Google Scholar]
- Luo, D.X.; Chen, Q.A.; Liu, L.W. Deformation Analysis in Deformation Zone during Asymmetric Rolling with Different Friction Coefficient. J. Iron Steel. Res. 2004, 16, 42–45. [Google Scholar]
- Han, G.M.; Li, H.B.; Yan, D.J. A mathematical model for longitudinal temperature evolution in strip deformation zone during cold rolling. Int. J. Term. Sci. 2023, 192, 108462. [Google Scholar] [CrossRef]
- Shigaki, Y.; Nakhoul, R.; Montmitonnet, P. Numerical Treatments of Slipping/No-Slip Zones in Cold Rolling of Thin Sheets with Heavy Roll Deformation. Lubricants 2015, 3, 113–131. [Google Scholar] [CrossRef]
- Yu, W.; Sun, G.J.; Shen, S. Forward slip theoretical model and simulation for variable gauge rolling of TRB sheet. Chin. J. Eng. 2014, 36, 241–245. [Google Scholar]
- Li, S.G.; Jia, D.P.; Mao, Z.Z. Finite Element Simulation Analysis of Thin Strip Rolling Process. Metall. Equip. 2022, 3, 44–49+102. [Google Scholar]
- Jiang, Z.Y.; Tieu, A.K.; Lu, C. A FEM modelling of the elastic deformation zones in flat rolling. J. Mater. Process. Technol. 2004, 146, 167–174. [Google Scholar] [CrossRef]
- Bu, H.; Yan, Z.; Zhang, D. A novel approach to improve the computing accuracy of rolling force and forward slip. Ironmak. Steelmak. 2019, 46, 269–276. [Google Scholar] [CrossRef]
- Shimura, M.; Kasai, D.; Otsuka, T. Mechanisms of Slip Generation in Cold Rolling of AHSS: Regular Article. ISIJ Int. 2023, 63, 2033–2041. [Google Scholar] [CrossRef]
- Bu, H.N.; Yan, Z.W.; Zhang, D.H. Comprehensive adaptation of rolling force model and forward slip model in tandem cold rolling process control. J. Shenyang Univ. Technol. 2015, 37, 299–303. [Google Scholar]
- Nam, Y.S.; Zamanian, A.; Shin, J.T. A Novel On-Line Model for the Prediction of Strip Profile in Cold Rolling. ISIJ Int. 2019, 60, 308–317. [Google Scholar] [CrossRef]
- Liu, Y.; Gu, Q.; Zhang, W. Improved model for calculating rolling load of ultra-high strength steel in cold rolling process. Iron Steel 2021, 56, 108–116. [Google Scholar]
- Máté, S.; György, K.; Lenard, J.G. The Difficulties of Predicting the Coefficient of Friction in Cold Flat Rolling. J. Tribol. 2021, 143, 101703. [Google Scholar] [CrossRef]
- Jeswiet, J. A comparison of friction coefficients in cold rolling. J. Mater. Process. Technol. 1998, 80, 239–244. [Google Scholar] [CrossRef]
- Meng, Y.J. Basic Knowledge of Steel Rolling, 1st ed.; Metallurgical Industry Press: Beijing, China, 2005; pp. 229–243. [Google Scholar]
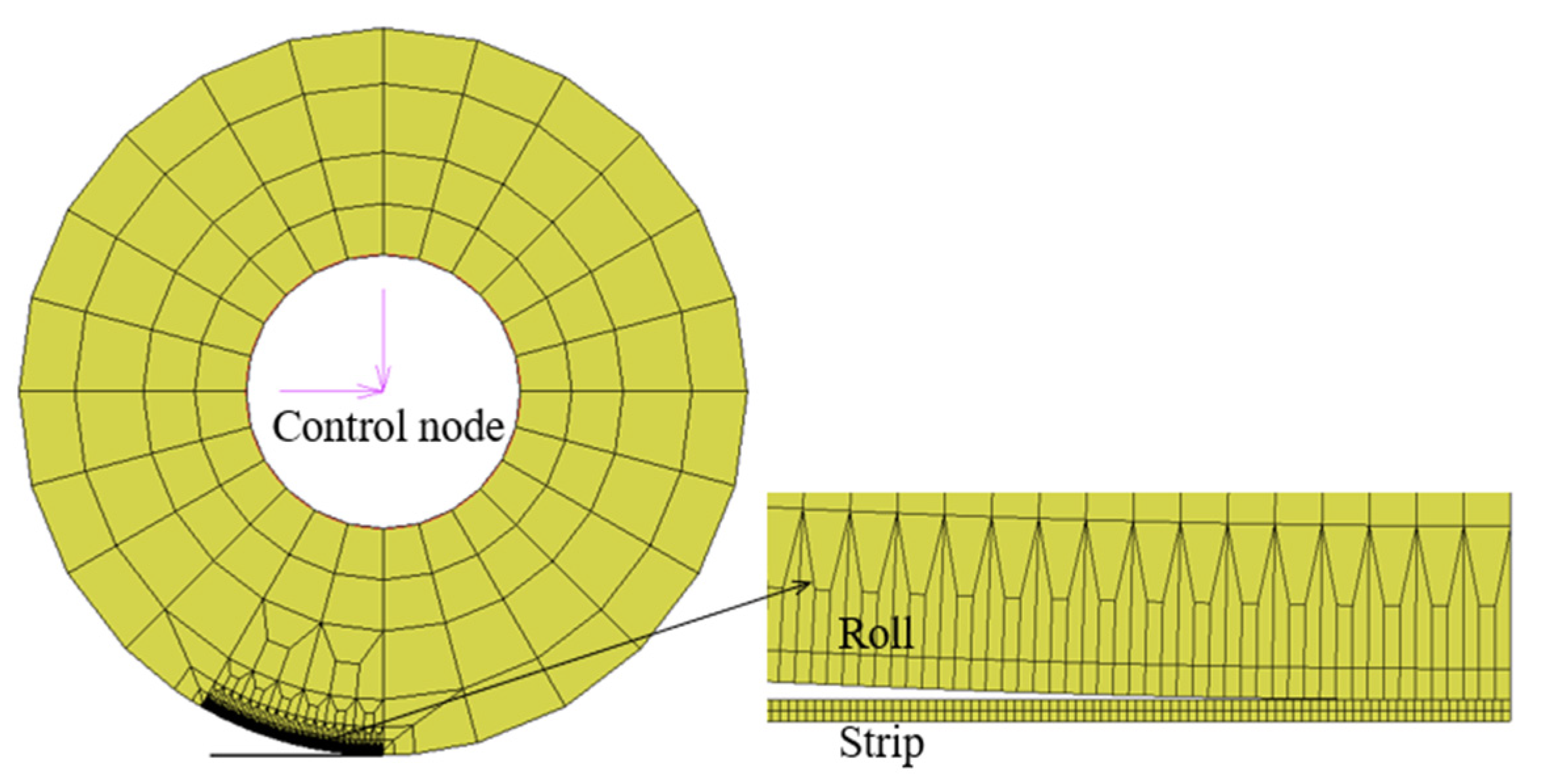




| Parameters | Value |
|---|---|
| Work roll diameter (mm) | 400 |
| Modulus of elasticity (MPa) | 210,000 |
| Poisson’s ratio | 0.3 |
| Strip inlet thickness (mm) | 0.5 |
| Strip outlet thickness (mm) | 0.36 |
| Strip yield strength (MPa) | 960 |
| Friction coefficient | 0.05 |
| Rolling Parameters | Experiment 1 | Experiment 2 | Experiment 3 |
|---|---|---|---|
| Inlet thickness (mm) | 2.0 | 1.6 | 1.3 |
| Outlet thickness (mm) | 1.6 | 1.3 | 1.1 |
| Deformation resistance (MPa) | 1161.7 | 1171.8 | 1266.7 |
| Work roll diameter (mm) | 400 | 400 | 400 |
| Rolling speed (m/min) | 190.8 | 250.0 | 301.8 |
| Strip export speed (m/min) | 249.8 | 301.5 | 353.4 |
| Friction coefficient | 0.05 | 0.03 | 0.03 |
| Rolling force (kN) | 1573.6 | 1423.0 | 1395.5 |
| Number | Experimental Results/% | Simulation Results/% | Relative Error/% |
|---|---|---|---|
| 1 | 30.9 | 30.4 | 1.6 |
| 2 | 20.8 | 23.0 | 8.2 |
| 3 | 17.1 | 18.7 | 9.4 |
| Process Parameter Variables | Value |
|---|---|
| Initial strip thickness (mm) | 0.5, 0.6, 0.7, 0.8, 1.0 |
| Reduction ratio (%) | 20, 40, 60, 80 |
| Friction coefficient | 0.05, 0.06, 0.07, 0.08, 0.12 |
| Yield strength (MPa) | 500, 600, 700, 800, 960 |
| Tension (MPa) | 0, 30, 60, 90 |
| Process Parameter Variables | Value |
|---|---|
| Roll diameter (mm) | 160, 180, 200, 220 |
| Friction coefficient | 0.05, 0.06, 0.07, 0.08 |
| Yield strength (MPa) | 560, 660, 760, 860, 960 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Bai, Z.; Gao, Y.; Shi, Z.; Guo, Z.; Li, X. Study on Contact Characteristics of Cold Rolled Deformation Zone of Ultra-High-Strength Steel. Metals 2025, 15, 311. https://doi.org/10.3390/met15030311
Wang J, Bai Z, Gao Y, Shi Z, Guo Z, Li X. Study on Contact Characteristics of Cold Rolled Deformation Zone of Ultra-High-Strength Steel. Metals. 2025; 15(3):311. https://doi.org/10.3390/met15030311
Chicago/Turabian StyleWang, Jianhui, Zhenhua Bai, Yuan Gao, Zhourun Shi, Zifei Guo, and Xuetong Li. 2025. "Study on Contact Characteristics of Cold Rolled Deformation Zone of Ultra-High-Strength Steel" Metals 15, no. 3: 311. https://doi.org/10.3390/met15030311
APA StyleWang, J., Bai, Z., Gao, Y., Shi, Z., Guo, Z., & Li, X. (2025). Study on Contact Characteristics of Cold Rolled Deformation Zone of Ultra-High-Strength Steel. Metals, 15(3), 311. https://doi.org/10.3390/met15030311








