Enhanced Compressive Properties of Additively Manufactured Ti-6Al-4V Gradient Lattice Structures
Abstract
1. Introduction
2. Experimental Procedures and Programs
2.1. Experimental Materials
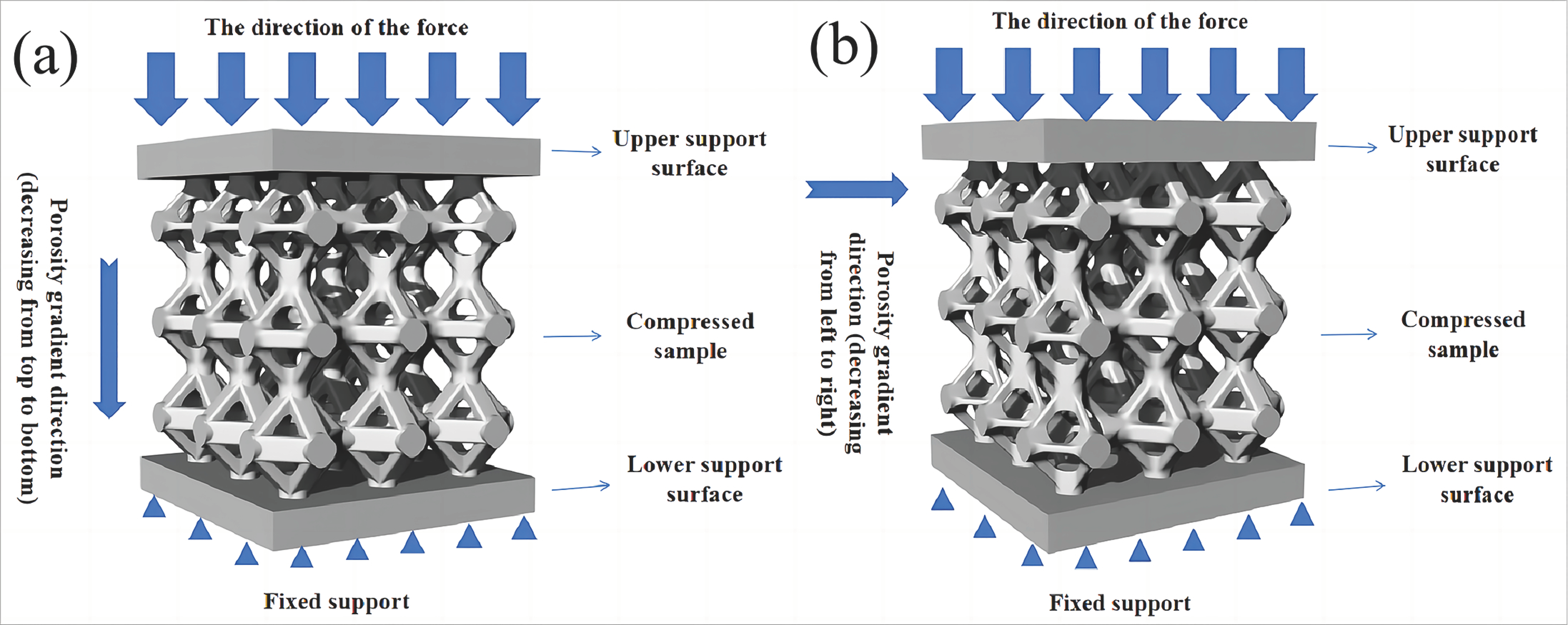
2.2. Lattice Structure Design and Fabrication
2.3. Quasi-Static Compression
2.4. Finite Element Analysis
3. Results and Discussion
3.1. Finite Element Simulations
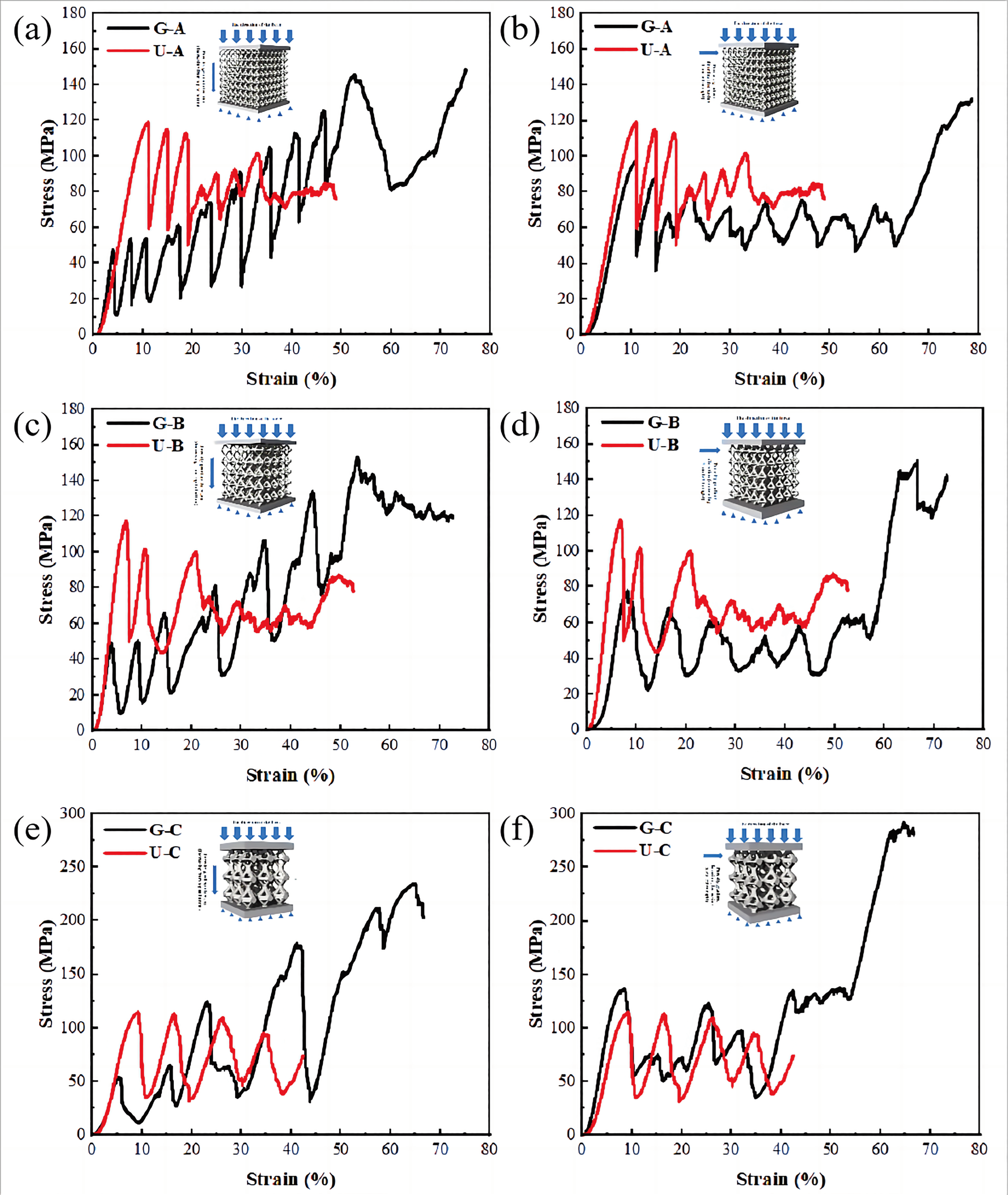
3.2. Deformation Behavior and Failure Mechanisms
3.3. Compression Deformation Characteristics
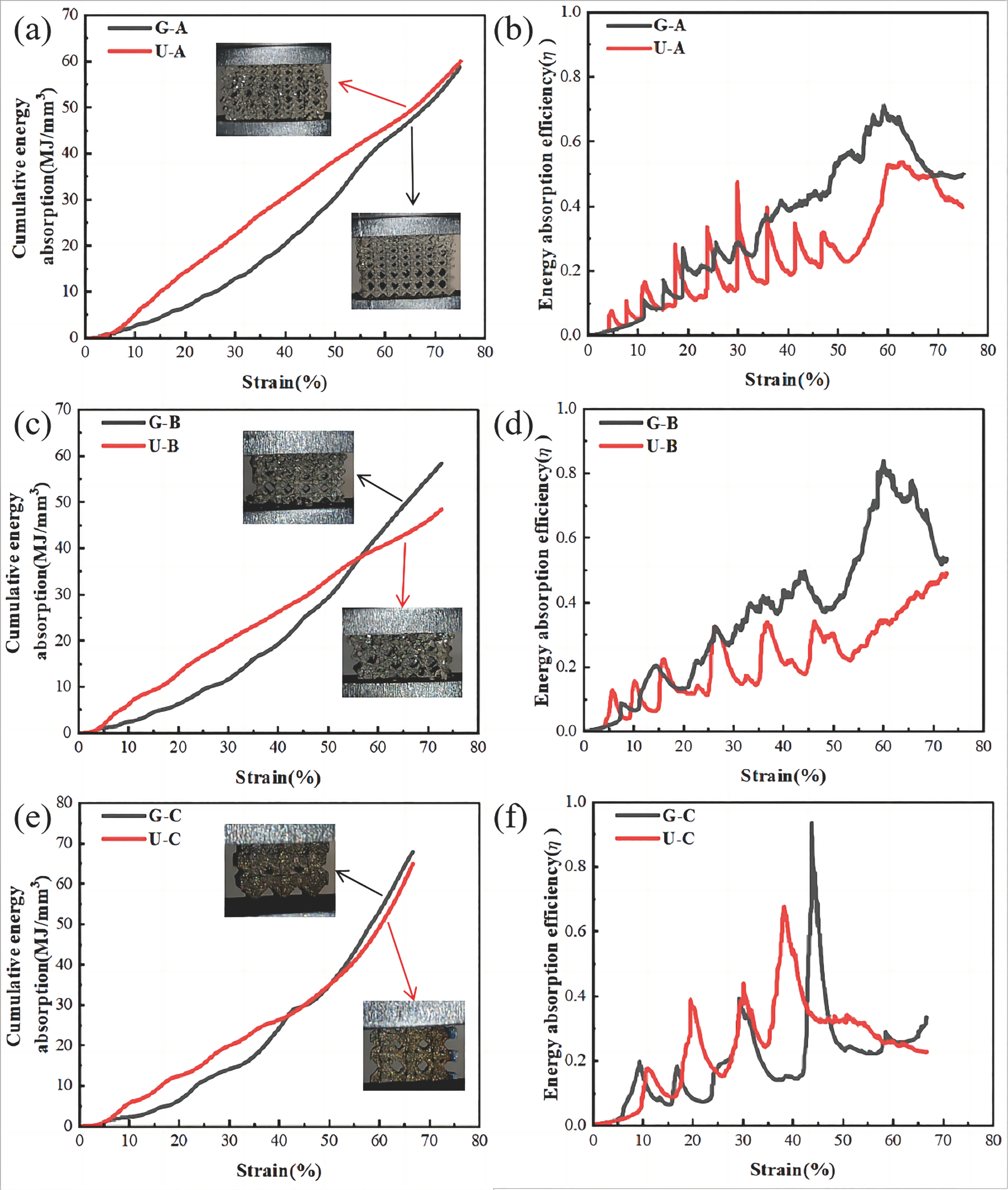
3.4. Cumulative Energy Absorption and Energy Absorption Efficiency Under Compressive Deformation Behavior
4. Conclusions
- (1)
- With the same microstructure and average porosity, the gradient lattice exhibits better compression performance, with a cumulative energy absorption capacity significantly superior to that of the uniform lattice structure.
- (2)
- This superior performance is attributed to the fact that, under compressive loading, the gradient lattice exhibits layer-by-layer shear failure, whereas the uniform lattice experiences overall random failure.
- (3)
- The gradient structure exhibits a greater total deformation before failure than the uniform lattice structure. However, as the deformation increases, the energy absorption efficiency slightly decreases after the deformation exceeds 50%. This indicates that the densification of the structure reduces its energy absorption efficiency.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hao, Y.-L.; Li, S.-J.; Yang, R. Biomedical titanium alloys and their additive manufacturing. Rare Met. 2016, 35, 661–671. [Google Scholar] [CrossRef]
- Qian, M.; Bourell, D.L. Additive Manufacturing of Titanium Alloys. JOM 2017, 69, 2677–2678. [Google Scholar] [CrossRef]
- Wang, M.; Lin, X.; Huang, W. Laser additive manufacture of titanium alloys. Mater. Technol. 2016, 31, 90–97. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Babamiri, B.B.; Zhou, Y.; Dargusch, M.; Hazeli, K.; Zhang, M.-X. Enhancing specific energy absorption of additively manufactured titanium lattice structures through simultaneous manipulation of architecture and constituent material. Addit. Manuf. 2022, 55, 102887. [Google Scholar] [CrossRef]
- Sun, G.; Chen, D.; Zhu, G.; Li, Q. Lightweight hybrid materials and structures for energy absorption: A state-of-the-art review and outlook. Thin-Walled Struct. 2022, 172, 108760. [Google Scholar] [CrossRef]
- Pan, X.; Qian, G.; Wu, S.; Fu, Y.; Hong, Y. Internal crack characteristics in very-high-cycle fatigue of a gradient structured titanium alloy. Sci. Rep. 2020, 10, 4742. [Google Scholar] [CrossRef] [PubMed]
- Zhan, Z.; Li, H.; Lam, K. Development of a novel fatigue damage model with AM effects for life prediction of commonly-used alloys in aerospace. Int. J. Mech. Sci. 2019, 155, 110–124. [Google Scholar] [CrossRef]
- He, S.; Zhu, J.; Jing, Y.; Long, S.; Tang, L.; Cheng, L.; Shi, Z. Effect of 3D-Printed Porous Titanium Alloy Pore Structure on Bone Regeneration: A Review. Coatings 2024, 14, 253. [Google Scholar] [CrossRef]
- Song, C.; Liu, L.; Deng, Z.; Lei, H.; Yuan, F.; Yang, Y.; Li, Y.; Yu, J. Research progress on the design and performance of porous titanium alloy bone implants. J. Mater. Res. Technol. 2023, 23, 2626–2641. [Google Scholar] [CrossRef]
- Bian, X.; Yuan, F.; Zhu, Y.; Wu, X. Gradient structure produces superior dynamic shear properties. Mater. Res. Lett. 2017, 5, 501–507. [Google Scholar] [CrossRef]
- Xiao, Z.; Yang, Y.; Xiao, R.; Bai, Y.; Song, C.; Wang, D. Evaluation of topology-optimized lattice structures manufactured via selective laser melting. Mater. Des. 2018, 143, 27–37. [Google Scholar] [CrossRef]
- Chen, L.; Che, J.; Liang, S.; Wang, Y. Multiscale topology optimization of gradient lattice structure based on volume parametric modeling. Compos. Struct. 2023, 328, 117746. [Google Scholar] [CrossRef]
- Li, J.; Huang, Z.; Liu, G.; An, Q.; Chen, M. Topology optimization design and research of lightweight biomimetic three-dimensional lattice structures based on laser powder bed fusion. J. Manuf. Process. 2021, 74, 220–232. [Google Scholar] [CrossRef]
- Li, T.; Sun, B.; Gan, N. Lattice infill structure design of topology optimization considering size effect. Math. Mech. Solids 2022, 28, 873–890. [Google Scholar] [CrossRef]
- Belda, R.; Megías, R.; Marco, M.; Vercher-Martínez, A.; Giner, E. Numerical analysis of the influence of triply periodic minimal surface structures morphometry on the mechanical response. Comput. Methods Programs Biomed. 2023, 230, 107342. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Liu, F.; Fu, G.; Zhang, D.Z.; Zhang, T.; Zhou, H. Improved Mechanical Properties and Energy Absorption of BCC Lattice Structures with Triply Periodic Minimal Surfaces Fabricated by SLM. Materials 2018, 11, 2411. [Google Scholar] [CrossRef] [PubMed]
- Bai, L.; Zhang, J.; Chen, X.; Yi, C.; Chen, R.; Zhang, Z. Configuration Optimization Design of Ti6Al4V Lattice Structure Formed by SLM. Materials 2018, 11, 1856. [Google Scholar] [CrossRef]
- Bahnini, I.; Rivette, M.; Rechia, A.; Siadat, A.; Elmesbahi, A. Additive manufacturing technology: The status, applications, and prospects. Int. J. Adv. Manuf. Technol. 2018, 97, 147–161. [Google Scholar] [CrossRef]
- Trevisan, F.; Calignano, F.; Lorusso, M.; Pakkanen, J.; Aversa, A.; Ambrosio, E.P.; Lombardi, M.; Fino, P.; Manfredi, D. On the Selective Laser Melting (SLM) of the AlSi10Mg Alloy: Process, Microstructure, and Mechanical Properties. Materials 2017, 10, 76. [Google Scholar] [CrossRef] [PubMed]
- Razavykia, A.; Brusa, E.; Delprete, C.; Yavari, R. An Overview of Additive Manufacturing Technologies—A Review to Technical Synthesis in Numerical Study of Selective Laser Melting. Materials 2020, 13, 3895. [Google Scholar] [CrossRef] [PubMed]
- Oropeza, D.; Seager, T.; Firdosy, S.; Guerra, J.; Billings, K.; Jones, J.-P.; Hofmann, D.C.; Roberts, S. Porosity control of copper-based alloys via powder bed fusion additive manufacturing for spacecraft applications. J. Porous Mater. 2024, 31, 779–791. [Google Scholar] [CrossRef]
- Yao, L.; Ramesh, A.; Xiao, Z.; Chen, Y.; Zhuang, Q. Multimetal Research in Powder Bed Fusion: A Review. Materials 2023, 16, 4287. [Google Scholar] [CrossRef] [PubMed]
- Hayat, M.D.; Singh, H.; He, Z.; Cao, P. Titanium metal matrix composites: An overview. Compos. Part A Appl. Sci. Manuf. 2019, 121, 418–438. [Google Scholar] [CrossRef]
- Gao, B.; Zhao, H.; Peng, L.; Sun, Z. A Review of Research Progress in Selective Laser Melting (SLM). Micromachines 2022, 14, 57. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Ren, D.; Li, S.; Wang, H.; Zhang, L.; Sercombe, T. Enhanced fatigue characteristics of a topology-optimized porous titanium structure produced by selective laser melting. Addit. Manuf. 2020, 32, 101060. [Google Scholar] [CrossRef]
- Chen, J.; Fan, M.; Zhou, L.; Chen, W.; Ren, Y.; Li, W.; Huang, W.; Niu, Y.; Li, Z.; Li, C. The effect of microstructure on the fatigue behavior of titanium alloy graded porous structures fabricated by selective laser melting. J. Mater. Res. Technol. 2023, 27, 4290–4304. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, H.; Liang, X.; Jia, M.; Lei, J. Microstructure and Biomechanical Properties in Selective Laser Melting of Porous Metal Implants. 3D Print. Addit. Manuf. 2021, 10, 1003–1014. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Ran, W.; Nie, Y.; Liu, Z.; Lou, C.; Li, J.; Chen, W. Excellent Mechanical Properties and Energy Absorption of Hexagonal-Body-Centered Lattice Structure Fabricated by Selective Laser Melting. Adv. Eng. Mater. 2023, 25, 2300431. [Google Scholar] [CrossRef]
- Li, H.; Yang, G.; Lv, S.; Zhou, Q.; Fan, L.; Liu, R.; Yao, J.; Tong, P. Effects of Unit Cell Topology on the Mechanical Properties of Porous Tantalum Structures via Laser Powder Bed Fusion. Adv. Eng. Mater. 2022, 25, 2201431. [Google Scholar] [CrossRef]
- Wang, Z.; Jiang, X.; Yang, G.; Song, B.; Sha, H. Design and mechanical performance analysis of T-BCC lattice structures. J. Mater. Res. Technol. 2024, 32, 1538–1551. [Google Scholar] [CrossRef]
- Pauly, S.; Schricker, C.; Scudino, S.; Deng, L.; Kühn, U. Processing a glass-forming Zr-based alloy by selective laser melting. Mater. Des. 2017, 135, 133–141. [Google Scholar] [CrossRef]
- Li, X.; Roberts, M.; O’Keeffe, S.; Sercombe, T. Selective laser melting of Zr-based bulk metallic glasses: Processing, microstructure and mechanical properties. Mater. Des. 2016, 112, 217–226. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, X.; Davies, C.H. Process variation in Laser Powder Bed Fusion of Ti-6Al-4V. Addit. Manuf. 2021, 41, 101987. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, X.; Tomus, D.; Davies, C.H. Surface roughness of Selective Laser Melted Ti-6Al-4V alloy components. Addit. Manuf. 2018, 21, 91–103. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, K.; Liu, J.; Wang, H.; Yang, Y.; Yan, L.; Tian, X.; Zhu, Y.; Huang, A. Investigation of fatigue behavior of laser powder bed fusion Ti-6Al-4V: Roles of heat treatment and microstructure. Int. J. Fatigue 2023, 176, 107839. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, K.; Liu, J.; Xu, Y.; Zhang, R.; Zeng, Z.; Zhu, Y.; Huang, A. In-situ investigation into the deformation behavior of Ti-6Al-4V processed by laser powder bed fusion. Mater. Charact. 2022, 194, 112434. [Google Scholar] [CrossRef]
- Aslan, B.; Yıldız, A.R. Optimum design of automobile components using lattice structures for additive manufacturing. Mater. Test. 2020, 62, 633–639. [Google Scholar] [CrossRef]
- ISO 13314-2011; Mechanical Testing of Metals—Ductility Testing—Compression Test for Porous and Cellular Metals. ISO: Geneva, Switzerland, 2011.
- Sugaya, K.; Imamura, T. Turbulent flow simulations of the common research model on Cartesian grids using recursive fitting approach. J. Comput. Phys. 2022, 467, 111460. [Google Scholar] [CrossRef]
- Hu, C.; Liu, C. Development of Cartesian grid method for simulation of violent ship-wave interactions. J. Hydrodyn. 2016, 28, 1003–1010. [Google Scholar] [CrossRef]
- Marker, C.; Shang, S.-L.; Zhao, J.-C.; Liu, Z.-K. Effects of alloying elements on the elastic properties of bcc Ti-X alloys from first-principles calculations. Comput. Mater. Sci. 2018, 142, 215–226. [Google Scholar] [CrossRef]
- Ren, Y.; Ma, Y.; Pan, Q. Effect of Microstructure on the Johnson-Cook Constitutive Model Parameters of Ti-6Al-4V Alloy. J. Phys. Conf. Ser. 2020, 1637, 012018. [Google Scholar] [CrossRef]
- Löschner, P.; Gupta, M.K.; Niesłony, P.; Korkmaz, M.E.; Jamil, M. Determination and Verification of the Johnson–Cook Constitutive Model Parameters in the Precision Machining of Ti6Al4V Alloy. Machines 2024, 12, 709. [Google Scholar] [CrossRef]
- Polley, C.; Radlof, W.; Hauschulz, F.; Benz, C.; Sander, M.; Seitz, H. Morphological and mechanical characterisation of three-dimensional gyroid structures fabricated by electron beam melting for the use as a porous biomaterial. J. Mech. Behav. Biomed. Mater. 2022, 125, 104882. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Xiao, L.; Song, W. Compressive behavior of selective laser melting printed Gyroid structures under dynamic loading. Addit. Manuf. 2021, 46, 102054. [Google Scholar] [CrossRef]
- Sun, Q.; Sun, J.; Guo, K.; Wang, L. Compressive mechanical properties and energy absorption characteristics of SLM fabricated Ti6Al4V triply periodic minimal surface cellular structures. Mech. Mater. 2022, 166, 104241. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, Y.; Wang, D.; Xiao, Z.; Song, C.; Weng, C. Effect of heat treatment on the microstructure and mechanical properties of Ti6Al4V gradient structures manufactured by selective laser melting. Mater. Sci. Eng. A 2018, 736, 288–297. [Google Scholar] [CrossRef]
- Choy, S.Y.; Sun, C.-N.; Leong, K.F.; Wei, J. Compressive properties of functionally graded lattice structures manufactured by selective laser melting. Mater. Des. 2017, 131, 112–120. [Google Scholar] [CrossRef]
- Cardeña, A.; Sancho, R.; Barba, D.; Gálvez, F. Dynamic behaviour of additively manufactured Ti6Al4V BCC lattice-based structures. Mater. Lett. 2023, 354, 135286. [Google Scholar] [CrossRef]
- Tan, Q.; Liu, P.; Du, C.; Wu, L.; He, G. Mechanical behaviors of quasi-ordered entangled aluminum alloy wire material. Mater. Sci. Eng. A 2009, 527, 38–44. [Google Scholar] [CrossRef]
- Wu, F.; Zhou, Z.; Yao, B.; Xiao, Z. Anisotropic Compressive Properties and Energy Absorption Efficiency of Porous Twisted Short Fiber Materials. Steel Res. Int. 2016, 87, 1534–1542. [Google Scholar] [CrossRef]
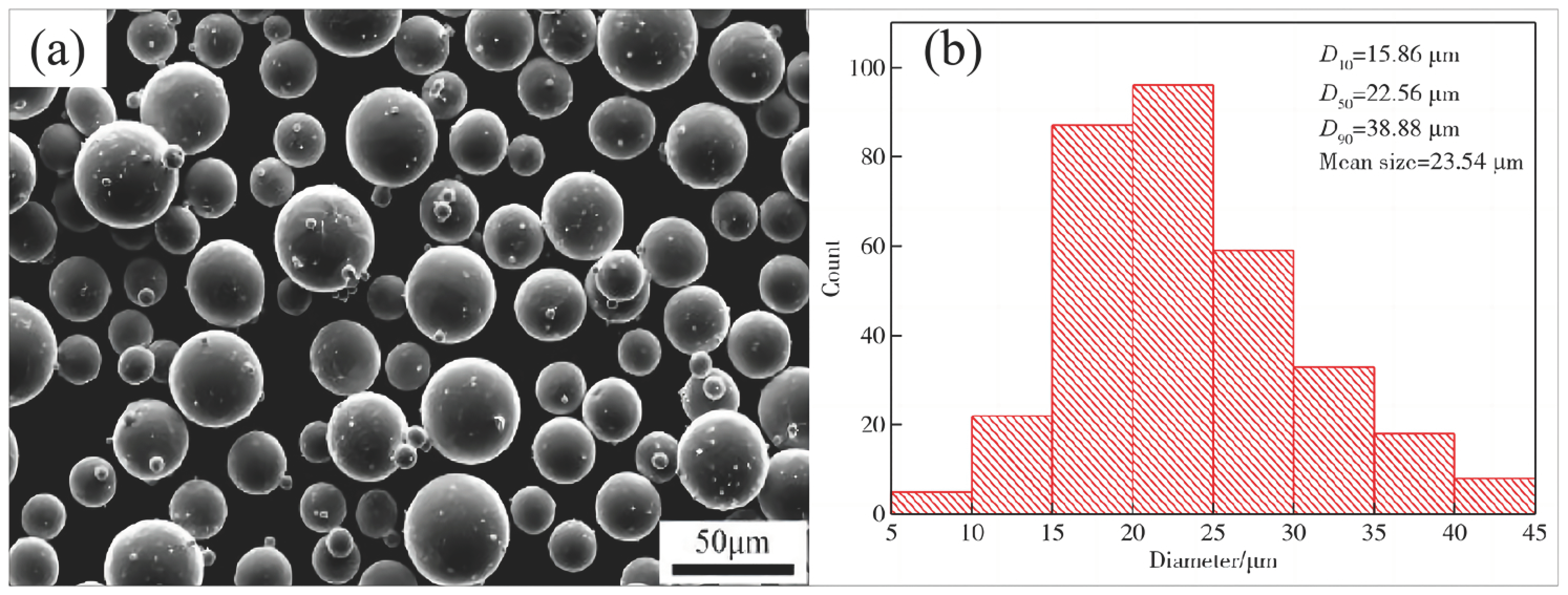







| Al | V | Fe | C | N | O | H | Ti |
|---|---|---|---|---|---|---|---|
| 6.42 | 4.22 | 0.044 | 0.052 | 0.012 | 0.097 | <0.0020 | Bal. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Ma, Y.; Ali, T.; Yang, Y.; Hou, J.; Li, S.; Wang, H. Enhanced Compressive Properties of Additively Manufactured Ti-6Al-4V Gradient Lattice Structures. Metals 2025, 15, 230. https://doi.org/10.3390/met15030230
Guo Z, Ma Y, Ali T, Yang Y, Hou J, Li S, Wang H. Enhanced Compressive Properties of Additively Manufactured Ti-6Al-4V Gradient Lattice Structures. Metals. 2025; 15(3):230. https://doi.org/10.3390/met15030230
Chicago/Turabian StyleGuo, Zhengjie, Yuting Ma, Tayyeb Ali, Yi Yang, Juan Hou, Shujun Li, and Hao Wang. 2025. "Enhanced Compressive Properties of Additively Manufactured Ti-6Al-4V Gradient Lattice Structures" Metals 15, no. 3: 230. https://doi.org/10.3390/met15030230
APA StyleGuo, Z., Ma, Y., Ali, T., Yang, Y., Hou, J., Li, S., & Wang, H. (2025). Enhanced Compressive Properties of Additively Manufactured Ti-6Al-4V Gradient Lattice Structures. Metals, 15(3), 230. https://doi.org/10.3390/met15030230







