Computational Modeling of Multiple-Phase Transformations in API X70 and X80 Steels

Abstract

Continuous cooling transformation (CCT) diagrams for two thermo-mechanically controlled processed (TMCP) steels were produced using a modified Johnson–Mehl–Avrami–Kolmogorov (JMAK) model, which accounted for the simultaneous transformation of multiple phases under non-isothermal conditions. A basin hopping algorithm was used to sequentially optimize the model parameters for each phase. Samples were prepared using a dilatometer which replicated the deformation and cooling rates experienced during TMCP. Scanning electron microscopy (SEM) and electron back-scattered diffraction (EBSD) were used to identify and quantify the phases present in each steel. CCT diagrams illustrating the start and stop temperatures of each phase were constructed for both steel samples. Through inclusion of the stop temperatures of each phase transformation, the utility of the CCT diagrams were expanded. This was done by introducing the possibility of applying the Scheil additive principle with respect to the beginning and end of each phase transformation. With this modification, the CCT diagrams are now more appropriately suited to predict the phase transformations that occur on the ROT, where non-continuous cooling occurs.

1. Introduction

Microalloyed steels are a type of alloy produced through small additions of niobium (Nb), titanium (Ti) and/or vanadium (V), and thermo-mechanically controlled processing (TMCP). As a subset of high-strength low-alloy steels (HSLA), these materials are engineered to exhibit high strength and toughness and are widely used in the automotive, construction, and pipeline industries [1,2,3,4,5,6]. The mechanical properties of HSLAs are derived from the alloy microstructure, which is a result of both the alloying and different stages of the production process.

Continuous cooling transformation (CCT) diagrams are a metallurgical tool used to map out the influence of cooling rate on the start of transformation of various product microstructures. These diagrams are typically constructed by measuring the dilation of an alloy as a function of cooling using a dilatometer. To extract phase transformation information from dilation curves, the lever rule can be applied on the section of the curve where the slope is variable with temperature [7]. This variable slope is the result of the formation of low-density base-centered cubic (BCC) product phases from the initial face-centered cubic (FCC) parent phase. There are three major factors that influence the observed austenite decomposition measured with the dilatometer: prior strain, cooling rate, and the specific alloying additions. In a CCT diagram, the start of transformation of a phase (1% start) as well as single-phase regions are illustrated. However, there are many occurrences when more than one phase is present in a given phase region (simultaneous transformation). Regions of simultaneous transformation may arise from the introduction of strain into the sample prior to transformation and/or through non-isothermal conditions.

Modification of the austenite to ferrite transformation can be achieved by straining the steel while below the recrystallization temperature. By imparting deformation without recrystallization, the number of nucleation sites increases drastically [8]. Since the formation of ferritic phases are nucleation and growth processes, by increasing the nucleation and decreasing growth, smaller final grains are achieved. Furthermore, different microstructures, such as bainitic ferrite (BF), may form on the deformation bands within the grains [8]. From previous research into this topic, it is suggested that an increase in deformation enhances the diffusion controlled austenite to ferrite and pearlite reactions [9,10]. This is attributed to an increase in defects in the lattice which can help promote diffusion and serve as nucleation sites [11]. On a CCT, this is typically illustrated by an increase in austenite decomposition temperature.

Accelerated cooling at temperatures around the austenite transformation range is also used to engineer the microstructure. This type of cooling occurs on the runout table (ROT) where water is used to cool the skelp. The ROT is the last section of the hot strip mill, prior to coiling, and consists of a series of headers and banks that expel water onto the skelp surface. At increased cooling rates, the $A_{r3}$ temperature is lowered and ferrite grain growth is retarded [8,12]. This observation has been attributed to the time at which metastable austenite exists prior to transformation ($A_3$ to $t_{start}$) [13]. At higher temperatures and times, there is a larger degree of carbon diffusion and redistribution along the austenite [13]. At severely high cooling rates, the formation of a coarse bainitic structure may occur, reducing the toughness of the steel [8]. This is the result of an increased stability of the supercooled austenite [13]. The stability of the supercooled austenite is also affected by the specific alloying of the steel [13]. With the exception of cobalt (Co), all other alloying elements shift the start transformation times to higher values [14]. For added austenite stabilizing elements such as copper (Cu), manganese (Mn), nickle (Ni), and carbon (C), there is a delay in the diffusional decomposition of the metastable austenite and decrease in $A_3$ temperature [14]. This observation is associated with the sluggish diffusion and change in solubility of C in the austenite and/or ferrite which results from induced lattice strains caused by the size of the alloying elements [14]. Ferrite stabilizers such as chrome (Cr), vanadium (V), molydbenum (Mo), and titanium (Ti) increase transformation times through their tendency to form carbides [14].

A drawback of using the lever technique on a dilation curve is that it is only valid when there is the formation of a single, non-partitioning phase [7]. For cases where a second phase is forming, the lever rule assumes the transformations are sequential, and that the second phase starts forming at the point of a second inflection in the curve or at a calculated temperature [7]. In HSLAs, such as the ones studied in this paper, straining and alloying create multi-phase regions where transformations involve two simultaneous processes: a change in the crystal lattice and a redistribution of alloying elements, particularly carbon. As austenite transforms, the newly formed phases do not retain the original composition, leading to a dynamic change in the carbon content of the remaining austenite. This ongoing enrichment alters the atomic volume and causes expansion in the material, with the product phases exhibiting different volume effects. Because these processes occur concurrently and the atomic volume of austenite depends on its evolving carbon concentration, it becomes difficult to clearly distinguish between the formation of product phases (sequentially or simultaneously formed) based on the dilation curve. This may result in the dilation curves not exhibiting a distinct second inflection point. This necessitates the need to develop different methods to extract fraction transformed data from the dilation data.

On such approach to determine the fractions of multiple product phases is through microstructure modeling. When modeling the decomposition of austenite into product phases, the classical JMAK equation is typically used. Using this equation, it can be assumed that the phase transformations proceed either sequentially or simultaneously, with the former case being less likely [15]. Jones et al. [15] modified the JMAK equation to account for the simultaneous transformation of two phases. This was done through the addition of proportionality constants that related the fractions of each phase and addressed the issues of hard and soft impingement. Furthermore, with the classical JMAK equation, it is assumed that the transformations occur isothermally, which is far from the reality of what is occurring on the ROT during TMCP. In a study by Venkatraman et al. [16], the non-isothermal decomposition of austenite was modeled through the introduction of a time constant $\tau$, which followed an Arrhenius-type equation.

In this paper, a microstructure model was developed that accounted for both non-isothermal conditions and the simultaneous formation of up to three phases. Dilatometer testing of X70 and X80 samples with cooling rates ranging from 1 to 120 °C/s were conducted. Each sample was processed differently and had varying chemistries. To validate the model, a combination of scanning electron microscopy (SEM) and electron back-scattered diffraction (EBSD) were used for phase identification and quantification. From using this model, the start and stop temperatures of each phase transformation could be predicted and then the modified CCT diagrams could be built.

2. Materials and Methods

2.1. Materials

Dilatometer tests were performed on commercial X70 and X80 samples to determine the effect of cooling rate on the decomposition of austenite.

Table 1. X70 and X80 samples used for dilatometry.

Grade	C	Mn	Cr + Ni + Mo + Cu	Nb	Ti	Si	B
X70	0.05	1.52	0.64	0.06	0.014	0.24	0
X80	0.06	1.69	0.83	0.04	0.007	0.12	0.0003

shows the partial chemistry of each sample, as provided by the manufacturer. The full composition cannot be provided for propietary reasons. Both samples contained the same microalloying elements, with the exception of 0.0003 wt% boron (B) in the X80 steel.

Dilatometery was conducted on a BÄHR DIL 805 thermo-mechanical simulator (BÄHR Thermoanalyse GmbH, Hüllhorst, Germany) with high accuracy linear variable differential transformer (LVDT) (±50 nm) and thermal profile (±2 °C/s). The samples were taken from the quarter thickness of 15 mm TMCP strips and then machined in cylinders with a length of 10 mm and diameter of 5 mm (for the X70 samples) and 4 mm (for the X80 samples). Figure 1 shows the processing profile used on each sample. The X70 steel was tested at cooling rates of 1-, 5-, 15-, 22-, 30-, 50-, 80-, and 120 °C/s. Meanwhile, the X80-A steel was tested at 1-, 3-, 10-, 25-, 30-, and 40 °C/s. For the X70, samples were heated up to 1200 °C at a rate of 10 °C/s and then held for 1 min. They were then cooled to 1050 °C at 3 °C/s and held for 5 s with 0.25 strain (0.1/s). This was followed by a cooling step to 850 °C at 5 °C/s, where they were held for 5 s with 0.25 strain (0.1/s) before being cooled at the rate being tested. For the X80, the samples were heated to 950 °C and held for 15 min prior to cooling. No strain was applied on these samples.

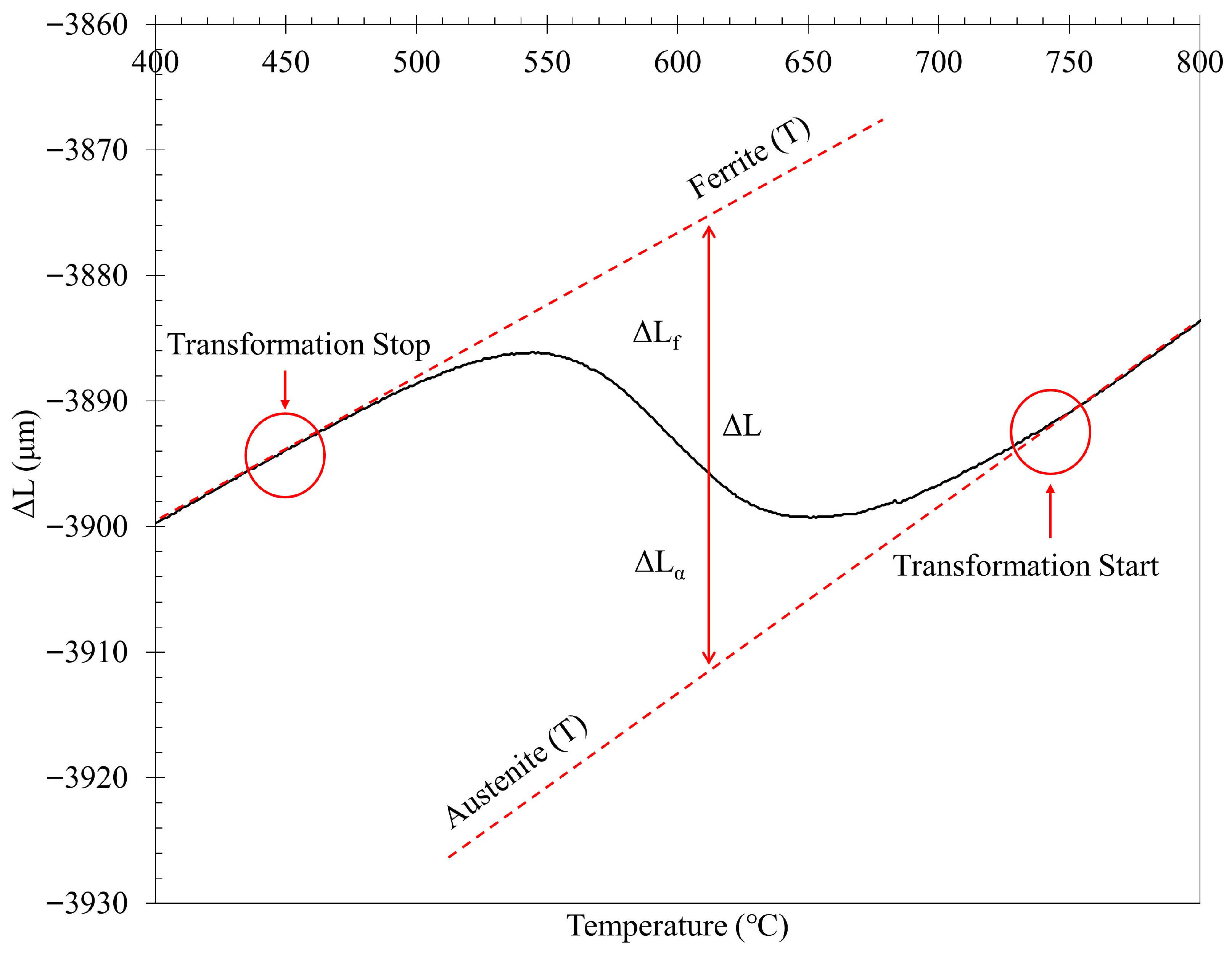
2.2. Dilatometry

Dilatometry measures the volume change of a sample at a fixed heating or cooling rate. In this work, the dilation as a function of temperature was determined and then related to the phase transition occurring. Prior to cooling at the testing rate, the sample was fully austenite. Austenite had a face-centered cubic (FCC) structure, where the packing factor was 0.74. As the sample cooled, FCC austenite transformed into a body-centered cubic (BCC) product. These BCC transformation products had a packing factor of 0.68, which resulted in dilation.

The dilation curve for the 15 °C/s sample is shown in Figure 2. This figure illustrates the main issue with relying on dilation data to determine phase transformations. In the dilation curve, only a single rebound can be observed, which would signify the formation of only one product phase. But characterization of this sample shows that two phases are present in the final microstructure (quasi-polygonal ferrite, QPF, and bainitic ferrite, BF). This means that dilation data cannot accurately capture the formation of multiple phases forming either sequentially or simultaneously. This highlights the necessity to develop a microstructure model that can extract the phase transformation(s) from dilation data.

Instead of using dilation data to measure product phase formation, in this work, it was used to measure the extent of austenite decomposition. As illustrated in Figure 2, tangent lines were included in the dilation curves for austenite (parent phase) and the product phases (QPF and BF in this case). Equations for the tangent lines were determined by finding the slope and intercept for the linear regions on the dilation curve corresponding to austenite and ferrite where no phase change is occurring. The regions considered predominately austenite and ferrite were above the A₃ temperature and the end of the transformation, respectively.

Using these tangent lines in correlation with the dilation curve, the austenite transformation start and stop temperatures could be determined. At approximately 740 °C, a rebound was observed, which signified the beginning of the austenite decomposition which continued until 450 °C.

Using the tangent lines, the fraction transformed at each temperature was then calculated using the lever rule [7]. In this method, the fraction of phases formed from austenite is assumed to be given by the ratio of dilation to maximum dilation. This is represented in Equation (1), where $\Delta L_a$, $\Delta L_f$, and $\Delta L$ are the austenite tangent, ferrite tangent, and the maximum dilation, respectively, at a given temperature:

$$f={\displaystyle \frac{\Delta L-\Delta L_a}{\Delta L_f-\Delta L_a}}.$$

(1)

By calculating the fraction transformed at each temperature between 740 °C and 450 °C, a complete austenite decomposition plot was generated for each dilatometer sample.

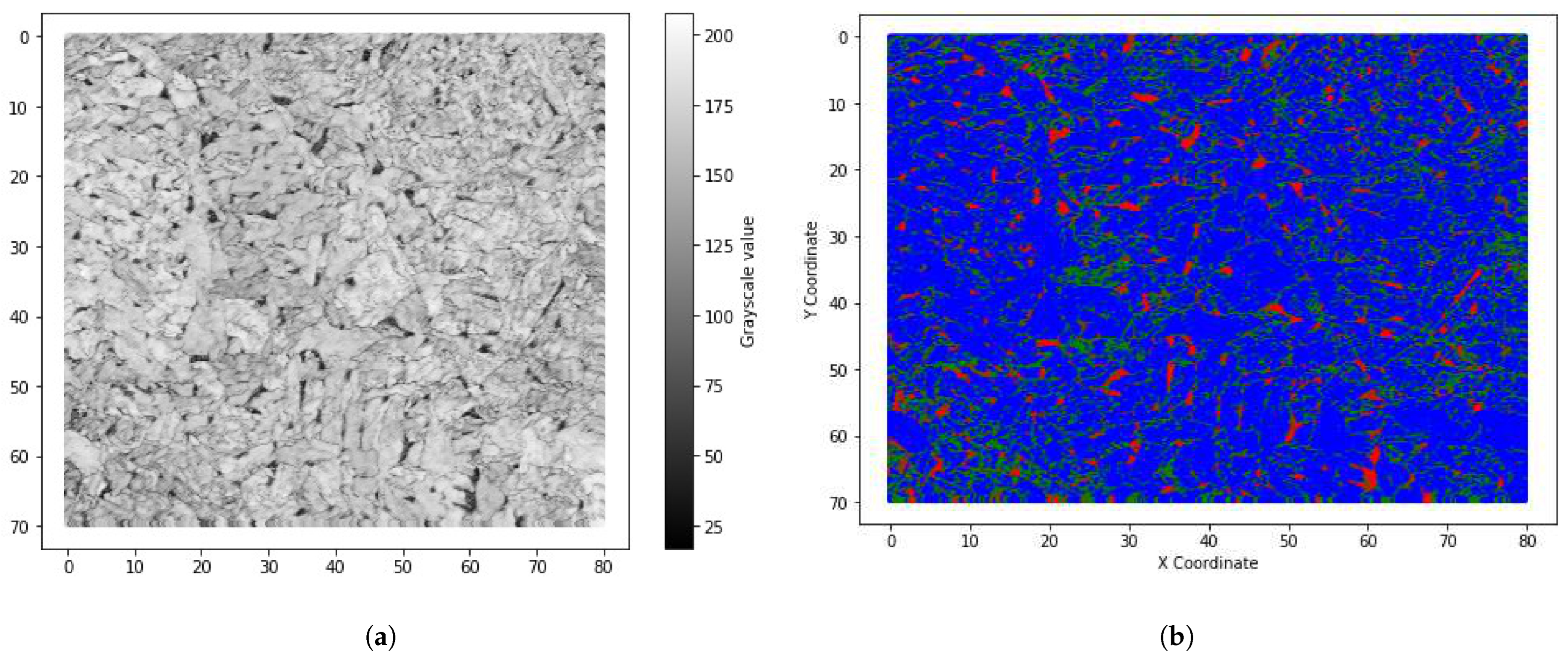
2.3. Scanning Electron Microscopy

SEM imaging was conducted on a Zeiss Sigma 300 VP-FESEM (Zeiss, Oberkochen, Germany). Samples were prepared by manually grinding and polishing down to 0.1 µm using a Buehler EcoMet 250 Grinder-Polisher (Buehler, Lake Bluff, IL, USA). Silicon carbide abrasive grinding papers of P120, P280, P400, P800, and P1200 were used before changing to alumina-, silica-, and diamond-polishing solutions. After grinding and polishing, the samples were etched with a 2% nital solution. In low-carbon steels, nital etching reveals the ferrite grain boundaries and colors them white while leaving phases such as bainite and pearlite dark [17]. Furthermore, it dissolves the ferrite grains, resulting in a topographical surface [17]. Images were taken at the quarter line using an accelerating voltage of 20 kV and magnification of 2000×. The images were obtained using secondary electrons to observe the topography.

2.4. Electron Back-Scattered Diffraction

EBSD was used to quantify the fraction of each phase present. The samples were prepared the same way as with SEM but without the final etching step. Prior to analysis, each sample was also cleaned with acetone in an ultrasonic bath for 10 min. Testing was conducted on a Zeiss Sigma FESEM using an operating voltage of 20 kV. Within the FESEM, the vacuum pressure was below 3 × 10⁻³ Pa, the aperture size was 60 µm, tilt was set to 70°, and the working distance was within 10–16 mm.

Band contrast images at the quarter line were generated for the X70 samples using a map size and step size of 90 × 63 µm and 0.1 µm, respectively. Band contrast images were converted to a gray scale, where a value of 0 is low contrast and a value of 255 is high contrast. The image quality (band contrast) is proportional to the sharpness of the Kikuchi pattern, which is influenced by crystalline defects such as dislocations. Based on this, low-temperature ferritic phases (bainitic ferrite and bainite) can be distinguished from those formed at higher temperatures (quasi-polygonal ferrite) through differences in pixel values.

The threshold pixel value that separates the phases was determined using a method developed by Wu et al. [18]. In this method, it is assumed that the overall distribution of pixel intensity values in a band contrast map is the summation of Gaussian peaks derived from the phases present [18]. To determine the threshold pixel value for the maps, the intersection point of the Gaussian curves was taken. Deconvolution of the pixel distributions into Gaussian peaks was done using OriginLab 2022b.

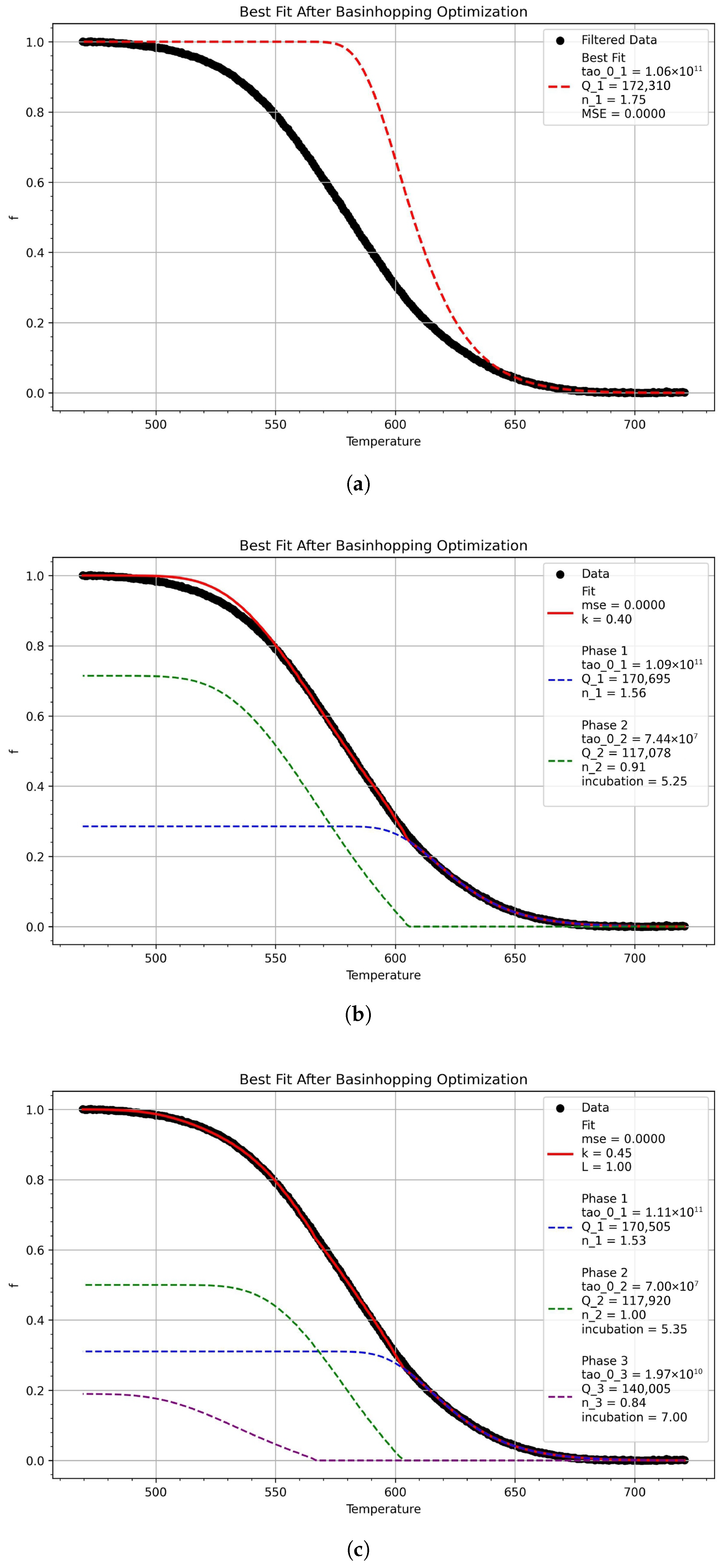
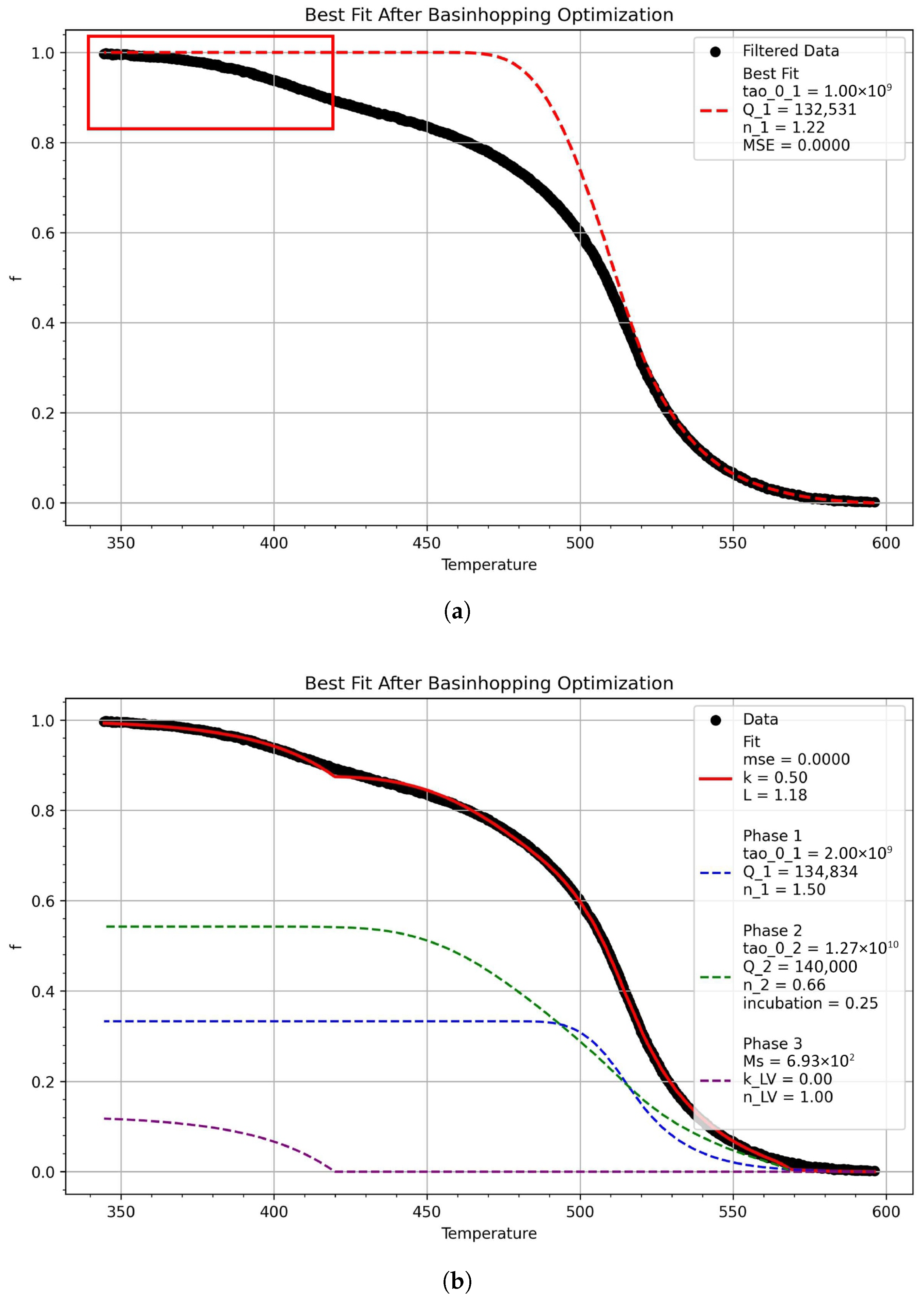
2.5. Microstructure Model

As previously stated, a drawback of using the lever rule to quantify austenite decomposition is that it assumes that only a single phase is being formed [7] or that the transformations are sequential. However, this is rarely the case, as revealed by the microstructural analysis of these samples (see Section 3.1). To circumvent this issue, a microstructure model was fit to the fraction transformed data.

To model the simultaneous formation of up to three phases, a sequential fitting process was used on the produced austenite decomposition curves, where three different forms of the JMAK equation were utilized. From assessing the provided CCT curves in the ASM Alloy Center Database, there are general temperature ranges in which the first, second, and potentially third phase are expected to form. Using these start temperature values, it was assumed that the potential start temperatures of ferrite, bainitic ferrite, and bainite were approximately 800 °C, 650 °C, and 550 °C, respectively, and that the martensite start temperature followed Equation (2) [19]. For the cases with sufficiently slow cooling (≤1 °C/s), pearlite was also assumed to form around 720 °C (if present).

$$\begin{array}{c}{M}_s(°\mathrm{C})=545-601.2(1-exp(-0.868C))-34.4Mn-13.7Si-17.3Ni-9.2Cr\hfill \\ \hfill -15.4Mo+10.8V+4.7Co-16.3Cu\end{array}$$

(2)

For the temperature range in which only a single phase is expected to form, the JMAK equation used by Venkatraman et al. [16] was fit to that portion of the data. In this form of the JMAK equation, the non-isothermal decomposition of austenite is modeled through the introduction of a time parameter $\tau$, which follows an Arrhenius-type equation, Equation (3). Equation (4) shows the form of the JMAK equation used, where constants ${\tau }_o$, Q, and R are the pre-exponential factor, activation energy, and universal gas constant, respectively, and a site-saturation mode is assumed.

$$\tau ={\tau }_{o}ex{p}^{{\displaystyle \frac{-Q}{RT}}}$$

(3)

$$f=1-exp\left(-{\left({\displaystyle \frac{t}{\tau }}\right)}^n\right)$$

(4)

As the temperature decreases into a range where two phases may be forming, a new form of the JMAK equation is needed. Equations (5) and (6) show the modified form of the JMAK equation produced by Jones et al. [15].

$${\zeta }_{\alpha }=\left({\displaystyle \frac{1}{1+K}}\right)\left(1-exp\left[-{\displaystyle \frac{1}{3}}\left(1+K\right)\pi G_{\alpha }^3{I}_{\alpha }^3{t}^4\right]\right)$$

(5)

$${\zeta }_{\beta }=\left({\displaystyle \frac{K}{1+K}}\right)\left(1-exp\left[-{\displaystyle \frac{1}{3}}\left({\displaystyle \frac{1+K}{K}}\right)\pi G_{\beta }^3{I}_{\beta }^3{t}^4\right]\right)$$

(6)

As these equations were derived for iso-thermal transformations, to convert them to a non-isothermal version, $\tau$ was incorporated in a similar manner as in Equations (3) and (4). This resulted in the formation of Equations (7) and (8), where the assumption that the fractions of phase one and phase two are linearly related was made.

$${\displaystyle \frac{V_{\beta }}{V}}=f_{\beta }=\left({\displaystyle \frac{K}{1+K}}\right)\left(1-exp{\left[-{\displaystyle \frac{t}{\tau }}\right]}^n\left({\displaystyle \frac{1+K}{K}}\right)\right)$$

(7)

$${\displaystyle \frac{V_{\alpha }}{V}}=f_{\alpha }=\left({\displaystyle \frac{1}{1+K}}\right)\left(1-exp{\left[-{\displaystyle \frac{t-t_{incubation}}{\tau }}\right]}^n\left(1+K\right)\right)$$

(8)

For the final fitting, a three-phase equation is used, where an assumption regarding the fractions of phase one ($\beta$), two ($\alpha$), and three ($\delta$) is made. Equation (9) shows the relationship between the phase fractions, where the sums are linearly related. Using these relations, Equations (10)–(12) are derived.

$$V_{\beta }=K·(V_{\alpha }+V_{\delta }),V_{\alpha }=L·(V_{\beta }+V_{\delta })$$

(9)

$${\displaystyle \frac{V_{\beta }}{V}}=f_{\beta }=\left({\displaystyle \frac{K}{K+1}}\right)\left(1-exp{\left[-{\displaystyle \frac{t}{\tau }}\right]}^n\left({\displaystyle \frac{K+1}{K}}\right)\right)$$

(10)

$${\displaystyle \frac{V_{\alpha }}{V}}=f_{\alpha }=\left({\displaystyle \frac{L}{L+1}}\right)\left(1-exp{\left[-{\displaystyle \frac{t-t_{incubation}}{\tau }}\right]}^n\left({\displaystyle \frac{L+1}{L}}\right)\right)$$

(11)

$${\displaystyle \frac{V_{\delta }}{V}}=f_{\delta }=\left({\displaystyle \frac{1-KL}{KL+K+L+1}}\right)\left(1-exp{\left[-{\displaystyle \frac{t-t_{incubation2}}{\tau }}\right]}^n\left({\displaystyle \frac{KL+K+L+1}{1-KL}}\right)\right)$$

(12)

For the instances where austenite decomposition does not occur in a range associated with martensite formation, Equations (10)–(12) are used. However, at higher cooling rates where a significant amount of transformation occurs, a different $V_{\delta }$ equation was used. The same three-phase proportionality constants were used, but the model proposed by Lee et al. [20] was substituted in for $V_{\delta }$, Equation (13), where $K_{LV}$ and $n_{LV}$ are constants related to the steel composition and $M_s$ is the martensite start temperature.

$$V_{\delta }=\left({\displaystyle \frac{1-KL}{KL+K+L+1}}\right)\left(1-exp\left[-K_{LV}{\left(M_s-T\right)}^{n_{LV}}\right]\left({\displaystyle \frac{KL+K+L+1}{1-KL}}\right)\right)$$

(13)

To fit Equations (3)–(13) to their corresponding sections of the austenite decomposition curve, a hand-tuning prior followed by a basin hopping method were used. A mean squared error cost function was also used to minimize the residuals for the optimization. Bounds were put on the equation constants that were characteristic to the expected phase. These bounds were determined by analyzing portions of select austenite decomposition curves that contained only a single phase. For the constant n, a value range between 0.01 and 2 was applied for each phase. For the activation energy, the Kissinger approximation was used, Equation (14), where $T_{\alpha }$ is the temperature to reach a certain amount of transformation, $CR$ is the cooling rate, and $Q_{\alpha }$ is the activation energy.

$$ln\left({\displaystyle \frac{T_{f_{\alpha }}}{CR}}\right)={\displaystyle \frac{Q_{f_{\alpha }}}{R{T}_{f_{\alpha }}}}+C$$

(14)

Figure 3 shows the fraction transformed curves for all of the X70 and X80 samples. The expected regions where each phase forms are highlighted and labeled. From these plots, it can be seen that single-phase regions for quasi-polygonal ferrite (QPF) and bainitic ferrite (BF) exist, but not for bainite (B) and martensite (M). As such, only the activation energies of QPF and BF could be solved for by plotting $ln\left({\displaystyle \frac{T_{\alpha }}{CR}}\right)$ vs. ${\displaystyle \frac{1}{T_{\alpha }}}$. Figure 4 shows the Kissinger approximation plots for QPF and BF, and based on the slopes of the curves, the activation energies were shown to vary between 170–280 kJ/mol and 117–138 kJ/mol, respectively. For bainite, an activation energy range of 140–203 kJ/mol was used based on values reported in the literature [21,22].

To begin the fitting process, the high-temperature region of the fraction transformed curves were fit using a reverse sigmoid weight function. A weight function was used to emphasize certain regions of the curve as to avoid over fitting. From this, the approximate model constants for the high temperature phase could be determined. The cutoff criteria for a good initial fit was taken to be a mean squared error (mse) of less than or equal to 0.0001. After obtaining the high temperature constants, the weight function was shifted to approximately 550 °C. This was done based on the assumption that the high-temperature phase forms in the temperature range of 750–650 °C, the medium temperature phase forms between 650 and 550 °C, and if a third low temperature phase forms, it is below 550 °C. With the weight function positioned around 550 °C, and the constants for the high-temperature phase determined, Equations (7) and (8) could be fit to this two-phase region of the curve. Based on this two-phase fit, if the rest of the transformation curve could be accurately predicted (mse of less than or equal to 0.0001), then the introduction of a third phase was ignored. In the case a third phase was needed, the constants previously calculated were plugged into Equations (10) and (11), while the constants for Equation (12) as well as K and L were determined. An important step during this optimization was to allow the values of K and L to have a large search space, as these values ultimately determine the final fractions of each phase.

3. Results and Discussion

3.1. Microstructural Analysis of X70 and X80

Figure 5 and Figure 6 show the SEM images for the X70 samples. From these images, it can be seen that at least two microstructures are formed at each cooling rate. For the 1 °C/s sample, polygonal ferrite (PF) and degenerate pearlite (DP) microstructures are formed. The PF can be delineated from quasi-polygonal ferrite (QPF) based on the smooth concave edges formed through impingement of growing ferrite grains [23]. This smooth shape is the result of low cooling rates, which allow for nucleation of allotriomorphic ferrite and subsequent equiaxed growth. At this low cooling rate, most of the prior austenite can be transformed into ferrite, which allows for a higher carbon saturation of any remaining austenite. The carbon saturation that occurs at this cooling rate leads to the formation of the DP. DP varies from lamellar pearlite (LP) as the ferrite and cementite is not layered and, as shown in Figure 5, has a more irregular morphology.

As the cooling rate increased to 5 °C/s and 15 °C/s, pearlite stopped forming, and the microstructure changed to PF and BF. The characteristic rough edges of the QPF that forms are the result of both the cooling rate and interstitial or substitutional atom partitioning at the migrating interface [23]. The BF accompanying the QPF is likely to have been formed through nucleation on deformation bands or at grain boundaries.

Figure 5d and Figure 6a show the microstructures for cooling rates of 22 °C/s and 30 °C/s. Unique to the rest of the X70 samples, at these cooling rates, there were three observed microstructures: QPF, BF, and B. The specific type of bainite forming appears to be upper bainite (UB), as suggested by the elongated and narrow bands.

Lastly, at cooling rates of 50 °C/s, 80 °C/s, and 120 °C/s, the microstructure is fully BF and UB, with some potential martensite. Furthermore, the amount of B and BF increases when the fraction of QPF decreases. This can be attributed to the competing nucleation mechanisms of the two. Both QPF and bainite nucleate at austenite grain boundaries [24]. Thus, by forming QPF at higher temperatures first, the amount of possible nucleation sites for bainite is reduced and the transformation is hindered [25]. Additionally, for the lower cooling rates, by inhibiting the bainite transformation, BF formation is promoted instead [25,26].

Figure 7 and Figure 8 show the SEM images of the X80 samples. The major difference observed between the X70 and X80 samples was the absence of BF in all X80 images. In the presence of dislocations, carbon tends to segregate to dislocations rather than precipitate as cementite, resulting in carbide-free BF [27]. Since the X80 samples did not undergo deformation prior to cooling, bainite formation was favored. Furthermore, different variants of bainite were also observed at different cooling rates.

At the lower cooling rates (1 °C/s and 5 °C/s), a blocky bainite microstructure was found in locations opposite of the QPF within the same prior austenite grain. This observation can be explained by the rejection of carbon into the surrounding austenite during nucleation and growth of allotriomorphic ferrite along the prior austenite grain boundaries. As the carbon diffuses faster along grain boundaries, the rejected excess carbon stabilizes other parts of the grain boundary, hindering any nucleation and growth of QPF. These untransformed regions may then stay untransformed until a temperature is reached, which allows for the formation of bainite.

As the cooling rates increased (10 °C/s, 25 °C/s, 30 °C/s, and 40 °C/s), the bainite took on more of a lathe morphology, similar to what was observed in the X70 samples. For similar reasons stated for the X70 samples, this may be the result of reduced QPF nucleation and growth at higher temperatures, which allows for more bainite formation.

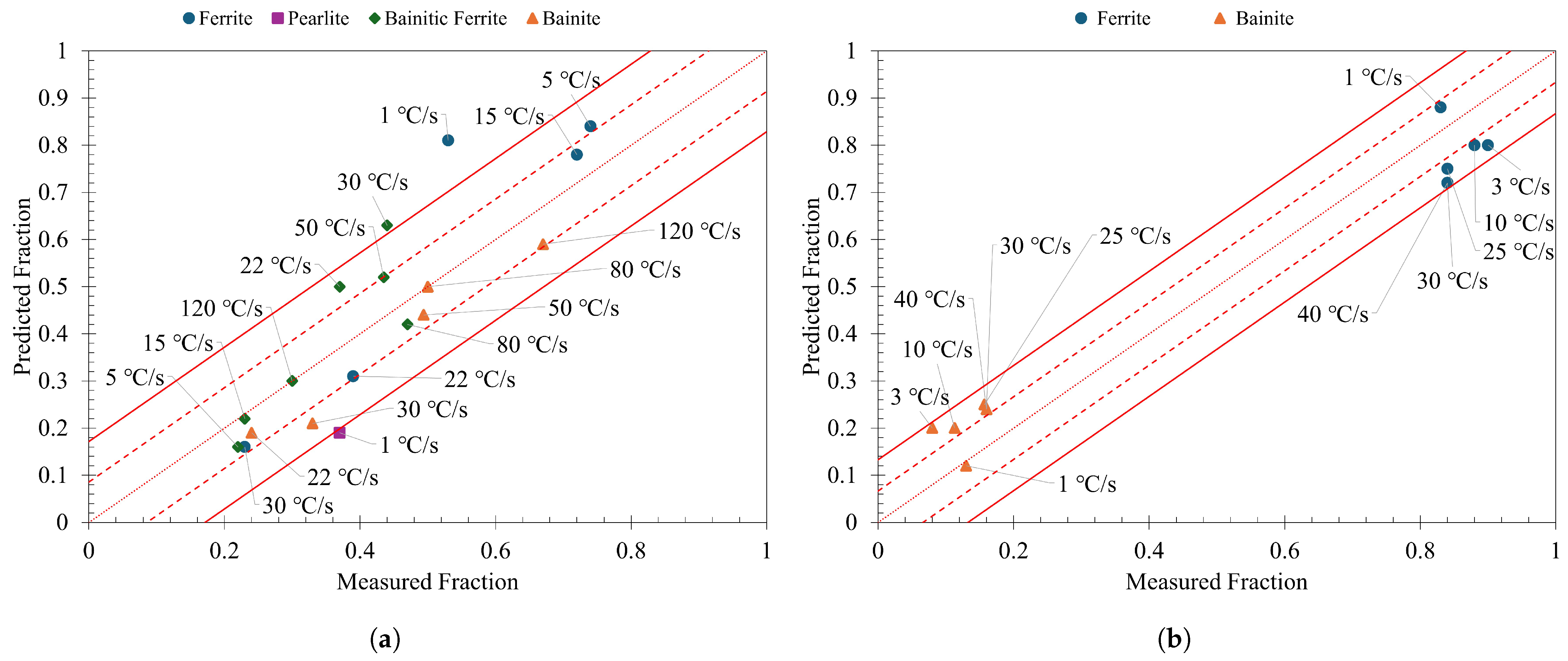
3.2. Phase Quantification of X70 and X80

For phase quantification, EBSD was used for the X70 samples, while the point=counting technique described in ASTM E562 was used for the X80 samples. Figure 9 shows the X70 15 °C/s sample band contrast image (a) produced through EBSD and the final colored image using the technique developed by Wu et al. [18] (b). In Figure 9b, blue is the high-temperature phase, green is the medium, and red is the low. Of note, the EBSD band contrast maps showed non-indexed regions, which are shown as black. These regions may be the result of martensite with retained austenite (MA) being present in the samples.

Figure 10 summarizes the measured fractions for each sample. The phases were labeled based on the observations from SEM. Similar between both samples was an initially lower amount of ferrite (at 1 °C/s) as well as a decrease in ferrite with increasing cooling rate. The observation of decreasing volume fraction of ferrite with increasing cooling rate is a commonly reported phenomena [28,29,30,31,32]. This is a result of the reconstructive mechanisms that occur during the austenite-to-ferrite phase transformation, facilitated by carbon diffusion [24]. As the cooling rate is increased, there is less time for the carbon to diffuse, which decreases nucleation and growth rates [24,32,33].

In the X70 samples, as the fraction of QPF decreased, there was a subsequent increase in BF. BF forms through a shear diffusional mechanism, where nucleation occurs at grain boundaries or dislocation bands [34,35]. These sites do not solely act as nucleation sites for BF, which is why, for the 1 °C/s sample, there is no observed BF given the same deformation band density [8]. But, as the cooling rate increases, the kinetics of QPF formation are reduced through the inhibiting of carbon diffusion [36]. This inhibiting of the QPF phase then promotes the formation of BF, as more nucleation sites are available at lower temperatures [33].

For the X80 samples, a similar explanation can be used to explain the slight increase in bainite content with increasing cooling rate. As the QPF or PF forms along the prior austenite grain boundaries, it not only consumes the available nucleation sites for bainite but also depletes the solid-solution atoms whose partitioning would otherwise stabilize the austenite, thereby suppressing bainite nucleation. Thus, by reducing the amount of QPF and/or PF nucleation through increased cooling rates, bainite formation can be promoted.

Finally, X70 samples were subjected to a high reheat of 1200 °C, which caused the dissolution of most of the niobium carbonitrides (Nb(CN)), followed by two steps of deformation. Despite the tendency of strain-induced precipitation of Nb, it is obvious that the remaining Nb in the solution supressed polygonal ferrite and promoted the formation of bainite from pancaked austenite, as seen in Figure 3 and Figure 10. In contrast, X80 samples were reheated to a low 950 °C temperature, insufficient for Nb(CN) dissolution. Furthermore, no deformation of austenite was carried out for the X80 samples. Although the Prior Austenite Grains were larger in the X80 than in the X70 samples (no deformation of austenite), it is clear that austenite transformed at higher temperatures and decomposed to more ferrite in X80 steel (Figure 3 and Figure 10). This can be attributed to the lack of Nb in solution in the X80 samples, which offset substantially the effect of larger grains of prior austenite and a lack of deformation in X80.

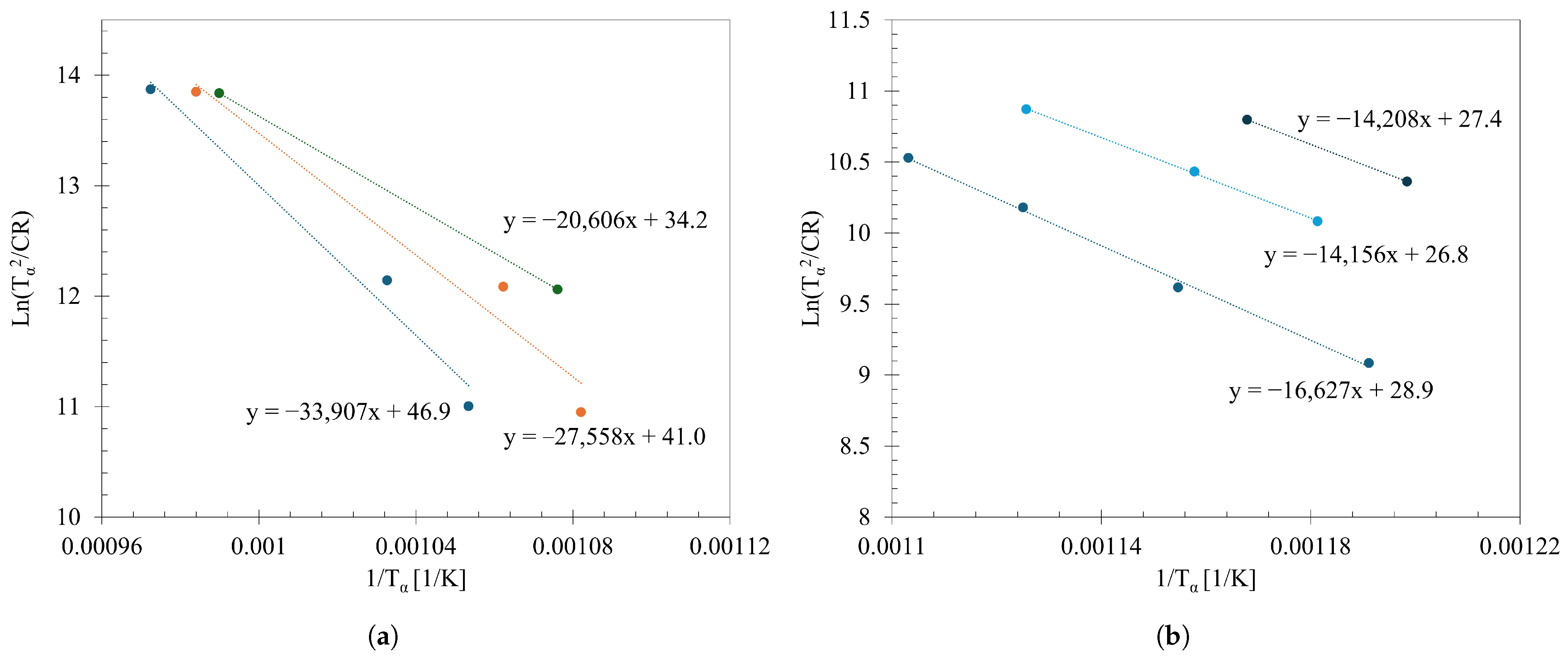
3.3. Model Predictions

Figure 11 and Figure 12 show the microstructure model results for two- and three-phase scenarios. In Figure 11a and Figure 12a, the results of fitting the single-phase version of the JMAK can be seen. To achieve these fits, Equation (4) was fit to the austenite data iteratively by beginning at the highest temperature and shifting the weight function to lower temperatures. As seen in these figures, Equation (4) was only able to model the austenite decomposition up until approximately 600 °C and 640 °C, at which point there was a departure from the austenite data. This departure from the austenite data signified the beginning of the formation of a second phase. Equations (7) and (8) were then used to model the remaining portion of the austenite decomposition curves in the same iterative manner. For Figure 11b, these equations were able to produce a fit with a mse of 0; however, as seen at 540 °C in Figure 12b, the fit again deviated from the austenite data. For the final fit shown in Figure 12c, no weight function was used, and Equations (10)–(12) were applied to the entire measured data set. As shown in these figures, the final error of fitting the microstructure model to the austenite data was 0. Using the final fitted results, information regarding the start and stop temperatures of individual phase transformations could be elucidated. Additionally, regions where simultaneous transformations occur could be observed.

Figure 13 illustrates the results of fitting the martensite version of the model to the austenite data. For samples that appeared to have martensite formation, there was an observed break from the continuity of the austenite curves (highlighted by the red box in Figure 13a). Given the characteristics of the martensite equation, Equation (13), the resulting curve has an abrupt concave down shape. This differs significantly from the more sigmoid shape produced from the modified JMAK equations, and results in the non-smooth final fitted curve (red).

Next, to assess the efficacy of the microstructure model, parity plots between the predicted and measured fractions of the phases were made, as seen in Figure 14a,b. Only the first and second primary phases were plotted (with the exception of X70 22 °C/s and 30 °C/s). From EBSD on the X70 samples, based on the non-indexed regions (black) in each EBSD map, it was suggested that MA was present at all cooling rates to some degree. But, through fitting the model to the data, in most cases, a third phase was not found. Furthermore, for the X80 samples, small fractions of DP were measured at cooling rates of 1 °C/s. 3 °C/s, and 10 °C/s, but only two phases were needed to achieve the proper fit. Additionally, in the higher cooling rate X80 samples (30 °C/s and 40 °C/s), martensite was included in the fit, yet no martensite was measured.

In Figure 14a,b, one and two standard deviation lines were included to identify any potential outliers. For the X70 samples, apart from the 1 °C/s and 30 °C/s predictions, it can be seen that there is good agreement between the measured and predicted data. Meanwhile, for all the X80 samples, the predictions fell within the standard deviation bounds. A potential reason for the minor deviations that are observed in all predictions may be due to the presence of MA (to some degree) being present in all samples. For the microstructure model used, unless the transformations entered a temperature range characteristic to martensite transformation, it was excluded from the fitting. But, from EBSD and SEM, there are signs of potential MA in the final microstructure. By not accounting for potential MA, this may be influencing the predicted fractions of the other phases. This would explain why the higher cooling rate samples (80 °C/s and 120 °C/s) for the X70, which did include martensite, produced predictions closest to the parity line (Figure 14a).

3.4. Continuous Cooling Transformation Diagrams

With the model being in good agreement with the measured EBSD and SEM results, CCT diagrams for the X70 and X80 samples were made. Figure 15 shows the CCT diagrams constructed from the microstructure model. In traditional CCT diagrams, only the solid lines would be shown, which would omit crucial information such as regions of simultaneous transformation, and where an individual phase stops forming. By including this information in the CCT diagrams, the usefulness of these curves are improved, as it gives the user a better understanding of the kinetics and thermodynamics of the steel they are working with.

In addition, by including the stop temperature of each phase transformation, it introduces the ability of these curves to be applied to non-continuous cooling profiles. It does this by allowing the user to apply the Scheil additivity principle with respect to the start and stop of the given phase transformation. This method is commonly used when working with time–temperature–transformation curves, which contain start and stop times for isothermal phase transformations. In most processing scenarios, such as TMCP, the steel is not cooled at a single cooling rate; instead, it is variable. By providing CCT users with the ability to perform additivity on cooling data, they can better approximate the final microstructure and phase fractions.

4. Conclusions

A microstructure model was developed to overcome the limitations of traditional dilatometry-based phase identification in microalloyed steels, particularly under conditions where austenite decomposes into multiple phases simultaneously. By integrating non-isothermal JMAK kinetics with simultaneous transformation models, the model successfully predicted the evolution of up to three product phases during continuous cooling. The model was validated using extensive dilatometer testing on X70 and X80 steels across a wide range of cooling rates (1–120 °C/s) along with a detailed microstructural quantification using SEM and EBSD.

The results show that cooling rate and prior deformation strongly influence austenite decomposition pathways. In the X70 steel, polygonal ferrite and pearlite formed at the lowest cooling rate, transitioning to quasi-polygonal ferrite and bainitic ferrite, and eventually quasi-polygonal ferrite, bainitic ferrite, and bainite as cooling rate increased. At the highest cooling rates, bainitic ferrite and bainite dominated, with small amounts of martensite possible. In the X80 steel samples, which were cooled without any prior deformation, bainitic ferrite was notably absent across all examined conditions, with ferrite and bainite dominating the microstructure. This highlights the role of plastic strain in promoting bainitic ferrite formation and altering transformation paths.

The predicted fractions of the product phases showed good agreement with microstructural observations. Using this model, CCT diagrams consistent with microstructural observations were constructed, providing both the starting and stopping points of individual transformations during austenite decomposition. The method is effective for predicting transformation kinetics from dilation curves under multi-phase, non-isothermal conditions typical of TMCP steels and provides clearer insight than conventional lever-rule interpretations. The ability to model simultaneous phase transformations under non-isothermal conditions represents a significant advance over most available kinetic approaches, which are typically limited to one product phase or sequential scenarios.

These results show the necessity of using approaches capable of capturing concurrent phase transformations during austenite decomposition in HSLA steels. The proposed microstructure model provides a more robust alternative to the classical lever rule, enabling a better prediction of phase evolution under industrially relevant cooling conditions and provides a basis for the development of more reliable CCT diagrams to support process design and property optimization in HSLA steels.