Mechanisms of Fine Mud Covering and Enhanced Dispersion for a Rutile Middling
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. The Slime
2.1.2. Experimental Materials
2.2. Experimental Methods
2.2.1. Zeta Potential Measurement
2.2.2. Contact Angle Tests
2.2.3. Other Measurements
2.3. Theoretical Calculation Methods of DLVO and EDLVO
3. Results and Discussions
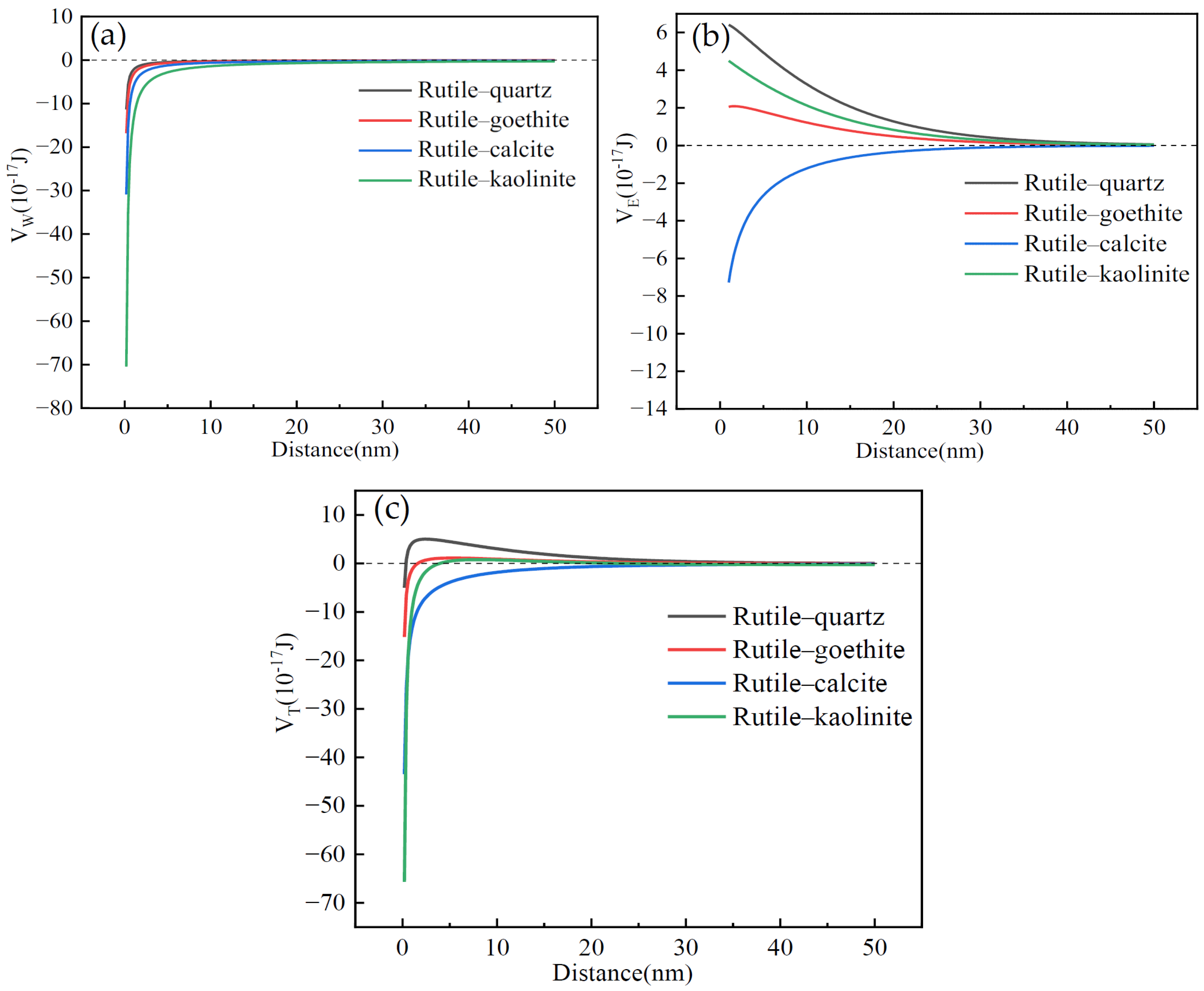
3.1. DLVO Theoretical Calculation
3.1.1. Interaction Energy Between Rutile and Gangue
3.1.2. Interaction Energy Between the Zircon and Gangue
3.2. EDLVO Theoretical Calculation
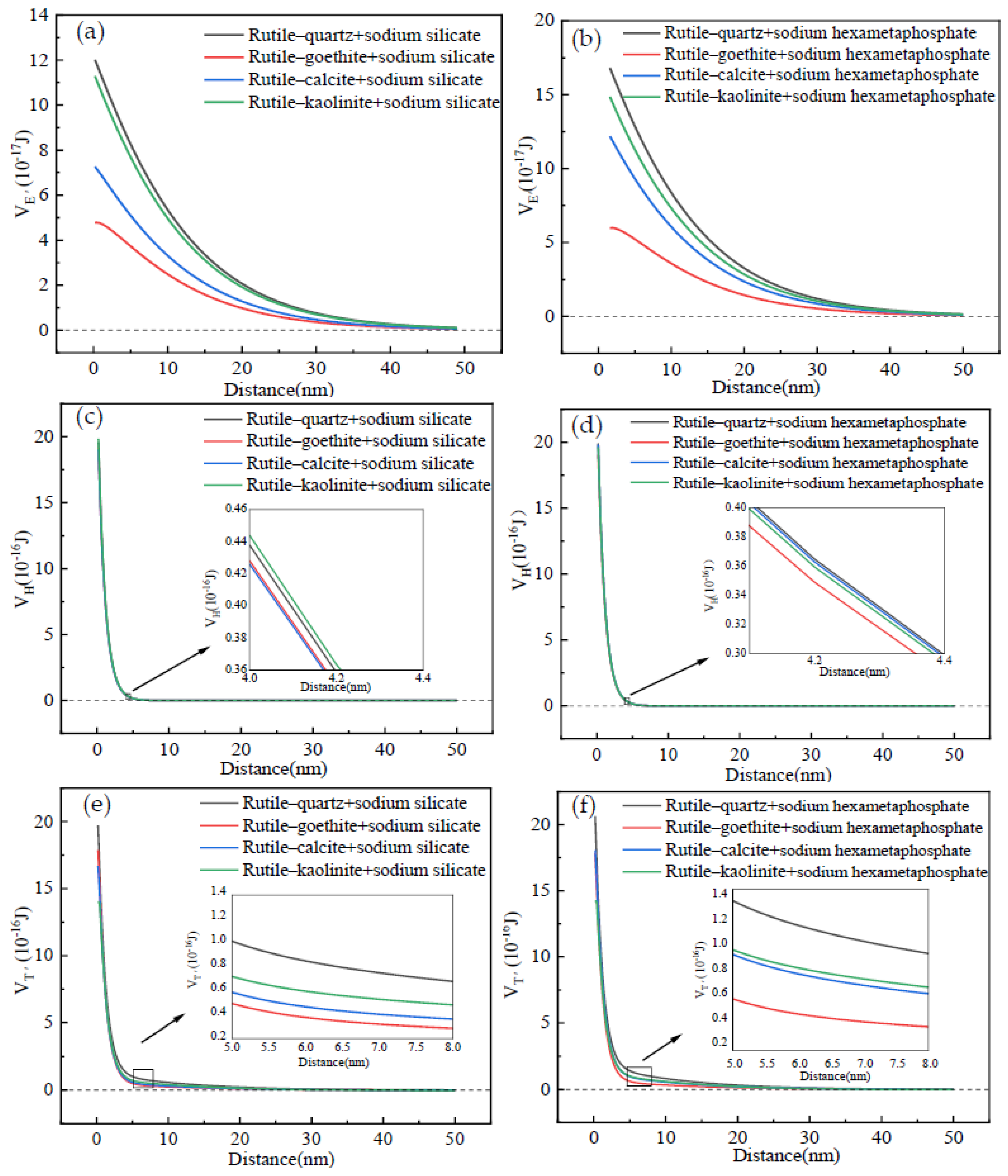
3.2.1. Interaction Energy Between the Rutile and Gangue After Adding Surfactants
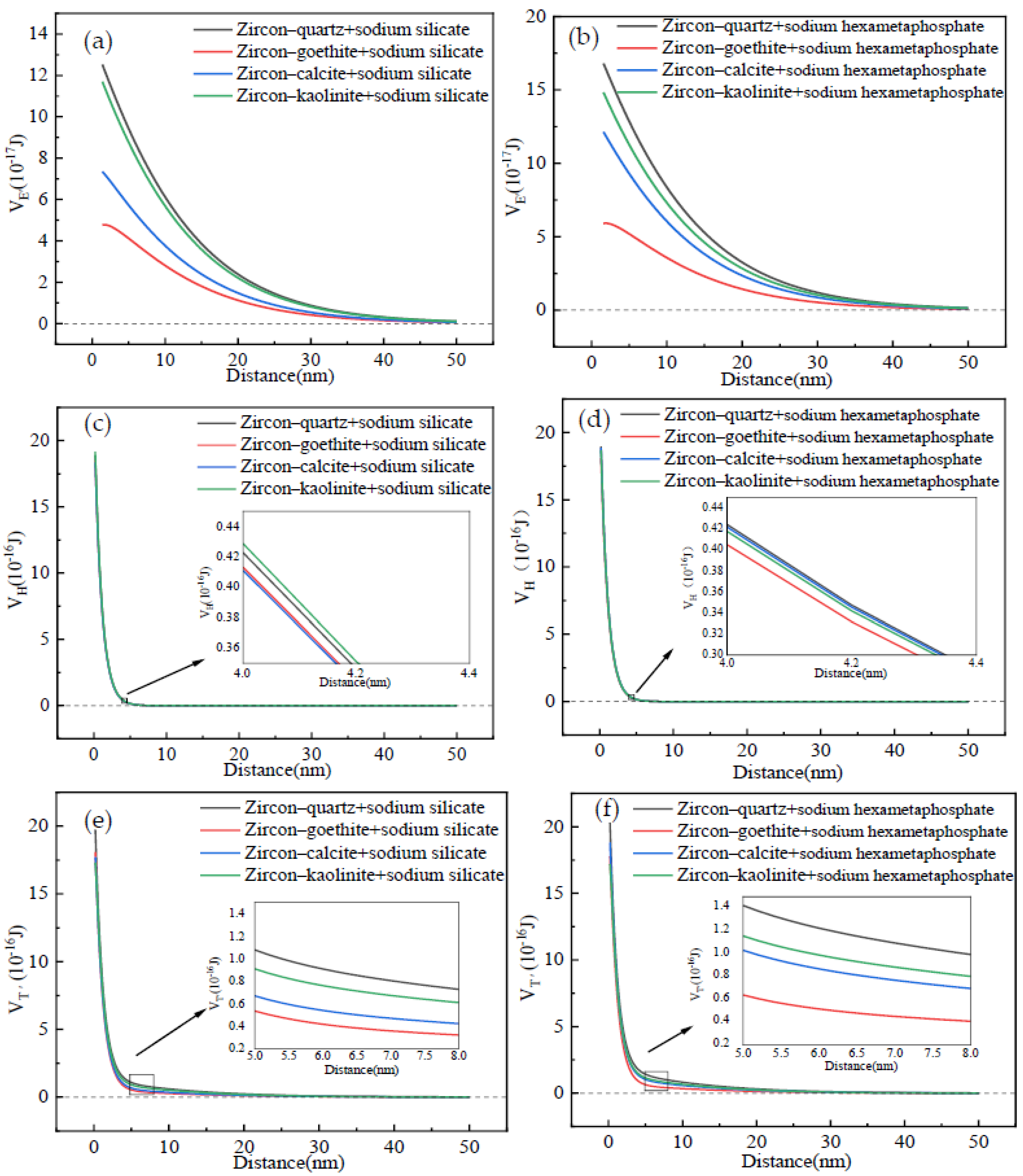
3.2.2. Interaction Energy Between the Zircon and Gangue After Adding Surfactants
4. Conclusions
- (1)
- The main gangue in the slime consisted of goethite, quartz, calcite, and kaolinite. In addition, a small amount of rutile and zircon also co-existed. Average particle size of the slime reached 11.06 μm.
- (2)
- The DLVO theoretical calculations demonstrated that the quartz was difficult to cover over the surface of zircon and rutile, whereas the calcite was prone to adhere to their surface. The covering capacity of goethite and kaolinite over the rutile was stronger than that over the zircon.
- (3)
- The EDLVO theoretical calculation verified that the addition of SS or SHMP promoted detachment of the gangue from the surface of rutile and zircon. Moreover, the gangue was more prone to detach from the zircon surface in contrast with the rutile. It was also found that the VH between the zircon/rutile and gangue after adding surfactants mainly contributed to the VT′. Comparing the SHMP with the SS, dispersion performance of the former surfactant was superior. These discoveries will provide an excellent theoretical reference for effectively removing fine mud from the surface of rutile ore.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Srivastava, M.; Jayakumar, V.; Udayan, Y.; SM, M.; Gautam, P.; Nag, A. Additive manufacturing of Titanium alloy for aerospace applications: Insights into the process, microstructure, and mechanical properties. Appl. Mater. Today 2024, 41, 102481. [Google Scholar] [CrossRef]
- Karadimas, G.; Salonitis, K. Ceramic matrix composites for aero engine applications—A review. Appl. Sci. 2023, 13, 3017. [Google Scholar] [CrossRef]
- Zhu, X.; Geng, Y.; Wu, D.; Houssini, K.; Gao, Z. Evaluating the security of China’s zirconium industry. Resour. Conserv. Recycl. 2023, 199, 107277. [Google Scholar] [CrossRef]
- Murty, V.; Upadhyay, R.; Asokan, S. Recovery of zircon from Sattankulam deposit in India-problems and prospects. In The 6th International Heavy Minerals Conference ‘Back to Basics’; The South African Institute of Mining and Metallurgy: Johannesburg, South Africa, 2007; pp. 69–74. [Google Scholar]
- Gong, P.; Ren, L.; Bao, S.; Zhang, Y.; Qin, W.; Nguyen, A.V. Flotation separation mechanism of rutile and chlorite using CMC as depressant. Miner. Eng. 2024, 217, 108957. [Google Scholar] [CrossRef]
- Liang, Q.-W.; Li, Y.-S.; Sun, Y.-C.; Zhai, D.-G.; Sun, H.-R.; Zhou, S.-X.; Zhang, B.-L.; Lü, X.; Xu, J.-C.; Li, X.-F. Distribution, types, metallogenic regularity and exploration potential analysis of zirconium deposit in China. China Geol. 2025, 8, 408–430. [Google Scholar] [CrossRef]
- Zeng, X. The Research of Mining System Scheme of Zr-Ti Placers in Baoding Sea. Master’s Thesis, Central South University, Changsha, China, 2014. [Google Scholar]
- Singh, R.; Venkatesh, A.; Sudhakar, C.; Sethy, S.N.; Babu, K.P. Exploration for strategic placer mineral deposits in a fluctuating shoreline: Depositional environment and mineralogical characterization of the NE Odisha coast placers, India. Ore Geol. Rev. 2020, 127, 103850. [Google Scholar] [CrossRef]
- Amosah, M.; Yvon, M.; Zhou, J.; Galvin, K. The role of enhanced desliming and gravity separation as a precursor to flotation in the upgrading of cassiterite from tailings. Miner. Eng. 2024, 208, 108581. [Google Scholar] [CrossRef]
- Wu, Y.; He, J.; Fan, R.; Wang, Q.; Sun, W.; Ralston, J.; Gao, Z. Effects of surface Chemistry, particle morphology and pretreatment on zircon flotation. Miner. Eng. 2022, 190, 107904. [Google Scholar] [CrossRef]
- Nouri, S.; Hoseinian, F.S.; Rezai, B.; Saberyan, K. New pretreatment method for high-tension electrical separation of zircon from quartz. Trans. Nonferrous Met. Soc. China 2019, 29, 1737–1743. [Google Scholar] [CrossRef]
- Nzeh, N.S.; Popoola, P.A. Physical beneficiation of heavy minerals–Part 2: A state of the art literature review on magnetic and electrostatic concentration techniques. Heliyon 2024, 10, e32201. [Google Scholar] [CrossRef]
- Wang, Z.; Zheng, Y.; Huang, X.; Wang, X.; Peng, J.; Dai, Z. Gravity separation tests of a complex rutile ore. Minerals 2024, 14, 68. [Google Scholar] [CrossRef]
- Yu, Y.; Ma, L.; Cao, M.; Liu, Q. Slime coatings in froth flotation: A review. Miner. Eng. 2017, 114, 26–36. [Google Scholar] [CrossRef]
- Li, Q.; Huang, L.; Hu, B.; Huang, S.; Zhou, J.; Xu, Y. Synthesis and utilization of a novel amidoxime collector for the flotation separation of cuprite from calcite. Sep. Purif. Technol. 2025, 353, 128447. [Google Scholar] [CrossRef]
- Yu, C.; Cai, G.; Hao, S.; Zhao, X.; Luo, X. Fractal characteristics of ore particle crushing under ultrasonic vibration. China Powder Sci. Technol. 2023, 29, 106558. [Google Scholar]
- Parsegian, V.A. Van der Waals Forces: A Handbook for Biologists, Chemists, Engineers, and Physicists; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Huang, G.; Pan, Z.; Wang, Y. Dispersion of praseodymium-doped zirconium silicate pigment in aqueous suspension by modified hydroxyl copolymer. Chem. Eng. Res. Des. 2020, 154, 86–100. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Kong, R. New insights into the interaction between low-rank coal particles and clay minerals and its role in flotation responses. Particuology 2024, 94, 48–58. [Google Scholar] [CrossRef]
- Wang, C.; Xu, C.; Zhao, S.; Hu, F.; Li, Q. Effect of Organic Matter Removal on Stability of Suspension of Loess Nanoparticles. Acta Pedol. Sin. 2020, 57, 119–129. [Google Scholar]
- Xu, D.; Zhu, S.; Zhu, Z.; Cui, H. Influences of sodium hexametaphosphate on interactions of coal and clay particles in flotation. J. Min. Sci. Technol. 2016, 1, 269–276. [Google Scholar]
- Wang, Y.; Jiang, W.; Qin, W.; Pan, Z.; Jia, L.; Hong, X.; Song, Z.; Luo, X. The origin of interparticle aggregation: Probing the long-range hydrophobic forces between particles induced by nanobubbles in aqueous solutions. Miner. Eng. 2024, 218, 109030. [Google Scholar] [CrossRef]
- Ma, X.; Chen, J.-Y.; Xu, J.-W.; Wu, X.-J.; Chi, H.-D.; Wei, Y.-D. Study on influence factors and mechanism of Floc-Bubble interaction in the flotation treatment of drilling wastewater. Sep. Purif. Technol. 2025, 377, 134300. [Google Scholar] [CrossRef]
- Shi, Z.; Ran, B.; Liu, L. Determining the interaction energy of a quartz–kaolinite system at different pH levels by atomic force microscopy and extended DLVO theory. Powder Technol. 2022, 409, 117842. [Google Scholar] [CrossRef]
- Gao, N.; Yang, Z.; Teng, Q.; Liu, S. Study on behavior and mechanism of reverse flotation desilication of magnetite enhanced by magnetic amylopectin. Sep. Purif. Technol. 2025, 361, 131286. [Google Scholar] [CrossRef]
- Fu, X.; Niu, Z.; Peng, C.; Han, H.; Sun, W.; Yue, T. Quantitative synergistic adsorption affinity of Ca (II) and sodium oleate to predict the surface reactivity of hematite and quartz. Sep. Purif. Technol. 2025, 360, 131196. [Google Scholar] [CrossRef]
- Kong, L.; Lv, J.; Li, J.; Ni, L.; Qin, L. The effects of pH regulators on the flotation separation of sphalerite and dolomite and their interaction mechanism. Appl. Surf. Sci. 2025, 680, 161450. [Google Scholar] [CrossRef]
- Yan, X.; Wei, L.; Meng, Q.; Wang, J.; Yang, Q.; Zhai, S.; Lu, J. A study on the mechanism of calcium ion in promoting the sedimentation of illite particles. J. Water Process Eng. 2021, 42, 102153. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, S.; Li, J.; Weng, L.; Wu, C.; Liu, K. Improvement on combustible matter recovery in coal slime flotation with the addition of sodium silicate. Colloids Surf. A Physicochem. Eng. Asp. 2020, 603, 125220. [Google Scholar] [CrossRef]
- Zhou, H.; Xu, L.; Wang, D.; Xue, K.; Tian, J. Selective adsorption mechanism of SHMP onto fine fluorite in bastnaesite flotation system. Colloids Surf. A Physicochem. Eng. Asp. 2023, 670, 131527. [Google Scholar] [CrossRef]
- Li, J.; Lv, J.; Kong, L.; Ni, L.; Qin, L. Enhancing flotation separation of fine-grained cassiterite and calcite with cetylpyridine bromide as a dispersant. Adv. Powder Technol. 2024, 35, 104606. [Google Scholar] [CrossRef]
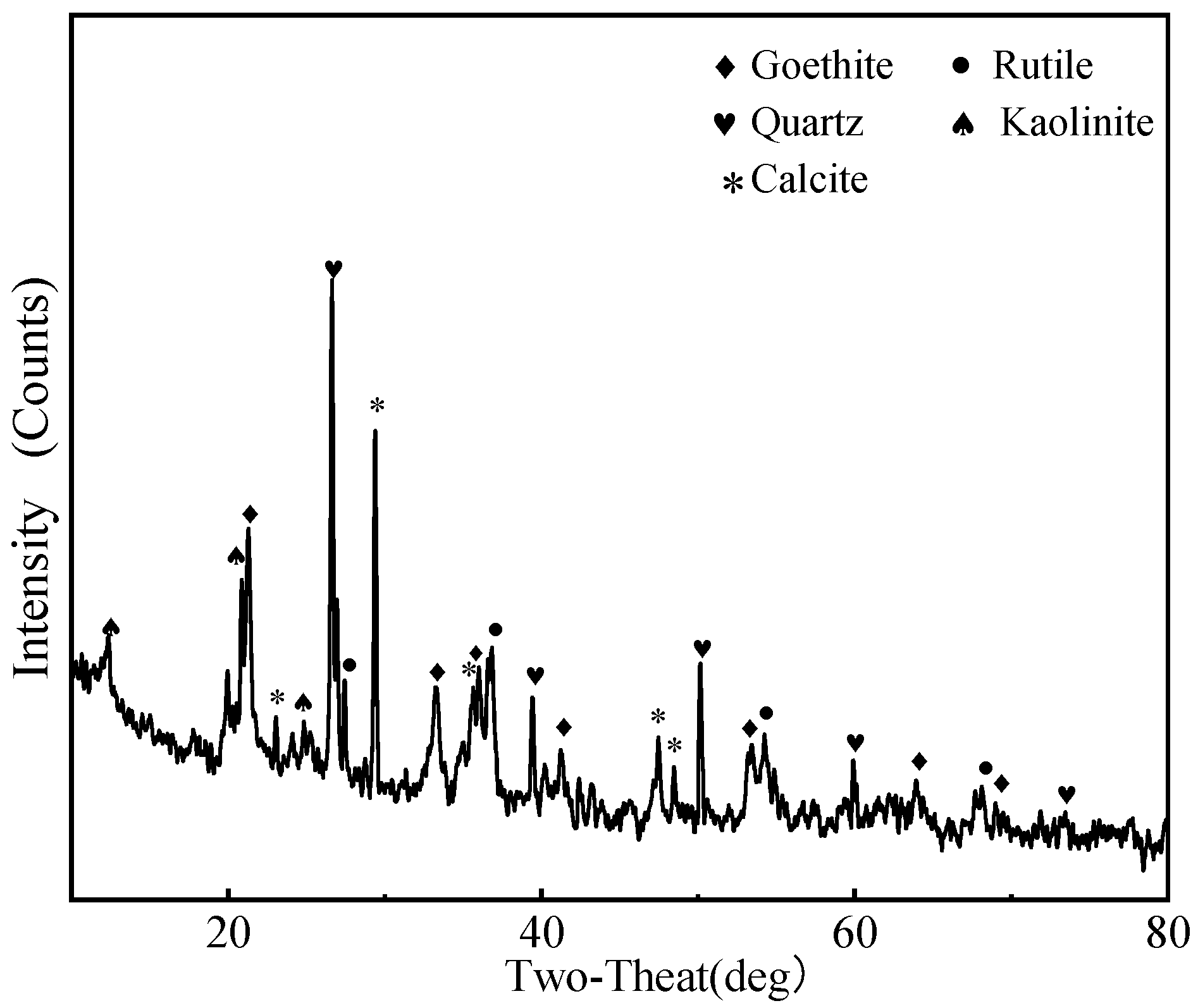

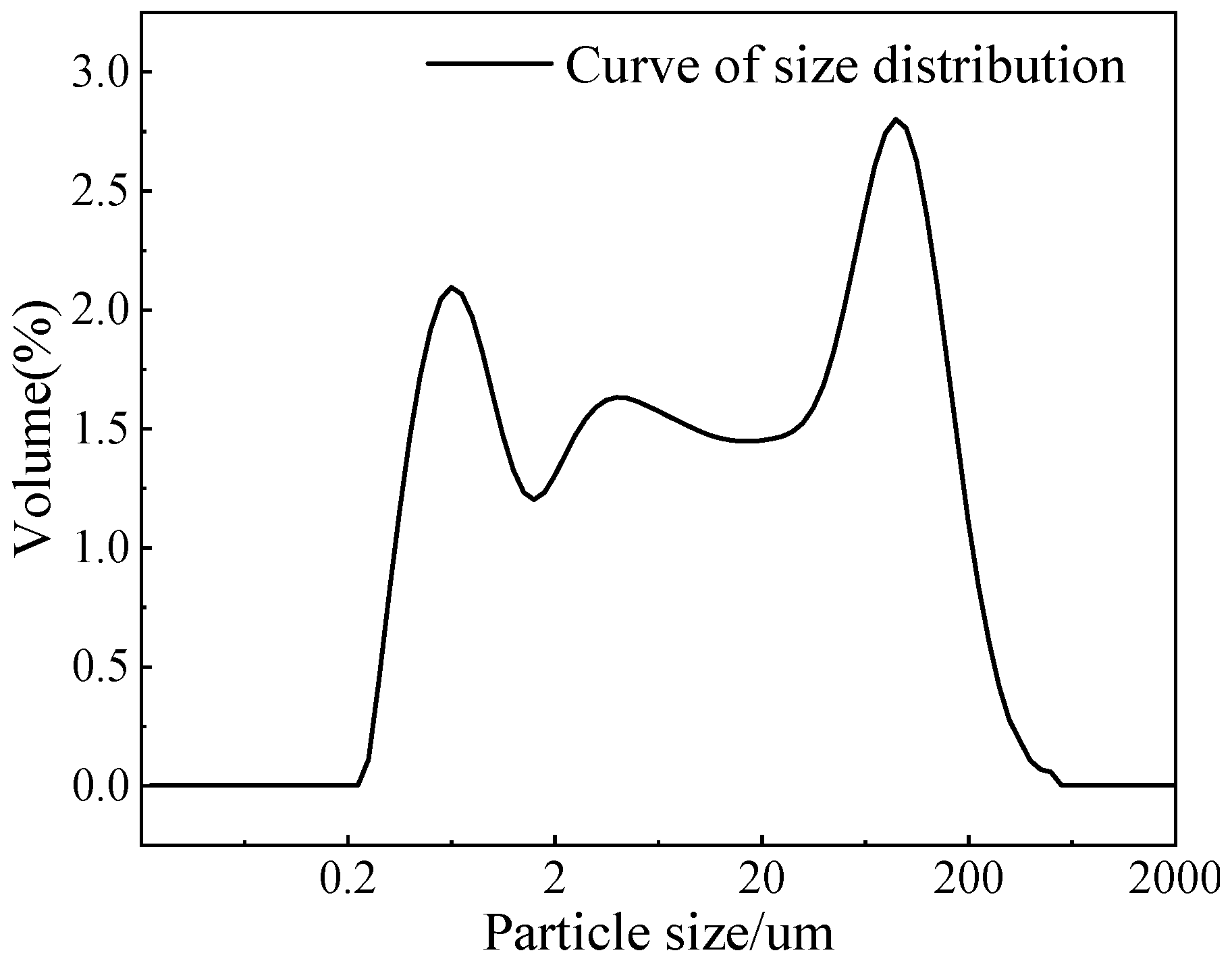
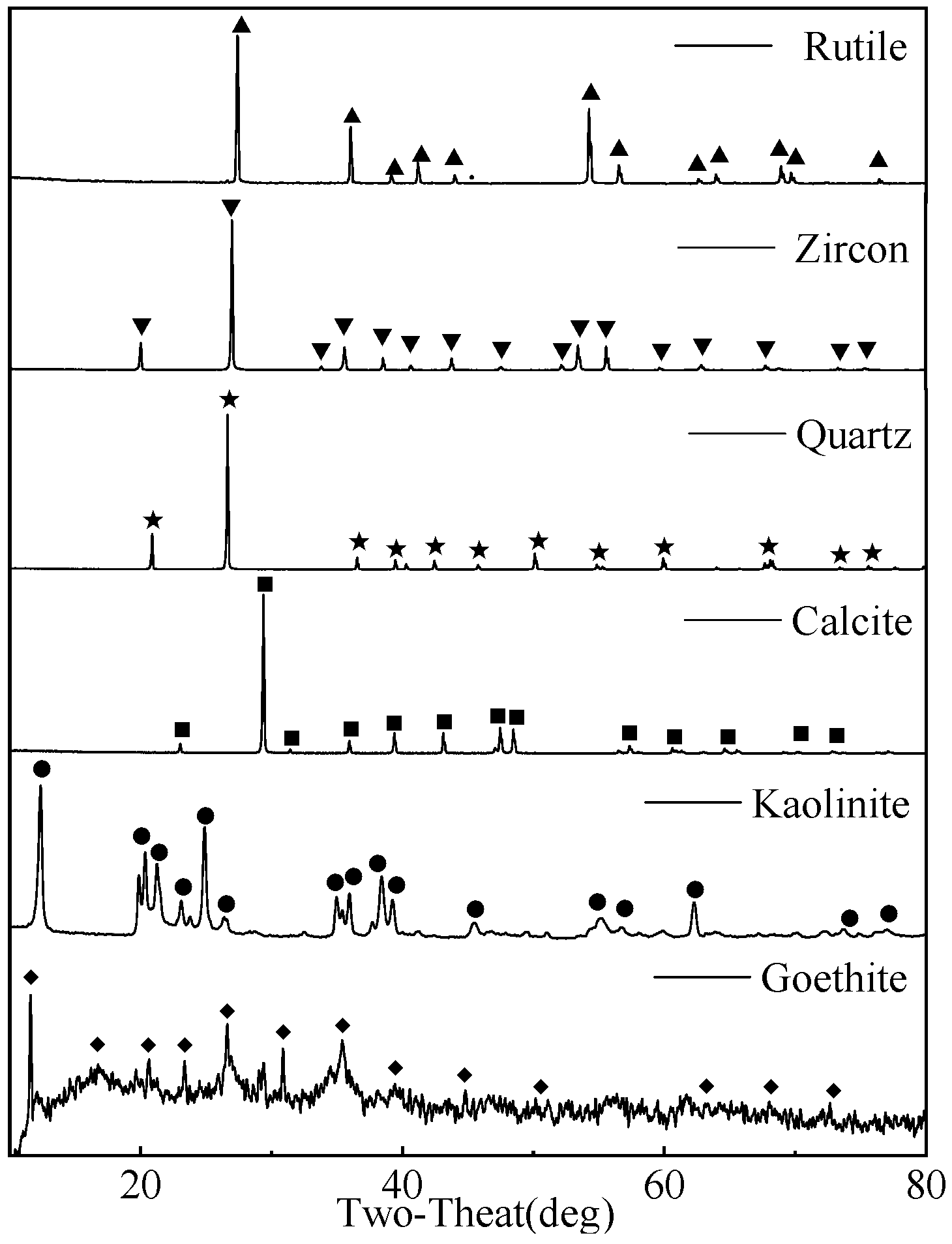

| Elements | O | Fe | Si | Al | Ca | Ti | Zr |
| Contents | 48.00 | 18.64 | 9.25 | 4.34 | 4.37 | 4.14 | 1.83 |
| Elements | Mg | K | P | S | Ce | Na | Cr |
| Contents | 0.48 | 0.33 | 0.28 | 0.19 | 0.18 | 0.12 | 0.12 |
| Elements | Nd | Ba | Mn | Th | Zn | La | Hf |
| Contents | 0.11 | 0.09 | 0.07 | 0.080 | 0.07 | 0.07 | 0.06 |
| Elements | Cl | Cu | Pb | Y | Nb | Sr | |
| Contents | 0.06 | 0.05 | 0.04 | 0.03 | 0.01 | 0.01 |
| Elements | Fe | Si | Al | Ca | Ti | Zr |
|---|---|---|---|---|---|---|
| Contents | 16.48 | 7.23 | 2.63 | 3.40 | 2.70 | 1.78 |
| Points | O | Si | Fe | Ti | Zr | Al | Ca | Mg |
|---|---|---|---|---|---|---|---|---|
| 1 | 50.09 | 49.91 | - | - | - | - | - | - |
| 2 | 53.33 | - | 2.73 | 37.23 | - | 1.77 | 0.31 | - |
| 3 | 50.85 | 21.02 | - | - | 28.10 | - | - | - |
| 4 | 48.52 | 26.31 | 4.44 | 0.99 | - | 18.12 | - | 0.88 |
| 5 | 49.24 | 35.42 | 3.95 | 1.36 | - | 7.84 | 0.40 | 0.41 |
| Minerals | Rutile [17] | Zircon [18] | Quartz [19] | Goethite [20] |
| Hamaker (J) | 18.1 × 10−20 | 8.86 × 10−20 | 6.3 × 10−20 | 7.8 × 10−20 |
| Minerals | Kaolinite [21] | Calcite [22] | Water [23] | |
| Hamaker (J) | 3.1 × 10−19 | 12.4 × 10−20 | 3.7 × 10−20 |
| Zeta Potentials | Rutile | Zircon | Quartz | Goethite | Kaolinite | Calcite |
|---|---|---|---|---|---|---|
| Without reagent | −29.6 | −25.4 | −42.4 | −16.3 | −27.33 | 9.84 |
| With SS | −43.0 | −45.6 | −51.9 | −24.8 | −48.1 | −32.3 |
| With SHMP | −52.0 | −52.6 | −61.5 | −27.5 | −53.6 | −44.5 |
| Contact Angle (°) | Rutile | Zircon | Quartz | Goethite | Kaolinite | Calcite |
|---|---|---|---|---|---|---|
| With SS | 30.3 | 40.1 | 22.4 | 21.3 | 22.8 | 38.2 |
| With SHMP | 30.0 | 39.8 | 18.8 | 20.3 | 22.1 | 30.2 |
| Contact Angle (°) | Rutile | Zircon | Quartz | Goethite | Kaolinite | Calcite |
|---|---|---|---|---|---|---|
| With SS | 40.6 | 51.1 | 33.1 | 31.0 | 34.1 | 49.3 |
| With SHMP | 40.1 | 50.1 | 30.8 | 30.1 | 33.2 | 41.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zheng, Y.; Ren, L.; Bai, S.; Huang, L.; Peng, J. Mechanisms of Fine Mud Covering and Enhanced Dispersion for a Rutile Middling. Metals 2025, 15, 1074. https://doi.org/10.3390/met15101074
Wang Y, Zheng Y, Ren L, Bai S, Huang L, Peng J. Mechanisms of Fine Mud Covering and Enhanced Dispersion for a Rutile Middling. Metals. 2025; 15(10):1074. https://doi.org/10.3390/met15101074
Chicago/Turabian StyleWang, Yang, Yongxing Zheng, Liuyi Ren, Shaojun Bai, Lingyun Huang, and Jieli Peng. 2025. "Mechanisms of Fine Mud Covering and Enhanced Dispersion for a Rutile Middling" Metals 15, no. 10: 1074. https://doi.org/10.3390/met15101074
APA StyleWang, Y., Zheng, Y., Ren, L., Bai, S., Huang, L., & Peng, J. (2025). Mechanisms of Fine Mud Covering and Enhanced Dispersion for a Rutile Middling. Metals, 15(10), 1074. https://doi.org/10.3390/met15101074









