Abstract
The resistance to near-threshold fatigue crack growth and its correlation with the microstructure of the Ti-5Al-3Mo-3V-2Zr-2Cr-1Nb-1Fe alloy were investigated. K-decreasing fatigue crack propagation rate tests were conducted on compact tension samples (ASTM standard) with a stress ratio R of 0.1 and a frequency of 15 HZ in a laboratory atmosphere. At a similar strength level of 1200 MPa, the sample with a fine basket-weave microstructure (F-BW) displayed the slowest near-threshold fatigue crack propagation rate compared with the samples with equiaxed (EM) and basket-weave (BW) microstructures. The fatigue threshold value (ΔKth) was 4.4 MPa·m1/2 for F-BW, 3.6 for BW, and 3.2 for EM. The fracture surfaces and crack profiles were observed by scanning electron microscopy (SEM) and electron backscatter diffraction (EBSD) to elucidate the mechanism of fatigue crack propagation in the near-threshold regime. The results revealed that the near-threshold crack growth in the three samples was primarily transgranular. The crack always propagated parallel to the crystal plane, with a high Schmid factor. In addition, the near-threshold fatigue crack growth behavior was synergistically affected by the crack tip plastic zone and crack bifurcation. The increased fatigue crack propagation resistance in F-BW was attributed to the better stress/strain compatibility and greater number of interface obstacles in the crack tip plastic zone.
1. Introduction
High-strength titanium alloys are extensively used in aerospace industries because of their excellent combination properties [1,2,3], such as high strength and fatigue crack growth resistance. Generally, fatigue crack growth can be divided into three stages: the near-threshold regime, the Paris regime, and the unstable growth rapid regime. Among the three regimes, the fatigue crack propagation regime accounts for most of the remaining life.
The fatigue crack propagation rate (FCPR) has been indicated to be influenced by the cyclic crack tip plastic zone (CTPZ) and crack bifurcation [4,5,6,7,8,9,10,11,12]. For the CTPZ at the crack tip, it was believed that energy consumption during plastic deformation could improve fatigue crack propagation resistance [4,5,6]. The local stress concentration in the CTPZ could slow local FCPR [7]. For the crack bifurcation behind the crack tip, it was believed that the rough crack profile behind the crack tip could reduce the effective stress intensity factor ΔKeff at the crack tip and decrease the FCPR [8,9,10,11].
The near-threshold fatigue crack propagation mechanisms are synergistically affected by the cyclic crack tip plastic zone and crack bifurcation, which are closely related to microstructures [12]. At a low stress intensity factor ΔK, the cyclic crack tip plastic zones are small, and the local microstructure in the cyclic crack tip plastic zone plays an important role in the FCPR [13,14]. With an increase in the size of the cyclic plastic zone, an increasing number of interface obstacles are encountered at the crack front, which in turn act on the crack tip and reduce the effective stress intensity factor at the crack tip. The FCP resistance is positively associated with crack roughness. Although the effects of crack bifurcations and cyclic crack tip plastic zones on near-threshold fatigue crack propagation have been commonly observed in titanium alloys, the synergistic effects of crack roughness and the cyclic crack tip plastic zone on FCP have not been fully investigated, particularly for high-strength titanium alloys with a strength of 1200 MPa.
Recently, as a newly developed damage tolerance alloy, Ti-5Al-3Mo-3V-2Zr-2Cr-1Nb-1Fe (Ti-5321) has been fabricated by forging, subsequent solution, and aging treatments to achieve excellent tensile properties [15,16]. The tensile strength of Ti-5321 alloy was above 1200 MPa and the elongation exceeded 10%. In this study, at a strength level of 1200 MPa, the near-threshold FCP behaviors of Ti-5321 alloys with equiaxed, basket-weave and fine basket-weave microstructures were studied. The synergistic effects of the cyclic crack tip plastic zone and crack bifurcation on the near-threshold FCP were revealed.
2. Materials and Experimental Methods
2.1. Materials
The 60 Kg Ti-5Al-3Mo-3V-2Zr-2Cr-1Nb-1Fe billets were produced via multidirectional forging and subsequent solution treatment and aging (STA) heat treatment. The β transformation temperature was determined to be 860 °C via a metallographic method [15].
Samples with an equiaxed microstructure (EM), basket-weave microstructure (BW), and fine basket-weave microstructure (F-BW) were obtained after different forging temperatures (810 °C, 870 °C, and 890 °C) and the same heat treatment [15]. The dimension of the three billets changes from the initial 150 mm × 150 mm × 220 mm to the final 90 mm × 90 mm × 500 mm. The thermo-mechanical process temperature plays an important role in microstructural evolution [17]. The processing schedules are illustrated in Figure 1a [15], and the details of the total forging process are shown in Table 1. The corresponding microstructures are shown in Figure 1b–d. The EM sample was characterized by the equiaxed α (αp) and secondary α (αs), as shown in Figure 1b. The average size of αp is approximately 2.2 ± 0.2 μm. The BW sample consisted of the basket-weave αl and αs, as shown in Figure 1c. The average width of the primary α lamellae is approximately 0.78 ± 0.2 μm. In contrast, the F-BW sample has finer basket-weave microstructure features, as illustrated in Figure 1d. The average width of the primary α lamellae is approximately 0.40 ± 0.2 μm. In addition, the elongated β grains and discontinuous β grain boundaries are also found. The quantitative statistics of αp and αl for EM, BW, and F-BW are displayed in Table 2. Ti-5321 alloy with EM, BW, and F-BW has been reported to exhibit excellent tensile strength (all above 1200 MPa) and elongation (above 10%) [15], as shown in Figure 2.
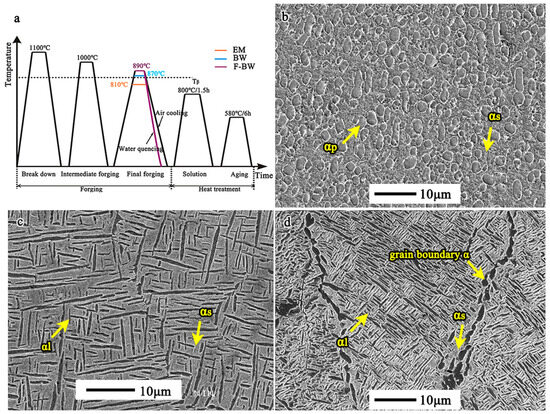
Figure 1.
Microstructures after forging and heat treatment of the Ti-5321 alloy. (a) Processing schematic; (b) EM; (c) BW; (d) F-BW.

Table 1.
Details of the total forging process.

Table 2.
Quantitative statistics of αp and αl for EM, BW, and F-BW.

Figure 2.
The tensile properties of Ti-5321 alloy with EM, BW, and F-BW samples [15].
2.2. Experimental Methods
2.2.1. Fatigue Crack Propagation Rate Test
The threshold stress intensity factor range (ΔKth) test was conducted on MTS370.10 fatigue equipment (MTS Systems Corporation, Tacoma, WA, USA) at a frequency of 15 Hz. A positive load ratio R of 0.1 was chosen for the test. The test was carried out with the ASTM E647-15 standard at room temperature [18]. Standard compact tension (CT) samples with precracks of approximately 2 mm were used. The sampling size is displayed in Figure 3. After the decreasing ΔK test, the curves of da/dN-ΔK were obtained. The value of ΔK corresponding to a da/dN of 10−7 mm/cycle was subsequently determined as the fatigue crack growth threshold value ΔKth. To obtain an accurate ΔKth, three CT samples were tested and average values were obtained for each microstructure. After the decreasing ΔK test, the crack path near the crack tip of one sample was studied. The other two fractured samples were used to observe the fracture surface.

Figure 3.
The size of fatigue samples used in this study (unit: mm).
2.2.2. Characterization
The fatigue crack paths were identified by scanning electron microcopy (SEM) with a JSM-6460 instrument (Instron Corporation, Boston, MA, USA) and electron backscatter diffraction (EBSD). The crystal orientation data of the α and β phases were obtained via Aztec crystal software 2.1.2. The slip traces and Schmid factor were calculated via MATLAB toolbox (Slip Trace Crystallography V 1.0) software [19]. The fracture surface roughness was measured via Profilometry. The roughness of the crack surface extracted at the near-threshold region for both samples was measured using a 3D Roughness Reconstruction tool. The area of the roughness measurement is a rectangular area of 0.5 × 0.5 mm in the central part of the crack surface. The measuring line length is about 700 μm. The average arithmetic deviation from the mean line to the measuring length is selected to be a parameter for evaluating surface roughness. The measuring length used for measuring roughness on the crack surfaces was about 2 mm.
3. Results
Figure 4a displays the fitted near-threshold FCPR curves for the EM, BW, and F-BW samples. The ΔKth is 3.2 ± 0.2 MPa·m1/2 for EM, 3.6 ± 0.1 MPa·m1/2 for BW, and 4.4 ± 0.2 MPa·m1/2 for F-BW. The F-BW samples display the highest fatigue threshold value at the same strength level of 1200 MPa. Compared with the EM and BW samples, the F-BW sample has the strongest near-threshold fatigue crack propagation resistance. In addition, the ultimate tensile strength and ΔKth for several typical titanium alloys are summarized, as shown in Figure 4b. It can be easily concluded that Ti-5321 alloy exhibits a superior comprehensive performance compared to other alloys.

Figure 4.
FCP rate curves of Ti-5321 alloy (a) and the ultimate tensile strength and ΔKth for several typical titanium alloys (b) [8,9,20,21].
The fractography of three samples in the near-threshold regime is shown in Figure 5(a1–c1). Obviously, some weak fatigue striations are uniformly distributed in the three microstructures, indicating crystallographic fracture [22,23]. In addition, many secondary cracks along the α/β phase interface are found in the BW sample (Figure 5(b1)). These secondary cracks are believed to reduce the effective stress intensity factor ΔKeff at the crack tip and decrease the FCPR [10]. The roughness reconstruction maps of the fracture surface in the near-threshold regime are shown in Figure 5(a2–c2). A rectangular area in the central part of 0.5 mm × 0.5 mm is chosen to measure the roughness of the crack surface. Four lines with different colors and different directions were selected (R1, R2, R3 and R4, in Figure 5(a2–c2)). The roughness values of the R1, R2, R3 and R4 lines are displayed in Figure 5(a3–c3). three samples are presented and summarized in Figure 5(a3–c3) and Table 3. The average roughness value for EM (13.25 μm) is the lowest, and the average roughness value for BW (18.91 μm) is the highest. The average roughness value of the F-BW sample with the highest ΔKth value is 17.10 μm. The average roughness is clearly non-proportional to the ΔKth value, indicating that the fracture roughness is not the determining factor influencing the near-threshold fatigue crack propagation behavior. To further explore the determining factors influencing the near-threshold fatigue crack propagation behavior of the Ti-5321 alloy at 1200 MPa, the detailed crack propagation path is discussed in the following text.
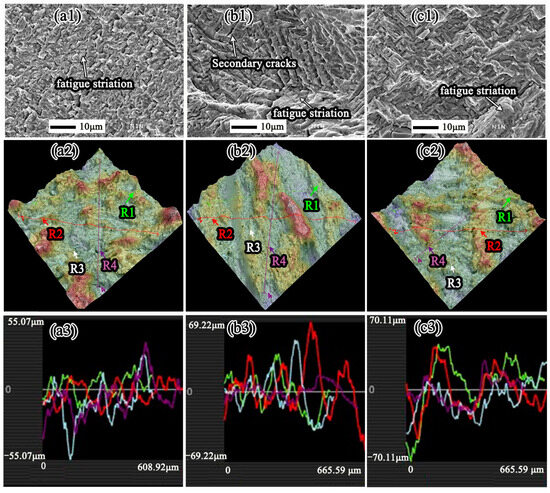
Figure 5.
Fracture surfaces and roughness analysis of the da/dN samples with EM (a1–a3), BW (b1–b3), and F-BW (c1–c3) in the near-threshold regime.

Table 3.
Roughness values of the EM, BW, and F-BW samples.
4. Discussion
4.1. Crack Propagation Path
As mentioned above, the FCP resistance has been reported to be synergistically affected by the CTPZ as well as the crack bifurcation behind the crack tip, which are closely related to microstructures [12]. To further explore the near-threshold FCP behavior, the effects of the microstructure on the deformation behavior of the CTPZ and the crack path are discussed below.
Both Figure 4a and Table 3 indicate that the sample with EM presents the lowest fatigue threshold and the minimum fracture roughness among the three samples. To investigate the crack growth mechanisms further, the near-threshold crack path in the EM is shown in Figure 6. Obviously, the crack path is relatively flat, and almost no obvious crack branching or secondary cracks are observed (Figure 6a). It can be easily concluded that the near-threshold crack path is primarily transgranular, and many cleavage faces can be found at the fracture surface (Figure 6b). The microstructures around the crack path in the EM are shown in Figure 6c,d. Numerous microvoids located at the αp/αp and αp/βt interfaces form, indicating a larger stress concentration at the interfaces.
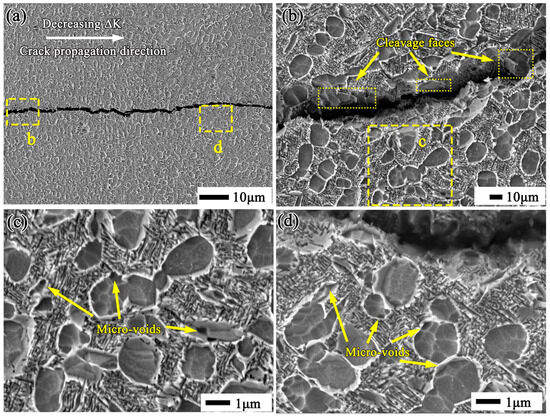
Figure 6.
SEM fractographs showing crack growth in the EM sample: (a) crack path at low magnification; (b) crack path at high magnification in rectangle (b) of (a); (c) crack path at high magnification in rectangle (c) of (b); (d) crack path at high magnification in rectangle (d) of (a).
Figure 7 shows the near-threshold crack path in BW. Many crack bifurcations and secondary cracks are observed during the propagation process. Most secondary cracks grow along the α/α and α/β interfaces, which is consistent with the fracture surface in Figure 5(b1). Many crack bifurcations and secondary cracks led to an increase in the fracture surface roughness (Figure 7b–d). The crack bifurcations have been widely reported to reduce ΔKeff at the crack tip by increasing the crack length and thus decreasing the FCPR [24,25,26,27]. In addition, the cracks in the BW sample are primarily translamellar. The cleavage faces can also be observed.

Figure 7.
SEM fractographs showing crack growth in the BW sample: (a) crack path at low magnification; (b–d) crack path at high magnification.
The near-threshold crack path for the F-BW sample is shown in Figure 8. Figure 8a shows that crack growth is primarily transgranular, and that the crack deflects when it encounters the grain boundary α plates. It can also be observed that the near-threshold crack propagation in a primitive β grain is primarily translamellar (Figure 8c). Unlike the deformation behavior in the EM and BW, microvoids and secondary cracks are rarely observed in the F-BW. Instead, large kink deformed alpha lamellae are observed in the vicinity of the fracture surface (Figure 8b). This is closely related to the better microscale strain compatibility in the F-BW. In addition, crack closure is observed in a primitive β grain, as shown in Figure 8d. The contact of the faceted surface could delay the crack propagation process.

Figure 8.
SEM fractographs showing crack growth in the F-BW sample: (a) crack path at low magnification; (b–d) crack path at high magnification.
As is known, under the fatigue load, the soft α phases deform preferentially, and are then constrained by the surrounding hard β phase, leading to the dislocations blocked at the αl/βt interfaces. The micro-scale incompatibility at interfaces dominates the micro-void nucleation and micro-crack growth. In order to reveal the stress/strain incompatibility and local stress concentration in EM, BW, and F-BW, macroscopic measurement of the back stress is conducted. The back stress can be estimated by the loading–unloading-reloading test, as schematically shown in the Figure 9a. The back stress (σb) can be established by the following equations:
where σf is the maximum stress during loading, σy is the yield stress during loading, and σrev is the yield strength during unloading. The hysteresis loops of Ti-5321 alloy are plotted in Figure 8b. Based on Equations (1)–(3), the back stress of three samples at different plastic strains are calculated and shown in Figure 8c. It can be easily concluded that the back stress increases with the increasing tensile true strain for the three samples. Furthermore, F-BW always shows lower back stress compared to the others at any true strain, indicating a lower stress concentration. As a result, micro-void and micro-crack development is more difficult and thus no signs of micro-cracks appear near the main crack of F-BW.
σb = σf − σeff
σeff = (σf − σrev)/2 + σ*/2
σ* = (σf − σy)
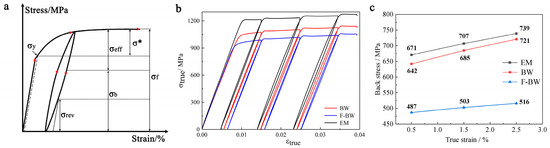
Figure 9.
The load–unload hysteresis loop and back stress of EM, BW, and F-BW samples. (a) Schematic hysteresis loop; (b) hysteresis loops of Ti-5321 alloy with EM, BW, and F-BW; (c) back stress of EM, BW, and F-BW samples at tensile true strains of 0.5%, 1.5%, and 2.5%.
4.2. Crystallographic Crack Propagation Mechanisms
As mentioned above, the near-threshold crack propagation in the Ti-5321 alloy is primarily translamellar. As reported, translamellar crack growth is dependent on the crystal orientation [28]; thus, the potential crystallographic crack propagation mechanisms are investigated. Taking the BW sample as an example, the SEM image and EBSD orientation maps containing translamellar and interlamellar crack segments are shown in Figure 10. The translamellar and interlamellar crack segments in the α1–α10 grains are reproduced by black lines in Figure 10c. Translamellar cracks are found in the α1, α3, α4, α5, α7, and α8 plates. The slip traces and the corresponding Schmid factor (SF) values for each grain are calculated via MATLAB toolbox (Slip Trace Crystallography V 1.0) software.
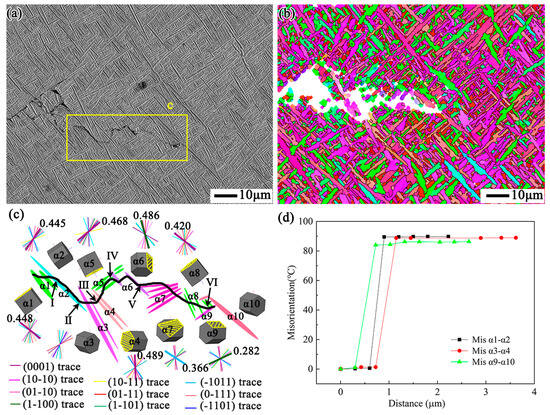
Figure 10.
SEM image and EBSD orientation maps containing crack paths in the BW sample: (a) SEM image in the vicinity of the crack path; (b) EBSD orientation maps in the vicinity of the crack path; (c) reconstructed map of crack propagation; (d) misorientation distribution map.
The slip plane of α1, α3, α4, α5, α7, and α8 grains are determined according to the slip criterion of the maximum Schmid factor. The trace lines of the slip planes are shown in bold in Figure 10c. The crack segments in the α1, α4, α5, and α8 plates are parallel to the (0001) basal slip plane with high SFs of 0.448, 0.489, 0.468, and 0.420, respectively, indicating that the near-threshold fatigue crack is mainly along the slip plane with a relatively high SF. In addition, interlamellar crack segments are found in the α2, α6, and α9 lamellae, and the slip traces and SF values are also displayed in Figure 10c. The crack in α2 is roughly along the (0001) basal slip plane with a high SF of 0.445. The cracks in α6 and α9 are along the (00) prismatic slip plane, and the SFs are 0.486 and 0.282, respectively. For the crack segment in α3, the growth direction is parallel to the horizontal axis, and the crack does not propagate through any slip plane. This finding indicates that the crack growth in α3 is largely influenced by the stress rather than the crystallographic orientation of the material.
In total, many crack deflections occurring at the interfaces can be found in BW. The interfaces can be roughly divided into the following categories: interfaces between the interlamellar segment and translamellar segment, such as deflection positions I, II, and VI; interfaces between the translamellar segment and the translamellar segment, such as deflection positions III; and interfaces between the interlamellar segment and the interlamellar segment, such as deflection positions IV and V (Figure 10c). The first deflection mode always results in a zigzag crack path. The factors affecting the change in the crack propagation mode can be summarized as stress factors and material factors. Generally, the stress factor refers to the external force, such as deflection position II, where the crack segment is strongly affected by the stress, and directly propagates along the horizontal direction. For material factors, for example, grain boundaries with a large misorientation, such as positions I and VI, where the misorientation angle reaches 90°, could hinder crack growth and promote changes in the crack propagation mode (Figure 10d). For the second type of crack deflection, the deflection mode is the most common in the near-threshold regime, where the crack propagates along the most favorable slip plane or cleavage plane. The grain boundaries become effective obstacles in the process of crack growth. For the interfaces between the interlamellar segment and the interlamellar segment, the misorientation angle of 90° between adjacent grains effectively hiders the crack translamellar propagation, resulting in a large crack deflection. For BW, the third type of crack deflection could easily result in a zigzag path in the process of interlamellar propagation because of its own basket-weave morphology.
Figure 11a shows the crack tip path in F-BW. The crack growth is easily found to be transgranular. Both translamellar and interlamellar crack segments could be observed in the original β grain. The local crack path and vicinal α orientation in the black rectangle of Figure 11a are revealed, as presented in Figure 11b. A random orientation distribution of α plates can be found. To investigate the crystallographic fatigue crack path, the crack path in the rectangle of Figure 11b is reproduced by black lines, as illustrated in Figure 11c. The cracks in α1, α3, α4, α5, α7, α8, α9, and α11 grains are intergranular. The slip traces as well as the SF are also presented below.
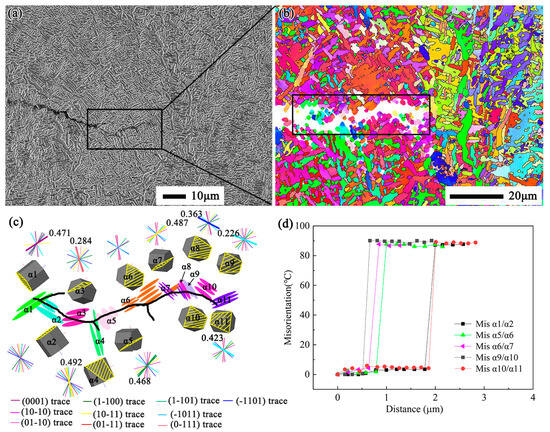
Figure 11.
SEM image and EBSD orientation maps containing crack paths in the F-BW sample: (a) SEM image in the vicinity of the crack path; (b) EBSD orientation maps in the vicinity of the crack path; (c) reconstructed map of crack propagation; (d) misorientation distribution map of the α plates in Figure 10c.
The crack in the α1 is along the (0001) basal plane, and the SF is 0.471. The cracks in the α3, α4, α5, α7, α8, α9, and α11 plates are along the {101} pyramidal plane, and the SFs are 0.284, 0.492, 0.468, 0.487, 0.363, 0.226, and 0.423, respectively. These results indicate that near-threshold crack propagation is linked to the crystallographic orientation of the material. The crack prefers to grow along the slip plane with a large Schmid factor. In addition, the interlamellar crack segments in the α2, α6, and α10 grains are shown in Figure 11c. The misorientation angles between adjacent α plates along the intergranular crack segments are analyzed in Figure 11d. Obviously, the misorientation angles (α1/α2, α5/α6, α6/α7, α9/α10, α10/α11) are all close to 90°. The grain boundaries with large crystallographic misorientation could strongly retard translamellar crack growth, resulting in interlamellar fracture.
4.3. Effects of Microstructures on Near-Threshold Fatigue Crack Propagation Behavior
Near-threshold crack advancement is reported to be affected by the microstructure characteristic scale, which is comparable to the cyclic plastic zone size (rc) at the crack tip [14]. The rc value at the crack tip in the near-threshold regime is given by:
where YS is the yield strength. A lower yield strength clearly results in a larger plastic zone size. The values of the cyclic plastic zone size and microstructure characteristic scale for the Ti-5321 alloy with three typical microstructures are listed in Table 4. For EM, in the near-threshold regime, the value of rc is far less than the diameter of the α phase. Thus, equiaxed α grains are expected to control the near-threshold FCP behavior. However, for BW and F-BW, the rc value is close to the width of the α lamellae at ΔKth, whereas at the final stage of the near-threshold regime, the rc value is far larger than the width of the α lamellae. The transition seems to occur at a ΔK, at which the cyclic plastic zone size becomes equal to the α lamellae. It can be concluded that α plates are the main microstructure units in the hypotransitional region. In the hyper-transitional region, the larger cyclic plastic zone at the crack tip contains more α lamellae, and the crack growth is affected by interface obstacles.

Table 4.
Values of the rc and α phase size for three typical microstructures.
At a low stress intensity factor ΔK, the cyclic plastic zone size is relatively small, and slip deformation in the CTPZ plays an important role in FCP behavior. Therefore, crack growth extends along these slip planes, resulting in transgranular fracture characteristics (Figure 4, Figure 6 and Figure 7). Thus, local deformation behaviors, which are affected by microstructure features and crystallographic orientation, have extremely significant influences on crack propagation. In this case, boundaries, instead of crack roughness, are the strongest obstacles for this transgranular crack propagation. For α/α and α/βt interfaces, the large misorientation angle (90°) could improve the crack deflection. For the F-BW sample, the fine α lamellae result in more and stronger interface obstacles, which contribute to the improvement in fatigue crack propagation resistance. In addition, at a similar strength level, the lower α/β interface stress (Figure 9) in the F-BW sample could also generate a lower stress/strain concentration at the crack tip, resulting in more energy consumption and relatively higher ΔKth values. Therefore, better stress/strain compatibility and stronger interface obstacles become the determining factor influencing the ΔKth value.
As ΔK increases, the rc value becomes far larger than the width of the α lamellae, especially at the final stage of the near-threshold regime (Table 4). As a result, the cracks encounter more interface obstacles in the crack tip plastic zone, and the cracks deflect as they propagate across the interfaces, suggesting that the interface obstacle factor must be considered. In the case of F-BW, owing to the smaller microstructure characteristic scale and larger cyclic plastic zone size, more interfaces are contained, and a lower FCPR is obtained. For F-BW, the better stress/strain compatibility and greater number of interface obstacles in the CTPZ could retard crack propagation, resulting in the strongest near-threshold FCP resistance. In addition, the fracture roughness factor should also be considered. The rough crack profile in F-BW could reduce the effective stress intensity factor ΔKeff and delay crack propagation. Therefore, owing to the synergistic influence of the CTPZ and crack bifurcation, the near-threshold FCP rate in F-BW tends to be much slower. The design for the aircraft was based on a damage-tolerant approach. Therefore, the fatigue crack growth data in titanium alloy with the tensile strength of 1200 MPa will gain importance. The Ti-5321 alloy with F-BW exhibits a high strength of 1200 MPa and a high ΔKth of 4.4 MPa·m1/2, meeting the needs of new-generation aircraft.
5. Conclusions
The near-threshold fatigue crack growth behavior of a high-strength Ti-5321 alloy with equiaxed, basket-weave and fine basket-weave microstructures has been studied, and several conclusions can be drawn as follows:
- (1)
- At a similar strength of 1200 MPa, the F-BW sample with a multilevel feature (e.g., mixtures of elongated βt matrix, discontinuous grain boundary α, intragranular α colonies, and fine α plates) exhibits a higher fatigue crack propagation threshold value (4.4 MPa·m1/2).
- (2)
- In the near-threshold regime, the main crack growth mode in the Ti-5321 alloy with EM, BW, and F-BW is translamellar, and the translamellar crack always propagates parallel to the crystal plane with a high SF.
- (3)
- At a similar strength of 1200 MPa, the increased FCP resistance in F-BW is attributed to the better stress/strain compatibility and greater number of interface obstacles in the CTPZ.
Author Contributions
Conceptualization, H.W. and Y.Z.; Methodology, P.G.; Software, F.Q.; Validation, F.Q., S.X. and L.Z.; Formal analysis, L.Z.; Investigation, Z.Q.; Resources, S.X.; Data curation, Z.Q.; Writing—original draft preparation, H.W.; Writing—review and editing, Y.Z.; Visualization, L.Z.; Supervision, Z.Q.; Project administration, P.G.; Funding acquisition, P.G. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financially supported by the National Key Research and Development Project of the Ministry of Science and Technology (2022YFB3705601), China Postdoctoral Science Foundation (2024M762659), and the Postdoctoral Grant Program of Shanxi Province (2023BSHGZZHQYXMZZ30).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Abbreviations
| Words | Symbols or Abbreviations |
| Fine basket-weave microstructure | F-BW |
| Equiaxed microstructure | EM |
| Basket-weave microstructures | BW |
| Electron backscatter diffraction | EBSD |
| Scanning electron microscopy | SEM |
| Threshold stress intensity factor range | ΔKth |
| Stress intensity factor range | ΔK |
| Effective stress intensity factor range | ΔKeff |
| Fatigue crack propagation rate | FCPR |
| Fatigue crack propagation | FCP |
| Crack tip plastic zone | CTPZ |
| Compact tension | CT |
| Yield stress | YS |
| Ultimate tensile stress | UTS |
| Elongation | El |
| Reduction in area | RA |
| Crack propagation rate | da/dN |
| Average roughness | Raver |
| Schmid factor | SF |
| Inverse pole of figure | IPF |
| Primary α | αp |
| Secondary α | αs |
References
- Banerjee, D.; Williams, J. Perspective on Titanium science and technology. Acta Mater. 2013, 61, 844–879. [Google Scholar] [CrossRef]
- Sadananda, K.; Vasudevan, A.K. Fatigue crack growth behavior of titanium alloys. Int. J. Fatigue 2005, 27, 1255–1266. [Google Scholar] [CrossRef]
- Su, M.; Feng, C.; Peng, C.; Xu, L.; Han, Y.; Zhao, L. A unifed approach for describing metallic fatigue short and long crack growth behaviors via plastic accumulated damage. Int. J. Fatigue 2023, 166, 107258. [Google Scholar] [CrossRef]
- Liu, X.; Qian, Y.; Fan, Q.; Zhou, Y.; Zhu, X.; Wang, D. Plastic deformation mode and α/β slip transfer of Ti–5Al-2.5Cr-0.5Fe-4.5Mo–1Sn–2Zr–3Zn titanium alloy at room temperature. J. Alloy Compd. 2020, 826, 154209. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Sun, B.; Ponge, D.; Jiang, C.; Raabe, D. The dual role of martensitic transformation in fatigue crack growth. Proc. Natl. Acad. Sci. USA 2022, 119, 2110139119. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.J.; Xue, Q.; Wang, H.; Huang, S.; Qiu, J.; Feng, X.; Lei, J.; Yang, R. Deformation twinning in fatigue crack tip plastic zone of Ti-6Al-4V alloy with Widmanstatten microstructure. Mater. Charact. 2017, 132, 338–347. [Google Scholar] [CrossRef]
- Carroll, J.D.; Abuzaid, W.Z.; Lambros, J.; Sehitoglu, H. On the interactions between strain accumulation, microstructure, and fatigue crack behavior. Int. J. Fatigue 2013, 180, 223–241. [Google Scholar] [CrossRef]
- Verdhan, N.; Bhende, D.D.; Kapoor, R.; Chakravartty, J.K. Effect of microstructure on the fatigue crack growth behaviour of a near-α Ti alloy. Int. J. Fatigue 2015, 74, 46–54. [Google Scholar] [CrossRef]
- Hasib, M.T.; Ostergaard, H.; Li, X.; Kruzic, J.J. Fatigue crack growth behavior of laser powder bed fusion additive manufactured Ti-6Al-4V: Roles of post heat treatment and build orientation. Int. J. Fatigue 2021, 142, 105955. [Google Scholar] [CrossRef]
- Kikuchi, S.; Imai, T.; Kubozono, H.; Nakai, Y.; Ota, M.; Ueno, A.; Ameyama, K. Effect of harmonic structure design with bimodal grain size distribution on near-threshold fatigue crack propagation in Ti-6Al-4V alloy. Int. J. Fatigue 2016, 92, 616–622. [Google Scholar] [CrossRef]
- Nalla, R.K.; Boyce, B.L.; Campbell, J.P.; Peters, J.O. Influence of microstructure on high-cycle fatigue of Ti-6Al-4V: Bimodal vs. lamellar structures. Metall. Mater. Trans. A. 2002, 33, 899–918. [Google Scholar] [CrossRef]
- Sarrazin-Baudoux, C. Abnormal near-threshold fatigue crack propagation of Ti alloys: Role of the microstructure. Int. J. Fatigue 2005, 27, 773–782. [Google Scholar] [CrossRef]
- Prasad, K.; Karamched, P.S.; Bhattacharjee, A.; Kumar, V.; Rao, K.B.S.; Sundararaman, M. Electron back scattered diffraction characterization of thermomechanical fatigue crack propagation of a near a titanium alloy Timetal 834. Mater. Des. 2015, 65, 297–311. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Dash, S.S.; Zhang, J.H.; Lyu, T.; Lang, L.; Chen, D.; Zou, Y. Fatigue crack growth behavior of an additively manufactured titanium alloy: Effects of spatial and crystallographic orientations of α lamellae. Int. J. Plast. 2024, 172, 103819. [Google Scholar] [CrossRef]
- Wang, H.; Xin, S.W.; Zhao, Y.Q.; Zhou, W.; Zeng, W.D. Forging-microstructure-tensile properties correlation in a new near beta high-strength titanium alloy. Rare Met. 2021, 40, 2109–2117. [Google Scholar] [CrossRef]
- Wu, C.; Zhao, Y.Q.; Huang, S.X.; Zhao, Y.; Lei, L.; Sun, Q.; Zhou, L. New insights in the development of α phase during continuously heating in a β-quenched Ti-5321 alloy. J. Mater. Sci. Technol. 2021, 151, 106348. [Google Scholar] [CrossRef]
- Ajabshir, S.Z.; Hare, C.; Sofia, D.; Barletta, D.; Poletto, M. Investigating the effect of temperature on powder spreading behaviour in powder bed fusion additive manufacturing process by Discrete Element Method. Powder Technol. 2024, 436, 119468. [Google Scholar] [CrossRef]
- ASTM E647-15; Standard Test Method for Measurement of Fatigue Crack Growth Rates. ASTM: West Conshohocken, PA, USA, 2015.
- Wei, S.; Zhu, G.; Tasan, C. Slip-twinning interdependent activation across phase boundaries: An in-situ investigation of a Ti-Al-V-Fe (α+β) alloy. Acta Mater. 2021, 206, 116520. [Google Scholar] [CrossRef]
- Guo, X.Y.; Zhao, L.F.; Liu, X.; Lu, F.G. Investigation on the resistance to fatigue crack growth for weld metals with different Ti addition in near-threshold regime. Int. J. Fatigue 2019, 120, 1–11. [Google Scholar] [CrossRef]
- Wang, F.; Lei, L.M.; Fu, X.; Shi, L.; Luo, X.M.; Song, Z.M.; Zhang, G.P. Toward developing Ti alloys with high fatigue crack growth resistance by additive manufacturing. J. Mater. Sci. Technol. 2023, 13, 166–178. [Google Scholar] [CrossRef]
- Zhai, Y.; Lados, D.A.; Brown, E.J.; Vigilante, G.N. Fatigue crack growth behavior and microstructural mechanisms in Ti-6Al-4V manufactured by laser engineered net shaping. Int. J. Fatigue 2016, 93, 51–63. [Google Scholar] [CrossRef]
- Ren, Y.; Lin, X.; Jian, Z.; Peng, H.; Huang, W. Long fatigue crack growth behavior of Ti-6Al-4V produced via high-power laser directed energy deposition. Mater. Sci. Eng. A 2021, 819, 141392. [Google Scholar] [CrossRef]
- Rui, S.S.; Shang, Y.B.; Su, Y.; Qiu, W.; Niu, L.-S.; Shi, H.-J.; Matsumoto, S.; Chuman, Y. EBSD analysis of cyclic load effect on final misorientation distribution of post-mortem low alloy steel: A new method for fatigue crack tip driving force prediction. Int. J. Fatigue 2018, 113, 264–276. [Google Scholar] [CrossRef]
- Suzuki, S.; Sakaguchi, M.; Domen, M.; Karato, T.; Suzuki, K. Temperature and ΔK dependence of grain boundary effect on fatigue crack propagation in a two-dimensional polycrystalline Ni-base superalloy. Acta Mater. 2022, 240, 118288. [Google Scholar] [CrossRef]
- Li, T.L.; Wu, H.P.; An, D.Y.; Chen, J.; Li, X.; Chen, J. By introducing heterogeneous interfaces: Improved fatigue crack growth resistance of a metastable β titanium alloy Fatigue crack branching in laser melting deposited Ti-55511 alloy. Scr. Mater. 2022, 220, 114921. [Google Scholar] [CrossRef]
- Shibata, A.; Gutierrez-Urrutia, I.; Nakamura, A.; Miyamoto, G.; Madi, Y.; Besson, J.; Hara, T.; Tsuzaki, K. Multi-scale three-dimensional analysis on local arrestability of intergranular crack in high-strength martensitic steel. Acta Mater. 2022, 234, 118053. [Google Scholar] [CrossRef]
- Margolin, H. Fracture toughness—A rationalization of the role of microstructure in an α-β titanium alloy. Metall. Trans. A 1982, 13A, 2191–2195. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).