A Data-Driven Methodology for Obtaining the Stress–Strain Curves of Metallic Materials Using Discrete Indentation Tests
Abstract
1. Introduction
- Coupled FE-Bayesian framework approach [19].
- Deep learning approach [14,20,21,22,23,24]. This approach consists of generating data of the stress–strain curve and its equivalent IIT force–displacement curve using finite element modeling of instrumented indentation tests and using this data to train a neural network architecture to predict stress–strain curve for a given force-displacement curve and possibly other parameters. The main differences between the various publications that implement this approach stem from the material model and its constant range used in the data generation procedure, the neural network architecture implemented, and the validation procedure.
- A train group, with which the model ‘learns’ how to make predictions.
- A validation group, utilized to fine-tune a model’s hyperparameters (i.e., parameters that control the learning process and affect how the algorithm operates).
- A test group is used to evaluate the model’s prediction capabilities using evaluation metrics (such as mean squared error) and thus see how well it generalizes to unseen data.
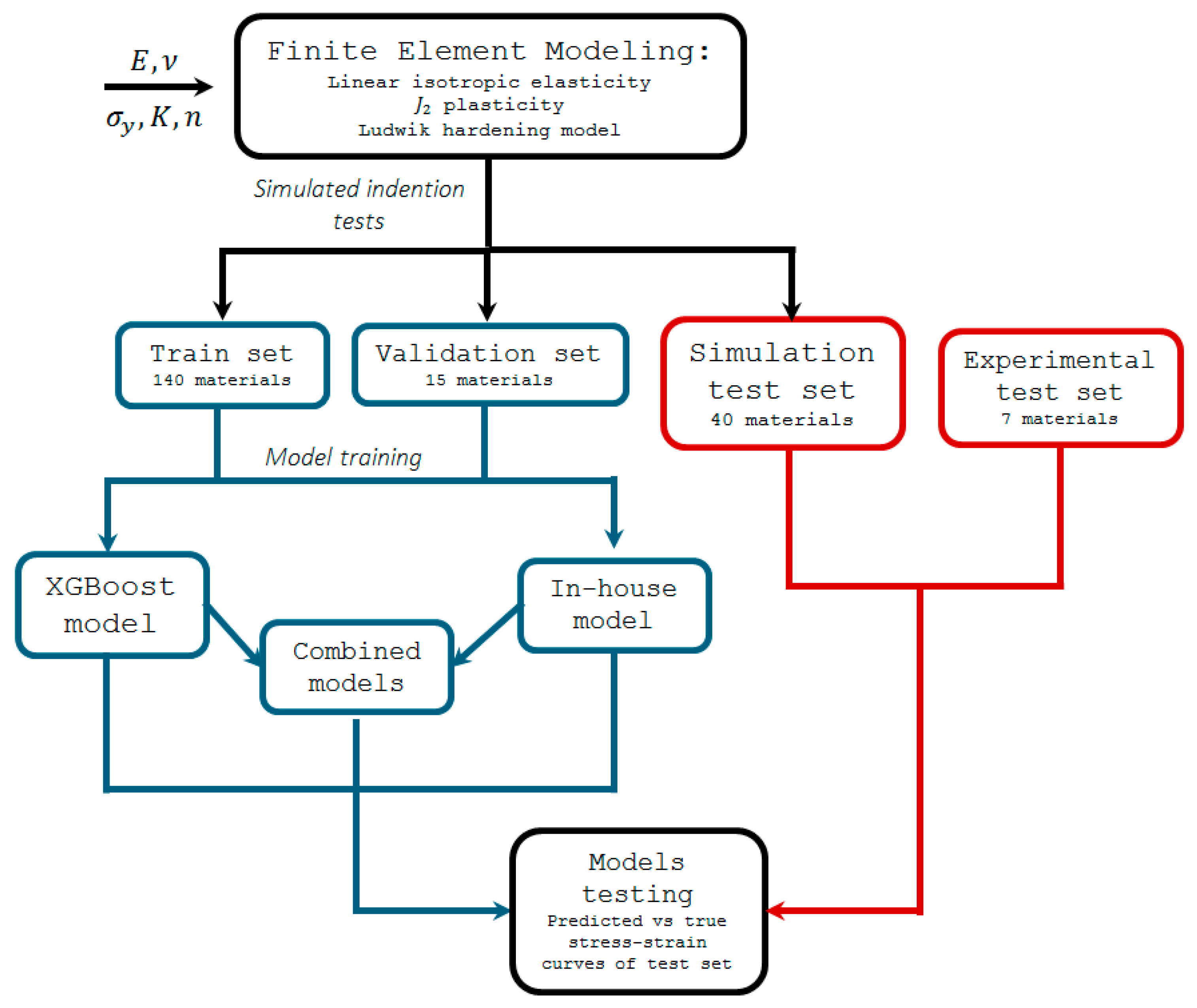
2. Methodology
- A database of Brinell indentation force–diameter trace pairs was created. The database was created using finite element modeling of Brinell indentation tests with various generated materials, together with several real indentation experiments on different metal alloys.
- Two models were considered in this study—an in-house learning model and the popular Extreme Gradient Boosting algorithm [35]. These two models were then fused to create two additional models (their architecture is shown in Section 5). All models were designed to use force–diameter trace pairs of a Brinell indentation test (requiring a minimum of two pairs) as input and generate a stress–plastic strain curve as output.
- All four models were trained using the database created in the first stage, and their prediction performance was analyzed and compared to that of the traditional Tabor model.
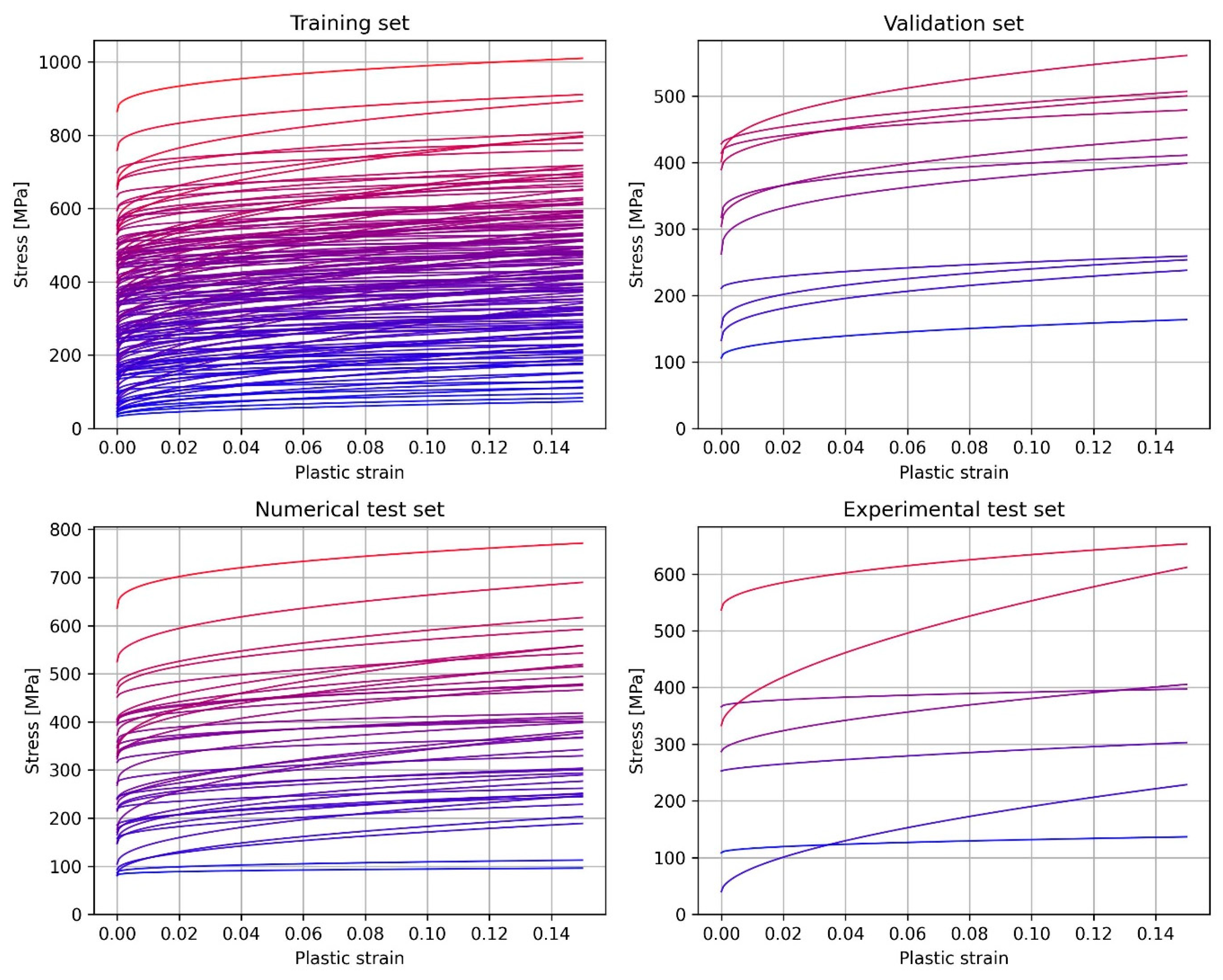
3. Database Creation for the Machine Learning Algorithm
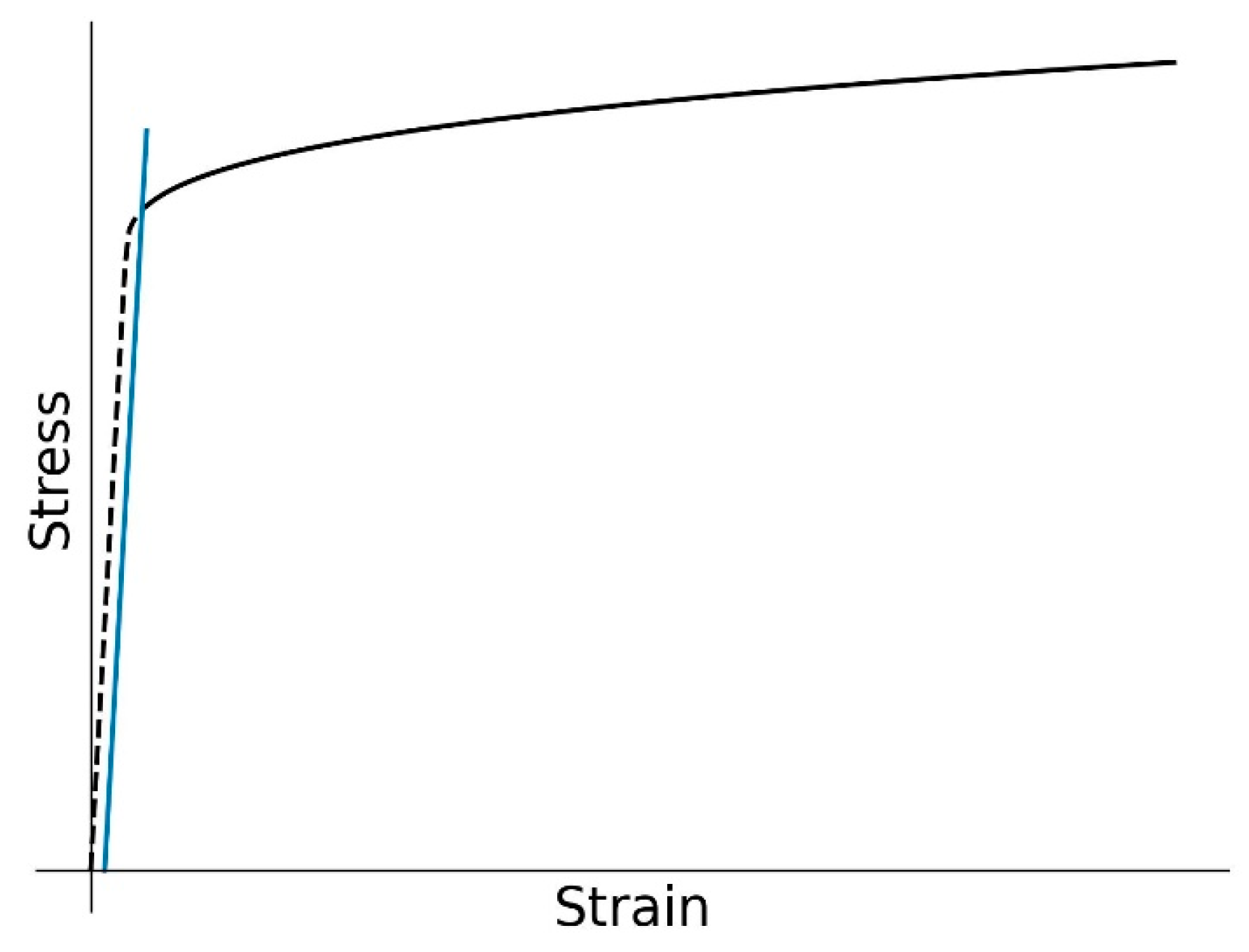
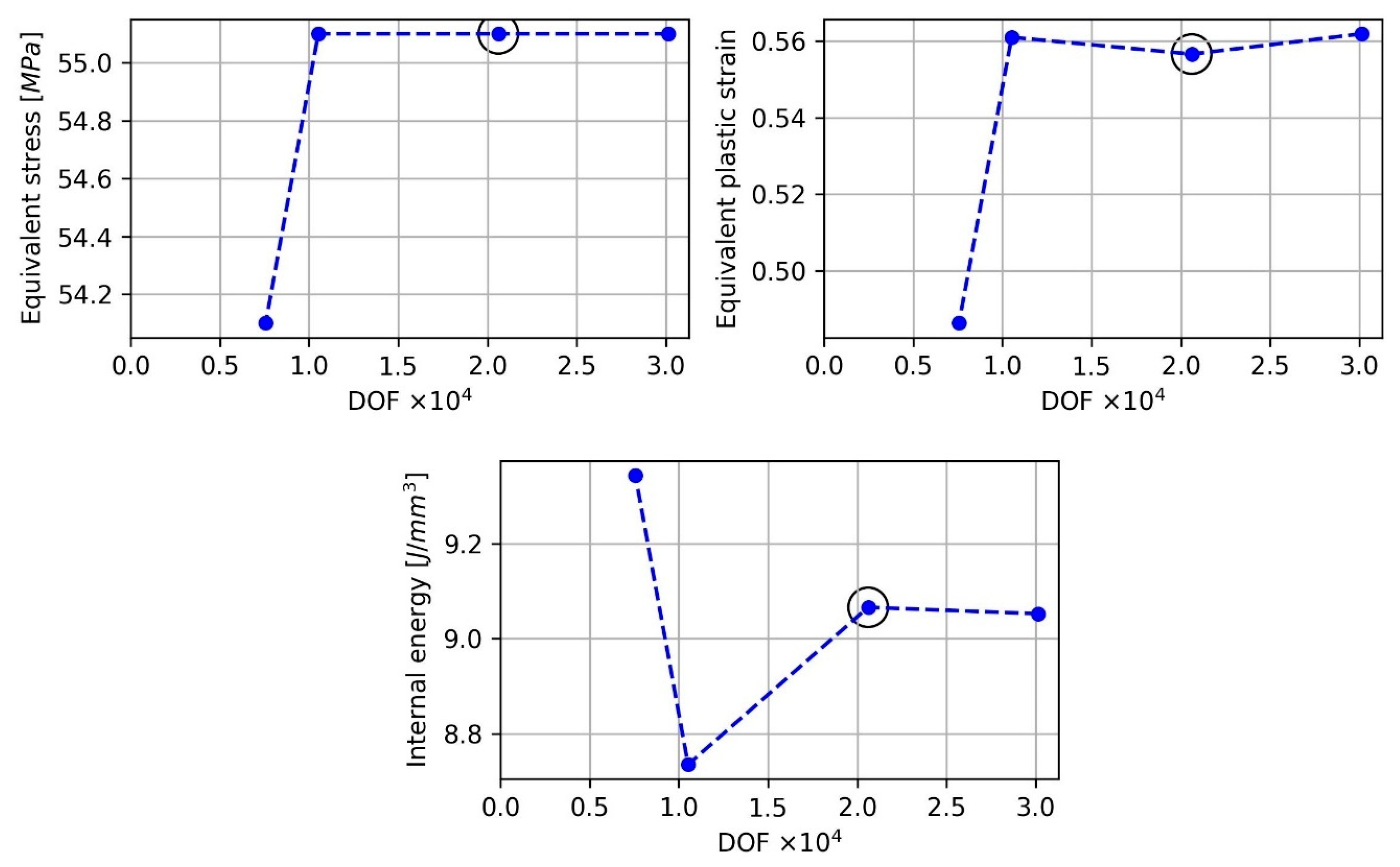
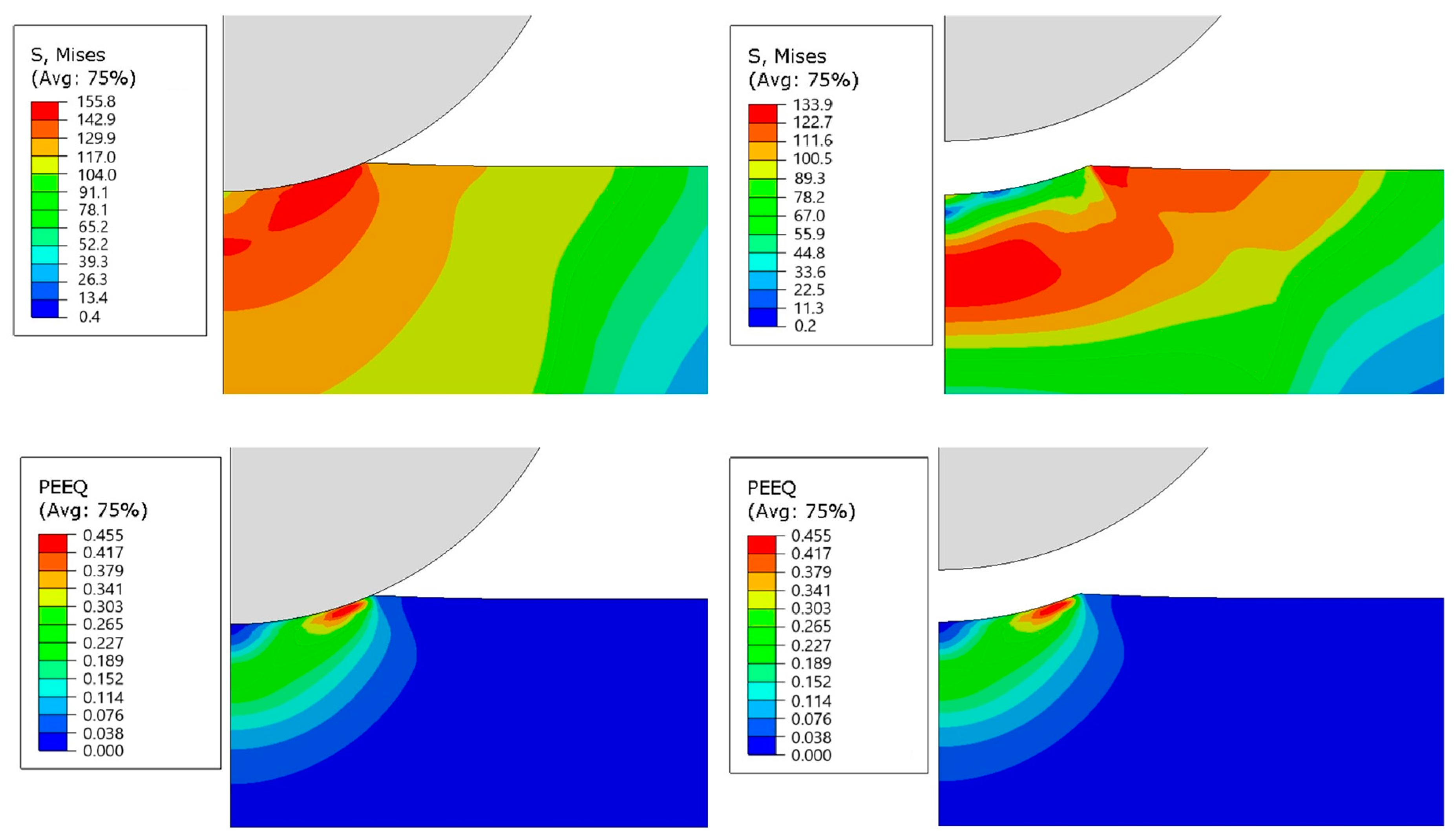
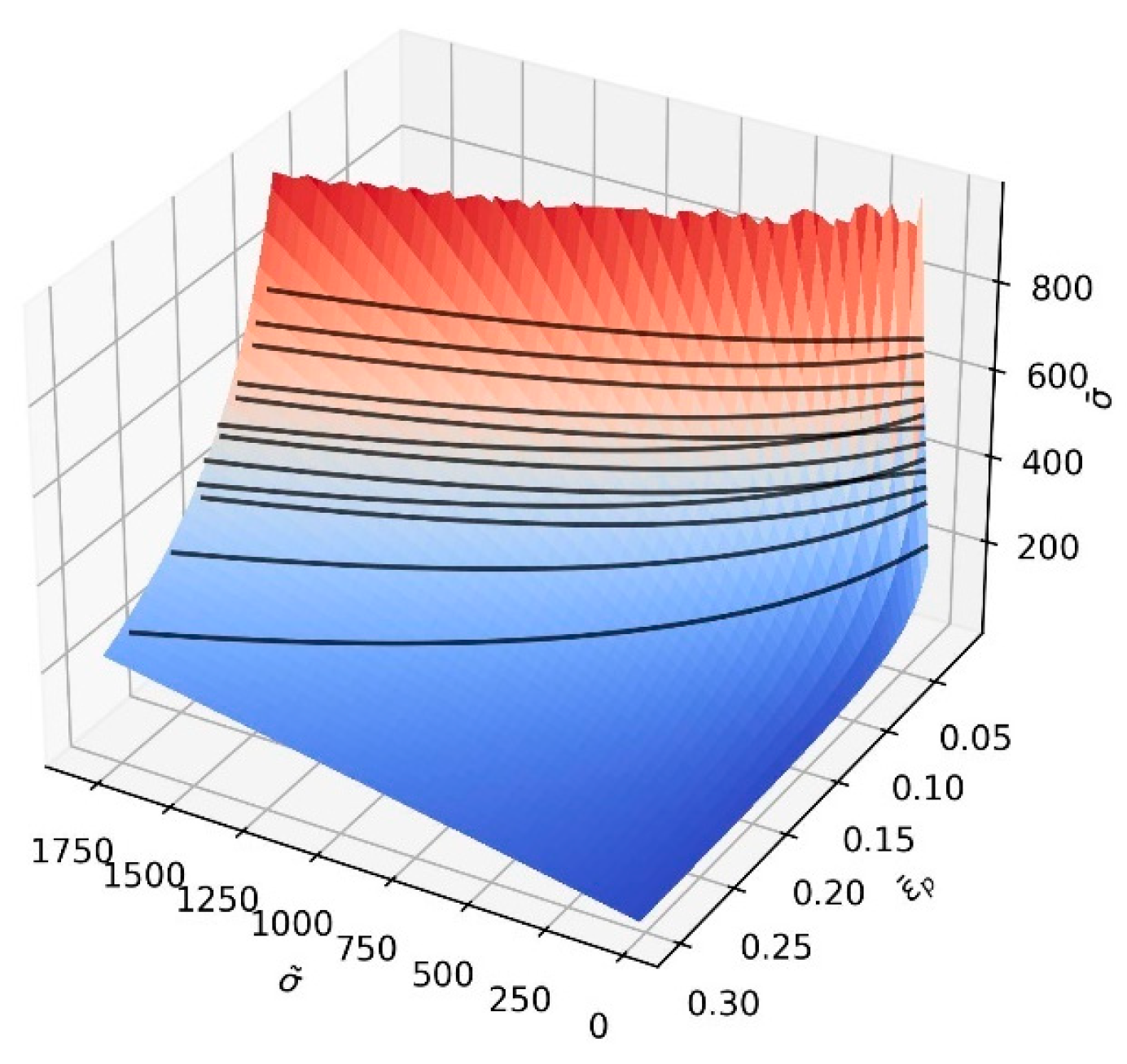
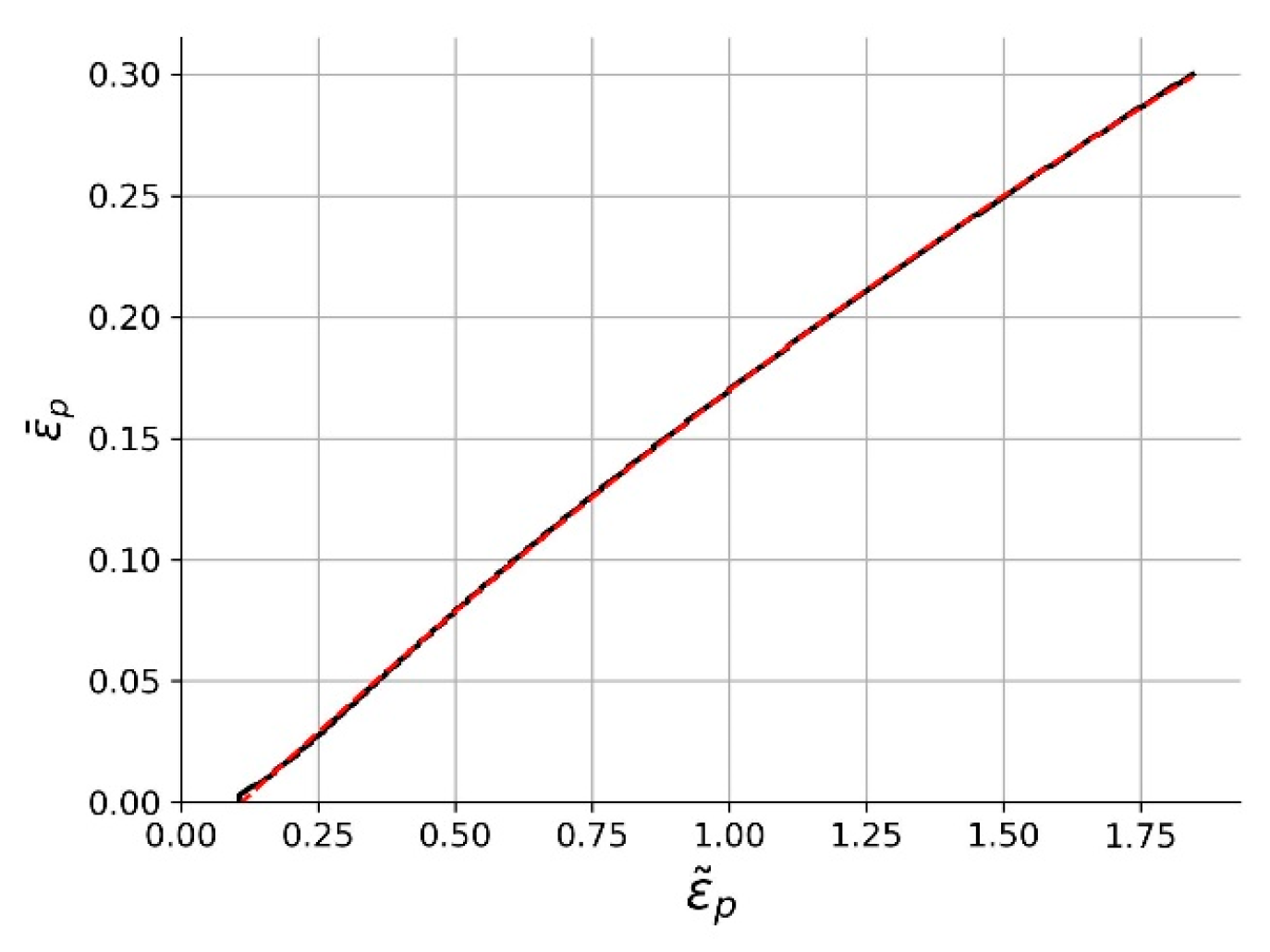
Finite Element Modeling
4. Machine Learning Models
4.1. In-House Statistical Algorithm
4.2. Model Training
4.3. XGBoost Algorithm
4.4. Model Training and Validation
5. Results
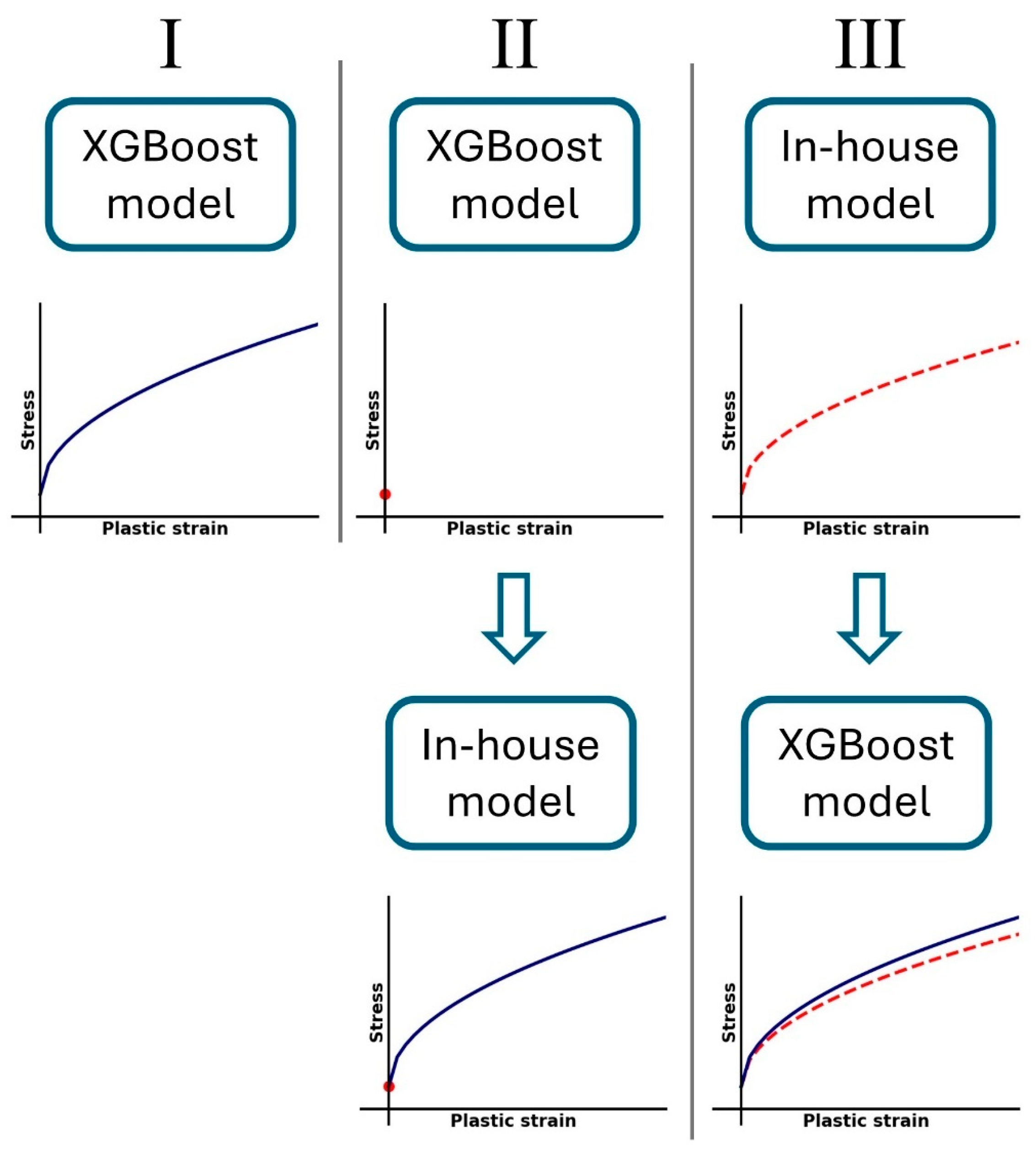
- An XGBoost model for predicting the entire flow stress curve.
- An XGBoost model for predicting the yield stress, and an in-house model for predicting the hardening curve. This split between the two models stems from the in-house model’s inability to predict the yield stress, as shown in Figure 11.
- An in-house model’s initial prediction for the entire flow stress curve, fed as an input to a subsequent XGBoost model for predicting the entire flow stress curve. This is performed in order to check whether the XGBoost model’s performance can be improved using the in-house model’s prediction (without the yield stress).
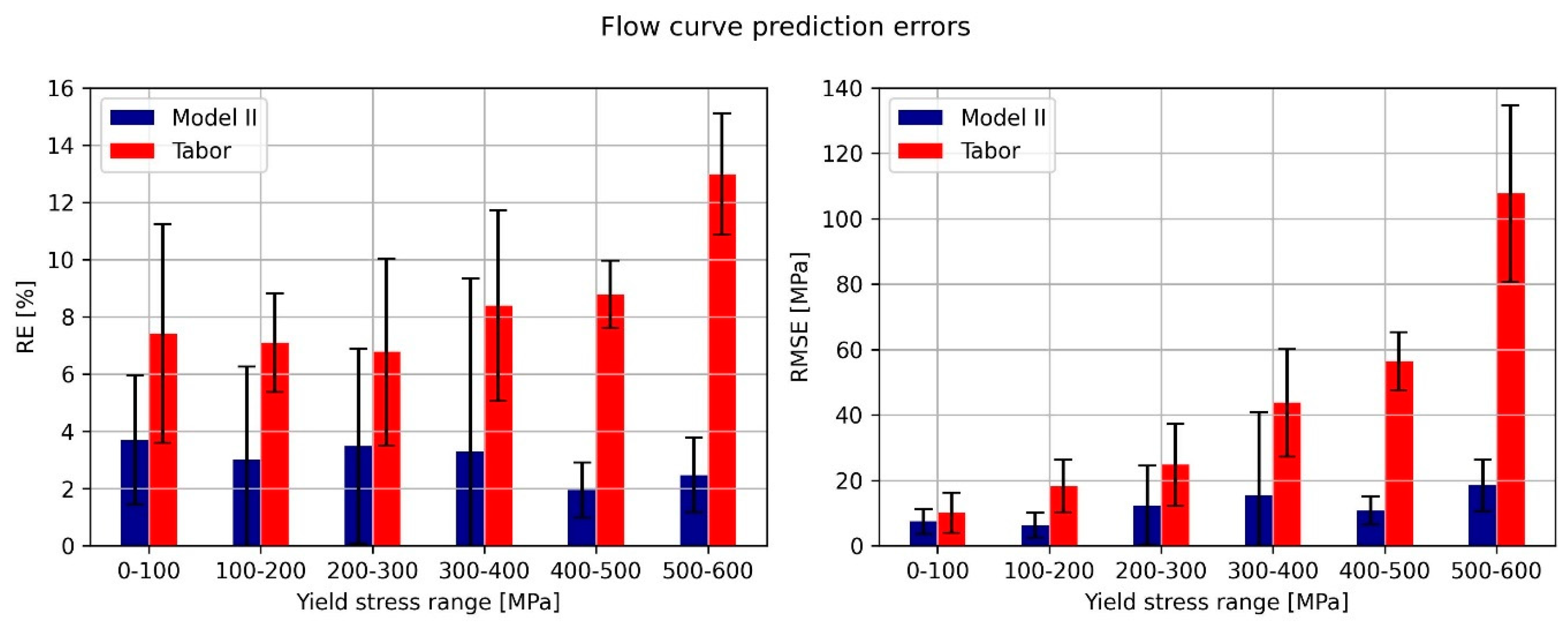
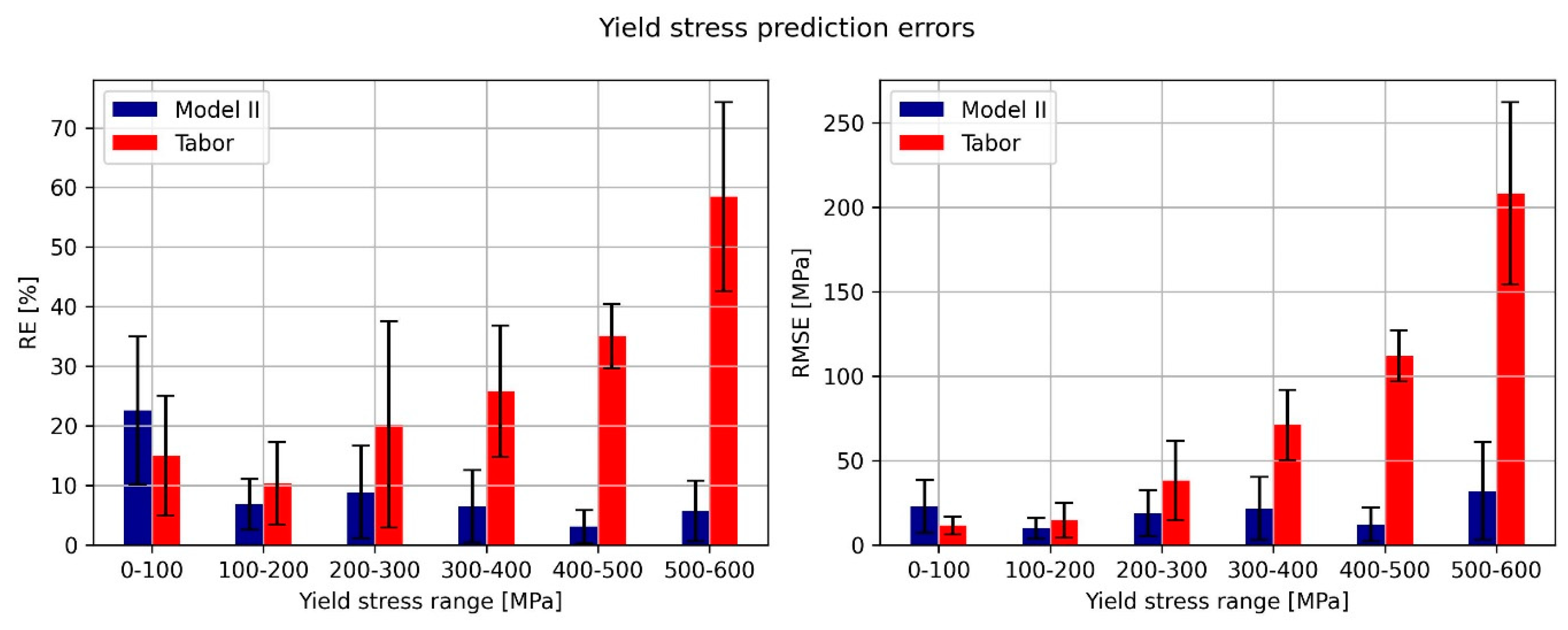
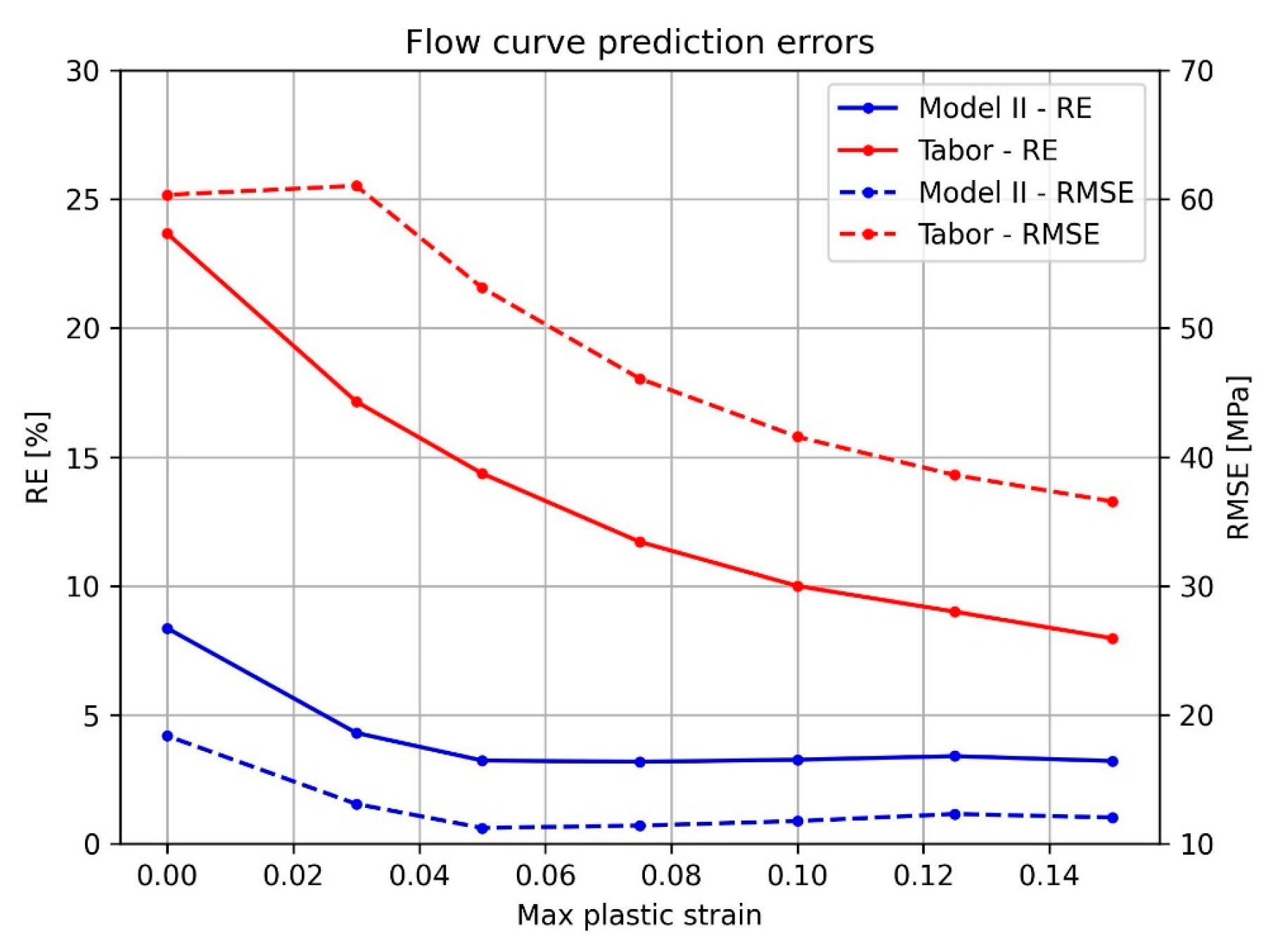
Prediction Results and Discussion
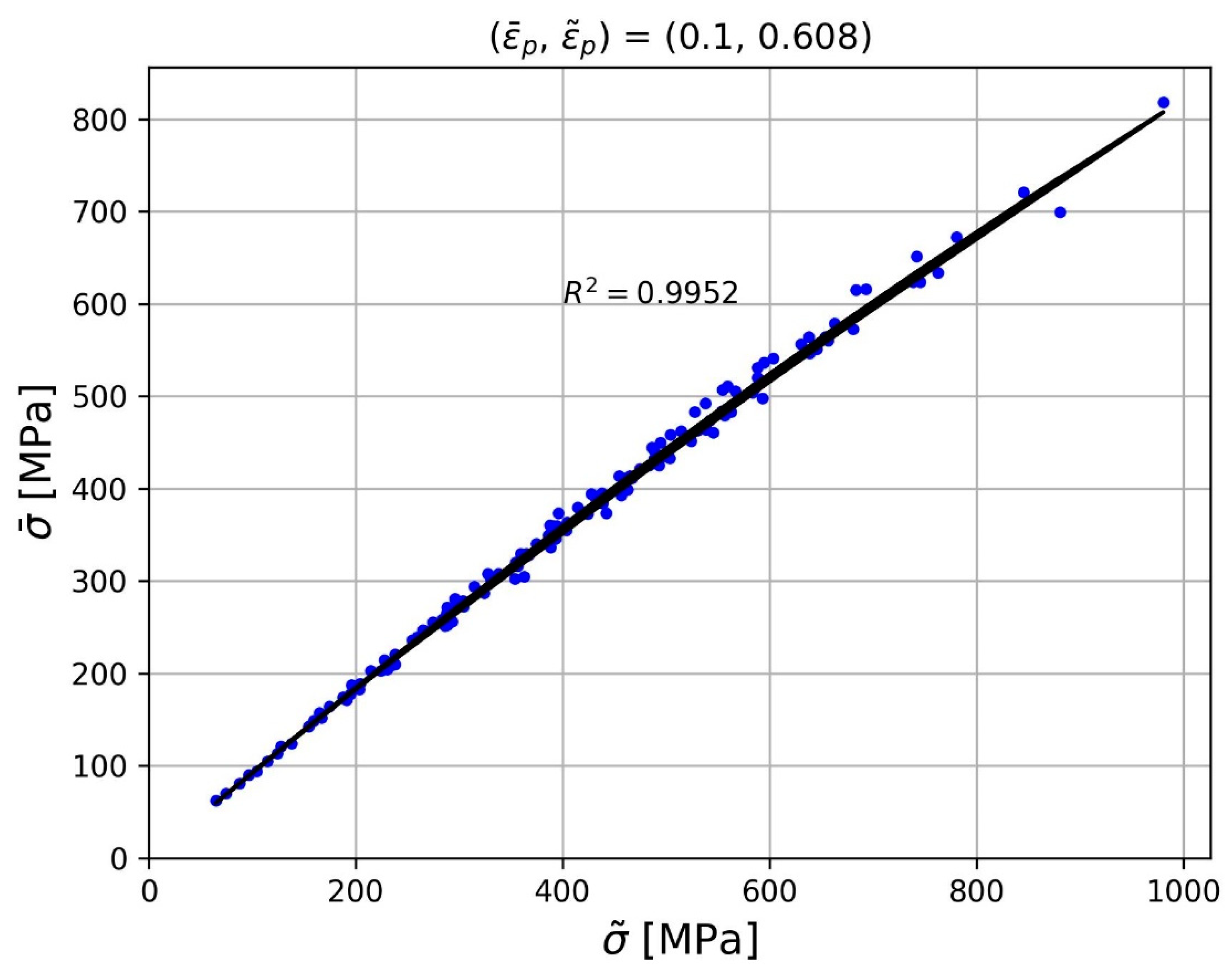
- The relative error defined as follows:
- The root mean squared error defined as follows:
- Performance based on the material’s yield stress:
- Performance based on the maximum plastic strain to be predicted:
- Prediction of materials used in real indentation tests:
6. Summary and Conclusions
- A Tabor model for predicting the yield stress of metals with a yield stress lower than 100 MPa.
- An XGBoost model for predicting the yield stress of metals with a yield stress higher than 100 MPa.
- An in-house developed model for predicting the hardening curve.
- Conduct Brinell hardness tests with different values of indentation forces. A minimum of two tests with different forces is required, although more test data will ensure more accurate results.
- Convert the force and trace diameter data from the hardness tests to the pseudo stress and pseudo strain values using Equation (4).
- Identify the Meyer coefficient of the material using the values calculated from Equation (4). Note that the model contains a tool for automatically identifying these coefficients (see the data availability statement for an online repository where the ML-model and tools can be found).
- Input the Meyer coefficients and the Brinell hardness values measured in the ML-model to generate the material hardening curve.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brinell, J.A. SaÈtt att bestaÈmma kroppars haÊrdhet jaÈmte naÊgra tillampningar af detsamma. Teknisk Tidskrift 1900, 30, 69–87. [Google Scholar]
- ASTM E10-15; Standard Test Method for Brinell Hardness of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2015.
- Meyer, E.; Ver, Z. Contribution to the knowledge of hardness and hardness testing. Z. Vereines Dtsch. Ingenieure 1908, 52, 645–654. [Google Scholar]
- Tabor, D. A simple theory of static and dynamic hardness. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 192, 247–274. [Google Scholar]
- Hill, R.; Storakers, B.; Zdunek, A.B. A theoretical study of the Brinell hardness test. Proc. R. Soc. Lond. A 1989, 423, 301–330. [Google Scholar]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Nix, W.D.; Dao, H. Indentation size effects in crystalline materials: A law for strain gradient plasticity. J. Mech. Phys. Solids 1998, 46, 411–425. [Google Scholar] [CrossRef]
- Bîrleanu, C.; Pustan, M.; Șerdean, F.; Merie, V. AFM Nanotribomechanical Characterization of Thin Films for MEMS Applications. Micromachines 2022, 13, 23. [Google Scholar] [CrossRef]
- Zak, S.; Trost, C.O.; Kreiml, P.; Cordill, M.J. Accurate measurement of thin film mechanical properties using nanoindentation. J. Mater. Res. 2022, 37, 1373–1389. [Google Scholar] [CrossRef]
- Zak, S. Controlling strain localization in thin films with nanoindenter tip sharpness. Sci. Rep. 2024, 14, 25500. [Google Scholar] [CrossRef] [PubMed]
- Khalfallah, A.; Khalfallah, A.; Benzarti, Z. Identification of Elastoplastic Constitutive Model of GaN Thin Films Using Instrumented Nanoindentation and Machine Learning Technique. Coatings 2024, 14, 683. [Google Scholar] [CrossRef]
- Soowan, P.; Karuppasamy, P.M.; Giyeol, H.; Hyungyil, L. Deep learning based nanoindentation method for evaluating mechanical properties of polymers. Int. J. Mech. Sci. 2023, 246, 108162. [Google Scholar]
- Niu, J.; Miao, B.; Guo, J.; Ding, Z.; He, Y.; Chi, Z.; Wang, F.; Ma, X. Leveraging Deep Neural Networks for Estimating Vickers Hardness from Nanoindentation Hardness. Materials 2024, 17, 148. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.T.; Watanabe, I. Data-driven estimation of plastic properties in work-hardening model combining power-law and linear hardening using instrumented indentation test. Sci. Technol. Adv. Mater. Methods 2022, 2, 416–424. [Google Scholar] [CrossRef]
- Dao, M.; Chollacoop, N.; Van Vliet, K.J.; Venkatesh, T.A.; Suresh, S. Computational modeling of the forward and reverse problems in instrumented sharp indentation. Acta Mater. 2001, 49, 3899–3918. [Google Scholar] [CrossRef]
- Bucaille, J.L.; Stauss, S.; Felder, E.; Michler, J. Determination of plastic properties of metals by instrumented indentation using different sharp indenters. Acta Mater. 2003, 51, 1663–1678. [Google Scholar] [CrossRef]
- Goto, K.; Watanabe, I.; Ohmura, T. Inverse estimation approach for elastoplastic properties using the load-displacement curve and pile-up topography of a single Berkovich indentation. Mater. Des. 2020, 194, 108925. [Google Scholar] [CrossRef]
- Kang, J.J.; Becker, A.A.; Sun, W. Determining elastic–plastic properties from indentation data obtained from finite element simulations and experimental results. Int. J. Mech. Sci. 2012, 62, 34–46. [Google Scholar] [CrossRef]
- Fernandez-Zelaia, P.; Joseph, V.R.; Kalidindi, S.R.; Melkote, S.N. Estimating mechanical properties from spherical indentation using Bayesian approaches. Mater. Des. 2018, 147, 92–105. [Google Scholar] [CrossRef]
- Lu, L.; Dao, M.; Kumar, P.; Ramamurty, U.; Karniadakis, G.E.; Suresh, S. Extraction of mechanical properties of materials through deep learning from instrumented indentation. Proc. Natl. Acad. Sci. USA 2020, 117, 7052–7062. [Google Scholar] [CrossRef]
- Karuppasamy, P.M. Physics-informed neural networks for spherical indentation problems. Mater. Des. 2023, 236, 112494. [Google Scholar]
- Haj-Ali, R.; Kim, H.K.; Koh, S.W.; Saxena, A.; Tummala, R. Nonlinear constitutive models from nanoindentation tests using artificial neural networks. Int. J. Plast. 2008, 24, 371–396. [Google Scholar] [CrossRef]
- Ma, Q.P.; Basterrech, S.; Halama, R.; Omacht, D.; Měsíček, J.; Hajnyš, J.; Platoš, J.; Petrů, J. Application of instrumented indentation test and neural networks to determine the constitutive model of in-situ austenitic strainless steel components. Arch. Civ. Mech. Eng. 2024, 24, 129. [Google Scholar] [CrossRef]
- Yongju, K. Novel deep learning approach for practical applications of indentation. Mater. Today Adv. 2022, 13, 100207. [Google Scholar]
- Dieter, G.E. Mechanical Metallurgy; McGraw-Hill Book Company: New York, NY, USA, 1961. [Google Scholar]
- Jayaraman, S.; Hahn, G.T.; Oliver, W.C.; Rubin, C.A.; Bastias, P.C. Determination of the monotonic stress-strain curve of hard materials from ultra-low-load indentation tests. Int. J. Solids Struct. 1998, 35, 365–381. [Google Scholar] [CrossRef]
- DiCarlo, A.; Yang, H.T.Y.; Chandrasekar, S. Prediction of stress-strain relation using cone indentation: Effect of friction. Int. J. Numer. Methods Eng. 2004, 60, 661–674. [Google Scholar] [CrossRef]
- Liu, X.; Peng, Q.; Pan, S.; Du, J.; Yang, S.; Han, J.; Lu, Y.; Yu, J.; Wang, C. Machine Learning Assisted Prediction of Microstructures and Young’s Modulus of Biomedical Multi-Component β-Ti Alloys. Metals 2022, 12, 796. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, H.; Zhang, S.; Cheng, J.; He, Y.; Zhou, G.; Liu, J.; Song, S.; Chen, L. A machine learning method approach for designing novel high strength and plasticity metastable β titanium alloys. Prog. Nat. Sci. Mater. Int. 2024. [Google Scholar] [CrossRef]
- Churyumov, A.Y.; Kazakova, A.A. Prediction of True Stress at Hot Deformation of High Manganese Steel by Artificial Neural Network Modeling. Materials 2023, 16, 1083. [Google Scholar] [CrossRef] [PubMed]
- Jeong, J.; Hong, D.; Yim, C. Deep Learning to Predict Deterioration Region of Hot Ductility in High-Mn Steel by Using the Relationship between RA Behavior and Time-Temperature-Precipitation. Metals 2022, 12, 1689. [Google Scholar] [CrossRef]
- Vivanco-Benavides, L.E.; Martínez-González, C.L.; Mercado-Zúñiga, C.; Torres-Torres, C. Machine learning and materials informatics approaches in the analysis of physical properties of carbon nanotubes: A review. Comput. Mater. Sci. 2022, 201, 110939. [Google Scholar] [CrossRef]
- Juan, Y.; Dai, Y.; Yang, Y.; Zhang, J. Accelerating materials discovery using machine learning. J. Mater. Sci. Technol. 2021, 79, 178–190. [Google Scholar] [CrossRef]
- Pan, S.; Wang, Y.; Yu, J.; Yang, M.; Zhang, Y.; Wei, H.; Chen, Y.; Wu, J.; Han, J.; Wang, C.; et al. Accelerated discovery of high-performance Cu-Ni-Co-Si alloys through machine learning. Mater. Des. 2021, 209, 109929. [Google Scholar] [CrossRef]
- Chet, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Richmond, O.; Morrison, H.; Devenpeck, M. Sphere indentation with application to the Brinell hardness test. Int. J. Mech. Sci. 1974, 16, 75–82. [Google Scholar] [CrossRef]
- ABAQUS, 2022; Dassault Systèmes: Providence, RI, USA, 2022.
- Rom, N.; Bortman, J.; Priel, E. Predicting ductile failure of aluminum components under general loading conditions: Computational implementation, model verification and experimental validation. Int. J. Solids Struct. 2023, 275, 112295. [Google Scholar] [CrossRef]
- Priel, E.; Mittelman, B.; Trabelsi, N.; Cohen, Y.; Koptiar, Y.; Oadan, R. A computational study of equal channel angular pressing of molybdenum validated by experiments. J. Mater. Process. Technol. 2019, 264, 469–485. [Google Scholar] [CrossRef]
- XGBoost Developers. XGBoost Documentation. Version 2.0.3. December 2023. Available online: https://xgboost.readthedocs.io/en/stable/index.html (accessed on 20 May 2024).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]





| 25 | 125 | 0.1 |
| 125 | 225 | 0.2 |
| 225 | 325 | 0.3 |
| 325 | 425 | 0.4 |
| 425 | 525 | 0.5 |
| -- | 825 | -- |
| Material | Al6061-T6 | Al7075-T6 | Al1100 | Copper | Al7075-400 |
|---|---|---|---|---|---|
| Experimental Indentation trace diameter [mm] | 0.602 | 0.504 | 1.046 | 0.667 | 0.564 |
| Computed indentation trace diameter [mm] | 0.62 | 0.49 | 0.992 | 0.602 | 0.548 |
| Relative error [%] | 2.9 | 2.8 | 5.1 | 9.7 | 2.8 |
| Parameter Name | Values Tested |
|---|---|
| n_estimators | 10,000 with an early stopping after 5 |
| learning_rate | [0.01, 0.1, 0.3] |
| max_depth | [3, 7, 10] |
| min_child_weight | [0, 5, 10] |
| subsample | [0.5, 0.7, 1] |
| colsample_bytree | [0.5, 1] |
| gamma | [0, 5, 10] |
| reg_alpha | [0.2, 0.8] |
| reg_lambda | [0.2, 0.8] |
| Cross-validation | 5 |
| Material | Relative Error [%] | Root Mean Squared Error [MPa] | ||
|---|---|---|---|---|
| Yield Stress | Entire Graph | Yield Stress | Entire Graph | |
| Al6061-T6 | 3.7 | 5.9 | 11.0 | 21.4 |
| Article1 | --- | 0.6 | --- | 3.3 |
| Article2 | --- | 8.0 | --- | 14.3 |
| Al1100-H | 2.1 | 11.4 | 2.3 | 15.0 |
| Al7075-T6 | 0.5 | 4.0 | 2.6 | 25.8 |
| Al7075-400 °C heat treated | 3.2 | 5.0 | 11.0 | 25.0 |
| Copper | 3.4 | 4.9 | 8.4 | 14.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rom, N.; Priel, E. A Data-Driven Methodology for Obtaining the Stress–Strain Curves of Metallic Materials Using Discrete Indentation Tests. Metals 2025, 15, 40. https://doi.org/10.3390/met15010040
Rom N, Priel E. A Data-Driven Methodology for Obtaining the Stress–Strain Curves of Metallic Materials Using Discrete Indentation Tests. Metals. 2025; 15(1):40. https://doi.org/10.3390/met15010040
Chicago/Turabian StyleRom, Nitzan, and Elad Priel. 2025. "A Data-Driven Methodology for Obtaining the Stress–Strain Curves of Metallic Materials Using Discrete Indentation Tests" Metals 15, no. 1: 40. https://doi.org/10.3390/met15010040
APA StyleRom, N., & Priel, E. (2025). A Data-Driven Methodology for Obtaining the Stress–Strain Curves of Metallic Materials Using Discrete Indentation Tests. Metals, 15(1), 40. https://doi.org/10.3390/met15010040







