Mathematical Modeling of Transient Submerged Entry Nozzle Clogging and Its Effect on Flow Field, Bubble Distribution and Interface Fluctuation in Slab Continuous Casting Mold
Abstract
1. Introduction
2. High-Temperature Velocity Measurement
3. Mathematical Model
3.1. Model Parameters and Boundary Conditions
3.2. Fluid Phase Hydrodynamics
3.3. Volume of Fluid (VOF) Model
3.4. Discrete Phase Model (DPM)
3.5. Porous Medium Model
4. Results and Discussion
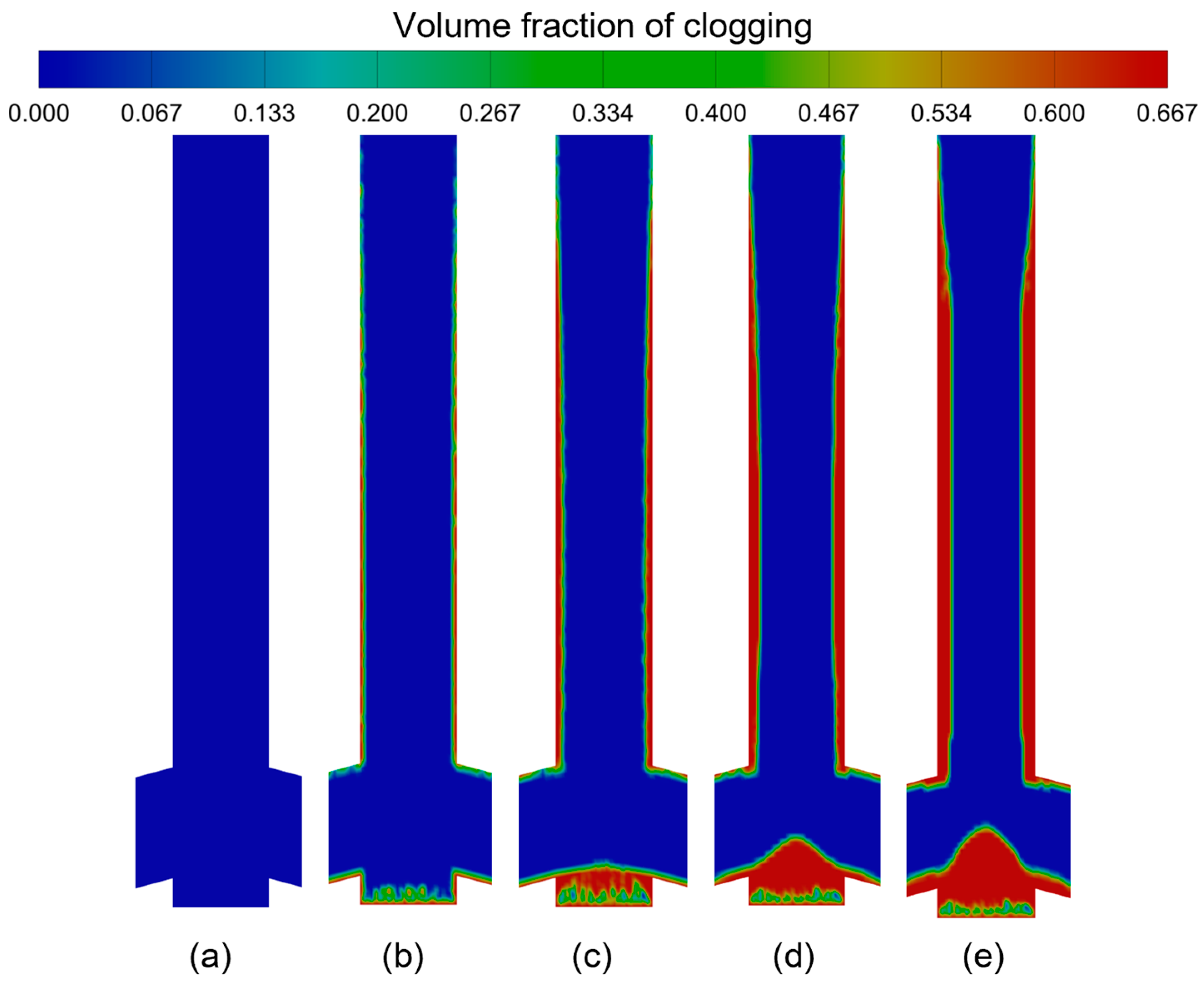
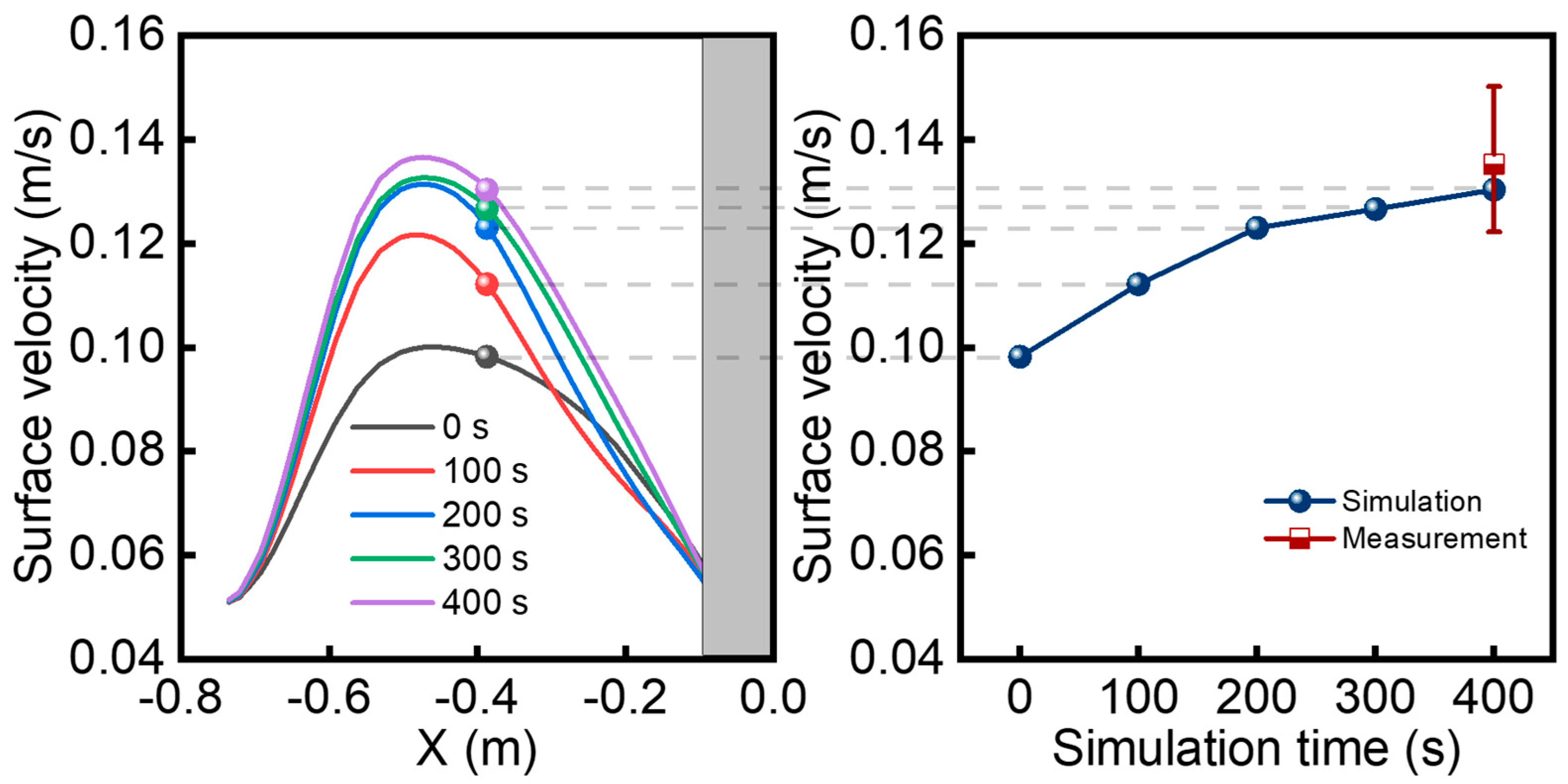
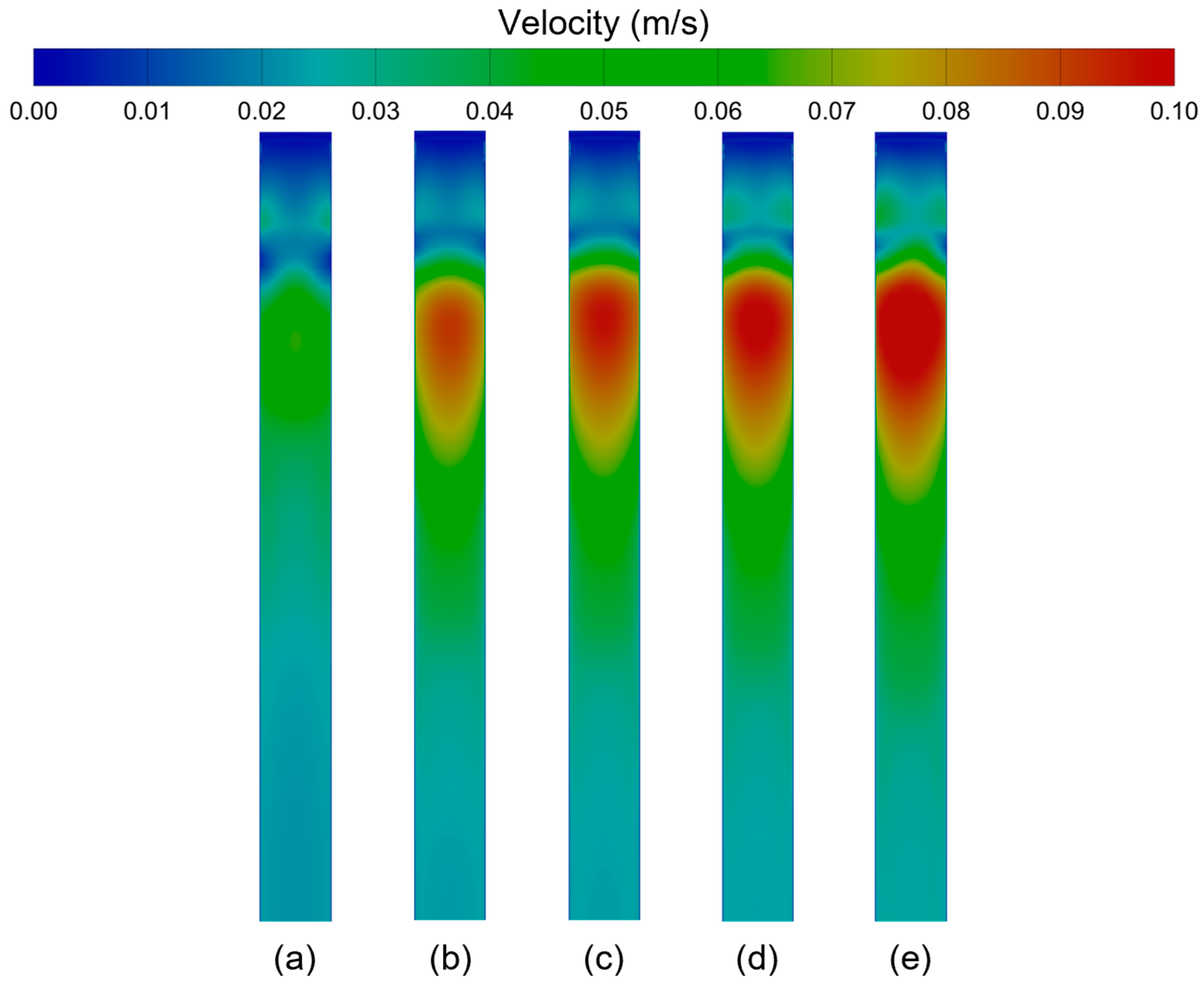
4.1. Model Verification
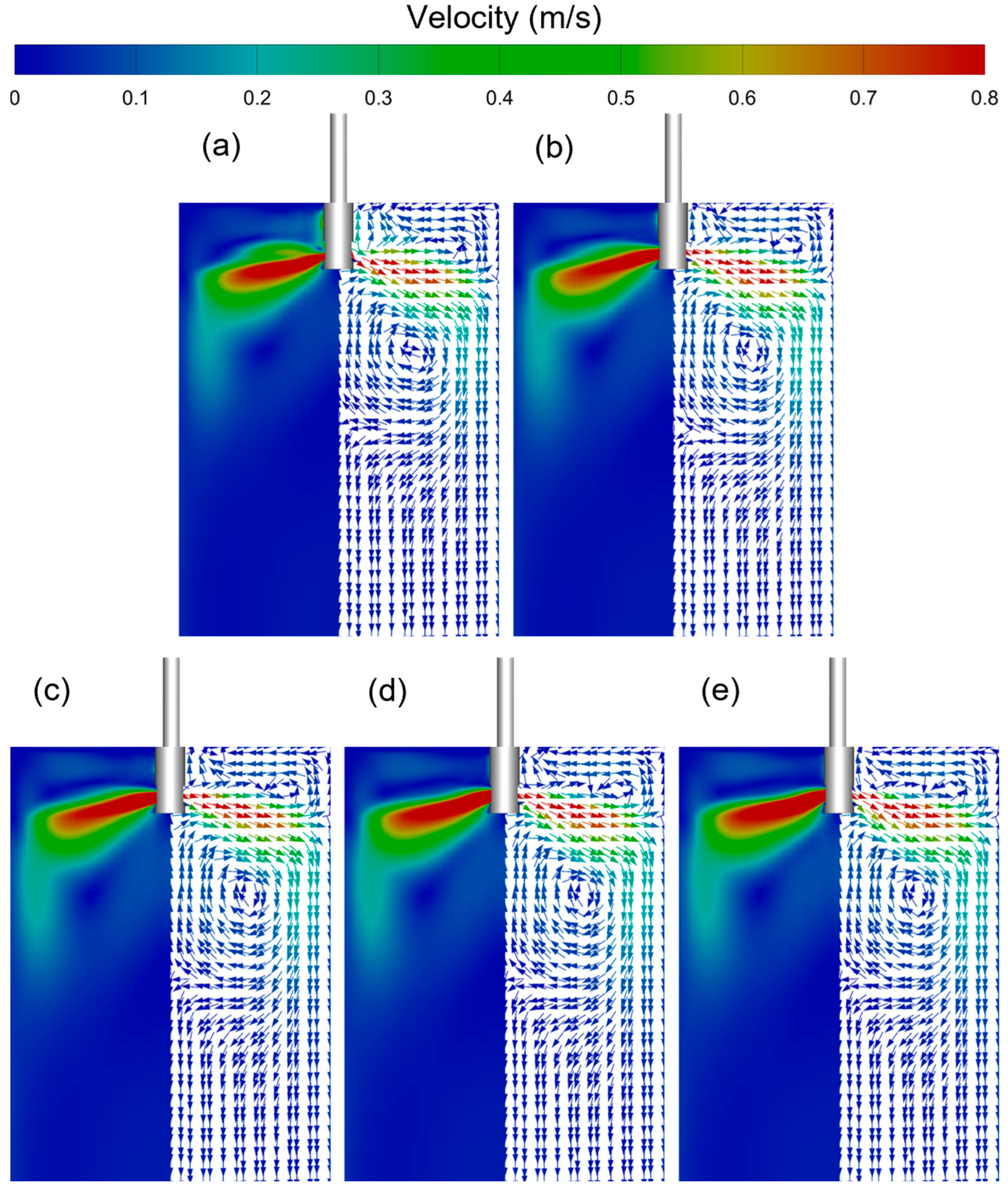
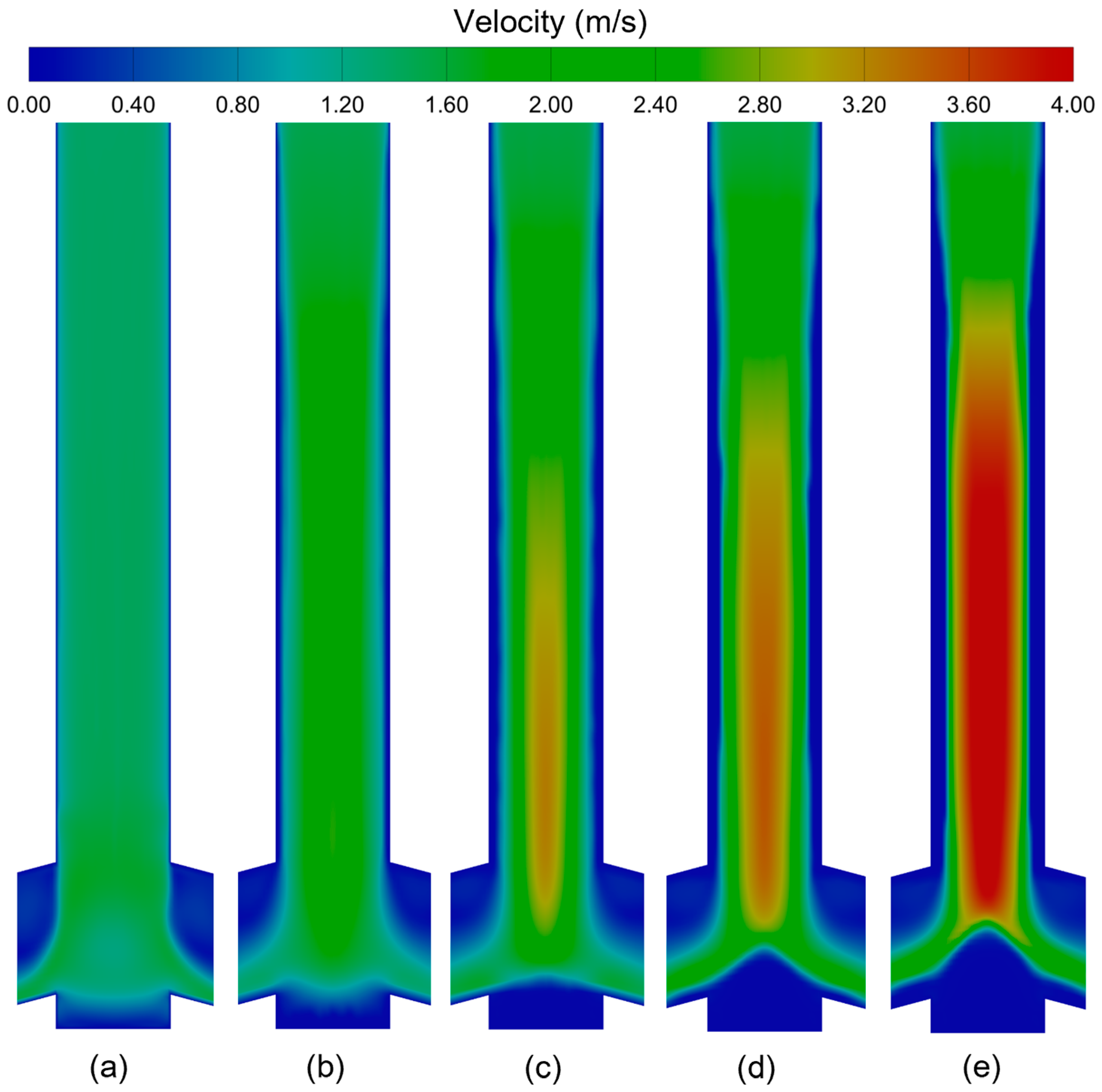
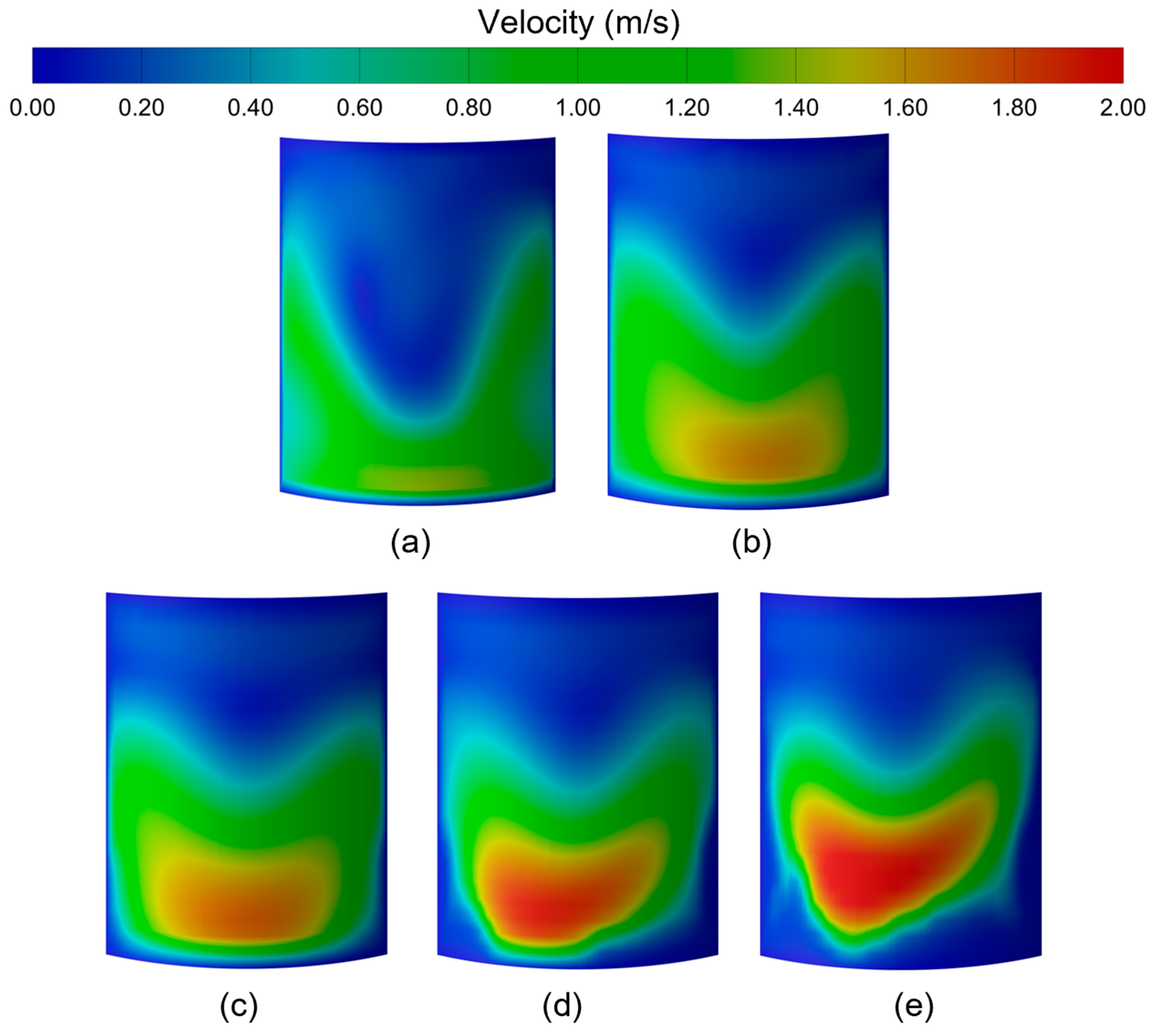
4.2. Effect of SEN Clogging on the Flow Field of the Mold
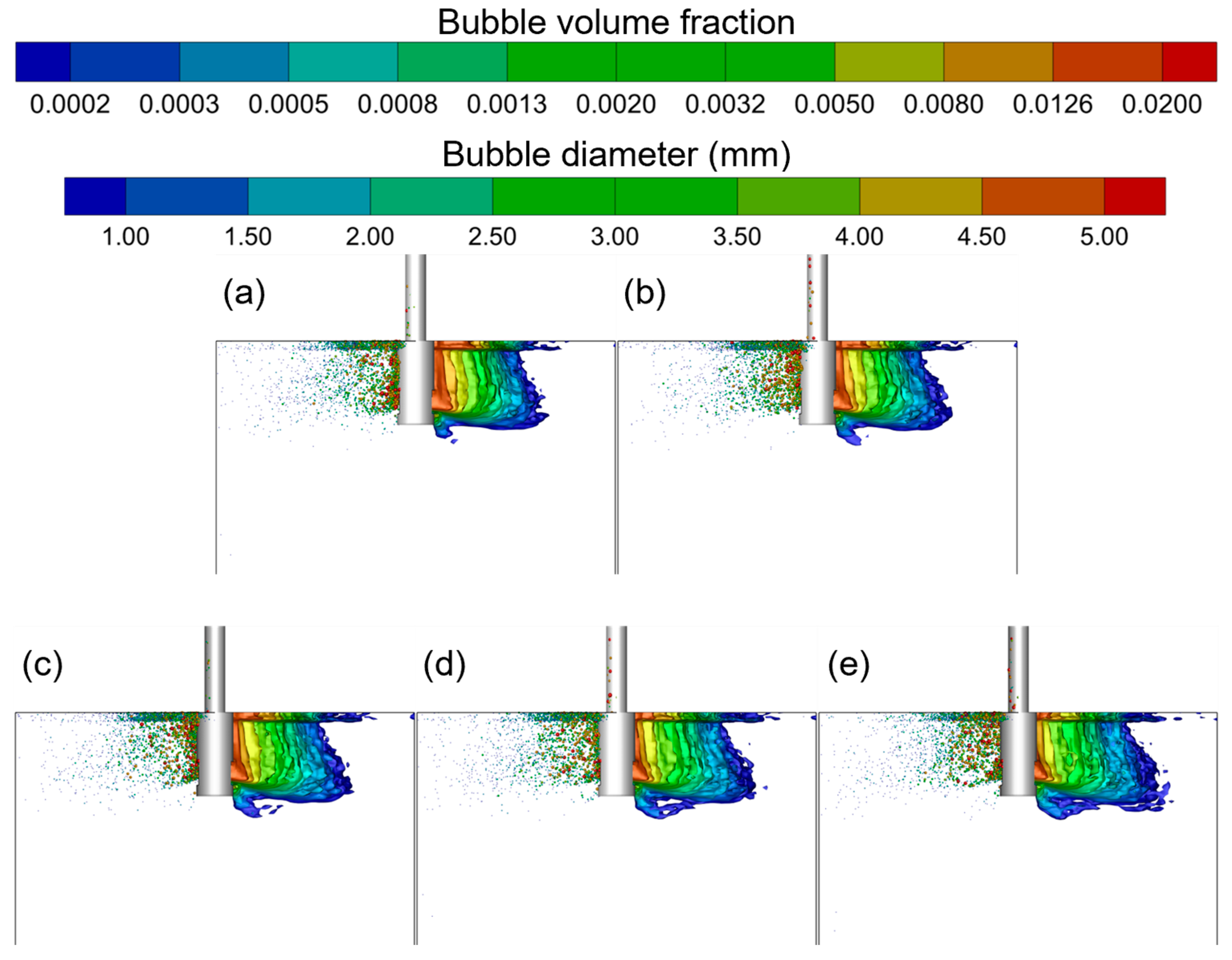
4.3. Effect of SEN Clogging on the Distribution of Argon Bubbles
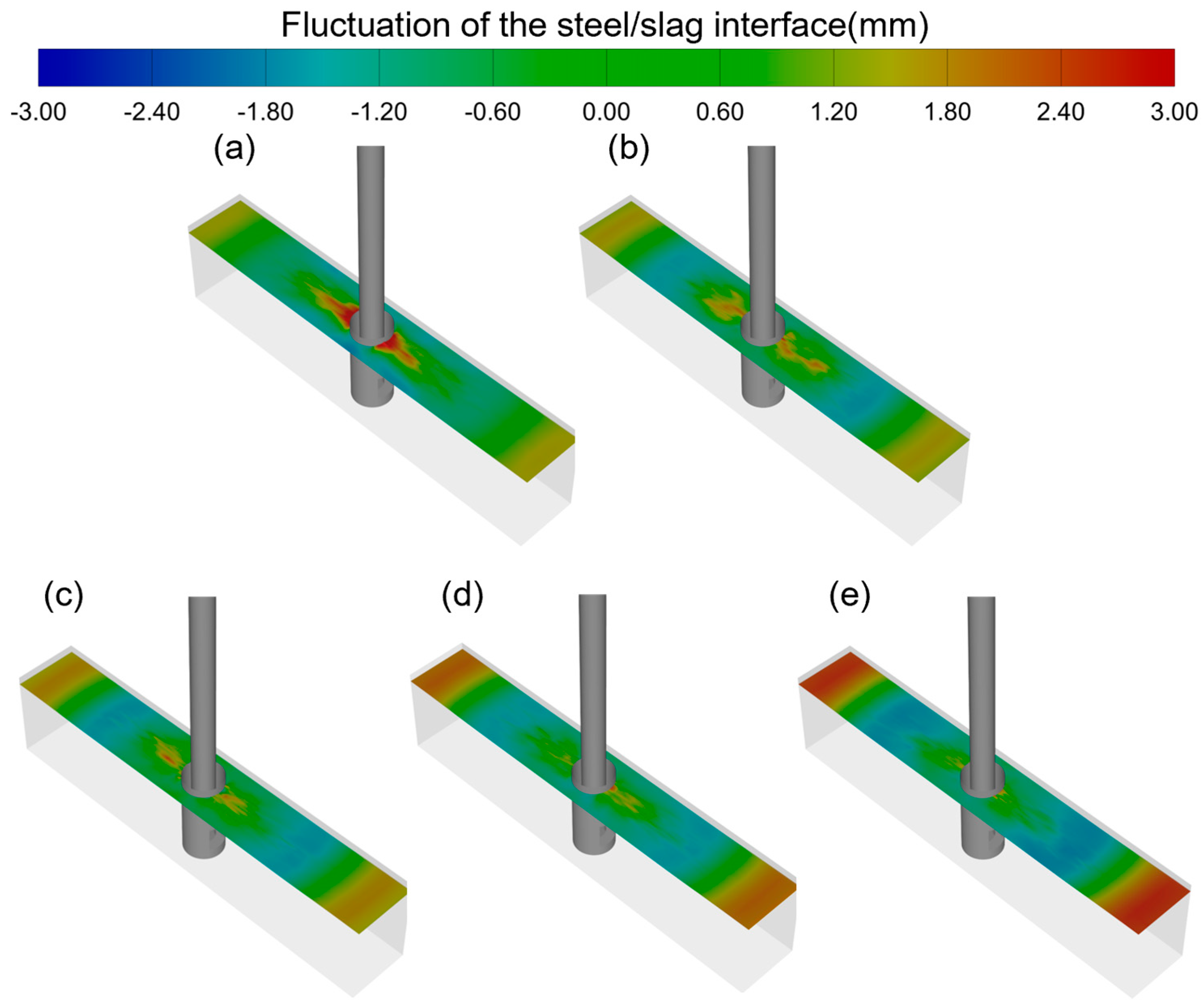
4.4. Effect of SEN Clogging on the Fluctuation of the Steel/Slag Interface
5. Conclusions
- The numerical simulation results of SEN clogging are in good agreement with the actual morphology and thicknesses of SEN clogging. In addition, the numerical simulation results of velocities near the 1/4 width of the mold at the late clogging stage are consistent with the measurement results of the surface flow velocity near the 1/4 width of the mold.
- The flow velocities of molten steel inside the SEN and at the outlet of the side hole increase with increasing simulation time and the degree of clogging, because the flow space is occupied with the clogging inclusions. This increases the strength of the upper circulation and lower circulation and increases the surface velocity of molten steel in the mold.
- The non-metallic inclusions are easy to adhere to the bottom of the SEN, because the flow velocities of molten steel and inclusions near the bottom are very low, which will make the growth rate of clogging at the bottom larger than those at the walls of the side holes and vertical part of SEN.
- With increasing the clogging simulation time and the clogging degree of the nozzle, the drag force of the molten steel jet to argon gas bubbles near the side holes of SEN will lead to an increase in the number of argon gas bubbles moving to the vicinity of the narrow walls.
- With increasing the clogging simulation time and the clogging degree of the nozzle, the fluctuation of the steel–slag interface near the narrow walls increases, resulting in the increased risk of slag entrapment caused by shear force.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hashimoto, Y.; Matsui, A.; Hayase, T.; Kano, M. Real-Time Estimation of Molten Steel Flow in Continuous Casting Mold. Metall. Mater. Trans. B 2020, 51, 581–588. [Google Scholar] [CrossRef]
- Hua, C.; Bao, Y.; Wang, M.; Xiao, W. Effect of nozzle clogging on flow and inclusion transport in GCr15 steel casting process. J. Mater. Res. Technol. 2022, 19, 2330–2345. [Google Scholar] [CrossRef]
- Li, G.; Lu, C.; Gan, M.; Wang, Q.; He, S. Influence of Submerged Entry Nozzle Clogging on the Flow Field and Slag Entrainment in the Continuous Casting Mold by the Physical Model. Metall. Mater. Trans. B 2022, 53, 1436–1445. [Google Scholar] [CrossRef]
- Srinivas, P.S.; Singh, A.; Korath, J.M.; Jana, A.K. A water-model experimental study of vortex characteristics due to nozzle clogging in slab caster mould. Ironmak. Steelmak. 2017, 44, 473–485. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, L.; Zhou, Q.; Chen, W.; Jiang, R.; Yin, K.; Yang, W. Clogging-Induced Asymmetrical and Transient Flow Pattern in a Steel Continuous Casting Slab Strand Measured Using Nail Boards. Steel Res. Int. 2021, 92, 2000547. [Google Scholar] [CrossRef]
- Luo, Y.; Ji, C.; He, W.; Liu, Y.; Yang, X.; Li, H. Fluid flow and heat transfer with nail dipping method in mould during continuous casting process. Can. Metall. Q. 2020, 59, 201–210. [Google Scholar] [CrossRef]
- Zhang, L.F.; Wang, Y.F.; Zuo, X.J. Flow Transport and Inclusion Motion in Steel Continuous-Casting Mold under Submerged Entry Nozzle Clogging Condition. Metall. Mater. Trans. B 2008, 39, 534–550. [Google Scholar] [CrossRef]
- Zhao, B.; Wu, W.; Zhi, J.; Su, C.; Zhang, J. Study on the formation mechanism of clogging layer of rare earth microalloyed Q355 steel’s submerged entry nozzle and process optimization. Ironmak. Steelmak. 2023, 50, 782–793. [Google Scholar] [CrossRef]
- Ji, S.; Yang, W.; Ren, Y.; Zhang, L. Clogging Growth on the Submerged Entry Nozzle During Continuous Casting of a Ca-Treated and Al-Killed Resulfurized Steel. Metall. Mater. Trans. B 2023, 54, 1630–1638. [Google Scholar] [CrossRef]
- Deng, Z.; Zhu, M.; Zhou, Y.; Sichen, D. Attachment of Alumina on the Wall of Submerged Entry Nozzle During Continuous Casting of Al-Killed Steel. Metall. Mater. Trans. B 2016, 47, 2015–2025. [Google Scholar] [CrossRef]
- Cui, H.; Bao, Y.-p.; Wang, M.; Wu, W.-S. Clogging behavior of submerged entry nozzles for Ti-bearing IF steel. Int. J. Miner. Metall. Mater. 2010, 17, 154–158. [Google Scholar] [CrossRef]
- Barati, H.; Wu, M.; Michelic, S.; Ilie, S.; Kharicha, A.; Ludwig, A.; Kang, Y.B. Mathematical Modeling of the Early Stage of Clogging of the SEN During Continuous Casting of Ti-ULC Steel. Metall. Mater. Trans. B 2021, 52, 4167–4178. [Google Scholar] [CrossRef]
- Barati, H.; Wu, M.; Kharicha, A.; Ludwig, A. Role of Solidification in Submerged Entry Nozzle Clogging During Continuous Casting of Steel. Steel Res. Int. 2020, 91, 2000230. [Google Scholar] [CrossRef]
- Hua, C.; Wang, M.; Bao, Y. Effect of Nozzle Clogging on the Fluid Flow Pattern in a Billet Mold with Particle Image Velocimetry Technology. Metall. Mater. Trans. B 2020, 51, 2871–2881. [Google Scholar] [CrossRef]
- Li, B.; Lu, H.; Shen, Z.; Sun, X.; Zhong, Y.; Ren, Z.; Lei, Z. Physical Modeling of Asymmetrical Flow in Slab Continuous Casting Mold due to Submerged Entry Nozzle Clogging with the Effect of Electromagnetic Stirring. ISIJ Int. 2019, 59, 2264–2271. [Google Scholar] [CrossRef]
- Srinivas, P.S.; Mishra, D.K.; Gupta, R.; Korath, J.M.; Jana, A.K. Vortex characteristics due to nozzle clogging in water caster mould: Modelling and validation. Can. Metall. Q. 2019, 58, 308–324. [Google Scholar] [CrossRef]
- Li, B.; Lu, H.; Zhong, Y.; Ren, Z.; Lei, Z. Influence of EMS on Asymmetric Flow with Different SEN Clogging Rates in a Slab Continuous Casting Mold. Metals 2019, 9, 1288. [Google Scholar] [CrossRef]
- Hua, C.; Bao, Y.; Wang, M. Numerical simulation and industrial application of nozzle clogging in bilateral-port nozzle. Powder Technol. 2021, 393, 405–420. [Google Scholar] [CrossRef]
- Vakhrushev, A.; Kharicha, A.; Wu, M.; Ludwig, A.; Tang, Y.; Hackl, G.; Nitzl, G.; Watzinger, J.; Bohacek, J. On Modelling Parasitic Solidification Due to Heat Loss at Submerged Entry Nozzle Region of Continuous Casting Mold. Metals 2021, 11, 1375. [Google Scholar] [CrossRef]
- Barati, H.; Wu, M.; Kharicha, A.; Ludwig, A. A transient model for nozzle clogging. Powder Technol. 2018, 329, 181–198. [Google Scholar] [CrossRef]
- Barati, H.; Wu, M.; Kharicha, A.; Ludwig, A. Calculation Accuracy and Efficiency of a Transient Model for Submerged Entry Nozzle Clogging. Metall. Mater. Trans. B 2019, 50, 1428–1443. [Google Scholar] [CrossRef]
- Liu, J.-Q.; Liu, Y.-B.; Sun, Q.; Lin, Y.; Du, L.; Meng, J.-S.; Yang, J. Numerical Simulation of Transient Submerged Entry Nozzle Clogging With Euler–Euler and Euler–Lagrange Frameworks. Metall. Mater. Trans. B 2023, 54, 2629–2650. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, J.; Jiang, P. Measurement of Molten Steel Velocity near the Surface and Modeling for Transient Fluid Flow in the Continuous Casting Mold. Metals 2019, 9, 36. [Google Scholar] [CrossRef]
- Dieguez Salgado, U.; Weiß, C.; Michelic, S.K.; Bernhard, C. Fluid Force-Induced Detachment Criteria for Nonmetallic Inclusions Adhered to a Refractory/Molten Steel Interface. Metall. Mater. Trans. B 2018, 49, 1632–1643. [Google Scholar] [CrossRef]
- Liu, Y.B.; Yang, J.; Lin, Z.Q. Mathematical Modeling of Mold Flow Field and Mold Flux Entrainment Assisted With High-Temperature Quantitative Velocity Measurement and Water Modeling. Metall. Mater. Trans. B 2022, 53, 2030–2050. [Google Scholar] [CrossRef]
- Thomas, B.G.; Huang, X.; Sussman, R.C. Simulation of Argon Gas Flow Effects in a Continuous Slab Caster. Metall. Mater. Trans. B 1994, 25, 527–547. [Google Scholar] [CrossRef]
- Brackbill, J.; Kothe, D.; Ca, Z. A Continuum Method for Modeling Surface Tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Jinbo, L.; Tao, Z.; Fubin, G.; Yankun, G.; Dan, Z. Analysis of nozzle clogging position in a continuous casting mold. Int. J. Chem. React. Eng. 2022, 20, 1027–1033. [Google Scholar] [CrossRef]
- Henry, C.; Minier, J.-P.; Lefèvre, G. Towards a description of particulate fouling: From single particle deposition to clogging. Adv. Colloid. Interface Sci. 2012, 185, 34–76. [Google Scholar] [CrossRef]
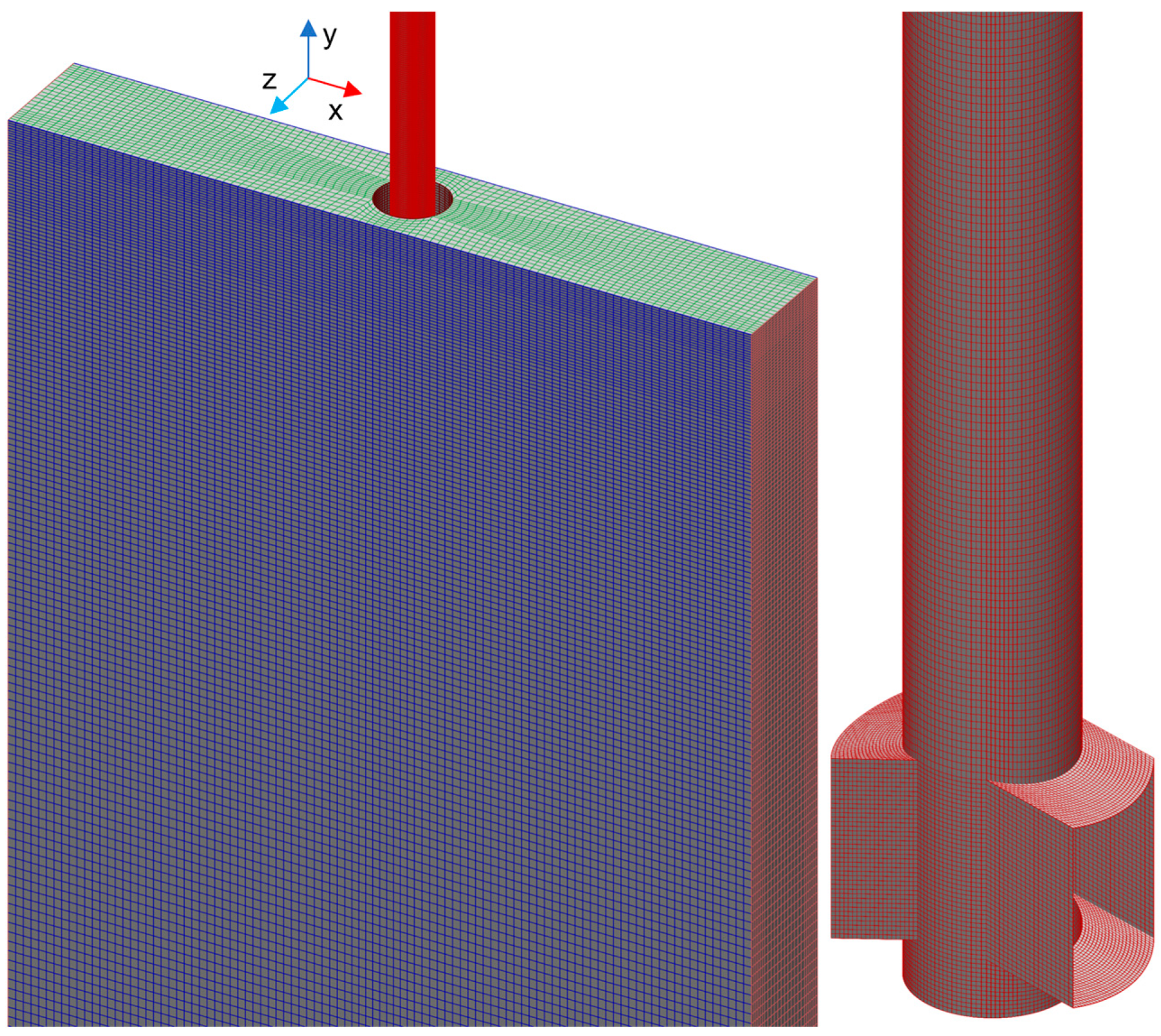
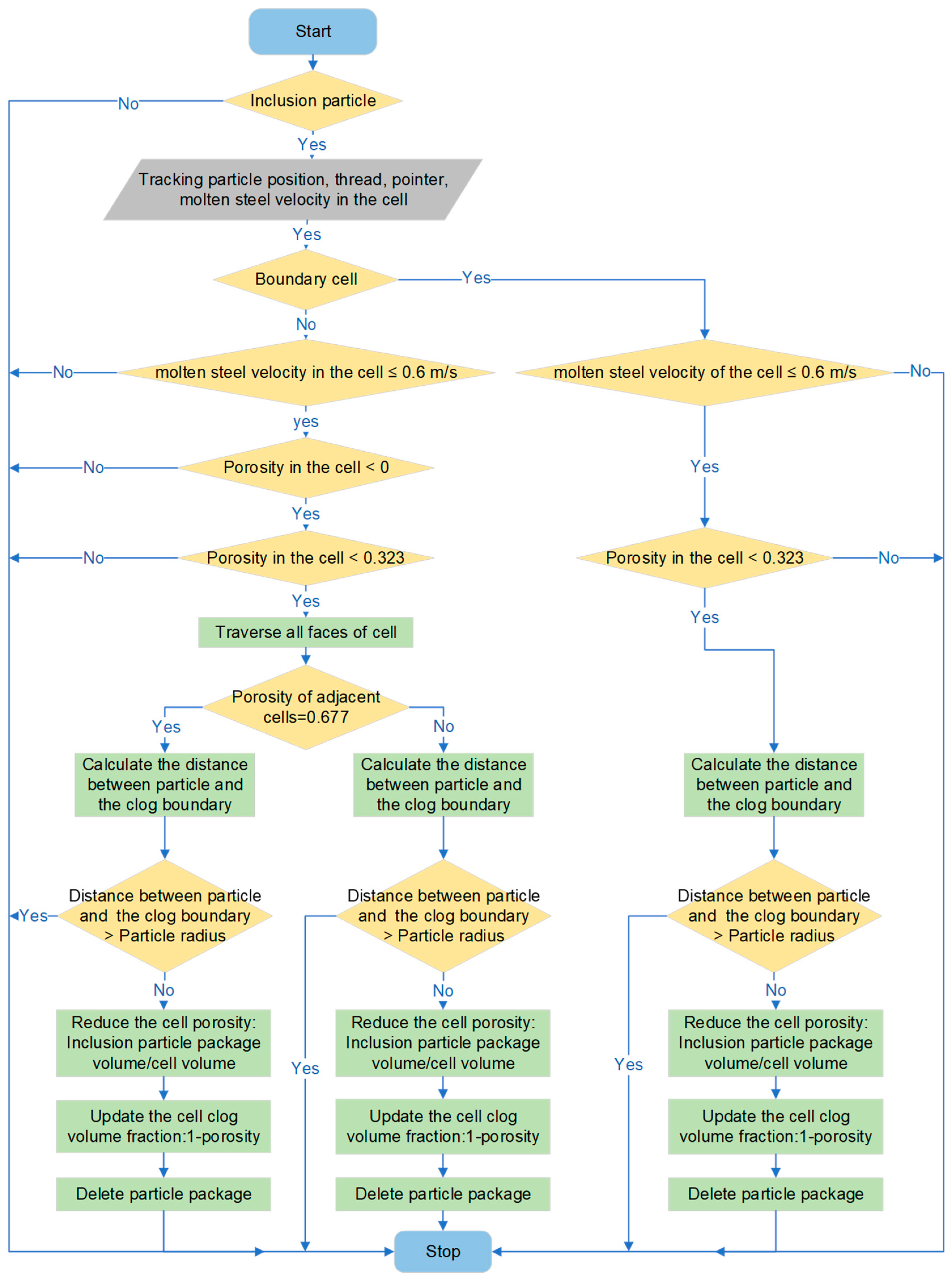
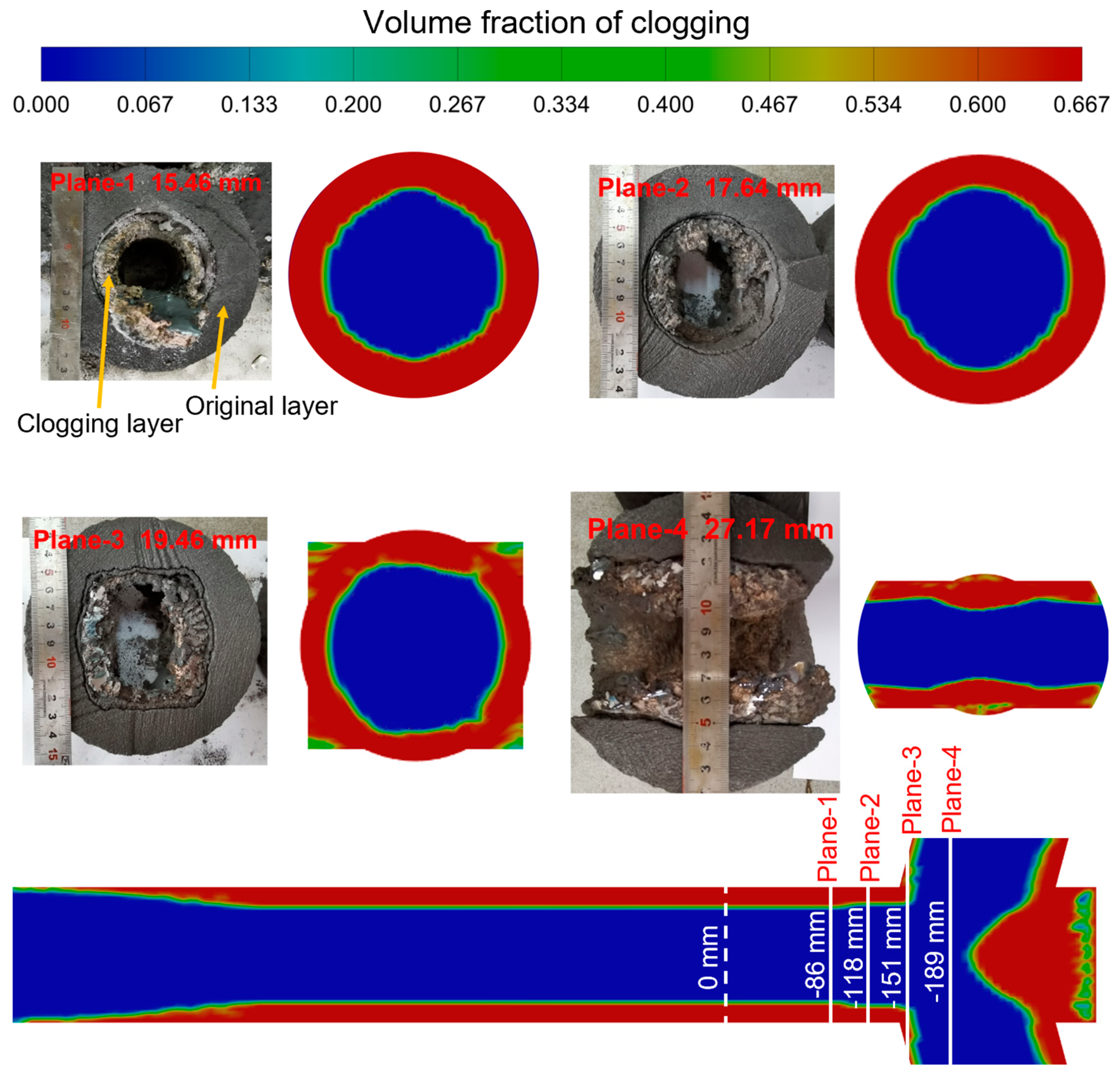
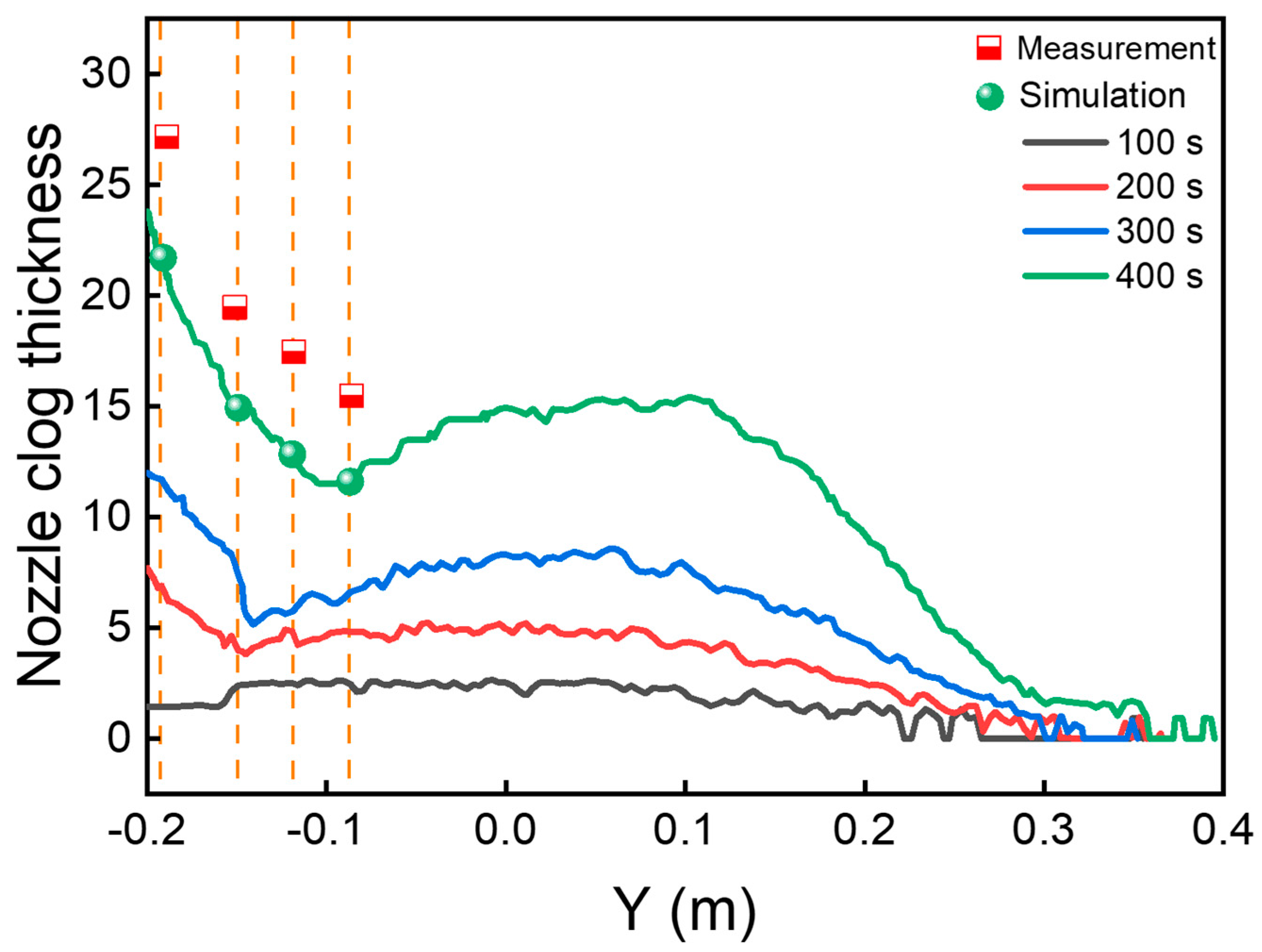
| Parameters | Values | Units |
|---|---|---|
| Mold width | 1500 | mm |
| Mold thickness | 230 | mm |
| Inner diameter/outer diameter of SEN | 78/140 | mm |
| Outlet size of SEN | 70 × 90 | mm × mm |
| Outlet angle of SEN(slope down) | 15 | ° |
| Argon gas flow rate | 6 | L·min−1 |
| Casting speed | 1 | m·min−1 |
| Immersion depth of SEN | 155 | mm |
| Thickness of the initial slag | 30 | mm |
| Density of molten steel | 7020 | kg·m−3 |
| Density of slag | 2600 | kg·m−3 |
| Viscosity of molten steel | 0.0062 | kg·s−1·m−1 |
| Viscosity of slag | 0.18 | kg·s−1·m−1 |
| Interfacial tension between molten steel and slag | 1.3 | N·m−1 |
| Density of argon gas | 0.27 | kg·m−3 |
| Density of inclusions | 3600 | kg·m−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; He, W.; Zhao, C.; Liu, J.; Yang, Z.; Zhao, Y.; Yang, J. Mathematical Modeling of Transient Submerged Entry Nozzle Clogging and Its Effect on Flow Field, Bubble Distribution and Interface Fluctuation in Slab Continuous Casting Mold. Metals 2024, 14, 742. https://doi.org/10.3390/met14070742
Li Y, He W, Zhao C, Liu J, Yang Z, Zhao Y, Yang J. Mathematical Modeling of Transient Submerged Entry Nozzle Clogging and Its Effect on Flow Field, Bubble Distribution and Interface Fluctuation in Slab Continuous Casting Mold. Metals. 2024; 14(7):742. https://doi.org/10.3390/met14070742
Chicago/Turabian StyleLi, Yuntong, Wenyuan He, Changliang Zhao, Jianqiu Liu, Zeyu Yang, Yuhang Zhao, and Jian Yang. 2024. "Mathematical Modeling of Transient Submerged Entry Nozzle Clogging and Its Effect on Flow Field, Bubble Distribution and Interface Fluctuation in Slab Continuous Casting Mold" Metals 14, no. 7: 742. https://doi.org/10.3390/met14070742
APA StyleLi, Y., He, W., Zhao, C., Liu, J., Yang, Z., Zhao, Y., & Yang, J. (2024). Mathematical Modeling of Transient Submerged Entry Nozzle Clogging and Its Effect on Flow Field, Bubble Distribution and Interface Fluctuation in Slab Continuous Casting Mold. Metals, 14(7), 742. https://doi.org/10.3390/met14070742





