Studying Plastic Deformation Mechanism in β-Ti-Nb Alloys by Molecular Dynamic Simulations
Abstract
1. Introduction
2. Computational Method
2.1. FS Potential Function
2.2. First-Principles Calculations
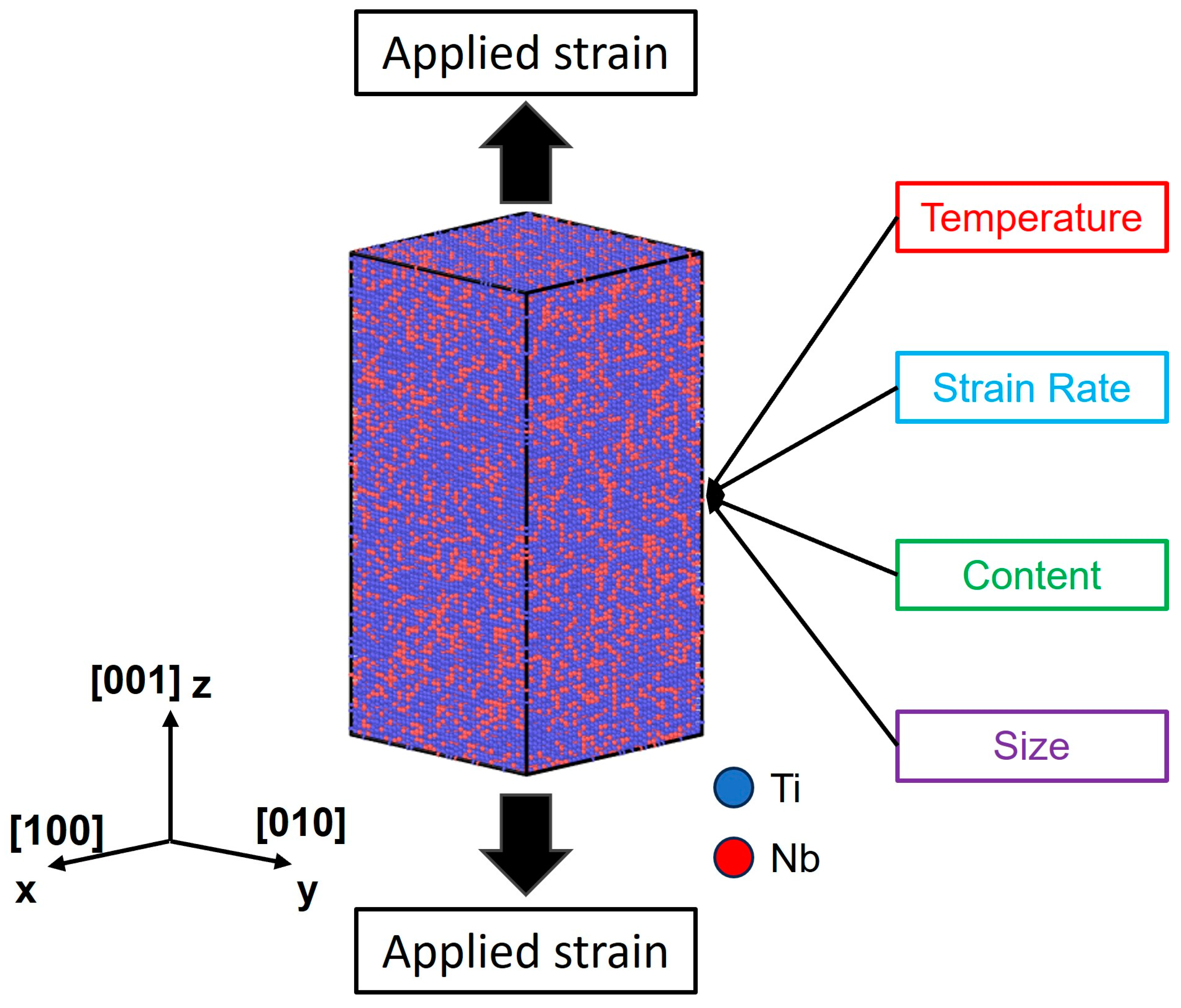
2.3. Molecular Dynamics (MD)
3. Results
3.1. Potential Function Validation
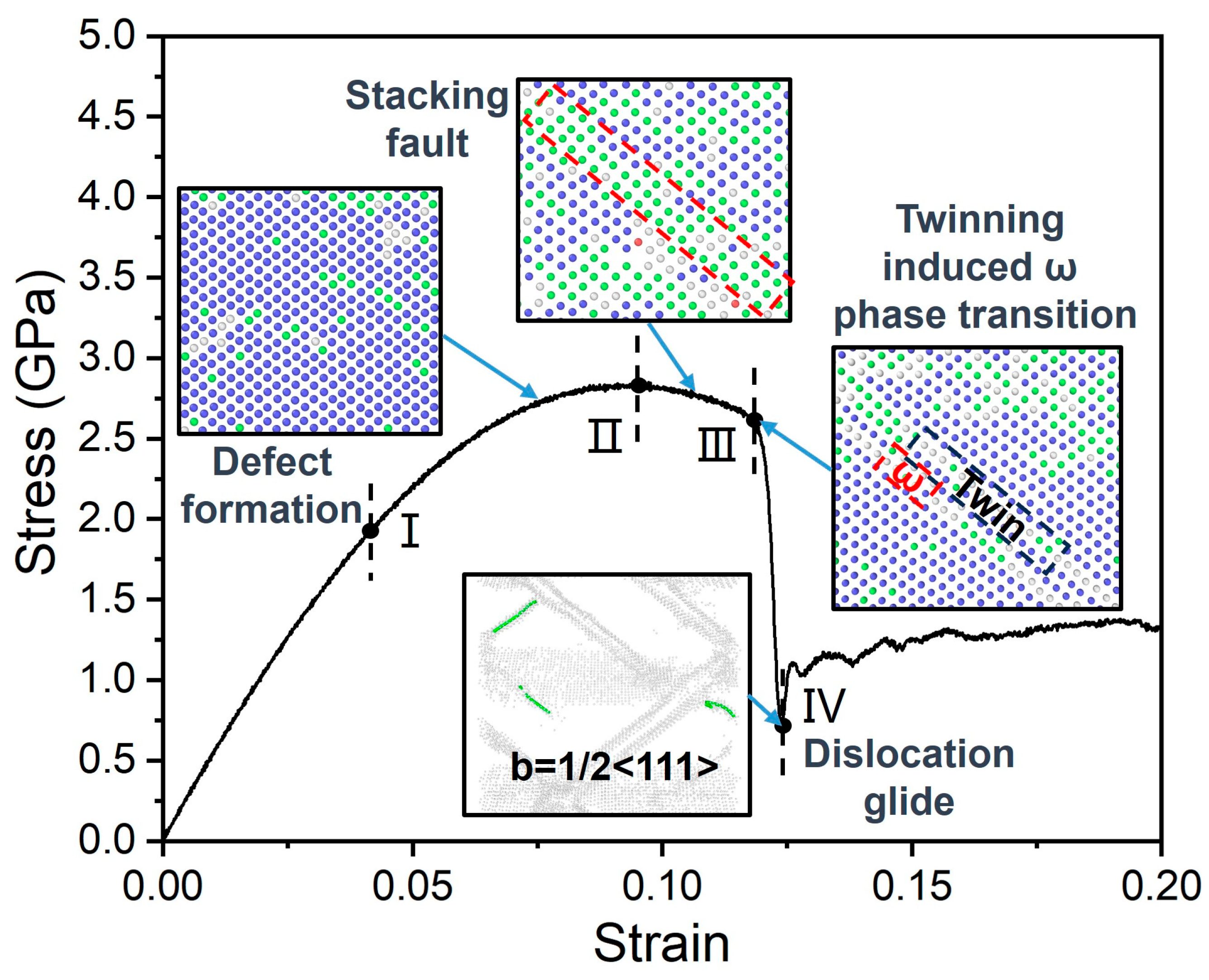
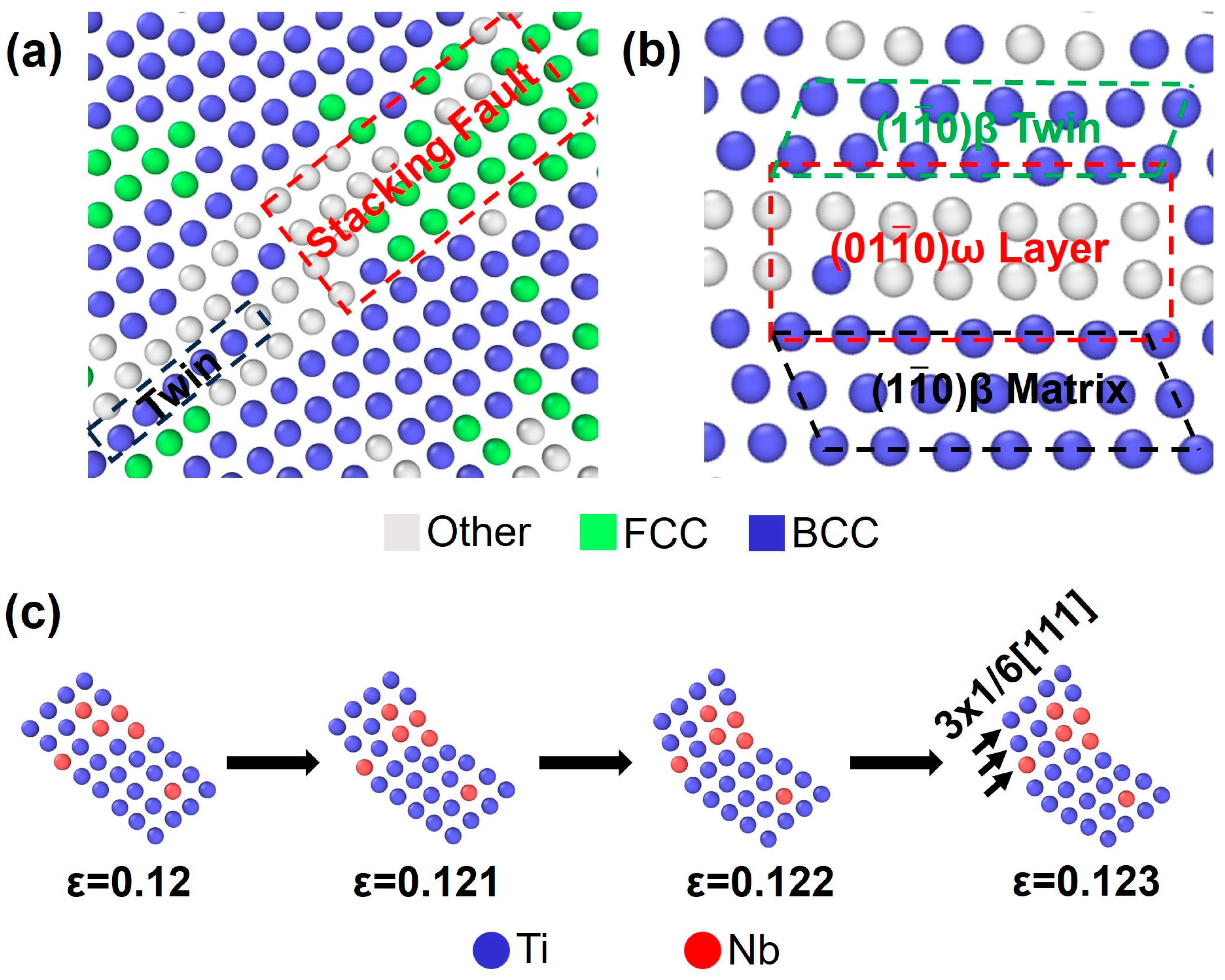
3.2. Analysis of Tensile Behavior
ω-Phase Transformation
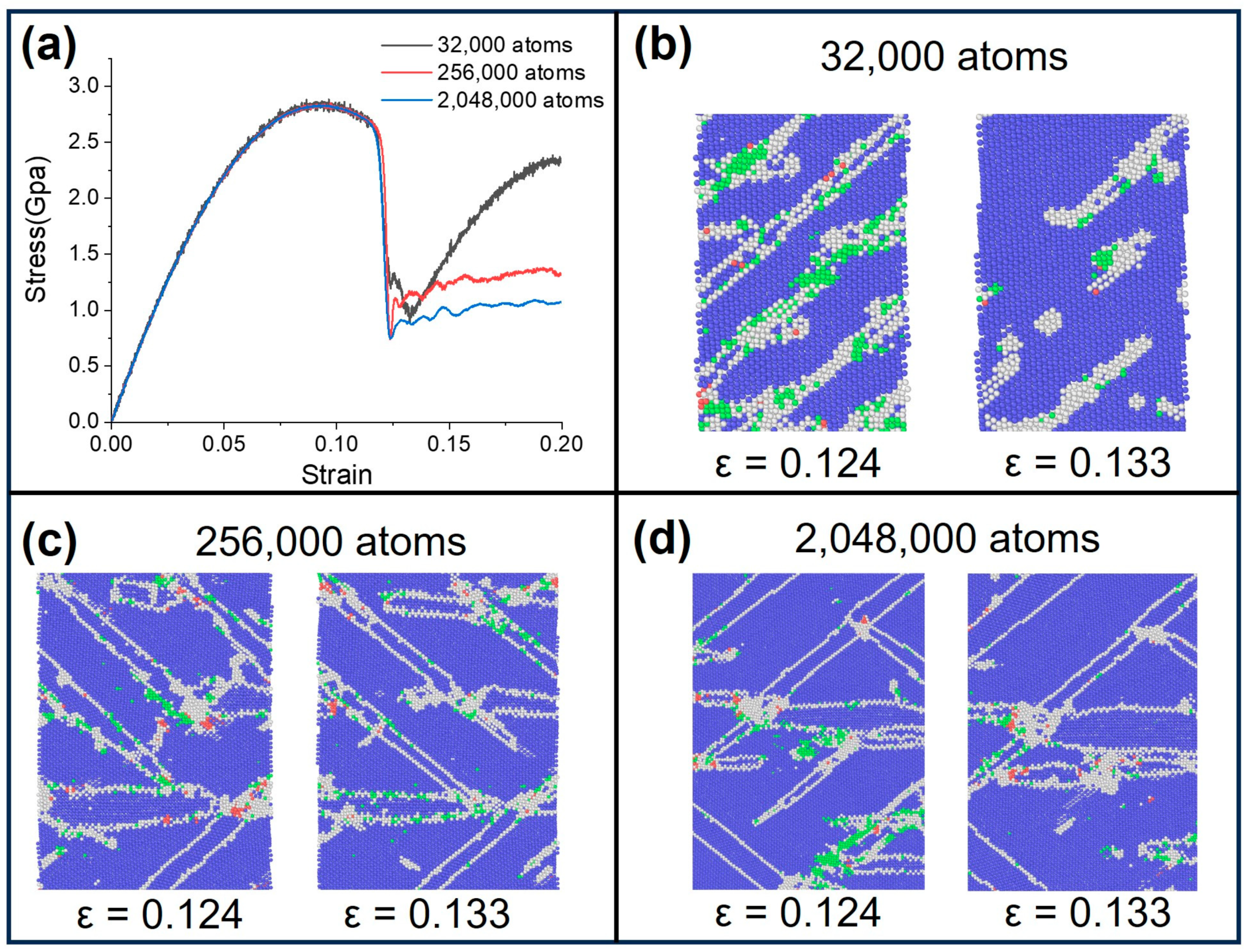
3.3. The Influence of Computational Cell Size on the Tensile Mechanical Properties of Ti-Nb Alloys
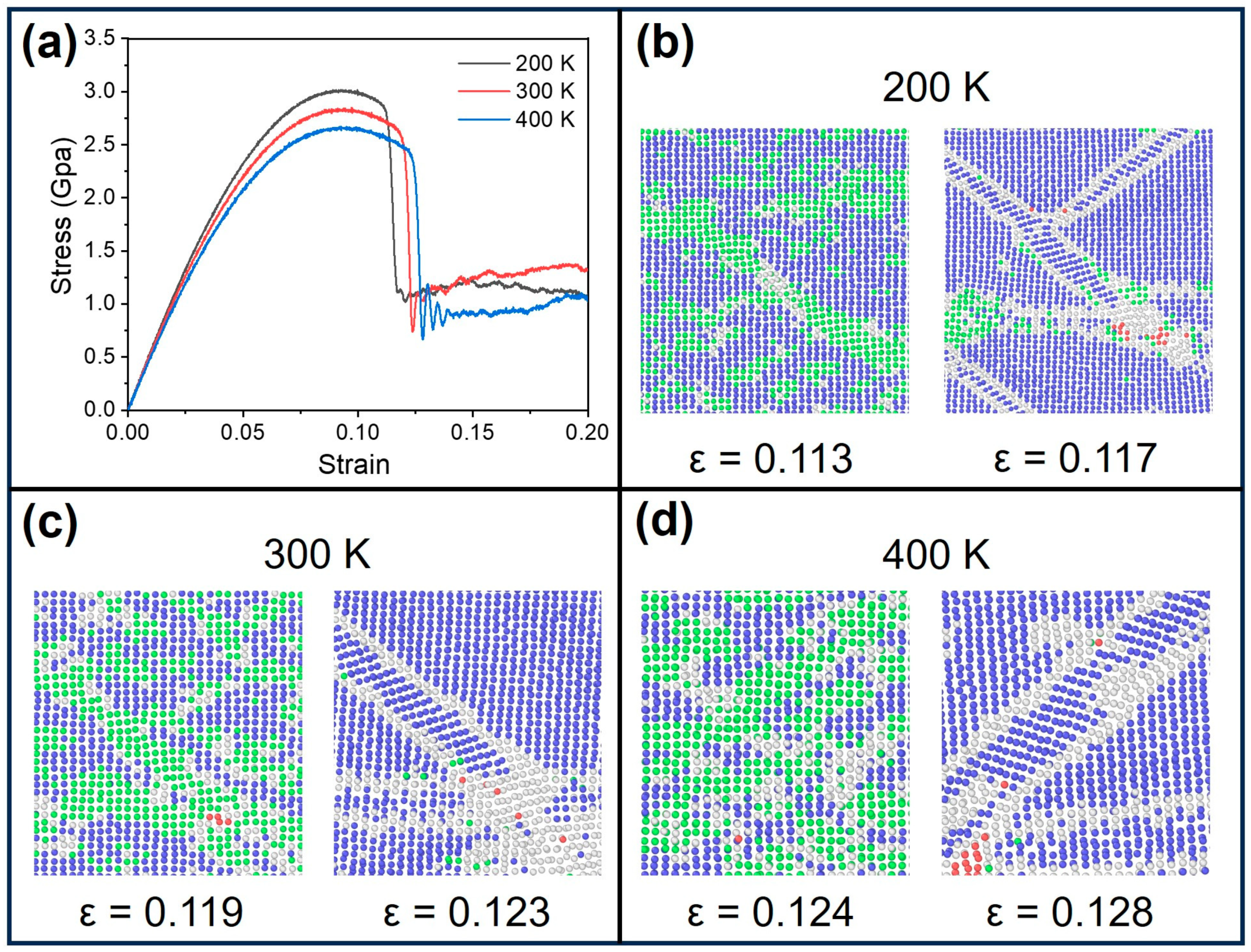
3.4. The Influence of Temperature on the Tensile Mechanical Properties of Ti-Nb Alloys
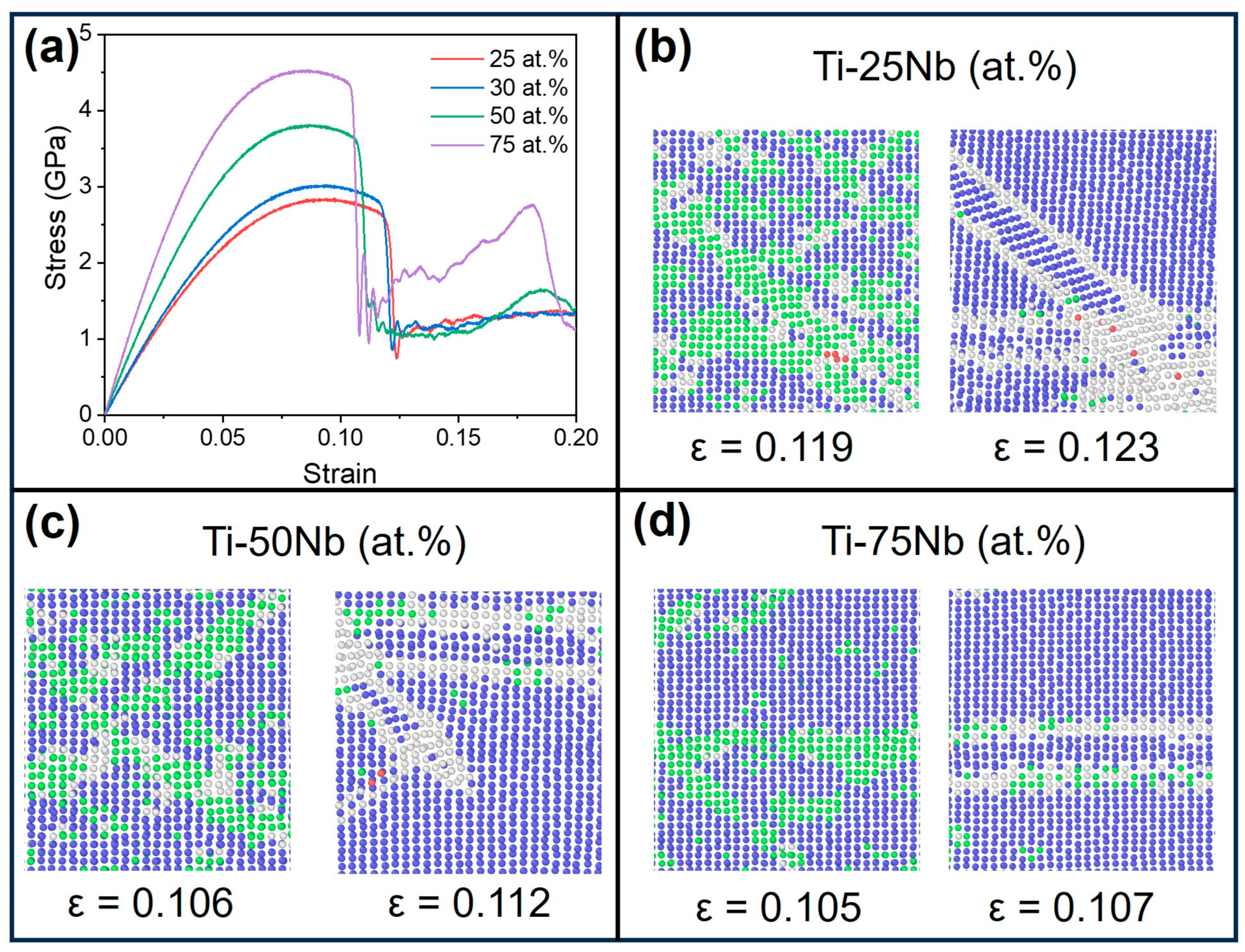
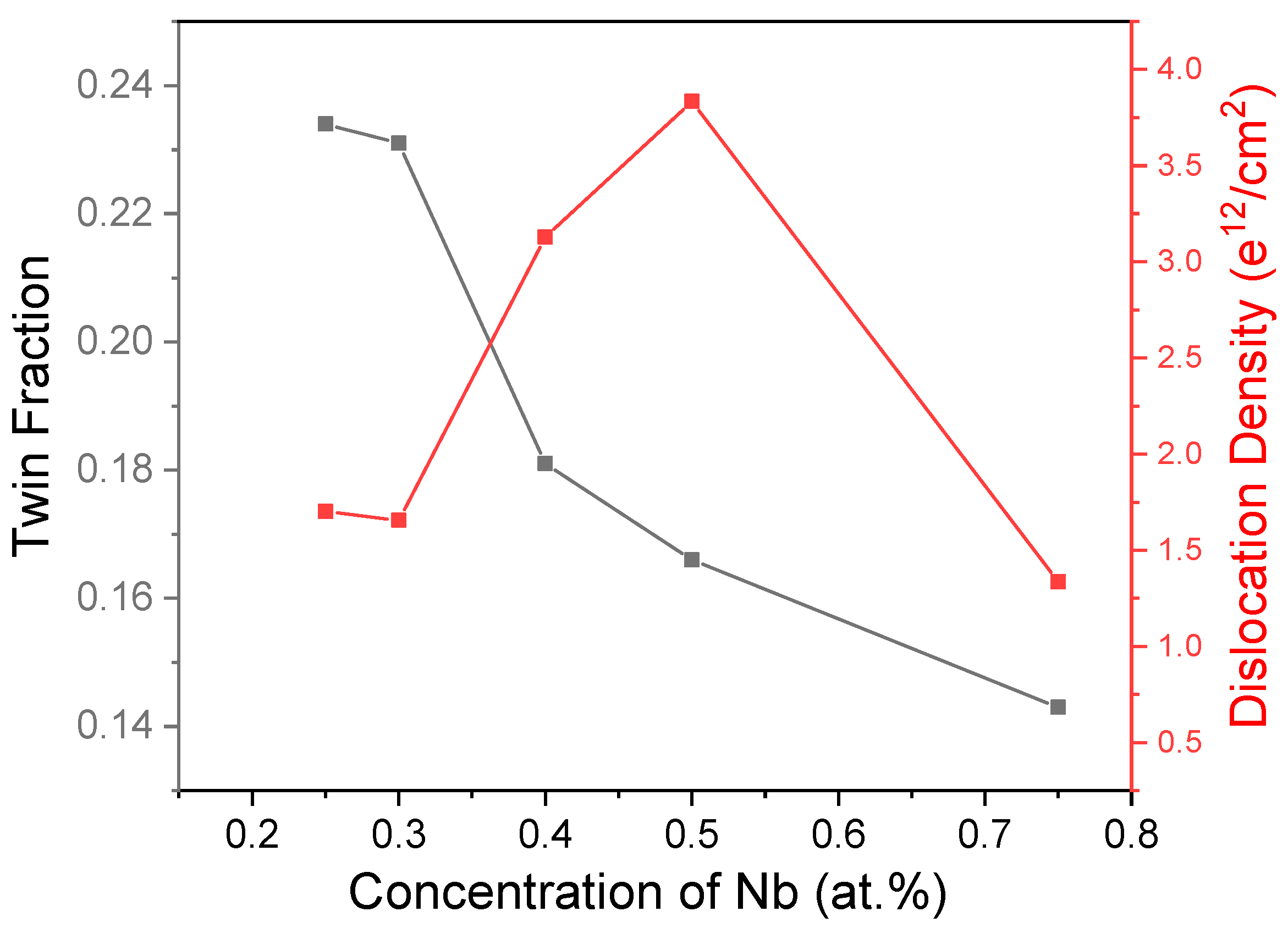
3.5. The Influence of Composition Variation on the Tensile Mechanical Properties of Ti-Nb Alloy
Dislocation and Twinning
3.6. The Influence of Strain Rate on the Tensile Mechanical Properties of Ti-Nb Alloy
4. Conclusions
- The overall deformation process of Ti-Nb alloys involves point-defect generation, followed by twinning and ω-phase transition, and ultimately, dislocation slip occurs. With the increase in the simulation model’s size, the deformed twins’ stability increases, and the strength of the material reduces. In addition, increasing temperature enhances the plasticity and reduces the strength of the material, while increasing composition has the opposite effect on the deformation.
- The elevated stresses resulting from molecular dynamics at higher strain rates cause the <111>{112} slip system to become more pronounced compared to experimental conditions. The interfacial ω-phase induced by the <111>{112} slip system also makes it easier to pass through the energy barrier of the phase transition, making its formation in the matrix easier.
- The predominant deformation mechanisms in Ti-Nb alloys involve twinning and dislocation slip, exhibiting a certain degree of competitiveness. At low Nb content, the number of twins increases with the increase in Nb content, making twinning the dominant mechanism in the overall deformation process. At high Nb content, dislocation slip is still active, but the addition of β-stability elements suppresses twinning deformation. The proportion of twinning decreases, leading to a shift in the plastic deformation mode from twinning to dislocation slip.
- At low strain rates, the twins disappear at a slight strain, while higher strain rates result in an increased number of twins. Moreover, the transition strain interval from stacking faults to twin dislocation slip significantly increases. Various deformation mechanisms work synergistically to enhance the material’s plasticity.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, W.; Lei, J.; Tan, C.; Sun, Q.; Chen, W.; Xiao, L.; Sun, J. A novel high-strength β-Ti alloy with hierarchical distribution of α-phase: The superior combination of strength and ductility. Mater. Des. 2019, 168, 107640. [Google Scholar] [CrossRef]
- Deng, C.; Dong, S.; Tan, W. Modelling for the flow behavior of a new metastable beta titanium alloy by GA-based Arrhenius equation. Mater. Res. Express 2018, 6, 026544. [Google Scholar] [CrossRef]
- Maghsoudlou, A.; Zarei-Hanzaki, A.; Abedi, H.R.; Barabi, A.; Pilehva, F.; Dietrich, D.; Lampke, T. The room temperature tensile deformation behavior of thermomechanically processed β metastable Ti-Nb-Ta-Zr bio-alloy: The role of deformation-induced martensite. Mater. Sci. Eng. A 2018, 738, 15–23. [Google Scholar] [CrossRef]
- Ahmed, M.; Wexler, D.; Casillas, G.; Ivasishin, O.M.; Pereloma, E.V. The influence of β phase stability on deformation mode and compressive mechanical properties of Ti–10V–3Fe–3Al alloy. Acta Mater. 2015, 84, 124–135. [Google Scholar] [CrossRef]
- Hanada, S.; Ozeki, M.; Izumi, O. Deformation characteristics in β phase Ti-Nb alloys. Metall. Trans. A 1985, 16, 789–795. [Google Scholar] [CrossRef]
- Talling, R.J.; Dashwood, R.J.; Jackson, M.; Dye, D. On the mechanism of superelasticity in Gum metal. Acta Mater. 2009, 57, 1188–1198. [Google Scholar] [CrossRef]
- Ballor, J.; Li, T.; Prima, F.; Boehlert, C.J.; Devaraj, A. A review of the metastable omega phase in beta titanium alloys: The phase transformation mechanisms and its effect on mechanical properties. Int. Mater. Rev. 2023, 68, 26–45. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Liu, B. Homogeneous shear-driven reversible α-to-α″phase transformation and superelasticity of titanium investigated by molecular dynamics simulations. Acta Mater. 2015, 93, 105–113. [Google Scholar] [CrossRef]
- Trinkle, D.R.; Hennig, R.G.; Srinivasan, S.G.; Hatch, D.M.; Jones, M.D.; Stokes, H.T.; Albers, R.C.; Wilkins, J.W. New mechanism for the α to ω martensitic transformation in pure titanium. Phys. Rev. Lett. 2003, 91, 025701. [Google Scholar] [CrossRef]
- Kuramoto, S.; Furuta, T.; Hwang, J.; Nishino, K.; Saito, T. Elastic properties of Gum Metal. Mater. Sci. Eng. A 2006, 442, 454–457. [Google Scholar] [CrossRef]
- Zhan, H.; Wang, G.; Kent, D.; Dargusch, M. The dynamic response of a metastable β Ti–Nb alloy to high strain rates at room and elevated temperatures. Acta Mater. 2016, 105, 104–113. [Google Scholar] [CrossRef]
- Ahmed, M.; Wexler, D.; Casillas, G.; Savvakin, D.G.; Pereloma, E.V. Strain rate dependence of deformation-induced transformation and twinning in a metastable titanium alloy. Acta Mater. 2016, 104, 190–200. [Google Scholar] [CrossRef]
- Ren, L.; Xiao, W.; Kent, D.; Wan, M.; Ma, C.; Zhou, L. Simultaneously enhanced strength and ductility in a metastable β-Ti alloy by stress-induced hierarchical twin structure. Scr. Mater. 2020, 184, 6–11. [Google Scholar] [CrossRef]
- Zhang, J.; Fu, Y.; Wu, Y.; Qian, B.; Chen, Z.; Inoue, A.; Wu, Y.; Yang, Y.; Sun, F.; Li, J.; et al. Hierarchical {332}<113> twinning in a metastable β Ti-alloy showing tolerance to strain localization. Mater. Res. Lett. 2020, 8, 247–253. [Google Scholar] [CrossRef]
- Rastogi, A.; Neelakantan, S. Enhanced thermo-mechanical processing through stress-induced martensitic transformation and its effect on grain refinement in metastable β titanium alloys. Scr. Mater. 2023, 226, 115222. [Google Scholar] [CrossRef]
- Fu, Y.; Xiao, W.; Rong, J.; Ren, L.; Peng, H.; Wen, Y.; Zhao, X.; Ma, C. Achieving large near-linear elasticity, low modulus, and high strength in a metastable β-Ti alloy by mild cold rolling. J. Mater. Sci. Technol. 2024, 189, 1–12. [Google Scholar] [CrossRef]
- Jamhari, F.I.; Foudzi, F.M.; Buhairi, M.A.; Sulong, A.B.; Radzuan, N.A.M.; Muhamad, N.; Mohamed, I.F.; Jamadon, N.H.; Tan, K.S. Influence of Heat Treatment Parameters on Microstructure and Mechanical Performance of Titanium Alloy: A Brief Review. J. Mater. Res. Technol. 2023, 24, 4091–4110. [Google Scholar] [CrossRef]
- Pilz, S.; Hariharan, A.; Günther, F.; Zimmermann, M.; Gebert, A. Influence of isothermal omega precipitation aging on deformation mechanisms and mechanical properties of a β-type Ti-Nb alloy. J. Alloys Compd. 2023, 930, 167309. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, X.Z.; Song, T.; Lu, S.L.; Dong, T.; Tang, H.P.; Qian, M. Laser directed energy deposition of Ti-1Al-8V-5Fe alloy: From zero to significant tensile plasticity. Scr. Mater. 2024, 239, 115814. [Google Scholar] [CrossRef]
- Ellis, D.E.; Painter, G.S. Discrete variational method for the energy-band problem with general crystal potentials. Phys. Rev. B 1970, 2, 2887. [Google Scholar] [CrossRef]
- Slater, J.C.; Phillips, J.C. Quantum Theory of Molecules and Solids Vol. 4: The Self Consistent Field for Molecules and Solids. Phys. Today 1974, 27, 49–50. [Google Scholar] [CrossRef]
- Morinaga, M.; Yukawa, H. Alloy design with the aid of molecular orbital method. Bull. Mater. Sci. 1997, 20, 805–815. [Google Scholar] [CrossRef]
- Abdel-Hady, M.; Hinoshita, K.; Morinaga, M. Morinaga. General approach to phase stability and elastic properties of β-type Ti-alloys using electronic parameters. Scr. Mater. 2006, 55, 477–480. [Google Scholar] [CrossRef]
- Bönisch, M.; Panigrahi, A.; Calin, M.; Waitz, T.; Zehetbauer, M.; Skrotzki, W.; Eckert, J. Thermal stability and latent heat of Nb–rich martensitic Ti-Nb alloys. J. Alloys Compd. 2017, 697, 300–309. [Google Scholar] [CrossRef]
- Qiu, R.; Chen, Y.; Liao, X.; Lin, Y.; Dou, Y.; He, X.; Yang, W.; Hu, W.; Deng, H. Development of a semi-empirical interatomic potential appropriate for the radiation defects in V-Ti-Ta-Nb high entropy alloy. J. Phys. Condens. Matter 2022, 35, 055701. [Google Scholar] [CrossRef]
- Finnis, M.W.; Sinclair, J.E. A simple empirical N-body potential for transition metals. Philos. Mag. A 1984, 50, 45–55. [Google Scholar] [CrossRef]
- Ackland, G.J.; Thetford, R. An improved N-body semi-empirical model for body-centred cubic transition metals. Philos. Mag. A 1987, 56, 15–30. [Google Scholar] [CrossRef]
- Bonny, G.; Pasianot, R.C. Gauge transformations to combine multi-component many-body interatomic potentials. Philos. Mag. Lett. 2010, 90, 559–563. [Google Scholar] [CrossRef]
- Johnson, R.A.; Oh, D.J. Analytic embedded atom method model for bcc metals. J. Mater. Res. 1989, 4, 1195–1201. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Larsen, P.M.; Schmidt, S.; Schiøtz, J. Robust structural identification via polyhedral template matching. Model. Simul. Mater. Sci. Eng. 2016, 24, 055007. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Huang, J.; Xing, H.; Sun, J. Structural stability and generalized stacking fault energies in β Ti Nb alloys: Relation to dislocation properties. Scr. Mater. 2012, 66, 682–685. [Google Scholar] [CrossRef]
- Kim, H.Y.; Ikehara, Y.; Kim, J.I.; Hosoda, H.; Miyazaki, S. Martensitic transformation, shape memory effect and superelasticity of Ti–Nb binary alloys. Acta Mater. 2006, 54, 2419–2429. [Google Scholar] [CrossRef]
- Ikehata, H.; Nagasako, N.; Furuta, T.; Fukumoto, A.; Miwa, K.; Saito, T. First-principles calculations for development of low elastic modulus Ti alloys. Phys. Rev. B 2004, 70, 174113. [Google Scholar] [CrossRef]
- Marker, C.; Shang, S.L.; Zhao, J.C.; Liu, Z.K. Effects of alloying elements on the elastic properties of bcc Ti-X alloys from first-principles calculations. Comput. Mater. Sci. 2018, 142, 215–226. [Google Scholar] [CrossRef]
- Nagasako, N.; Asahi, R.; Hafner, J. Ideal tensile and shear strength of a gum metal approximant: Ab initio density functional calculations. Phys. Rev. B 2012, 85, 024122. [Google Scholar] [CrossRef]
- Ju, S.P.; Li, C.C. Role of Local FCC Structure to the BCC Polycrystalline NbMoTaWV High Entropy Refractory Alloy under Plastic Deformation. Phys. Status Solidi A 2022, 219, 2100834. [Google Scholar] [CrossRef]
- Machová, A.; Beltz, G.E.; Chang, M. Chang. Atomistic simulation of stacking fault formation in bcc iron. Model. Simul. Mater. Sci. Eng. 1999, 7, 949. [Google Scholar] [CrossRef]
- Zhan, H.; Zeng, W.; Wang, G.; Kent, D.; Dargusch, M. On the deformation mechanisms and strain rate sensitivity of a metastable β Ti–Nb alloy. Scr. Mater. 2015, 107, 34–37. [Google Scholar] [CrossRef]
- Chen, C.Q.; Florando, J.N.; Kumar, M.; Ramesh, K.T.; Hemker, K.J. Incipient deformation twinning in dynamically sheared bcc tantalum. Acta Mater. 2014, 69, 114–125. [Google Scholar] [CrossRef]
- Sleeswyk, A.W. ½< 111> screw dislocations and the nucleation of {112}< 111> twins in the bcc lattice. Philos. Mag. 1963, 8, 1467–1486. [Google Scholar] [CrossRef]
- Marian, J.; Cai, W.; Bulatov, V.V. Dynamic transitions from smooth to rough to twinning in dislocation motion. Nat. Mater. 2004, 3, 158–163. [Google Scholar] [CrossRef]
- Lai, M.J.; Tasan, C.C.; Zhang, J.; Grabowski, B.; Huang, L.F.; Raabe, D. Origin of shear induced β to ω transition in Ti–Nb-based alloys. Acta Mater. 2015, 92, 55–63. [Google Scholar] [CrossRef]
- Moreno, J.G.; Bönisch, M.; Panagiotopoulos, N.T.; Calin, M.; Papageorgiou, D.G.; Gebert, A.; Eckert, J.; Evangelakis, G.A.; Lekka, C.E. Ab-initio and experimental study of phase stability of Ti Nb alloys. J. Alloys Compd. 2017, 696, 481–489. [Google Scholar] [CrossRef]
- Samiee, A.; Casillas, G.; Ahmed, M.; Savvakin, D.G.; Naseri, R.; Pereloma, E. Formation of deformation-induced products in a metastable-β titanium alloy during high temperature compression. Metals 2018, 8, 100. [Google Scholar] [CrossRef]
- Ehemann, R.C.; Wilkins, J.W. Force-matched empirical potential for martensitic transitions and plastic deformation in Ti-Nb alloys. Phys. Rev. B 2017, 96, 184105. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, S.Q.; Li, G.P.; Li, Y.L.; Lu, Y.F.; Yang, K.; Ge, P. Evolution of deformation mechanisms of Ti–22.4 Nb–0.73 Ta–2Zr–1.34 O alloy during straining. Acta Mater. 2010, 58, 2778–2787. [Google Scholar] [CrossRef]
- Li, Z.; Gao, Y.; Zhan, S.; Fang, H.; Zhang, Z. Molecular dynamics study on temperature and strain rate dependences of mechanical properties of single crystal Al under uniaxial loading. AIP Adv. 2020, 10, 075321. [Google Scholar] [CrossRef]
- Morkina, A.Y.; Babicheva, R.I.; Korznikova, E.A.; Enikeev, N.A.; Edalati, K.; Dmitriev, S.V. A Molecular Dynamics Simulation to Shed Light on the Mechanical Alloying of an Al-Zr Alloy Induced by Severe Plastic Deformation. Metals 2023, 13, 1595. [Google Scholar] [CrossRef]
- Huang, X.; Li, J.S.; Lai, M.J. Influences of grain size on the deformation behavior of a twinning-induced plasticity metastable β titanium alloy. J. Alloys Compd. 2023, 937, 168274. [Google Scholar] [CrossRef]
- Lu, H.; Shi, H.; Zhang, H.; Ma, W.; Guo, Y.; Liang, S.; Zhang, J.; Zhang, X.; Zhang, S.; Liu, R. Enhanced yield strength by fine grain strengthening and TRIP/TWIP effect of metastable β-type Ti-4V-2Mo-2Fe alloy with high ductility. Mater. Charact. 2024, 207, 113591. [Google Scholar] [CrossRef]
- Li, L.; Han, M. Molecular dynamics simulations on tensile behaviors of single-crystal bcc Fe nanowire: Effects of strain rates and thermal environment. Appl. Phys. A 2017, 123, 450. [Google Scholar] [CrossRef]
- Veerababu, J.; Nagesha, A. Competition between full slip and twinning in BCC-Fe: Effect of preloaded stress and temperature. J. Appl. Phys. 2023, 134, 055102. [Google Scholar] [CrossRef]
- Hanada, S.; Izumi, O. Correlation of tensile properties, deformation modes, and phase stability in commercial β-phase titanium alloys. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 1987, 18, 265–271. [Google Scholar] [CrossRef]
- Manero, J.M.; Gil, F.J.; Planell, J.A. Deformation mechanisms of Ti–6Al–4V alloy with a martensitic microstructure subjected to oligocyclic fatigue. Acta Mater. 2000, 48, 3353–3359. [Google Scholar] [CrossRef]
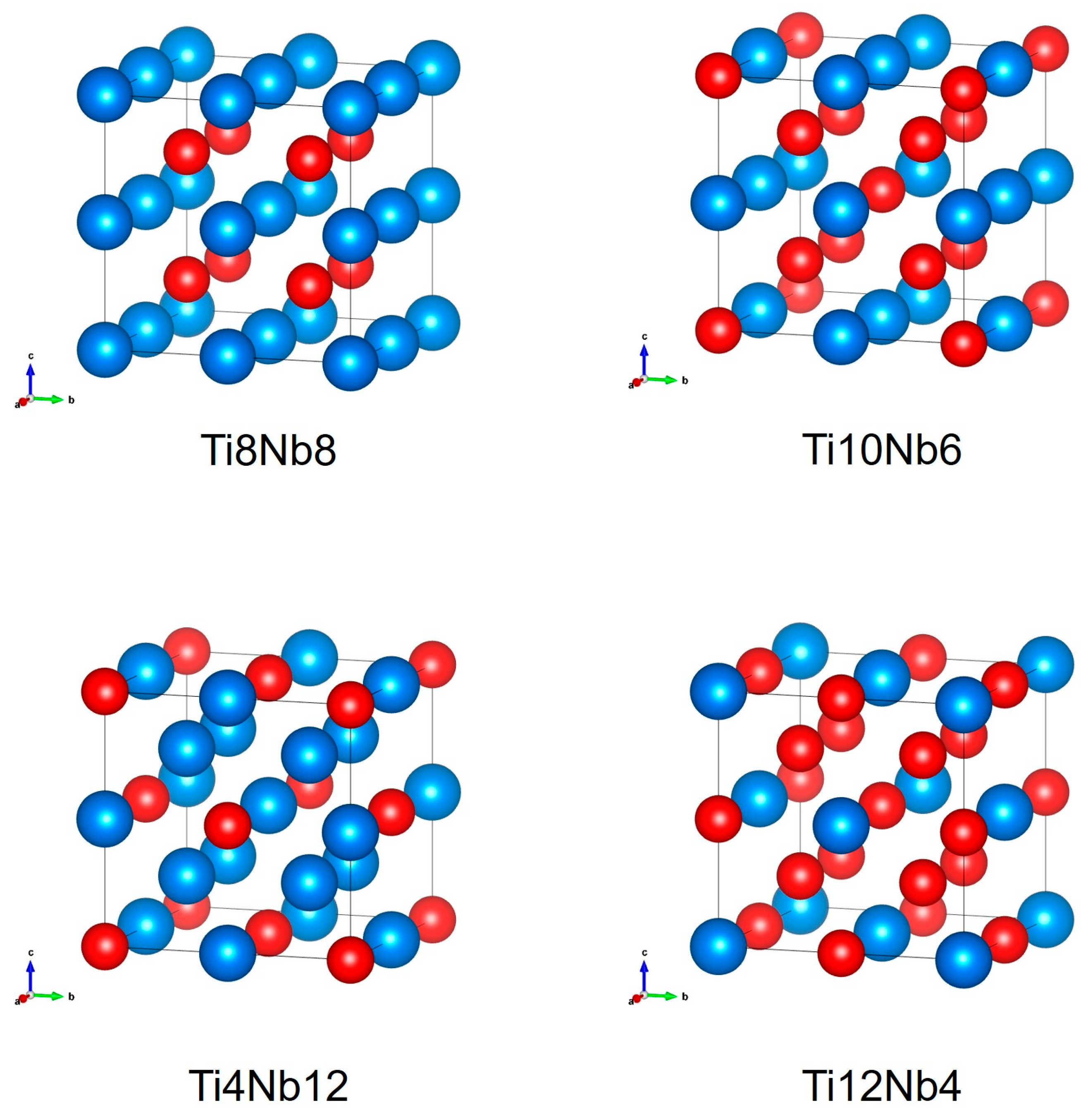

| Ti4Nb12 | Ti8Nb8 | Ti10Nb6 | Ti12Nb4 | ||
|---|---|---|---|---|---|
| Lattice Constant/Å | MD (This work) | 3.317 | 3.324 | 3.278 | 3.265 |
| DFT (This work) | 3.302 | 3.271 | 3.267 | 3.264 | |
| [38] | 3.289 | 3.286 | |||
| Cohesive Energy/eV | MD (This work) | −6.838 | −6.038 | −5.739 | −5.429 |
| DFT (This work) | −6.554 | −6.185 | −6.020 | −5.855 |
| γus on {110} (J m−2) | γus on {112} (J m−2) | |
|---|---|---|
| Ti-25Nb (at.%) | 0.408 | 0.381 |
| DFT [37] | 0.307 | 0.296 |
| Ti-50Nb (at.%) | 0.501 | 0.459 |
| DFT [37] | 0.329 | 0.371 |
| Ti-75Nb (at.%) | 0.581 | 0.531 |
| DFT [37] | 0.494 | 0.534 |
| Nb | 0.657 | 0.714 |
| DFT [37] | 0.678 | 0.781 |
| Content | Elastic Constant | This Work | [39] | [40] |
|---|---|---|---|---|
| Ti-25Nb (at.%) | C11 | 123.9 | 128.5 | 140 ± 11 |
| C12 | 85.5 | 115.5 | 116 ± 13 | |
| C44 | 51.7 | 14.9 | 34 ± 10 | |
| B | 98.3 | 124 ± 13 | ||
| G | 19.2 | 22 ± 13 | ||
| Ti-50Nb (at.%) | C11 | 167.5 | 155.4 | 181 ± 9 |
| C12 | 88.3 | 124.7 | 121 ± 2 | |
| C44 | 52.2 | 12.8 | 31 ± 10 | |
| B | 114.7 | 141 ± 9 | ||
| G | 39.6 | 31 ± 10 | ||
| Ti-75Nb (at.%) | C11 | 198.1 | 203.5 | 208 ± 3 |
| C12 | 104.0 | 126.8 | 130 ± 4 | |
| C44 | 43.7 | 21.3 | 15 ± 10 | |
| B | 135.4 | 156 ± 4 | ||
| G | 47.1 | 22 ± 10 |
| Computational Cell Size | 32,000 atoms | 256,000 atoms | 2,048,000 atoms |
|---|---|---|---|
| Twinning fraction (%) | 0.109 | 0.252 | 0.263 |
| Temperature | 200 K | 300 K | 400 K |
|---|---|---|---|
| Other structure concentration (%) | 3.1 | 7.9 | 15.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Huang, B.; Hu, W.; Huang, J. Studying Plastic Deformation Mechanism in β-Ti-Nb Alloys by Molecular Dynamic Simulations. Metals 2024, 14, 318. https://doi.org/10.3390/met14030318
Wang H, Huang B, Hu W, Huang J. Studying Plastic Deformation Mechanism in β-Ti-Nb Alloys by Molecular Dynamic Simulations. Metals. 2024; 14(3):318. https://doi.org/10.3390/met14030318
Chicago/Turabian StyleWang, Hongbo, Bowen Huang, Wangyu Hu, and Jian Huang. 2024. "Studying Plastic Deformation Mechanism in β-Ti-Nb Alloys by Molecular Dynamic Simulations" Metals 14, no. 3: 318. https://doi.org/10.3390/met14030318
APA StyleWang, H., Huang, B., Hu, W., & Huang, J. (2024). Studying Plastic Deformation Mechanism in β-Ti-Nb Alloys by Molecular Dynamic Simulations. Metals, 14(3), 318. https://doi.org/10.3390/met14030318







