A Hybrid Design of Experiment Approach in Analyzing the Electrical Discharge Machining Influence on Stir Cast Al7075/B4C Metal Matrix Composites
Abstract
1. Introduction
1.1. Metal Matrix Composites
1.2. Design of Experiments
- -
- OA is applied with the scope to ensure an efficient and balanced testing combination of different levels of factors. The signal-to-noise ratio (SNR) defines the ratio of deviation of the target value to the variability of the experimental values.
- -
- SNR is used to analyze the performance of the processes. There are three objectives of SNR used for the analysis depending upon the nature of response variables [8,9], named as: (i) the smaller the better, (ii) the larger the better, and (iii) the nominal the better. OA and SNR are used in efficient experimentation and analysis of data to assist in decision-making and cost-effective improvements.
2. Materials and Methodology
2.1. Taguchi Method
2.2. Multiple Response Optimization
2.3. Entropy Weight Method Procedure
2.4. Grey Relational Analysis Procedure
- 1.
- Lower the better criterion:
- 2.
- Higher the better criterion
3. Results and Discussion
3.1. Entropy Weight Method
3.2. Grey Relational Analysis
3.3. SEM Analysis
4. Conclusions and Recommendations
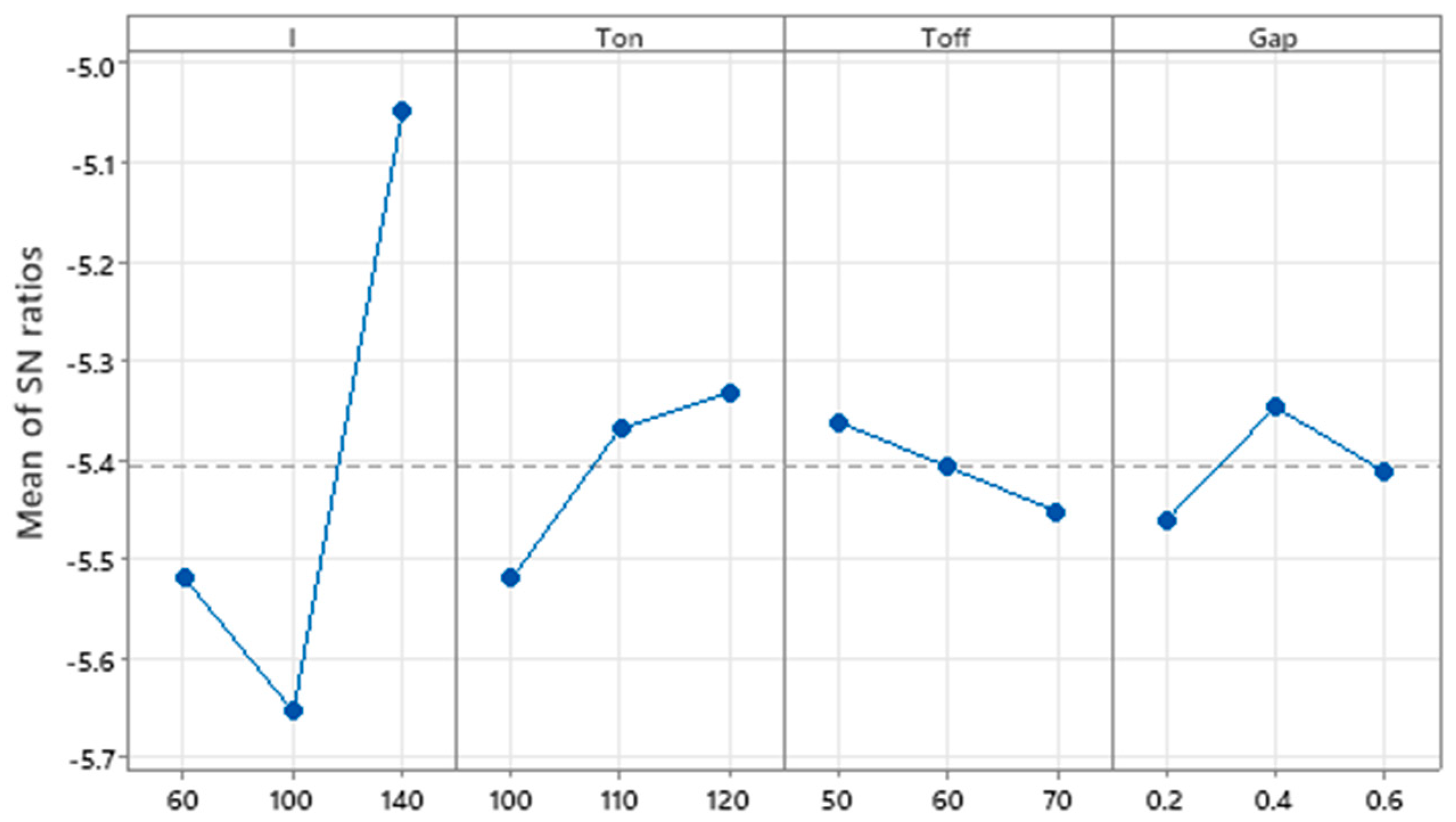
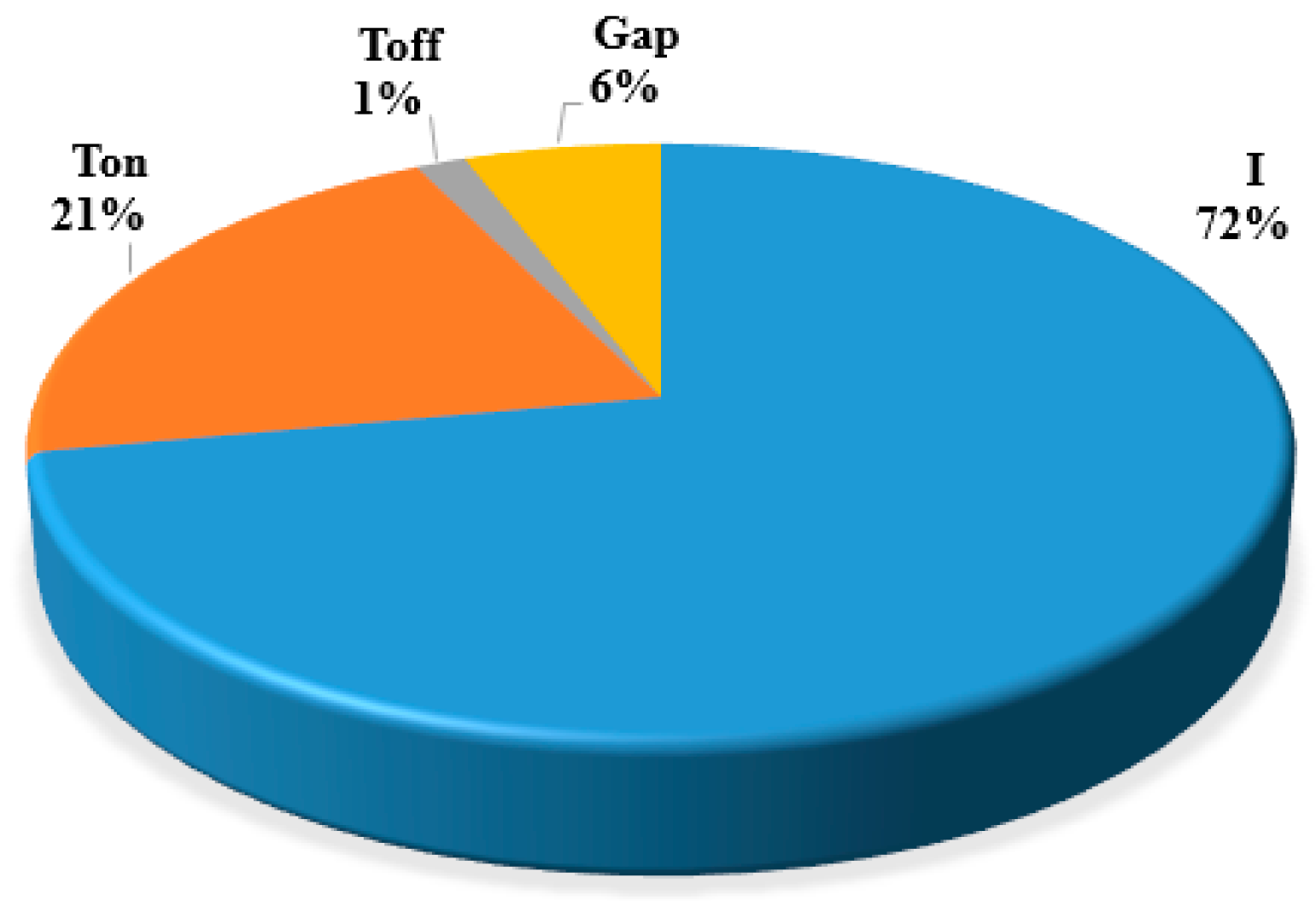
- MRR: All the selected process parameters played a significant role in MRR. The maximum MRR can be achieved at the higher setting of current and pulse ON time, lower setting of pulse OFF time, and electrode gap values. The optimum parameter combination of values for maximum MRR was current = 140 A, Ton = 120 ms, Toff = 50 ms, and Gap = 0.4 mm.
- TWR: The input process parameters current, pulse ON time, pulse off time, and electrode gap contributed to the TWR. The minimum TWR obtained at the combination parameter values was 140 A, 120 ms, 40 ms, and 0.4 mm, respectively.
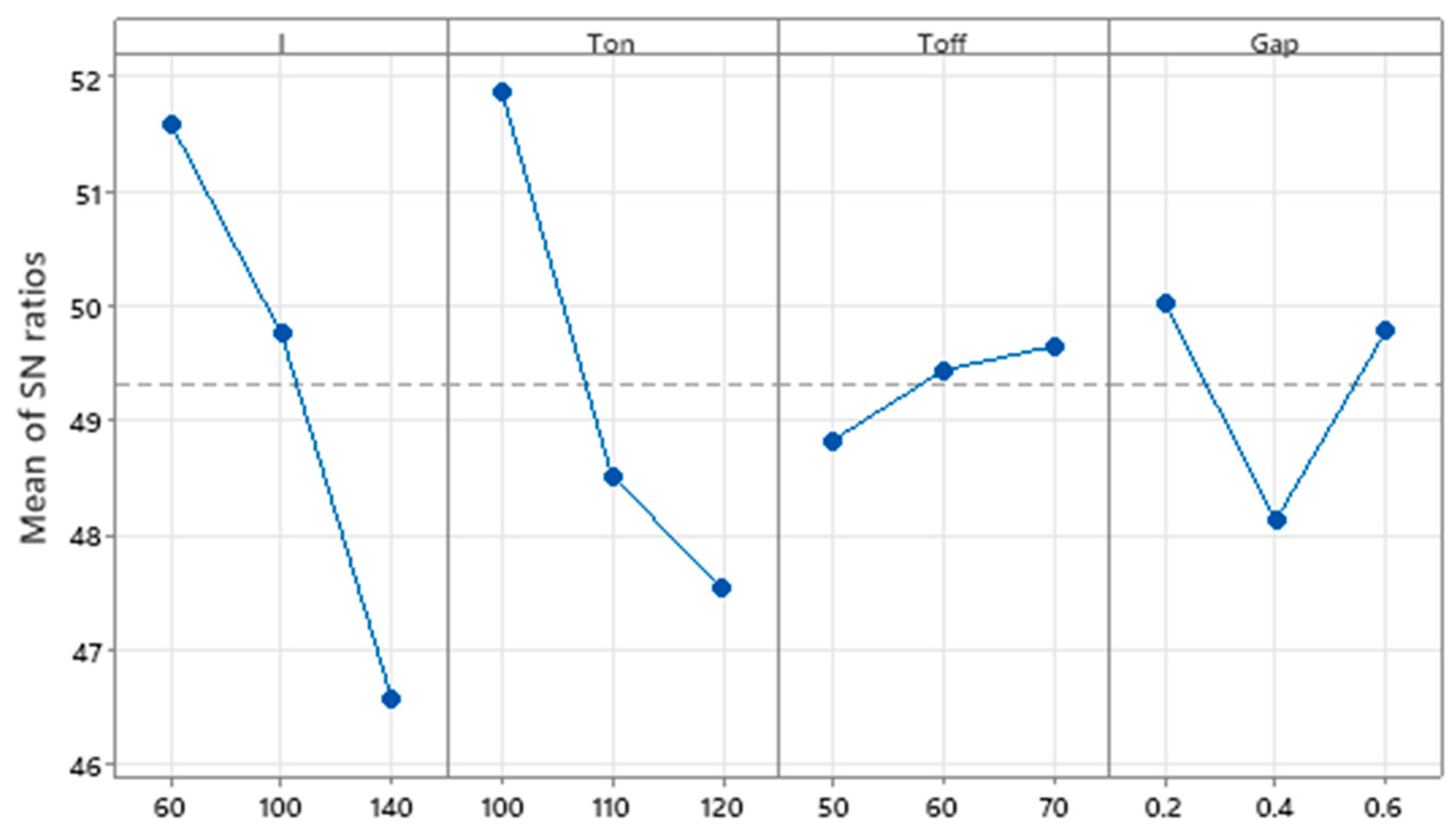
- SR: The current, pulse ON time, and electrode gap were the most significant factors affecting the surface roughness of the machined materials. The optimum surface roughness obtained at the process parameter values were current = 140 A, Ton = 120 ms, Toff = 50 ms, and Gap = 0.6 mm.
- The results showed that an increase in current and pulse ON time increased MRR, TWR, and SR values. An increase in pulse OFF time and electrode gap reduced MRR, TWR, and SR values.
- The weightage of the response parameters, calculated through EWM, had a significant role in the multi-response optimization process. The weightage of the response parameters was MRR = 0.3343, TWR = 0.3314, and SR = 0.3343.
- Grey relational analysis was utilized for the optimization process. The optimum value of the response parameters was MRR=0.5628 mm3/min, TWR = 0.0048 mm3/min, and SR = 4.4034. The optimum process parameter values to obtain better results were current = 140 A, pulse ON time = 120 ms, pulse OFF time = 50 ms, and electrode gap = 0.4 mm.
- The confirmation experiment was conducted based on the optimized process parameter values and the results were compared to the initial parameter values results. The comparison showed the improvement of the Grey response grade of 81%.
- Hybrid multi-objective optimization of the EWM, GRA incorporated with ANOVA technique was applied to analyze the results to determine the optimum parameter combination values to obtain better output results.
- SEM analysis showed optimum parameter level machined surface condition of minimum debris and cracks without recast layer formation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Al7075 | Aluminum 7075 |
| AMCs | Aluminum-based metal matrix composites |
| AlSi | Silicon-reinforced aluminum metal matrix composite |
| ANOVA | Analysis of variance |
| B4C | Boron carbide |
| CNC | Computer numerical controlled |
| DF | Desirability function |
| DoE | Design of experiment |
| ECSM | Electrochemical spark machining |
| EDD | Electric discharge drilling |
| EDDG | Electric discharge diamond grinding |
| EDM | Electrical discharge machining |
| EWR | Electrode or tool wear rate |
| EWM | Entropy weight method |
| Gap | Electrode gap |
| GRA | Grey relational analysis |
| GRG | Grey relational grade |
| I | Current intensity |
| LB | The larger the better (objective) |
| MMCs | Metal matrix composites |
| MRR | Material removal rate |
| OA | Orthogonal array |
| PMEDM | Powder mixed electrical discharge machining |
| RA | Regression analysis |
| RSM | Response surface methodology |
| SB | The smaller the better (objective) |
| SEM | Scanning electron microscope |
| SNR | Signal-to-noise ratio |
| SR | Surface roughness |
| TiC | Titanium carbide |
| Ton | Pulse ON time |
| Toff | Pulse OFF time |
| TOPSIS | Technique for order of preference by similarity to ideal solution |
| TWR | Tool wear rate |
| WGRA | Weighted Grey relational analysis |
References
- Singh, N.K.; Singh, Y.; Sharma, A.; Singla, A.; Negi, P. An Environmental-Friendly Electrical Discharge Machining Using Different Sustainable Techniques: A Review. Adv. Mater. Process. Technol. 2021, 7, 537–566. [Google Scholar] [CrossRef]
- Bodukuri, A.K.; Chandramouli, S.; Eswaraiah, K.; Laxman, J. Experimental Investigation and Optimization of EDM Process Parameters on Aluminum Metal Matrix Composite. Mater. Today Proc. 2018, 5, 24731–24740. [Google Scholar] [CrossRef]
- Singh, P.N.; Raghukandan, K.; Pai, B.C. Optimization by Grey Relational Analysis of EDM Parameters on Machining Al–10% SiCP Composites. J. Mater. Process. Technol. 2004, 155, 1658–1661. [Google Scholar] [CrossRef]
- Tharian, B.K.; Jacob, E.; Johnson, J.; Hari, V. Multi-Objective Parametric Optimization in EDM Using Grey Relational Analysis. Mater. Today Proc. 2019, 16, 1013–1019. [Google Scholar] [CrossRef]
- Mohankumar, V.; Soorya Prakash, K.; Sendhil Kumar, S. Investigation of Electrical Discharge Machining Properties of Reinforced Cryogenic Treated AA7075 Composites. Chiang Mai J. Sci. 2022, 49, 1184–1204. [Google Scholar]
- Devi, M.B.; Birru, A.K.; Bannaravuri, P.K. The Recent Trends of EDM Applications and Its Relevance in the Machining of Aluminium MMCs: A Comprehensive Review. Mater. Today Proc. 2021, 47, 6870–6873. [Google Scholar] [CrossRef]
- Nahak, B.; Gupta, A. A Review on Optimization of Machining Performances and Recent Developments in Electro Discharge Machining. Manuf. Rev. 2019, 6, 2. [Google Scholar] [CrossRef]
- Singh, V.; Bhandari, R.; Yadav, V.K. An Experimental Investigation on Machining Parameters of AISI D2 Steel Using WEDM. Int. J. Adv. Manuf. Technol. 2017, 93, 203–214. [Google Scholar] [CrossRef]
- Chaudhari, R.; Vora, J.; Parikh, D.M.; Wankhede, V.; Khanna, S. Multi-Response Optimization of WEDM Parameters Using an Integrated Approach of RSM–GRA Analysis for Pure Titanium. J. Inst. Eng. (India) Ser. D 2020, 101, 117–126. [Google Scholar] [CrossRef]
- Gopal, P.M.; Prakash, K.S.; Jayaraj, S. WEDM of Mg/CRT/BN Composites: Effect of Materials and Machining Parameters. Mater. Manuf. Process. 2018, 33, 77–84. [Google Scholar] [CrossRef]
- Kavimani, V.; Prakash, K.S.; Thankachan, T. Multi-Objective Optimization in WEDM Process of Graphene–SiC-Magnesium Composite through Hybrid Techniques. Measurement 2019, 145, 335–349. [Google Scholar] [CrossRef]
- Alqahtani, K.N.; Dabwan, A.; Abualsauod, E.H.; Anwar, S.; Al-Samhan, A.M.; Kaid, H. Multi-Response Optimization of Additively Manufactured Ti6Al4V Component Using Grey Relational Analysis Coupled with Entropy Weights. Metals 2023, 13, 1130. [Google Scholar] [CrossRef]
- Abhilash, P.M.; Chakradhar, D. Multi-Response Optimization of Wire EDM of Inconel 718 Using a Hybrid Entropy Weighted GRA-TOPSIS Method. Process Integr. Optim. Sustain. 2022, 6, 61–72. [Google Scholar] [CrossRef]
- Mahapatra, S.S.; Patnaik, A. Optimization of Wire Electrical Discharge Machining (WEDM) Process Parameters Using Taguchi Method. Int. J. Adv. Manuf. Technol. 2007, 34, 911–925. [Google Scholar] [CrossRef]
- Li, H.; Li, X.; Liu, X.; Li, H.; Bu, X.; Chen, S.; Lyu, Q. Evaluation and Prediction Models for Blast Furnace Operating Status Based on Big Data Mining. Metals 2023, 13, 1250. [Google Scholar] [CrossRef]
- Mohanty, S.; Mishra, A.; Nanda, B.K.; Routara, B.C. Multi-Objective Parametric Optimization of Nano Powder Mixed Electrical Discharge Machining of AlSiCp Using Response Surface Methodology and Particle Swarm Optimization. Alex. Eng. J. 2018, 57, 609–619. [Google Scholar] [CrossRef]
- Majumder, A.; Das, P.K.; Majumder, A.; Debnath, M. An Approach to Optimize the EDM Process Parameters Using Desirability-Based Multi-Objective PSO. Prod. Manuf. Res. 2014, 2, 228–240. [Google Scholar] [CrossRef]
- Lin, J.L.; Lin, C.L. The Use of the Orthogonal Array with Grey Relational Analysis to Optimize the Electrical Discharge Machining Process with Multiple Performance Characteristics. Int. J. Mach. Tools Manuf. 2002, 42, 237–244. [Google Scholar] [CrossRef]
- Singh, S.; Doddamani, M.; Powar, S. Multi-Objective Optimization of Machining Parameter in Laser Drilling of Glass Microballoon/Epoxy Syntactic Foams. J. Mater. Res. Technol. 2023, 23, 3869–3879. [Google Scholar] [CrossRef]
- Jung, J.H.; Kwon, W.T. Optimization of EDM Process for Multiple Performance Characteristics Using Taguchi Method and Grey Relational Analysis. J. Mech. Sci. Technol. 2010, 24, 1083–1090. [Google Scholar] [CrossRef]
- Lin, C.L.; Lin, J.L.; Ko, T.C. Optimisation of the EDM Process Based on the Orthogonal Array with Fuzzy Logic and Grey Relational Analysis Method. Int. J. Adv. Manuf. Technol. 2002, 19, 271–277. [Google Scholar] [CrossRef]
- Rajyalakshmi, G.; Venkata Ramaiah, P. Multiple Process Parameter Optimization of Wire Electrical Discharge Machining on Inconel 825 Using Taguchi Grey Relational Analysis. Int. J. Adv. Manuf. Technol. 2013, 69, 1249–1262. [Google Scholar] [CrossRef]
- Pawade, R.S.; Joshi, S.S. Multi-Objective Optimization of Surface Roughness and Cutting Forces in High-Speed Turning of Inconel 718 Using Taguchi Grey Relational Analysis (TGRA). Int. J. Adv. Manuf. Technol. 2011, 56, 47–62. [Google Scholar] [CrossRef]
- Chauhan, N.K.; Das, A.K.; Rajesha, S. Optimization of Process Parameters Using Grey Relational Analysis and Taguchi Method during Micro-EDMing. Mater. Today Proc. 2018, 5, 27178–27184. [Google Scholar] [CrossRef]
- Gohil, V.; Puri, Y.M. Multi-Objective Optimization of Material Removal Rate and Surface Roughness in Electrical Discharge Turning of Titanium Alloy (Ti-6Al-4V). Indian J. Eng. Mater. Sci. (IJEMS) 2017, 24, 429–436. [Google Scholar]
- Moghaddam, A.O.; Shaburova, N.; Naseri, M.; Latfulina, Y.; Samodurova, M.; Krymsky, V.; Litvinyuk, K.; Trofimov, E. Detonation Spraying of Ni-Based Composite Coatings Reinforced by High-Entropy Intermetallic Particles. Metals 2023, 13, 1807. [Google Scholar] [CrossRef]
- Shah, A.H.A.; Azmi, A.I.; Khalil, A.N.M. Grey Relational Analyses for Multi-Objective Optimization of Turning S45C Carbon Steel. IOP Conf. Ser. Mater. Sci. Eng. 2016, 114, 12023. [Google Scholar] [CrossRef]
- Hsiao, Y.F.; Tarng, Y.S.; Huang, W.J. Optimization of Plasma Arc Welding Parameters by Using the Taguchi Method with the Grey Relational Analysis. Mater. Manuf. Process. 2007, 23, 51–58. [Google Scholar] [CrossRef]
- Azmi, A.I. Multi-Objective Optimisation of Machining Fibre Reinforced Composites. J. App. Sci. 2012, 12, 2360–2367. [Google Scholar] [CrossRef]
- Kalyon, A. Optimization of Machining Parameters in Sinking Electrical Discharge Machine of Caldie Plastic Mold Tool Steel. Sādhanā 2020, 45, 65. [Google Scholar] [CrossRef]
- Ganapathy, S.; Palanivendhan, M.; Susitra, K.; Balasubramanian, P. Optimization of Machining Parameters in EDM Using Taguchi Based Grey Relational Analysis. Mater. Today Proc. 2023, 82, 43–46. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Bara, A.; Bhaskar, P.; Sai, K.K.; Rajiv, L.S.; Singh, S.L. Optimization of Process Parameters Based on RSM and GRA Method for Machining of Inconel-600 by Electric Discharge Machining. Mater. Today Proc. 2021, 44, 2551–2555. [Google Scholar] [CrossRef]
- Paulson, D.M.; Saif, M.; Zishan, M. Optimization of Wire-EDM Process of Titanium Alloy-Grade 5 Using Taguchi’s Method and Grey Relational Analysis. Mater. Today Proc. 2023, 72, 144–153. [Google Scholar] [CrossRef]
- Palanisamy, A.; Rekha, R.; Sathiya Narayanan, C. Multi-Objective Optimization of EDM Parameters Using Grey Relational Analysis for Titanium Alloy (Ti–6Al–4V). Appl. Mech. Mater. 2014, 592, 540–544. [Google Scholar] [CrossRef]
- Sivam, S.P.; Michaelraj, A.L.; Kumar, S.S.; Prabhakaran, G.; Dinakaran, D.; Ilankumaran, V. Statistical Multi-Objective Optimization of Electrical Discharge Machining Parameters in Machining Titanium Grade 5 Alloy Using Graphite Electrode. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2014, 228, 736–743. [Google Scholar] [CrossRef]
- Sahu, A.K.; Mohanty, P.P.; Sahoo, S.K. Electro Discharge Machining of Ti-Alloy (Ti6Al4V) and 316L Stainless Steel and Optimization of Process Parameters by Grey Relational Analysis (GRA) Method. In Advances in 3D Printing & Additive Manufacturing Technologies; Springer: Singpore, 2017; pp. 65–78. [Google Scholar]
- Işık, A.T.; Çakıroğlu, R.; Günay, M. Multiresponse Optimization of Performance Indicators through Taguchi-Grey Relational Analysis in EDM of Cemented Carbide. CIRP J. Manuf. Sci. Technol. 2023, 41, 490–500. [Google Scholar] [CrossRef]
- Gopalakannan, S.; Senthilvelan, T.; Ranganathan, S. Statistical Optimization of EDM Parameters on Machining of Aluminium Hybrid Metal Matrix Composite by Applying Taguchi Based Grey Analysis. J. Sci. Ind. Res. 2013, 72, 358–365. [Google Scholar]
- Balraj, U.S.; Krishna, A.G. Multi-Objective Optimization of EDM Process Parameters Using Taguchi Method, Principal Component Analysis and Grey Relational Analysis. Int. J. Manuf. Mater. Mech. Eng. 2014, 4, 29–46. [Google Scholar] [CrossRef]
- Alvarado, K.; Janeiro, I.; Florez, S.; Flipon, B.; Franchet, J.-M.; Locq, D.; Dumont, C.; Bozzolo, N.; Bernacki, M. Dissolution of the Primary Γ′ Precipitates and Grain Growth during Solution Treatment of Three Nickel Base Superalloys. Metals 2021, 11, 1921. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, S.; Bilga, P.S.; Singh, J.; Singh, S.; Scutaru, M.-L.; Pruncu, C.I. Revealing the Benefits of Entropy Weights Method for Multi-Objective Optimization in Machining Operations: A Critical Review. J. Mater. Res. Technol. 2021, 10, 1471–1492. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, D.; Yan, F. Effectiveness of Entropy Weight Method in Decision-Making. Math. Probl. Eng. 2020, 2020, 1–5. [Google Scholar] [CrossRef]
- Sharma, A.; Belokar, R.M.; Kumar, S. Multi-Response Optimization of Al2024/Red Mud MMC Using Hybrid Taguchi-GRA-Entropy Optimization Technique. Mater. Today Proc. 2018, 5, 4748–4760. [Google Scholar] [CrossRef]
- Yang, X.; Chen, X.; Zhang, T.; Ye, J.; Lv, G.; Zhang, J. Study on Reductive Smelting of High-Iron Red Mud for Iron Recovery. Metals 2022, 12, 639. [Google Scholar] [CrossRef]
- Meel, R.; Singh, V.; Katyal, P.; Gupta, M. Optimization of Process Parameters of Micro-EDD/EDM for Magnesium Alloy Using Taguchi Based GRA and TOPSIS Method. Mater. Today Proc. 2022, 51, 269–275. [Google Scholar] [CrossRef]
- Adalarasan, R.; Santhanakumar, M.; Rajmohan, M. Optimization of Laser Cutting Parameters for Al6061/SiCp/Al2O3 Composite Using Grey Based Response Surface Methodology (GRSM). Measurement 2015, 73, 596–606. [Google Scholar] [CrossRef]
- Sathish, T.; Karthick, S. Wear Behaviour Analysis on Aluminium Alloy 7050 with Reinforced SiC through Taguchi Approach. J. Mater. Res. Technol. 2020, 9, 3481–3487. [Google Scholar] [CrossRef]
- Venkatesan, S.; Xavior, M.A. Wear Characteristics Studies on Graphene Reinforced AA7050 Based Composite. Mater. Res. Express 2019, 6, 56501. [Google Scholar] [CrossRef]
- Budapanahalli, S.H.; Mallur, S.B.; Patil, A.Y.; Alosaimi, A.M.; Khan, A.; Hussein, M.A.; Asiri, A.M. A Tribological Study on the Effect of Reinforcing SiC and Al2O3 in Al7075: Applications for Spur Gears. Metals 2022, 12, 1028. [Google Scholar] [CrossRef]
- Baradeswaran, A.; Elayaperumal, A.; Issac, R.F. A Statistical Analysis of Optimization of Wear Behaviour of Al-Al2O3 Composites Using Taguchi Technique. Procedia Eng. 2013, 64, 973–982. [Google Scholar] [CrossRef]
- Suresh, S.; Gowd, G.H.; Deva Kumar, M.L.S. Tribological Behavior of Al 7075/SiC Metal Matrix Nano-Composite by Stir Casting Method. J. Inst. Eng. (India) Ser. D 2019, 100, 97–103. [Google Scholar] [CrossRef]
- Woźnicki, A.; Leszczyńska-Madej, B.; Włoch, G.; Grzyb, J.; Madura, J.; Leśniak, D. Homogenization of 7075 and 7049 Aluminium Alloys Intended for Extrusion Welding. Metals 2021, 11, 338. [Google Scholar] [CrossRef]
- Vigneshkumar, M.; Sekar, P. Multi-Objective Optimization of Process Parameters in Dry Sliding Wear Characteristics of Al/Sic Composites Using Taguchi Grey Relation Analysis. Mater. Today Proc. 2021, 45, 1882–1886. [Google Scholar]
- Sivakumar, V.R.; Kavitha, V.; Saravanan, N.S.; Nanjundamoorthi, T.T.; Chanakyan, C. Tribological Behavior on Stir Casted Metal Matrix Composites of Al 6070 and TiC Reinforcement with Taguchi S/N Ratios. Mater. Today Proc. 2023, 77, 455–461. [Google Scholar] [CrossRef]
- Selvarajan, L.; Sasikumar, R.; Kumar, N.S.; Kolochi, P.; Kumar, P.N. Effect of EDM Parameters on Material Removal Rate, Tool Wear Rate and Geometrical Errors of Aluminium Material. Mater. Today Proc. 2021, 46, 9392–9396. [Google Scholar] [CrossRef]
- Routara, B.C.; Das, D.; Satpathy, M.P.; Nanda, B.K.; Sahoo, A.K.; Singh, S.S. Investigation on Machining Characteristics of T6-Al7075 during EDM with Cu Tool in Steady and Rotary Mode. Mater. Today Proc. 2020, 26, 2143–2150. [Google Scholar] [CrossRef]
- Saravanan, C.; Sathivel, P.; Kajendirakumar, S.V.; Kumar, B.S. Mechanical and Wear Behaviour of AA7075 Alloy Reinforced with Graphite. Mater. Today Proc. 2021, 37, 868–871. [Google Scholar] [CrossRef]
- Kavimani, V.; Prakash, K.S.; Thankachan, T.; Nagaraja, S.; Jeevanantham, A.K.; Jhon, J.P. WEDM Parameter Optimization for Silicon@ R-GO/Magneisum Composite Using Taguchi Based GRA Coupled PCA. Silicon 2020, 12, 1161–1175. [Google Scholar] [CrossRef]
- Gopal, P.M.; Prakash, K.S. Minimization of Cutting Force, Temperature and Surface Roughness through GRA, TOPSIS and Taguchi Techniques in End Milling of Mg Hybrid MMC. Measurement 2018, 116, 178–192. [Google Scholar] [CrossRef]
- Priyadarshini, M.; Behera, A.; Swain, B.; Patel, S. Multi-Objective Optimization of EDM Process for Titanium Alloy. Mater. Today Proc. 2020, 33, 5526–5529. [Google Scholar] [CrossRef]
- Pradeep, M.; Rajesh, S.; Uthayakumar, M.; Mathalai Sundaram, C.; Korniejenko, K.; Miernik, K.; Majid, M.S.A. Experimental Investigation on Bio-Machining of Nickel, Titanium and Nitinol (Shape Memory Alloys) Using Acidithiobacillus ferrooxidans Microorganisms. J. Compos. Sci. 2023, 7, 262. [Google Scholar] [CrossRef]
- Julong, D. Introduction to Grey System Theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Ramanujam, R.; Shinde, P.A.; Kadam, R.; Dey, A.; Shinde, H. Estimation of Optimum Machining Parameters and Surface Characterization for WEDM of AA7075/10/Al2O3 (p) MMC through Multi-Objective Optimization. Mater. Today Proc. 2018, 5, 12330–12338. [Google Scholar] [CrossRef]
- Kumar, R.; Roy, S.; Gunjan, P.; Sahoo, A.; Sarkar, D.D.; Das, R.K. Analysis of MRR and Surface Roughness in Machining Ti-6Al-4V ELI Titanium Alloy Using EDM Process. Procedia Manuf. 2018, 20, 358–364. [Google Scholar] [CrossRef]
- Murugesan, S.; Balamuruga, K. Optimization by Grey Relational Analysis of EDM Parameters in Machining Al-15% SiC MMC Using Multihole Electrode. J. Appl. Sci. 2012, 12, 963–970. [Google Scholar] [CrossRef]
- Lin, C.L. Use of the Taguchi Method and Grey Relational Analysis to Optimize Turning Operations with Multiple Performance Characteristics. Mater. Manuf. Process. 2004, 19, 209–220. [Google Scholar] [CrossRef]
- Fatatit, A.Y.; Kalyon, A. Determination of Multi-Performance Characteristics in Electric Discharge Machining of DIN 1.2767 Steel Using Grey Relational Analysis. ARO-Sci. J. Koya Univ. 2021, 9, 1–7. [Google Scholar] [CrossRef]
- Gajalakshmi, K.; Senthilkumar, N.; Prabu, B. Multi-Response Optimization of Dry Sliding Wear Parameters of AA6026 Using Hybrid Gray Relational Analysis Coupled with Response Surface Method. Meas. Control 2019, 52, 540–553. [Google Scholar] [CrossRef]
- Perumal, A.; Kailasanathan, C.; Stalin, B.; Suresh Kumar, S.; Rajkumar, P.R.; Gangadharan, T.; Venkatesan, G.; Nagaprasad, N.; Dhinakaran, V.; Krishnaraj, R. Multiresponse Optimization of Wire Electrical Discharge Machining Parameters for Ti-6Al-2Sn-4Zr-2Mo (α-β) Alloy Using Taguchi-Grey Relational Approach. Adv. Mater. Sci. Eng. 2022, 2022, 1–13. [Google Scholar] [CrossRef]
- Tsai, C.-H.; Chang, C.-L.; Chen, L. Applying Grey Relational Analysis to the Decathlon Evaluation Model. Int. J. Comput. Internet Manag. 2003, 11, 55–62. [Google Scholar]
- Wang, Z.; Zhu, L.I.; Wu, J.H. Grey Relational Analysis of Correlation of Errors in Measurement. J. Grey Syst. 1996, 8, 73–78. [Google Scholar]
- Kuo, Y.; Yang, T.; Huang, G.-W. The Use of a Grey-Based Taguchi Method for Optimizing Multi-Response Simulation Problems. Eng. Optim. 2008, 40, 517–528. [Google Scholar] [CrossRef]
- Tosun, N.; Pihtili, H. Gray Relational Analysis of Performance Characteristics in MQL Milling of 7075 Al Alloy. Int. J. Adv. Manuf. Technol. 2010, 46, 509–515. [Google Scholar] [CrossRef]
- Suhail, A.H.; Ismail, N.; Wong, S.V.; Abdul Jalil, N.A. Surface Roughness Identification Using the Grey Relational Analysis with Multiple Performance Characteristics in Turning Operations. Arab. J. Sci. Eng. 2012, 37, 1111–1117. [Google Scholar] [CrossRef]
- Bhaumik, M.; Maity, K.P. Multi Response Optimization by Using the Hybrid Technique in Electro Discharge Machining of AISI 304. Int. J. Eng. Res. Afr. 2016, 26, 68–75. [Google Scholar] [CrossRef]
- Bhaumik, M.; Maity, K. Multi-Response Optimization of EDM Parameters Using Grey Relational Analysis (GRA) for Ti-5Al-2.5 Sn Titanium Alloy. World J. Eng. 2021, 18, 50–57. [Google Scholar] [CrossRef]
- Karthikeyan, K.M.B.; Yuvaraj, C.; Balasubramanian, T. A Hybrid Taguchi Based Grey Relational Analysis of Hard Turning of Subzero Treated EN24 Alloy Steel. Mater. Today Proc. 2021, 46, 3275–3281. [Google Scholar] [CrossRef]
- Singh, B.; Kumar, J.; Kumar, S. Influences of Process Parameters on MRR Improvement in Simple and Powder-Mixed EDM of AA6061/10% SiC Composite. Mater. Manuf. Process. 2015, 30, 303–312. [Google Scholar] [CrossRef]
- Madugula, A.S.; Baratam, M.K.; Gurugubelli, S.N. Electric Discharge Machining of AA2024 with Specific Wt% of Red Mud Hybrid Composites. Mater. Today Proc. 2021, 39, 1390–1395. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Wang, A.-C.; Wang, D.-A.; Chen, C.-C. Machining Performance and Optimizing Machining Parameters of Al2O3–TiC Ceramics Using EDM Based on the Taguchi Method. Mater. Manuf. Process. 2009, 24, 667–674. [Google Scholar] [CrossRef]

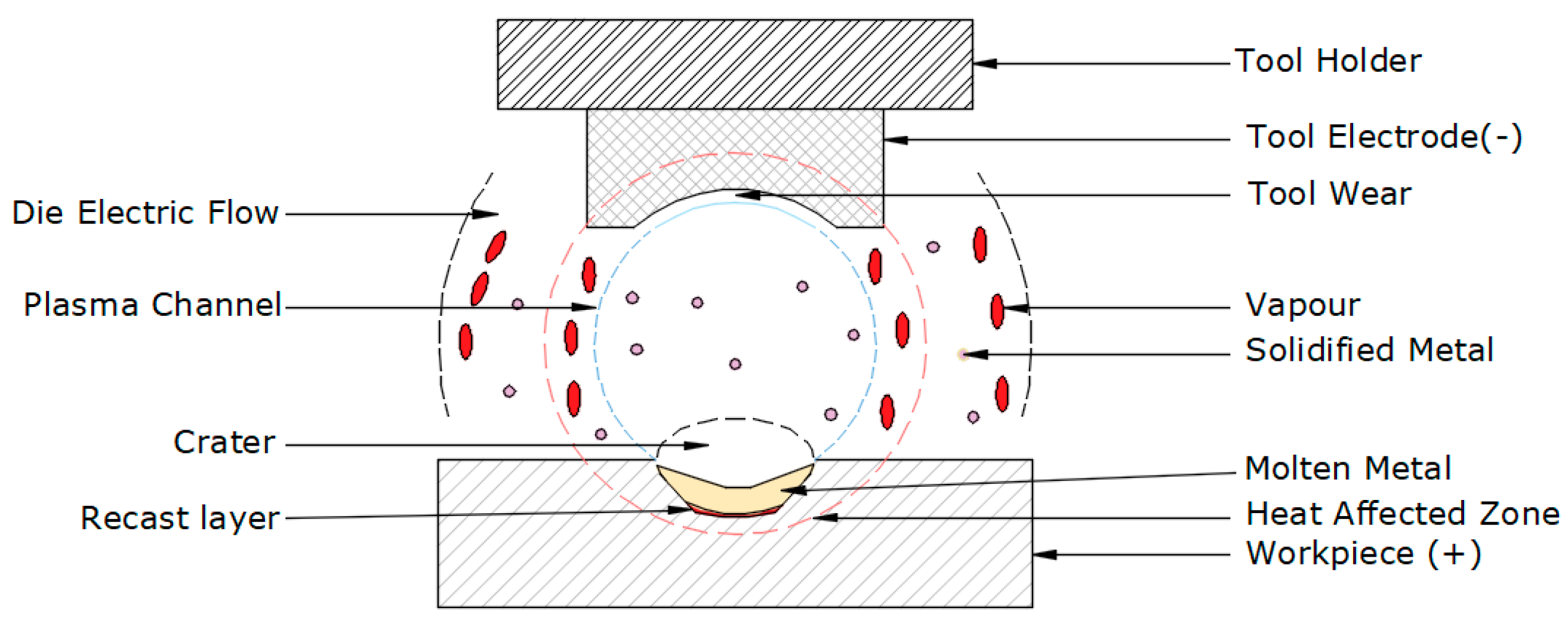






| Constituents | Si | Fe | Cu | Mn | Mg | Cr | Zi | Ti | Others | Al |
|---|---|---|---|---|---|---|---|---|---|---|
| % | 0.4 | 0.5 | 1.2–2 | 0.3 | 2.1–2.9 | 0.18–2 | 5.1–6.1 | 0.2 | 0.15 | Balance |
| Parameter | Parameter Values | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| Current (I) | 60 | 100 | 140 |
| Pulse ON Time (Ton) | 100 | 110 | 120 |
| Pulse OFF time (Toff) | 50 | 60 | 70 |
| Electrode Gap (Gap) | 0.2 | 0.4 | 0.6 |
| Workpiece | Al7075 MMC-Thickness 10 mm |
|---|---|
| Electrode | Brass-Diameter 0.3 mm |
| Dielectric Fluid | Kerosene |
| Polarity | Workpiece: Negative; Electrode: Positive |
| Electrode Rotation Speed | 120 RPM |
| Machine | SODICK AQ300L |
|---|---|
| Max. travel of X, Y, Z axes (mm) | 300 × 200 × 200 |
| Max. travel of U, V axes (mm) | 80 × 80 |
| Max. Machining size (mm) | 500 × 300 × 180 |
| Machine tool dimension (mm) | 1300 × 2400 × 2210 |
| I | Ton | Toff | Gap | MRR | TWR | SR | SNR-MRR | SNR-TWR | SNR-SR |
|---|---|---|---|---|---|---|---|---|---|
| 60 | 100 | 50 | 0.2 | 0.5165 | 0.0015 | 3.9271 | −5.7386 | 56.4782 | −11.8814 |
| 60 | 100 | 60 | 0.2 | 0.5117 | 0.0013 | 3.9189 | −5.8197 | 57.7211 | −11.8633 |
| 60 | 100 | 70 | 0.2 | 0.5084 | 0.0012 | 3.9126 | −5.8759 | 58.4164 | −11.8493 |
| 100 | 110 | 50 | 0.4 | 0.5231 | 0.0032 | 4.1352 | −5.6283 | 49.8970 | −12.3299 |
| 100 | 110 | 60 | 0.4 | 0.5198 | 0.0029 | 4.1328 | −5.6833 | 50.7520 | −12.3249 |
| 100 | 110 | 70 | 0.4 | 0.5169 | 0.0029 | 4.1302 | −5.7319 | 50.7520 | −12.3194 |
| 140 | 120 | 50 | 0.6 | 0.5571 | 0.0042 | 4.3968 | −5.0813 | 47.5350 | −12.8627 |
| 140 | 120 | 60 | 0.6 | 0.5559 | 0.0039 | 4.3942 | −5.1001 | 48.1787 | −12.8576 |
| 140 | 120 | 70 | 0.6 | 0.5538 | 0.0039 | 4.3908 | −5.1329 | 48.1787 | −12.8509 |
| 100 | 120 | 50 | 0.2 | 0.5288 | 0.0046 | 4.1376 | −5.5342 | 46.7448 | −12.3350 |
| 100 | 120 | 60 | 0.2 | 0.5263 | 0.0042 | 4.1237 | −5.5753 | 47.5350 | −12.3057 |
| 100 | 120 | 70 | 0.2 | 0.5236 | 0.004 | 4.1182 | −5.6200 | 47.9588 | −12.2941 |
| 140 | 100 | 50 | 0.4 | 0.5626 | 0.0047 | 4.4032 | −4.9960 | 46.5580 | −12.8754 |
| 140 | 100 | 60 | 0.4 | 0.5598 | 0.0046 | 4.3982 | −5.0393 | 46.7448 | −12.8655 |
| 140 | 100 | 70 | 0.4 | 0.5563 | 0.0046 | 4.3956 | −5.0938 | 46.7448 | −12.8604 |
| 60 | 110 | 50 | 0.6 | 0.5376 | 0.0032 | 4.5228 | −5.3908 | 49.8970 | −13.1081 |
| 60 | 110 | 60 | 0.6 | 0.5351 | 0.0032 | 4.5192 | −5.4313 | 49.8970 | −13.1012 |
| 60 | 110 | 70 | 0.6 | 0.5332 | 0.0031 | 4.5146 | −5.4622 | 50.1728 | −13.0924 |
| 140 | 110 | 50 | 0.2 | 0.5651 | 0.0057 | 4.4134 | −4.9575 | 44.8825 | −12.8955 |
| 140 | 110 | 60 | 0.2 | 0.5623 | 0.0057 | 4.3875 | −5.0006 | 44.8825 | −12.8443 |
| 140 | 110 | 70 | 0.2 | 0.5601 | 0.0053 | 4.3826 | −5.0347 | 45.5145 | −12.8346 |
| 60 | 120 | 50 | 0.4 | 0.5456 | 0.0048 | 4.5323 | −5.2625 | 46.3752 | −13.1264 |
| 60 | 120 | 60 | 0.4 | 0.5424 | 0.0042 | 4.5284 | −5.3136 | 47.5350 | −13.1189 |
| 60 | 120 | 70 | 0.4 | 0.5383 | 0.0041 | 4.5192 | −5.3795 | 47.7443 | −13.1012 |
| 100 | 100 | 50 | 0.6 | 0.5205 | 0.0028 | 4.1321 | −5.6716 | 51.0568 | −12.3234 |
| 100 | 100 | 60 | 0.6 | 0.5186 | 0.0026 | 4.1293 | −5.7033 | 51.7005 | −12.3175 |
| 100 | 100 | 70 | 0.6 | 0.5162 | 0.0027 | 4.1278 | −5.7436 | 51.3727 | −12.3144 |
| Level | I | Ton | Toff | Gap |
|---|---|---|---|---|
| 1 | −5.519 | −5.52 | −5.362 | −5.462 |
| 2 | −5.655 | −5.369 | −5.407 | −5.348 |
| 3 | −5.048 | −5.333 | −5.453 | −5.413 |
| Delta | 0.606 | 0.187 | 0.09 | 0.114 |
| Rank | 1 | 2 | 4 | 3 |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value | Contribution % |
|---|---|---|---|---|---|---|
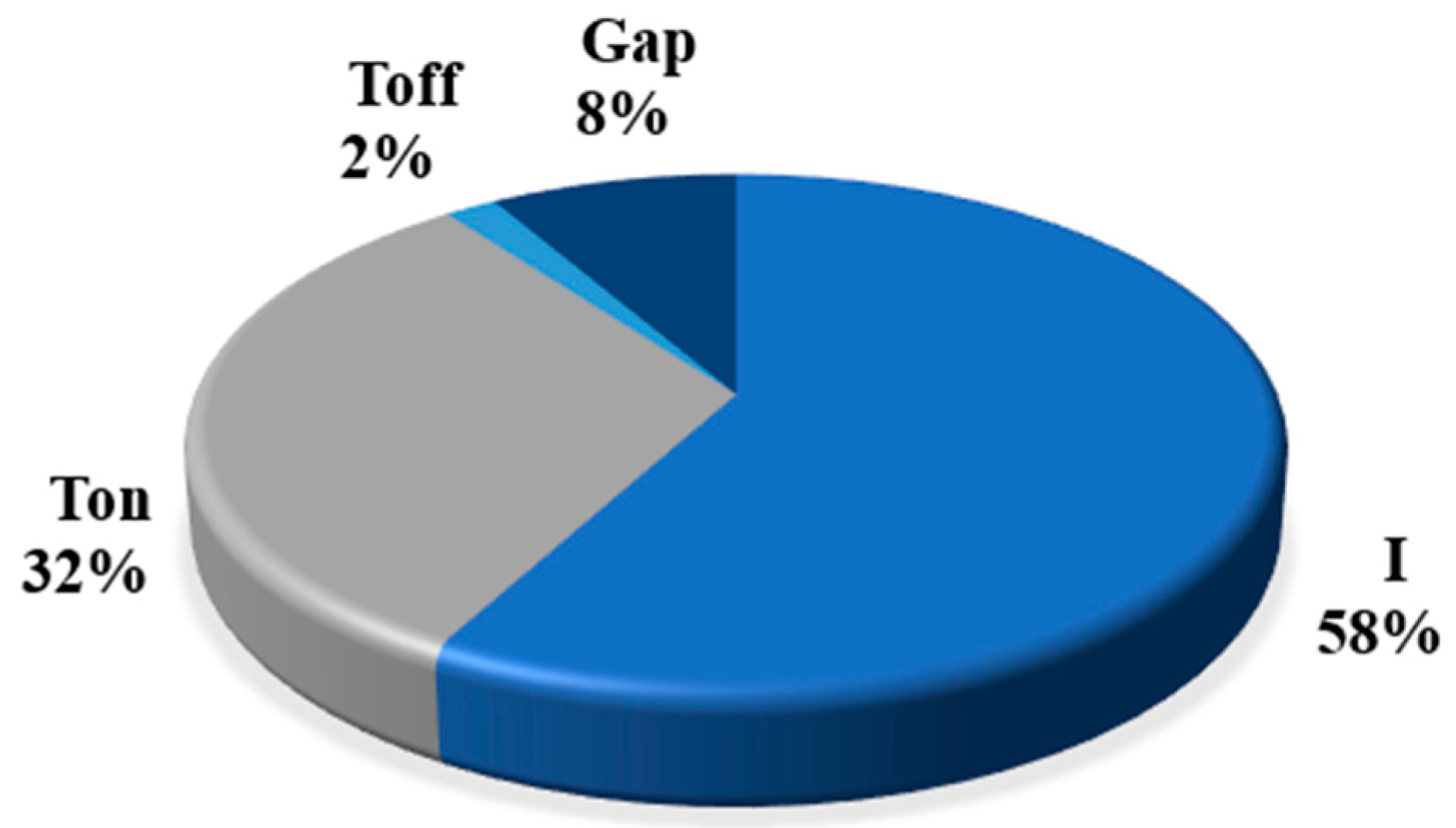
| I | 2 | 0.049088 | 0.024544 | 22.05 | 0 | 72.06% |
| Ton | 2 | 0.014016 | 0.007008 | 6.3 | 0.008 | 20.59% |
| Toff | 2 | 0.001032 | 0.000516 | 0.46 | 0.636 | 1.50% |
| Gap | 2 | 0.003987 | 0.001994 | 1.79 | 0.195 | 5.85% |
| Error | 18 | 0.020033 | 0.001113 | |||
| Total | 26 | 0.088157 |
| Level | I | Ton | Toff | Gap |
|---|---|---|---|---|
| 1 | 51.58 | 51.87 | 48.82 | 50.01 |
| 2 | 49.75 | 48.52 | 49.44 | 48.12 |
| 3 | 46.58 | 47.53 | 49.65 | 49.78 |
| Delta | 5 | 4.33 | 0.83 | 1.89 |
| Rank | 1 | 2 | 4 | 3 |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value | Contribution % |
|---|---|---|---|---|---|---|
| I | 2 | 0.000016 | 0.000008 | 12.75 | 0 | 58.06% |
| Ton | 2 | 0.000009 | 0.000004 | 6.95 | 0.006 | 31.65% |
| Toff | 2 | 0 | 0 | 0.4 | 0.676 | 1.82% |
| Gap | 2 | 0.000002 | 0.000001 | 1.86 | 0.185 | 8.47% |
| Error | 18 | 0.000011 | 0.000001 | |||
| Total | 26 | 0.000039 |
| Level | I | Ton | Toff | Gap |
|---|---|---|---|---|
| 1 | −12.69 | −12.35 | −12.64 | −12.34 |
| 2 | −12.32 | −12.76 | −12.62 | −12.77 |
| 3 | −12.86 | −12.76 | −12.61 | −12.76 |
| Delta | 0.54 | 0.41 | 0.02 | 0.42 |
| Rank | 1 | 3 | 4 | 2 |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value | Contribution % |
|---|---|---|---|---|---|---|
| I | 2 | 0.33962 | 0.169811 | 12.66 | 0 | 41.06% |
| Ton | 2 | 0.23866 | 0.119328 | 8.89 | 0.002 | 28.84% |
| Toff | 2 | 0.00067 | 0.000337 | 0.03 | 0.975 | 0.10% |
| Gap | 2 | 0.24812 | 0.124062 | 9.25 | 0.002 | 30.00% |
| Error | 18 | 0.24153 | 0.013418 | |||
| Total | 26 | 1.0686 |
| Normalization Values | Entropy Measure | ||||
|---|---|---|---|---|---|
| MRR | TWR | SR | MRR | TWR | SR |
| 0.0356 | 0.0151 | 0.0340 | −0.1188 | −0.0634 | −0.1149 |
| 0.0353 | 0.0131 | 0.0339 | −0.1180 | −0.0569 | −0.1147 |
| 0.0351 | 0.0121 | 0.0338 | −0.1175 | −0.0534 | −0.1146 |
| 0.0361 | 0.0323 | 0.0358 | −0.1199 | −0.1109 | −0.1191 |
| 0.0359 | 0.0293 | 0.0357 | −0.1193 | −0.1033 | −0.1191 |
| 0.0357 | 0.0293 | 0.0357 | −0.1189 | −0.1033 | −0.1190 |
| 0.0384 | 0.0424 | 0.0380 | −0.1252 | −0.1340 | −0.1243 |
| 0.0383 | 0.0394 | 0.0380 | −0.1251 | −0.1273 | −0.1243 |
| 0.0382 | 0.0394 | 0.0380 | −0.1247 | −0.1273 | −0.1242 |
| 0.0365 | 0.0464 | 0.0358 | −0.1208 | −0.1425 | −0.1192 |
| 0.0363 | 0.0424 | 0.0357 | −0.1204 | −0.1340 | −0.1189 |
| 0.0361 | 0.0404 | 0.0356 | −0.1200 | −0.1296 | −0.1188 |
| 0.0388 | 0.0474 | 0.0381 | −0.1261 | −0.1446 | −0.1245 |
| 0.0386 | 0.0464 | 0.0380 | −0.1257 | −0.1425 | −0.1244 |
| 0.0384 | 0.0464 | 0.0380 | −0.1251 | −0.1425 | −0.1243 |
| 0.0371 | 0.0323 | 0.0391 | −0.1222 | −0.1109 | -0.1268 |
| 0.0369 | 0.0323 | 0.0391 | −0.1218 | −0.1109 | −0.1267 |
| 0.0368 | 0.0313 | 0.0390 | −0.1215 | −0.1084 | −0.1266 |
| 0.0390 | 0.0575 | 0.0382 | −0.1265 | −0.1643 | −0.1247 |
| 0.0388 | 0.0575 | 0.0379 | −0.1261 | −0.1643 | −0.1241 |
| 0.0386 | 0.0535 | 0.0379 | −0.1257 | −0.1566 | −0.1240 |
| 0.0376 | 0.0484 | 0.0392 | −0.1234 | −0.1466 | −0.1270 |
| 0.0374 | 0.0424 | 0.0392 | −0.1229 | −0.1340 | −0.1269 |
| 0.0371 | 0.0414 | 0.0391 | −0.1223 | −0.1318 | −0.1267 |
| 0.0359 | 0.0283 | 0.0357 | −0.1195 | −0.1008 | −0.1191 |
| 0.0358 | 0.0262 | 0.0357 | −0.1192 | −0.0955 | −0.1190 |
| 0.0356 | 0.0272 | 0.0357 | −0.1188 | −0.0982 | −0.1190 |
| MRR | TWR | SR | |
|---|---|---|---|
| Wi | 0.3343 | 0.3314 | 0.3343 |
| Normalization Values | Deviation Sequence | Grey Relational Coefficient | GRG | Rank | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MRR | TWR | SR | MRR | TWR | SR | MRR | TWR | SR | ||
| 0.1495 | 0.1432 | 0.0252 | 0.8505 | 0.8568 | 0.9748 | 0.3702 | 0.3685 | 0.3390 | 0.1197 | 25 |
| 0.0612 | 0.0514 | 0.0109 | 0.9388 | 0.9486 | 0.9891 | 0.3475 | 0.3452 | 0.3358 | 0.1143 | 26 |
| 0.0000 | 0.0000 | 0.0000 | 1.0000 | 1.0000 | 1.0000 | 0.3333 | 0.3333 | 0.3333 | 0.1111 | 27 |
| 0.2696 | 0.6295 | 0.3763 | 0.7304 | 0.3705 | 0.6237 | 0.4064 | 0.5744 | 0.4450 | 0.1583 | 19 |
| 0.2097 | 0.5663 | 0.3724 | 0.7903 | 0.4337 | 0.6276 | 0.3875 | 0.5355 | 0.4434 | 0.1517 | 20 |
| 0.1568 | 0.5663 | 0.3681 | 0.8432 | 0.4337 | 0.6319 | 0.3723 | 0.5355 | 0.4417 | 0.1499 | 22 |
| 0.8652 | 0.8040 | 0.7936 | 0.1348 | 0.1960 | 0.2064 | 0.7876 | 0.7184 | 0.7078 | 0.2460 | 9 |
| 0.8448 | 0.7564 | 0.7895 | 0.1552 | 0.2436 | 0.2105 | 0.7631 | 0.6724 | 0.7038 | 0.2377 | 11 |
| 0.8090 | 0.7564 | 0.7843 | 0.1910 | 0.2436 | 0.2157 | 0.7236 | 0.6724 | 0.6986 | 0.2328 | 12 |
| 0.3721 | 0.8624 | 0.3803 | 0.6279 | 0.1376 | 0.6197 | 0.4433 | 0.7842 | 0.4465 | 0.1858 | 16 |
| 0.3273 | 0.8040 | 0.3574 | 0.6727 | 0.1960 | 0.6426 | 0.4264 | 0.7184 | 0.4376 | 0.1756 | 17 |
| 0.2786 | 0.7727 | 0.3483 | 0.7214 | 0.2273 | 0.6517 | 0.4094 | 0.6875 | 0.4342 | 0.1699 | 18 |
| 0.9581 | 0.8762 | 0.8035 | 0.0419 | 0.1238 | 0.1965 | 0.9226 | 0.8015 | 0.7178 | 0.2713 | 4 |
| 0.9109 | 0.8624 | 0.7957 | 0.0891 | 0.1376 | 0.2043 | 0.8487 | 0.7842 | 0.7099 | 0.2603 | 6 |
| 0.8516 | 0.8624 | 0.7917 | 0.1484 | 0.1376 | 0.2083 | 0.7711 | 0.7842 | 0.7059 | 0.2512 | 8 |
| 0.5282 | 0.6295 | 0.9857 | 0.4718 | 0.3705 | 0.0143 | 0.5145 | 0.5744 | 0.9722 | 0.2291 | 13 |
| 0.4841 | 0.6295 | 0.9803 | 0.5159 | 0.3705 | 0.0197 | 0.4922 | 0.5744 | 0.9621 | 0.2255 | 14 |
| 0.4505 | 0.6091 | 0.9734 | 0.5495 | 0.3909 | 0.0266 | 0.4764 | 0.5612 | 0.9495 | 0.2209 | 15 |
| 1.0000 | 1.0000 | 0.8192 | 0.0000 | 0.0000 | 0.1808 | 1.0000 | 1.0000 | 0.7344 | 0.3037 | 1 |
| 0.9530 | 1.0000 | 0.7792 | 0.0470 | 0.0000 | 0.2208 | 0.9141 | 1.0000 | 0.6936 | 0.2896 | 2 |
| 0.9159 | 0.9533 | 0.7716 | 0.0841 | 0.0467 | 0.2284 | 0.8561 | 0.9146 | 0.6864 | 0.2729 | 3 |
| 0.6679 | 0.8897 | 1.0000 | 0.3321 | 0.1103 | 0.0000 | 0.6009 | 0.8193 | 1.0000 | 0.2689 | 5 |
| 0.6122 | 0.8040 | 0.9941 | 0.3878 | 0.1960 | 0.0059 | 0.5632 | 0.7184 | 0.9884 | 0.2523 | 7 |
| 0.5405 | 0.7885 | 0.9803 | 0.4595 | 0.2115 | 0.0197 | 0.5211 | 0.7028 | 0.9621 | 0.2429 | 10 |
| 0.2225 | 0.5438 | 0.3712 | 0.7775 | 0.4562 | 0.6288 | 0.3914 | 0.5229 | 0.4430 | 0.1507 | 21 |
| 0.1879 | 0.4962 | 0.3666 | 0.8121 | 0.5038 | 0.6334 | 0.3811 | 0.4981 | 0.4412 | 0.1466 | 23 |
| 0.1440 | 0.5204 | 0.3642 | 0.8560 | 0.4796 | 0.6358 | 0.3687 | 0.5104 | 0.4402 | 0.1465 | 24 |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value | Contribution % |
|---|---|---|---|---|---|---|
| Linear | 4 | 0.031008 | 0.007752 | 2.98 | 0.041 | |
| I | 1 | 0.01875 | 0.01875 | 7.22 | 0.013 | 60.47% |
| Ton | 1 | 0.010756 | 0.010756 | 4.14 | 0.054 | 34.67% |
| Toff | 1 | 0.001021 | 0.001021 | 0.39 | 0.537 | 3.27% |
| Gap | 1 | 0.000482 | 0.000482 | 0.19 | 0.671 | 1.59% |
| Error | 22 | 0.057149 | 0.002598 | |||
| Total | 26 | 0.088157 |
| S | R-sq | R-sq(adj) | R-sq(pred) |
|---|---|---|---|
| 0.00644 | 99.34% | 98.78% | 97.40% |
| Parameter | Level 1 | Level 2 | Level 3 | Deviation | Rank |
|---|---|---|---|---|---|
| I | 0.0661 | 0.0532 | 0.0876 | 0.0345 | 1 |
| Ton | 0.0582 | 0.0741 | 0.0745 | 0.0163 | 2 |
| Toff | 0.0716 | 0.0687 | 0.0666 | 0.0050 | 4 |
| Gap | 0.0645 | 0.0743 | 0.0680 | 0.0098 | 3 |
| Total mean value of Grey relational grade | 0.0690 | ||||
| Test Condition | Levels | C | Ton | Toff | Gap | MRR | TWR | SR | GRG |
|---|---|---|---|---|---|---|---|---|---|
| Initial parameters | A3B3C3D3 | 140 | 120 | 70 | 0.6 | 0.5538 | 0.0039 | 4.3908 | 0.2328 |
| Optimum parameters | A3B3C1D2 | 140 | 120 | 50 | 0.4 | 0.5628 | 0.0048 | 4.4034 | 0.2746 |
| % of Improvement: | 118% | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohankumar, V.; Kapilan, S.; Karthik, A.; Bhuvaneshwaran, M.; Santulli, C.; Kumar, D.T.; Palanisamy, S.; Fragassa, C. A Hybrid Design of Experiment Approach in Analyzing the Electrical Discharge Machining Influence on Stir Cast Al7075/B4C Metal Matrix Composites. Metals 2024, 14, 205. https://doi.org/10.3390/met14020205
Mohankumar V, Kapilan S, Karthik A, Bhuvaneshwaran M, Santulli C, Kumar DT, Palanisamy S, Fragassa C. A Hybrid Design of Experiment Approach in Analyzing the Electrical Discharge Machining Influence on Stir Cast Al7075/B4C Metal Matrix Composites. Metals. 2024; 14(2):205. https://doi.org/10.3390/met14020205
Chicago/Turabian StyleMohankumar, Velusamy, Sunderraj Kapilan, Aruchamy Karthik, Mylsamy Bhuvaneshwaran, Carlo Santulli, Durairaj Thresh Kumar, Sivasubramanian Palanisamy, and Cristiano Fragassa. 2024. "A Hybrid Design of Experiment Approach in Analyzing the Electrical Discharge Machining Influence on Stir Cast Al7075/B4C Metal Matrix Composites" Metals 14, no. 2: 205. https://doi.org/10.3390/met14020205
APA StyleMohankumar, V., Kapilan, S., Karthik, A., Bhuvaneshwaran, M., Santulli, C., Kumar, D. T., Palanisamy, S., & Fragassa, C. (2024). A Hybrid Design of Experiment Approach in Analyzing the Electrical Discharge Machining Influence on Stir Cast Al7075/B4C Metal Matrix Composites. Metals, 14(2), 205. https://doi.org/10.3390/met14020205











