Experimental Determination of the Standard Gibbs Energy of Formation of Fe3–xVxO4 at 1473 K
Abstract
1. Introduction
2. Principle and Experimental
2.1. Principle of Determining the Gibbs Energy of Fe3–xVxO4
2.2. Experimental Procedure for Measuring in the Solid-Solution Phase Fe3–xVxO4
3. Results and Discussion
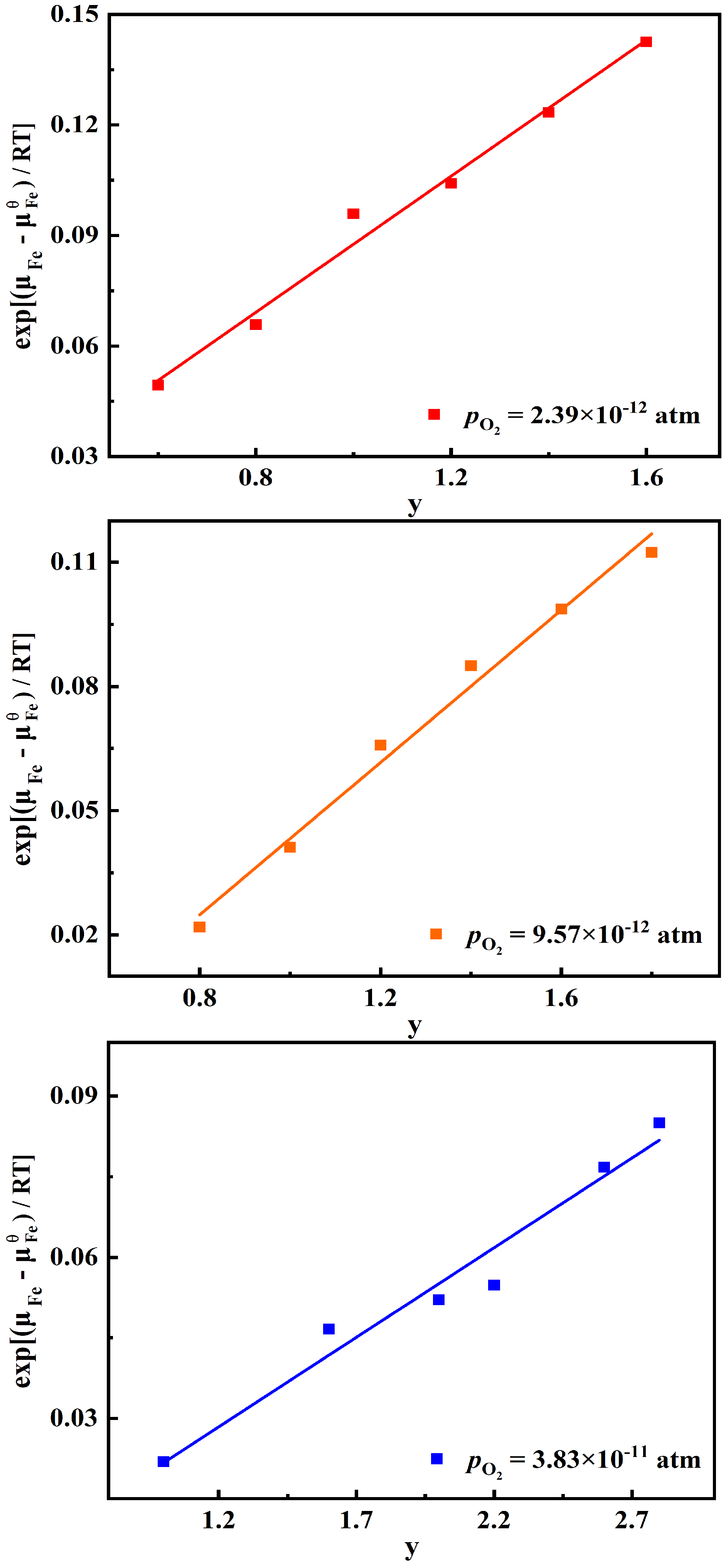
3.1. Chemical Potential of Fe in the Fe3–xVxO4 under Different Oxygen Partial Pressures
3.2. Chemical Potential of V in the Fe3–xVxO4 under Different Oxygen Partial Pressure
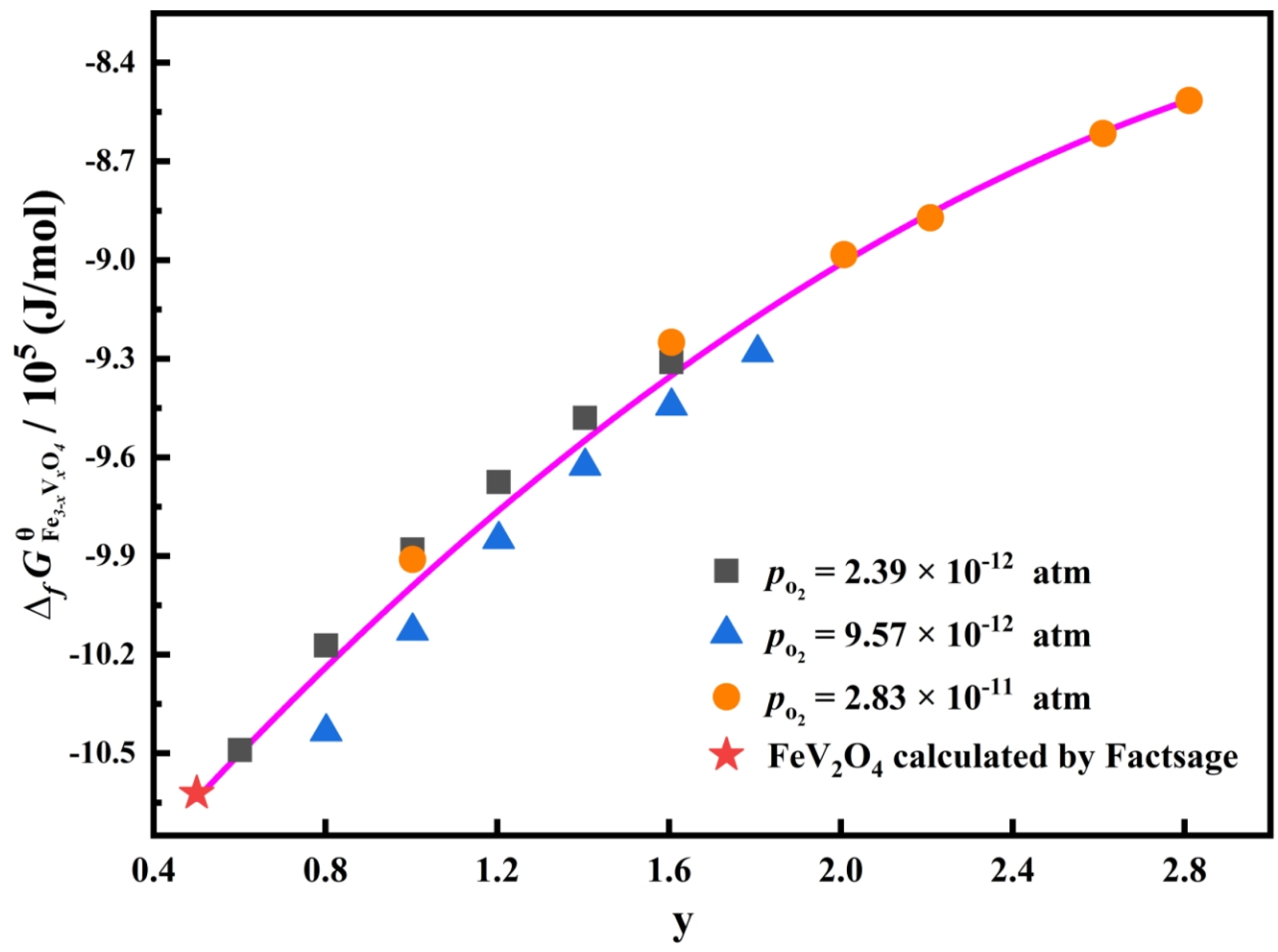
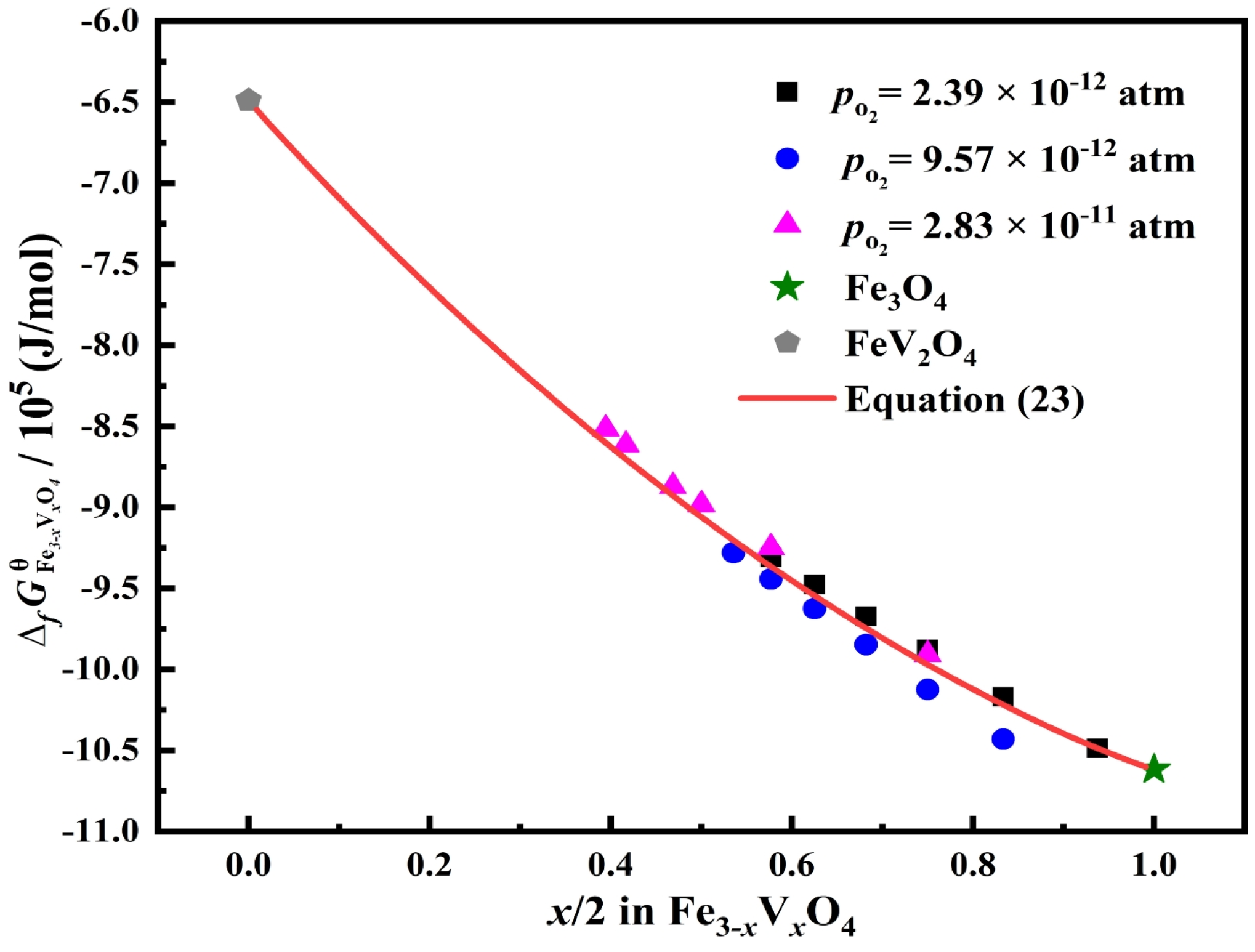
3.3. Standard Gibbs Energy of Formation of Fe3–xVxO4 at 1473 K
4. Conclusions
- The approach of determining consists of two steps. The first is to measure the chemical potential of Fe () in Fe3–xVxO4 under fixed oxygen partial pressure by using liquid copper as the equilibrating phase, thereby obtaining the composition-dependent relation of . The second is to calculate the by utilizing the Gibbs–Duhem relation.
- The standard Gibbs energies of the formation of a variety of Fe3–xVxO4 compounds were determined through this approach, and its reliability was verified by comparing the determined with the reported value of FeV2O4.
- In the oxygen partial pressure range from 2.39 × 10−12 to 3.83 × 10−11 atm, the standard Gibbs energies of formation of Fe3–xVxO4 is mainly decided by the Fe/V molar ratio and almost not related to the oxygen partial pressure.
- The standard Gibbs energies of the formation of Fe3–xVxO4 can be modeled satisfactorily using the regular solution model with Fe3O4 and FeV2O4 as the solution end members.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, R.W.; Ren, X.L.; Zhan, C.Z.; Wang, C.; Lv, R.; Shen, W.; Kang, F.; Huang, Z.-H. Facile synthesis of FeVO@C materials as high-performance composite cathode for lithium-ion hybrid capacitor. J. Alloys Compd. 2020, 835, 155398. [Google Scholar] [CrossRef]
- Xie, W.; Xin, X.R.; Cao, Z.M. Thermodynamic assessment of the Fe–V–O system. CALPHAD Comput. Coupling Phase Diagr. Thermochem. 2020, 71, 102213. [Google Scholar] [CrossRef]
- Li, S.-R.; Ge, S.-Y.; Qiao, Y.; Chen, Y.-M.; Feng, X.-Y.; Zhu, J.-F.; Chen, C.-H. Three-dimensional porous Fe0.1V2O5.15 thin film as a cathode material for lithium ion batteries. Eectrochimica Acta 2012, 64, 81–86. [Google Scholar] [CrossRef]
- Xie, W.; Xin, X.R.; Cao, Z.M. Thermodynamic, lattice dynamical, and elastic properties of iron-vanadium oxides from experiments and first principles. J. Am. Ceram. Soc. 2020, 103, 3797–3811. [Google Scholar] [CrossRef]
- Muller, J.; Joubert, J.C.; Marezio, M. The synthesis of the crystalline structure of the new oxide FeV3O8 (FexV1-xO2, x = 0.25). J. Solid State Chem. 1979, 27, 191–199. [Google Scholar] [CrossRef]
- Mawuse, A.A.; Song, N.; Jeong, I.H. All layered iron vanadate (FeV3O9.2.1H2O) as electrode for symmetric supercapacitor application in aqueous electrolyte. J. Alloys Compd. 2023, 938, 168641. [Google Scholar]
- Sharma, A.; Ashoka, S.; Nishchith, B.S.; Kalegowda, Y. Electrochemical quantification of glycine using amorphous iron vanadate nanoparticles modified pencil electrode. Inorg. Chem. Commun. 2023, 153, 110766. [Google Scholar] [CrossRef]
- Zhang, C.L.; Sang, H.R.; Yang, H.P.; Hu, L.; Wu, B.; Yin, Y. Establishment of a novel Fenton-like enhanced low-temperature selective catalytic reduction over FeVO4 catalysts. J. Environ. Chem. Eng. 2023, 11, 109634. [Google Scholar] [CrossRef]
- Wang, D.Y.; Li, F.; Yan, B.J. Synthetic mechanism and kinetics of Fe2VO4 at 1273–1473 K from Fe2O3 and V2O3 under reducing atmosphere. J. Alloys Compd. 2019, 797, 1050–1058. [Google Scholar] [CrossRef]
- Kawaguchi, S.; Ishibashi, H.; Nishihara, S.; Miyagawa, M.; Inoue, K.; Mori, S.; Kubota, Y. Anomalous magnetization behaviour in a single crystal of vanadium spinel FeV2O4. J. Phys. Condens. Matter 2013, 25, 416005. [Google Scholar] [CrossRef]
- Cevik, E.; Bozkurt, A.; Gunday, S.T.; Qahtan, T.F.; Drmosh, Q.A.; Elsayed, K.A.; Akhtar, S.; Mustafa, A. Synthesis of NiO/Fe2VO4 nano-hybrid structures via sonication induced approach for electrochemical energy storage in non-aqueous medium. J. Energy Storage 2023, 68, 107873. [Google Scholar] [CrossRef]
- Kang, J.S.; Hwang, J.; Kim, D.H.; Lee, E.; Kim, W.-J.; Kim, C.-S.; Kwon, S.; Lee, S.; Kim, J.; Ueno, T.; et al. Valence states and spin structure of spinel FeV2O4 with different orbital degrees of freedom. Phys. Rev. B 2012, 85, 165136. [Google Scholar] [CrossRef]
- Abe, M.; Karachi, M.; Nomura, S. Mossbauer study of the FeV2O4–Fe3O4 system. J. Solid State Chem. 1974, 10, 351–356. [Google Scholar] [CrossRef]
- Wakihara, M.; Shimizu, Y.; Katsura, T. Preparation and Magnetic properties FeV2O4–Fe3O4 system. J. Solid State Chem. 1971, 3, 478–483. [Google Scholar] [CrossRef]
- Jin, C.; Liz, J.; Zheng, D.X.; Tang, M.; Li, P.; Bai, H. Effect of cation substitution on the magnetic and magnetotransport properties of epitaxial Fe3−xVxO4 films. Appl. Surf. Sci. 2015, 332, 70–75. [Google Scholar] [CrossRef]
- Pool, V.L.; Kleb, M.T.; Chorney, C.L.; Lee, J.H.; Park, J.Y.; Kim, S.J. Enhanced magnetization in VxFe3−xO4 nanoparticles. J. Magn. Magn. Mater. 2015, 396, 304–307. [Google Scholar] [CrossRef]
- Kim, K.J.; Choi, S.L.; Lee, H.J.; Lee, J.H.; Park, J.Y. Evolution of structural and optical-absorption properties in VxFe3−xO4. Solid State Commun. 2007, 143, 285–288. [Google Scholar] [CrossRef]
- Häggblad, R.; Massa, M.; Andersson, A. Stability and performance of supported Fe–V-oxide catalysts in methanol oxidation. J. Catal. 2009, 266, 218–227. [Google Scholar] [CrossRef]
- Coetsee, T.; Pistorius, C. Preliminary Observations on Phase Relations in the “V2O3–FeO” and V2O3–TiO2 Systems from 1400 °C to 1600 °C in Reducing Atmospheres. J. Am. Ceram. Soc. 2000, 83, 1485–1488. [Google Scholar] [CrossRef]
- Wakihara, M.; Katsura, T. The Phase Equilibria in the FeO-Fe2O3-V2O3 System at 1500°K. Bull. Chem. Soc. Jpn. 1971, 44, 3043–3046. [Google Scholar] [CrossRef]
- Yan, B.; Wang, D.; Qiu, Q.; Deng, T. Phase relations in the “FeO-V2O3” system at 1473 K and the magnetic properties of spinel phase Fe3-xVxO4. Ceram. Int. 2020, 46, 6160–6167. [Google Scholar] [CrossRef]
- Du, W.T.; Jung, I.H. Critical evaluation and thermodynamic modeling of the Fe-V-O (FeO-Fe2O3-VO-V2O3-VO-V2O5) system. CALPHAD Comput. Coupling Phase Diagr. Thermochem. 2019, 67, 101682. [Google Scholar] [CrossRef]
- Malan, W.D.; Akdogan, G.; Taskinen, P.; Zietsman, J. Phase equilibria and thermodynamic evaluation of the Fe-Ti-V-O system in air. CALPHAD Comput. Coupling Phase Diagr. Thermochem. 2019, 65, 141–154. [Google Scholar] [CrossRef]
- Jantzen, T.; Yazhenskikh, E.; Hack, K.; Baben, M.; Wu, G.; Müller, M. Addition of V2O5 and V2O3 to the CaO–FeO–Fe2O3–MgO–SiO2 database for vanadium distribution and viscosity calculations. CALPHAD Comput. Coupling Phase Diagr. Thermochem. 2021, 74, 102284. [Google Scholar] [CrossRef]
- Chipman, J.; Dastur, M.N. Vanadium-oxygen equilibrium in liquid iron. JOM 1951, 191, 111–115. [Google Scholar] [CrossRef]
- The FactSage System. Available online: http://www.factsage.com/ (accessed on 1 July 2023).
- Hillert, M. Phase Equilibria, Phase Diagrams and Phase Transformations, 2nd ed.; Cambridge University Press: Cambridge, UK, 2007; p. 49. [Google Scholar]
- Wang, D.; Shu, Q.; Yan, B.; Wu, L.; Wang, J.; Dong, Y. Thermodynamics of the CaO–SiO2–VOx system at 1873 K under the oxygen partial pressure of 6.93 × 10−11 atm. J. Am. Ceram. Soc. 2017, 100, 4912–4927. [Google Scholar] [CrossRef]
- Yan, B.; Wang, D.; Deng, T.; Wu, L.; Dong, Y. Effects of oxygen partial pressure on the thermodynamics of CaO–SiO2–VOx system at 1873 K. J. Am. Ceram. Soc. 2020, 103, 2114–2127. [Google Scholar] [CrossRef]
- Sigworth, G.K.; Elliott, J.F. The thermodynamics of dilute liquid copper alloys. Can. Metall. Q. 1974, 13, 455–461. [Google Scholar] [CrossRef]
| No. of Samples | Fe/V Molar Ratio | Volume Ratio of CO to CO2 | Oxygen Partial Pressure (atm) |
|---|---|---|---|
| 1-1 | 1.6 | 2 | 2.39 × 10−12 |
| 1-2 | 1.4 | ||
| 1-3 | 1.2 | ||
| 1-4 | 1.0 | ||
| 1-5 | 0.8 | ||
| 1-6 | 0.6 | ||
| 2-1 | 1.8 | 1 | 9.57 × 10−12 |
| 2-2 | 1.6 | ||
| 2-3 | 1.4 | ||
| 2-4 | 1.2 | ||
| 2-5 | 1.0 | ||
| 2-6 | 0.8 | ||
| 3-1 | 2.8 | 0.5 | 3.83 × 10−11 |
| 3-2 | 2.6 | ||
| 3-3 | 2.2 | ||
| 3-4 | 2.0 | ||
| 3-5 | 1.6 | ||
| 3-6 | 1.0 |
| Oxygen Partial Pressure | Compositional Limitations | |
|---|---|---|
| 2.39 × 10−12 | 0.524 | 1.604 |
| 9.57 × 10−12 | 0.565 | 2.300 |
| 3.83 × 10−11 | 0.567 | 3.098 |
| Equilibrating Experimental Conditions | Results | ||||
|---|---|---|---|---|---|
| No. | Mass % of Fe in Cu | (J/mol) | |||
| 1-1 | 1.6 | 2.39 × 10−12 | 0.52 | 0.0059 | −23,861.3 |
| 1-2 | 1.4 | 0.45 | 0.0051 | −25,630.8 | |
| 1-3 | 1.2 | 0.38 | 0.0043 | −27,700.2 | |
| 1-4 | 1.0 | 0.35 | 0.0040 | −28,706.8 | |
| 1-5 | 0.8 | 0.24 | 0.0027 | −33,325.5 | |
| 1-6 | 0.6 | 0.18 | 0.0020 | −36,847.6 | |
| 2-1 | 1.8 | 9.57 × 10−12 | 0.41 | 0.0047 | −26,770.1 |
| 2-2 | 1.6 | 0.36 | 0.0041 | −28,362.0 | |
| 2-3 | 1.4 | 0.31 | 0.0035 | −30,192.4 | |
| 2-4 | 1.2 | 0.24 | 0.0027 | −33,325.5 | |
| 2-5 | 1.0 | 0.15 | 0.0017 | −39,079.9 | |
| 2-6 | 0.8 | 0.08 | 0.0009 | −46,777.0 | |
| 3-1 | 2.8 | 3.83 × 10−11 | 0.31 | 0.0035 | −30,192.4 |
| 3-2 | 2.6 | 0.28 | 0.0032 | −31,438.4 | |
| 3-3 | 2.2 | 0.20 | 0.0023 | −35,557.6 | |
| 3-4 | 2.0 | 0.19 | 0.0022 | −36,185.6 | |
| 3-5 | 1.6 | 0.17 | 0.0019 | −37,547.4 | |
| 3-6 | 1.0 | 0.08 | 0.0009 | −46,777.0 | |
| 2.39 × 10−12 | |
| 9.57 × 10−12 | 𝜇𝐹𝑒 = 𝜇𝐹𝑒𝜃 + 𝑅𝑇𝑙𝑛 − 0.0488 + 0.092𝑦 |
| 3.83 × 10−11 |
| Equilibrating Experimental Conditions | Results | |||
|---|---|---|---|---|
| No. | (J/mol) | (J/mol) | ||
| 1-1 | 1.6 | 2.39 × 10−12 | −23,861.3 | −200,496.5 |
| 1-2 | 1.4 | −25,630.8 | −197,958.8 | |
| 1-3 | 1.2 | −27,700.2 | −195,406.8 | |
| 1-4 | 1.0 | −28,706.8 | −192,835.2 | |
| 1-5 | 0.8 | −33,325.5 | −190,234.6 | |
| 1-6 | 0.6 | −36,847.6 | −187,586.3 | |
| 2-1 | 1.8 | 9.57 × 10−12 | −26,770.1 | −237,836.0 |
| 2-2 | 1.6 | −28,362.0 | −234,273.1 | |
| 2-3 | 1.4 | −30,192.4 | −230,479.1 | |
| 2-4 | 1.2 | −33,325.5 | −226,331.9 | |
| 2-5 | 1.0 | −39,079.9 | −221,577.7 | |
| 2-6 | 0.8 | −46,777.0 | −215,523.2 | |
| 3-1 | 2.8 | 3.83 × 10−11 | −30,192.4 | −249,849.2 |
| 3-2 | 2.6 | −31,438.4 | −247,033.0 | |
| 3-3 | 2.2 | −35,557.6 | −241,291.1 | |
| 3-4 | 2.0 | −36,185.6 | −238,348.9 | |
| 3-5 | 1.6 | −37,547.4 | −232,253.9 | |
| 3-6 | 1.0 | −46,777.0 | −222,086.1 | |
| No. | |||
|---|---|---|---|
| 1-1 | 1.6 | 2.39 × 10−12 | −930,820.9 |
| 1-2 | 1.4 | −947,729.6 | |
| 1-3 | 1.2 | −967,218.6 | |
| 1-4 | 1.0 | −987,740.2 | |
| 1-5 | 0.8 | −1,016,918.9 | |
| 1-6 | 0.6 | −1,048,605.1 | |
| 2-1 | 1.8 | 9.57 × 10−12 | −927,899.3 |
| 2-2 | 1.6 | −944,122.7 | |
| 2-3 | 1.4 | −962,382.6 | |
| 2-4 | 1.2 | −984,614.1 | |
| 2-5 | 1.0 | −1,012,433.4 | |
| 2-6 | 0.8 | −1,043,021.7 | |
| 3-1 | 2.8 | 3.83 × 10−11 | −851,470.1 |
| 3-2 | 2.6 | −861,457.0 | |
| 3-3 | 2.2 | −887,027.6 | |
| 3-4 | 2.0 | −898,199.8 | |
| 3-5 | 1.6 | −924,783.2 | |
| 3-6 | 1.0 | −990,774.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, Q.; Li, M.; Yan, B. Experimental Determination of the Standard Gibbs Energy of Formation of Fe3–xVxO4 at 1473 K. Metals 2023, 13, 1498. https://doi.org/10.3390/met13081498
Miao Q, Li M, Yan B. Experimental Determination of the Standard Gibbs Energy of Formation of Fe3–xVxO4 at 1473 K. Metals. 2023; 13(8):1498. https://doi.org/10.3390/met13081498
Chicago/Turabian StyleMiao, Qingdong, Ming Li, and Baijun Yan. 2023. "Experimental Determination of the Standard Gibbs Energy of Formation of Fe3–xVxO4 at 1473 K" Metals 13, no. 8: 1498. https://doi.org/10.3390/met13081498
APA StyleMiao, Q., Li, M., & Yan, B. (2023). Experimental Determination of the Standard Gibbs Energy of Formation of Fe3–xVxO4 at 1473 K. Metals, 13(8), 1498. https://doi.org/10.3390/met13081498







