Numerical Simulations and Experimental Verification of T-Structure Welding Deformation Using the Step-by-Step Loading Inherent Strain Method
Abstract
1. Introduce
2. Welding Deformation Prediction Methods and Theory
2.1. Thermal Elastic–Plastic Finite Element Method (TEP-FEM)
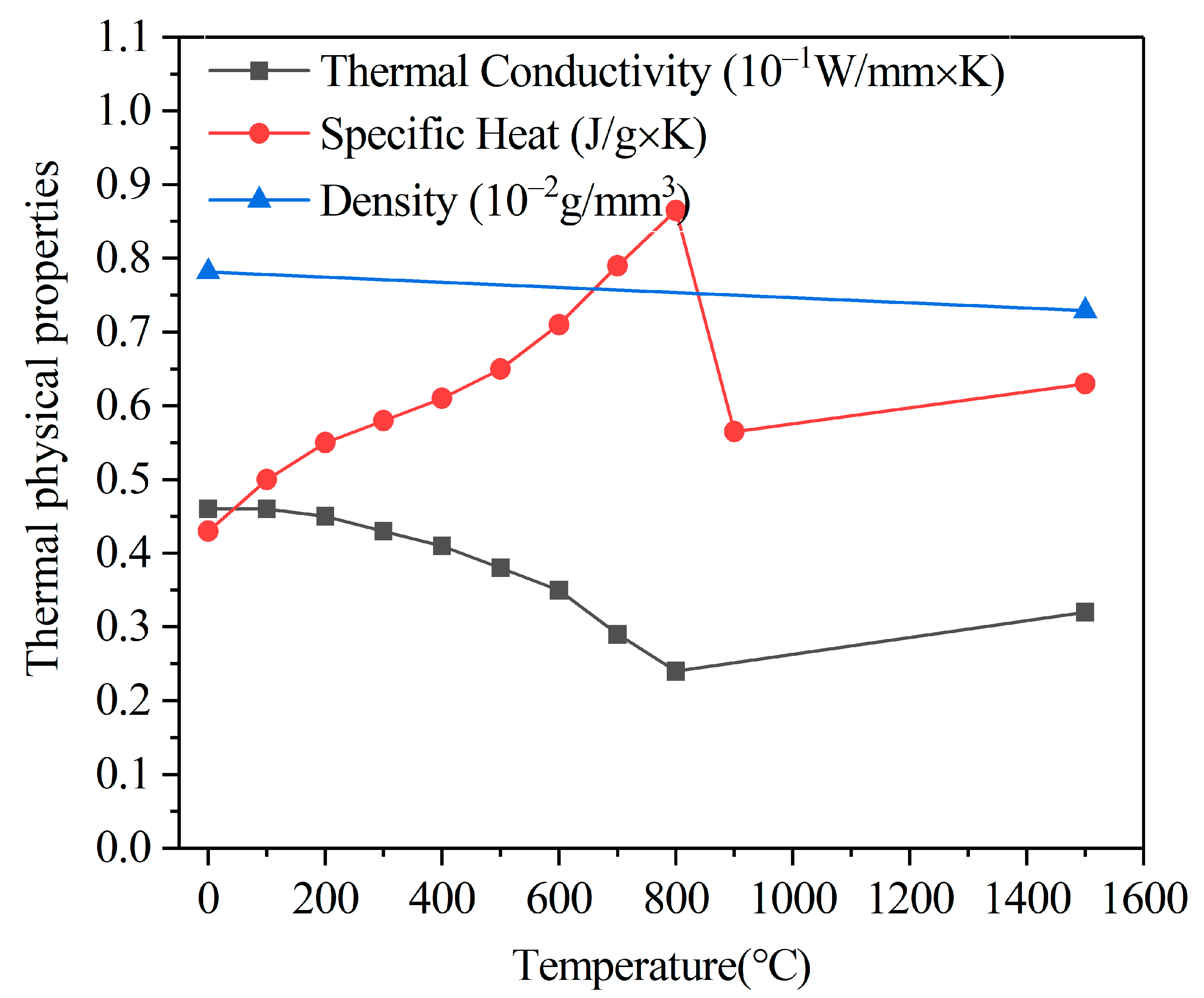
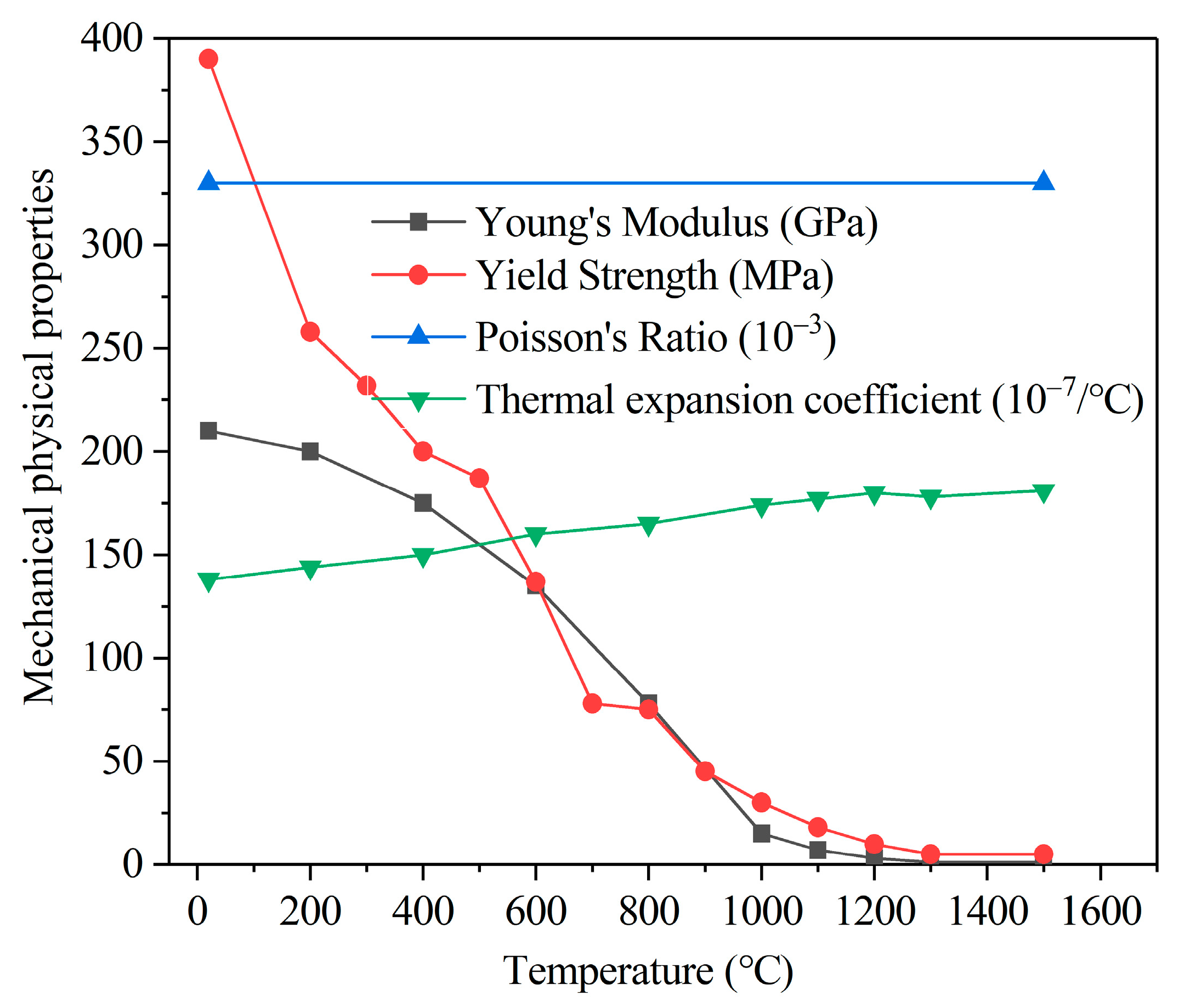
2.1.1. Thermal Analysis
2.1.2. Mechanical Analysis
2.2. Inherent Strain Method (ISM)
2.2.1. Inherent Strain Theory
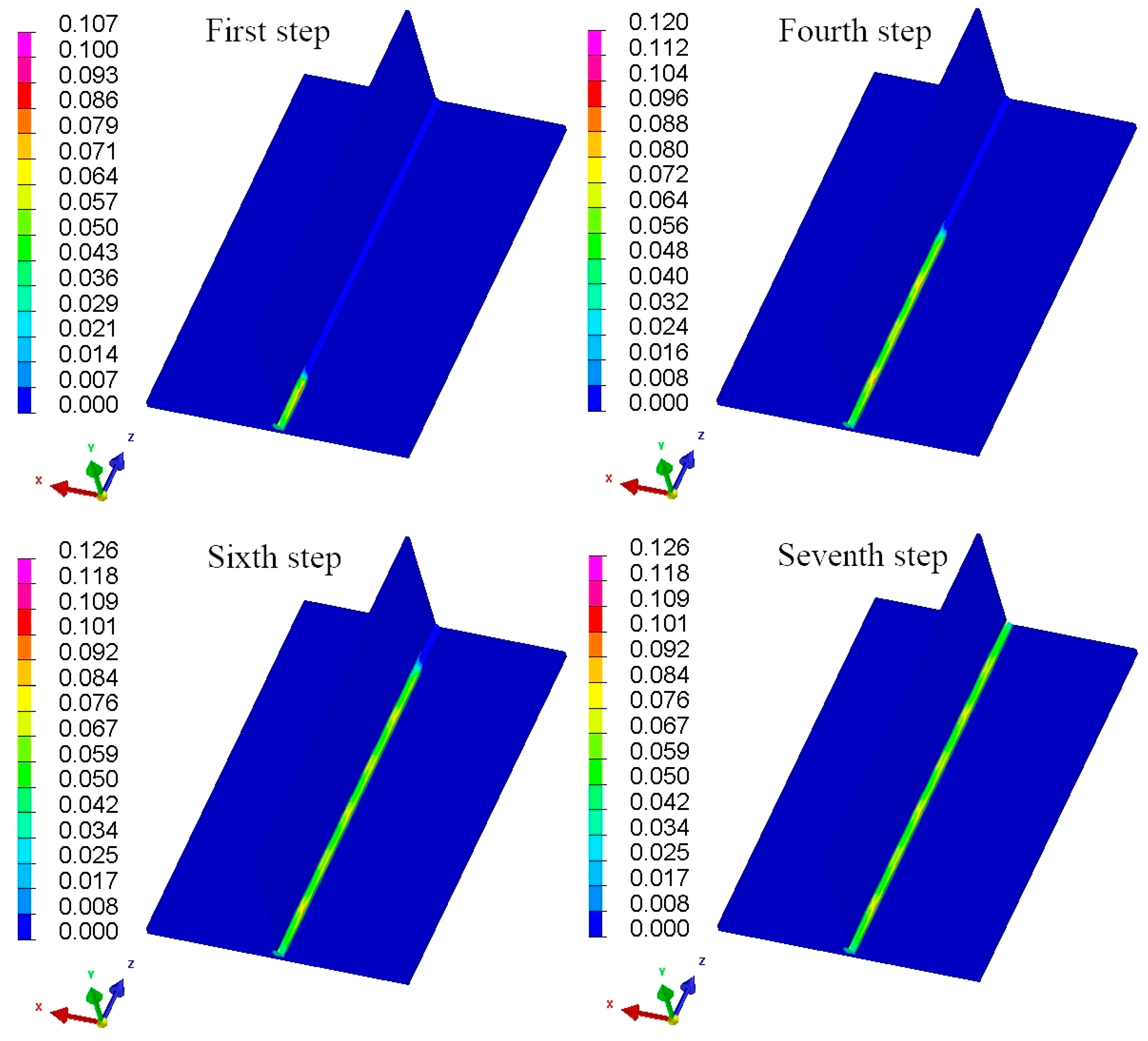
2.2.2. Inherent Strain Acquisition and Loading Methods
3. Numerical Simulation of Local Finite Element Welding Deformation Based on TEP-FEM
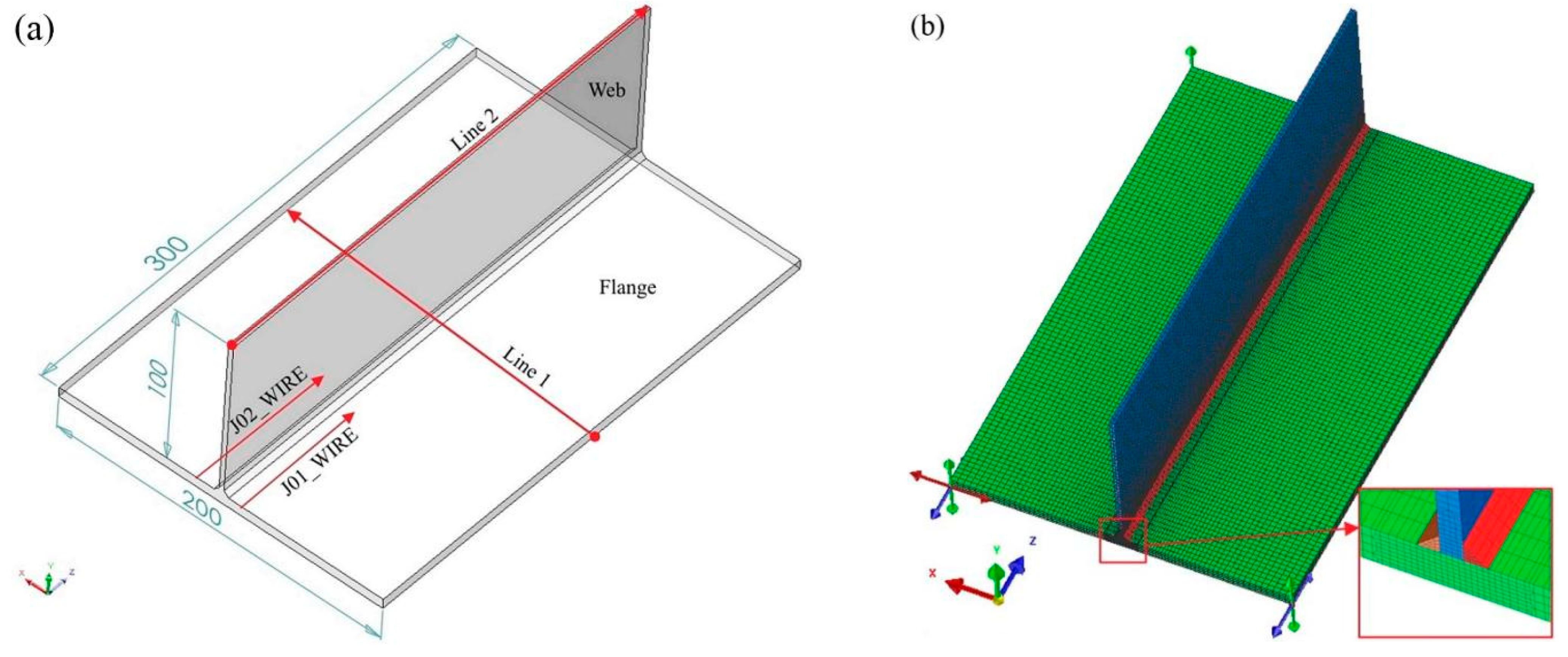
3.1. Local Finite Element Creation and Constraints
3.2. Finding the Optimum Welding Parameters Based on TEP-FEM
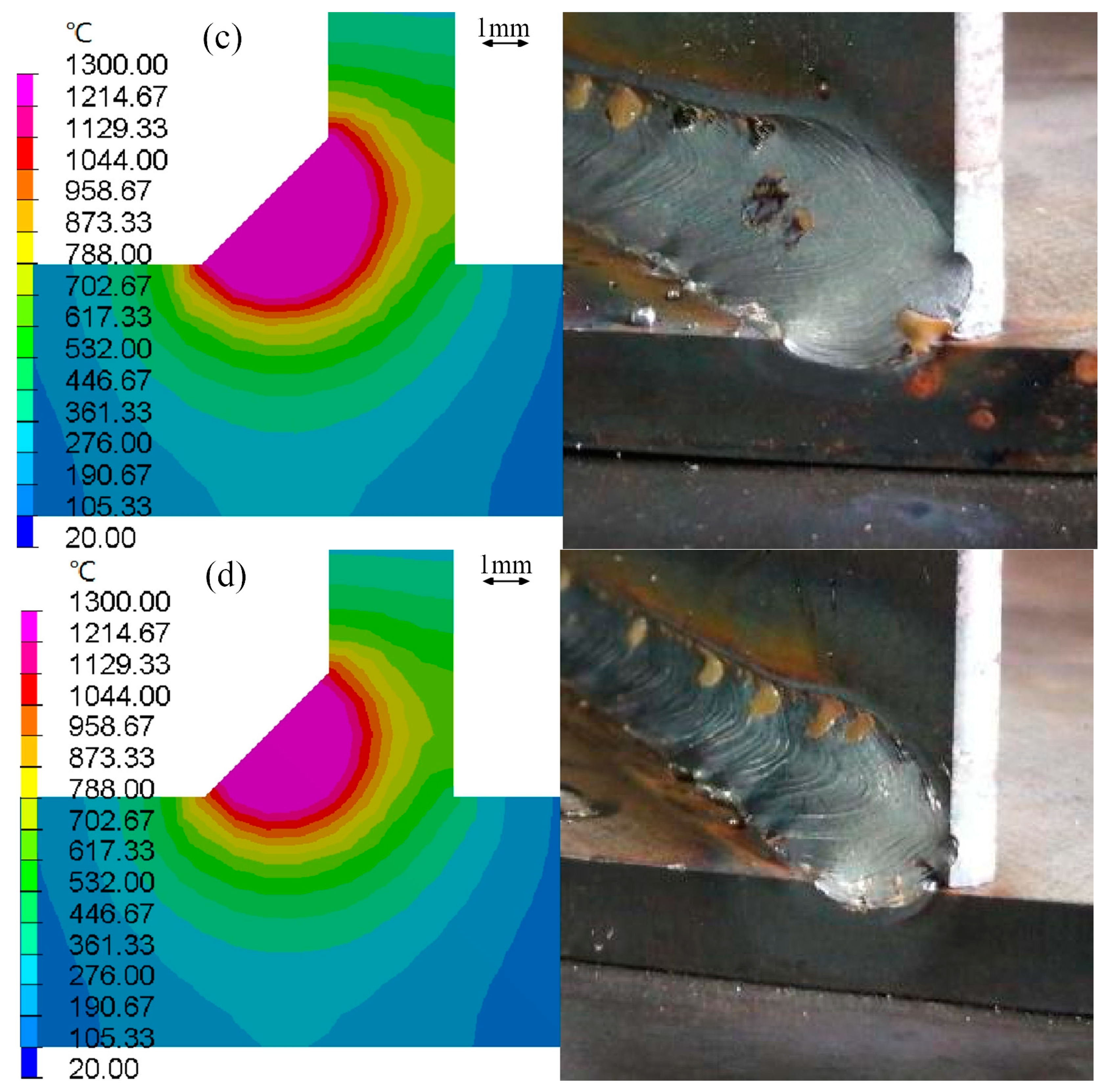
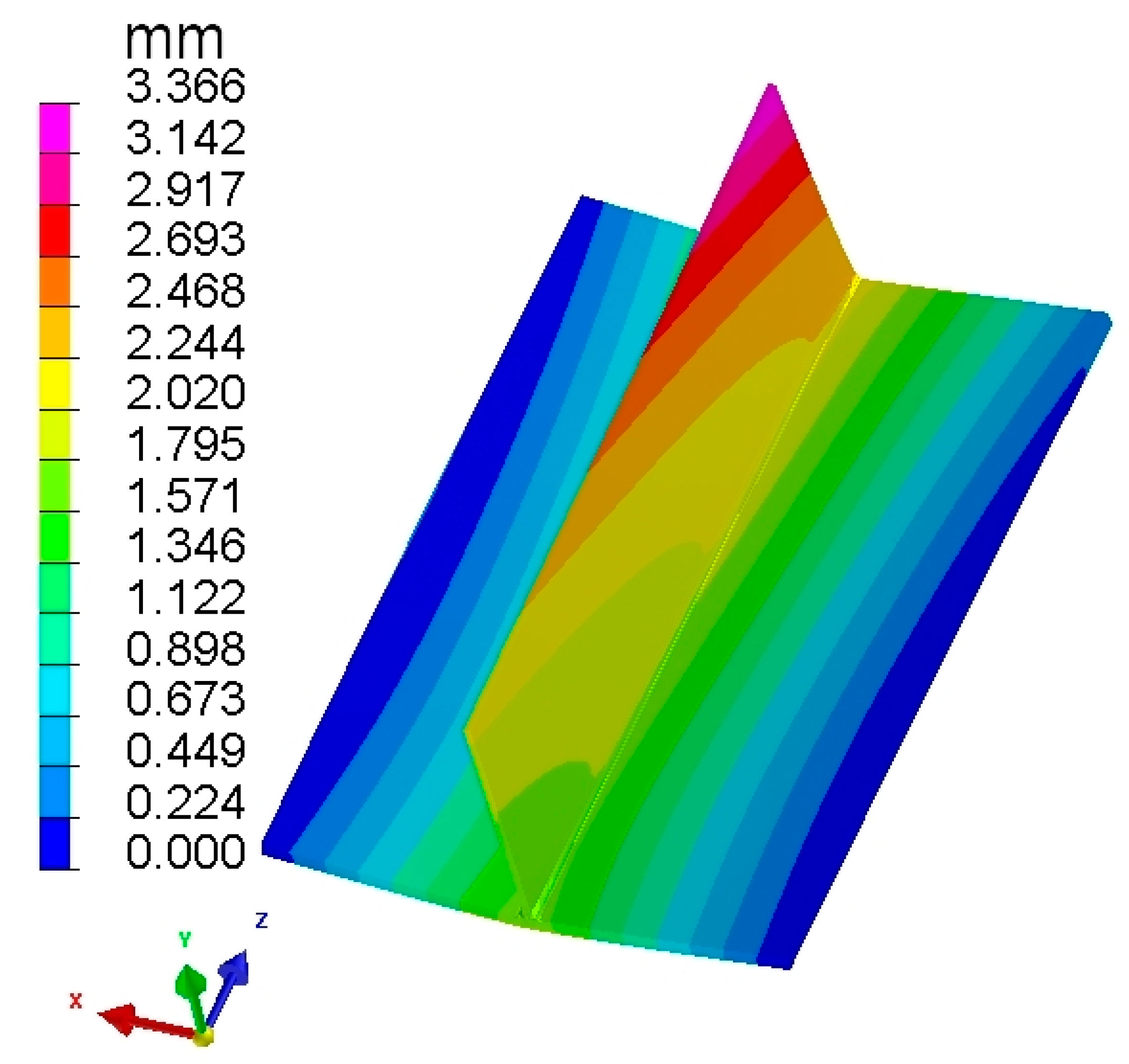
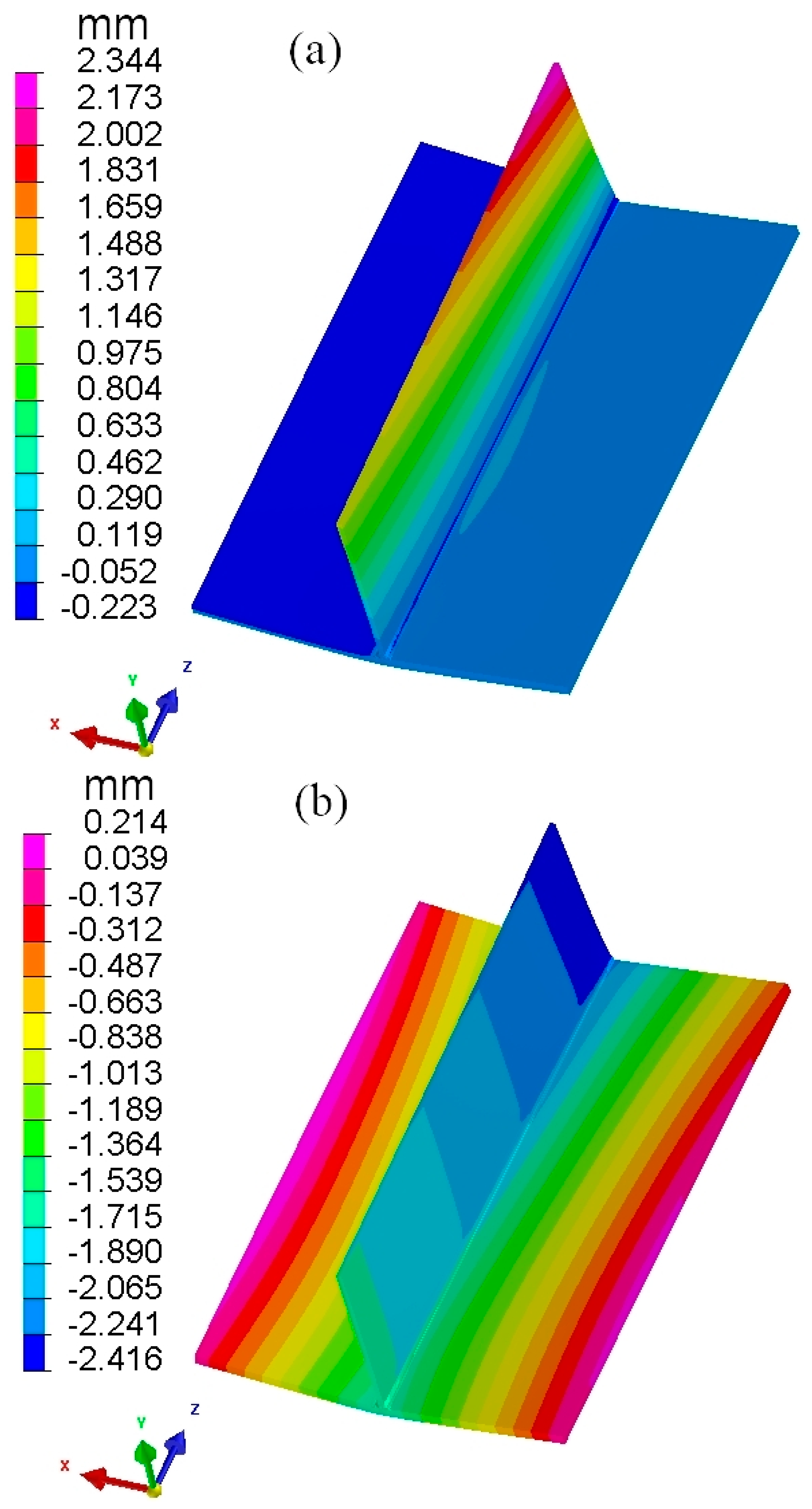
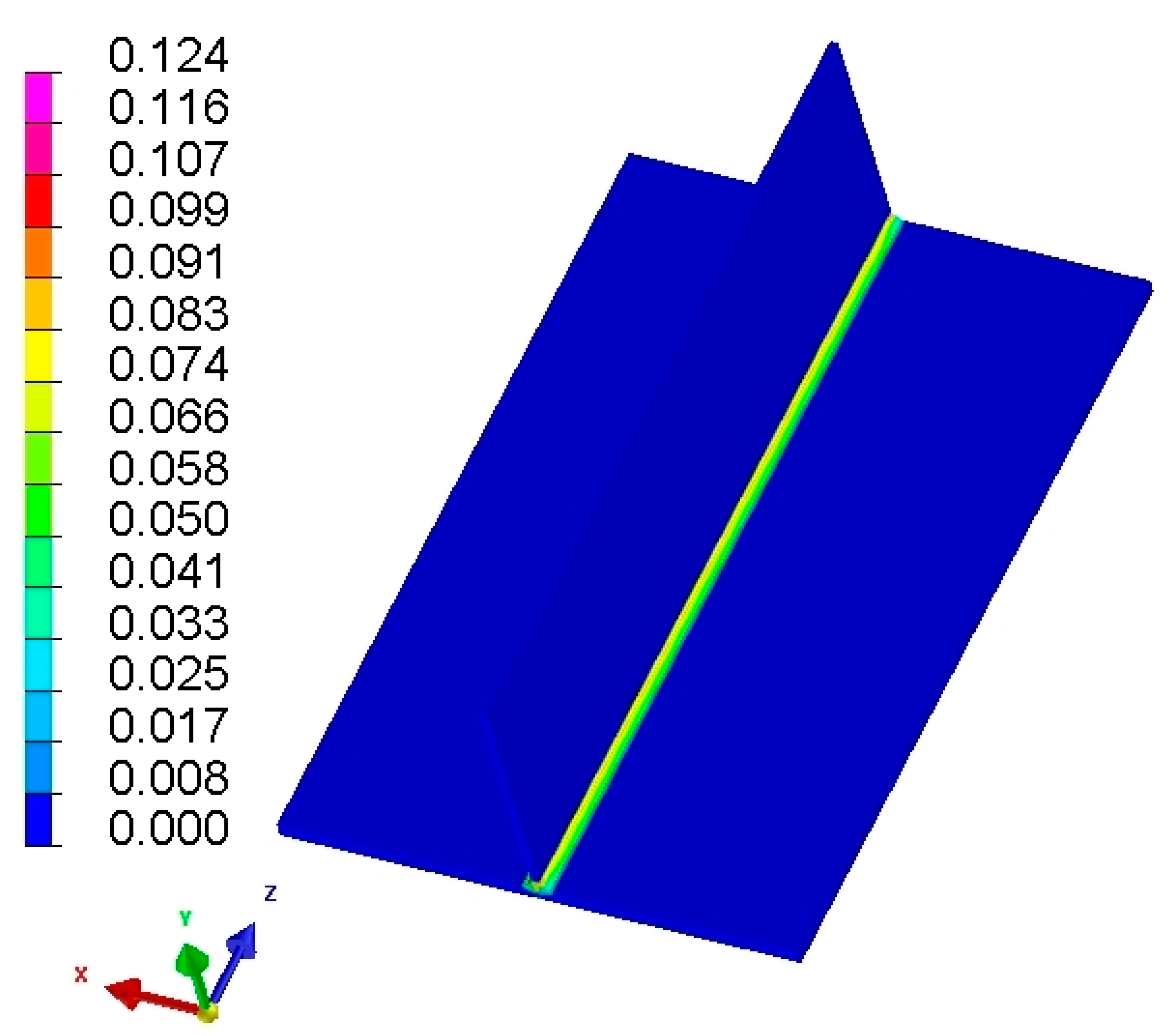
3.3. Numerical Analysis of Local Finite Element Welding Deformation
4. Numerical Simulation of Local Finite Element Welding Deformation Based on ISM
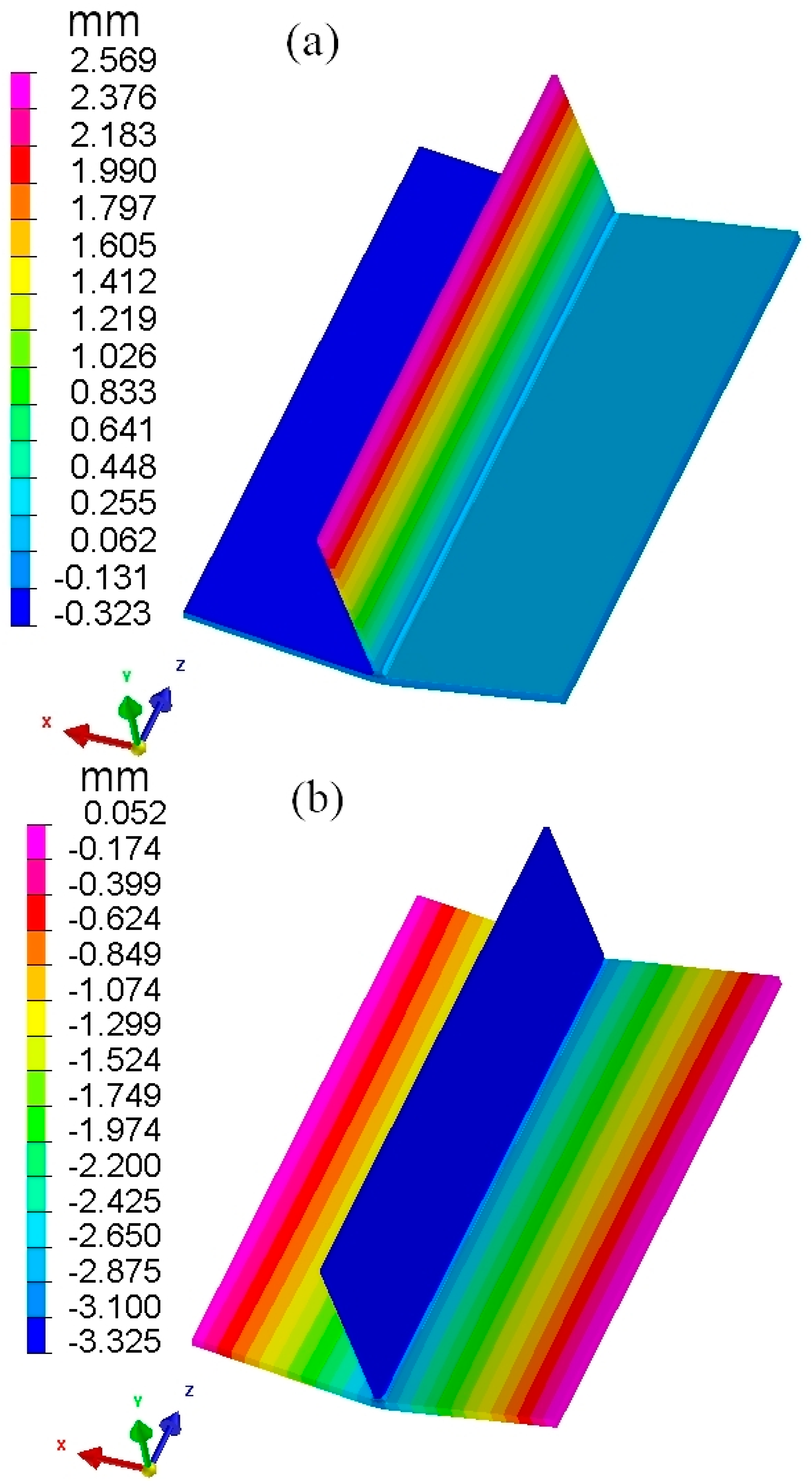
4.1. Numerical Simulation of Local Finite Element Welding Deformation Based on Traditional Inherent Strain Method
4.2. Numerical Simulation of Local Finite Element Welding Deformation Based on the Step-by-Step Loading Inherent Strain Method
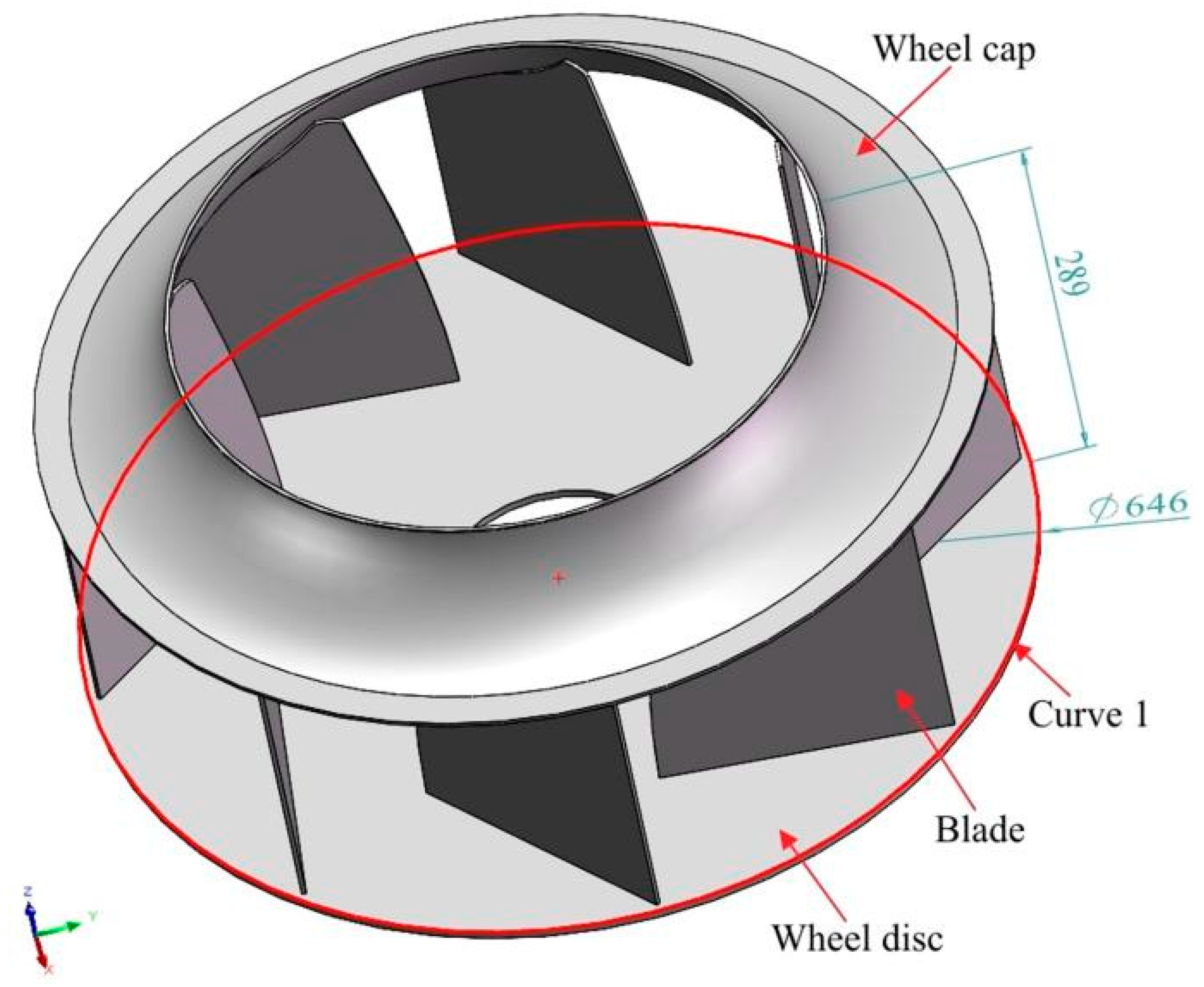
5. Prediction of Welding Deformation for the Backward Centrifugal Fan Impeller
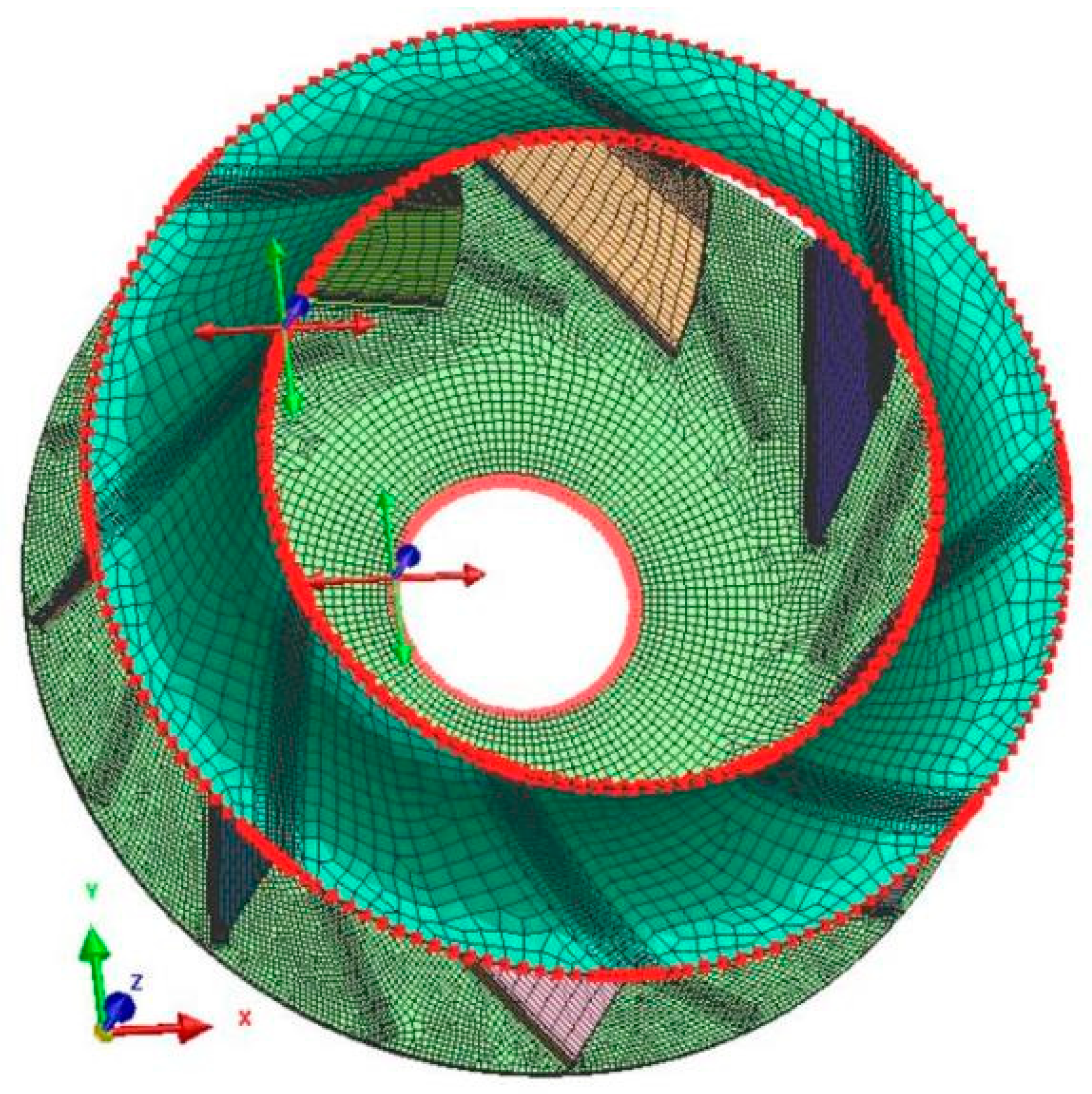
5.1. The Mesh and Constraints of the Backward Centrifugal Fan Impeller
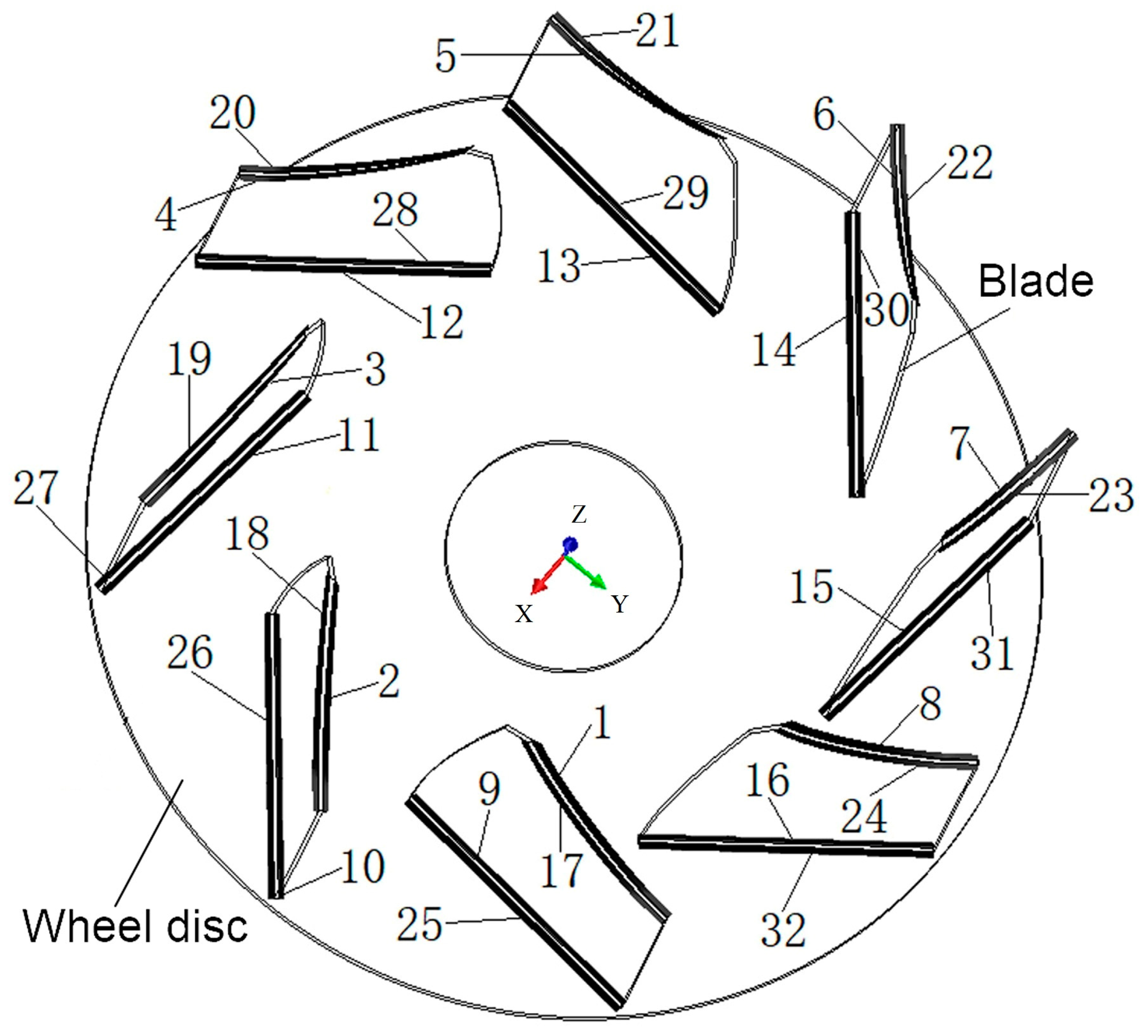
5.2. Welding Sequence Schemes of the Backward Centrifugal Fan Impeller
6. Results and Discussion
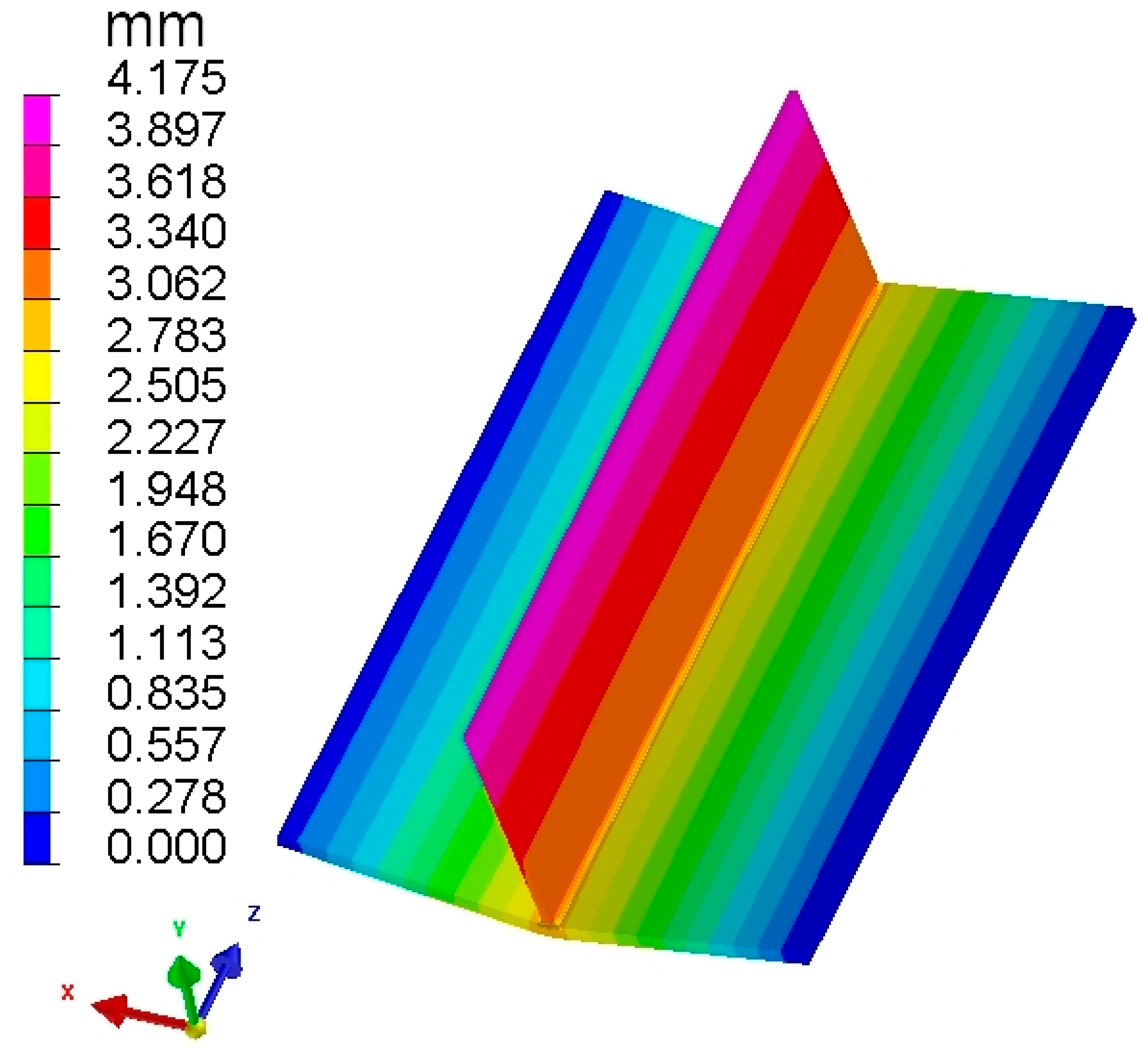
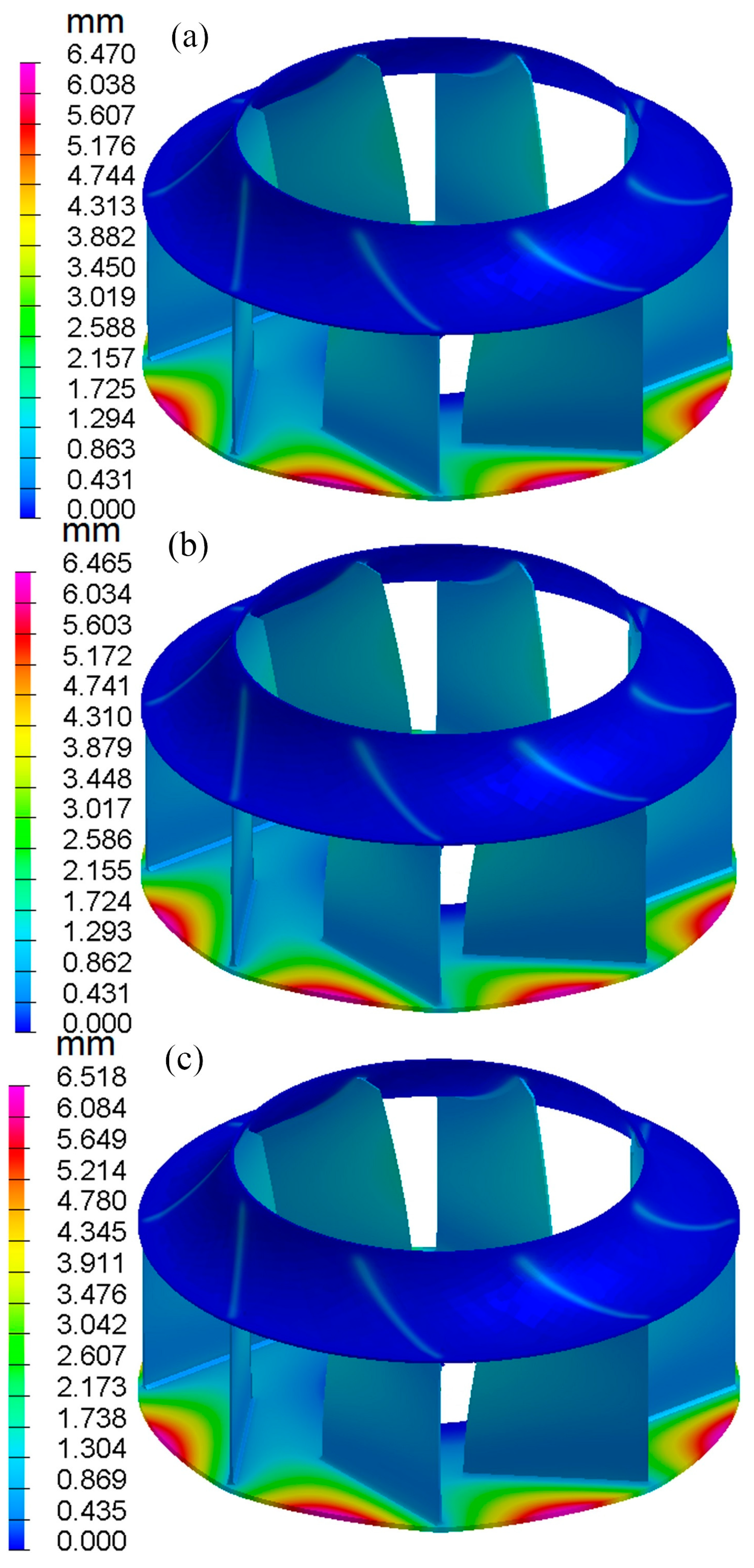
6.1. OS-ISM-Calculated Welding Deformation
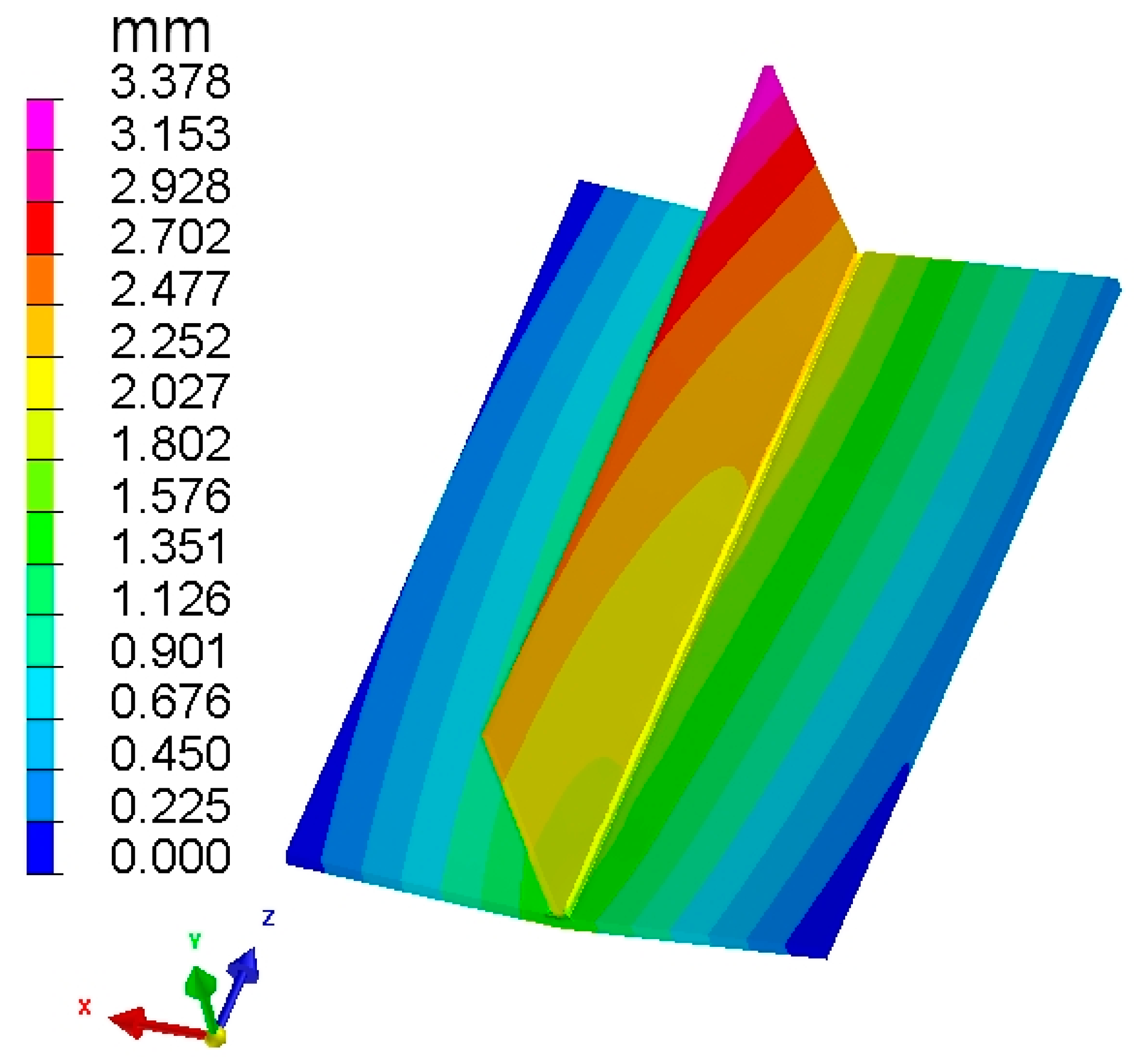
6.2. SBS-ISM-Calculated Welding Deformation
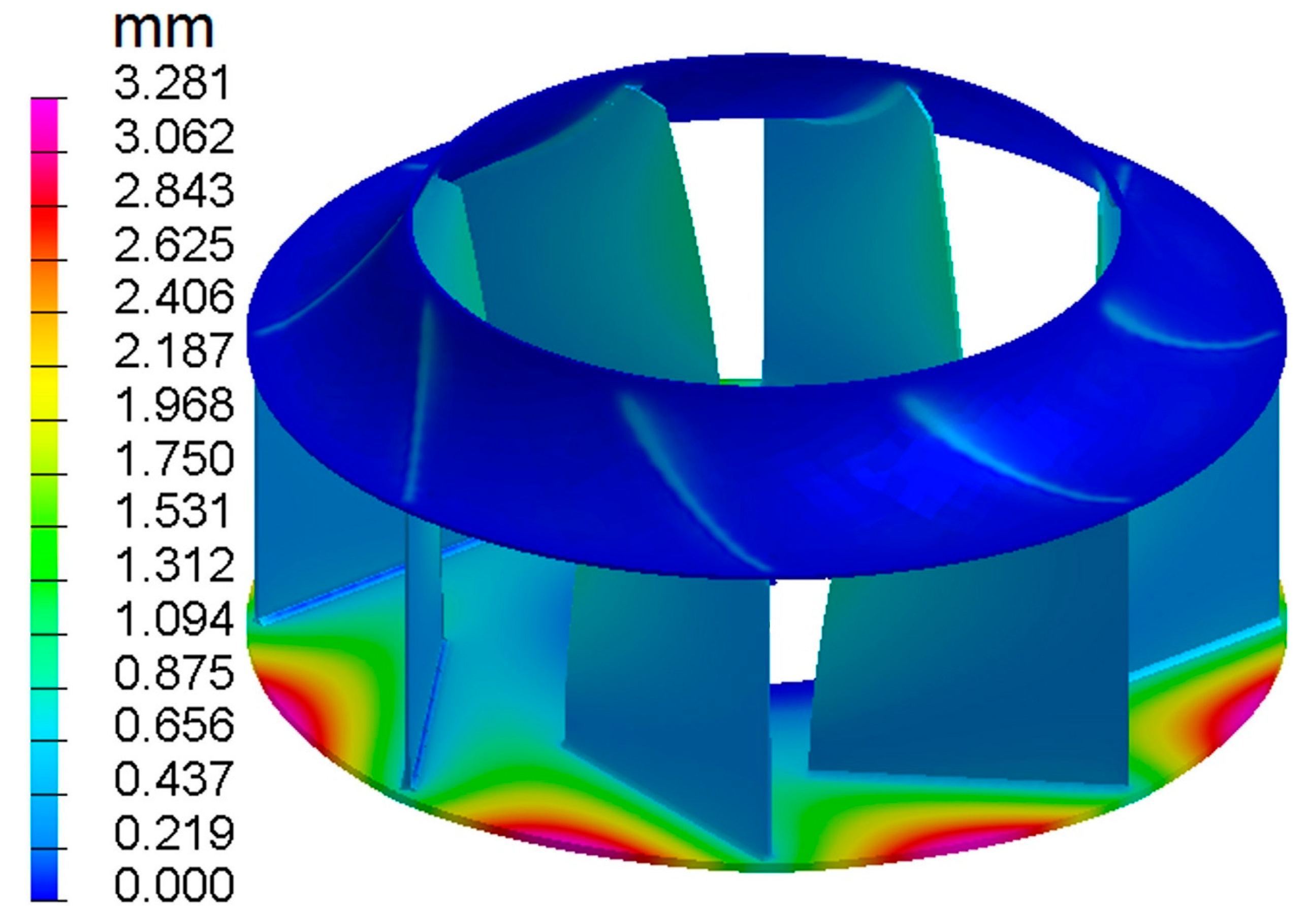
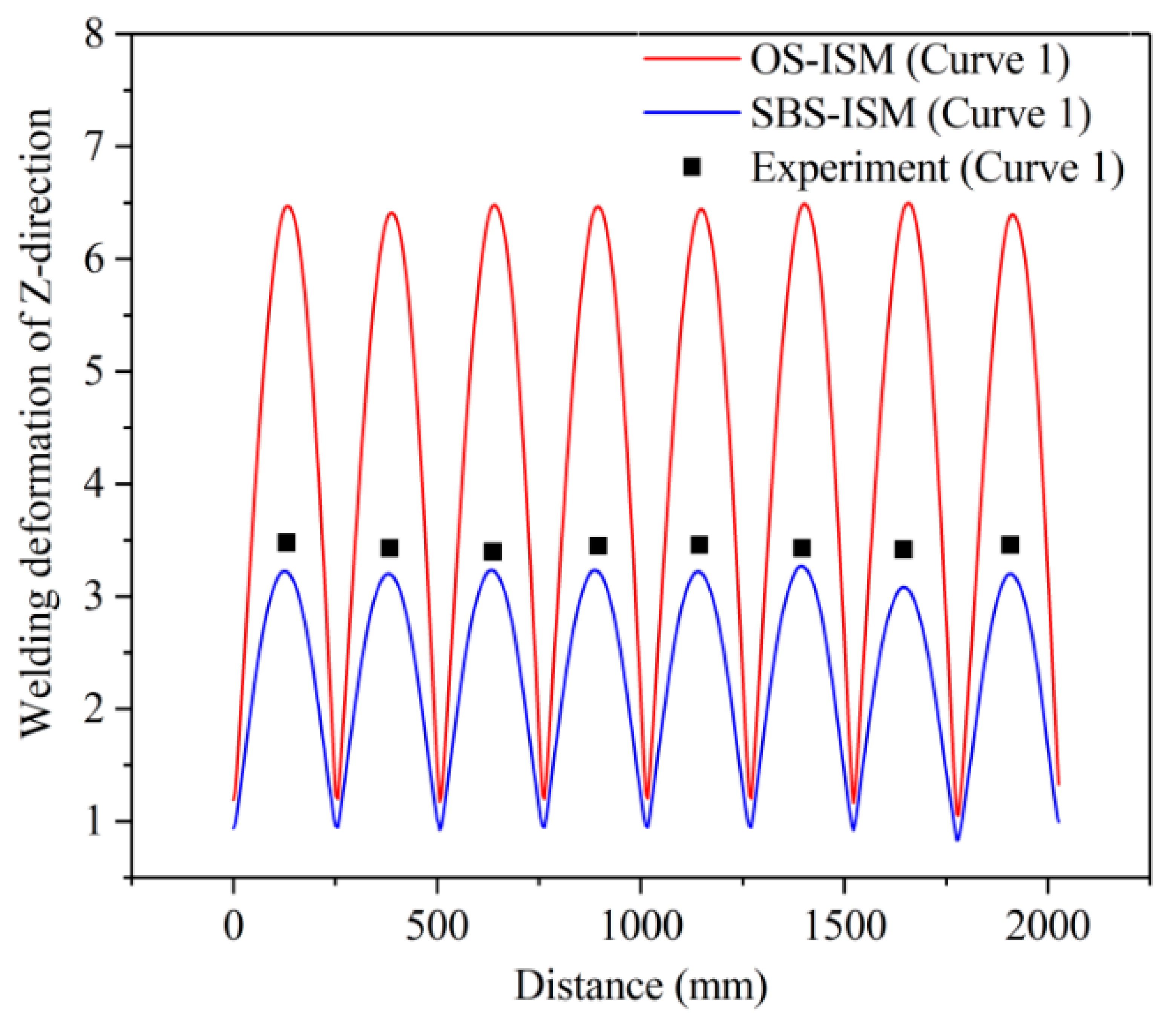
6.3. Comparison of Numerical Simulations with Actual Welding Deformation Produced by Welding
7. Conclusions
- (1)
- Use of the TEP-FEM in combination with a double ellipsoidal heat source model enables accurate simulation of welding pools in accordance with welding parameters, leading to the discovery of optimal welding process parameters and greatly reducing the problem of finding optimal welding parameters experimentally.
- (2)
- The TEP-FEM, used to obtain the residual plastic strain of the local model welded joint, and then combined with the inherent strain-based method, can quickly simulate the welding deformation of different welding sequences, so as to find the optimal welding sequence according to the deformation situation.
- (3)
- For thin-walled T-shaped structures, the step-by-step loading inherent strain method (SBS-ISM) is more in line with the actual process of residual plastic strain generation during welding. Consequently, the welding deformation trends and magnitudes simulated using the SBS-ISM are more consistent with those obtained from TEP-FEM simulations.
- (4)
- Combining the TEP-FEM with the SBS-ISM enables accurate simulation of welding deformation in large and complex thin-walled T-shaped structures such as the backward centrifugal fan impeller. This provides an effective solution for simulating welding deformation in more complex welded structural components.
- (5)
- The SBS-ISM is computed linearly, and although it takes longer than the OS-ISM, its prediction accuracy is comparable to that of the TEP-FEM, and the computational time spent is significantly reduced compared to the TEP-FEM.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Yi, B. Benchmark Investigation of Welding-Induced Buckling and Its Critical Condition during Thin Plate Butt Welding. J. Manuf. Sci. Eng. Trans. ASME 2019, 141, 071010. [Google Scholar] [CrossRef]
- Iranmanesh, M.; Azad, N.; Zabihpoor, M. A New Algorithm on Welding Process of T-Shaped Plates in Ship Hull Structure to Minimize Distortion Based on Thermal Simulation. Ships Offshore Struct. 2014, 9, 489–497. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, J.; Zhang, H.; Liu, J.; Mo, Z. Prediction and Mitigation of Out-of-Plane Welding Distortion of a Typical Block in Fabrication of a Semi-Submersible Lifting and Disassembly Platform. Mar. Struct. 2021, 77, 102964. [Google Scholar] [CrossRef]
- Ueda, Y.; Yamakawa, T. Analysis of Thermal Elastic–Plastic Stress and Strain during Welding by Finite Element Method. Trans. Jpn. Weld Soc. 1971, 2, 186–196. [Google Scholar]
- Ueda, Y.; Murakava, H. Establishment of Computational Welding Mechanics. Weld. Surf. Rev. 1997, 24, 73–86. [Google Scholar]
- Deng, D.; Murakawa, H. Numerical Simulation of Temperature Field and Residual Stress in Multi-Pass Welds in Stainless Steel Pipe and Comparison with Experimental Measurements. Comput. Mater. Sci. 2006, 37, 269–277. [Google Scholar] [CrossRef]
- Ye, Y.; Cai, J.; Jiang, X.; Dai, D.; Deng, D. Influence of Groove Type on Welding-Induced Residual Stress, Deformation and Width of Sensitization Region in a SUS304 Steel Butt Welded Joint. Adv. Eng. Softw. 2015, 86, 39–48. [Google Scholar] [CrossRef]
- Rong, Y.; Chang, Y.; Xu, J.; Huang, Y.; Lei, T.; Wang, C. Numerical Analysis of Welding Deformation and Residual Stress in Marine Propeller Nozzle with Hybrid Laser-Arc Girth Welds. Int. J. Press. Vessel. Pip. 2017, 158, 51–58. [Google Scholar] [CrossRef]
- Bajpei, T.; Chelladurai, H.; Ansari, M.Z. Experimental Investigation and Numerical Analyses of Residual Stresses and Distortions in GMA Welding of Thin Dissimilar AA5052-AA6061 Plates. J. Manuf. Process. 2017, 25, 340–350. [Google Scholar] [CrossRef]
- Hu, J.; Tsai, H.L. Modelling of Transport Phenomena in 3D GMAW of Thick Metals with v Groove. J. Phys. D Appl. Phys. 2008, 41, 065202. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Babu, A.; Kleijn, C.R.; Hermans, M.J.M.; Richardson, I.M. The Effect of Groove Shape on Molten Metal Flow Behaviour in Gas Metal Arc Welding. Materials 2021, 14, 7444. [Google Scholar] [CrossRef] [PubMed]
- Ueda, Y.; Yuan, M.G. Prediction of Welding Residual Stresses in T and I Joints Using Inherent Strains. 3rd Report: Method for Prediction of Welding Residual Stress Using Residual Stress Generation Source. Weld. Int. 1992, 6, 263–269. [Google Scholar] [CrossRef]
- Ueda, Y.; Yuan, M.G.; Mochizuki, M.; Umezawa, S.; Enomoto, K. Experimental Verification of a Method for Prediction of Welding Residual Stresses in T Joints Using Inherent Strains 4th Report: Method for Prediction Using Source of Residual Stress. Weld. Int. 1993, 7, 863–869. [Google Scholar] [CrossRef]
- Deng, D.; Murakawa, H.; Liang, W. Numerical Simulation of Welding Distortion in Large Structures. Comput. Methods Appl. Mech. Eng. 2007, 196, 4613–4627. [Google Scholar] [CrossRef]
- Deng, D.; Murakawa, H. Prediction of Welding Distortion and Residual Stress in a Thin Plate Butt-Welded Joint. Comput. Mater. Sci. 2008, 43, 353–365. [Google Scholar] [CrossRef]
- Deng, D.; Murakawa, H. FEM Prediction of Buckling Distortion Induced by Welding in Thin Plate Panel Structures. Comput. Mater. Sci. 2008, 43, 591–607. [Google Scholar] [CrossRef]
- Sulaiman, M.S.; Manurung, Y.H.P.; Haruman, E.; Rahim, M.R.A.; Redza, M.R.; Lidam, R.N.A.; Abas, S.K.; Tham, G.; Chau, C.Y. Simulation and Experimental Study on Distortion of Butt and T-Joints Using WELD PLANNER. J. Mech. Sci. Technol. 2011, 25, 2641–2646. [Google Scholar] [CrossRef]
- Manurung, Y.H.P.; Sulaiman, M.S.; Abas, S.K.; Tham, G.; Haruman, E. Investigation on Welding Distortion of Combined Butt and T-Joints with 9-Mm Thickness Using FEM and Experiment. Int. J. Adv. Manuf. Technol. 2015, 77, 775–782. [Google Scholar] [CrossRef]
- Shen, Y.; Liu, S.; Yuan, M.; Dai, X.; Lan, J. Immune Optimization of Double-Sided Welding Sequence for Medium-Small Assemblies in Ships Based on Inherent Strain Method. Metals 2022, 12, 1091. [Google Scholar] [CrossRef]
- Chino, T.; Kunugi, A.; Kawashima, T.; Watanabe, G.; Can, C.; Ma, N. Fast Prediction for Resistance Spot Welding Deformation Using Inherent Strain Method and Nugget Model. Materials 2021, 14, 7180. [Google Scholar] [CrossRef]
- Liang, W.; Deng, D.; Sone, S. Prediction of Welding Distortion by Elastic Finite Element Analysis using Inherent Deformation Estimated Through Inverse Analysis. Weld. World. 2005, 49, 30–39. [Google Scholar] [CrossRef]
- Wang, J.; Shi, X.; Zhou, H.; Yang, Z.; Liu, J. Dimensional Precision Controlling on Out-of-Plane Welding Distortion of Major Structures in Fabrication of Ultra Large Container Ship with 20000TEU. Ocean. Eng. 2020, 199, 106993. [Google Scholar] [CrossRef]
- Ma, N.; Tateishi, J.; Hiroi, S.; Kunugi, A.; Huang, H. Fast Prediction of Welding Distortion of Large Structures Using Inherent Deformation Database and Comparison with Measurement. Q. J. Jpn. Weld. Soc. 2017, 35, 137s–140s. [Google Scholar] [CrossRef]
- Hammad, A.; Churiaque, C.; Sánchez-Amaya, J.M.; Abdel-Nasser, Y. Experimental and Numerical Investigation of Hybrid Laser Arc Welding Process and the Influence of Welding Sequence on the Manufacture of Stiffened Flat Panels. J. Manuf. Process. 2021, 61, 527–538. [Google Scholar] [CrossRef]
- Lu, Y.; Zhu, S.; Zhao, Z.; Chen, T.; Zeng, J. Numerical Simulation of Residual Stresses in Aluminum Alloy Welded Joints. J. Manuf. Process. 2020, 50, 380–393. [Google Scholar] [CrossRef]
- Suman, S.; Biswas, P. Finite Element Analysis of In- Process Thermal Mitigation of Welding Induced Residual Stresses in 9Cr-1Mo-V Steel Butt Joint Considering Phase Transformation. J. Manuf. Process. 2021, 70, 361–375. [Google Scholar] [CrossRef]
- Ghafouri, M.; Ahola, A.; Ahn, J.; Björk, T. Numerical and Experimental Investigations on the Welding Residual Stresses and Distortions of the Short Fillet Welds in High Strength Steel Plates. Eng. Struct. 2022, 260, 114269. [Google Scholar] [CrossRef]
- ESI Group. Visual-Environment (Version 18.0)-Material Database. Windows. Paris. ESI Group. Available online: https://myesi.esi-group.com/downloads/software-downloads/visual-environment-18.0 (accessed on 12 June 2023).
- ESI Group. Visual-Environment (Version 18.0)-Visual-Weld. Windows. Paris. ESI Group. Available online: https://myesi.esi-group.com/downloads/software-documentation/visual-environment-18.0-user-guide-visual-weld-online (accessed on 12 June 2023).
- Chen, J.; Wu, C.S.; Chen, M.A. Improvement of Welding Heat Source Models for TIG-MIG Hybrid Welding Process. J. Manuf. Process. 2014, 16, 485–493. [Google Scholar] [CrossRef]
- Goldak, J.; Chakravarti, A.; Bibby, M. A New Finite Element Model for Welding Heat Sources. Metall. Trans. B 1984, 15, 299–305. [Google Scholar] [CrossRef]
- Yang, Y.P. Recent Advances in the Prediction of Weld Residual Stress and Distortion’ Part 1: A Comprehensive Review of the Numerical Modeling Theory and Methods for Predicting Weld Residual Stress and Distortion. Weld. J. 2021, 100, 151S–170S. [Google Scholar] [CrossRef]
- Hu, X.; Feng, G.; Wang, Y.; Zhang, C.; Deng, D. Influence of Lumping Passes on Calculation Accuracy and Efficiency of Welding Residual Stress of Thick-Plate Butt Joint in Boiling Water Reactor. Eng. Struct. 2020, 222, 111136. [Google Scholar] [CrossRef]
- Zhang, K.; Dong, W.; Lu, S. Finite Element and Experiment Analysis of Welding Residual Stress in S355J2 Steel Considering the Bainite Transformation. J. Manuf. Process. 2021, 62, 80–89. [Google Scholar] [CrossRef]
- Zubairuddin, M.; Albert, S.K.; Vasudevan, M.; Mahadevan, S.; Chaudhari, V.; Suri, V.K. Numerical Simulation of Multi-Pass GTA Welding of Grade 91 Steel. J. Manuf. Process. 2017, 27, 87–97. [Google Scholar] [CrossRef]
- Chen, Q.; Yang, J.; Liu, X.; Tang, J.; Huang, B. Effect of the Groove Type When Considering a Thermometallurgical-Mechanical Model of the Welding Residual Stress and Deformation in an S355JR-316L Dissimilar Welded Joint. J. Manuf. Process. 2019, 45, 290–303. [Google Scholar] [CrossRef]
- Li, S.; Hu, L.; Dai, P.; Bi, T.; Deng, D. Influence of the Groove Shape on Welding Residual Stresses in P92/SUS304 Dissimilar Metal Butt-Welded Joints. J. Manuf. Process. 2021, 66, 376–386. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Q.; Qian, L.; Yang, Y. A Modified Inherent Strain Model with Consideration of the Variance of Mechanical Properties in Metal Additive Manufacturing. J. Manuf. Process. 2021, 72, 115–125. [Google Scholar] [CrossRef]
- Lu, Y.; Lu, C.; Zhang, D.; Chen, T.; Zeng, J.; Wu, P. Numerical Computation Methods of Welding Deformation and Their Application in Bogie Frame for High-Speed Trains. J. Manuf. Process. 2019, 38, 204–213. [Google Scholar] [CrossRef]
- Biswas, P.; Mandal, N.R.; Das, S. Prediction of Welding Deformations of Large Stiffened Panels Using Average Plastic Strain Method. Sci. Technol. Weld. Join. 2011, 16, 227–231. [Google Scholar] [CrossRef]





| Parameter | af (mm) | ar (mm) | b (mm) | c (mm) | ff | fr |
|---|---|---|---|---|---|---|
| Value | 5 | 10 | 2.15 | 2.3 | 0.67 | 1.33 |
| Welding Method | Current (A) | Voltage (V) | Diameter of Welding Wire (mm) | Welding Speed (m/min) | Welding Efficiency () | Protective Gases | Gas Flow Rate (L/min) |
|---|---|---|---|---|---|---|---|
| MAG | 160 | 22 | 1.2 | 0.35 | 0.8 | 80%Ar + 20%CO2 | 15 |
| 0.45 | |||||||
| 0.55 | |||||||
| 0.65 |
| Welding Methods | Current (A) | Voltage (V) | Diameter of Welding Wire (mm) | Welding Speed (m/min) | Welding Efficiency () | Protective Gases | Gas Flow Rate (L/min) |
|---|---|---|---|---|---|---|---|
| MAG | 160 | 22 | 1.2 | 0.55 | 0.8 | 80%Ar + 20%CO2 | 15 |
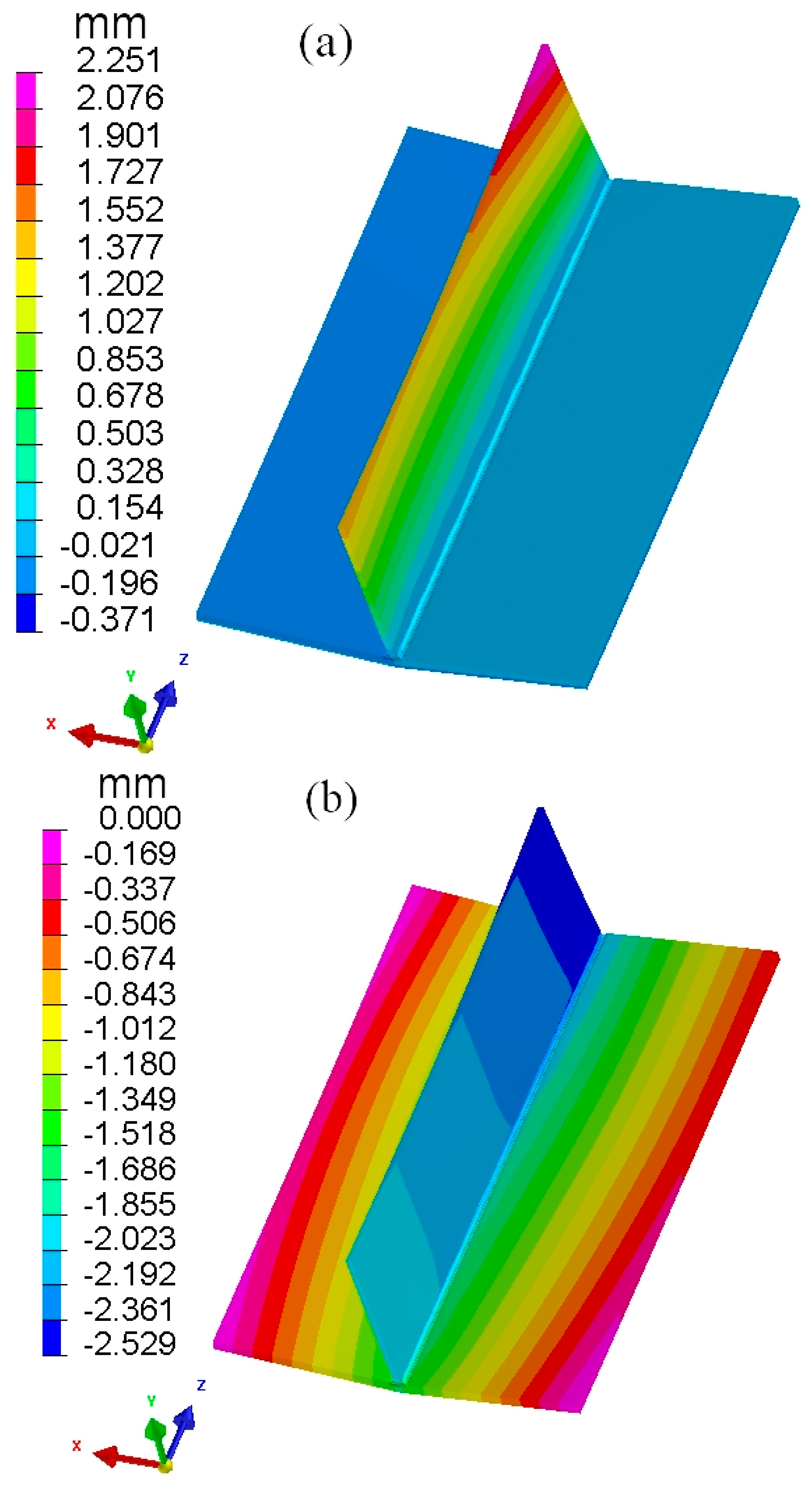
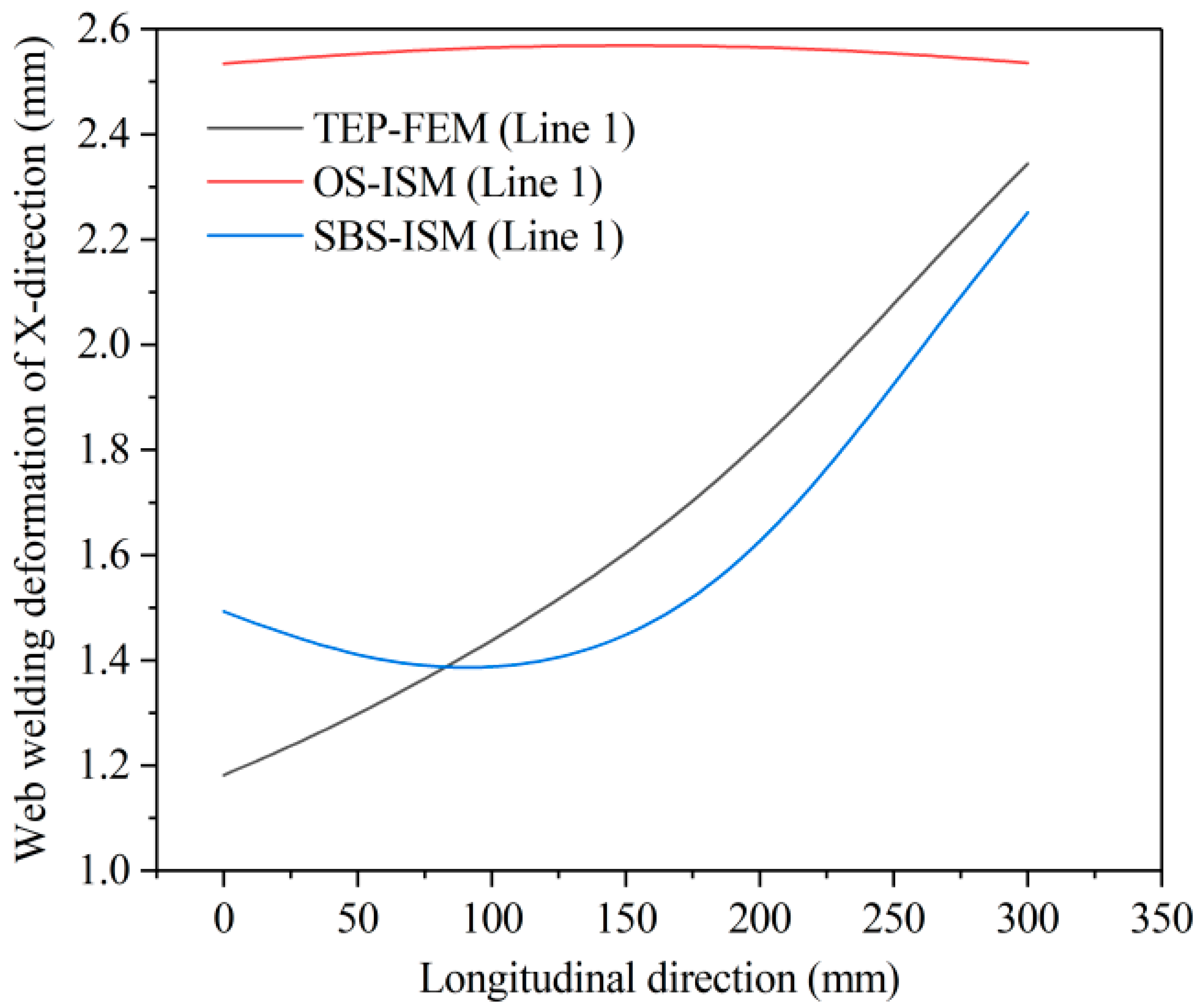
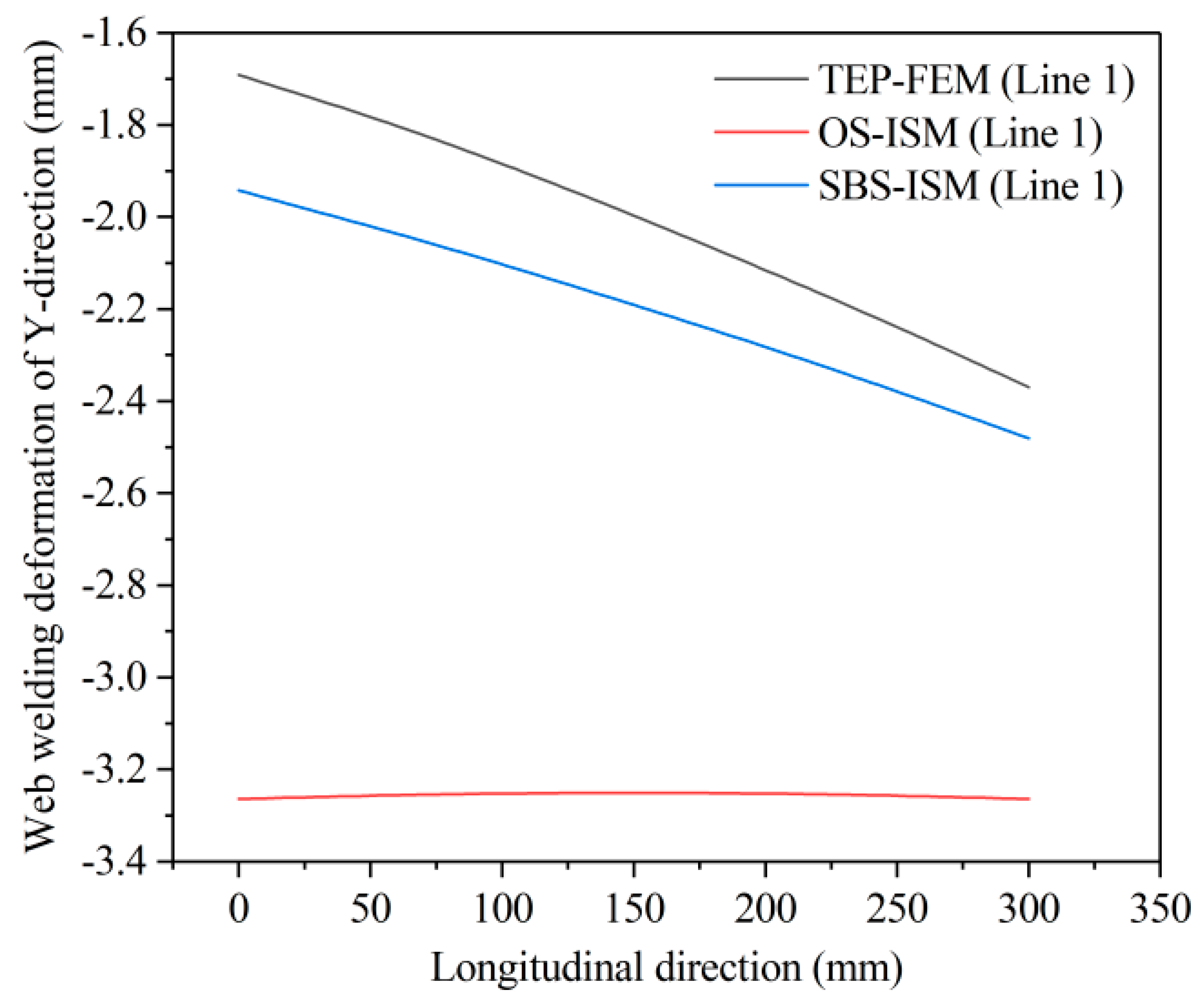
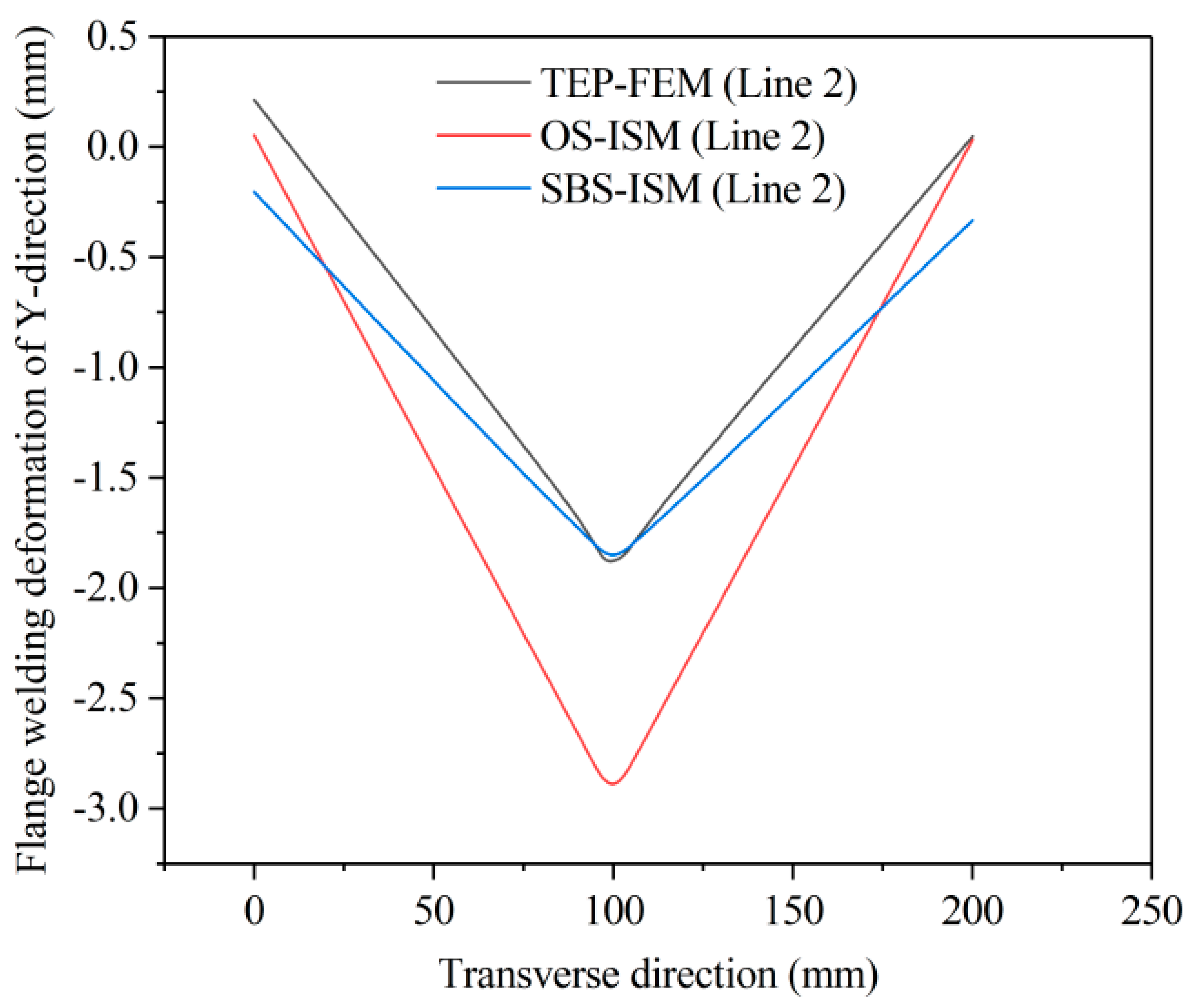
| Methods | Overall Maximum Deformation (with TEP-FEM Errors) | Maximum Deformation in X-Direction (with TEP-FEM Errors) | Maximum Deformation in Y-Direction (with TEP-FEM Errors) |
|---|---|---|---|
| TEP-FEM | 3.366 | 2.344 | −2.416 |
| OS-ISM | 4.175 (24%) | 2.569 (9.6%) | −3.325 (37.6%) |
| SBS-ISM | 3.378 (0.35%) | 2.251 (3.97%) | −2.529 (4.67%) |
| Schemes | Welding Sequences |
|---|---|
| 1 | 1 → 2 → 3 → 4 → 5 → 6 → 7 → 8 → 9 → 10 → 11 → 12 → 13 → 14 → 15 → 16 → 17 → 18 → 19 → 20 → 21 → 22 → 23 → 24 → 25 → 26 → 27 → 28 → 29 → 30 → 31 → 32 |
| 2 | 1 → 9 → 2 → 10 → 3 → 11 → 4 → 12 → 5 → 13 → 6 → 14 → 7 → 15 → 8 → 16 → 17 → 25 → 18 → 26 → 19 → 27 → 20 → 28 → 21 → 29 → 22 → 30 → 23 → 31 → 24 → 32 |
| 3 | 24 → 32 → 1 → 9 → 17 → 25 → 2 → 10 → 18 → 26 → 3 → 11 → 19 → 27 → 4 → 12 → 20 → 28 → 5 → 13 → 21 → 29 → 6 → 14 → 22 → 30 → 7 → 15 → 23 → 31 → 8 → 16 |
| Schemes | Overall Deformation | X-Direction | Y-Direction | Z-Direction |
|---|---|---|---|---|
| 1 | 6.470 | 1.531 | 1.518 | 6.451 |
| 2 | 6.465 | 1.511 | 1.478 | 6.447 |
| 3 | 6.518 | 1.405 | 1.339 | 6.500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Miao, Y.; Hu, G.; Zhao, Y.; Deng, Q. Numerical Simulations and Experimental Verification of T-Structure Welding Deformation Using the Step-by-Step Loading Inherent Strain Method. Metals 2023, 13, 1312. https://doi.org/10.3390/met13071312
Wang L, Miao Y, Hu G, Zhao Y, Deng Q. Numerical Simulations and Experimental Verification of T-Structure Welding Deformation Using the Step-by-Step Loading Inherent Strain Method. Metals. 2023; 13(7):1312. https://doi.org/10.3390/met13071312
Chicago/Turabian StyleWang, Lin, Yugang Miao, Guangxu Hu, Yuyang Zhao, and Qingwen Deng. 2023. "Numerical Simulations and Experimental Verification of T-Structure Welding Deformation Using the Step-by-Step Loading Inherent Strain Method" Metals 13, no. 7: 1312. https://doi.org/10.3390/met13071312
APA StyleWang, L., Miao, Y., Hu, G., Zhao, Y., & Deng, Q. (2023). Numerical Simulations and Experimental Verification of T-Structure Welding Deformation Using the Step-by-Step Loading Inherent Strain Method. Metals, 13(7), 1312. https://doi.org/10.3390/met13071312





