Damage Distribution Map Based Damage Accumulation Calculation Approach for Welded Joints
Abstract
1. Introduction
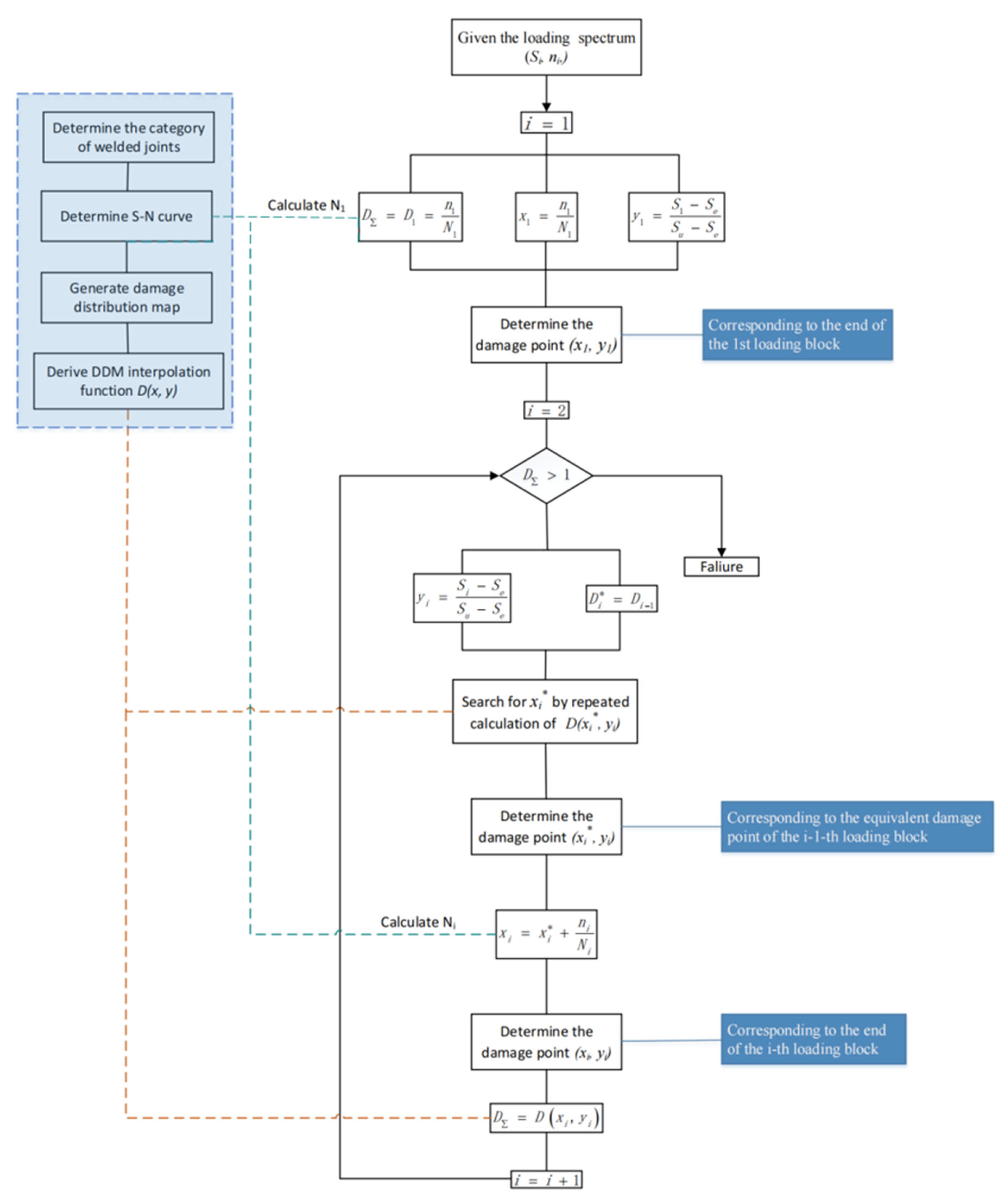
2. The Proposed Approach and Its Calculation Process
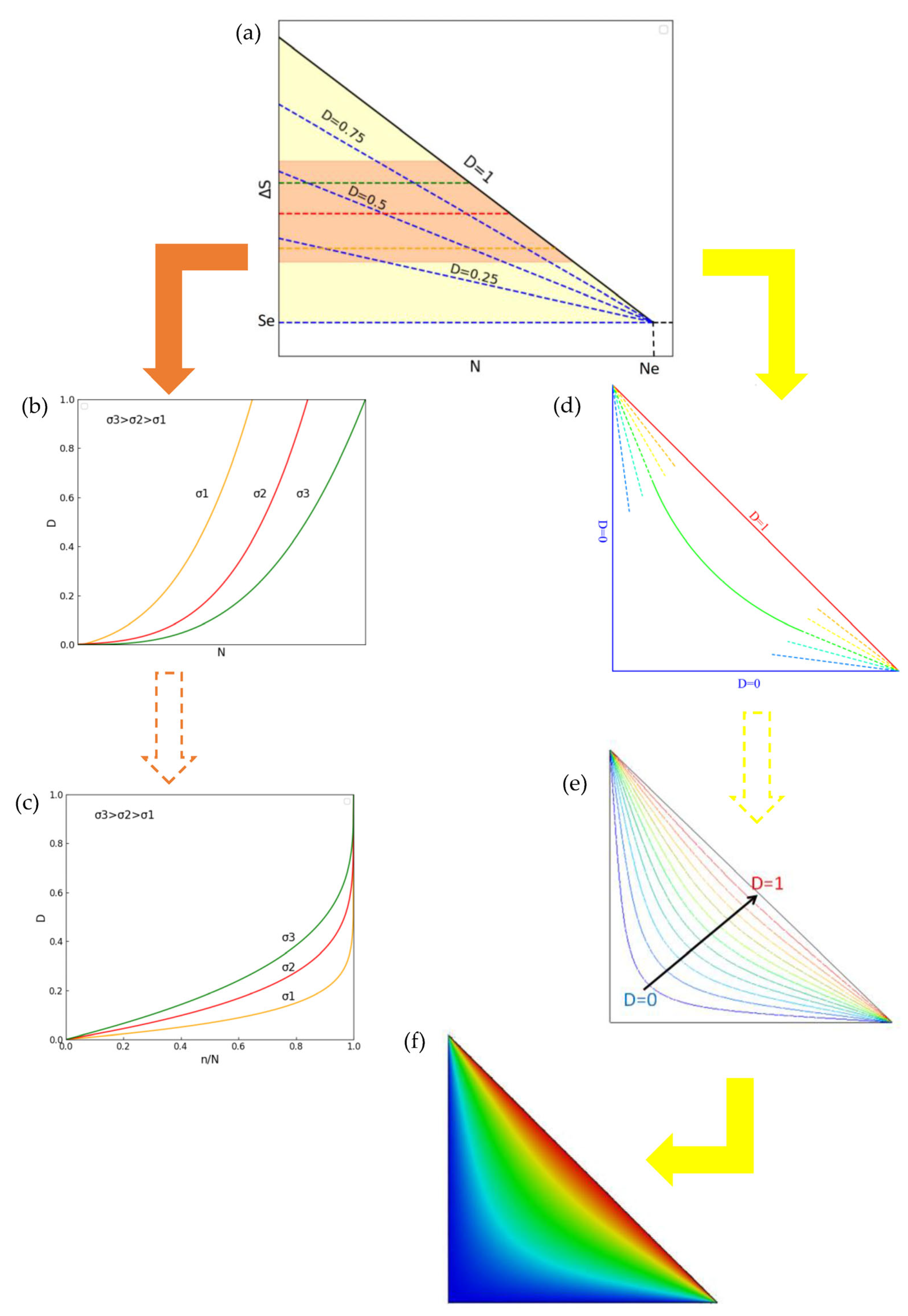
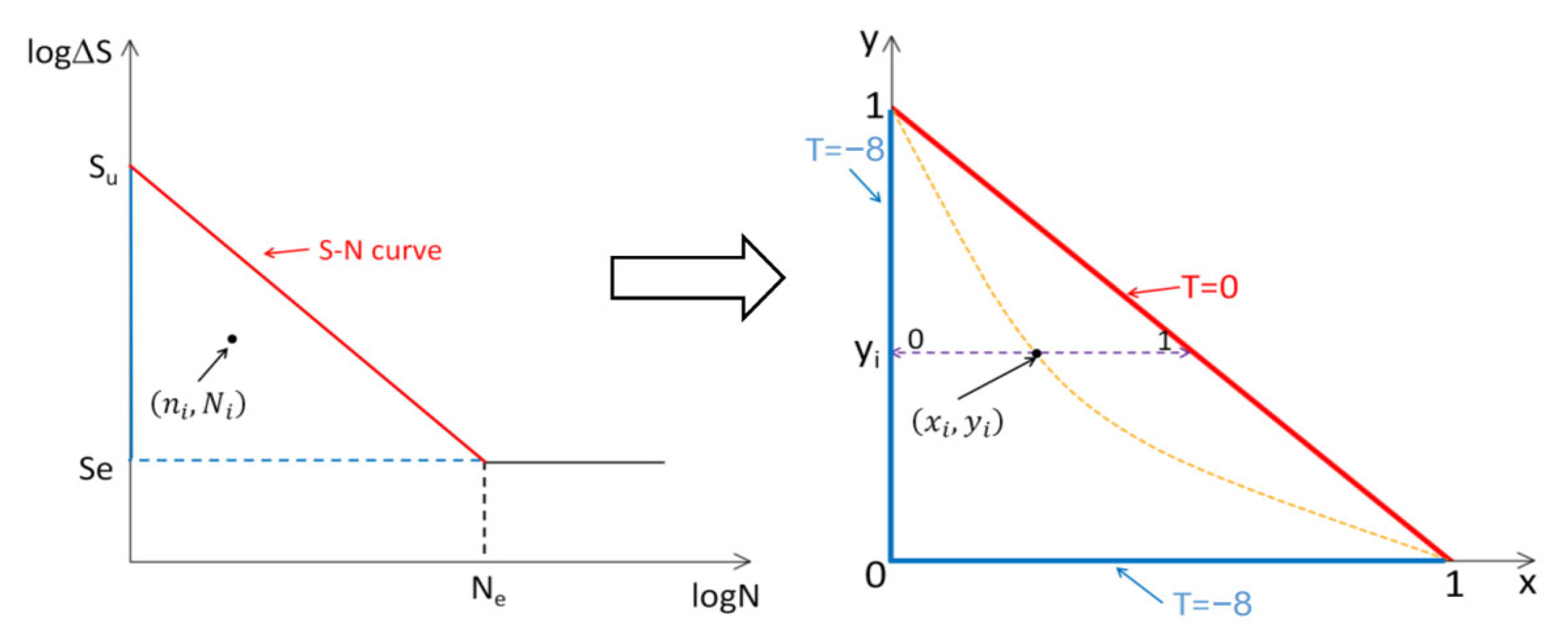
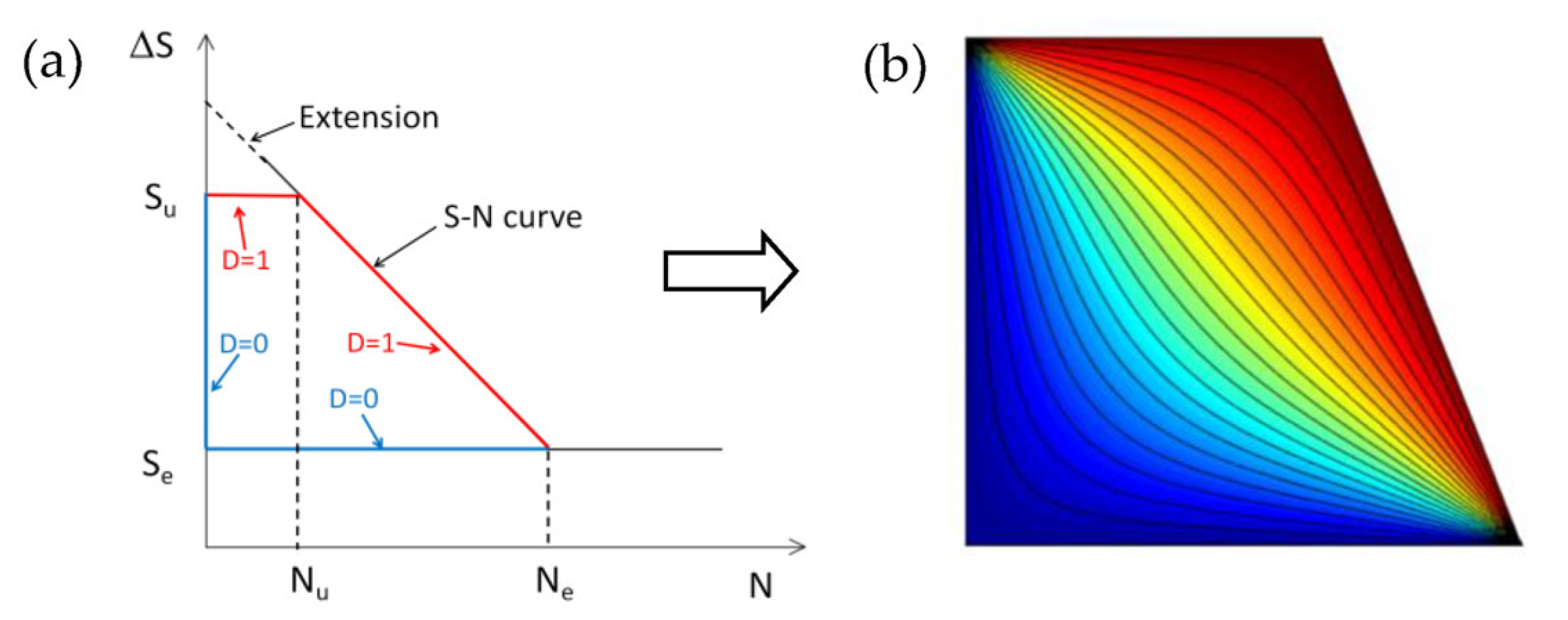
2.1. Damage Distribution Map (DDM)
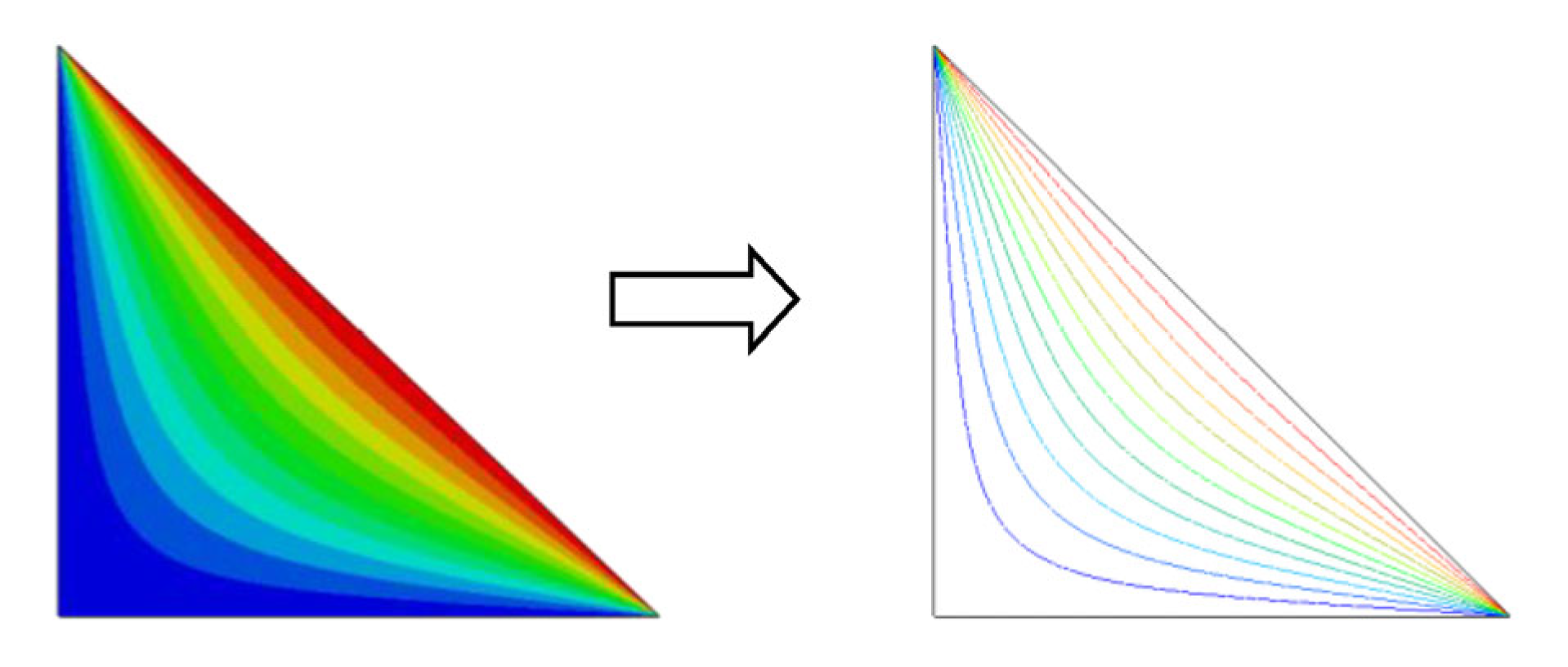
2.2. Construction and Preprocessing of DDM
2.3. Damage Accumulation Calculation Process
3. Fatigue Tests of Welded Joints
3.1. Fatigue Test Configuration
3.2. DDM Construction for Welded Joints
3.3. Cumulative Damage Calculation
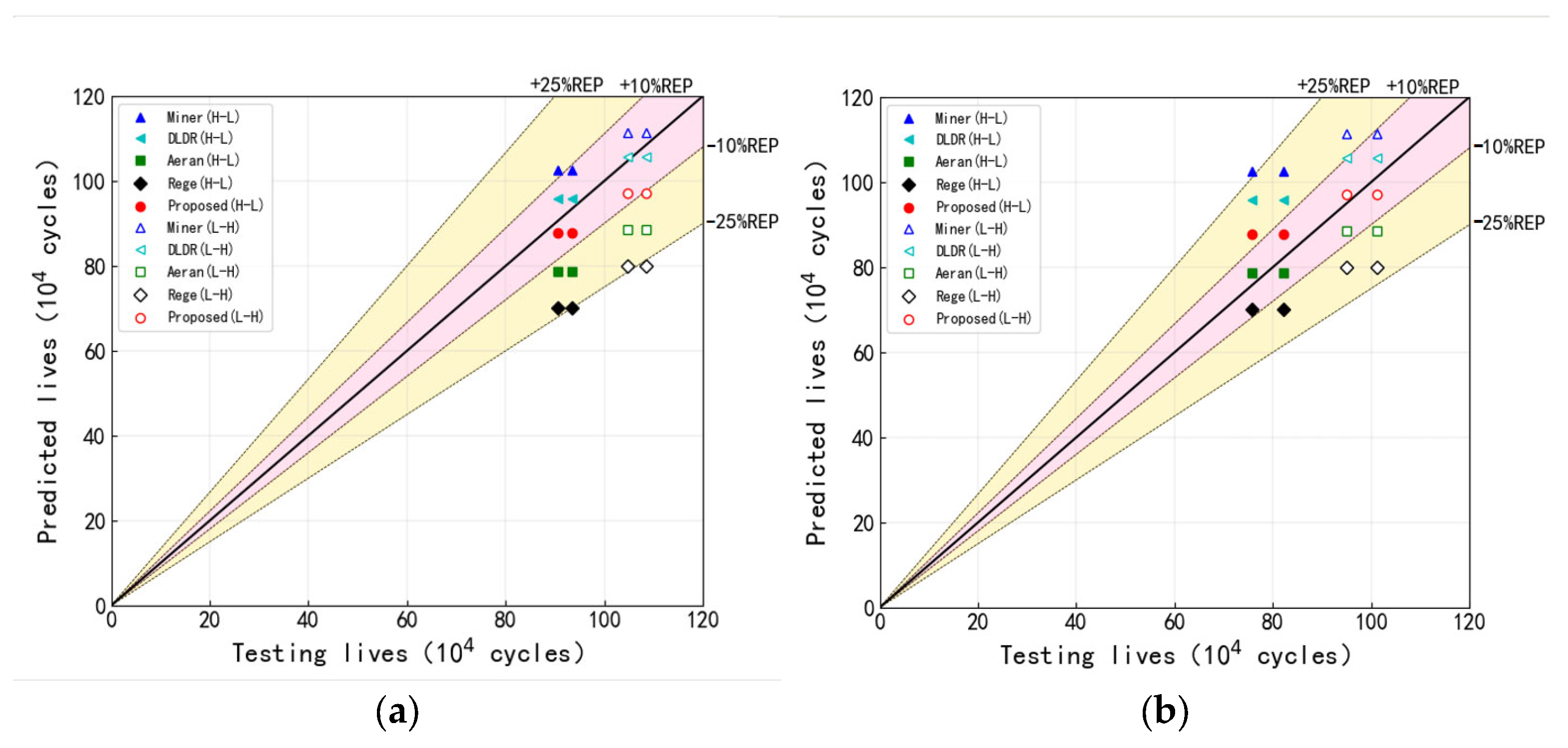
3.4. Fatigue Life Prediction
4. Conclusions
- (1)
- Based on Pavlou’s theory, the fatigue damage envelope for welded joints can be reasonably constructed by directly adopting S-N curves provided in welded structure fatigue design standards and codes. According to the FEA solution for a heat transfer problem, the damage distribution map can be generated, and the corresponding polynomial fitting function can be derived. Then, the cumulative damage and fatigue life for welded joints under variable amplitude loadings can be predicted.
- (2)
- For cruciform joints and T joints, respectively, simple tensile and three-point-bending fatigue tests under two-level loading block sequences were conducted. An S-N curve with 97.7% failure probability for F class in BS7608 was adopted, and the boundary condition corresponding to damage D = 0 of the heat transfer FEA model was set as −8 °C. The cumulative damage was calculated based on the Miner, DLDR, Aeran, and Rege models and the proposed model. The prediction results show that the proposed approach is in best agreement with the experimental results. It is interesting that nonlinear models do not seem better than linear models for overall fatigue life prediction, which may be because the overall fatigue lives ignore the dominant damage differences among different fatigue stages.
- (3)
- Comparison of the damage prediction results according to the five models shows that nonlinear models have significant advantages in describing the damage characteristics in the fatigue early stage of weld toe cracks. Therefore, from aspects of both life prediction accuracy and crack damage process description, the proposed model is superior to others.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| fatigue life | stress range | ||
| specific heat | density | ||
| a constant of material | R | stress ratio | |
| the number of standard deviation less than the mean | mean square error | ||
| damage | R-Square | square of correlation coefficient | |
| cumulative damage | fatigue limit | ||
| interpolation function of damage | stress range of loading block i | ||
| thermal conductivity | sum of squares of fitting errors | ||
| inverse slope of S-N curve | ultimate strength | ||
| cycles of loading block i | time | ||
| life under constant amplitude loading Si | T | function of temperature | |
| σ | standard deviation | load interaction factor |
References
- Łagoda, T.; Głowacka, K. Fatigue life prediction of welded joints from nominal system to fracture mechanics. Int. J. Fatigue 2020, 137, 105647. [Google Scholar] [CrossRef]
- Murakami, Y.; Endo, M. The reality of the concept of fatigue damage in multiple step amplitude loadings: Reason for unsuccessful results of existing damage counting models. Int. J. Fatigue 2022, 154, 106529. [Google Scholar] [CrossRef]
- Fernández-Canteli, A.; Castillo, E.; Blasón, S. A methodology for phenomenological analysis of cumulative damage processes. Application to fatigue and fracture phenomena. Int. J. Fatigue 2021, 150, 106311. [Google Scholar] [CrossRef]
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. 1945, 67, A159–A164. [Google Scholar] [CrossRef]
- Mesmacquea, G.; Garciab, S.; Amrouchea, A.; Rubio-Gonzalezb, C. Sequential law in multiaxial fatigue, a new damage indicator. Int. J. Fatigue 2005, 27, 461–467. [Google Scholar] [CrossRef]
- Lu, X.; Zheng, S. Changes in mechanical properties of vehicle components after strengthening under low-amplitude loads below the fatigue limit. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 847–855. [Google Scholar]
- Marco, S.M.; Starkey, W.L. A concept of fatigue damage. Trans. ASME 1954, 76, 627–632. [Google Scholar] [CrossRef]
- Manson, S.S.; Halford, G.R. Practical implementation of the double linear damage rule and damage curve approach for treating cumulative fatigue damage. Int. J. Fract. 1981, 17, 169–192. [Google Scholar] [CrossRef]
- Xue, Q.; Du, X. Welding fatigue design based on nonlinear damage theory. J. Mech. Eng. 2019, 55, 32–38. [Google Scholar]
- Gao, K.; Liu, G.; Tang, W. An improved Manson-Halford model for multi-level nonlinear fatigue life prediction. Int. J. Fatigue 2021, 151, 106393. [Google Scholar] [CrossRef]
- Zhao, G.; Liu, Y.; Ye, N. An improved fatigue accumulation damage model based on load interaction and strength degradation. Int. J. Fatigue 2022, 156, 106636. [Google Scholar] [CrossRef]
- Miller, K.J.; Zachariah, K.P. Cumulative damage laws for fatigue crack initiation and stage I propagation. J. Strain Anal. Eng. Des. 1977, 12, 262–270. [Google Scholar] [CrossRef]
- Chaboche, J.L. A differential law for nonlinear cumulative fatigue damage. In Materials and Building Research; Annales de l’ITBTP, HS No. 39; Paris Institut Technique du Batiment et des Travaus Publies: Paris, France, 1974; pp. 117–124. [Google Scholar]
- Chaboche, J.L. Continuum damage mechanics and its application to structural lifetime predictions. La Rech. Aerosp. (Engl. Ed.) 1987, 4, 37–54. [Google Scholar]
- Lemaitre, J.; Chaboche, J.L. Mechanics of Solid Materials. J. Eng. Mech. 1993, 119, 642–643. [Google Scholar] [CrossRef]
- Wang, J. A continuum damage mechanics model for low-cycle fatigue failure of metals. Eng. Fract. Mech. 1992, 41, 437–441. [Google Scholar]
- Wang, T.; Lou, Z. A continuum damage model for weld heat affected zone under low cycle fatigue loading. Eng. Fract. Mech. 1990, 37, 825–829. [Google Scholar] [CrossRef]
- Subramanyan, S. A cumulative damage rule based on the knee point of the S-N curve. J. Eng. Mater. Technol. 1976, 98, 316–321. [Google Scholar] [CrossRef]
- Pavlou, D.G. A phenomenological fatigue damage accumulation rule based on hardness increasing, for the 2024-T42 aluminium. Eng. Struct. 2002, 24, 1363–1368. [Google Scholar] [CrossRef]
- Hectors, K.; De Waele, W. Cumulative damage and life prediction models for high-cycle fatigue of metals: A review. Metals 2021, 11, 204. [Google Scholar] [CrossRef]
- Muñiz-Calvente, M.; Álvarez-Vázquez, A.; Pelayo, F.; Aenlle, M.; García-Fernández, N.; Lamela-Rey, M.J. A comparative review of time-and frequency-domain methods for fatigue damage assessment. Int. J. Fatigue 2022, 163, 107069. [Google Scholar] [CrossRef]
- Aeran, A.; Siriwardane, S.C.; Mikkelsen, O.; Langen, I. A new nonlinear fatigue damage model based only on S-N curve parameters. Int. J. Fatigue 2017, 103, 327–341. [Google Scholar] [CrossRef]
- Rege, K.; Pavlou, D.G. A one-parameter nonlinear fatigue damage accumulation model. Int. J. Fatigue 2017, 98, 234–246. [Google Scholar] [CrossRef]
- Zhu, S.-P.; Liao, D.; Liu, Q.; Correia, J.A.; De Jesus, A.M. Nonlinear fatigue damage accumulation:Isodamage curve-based model and life prediction aspects. Int. J. Fatigue 2019, 128, 105185. [Google Scholar] [CrossRef]
- Hashin, Z.; Rotem, A. A cumulative damage theory of fatigue failure. Mater. Sci. Eng. 1978, 34, 147–160. [Google Scholar] [CrossRef]
- Pavlou, D.G. The theory of the S-N fatigue damage envelope: Generalization of linear, double-linear, and non-linear fatigue damage models. Int. J. Fatigue 2018, 110, 204–214. [Google Scholar] [CrossRef]
- Klesnil, M.; Lukáš, P. Influence of strength and stress history on growth and stabilisation of fatigue cracks. Eng. Fract. Mech. 1972, 4, 77–92. [Google Scholar] [CrossRef]
- Schijve, J. Effect of load sequences on crack propagation under random and program loading. Eng. Fract. Mech. 1973, 5, 269–280. [Google Scholar] [CrossRef]
- Meneghetti, G.; Campagnolo, A. State-of-the-art review of peak stress method for fatigue strength assessment of welded joints. Int. J. Fatigue 2020, 139, 105705. [Google Scholar] [CrossRef]
- Aeran, A.; Acosta, R.; Siriwardane, S.C.; Starke, P.; Mikkelsen, O.; Langen, I.; Walther, F. A nonlinear fatigue damage model: Comparison with experimental damage evolution of S355 (SAE 1020) structural steel and application to offshore jacket structures. Int. J. Fatigue 2020, 135, 105568. [Google Scholar] [CrossRef]
- Bjørheim, F.; Siriwardane, S.C.; Pavlou, D. A review of fatigue damage detection and measurement techniques. Int. J. Fatigue 2022, 154, 106556. [Google Scholar] [CrossRef]
- Leonetti, D.; Maljaars, J.; Snijder, H.H.B. Fracture mechanics based fatigue life prediction for a weld toe crack under constant and variable amplitude random block loading—Modeling and uncertainty estimation. Eng. Fract. Mech. 2021, 242, 107487. [Google Scholar] [CrossRef]
- Remes, H.; Gallo, P.; Jelovica, J. Fatigue strength modelling of high-performing welded joints. Int. J. Fatigue 2020, 135, 105555. [Google Scholar] [CrossRef]
- Haghshenas, A.; Khonsari, M.M. Damage accumulation and crack initiation detection based on the evolution of surface roughness parameters. Int. J. Fatigue 2018, 107, 130–144. [Google Scholar] [CrossRef]
- Guerchais, R.; Saintier, N.; Morel, F.; Robert, C. Micromechanical investigation of the influence of defects in high cycle Fatigue. Int. J. Fatigue 2014, 67, 159–172. [Google Scholar] [CrossRef]
- Schork, B.; Kucharczyk, P.; Madia, M.; Zerbst, U.; Hensel, J.; Bernhard, J.; Tchuindjang, D.; Kaffenberger, M.; Oechsner, M. The effect of the local and global weld geometry as well as material defects on crack initiation and fatigue strength. Eng. Fract. Mech. 2018, 198, 103–122. [Google Scholar] [CrossRef]
- Yıldırım, H.C.; Remes, H.; Nussbaumer, A. Fatigue properties of as-welded and post-weld-treated high-strength steel joints: The influence of constant and variable amplitude loads. Int. J. Fatigue 2020, 138, 105687. [Google Scholar] [CrossRef]
- Zerbst, U.; Hensel, J. Application of fracture mechanics to weld fatigue. Int. J. Fatigue 2020, 139, 105801. [Google Scholar] [CrossRef]
- Raftar, H.R.; Dabiri, E.; Ahola, A.; Björk, T. Weld root fatigue assessment of load-carrying fillet welded joints: 4R method compared to other methods. Int. J. Fatigue 2022, 156, 106623. [Google Scholar] [CrossRef]
- Rozumek, D.; Lewandowski, J.; Lesiuk, G.; Correia, J.A. The influence of heat treatment on the behavior of fatigue crack growth in welded joints made of S355 under bending loading. Int. J. Fatigue 2020, 131, 105328. [Google Scholar] [CrossRef]

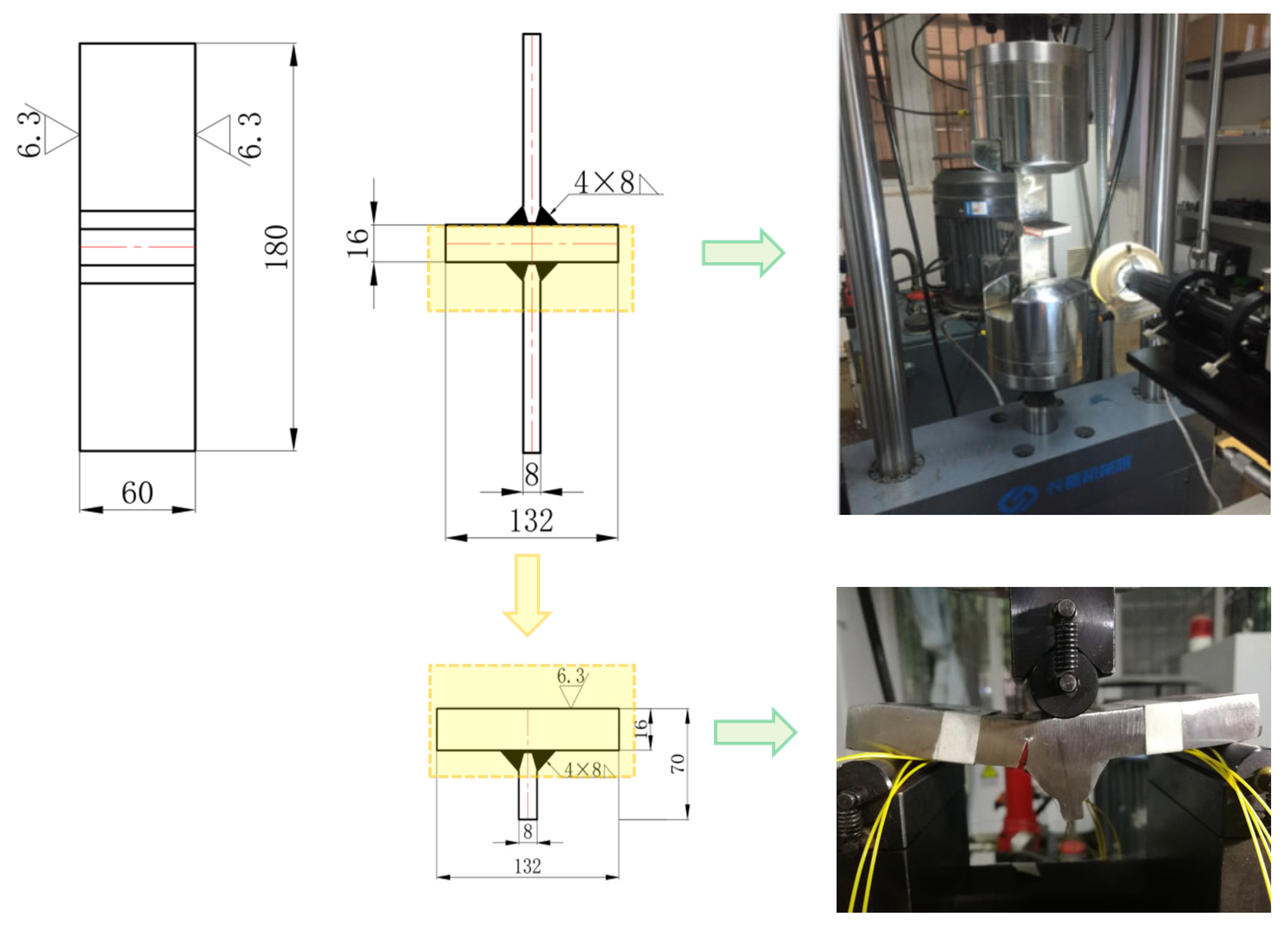

| Yield Strength | Ultimate Tensile Strength | Elongation (%) | Young’s Modulus E (Mpa) | Poisson’s Ratio |
|---|---|---|---|---|
| 358 | 564 | ≤22.3 | 2.08 × 105 | 0.31 |
| C | Si | Mn | P | S |
|---|---|---|---|---|
| 0.150 | 0.380 | 1.360 | 0.030 | 0.028 |
| Welding Current I (A) | Welding Voltage U (V) | Welding Speed | Gas | Gas Flow Rate |
|---|---|---|---|---|
| 240 | 25 | 0.8 | Ar-20%CO2 | 20 |
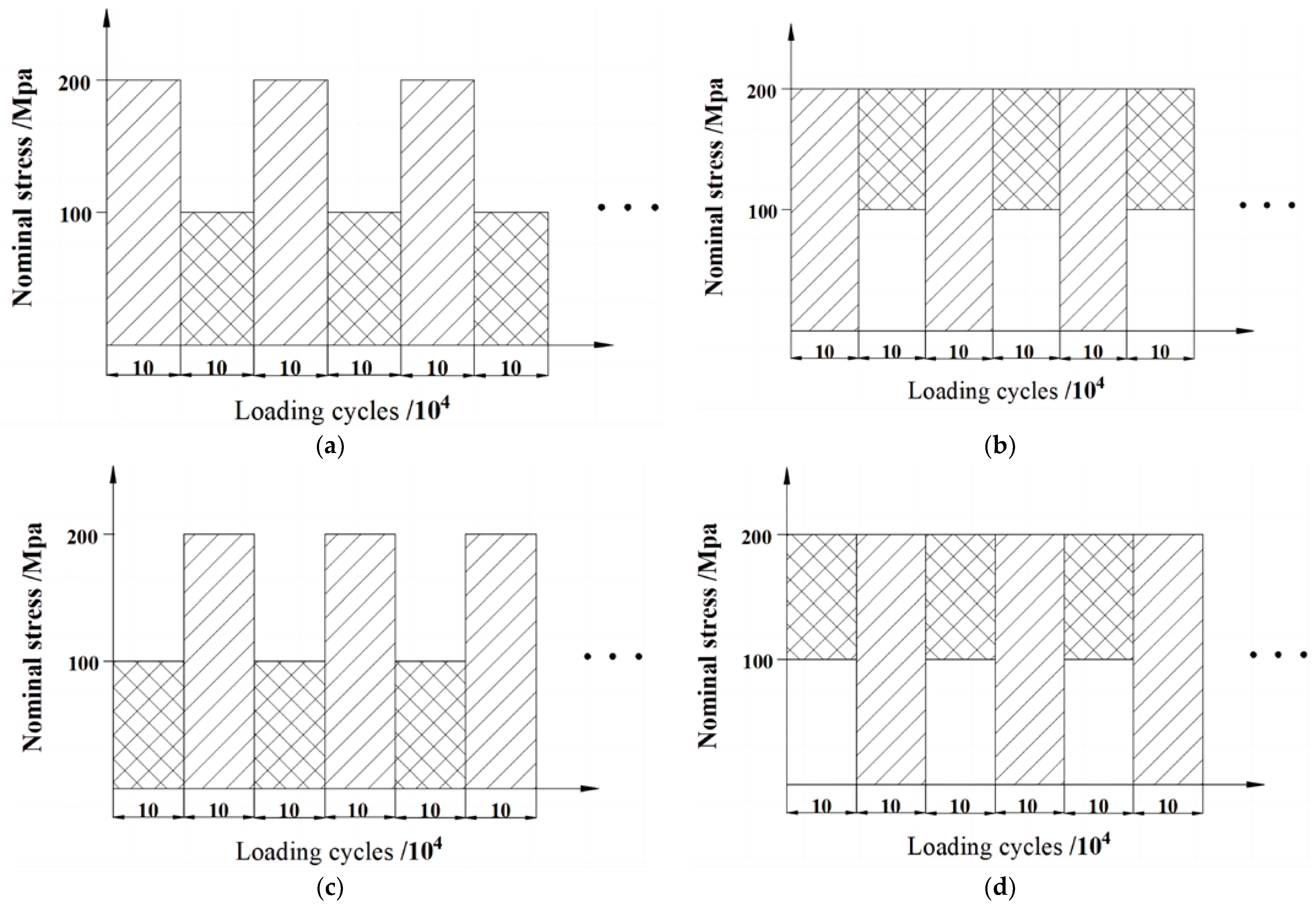
| No. of Specimens | Testing Lives (104 Cycles) | Loading Spectrum Type | Memo | |
|---|---|---|---|---|
| C01 | 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 0.5 | =90.5 | a (H-L) | cruciform joint specimens under simple tensile loading |
| C02 | 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 3.4 | =93.4 | b (H-L) | |
| C03 | 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 8.4 | =108.4 | c (L-H) | |
| C04 | 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 4.7 | =104.7 | d (L-H) | |
| T01 | 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 2.1 | =82.1 | a (H-L) | T joint specimens under three-point-bending loading |
| T02 | 10 + 10 + 10 + 10 + 10 + 10 + 10 + 5.8 | =75.8 | b (H-L) | |
| T03 | 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 4.9 | =94.9 | c (L-H) | |
| T04 | 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 1.3 | =101.3 | d (L-H) | |
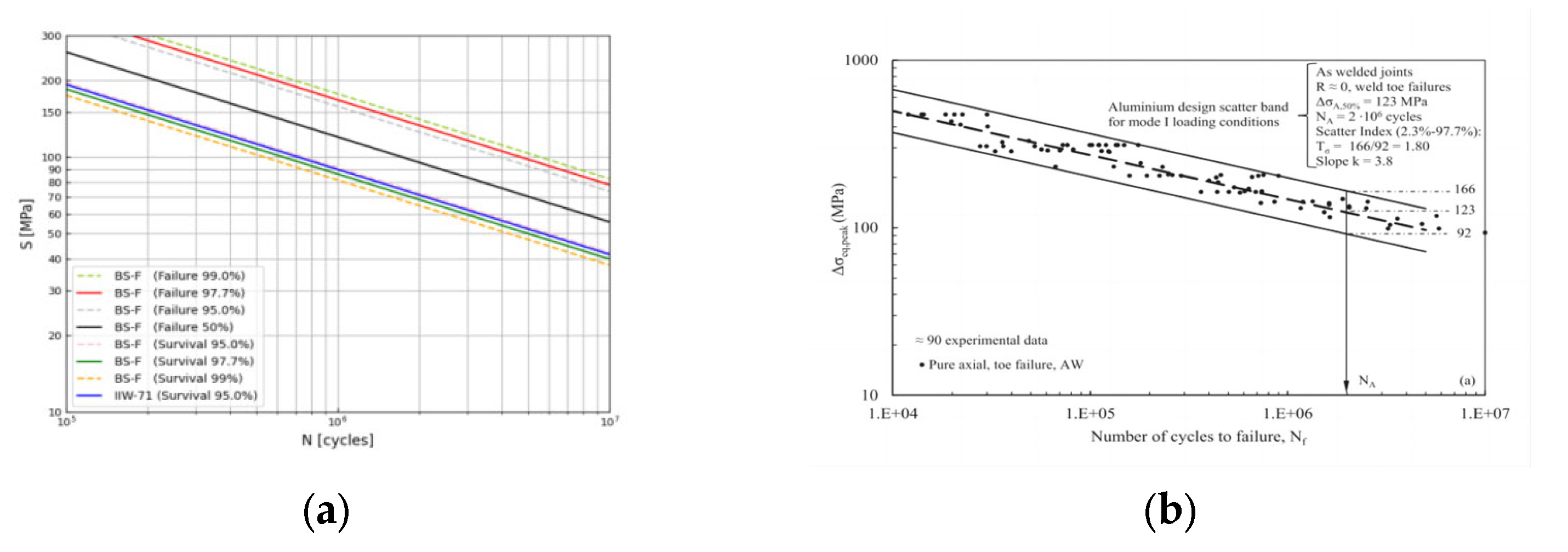
| No. | m | C0 | LogC0 | d | Failure Probability | Extrapolated Su (MPa) | Standard |
|---|---|---|---|---|---|---|---|
| 1 | 3 | 5.56 × 1012 | 12.74 | 2.33 | 99.0% | 17,712 | |
| 2 * | 3 | 4.72 × 1012 | 12.67 | 2.00 | 97.7% | 16,771 | |
| 3 | 3 | 3.95 × 1012 | 12.60 | 1.65 | 95.0% | 15,802 | |
| 4 | 3 | 1.73 × 1012 | 12.24 | 0.00 | 50.0% | 11,995 | BS7608 |
| 5 | 3 | 7.55 × 1011 | 11.88 | −1.65 | 5.0% | 9106 | |
| 6 | 3 | 6.32 × 1011 | 11.80 | −2.00 | 2.3% | 8580 | |
| 7 | 3 | 5.36 × 1011 | 11.73 | −2.33 | 1.0% | 8124 | |
| 8 | 3 | 7.16 × 1011 | 11.85 | / | 50.0% (with 75% two-sided confidence level) | 8945 | IIW |
| Block No. | Miner | DLDR | Aeran | Rege | Proposed |
|---|---|---|---|---|---|
| 1 | 0.1696 | 0.1696 | 0.0411 | 1.39 × 10−6 | 7.06 × 10−7 |
| 2 | 0.1908 | 0.1898 | 0.1861 | 4.95 × 10−6 | 8.86 × 10−7 |
| 3 | 0.3604 | 0.3525 | 0.0972 | 2.79 × 10−4 | 3.01 × 10−5 |
| 4 | 0.3816 | 0.3753 | 0.4954 | 9.98 × 10−4 | 5.03 × 10−5 |
| 5 | 0.5512 | 0.5467 | 0.1838 | 0.0129 | 0.0008 |
| 6 | 0.5724 | 0.5993 | 1.6044 | 0.0471 | 0.0021 |
| 7 | 0.7420 | 0.7652 | 0.4839 | 0.3218 | 0.0277 |
| 8 | 0.7632 | 0.8655 | 1 * | 1.1943 | 0.0987 |
| 9 | 0.9329 | 0.9786 | / | / | 1 * |
| 10 | 0.9541 | 1.0328 | / | / | / |
| 11 | 1.1237 | / | / | / | / |
| Lives (104 cycles) | 102.71 | 95.75 | 70.10 | 78.65 | 87.81 |
| Block No. | Miner | DLDR | Aeran | Rege | Proposed |
|---|---|---|---|---|---|
| 1 | 0.0212 | 0.0212 | 0.0040 | 2.03 × 10−37 | 1.17 × 10−8 |
| 2 | 0.1908 | 0.4413 | 0.0423 | 1.39 × 10−6 | 8.21 × 10−7 |
| 3 | 0.2120 | 0.4852 | 0.1922 | 4.95 × 10−6 | 1.03 × 10−6 |
| 4 | 0.3816 | 0.6265 | 0.0990 | 2.79 × 10−4 | 3.38 × 10−5 |
| 5 | 0.4028 | 0.6590 | 0.5068 | 9.98 × 10−4 | 5.80 × 10−5 |
| 6 | 0.5724 | 0.7689 | 0.1869 | 0.0129 | 0.0009 |
| 7 | 0.5936 | 0.7886 | 1.7452 | 0.0471 | 0.0024 |
| 8 | 0.7632 | 0.8623 | 0.5259 | 0.3218 | 0.0306 |
| 9 | 0.7844 | 0.9155 | 1 * | 1.1943 | 0.1177 |
| 10 | 0.9541 | 0.9735 | / | / | 1 * |
| 11 | 0.9753 | 1.0091 | / | / | / |
| 12 | 1.1449 | / | / | / | / |
| Lives (104 cycles) | 111.46 | 105.71 | 80.06 | 88.65 | 97.23 |
| Damage | Predicted Lives (104 Cycles)/Life Ratio (%) | |||||
|---|---|---|---|---|---|---|
| Miner | DLDR | Aeran | Rege | Proposed | ||
| H-L | D = 0.01 | 0.59/0.69% | 0.59/0.69% | 2.64/3.09% | 48.89/57.19% | 50.11/58.62% |
| D = 0.1 | 5.89/6.89% | 5.89/6.89% | 20.98/24.54% | 63.75/74.58% | 80.02/93.61% | |
| L-H | D = 0.01 | 4.71/4.60% | 4.71/4.60% | 2.52/2.46% | 58.89/57.55% | 75.56/73.84% |
| D = 0.1 | 14.65/14.32% | 10.28/14.32% | 20.01/19.55% | 73.75/72.07% | 89.34/87.31% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, H.; Dang, Z.; Wei, G. Damage Distribution Map Based Damage Accumulation Calculation Approach for Welded Joints. Metals 2023, 13, 1203. https://doi.org/10.3390/met13071203
Duan H, Dang Z, Wei G. Damage Distribution Map Based Damage Accumulation Calculation Approach for Welded Joints. Metals. 2023; 13(7):1203. https://doi.org/10.3390/met13071203
Chicago/Turabian StyleDuan, Haochun, Zhang Dang, and Guoqian Wei. 2023. "Damage Distribution Map Based Damage Accumulation Calculation Approach for Welded Joints" Metals 13, no. 7: 1203. https://doi.org/10.3390/met13071203
APA StyleDuan, H., Dang, Z., & Wei, G. (2023). Damage Distribution Map Based Damage Accumulation Calculation Approach for Welded Joints. Metals, 13(7), 1203. https://doi.org/10.3390/met13071203






