Optimization of a Certain Type of Aero-Engine Three-Tooth Mortise and Tenon Joint Structure against Fretting Fatigue
Abstract
1. Introduction
2. Parametric Model of Three-Tooth Tenon Joint Structure
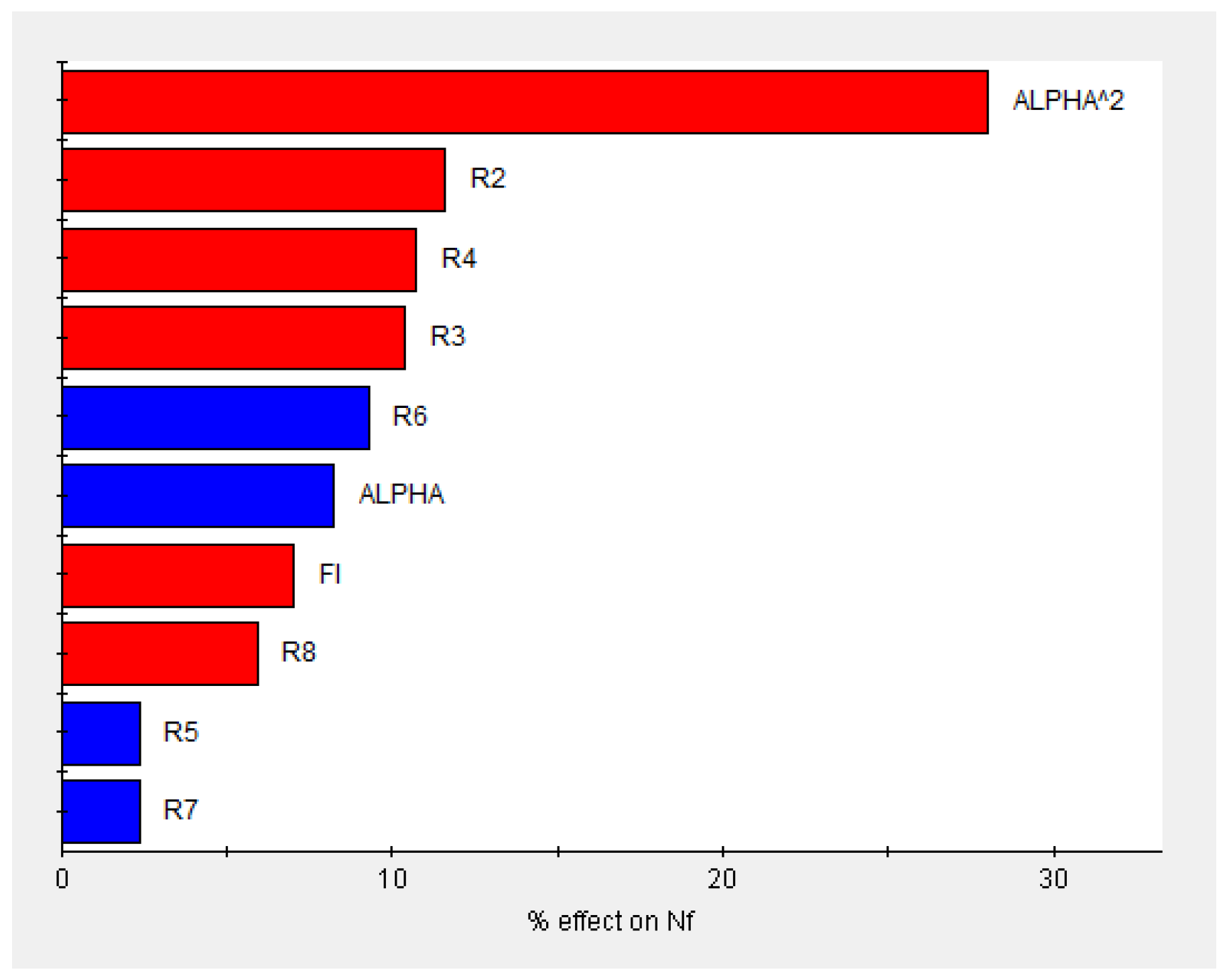
3. Sensitivity Analysis
4. Optimized Design of Three-Tooth Mortise and Tenon Joint Structure
4.1. Description of the Optimization Problem
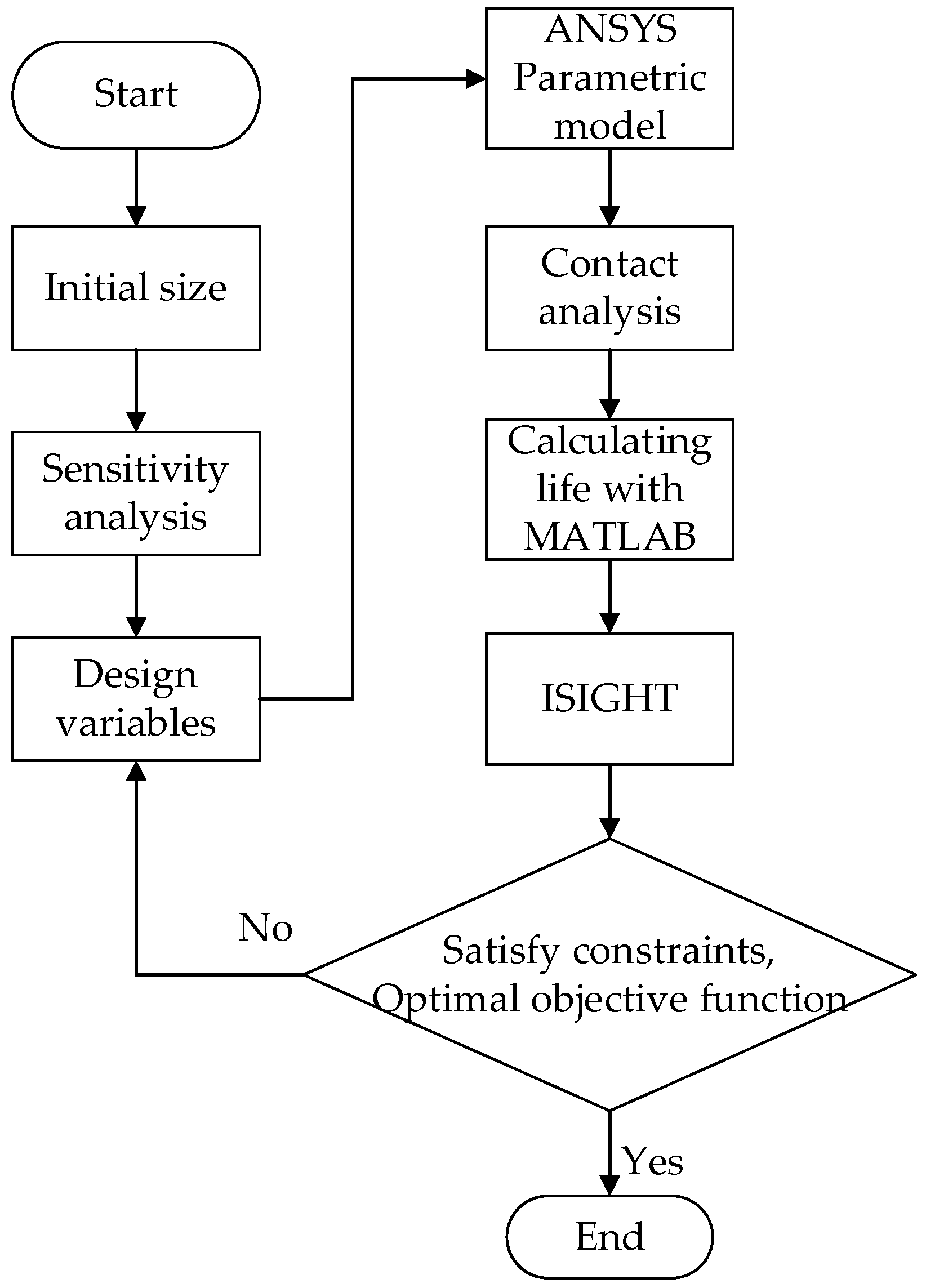
4.2. Optimization Processes
- First, input the design variable values into ISIGHT. Update the parametric model and mesh the three-tooth mortise and tenon joint construction in ANSYS using a batch file. At the peak and valley of the load, non-linear contact analysis must be conducted. Identify each node’s stress and strain statistics in the contact zone under peak and valley loads. Create a result file;
- Import the output file into MATLAB, and then use ISIGHT to run the MATLAB program to determine the structure’s fretting fatigue life based on non-linear fatigue damage;
- The IGHGHT optimization module can be used to determine the constraints and goal functions. Change the design variables to move on to step 1 if the objective function is not convergent or the constraint is not met. The optimization is finished if the objective function is optimal and the restriction is met.
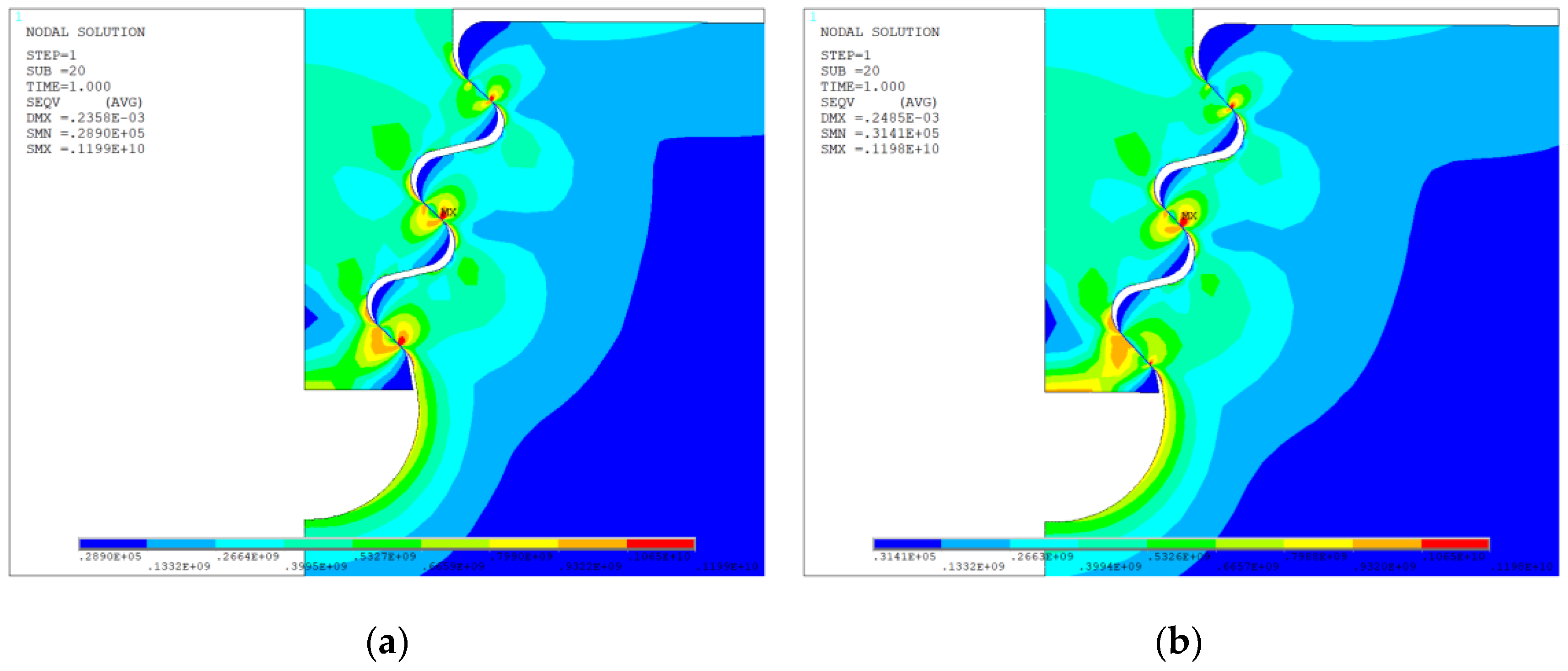
4.3. Optimization Results and Analysis
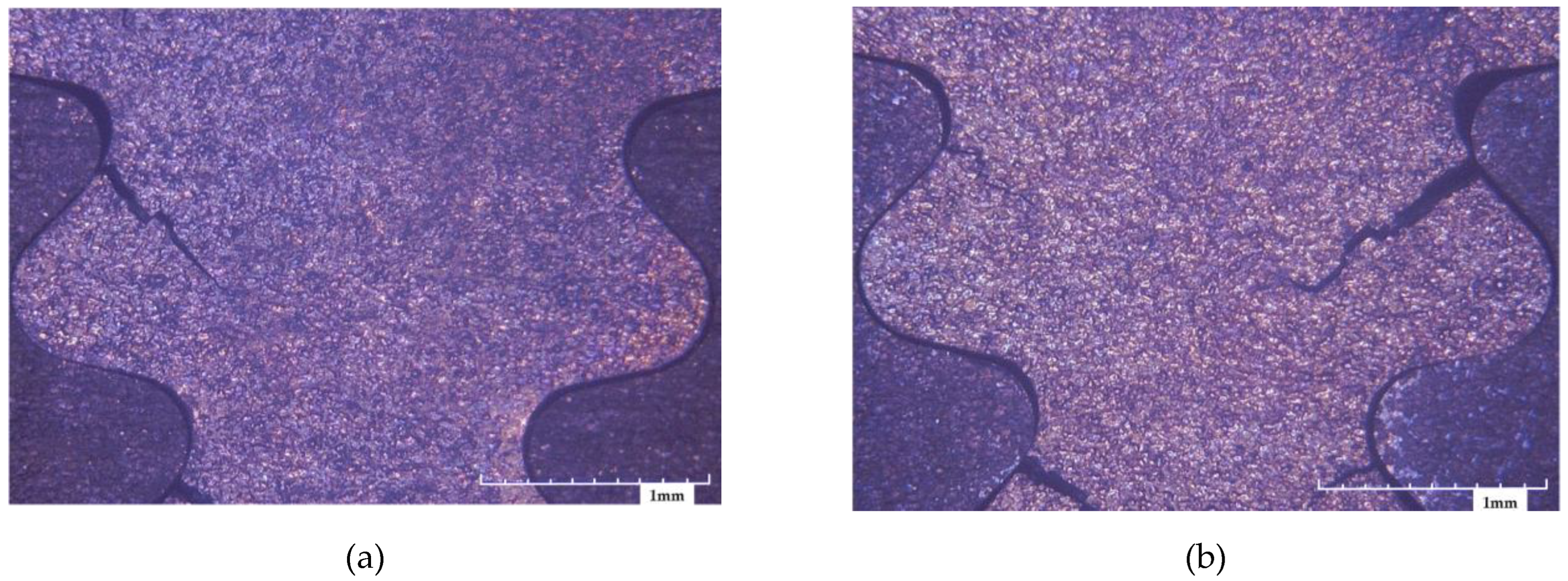
5. Verification by Fretting Fatigue Test
6. Conclusions
- The primary characteristic parameters for the three-tooth mortise and tenon joint structure are ALPHA, R2, R3, R4, R6, and FI.
- With mostly constant maximum equivalent forces, optimization increases the fretting fatigue life of the mortise and tenon joint structure while lowering the maximum contact pressure and maximum slip amplitude and enhancing the stress distribution in the structure.
- The effectiveness of the optimization method was verified by the fretting fatigue test. The optimization results have a certain reference value for the design of the three-tooth mortise and tenon joint structure of the turbine.
Author Contributions
Funding
Conflicts of Interest
References
- Zhou, Z.; Vincent, L. Fretting Wear, 1st ed.; Science Press: Beijing, China, 2002. [Google Scholar]
- Zhou, Z.; Zhu, M. Composite Fretting Wear, 1st ed.; Shanghai Jiao Tong University Press: Shagnhai, China, 2004. [Google Scholar]
- He, M. Fretting Fatigue of Mechanical Components, 1st ed.; National Defense Industry Press: Beijing, China, 1994. [Google Scholar]
- Zong, H.; Tao, H.; Gao, Q.; Tan, C. Structural Analysis and Optimization of Gas Turbine Fir-Tree Attachment with Various Tooth Profile Parameters. Aeroengine 2016, 42, 64–69. [Google Scholar] [CrossRef]
- Hao, Y.-H.; Huang, Z.-J. Optimization design of tenon connection structure based on coordinate correlation method. J. Aerosp. Power 2014, 29, 2716–2721. [Google Scholar] [CrossRef]
- Yu, D.; Zhang, X.; Yang, J.; Cheng, K.; Li, M. Structural Optimization of Fir-Tree Root and Groove for Turbine Blade With Superellipse and P-Norm Aggregation Function. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019. [Google Scholar]
- Yu, D.; Li, F.; Yang, J.; Kai, C.; Weilin, S.; Lv, K.; Li, M. Structural Optimization of Fir-Tree Root and Groove for Turbine Blade With Splines and Genetic Algorithm. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Republic of Korea, 13–17 June 2016. [Google Scholar]
- You, Y.; Lu, S. Optimization design method for twin-web turbine disk/tenon structure based on static strength and life reliability. J. Aerosp. Power 2017, 32, 1388–1393. [Google Scholar] [CrossRef]
- Chen, Z.-Y.; Wang, C.; Zhou, P. Research on Robust Optimization of Fatigue Life for Blade-Disk Considering Contact Gap between Tenon and Mortise. J. Propuls. Technol. 2018, 39, 857–864. [Google Scholar] [CrossRef]
- Sapronov, D.; Mezencev, M.; Karimbaev, T.; Reznik, S.; Prosuntsov, P. Complex Design Method of Ceramic Blades and Metal Disk Connection. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019. [Google Scholar]
- Yang, M.-C.; Sun, S.-Y. Structural optimization of turbine tenon/mortise. J. Aerosp. Power 2010, 1876–1882. [Google Scholar] [CrossRef]
- Tao, Y.; Tian, L.; Zhang, Y.; Lu, S. Optimal design of turbine mortise and tenon structure based on ansys. Mech Eng. 2013, 51, 11–14. [Google Scholar]
- Niu, X.; Zhu, S.; Gao, J.; Liao, D.; He, J. Fatigue Reliability Analysis and Optimization Design of Turbine Blade Disks under Multi-Source Uncertainties. J. Propuls. Technol. 2022, 43, 228–236. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, H.; Xing, Z.; Yu, Z.; Cui, H.; Wen, W. Optimization of turbine tenon structure against fretting fatigue damage. Gas Turbine Exp. Res. 2022, 35, 36–40. [Google Scholar]
- Du, Q.; Zhang, J.; Zhang, H.; Liang, Z.; Chen, Y.; Li, J.; Xu, S. Research on fatigue life optimization design and verification method for large size disk and tenon structural parts. J. Propuls. Technol. 2023, 1–8. Available online: http://kns.cnki.net/kcms/detail/11.1813.V.20230303.0938.005.html (accessed on 18 April 2023).
- Yu, M.; Wu, D.; Zhao, J.; Liu, S.; Gong, K.; Qu, Z. Vibration characteristics analysis of a type of turbine disk-blade assembly system in the civil aero-engine. Adv. Mech. Eng. 2022, 14, 1–11. [Google Scholar] [CrossRef]
- Tan, C.; Gao, H.; Li, L.; Sun, S.; Yang, W. Turbine blade arc tenon/mortise structure and optimization method based on parameterized mesh deformation. Struct. Multidiscip. Optim. 2022, 65, 239. [Google Scholar] [CrossRef]
- Xu, Y.; Cui, H.; Chen, W. Microdynamic fatigue life prediction of dovetail joint structures based on the critical surface method. J. Aerosp. Power 2013, 28(3), 489–493. [Google Scholar] [CrossRef]
- Shi, W.; Wen, W.; Cui, H. Research on fretting fatigue life of dovetail joints. J. Aerosp. Power 2014, 29, 104–110. [Google Scholar]
- Wang, N.; Cui, H.; Zhang, H. Low cycle fretting fatigue tests of dovetail structure at elevated temperature. J. Aerosp. Power 2018, 33, 3007–3012. [Google Scholar] [CrossRef]
- Yan, L.; Hu, D.; Tian, T.; Mao, J.; Wang, R. Design and experiment of simulated specimen for fretting fatigue of turbine attachment. J. Aerosp. Power 2022, 1–9. [Google Scholar] [CrossRef]
- Qu, Z.; Liu, K.; Wang, B.; Chen, Z. Fretting Fatigue Experiment and Finite Element Analysis for Dovetail Specimen at High Temperature. Appl. Sci. 2021, 11, 9913. [Google Scholar] [CrossRef]
- Hu, C.; Wei, D.; Wang, Y.; Shi, L. Experimental and numerical study of fretting fatigue in dovetail assembly using a total life prediction model. Eng. Fract. Mech. 2019, 205, 301–318. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, H.; Cui, H.; Wang, N. High-temperature fretting fatigue life prediction model based on continuum damage mechanics. J. Aerosp. Power 2019, 34, 656–663. [Google Scholar]
- Zhang, H.; Yang, X.; Cui, H.; Wen, W. Study on the Effect of Laser Quenching on Fretting Fatigue Life. Metals 2019, 9, 566. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, H.; Cui, H.; Wen, C. Effect of Laser Shock Peening on Fretting Fatigue Life of TC11 Titanium Alloy. Materials 2020, 13, 4711. [Google Scholar] [CrossRef]
- Xing, Z.; Zhang, H.; Yu, Z.; Cui, B.; Wen, W. Fretting fatigue test of ZSGH4169 dovetail structure. J. Aerosp. Power 2021, 36, 2410–2417. [Google Scholar]
- Xing, Z. Research on Fretting Fatigue Mechanism and Life Model of ZSGH4169/DZ125 Contact Pairs. Master Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2021. [Google Scholar]
- Xu, K.; Li, W.; Huang, Y.; Yu, Q.; Ma, G.; Hu, W. A fretting fatigue total life prediction method for dovetail attachment. J. Beijing Univ. Aeronaut. Astronaut. 2020, 1890–1898. [Google Scholar] [CrossRef]
- Jin, O.; Mall, S. Shear force effects on fretting fatigue behavior of Ti-6Al-4V. Metall. Mater. Trans. A 2004, 35, 131–138. [Google Scholar] [CrossRef]
- Jin, R.; Chen, W.; Sudjianto, A. An efficient algorithm for constructing optimal design of computer experiments. J. Stat. Plan. Inference. 2005, 134, 268–287. [Google Scholar] [CrossRef]
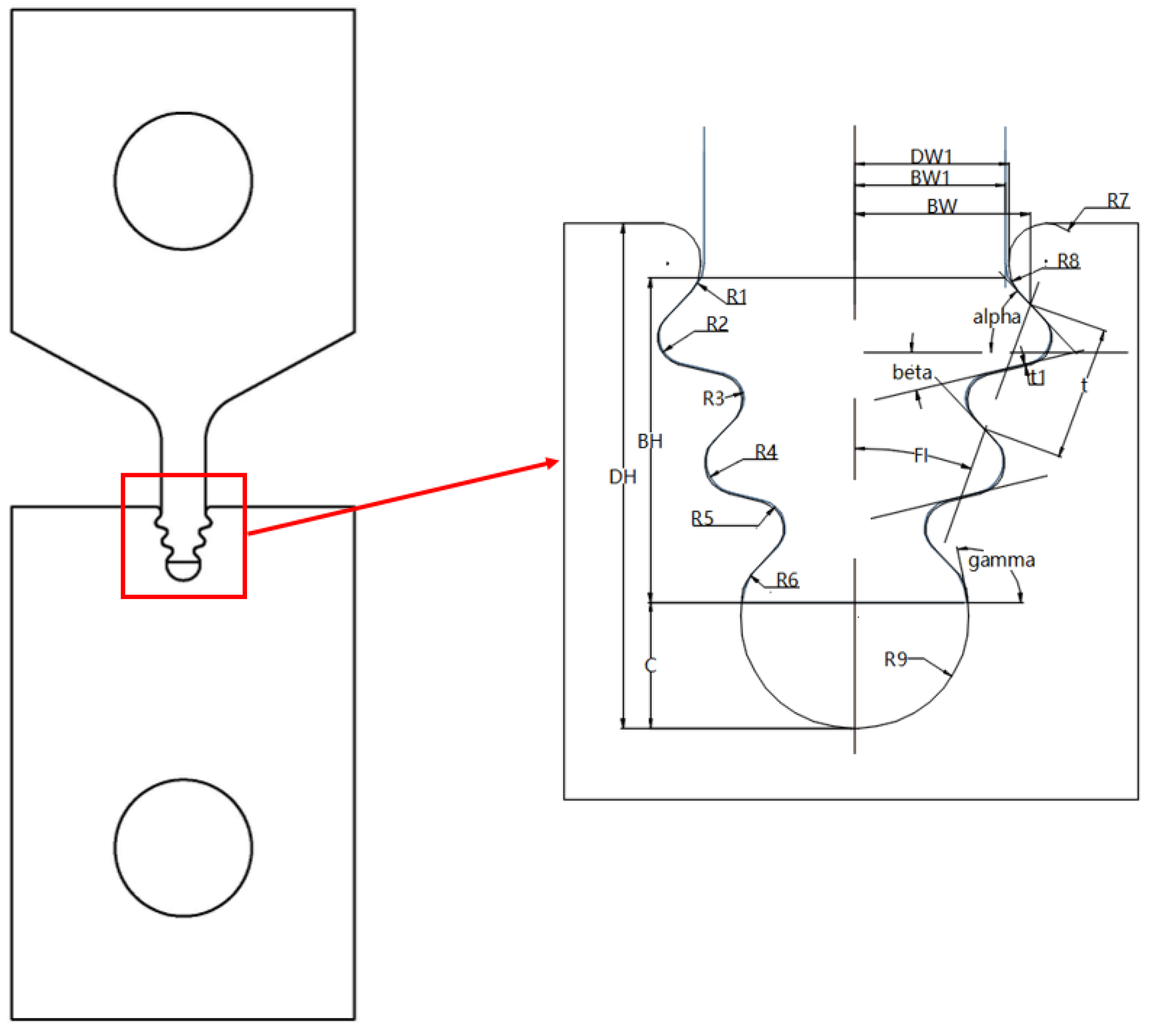








| Parameter | Description | Parameter | Description |
|---|---|---|---|
| BW | Shoulder width of the tenon | BW1 | Neck width of the tenon |
| DW1 | Neck width of the mortise | BH | Height of the tenon |
| DH | Height of the mortise | C | Clearance at the bottom of the mortise |
| alpha | Upward inclination | beta | Downward inclination |
| FI | Wedge angle | gamma | The inclination of the bottom of the mortise |
| t | Pitch | t1 | Clearance between teeth |
| R1 | Radius of the transition arc between tenon teeth 1 | R2 | The radius of the transition arc of tooth top 1 |
| R3 | The transition arc radius of tooth root 1 | R4 | The radius of the transition arc of tooth top 2 |
| R5 | The transition arc radius of tooth root 2 | R6 | The radius of the transition arc between the teeth of tenon 2 |
| R7 | The arc radius of the transition arc on the top surface of mortise | R8 | The radius of the transition arc between the teeth of the mortise |
| R9 | The transition arc radius at the bottom of the mortise |
| Parameters | Before | Minimum Limit | Maximum Limit | After |
|---|---|---|---|---|
| ALPHA (°) | 43.5 | 40 | 48 | 42.5 |
| FI (°) | 20 | 12 | 22 | 19.5 |
| R2 (mm) | 0.58 | 0.48 | 0.68 | 0.50 |
| R3 (mm) | 0.55 | 0.45 | 0.65 | 0.614 |
| R4 (mm) | 0.68 | 0.58 | 0.78 | 0.597 |
| R6 (mm) | 0.6 | 0.5 | 0.7 | 0.676 |
| Nf | 9347 | \ | \ | 17,206 |
| Before | After | |
|---|---|---|
| Maximum equivalent stress (MPa) | 1199 | 1198 |
| Contact pressure (MPa) | 2029 | 2018 |
| Maximum slip amplitude (μm) | 9.036 × 10−2 | 7.859 × 10−2 |
| Temperature (°C) | Peak Load (kN) | Life (Cycle) | Average Life (Cycle) | |
|---|---|---|---|---|
| Before | 650 | 14 | 8422 | 7613 |
| 6804 | ||||
| After | 10,889 | 11,518 | ||
| 12,146 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, Z.; Mi, D.; Cheng, B.; Deng, L.; Li, S.; Zhang, H.; Cui, H. Optimization of a Certain Type of Aero-Engine Three-Tooth Mortise and Tenon Joint Structure against Fretting Fatigue. Metals 2023, 13, 1116. https://doi.org/10.3390/met13061116
Qian Z, Mi D, Cheng B, Deng L, Li S, Zhang H, Cui H. Optimization of a Certain Type of Aero-Engine Three-Tooth Mortise and Tenon Joint Structure against Fretting Fatigue. Metals. 2023; 13(6):1116. https://doi.org/10.3390/met13061116
Chicago/Turabian StyleQian, Zhengming, Dong Mi, Benlin Cheng, Lijun Deng, Shaomeng Li, Hongjian Zhang, and Haitao Cui. 2023. "Optimization of a Certain Type of Aero-Engine Three-Tooth Mortise and Tenon Joint Structure against Fretting Fatigue" Metals 13, no. 6: 1116. https://doi.org/10.3390/met13061116
APA StyleQian, Z., Mi, D., Cheng, B., Deng, L., Li, S., Zhang, H., & Cui, H. (2023). Optimization of a Certain Type of Aero-Engine Three-Tooth Mortise and Tenon Joint Structure against Fretting Fatigue. Metals, 13(6), 1116. https://doi.org/10.3390/met13061116







