Characteristics of Bubble Behavior and Inclusion Removal in Liquid Steel Based on Industrial Trials of Argon Injection into Ladle Shroud
Abstract
1. Introduction
2. Materials and Methods
2.1. Industrial Trials of Argon Injection into Ladle Shroud (AIILS)
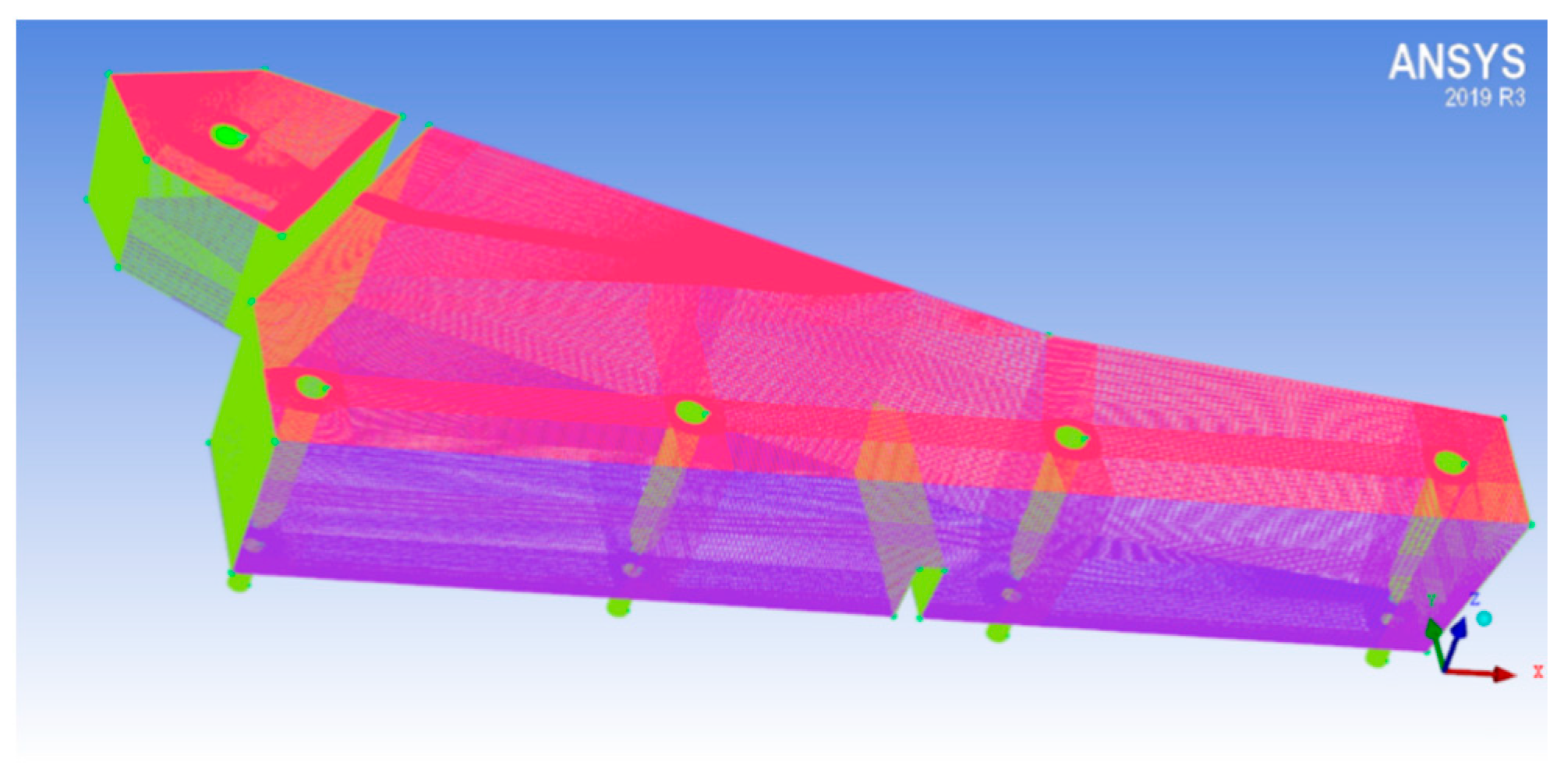
2.2. Numerical Simulation of Bubble Motion and Distribution in Tundish
3. Results and Discussion
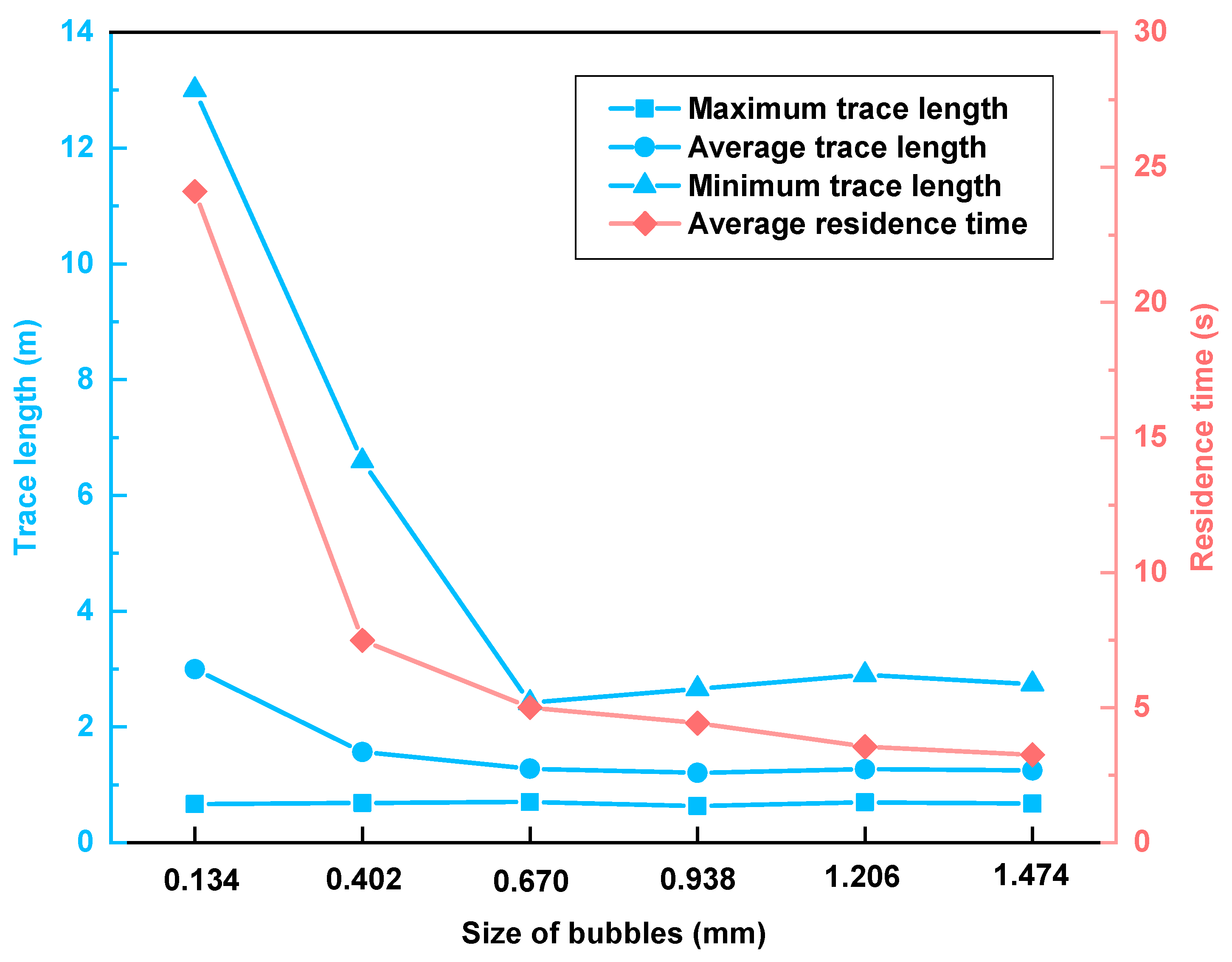
3.1. Morphological Characteristics of Bubbles
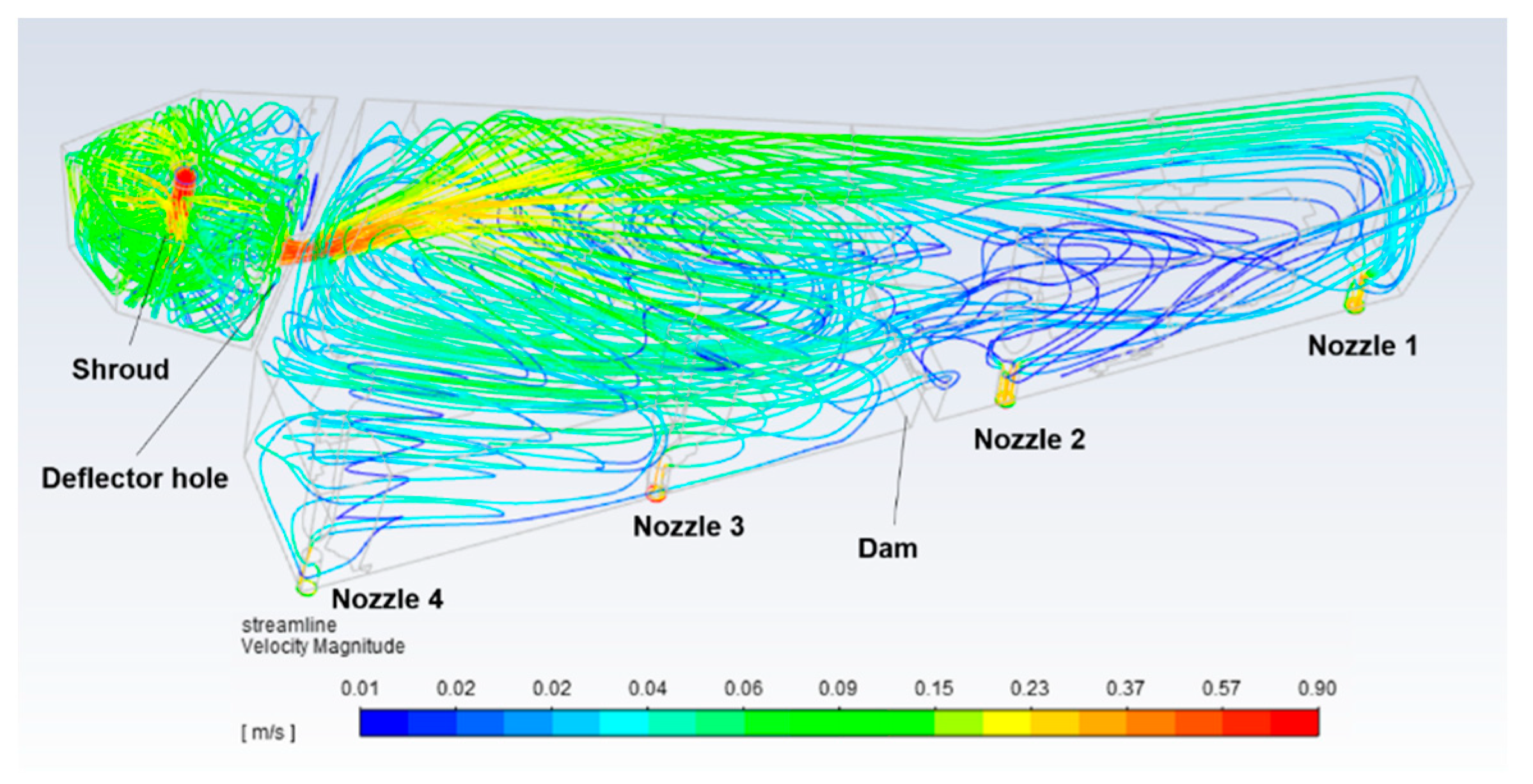
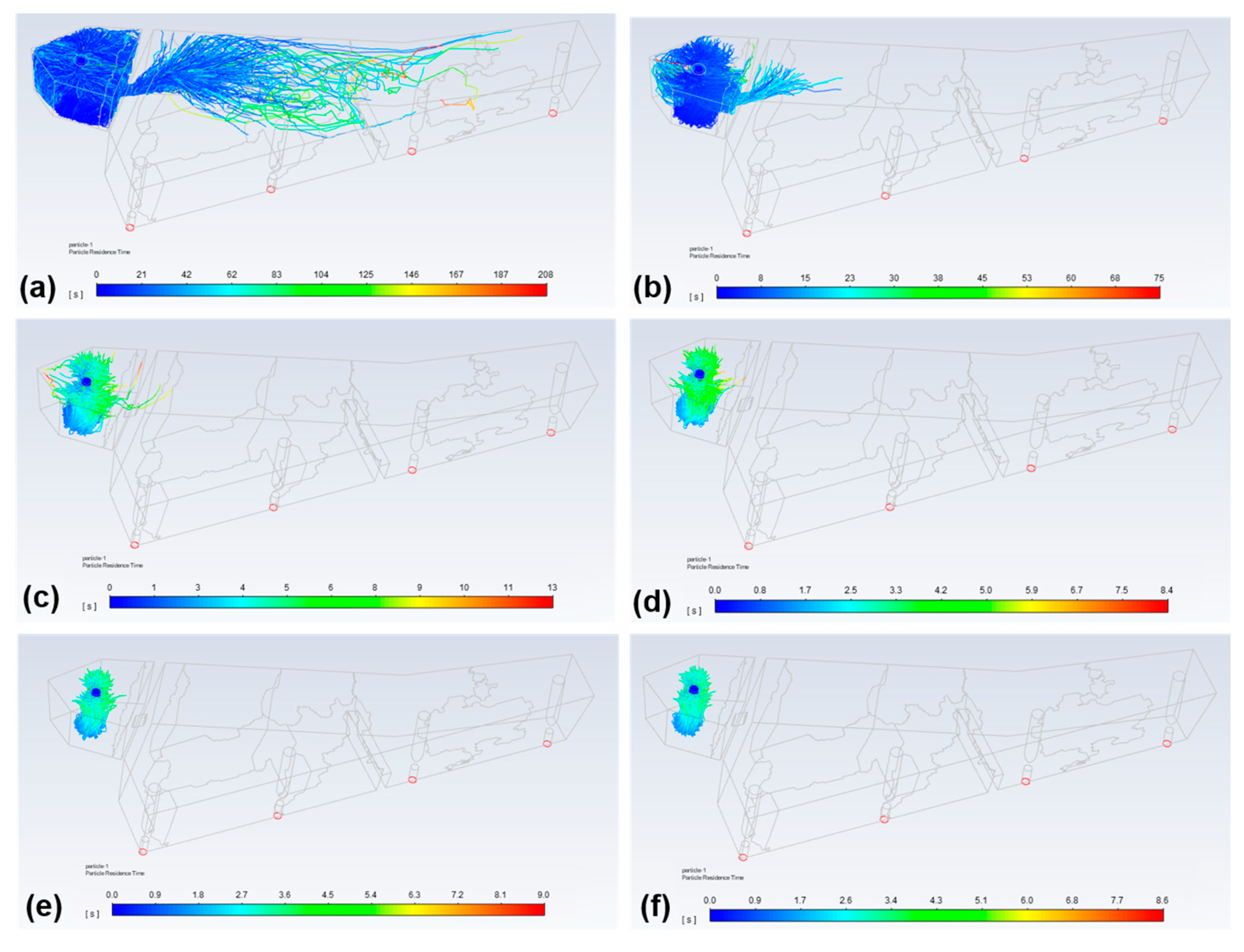
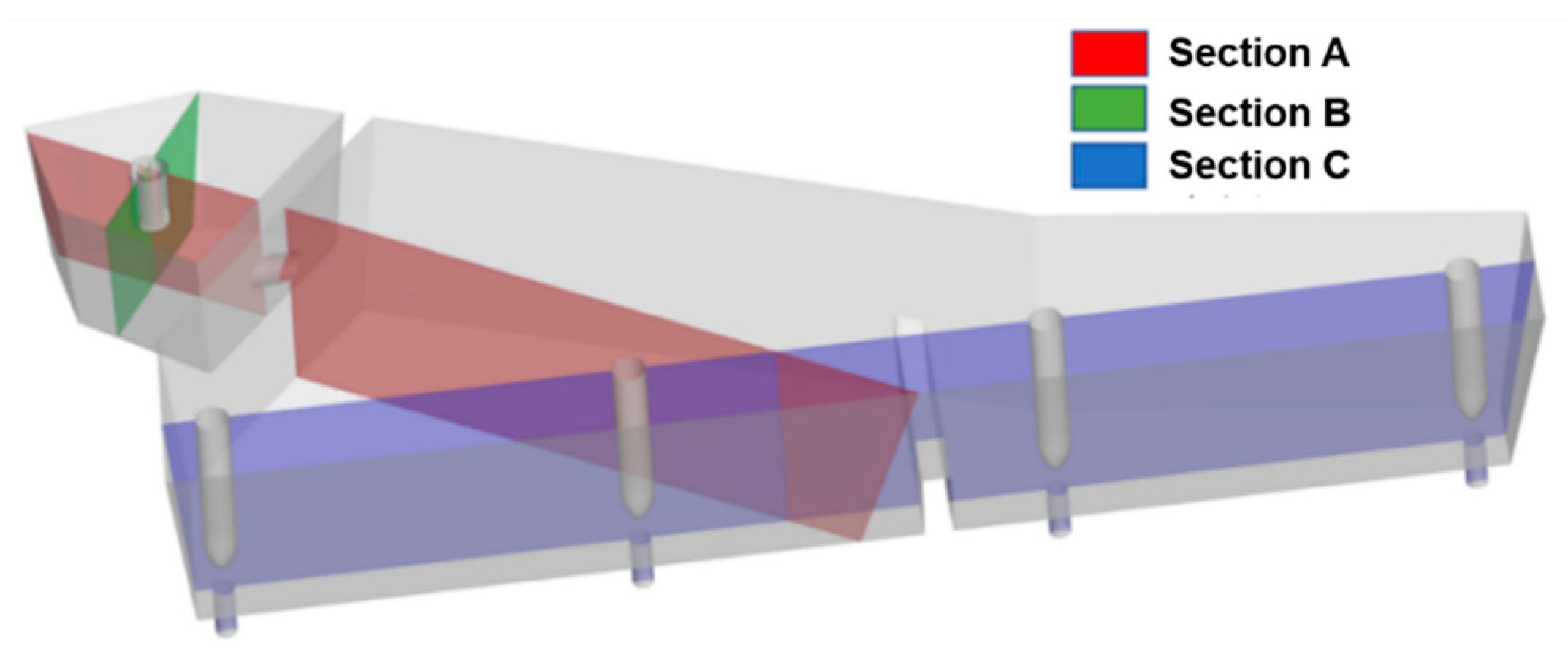
3.2. Motion Behaviors of Bubbles in Tundish
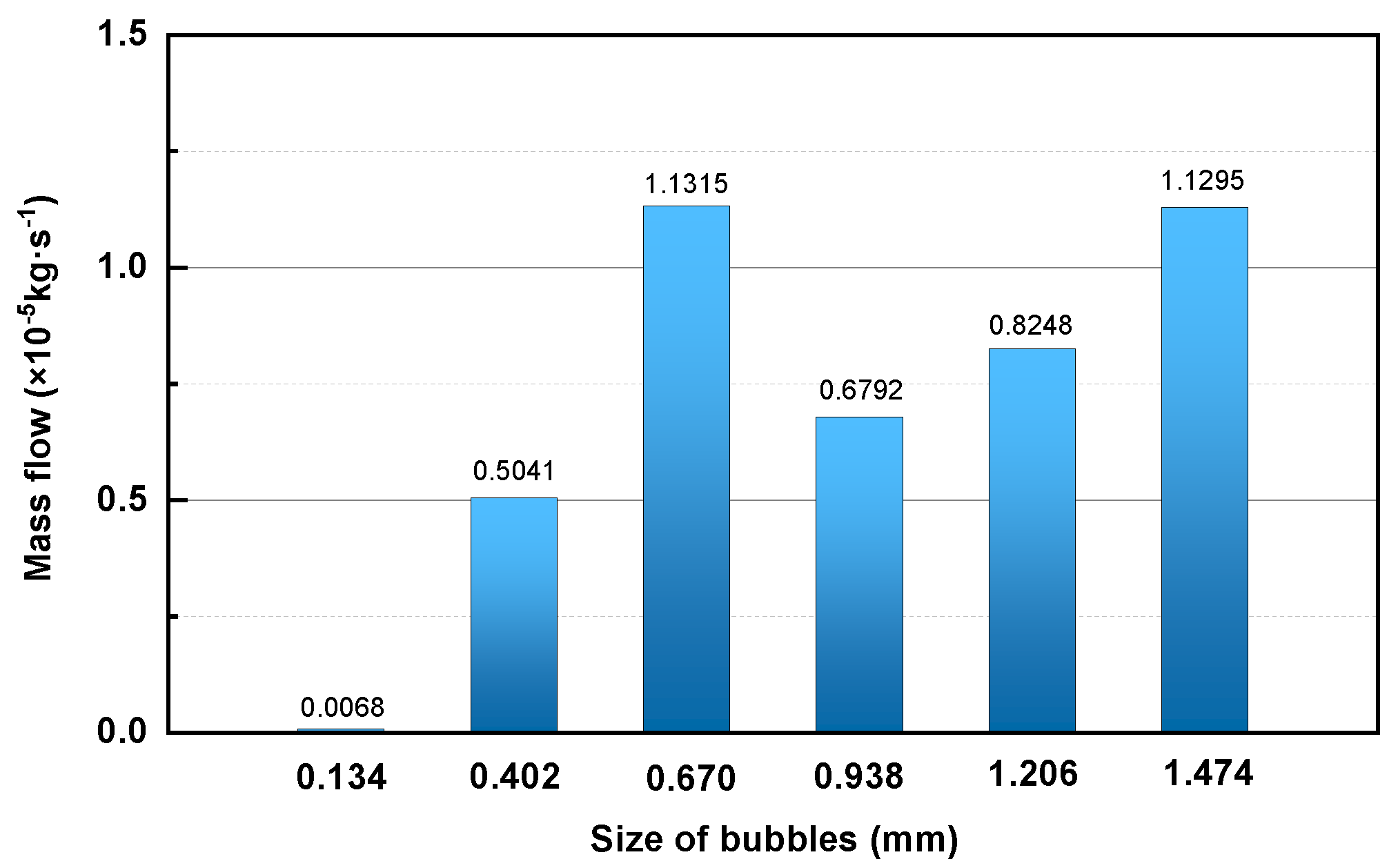
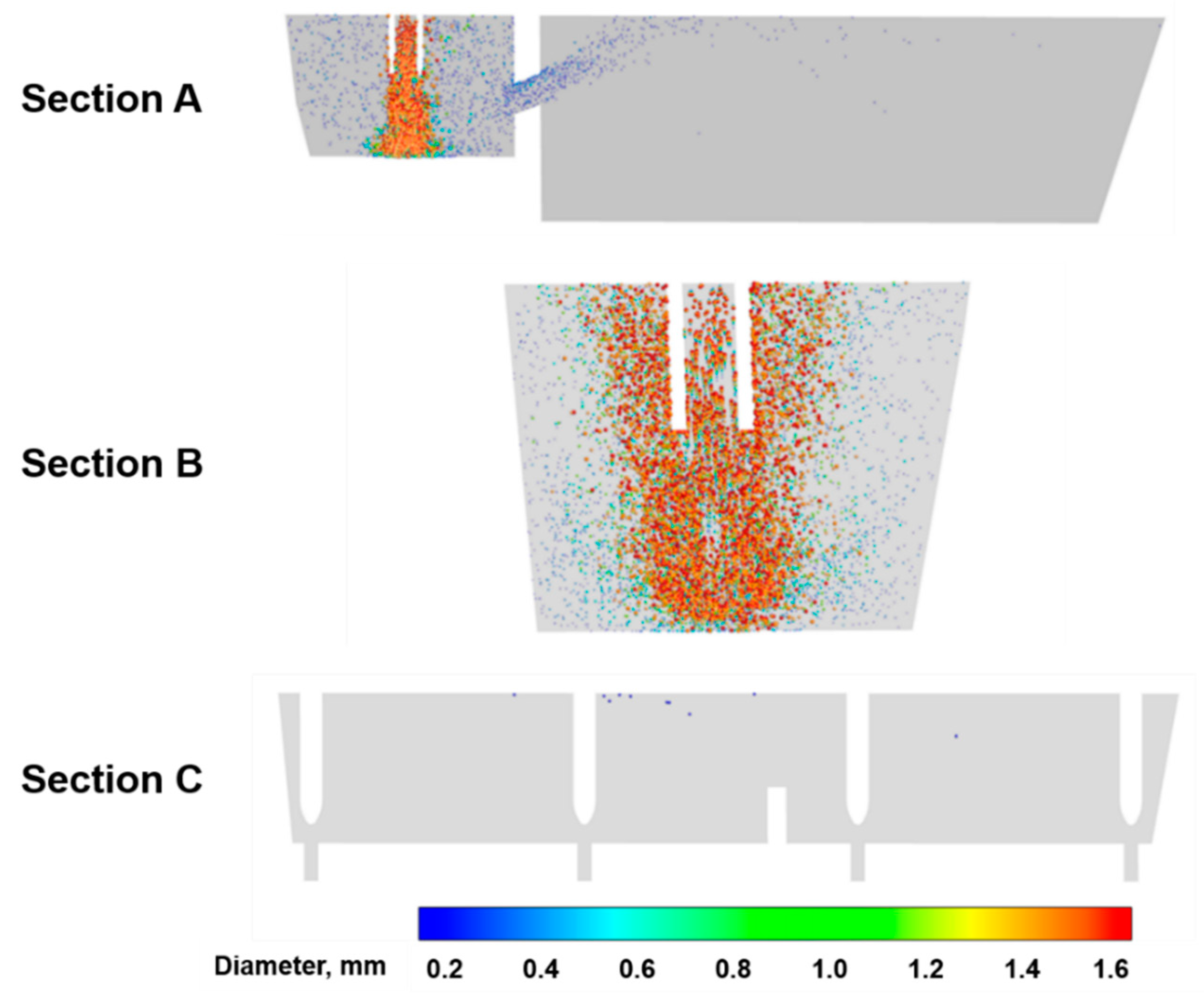
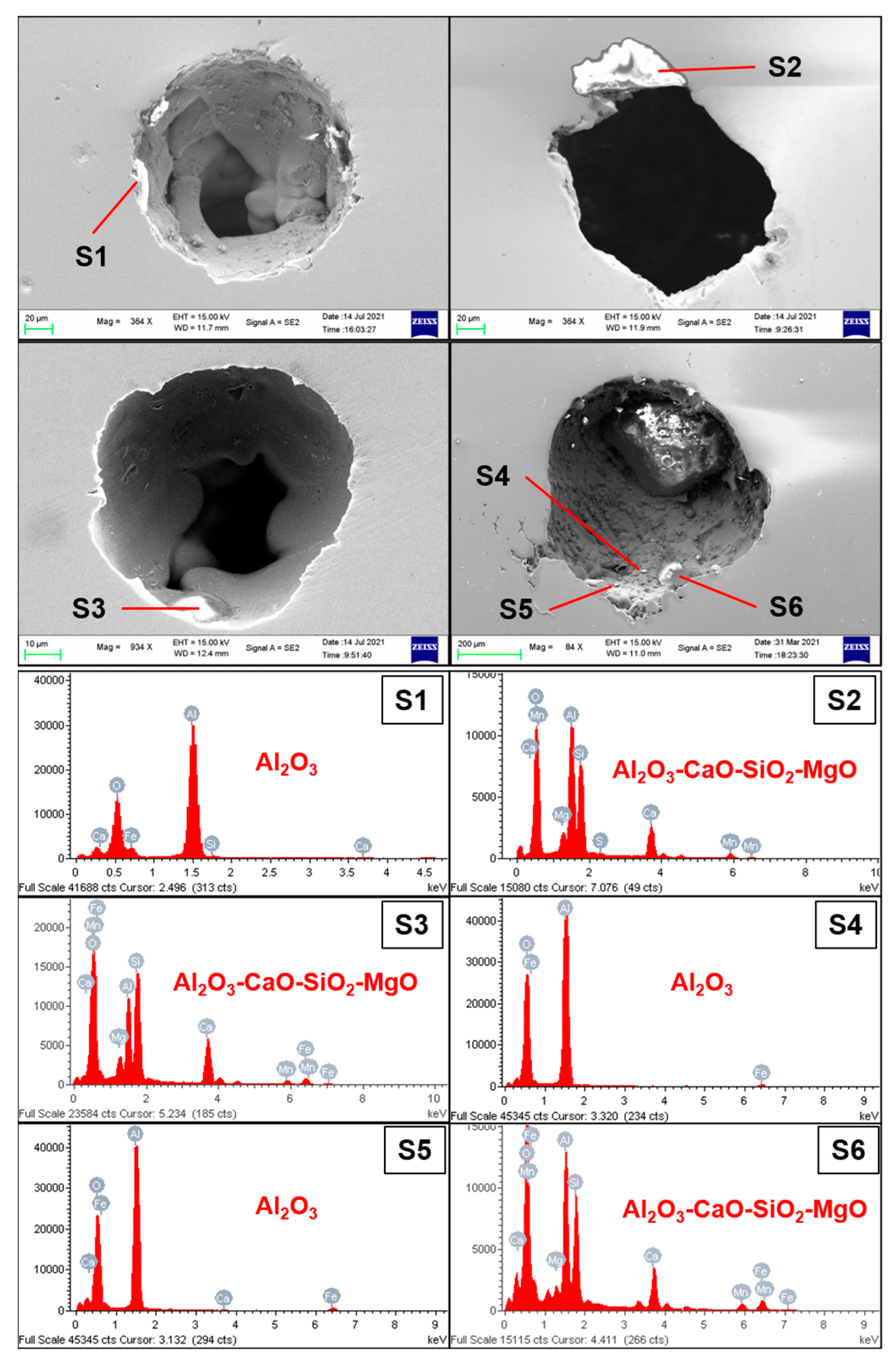
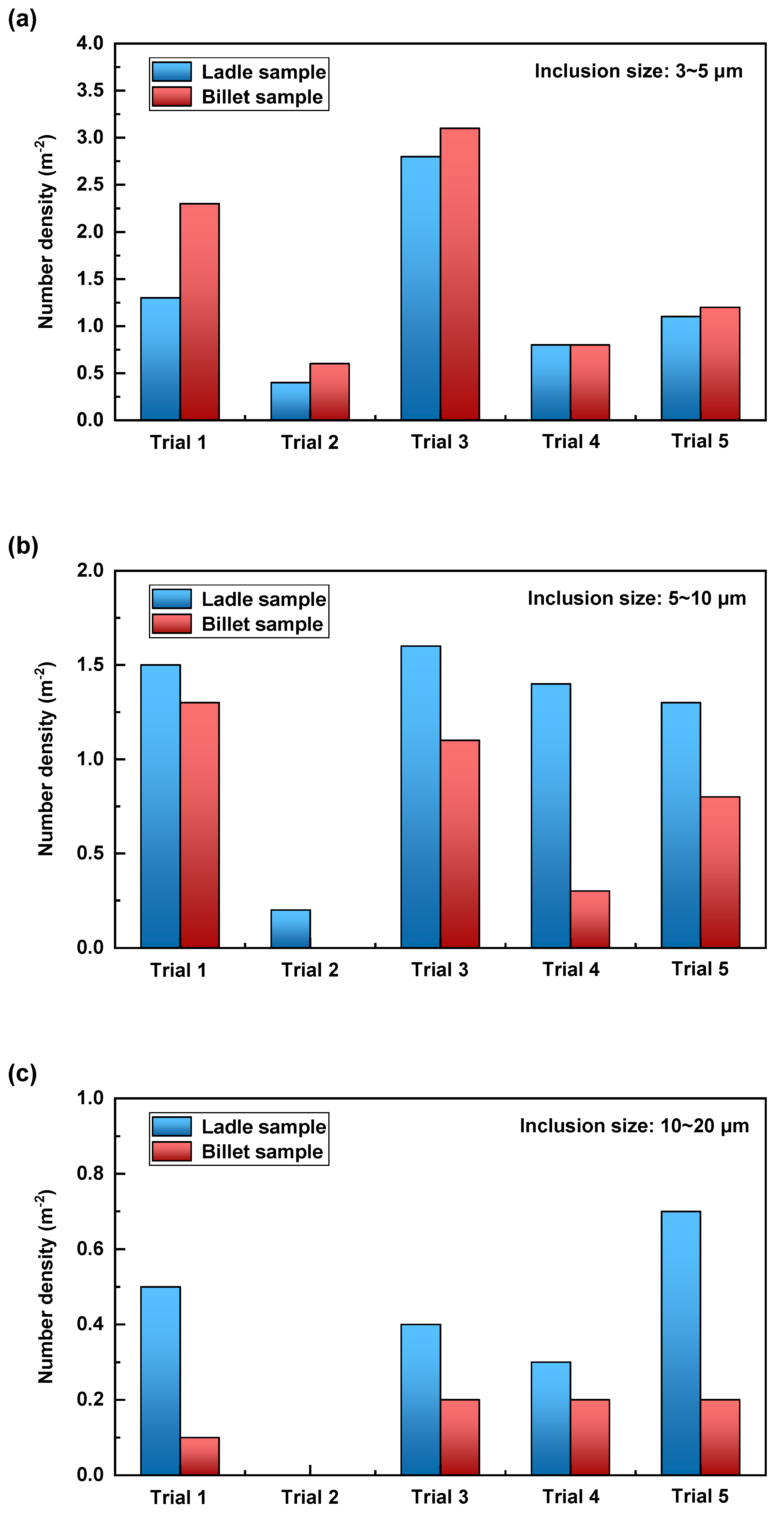
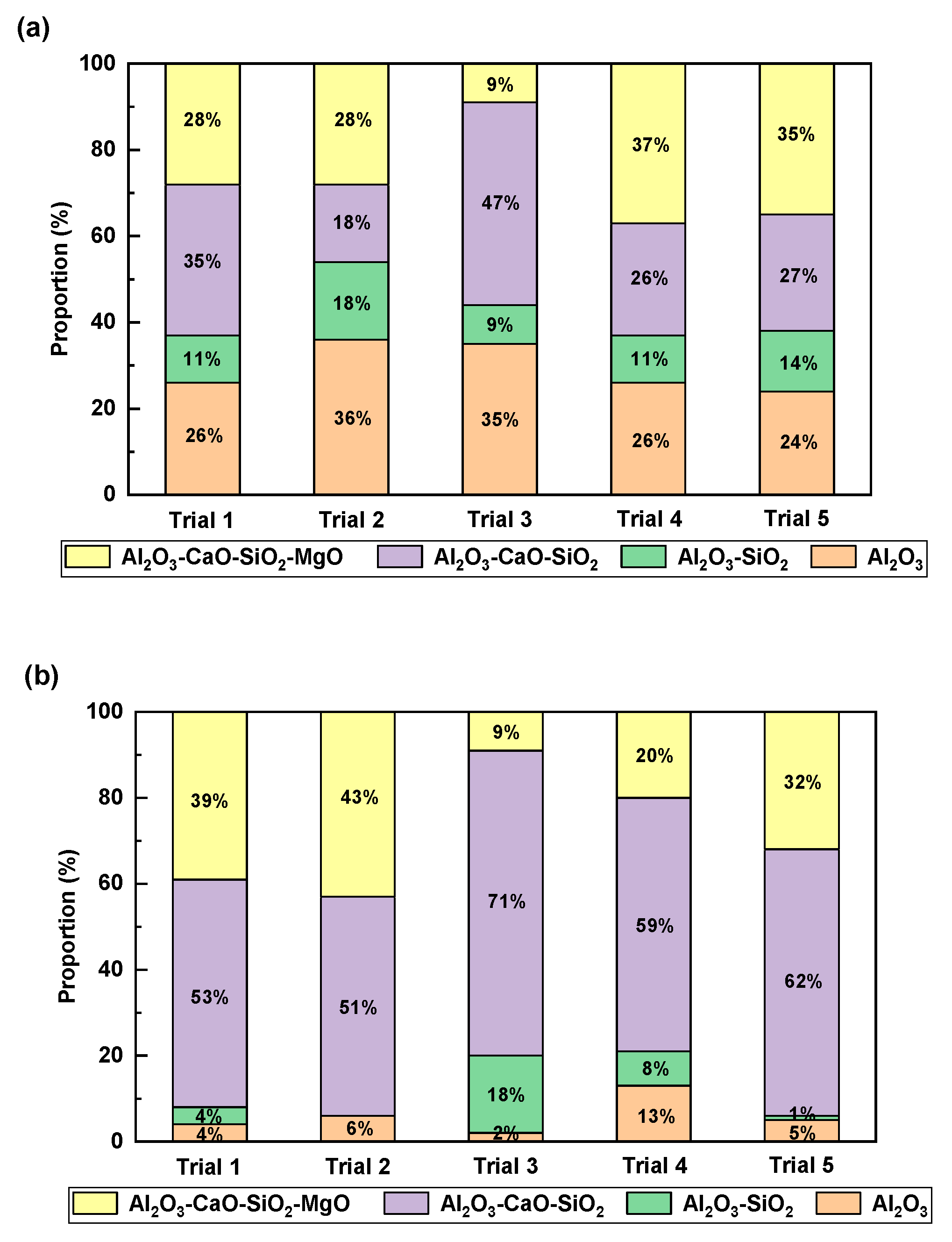
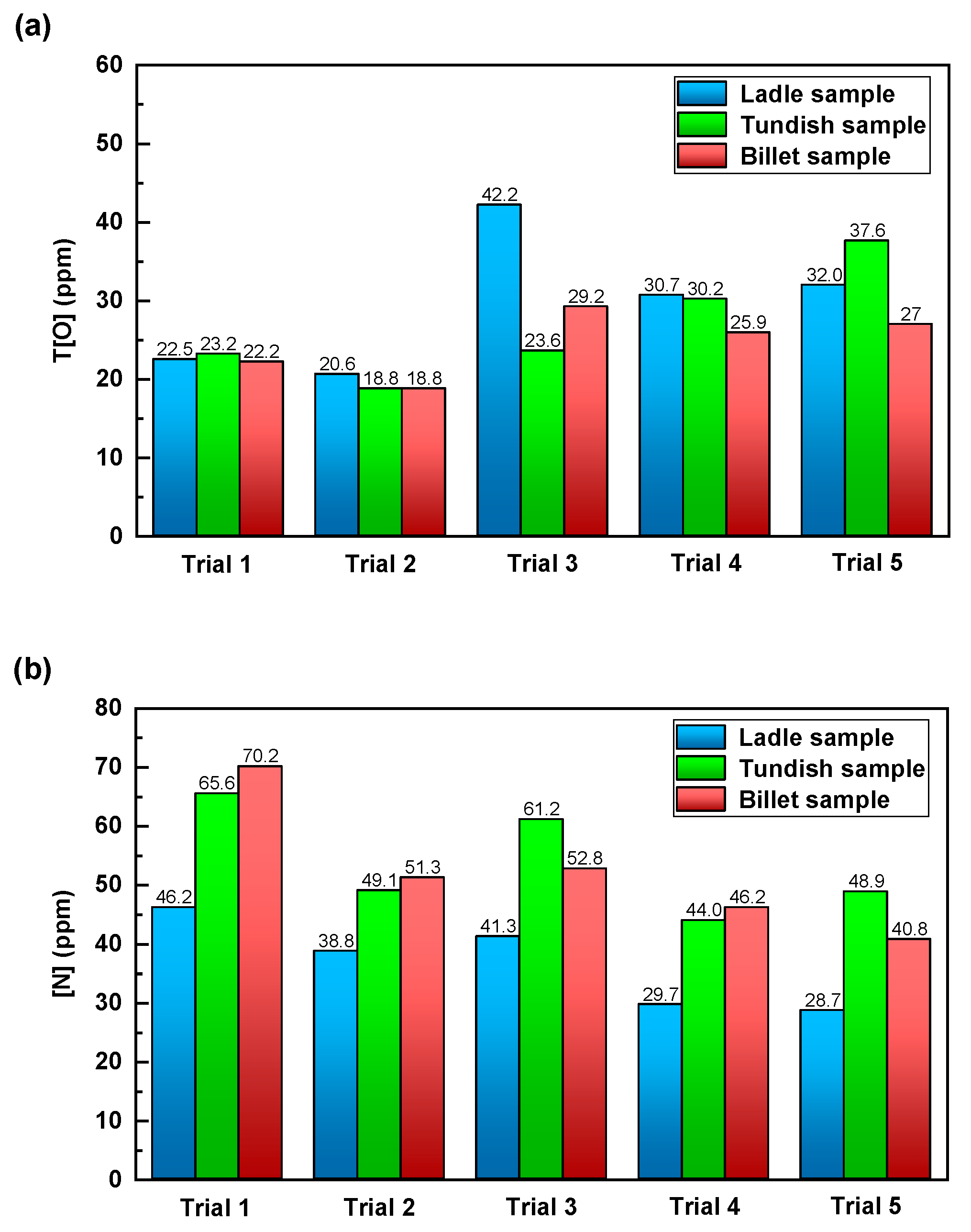
3.3. Inclusion Removal by Bubbles
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Holzinger, G.; Thumfart, M. Flow interaction in continuous casting tundish due to bubble curtain operation. Steel Res. Int. 2019, 90, 1800642. [Google Scholar] [CrossRef]
- Souza, G.M.; Mendonça, A.F.G.; Tavares, R.P. Physical and mathematical modeling of inclusion behavior in a tundish with gas curtain. REM Int. Eng. J. 2020, 73, 531–538. [Google Scholar] [CrossRef]
- Sheng, D.Y. Mathematical Modelling of Multiphase Flow and Inclusion Behavior in a Single-Strand Tundish. Metals 2020, 10, 1213. [Google Scholar] [CrossRef]
- Xue, Z.L.; Wang, Y.F.; Wang, L.T.; Li, Z.B.; Zhang, J.W. Inclusion removal from molten steel by attachment small bubbles. Acta Metall. Sin. 2003, 39, 431–434. [Google Scholar]
- Rogler, J.P.; Heaslip, L.J.; Mehrvar, M. Physical modelling of inclusion removal in a tundish by gas bubbling. Can. Metall. Quart. 2005, 44, 357–368. [Google Scholar] [CrossRef]
- Zhang, J.; He, Y.; Liu, J.H.; Yan, B.J.; Zhang, S.; Li, W. The effects of soluble gas floatation technology on the flow filed of ladle and inclusion removal in RH refine process. Vacuum 2019, 168, 108803. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, B.J.; Liu, J.H.; He, Y.; Li, W.; Liu, H.B. Water model study of the removal effect of soluble gas floatation technology (SGFT) on inclusions with different characteristics. Vacuum 2021, 186, 110050. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, J.H.; He, Y.; Zhou, C.H.; Yuan, B.H.; MacLean, A. Bubble formation by argon injection through the down-leg snorkel with Ruhrstahl-Heraeus (RH) circulating flow. J. Mater. Process. Tech. 2022, 306, 117647. [Google Scholar] [CrossRef]
- Yang, X.F.; Chang, W.J.; Zhong, L.C.; Li, X.X.; Ji, W.Y.; Hao, P.F. Experiment of bubble behavior in argon blowing through long shroud of continuous casting. Steelmaking 2018, 34, 12–18. [Google Scholar]
- Mazumdar, D.; Singh, P.K.; Tiwari, R.K. Shrouded transfer of molten steel from ladle to tundish: Current understanding, mathematical modelling and new insight. ISIJ Int. 2018, 58, 1545–1547. [Google Scholar] [CrossRef]
- Wang, L.; Lee, H.G.; Hayes, P. A new approach to molten steel refining using fine gas bubbles. ISIJ Int. 1996, 36, 17–24. [Google Scholar] [CrossRef]
- Zhang, Q.Y.; Wang, L.T.; Xu, Z.R. A new method of removing inclusions in molten steel by injecting gas from the shroud. ISIJ Int. 2006, 46, 1177–1182. [Google Scholar] [CrossRef]
- Li, J.; Wen, G.; Zhu, M.M.; Tang, P. A new application of turbulator in removing inclusions by injecting gas from the shroud. Metal. Int. 2012, 17, 57–62. [Google Scholar]
- Fan, A.Y.; Wen, G.H.; Li, J.X.; Tang, P. Present situation and prospect of fine gas bubbles formation in the ladle shroud. Steelmaking 2015, 32, 67–72. [Google Scholar]
- Chang, S.; Cao, X.E.; Zou, Z.S.; Isac, M.; Guthrie, R.I.L. Microbubble swarms in a full-scale water model tundish. Metall. Mater. Trans. B 2016, 47, 2732–2743. [Google Scholar] [CrossRef]
- Bao, Y.P.; Liu, J.H.; Xu, B.M. Behaviors of fine bubbles in the shroud nozzle of ladle and tundish. Int. J. Min. Met. Mater. 2003, 10, 20–23. [Google Scholar]
- Singh, P.K.; Mazumdar, D.A. Physical model study of two-phase gas-liquid flows in a ladle shroud. Metall. Mater. Trans. B 2018, 49, 1945–1962. [Google Scholar] [CrossRef]
- Chatterjee, S.; Chattopadhyay, K. Physical modeling of slag ‘eye’ in an inert gas-shrouded tundish using dimensional analysis. Metall. Mater. Trans. B 2016, 47, 508–521. [Google Scholar] [CrossRef]
- Chattopadhyay, K.; Isac, M.; Guthrie, R.I.L. Physical and mathematical modelling of inert gas shrouding in a tundish. ISIJ Int. 2011, 51, 573–580. [Google Scholar] [CrossRef]
- Chatterjee, S.; Chattopadhyay, K. Formation of slag “eye” in an inert gas shrouded tundish. ISIJ Int. 2015, 55, 1416–1424. [Google Scholar] [CrossRef]
- Liu, J.H.; Li, W.; He, Y.; Su, X.F.; Zhang, J.; Chang, F.R. Industrial experimental study on the formation of microbubbles by argon injection into ladle shroud. Chin. J. Eng. 2022, 44, 1183–1191. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Method. Appl. M. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Merder, T.; Warzecha, M. Optimization of a six-strand continuous casting tundish: Industrial measurements and numerical investigation of the tundish modifications. Metall. Mater. Trans. B 2012, 43, 856–868. [Google Scholar] [CrossRef]
- Bai, H.; Thomas, B.G. Bubble formation during horizontal gas injection into downward-flowing liquid. Metall. Mater. Trans. B 2001, 32, 1143–1159. [Google Scholar] [CrossRef]
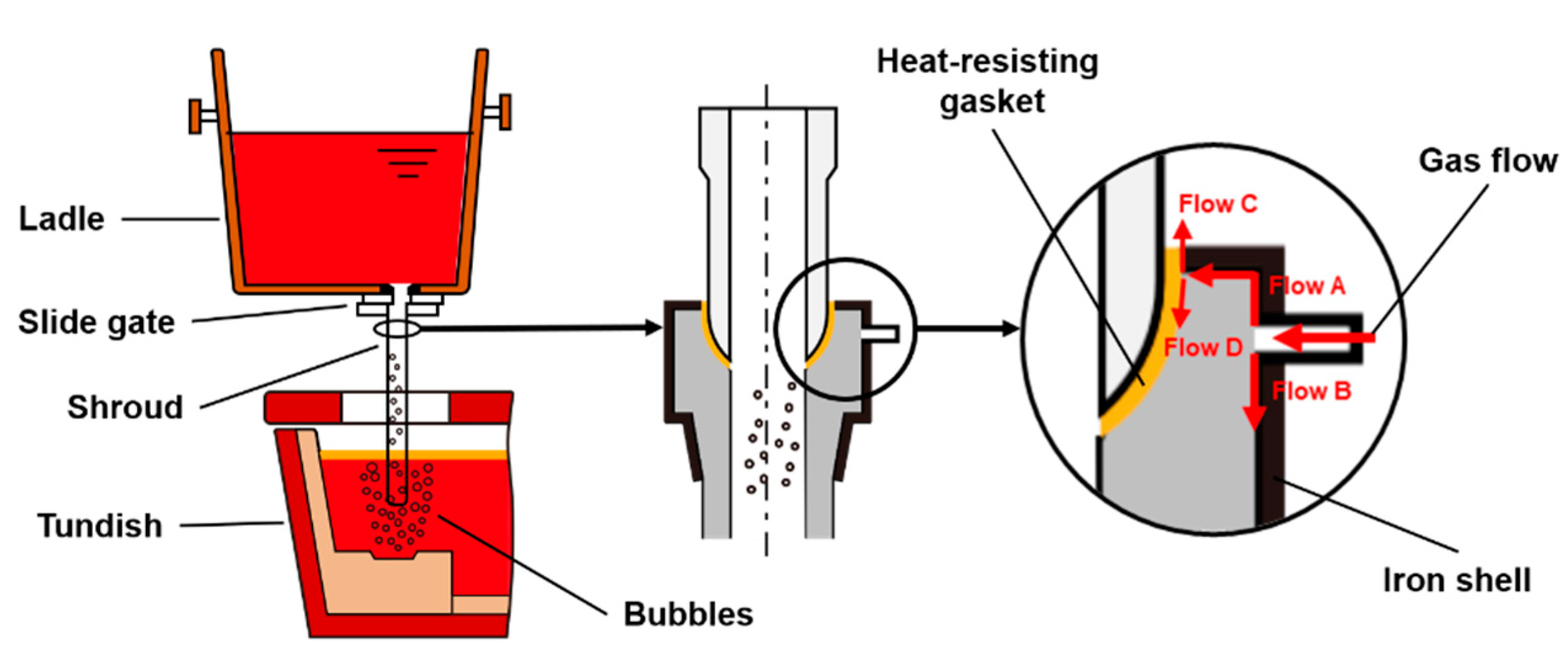






| C1 | C2 | Cμ | σε | σk |
|---|---|---|---|---|
| 1.44 | 1.92 | 0.09 | 1.3 | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Liu, J.; Su, X.; Li, W.; Pan, Y.; Wang, D. Characteristics of Bubble Behavior and Inclusion Removal in Liquid Steel Based on Industrial Trials of Argon Injection into Ladle Shroud. Metals 2023, 13, 593. https://doi.org/10.3390/met13030593
He Y, Liu J, Su X, Li W, Pan Y, Wang D. Characteristics of Bubble Behavior and Inclusion Removal in Liquid Steel Based on Industrial Trials of Argon Injection into Ladle Shroud. Metals. 2023; 13(3):593. https://doi.org/10.3390/met13030593
Chicago/Turabian StyleHe, Yang, Jianhua Liu, Xiaofeng Su, Wei Li, Yukang Pan, and Daya Wang. 2023. "Characteristics of Bubble Behavior and Inclusion Removal in Liquid Steel Based on Industrial Trials of Argon Injection into Ladle Shroud" Metals 13, no. 3: 593. https://doi.org/10.3390/met13030593
APA StyleHe, Y., Liu, J., Su, X., Li, W., Pan, Y., & Wang, D. (2023). Characteristics of Bubble Behavior and Inclusion Removal in Liquid Steel Based on Industrial Trials of Argon Injection into Ladle Shroud. Metals, 13(3), 593. https://doi.org/10.3390/met13030593








