Buckling of Bisegment Pressure Hulls Fabricated through Free Bulging
Abstract
1. Introduction
2. Experimental Analysis
2.1. Material and Methods
2.1.1. Problem Statement
2.1.2. Measuring and Testing
2.2. Experimental Results and Discussion
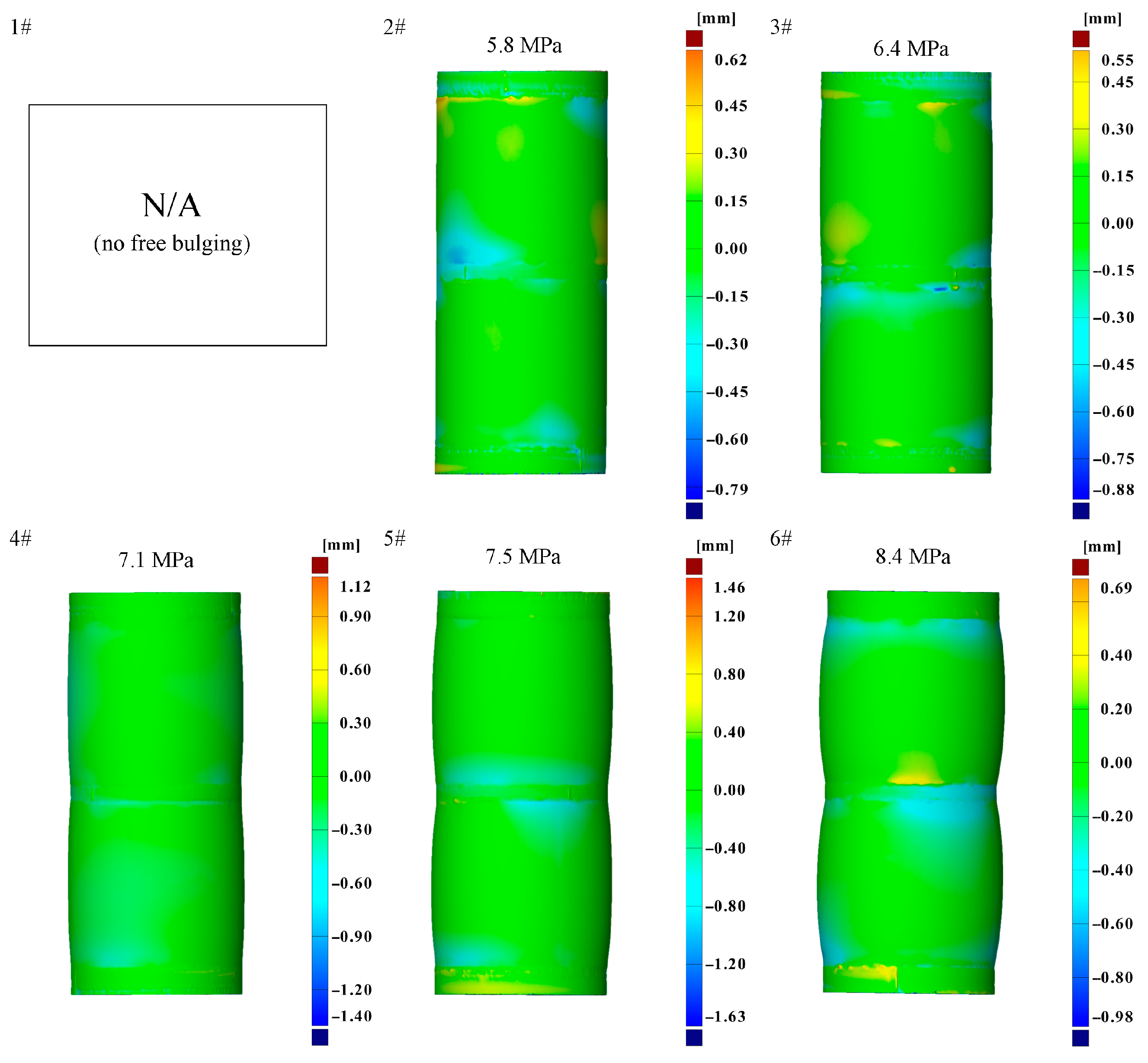
2.2.1. Measuring Analysis
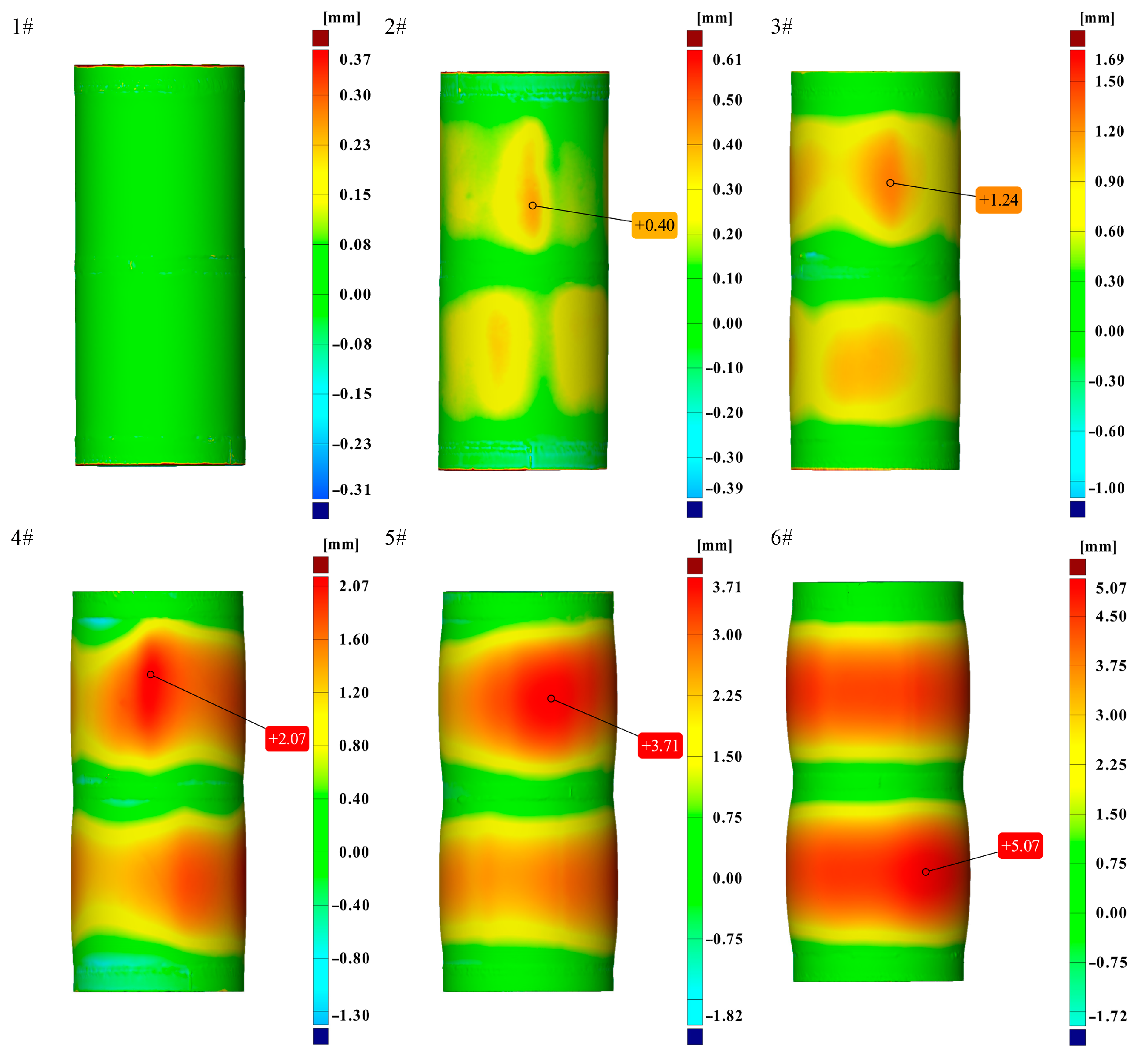
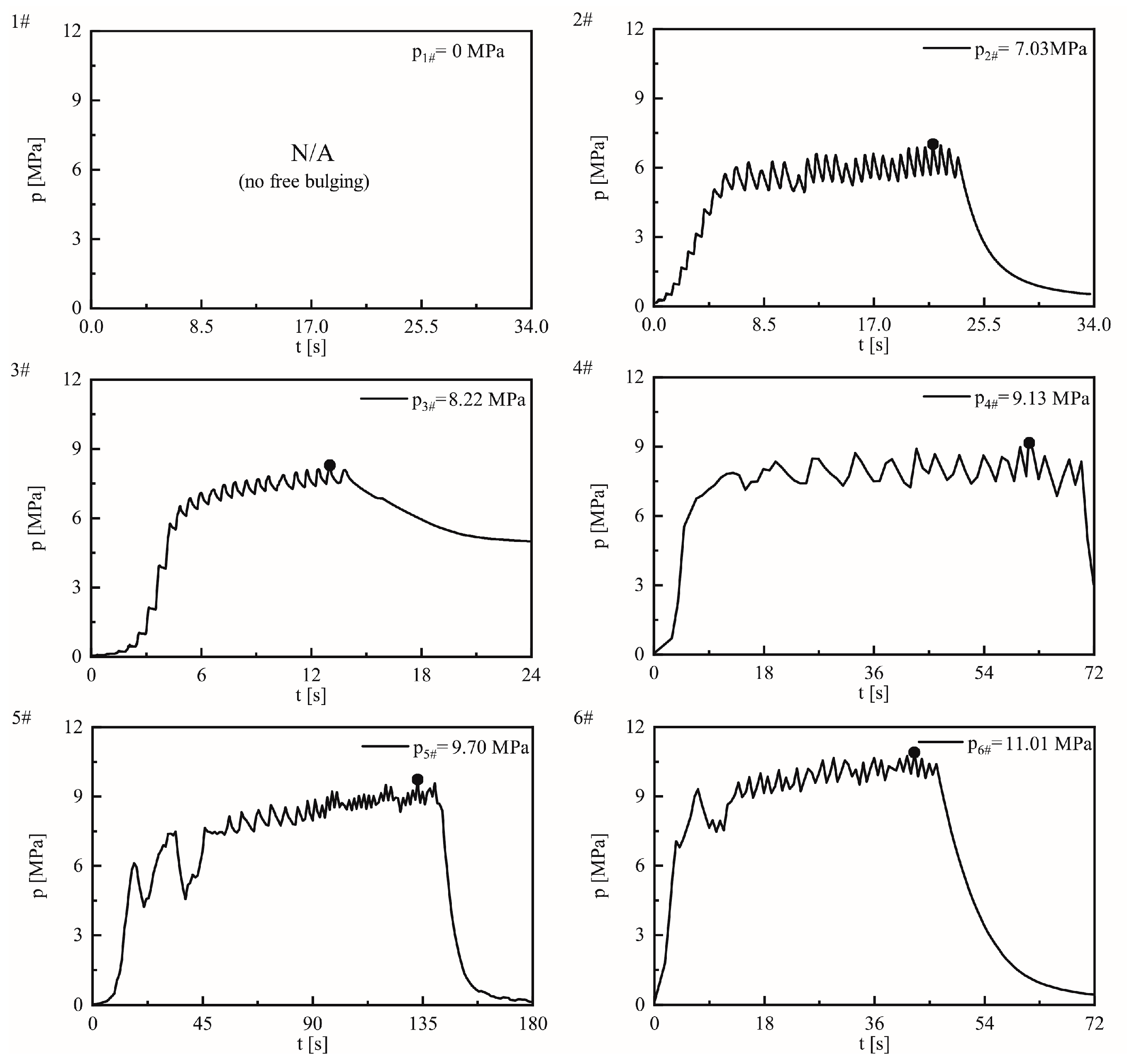
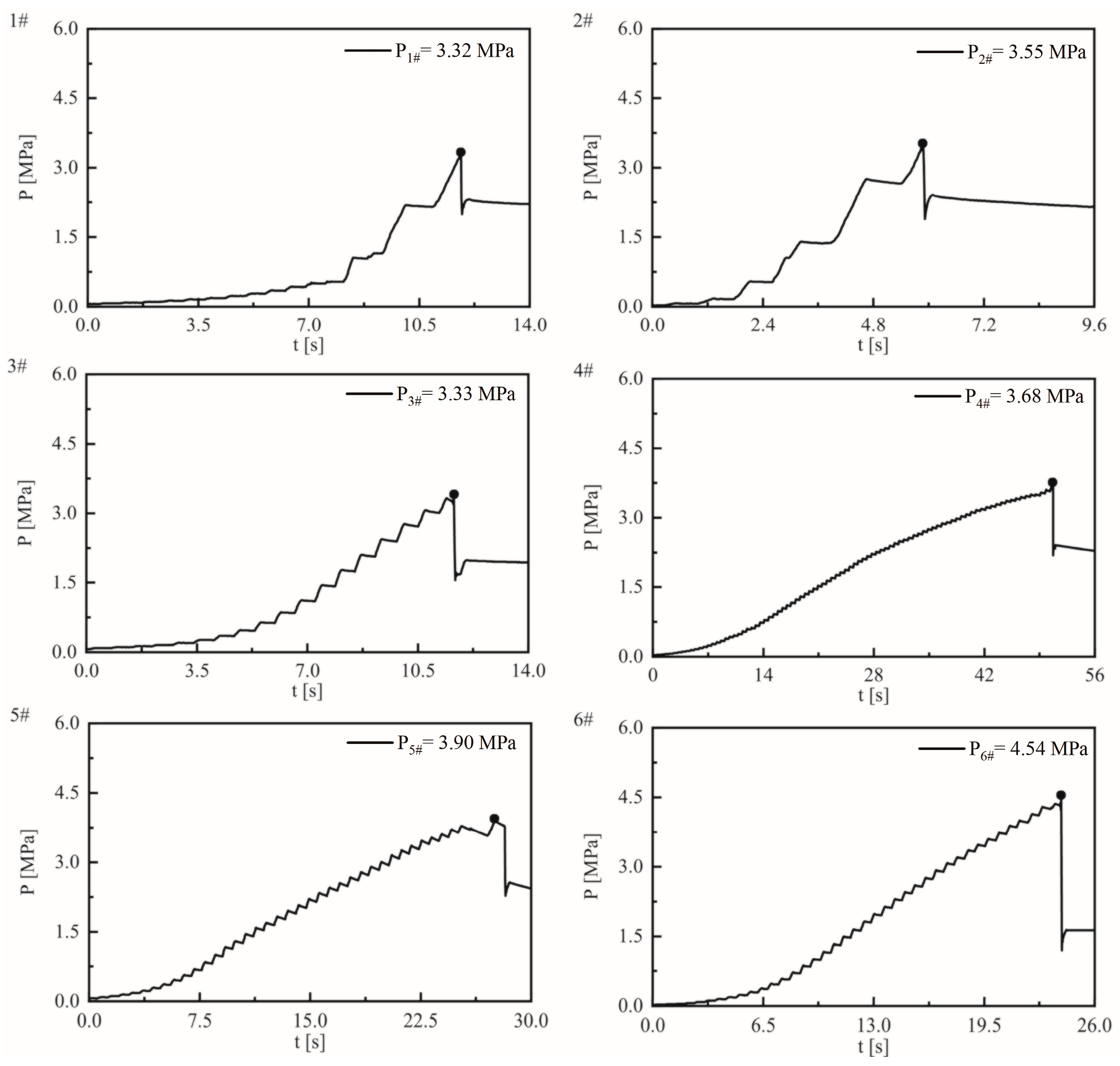
2.2.2. Test Results
3. Numerical Analysis
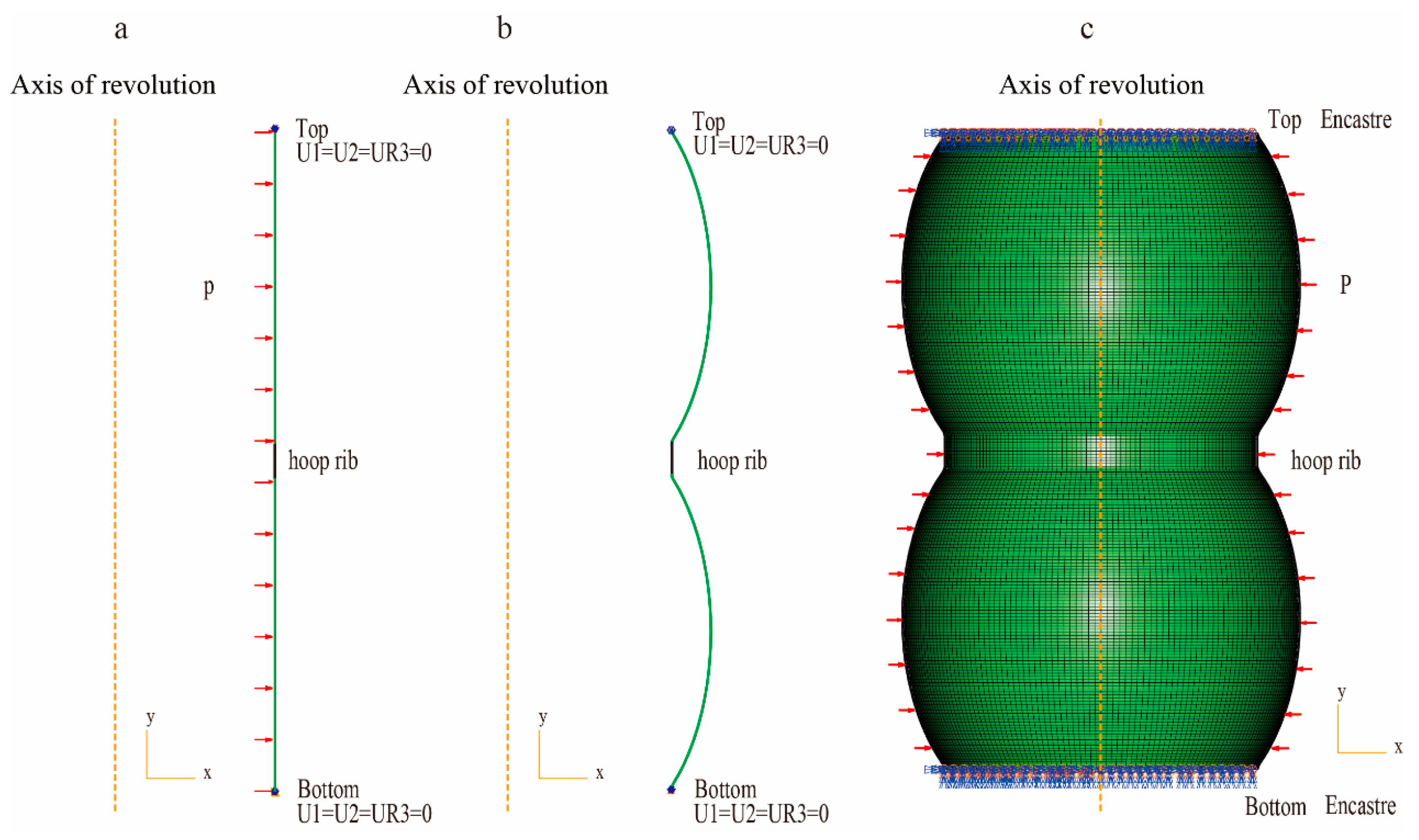
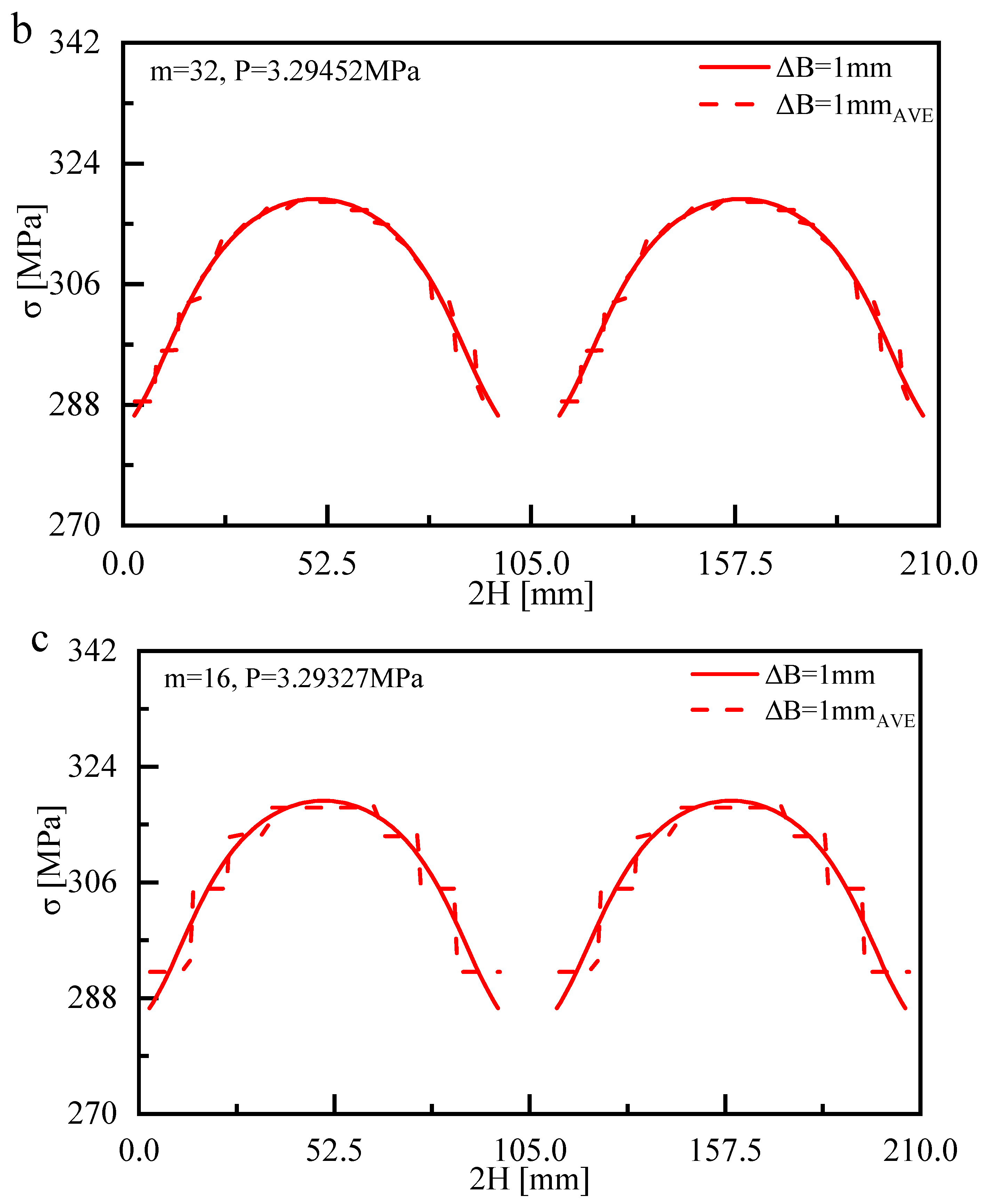
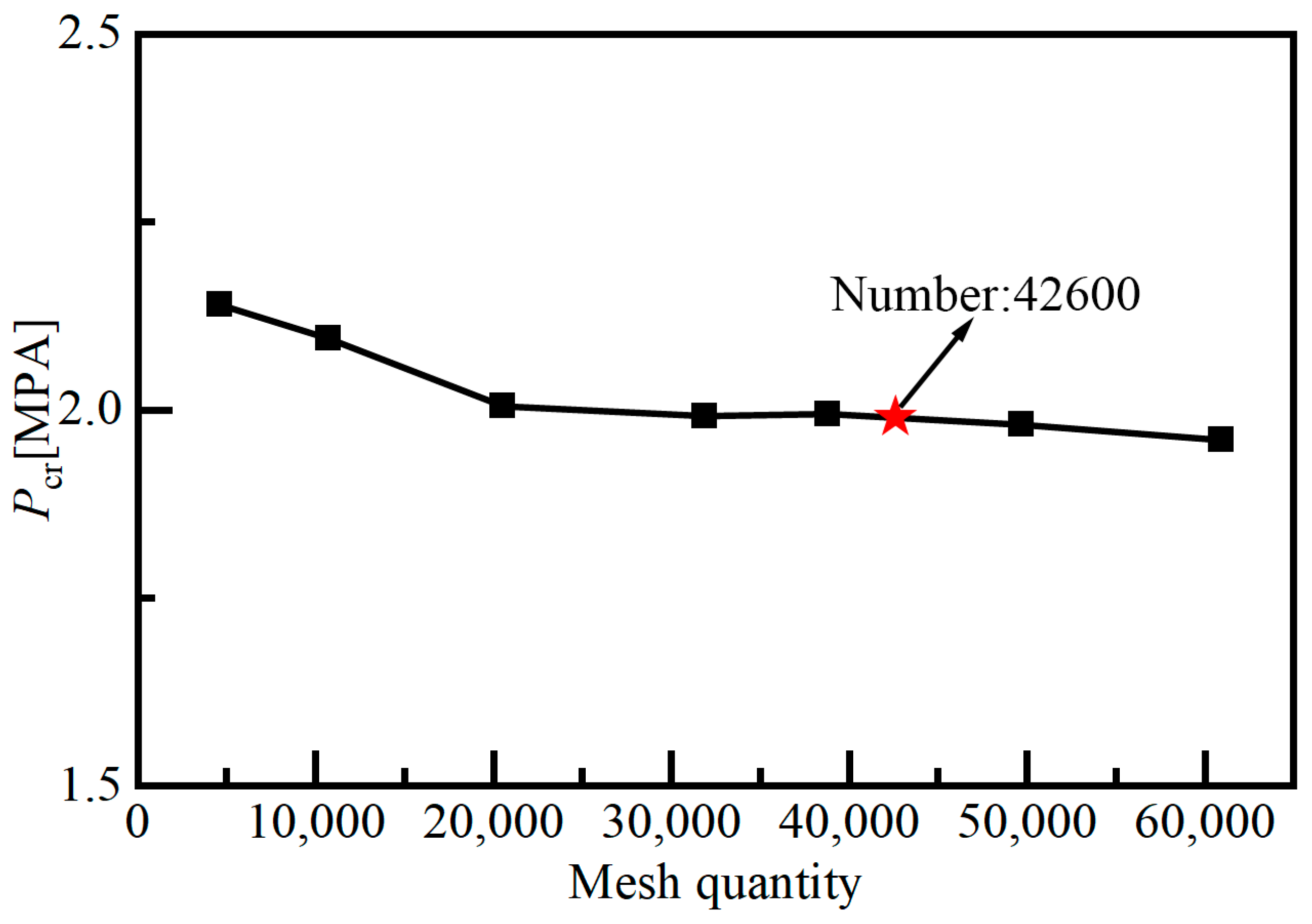
3.1. Numerical Modelling
3.2. Numerical Results and Discussion
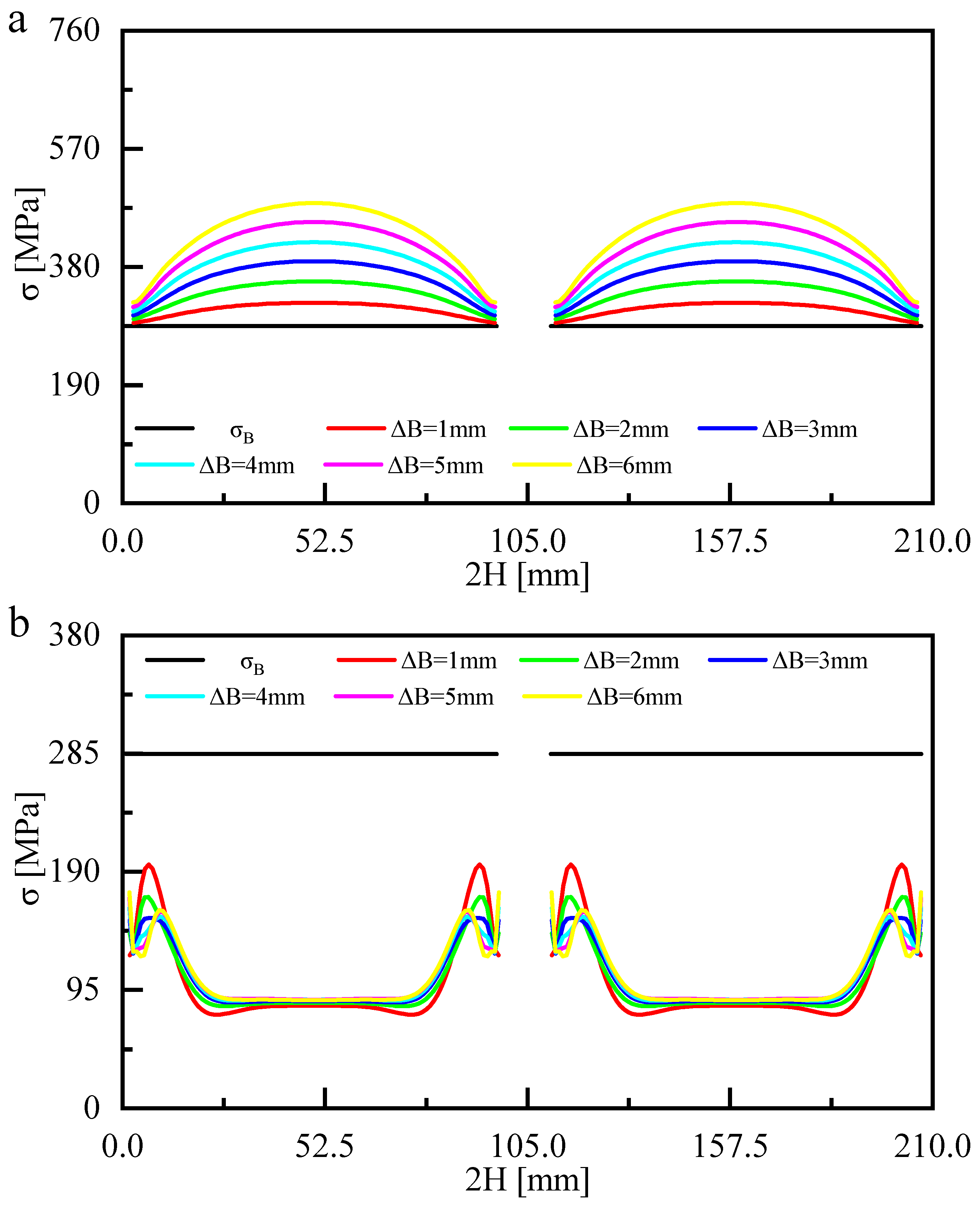
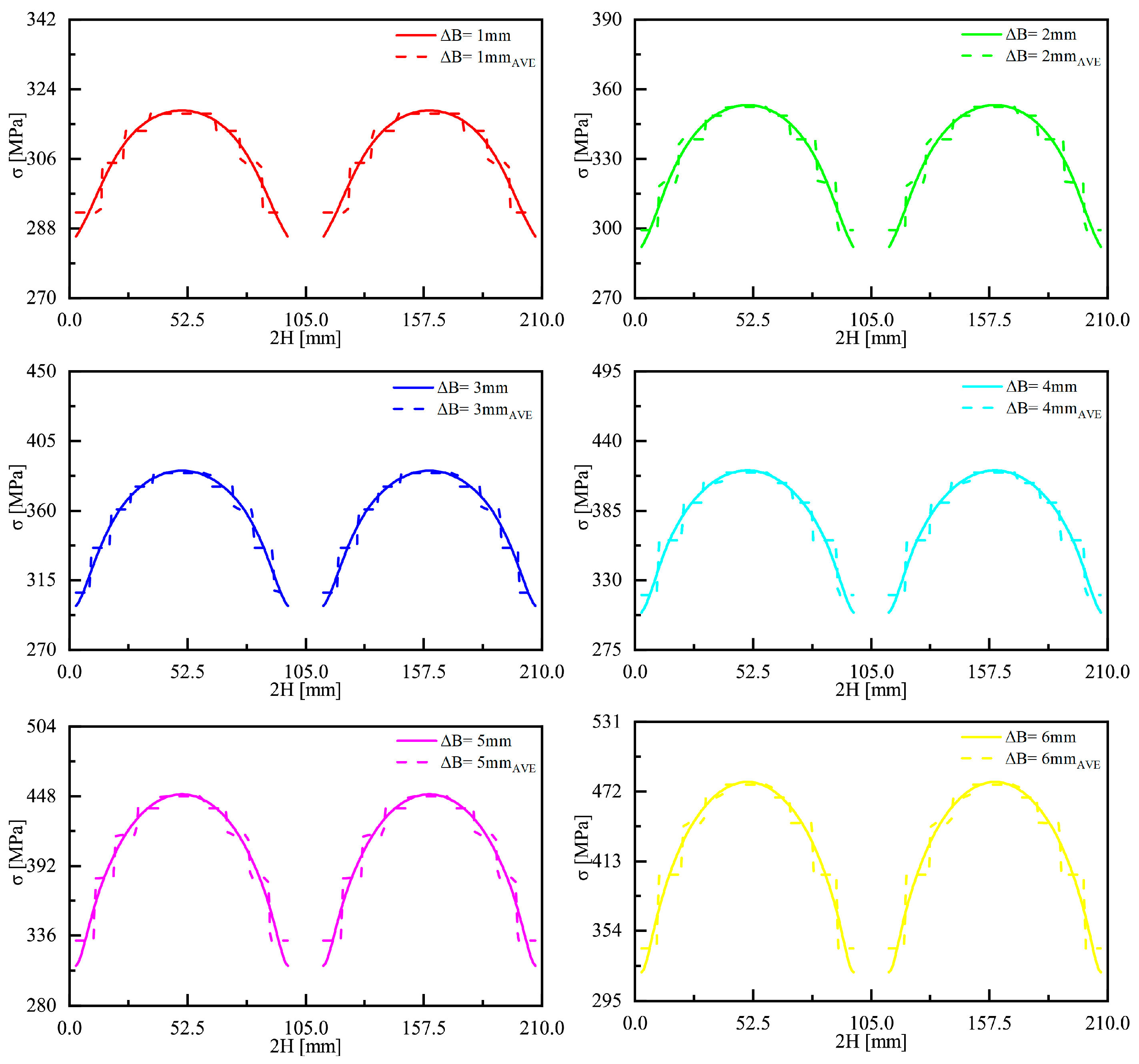
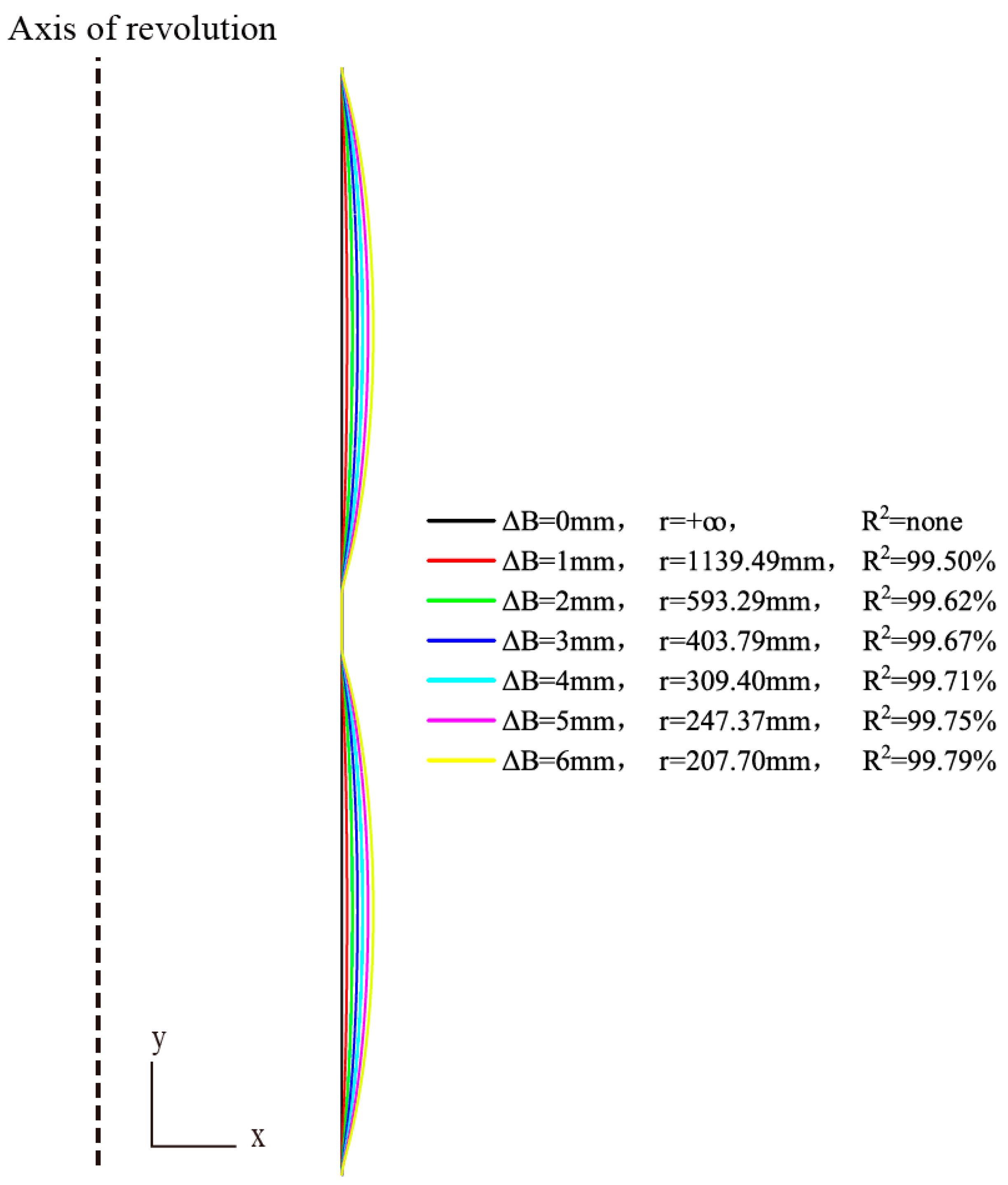
3.2.1. Bulging Analysis
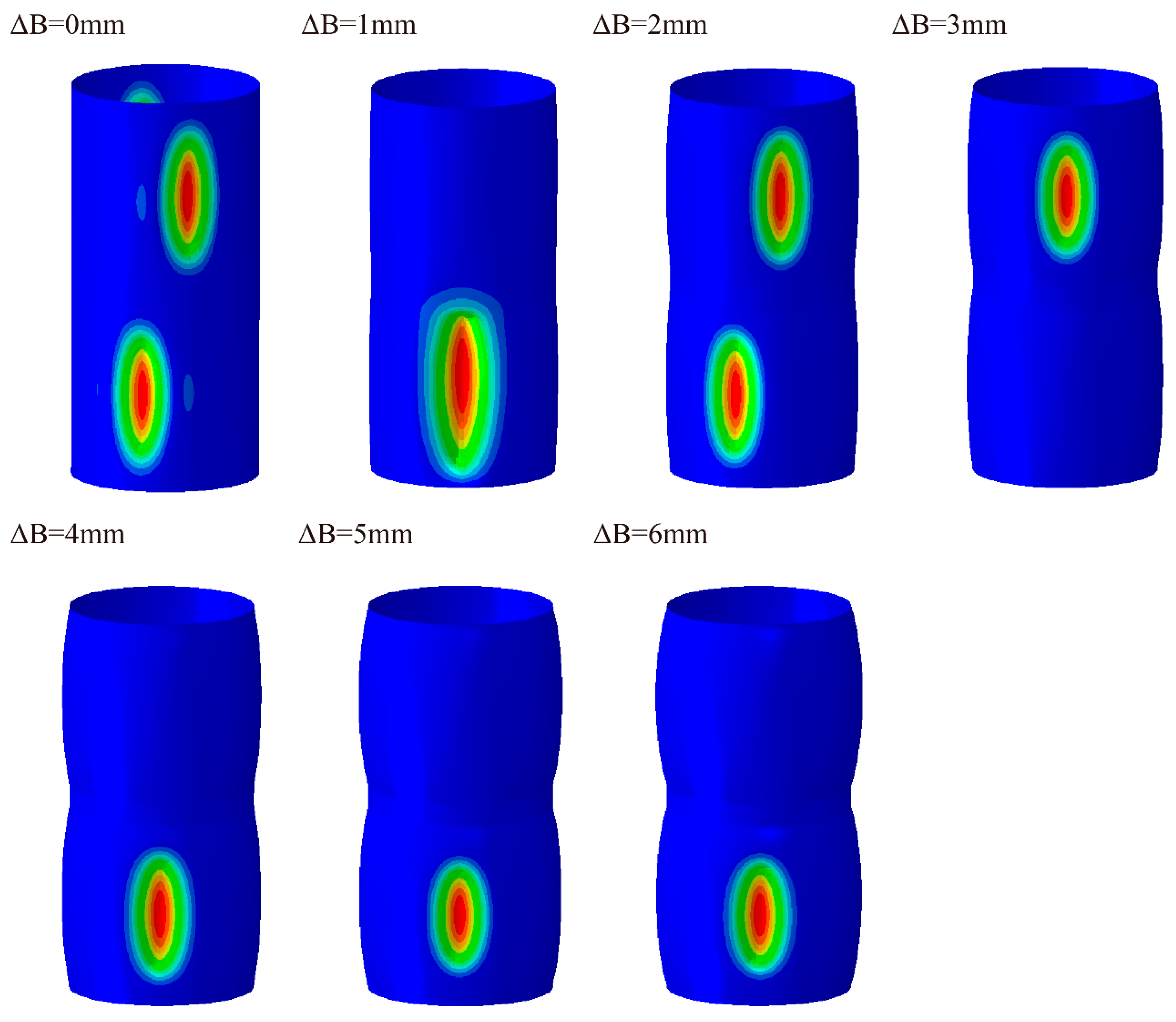
3.2.2. Buckling Analysis
4. Conclusions
- (1)
- Six bi-segment cylindrical preforms were fabricated through the TIG technique and exhibited favourable symmetry and machinability. Owing to the thick steel plates at the ends of the preforms, six bi-segment cylindrical hulls were produced through a quasi–static free bulging process; the hulls exhibited favourable geometric symmetry and a favourable thickness distribution around the axis of rotation. The hoop rib was not displaced during the free bulging process, and this can be attributed to the deformation consistency of the hulls. This thus verifies the reliability of the design parameters.
- (2)
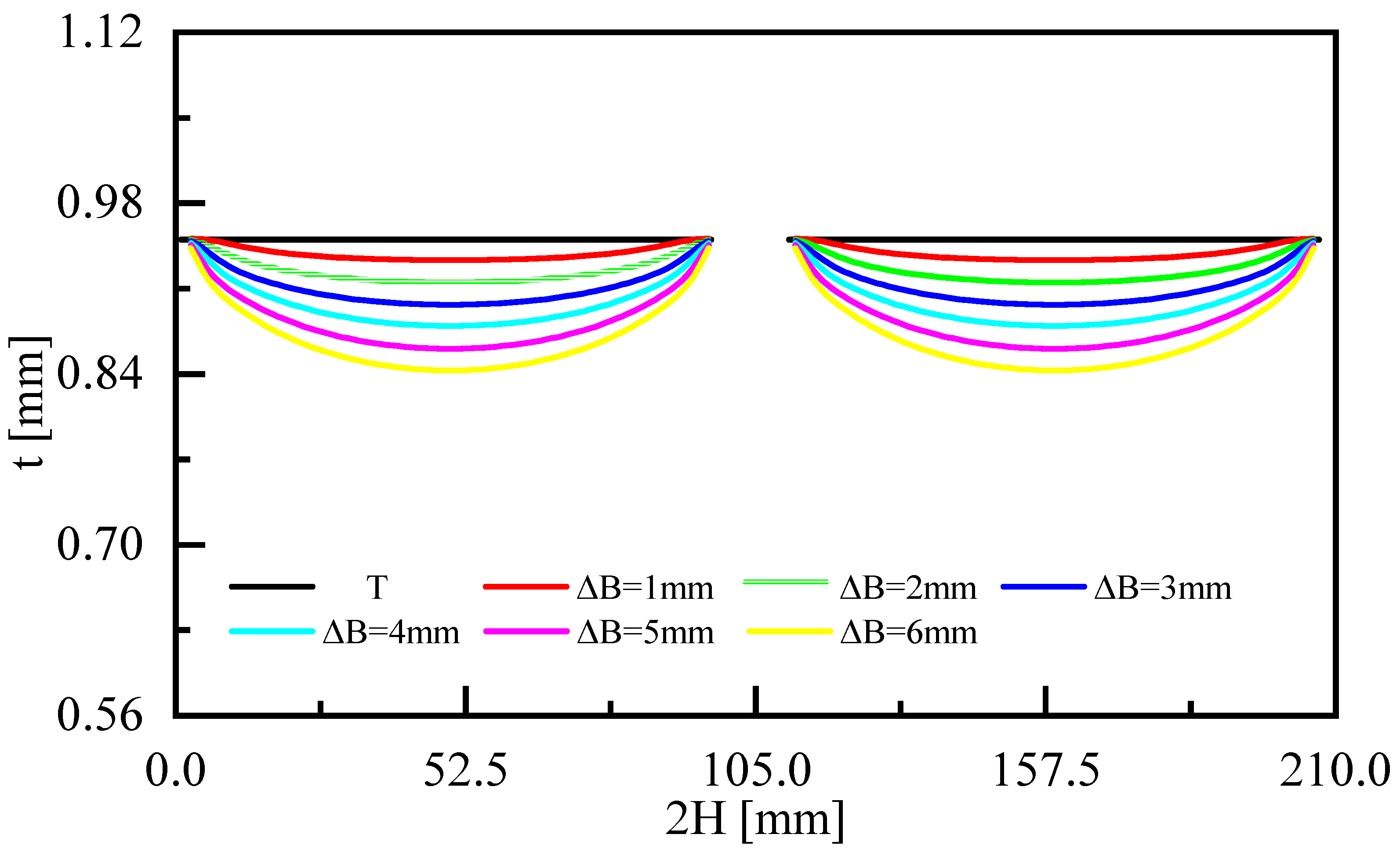
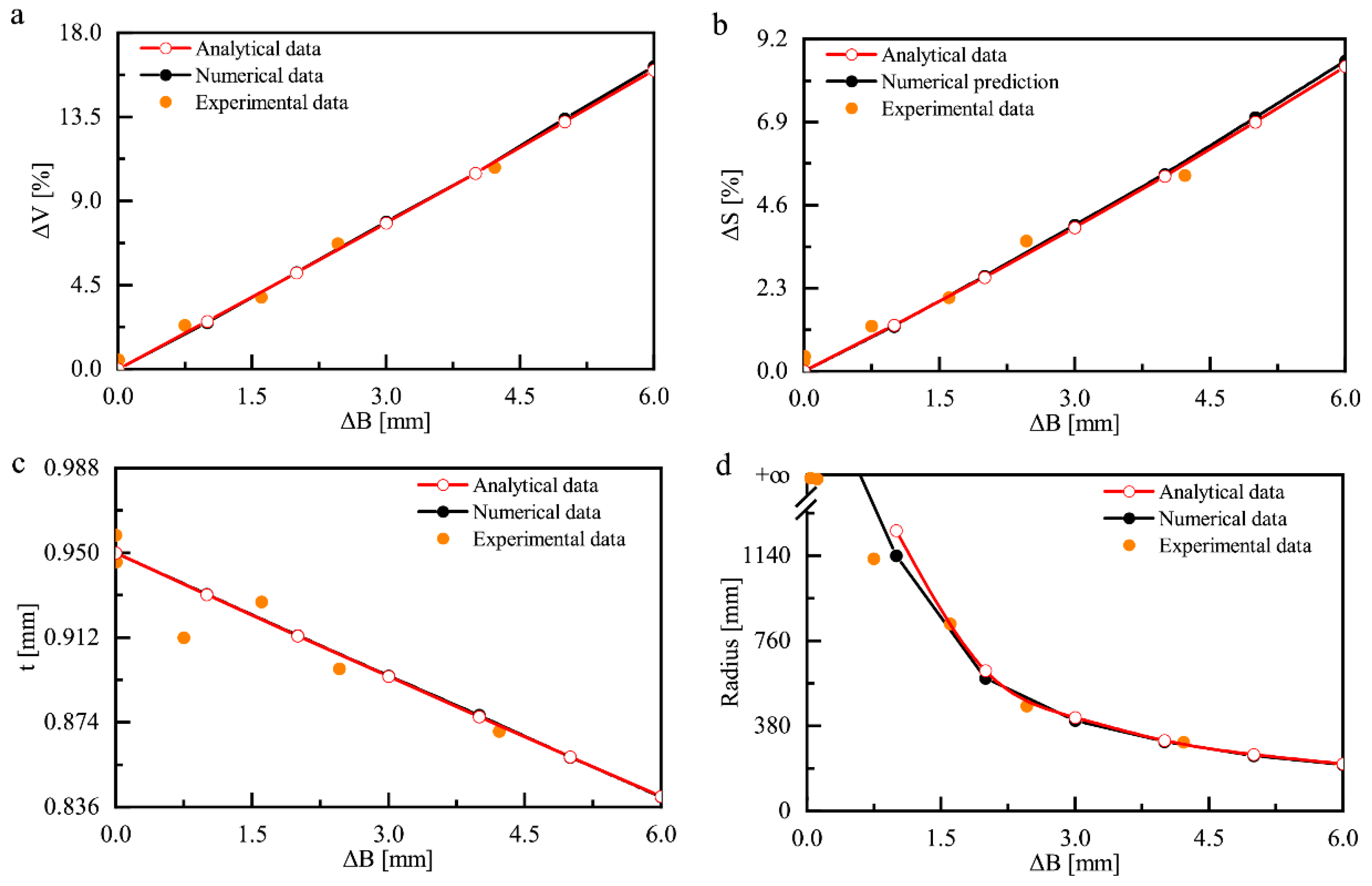
- Free bulging increased the volume and surface area and decreased the thickness of a bi-segment pressure hull. This study revealed that the maximum bulging magnitude for the bi-segment pressure hulls was 4.218 mm. The hulls had a volume growth rate of 10.81%, surface area growth rate of 5.43%, and maximum thickness reduction of 11.58%.
- (3)
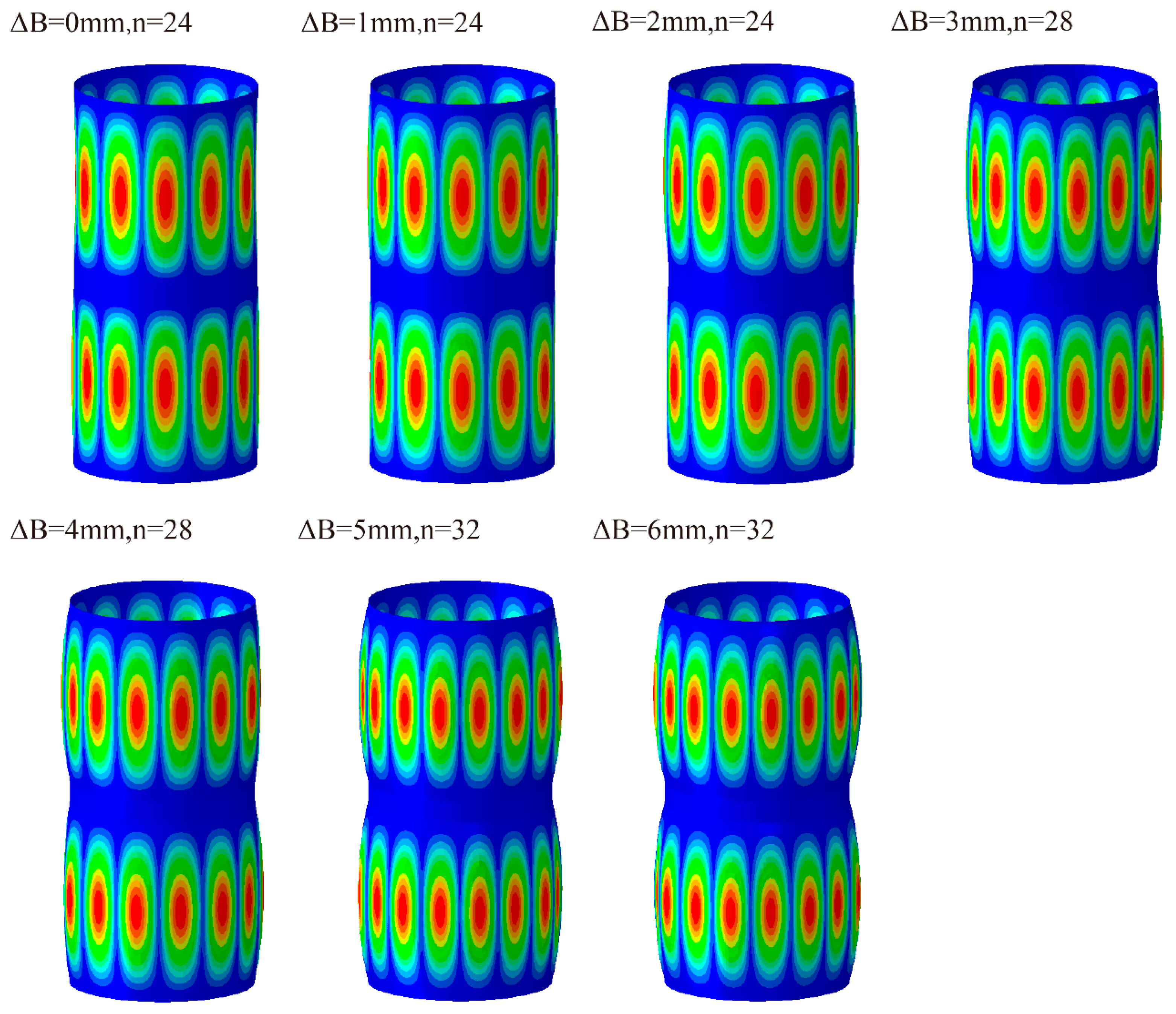
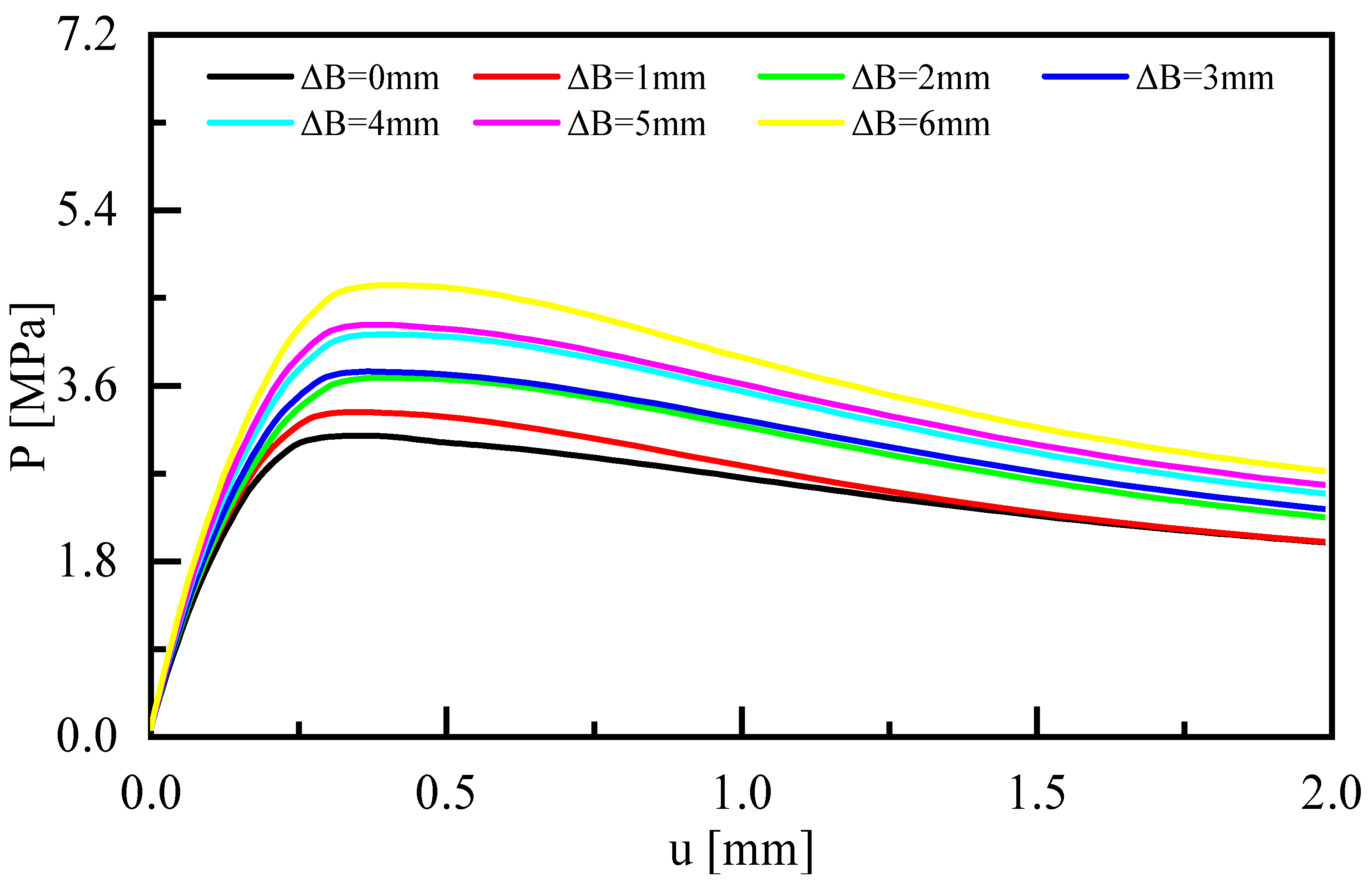
- The buckling loads of the six bi-segment pressure hulls produced in this study increased with the bulging magnitude under uniform hydrostatic pressure. Compared with buckling load of the control preform (preform 1) that was not subjected to a bulging load, the buckling loads of the other bulged hulls were increased by 6.93%, 0.31%, 10.84%, 17.47%, and 36.75%. The buckling modes of the bi-segment pressure hulls were characterised by local pits, whose location was related to the initial geometrical imperfections of the preform and the thickness distribution after free bulging.
- (4)
- Our numerical analysis of free bulging revealed that the growth rates of the volume and surface area of the bi-segment pressure hulls and the reduction rate of the thinnest points of the bi-segment pressure hulls increased linearly with the bulging magnitude. In contrast, the radius of the meridian decreased as the bulging magnitude increased. The numerical simulation results were in good agreement with the experimental and analytical results.
- (5)
- Our numerical buckling analysis indicated that the external pressure buckling capacity of the bi-segment pressure hulls fabricated through free bulging was relatively high. Both the linear and nonlinear buckling loads of the bi-segment pressure hulls increased linearly with the bulging magnitude. The linear buckling modes were observed using 24–32 latitudinal waves and half of a meridional wave. The nonlinear buckling modes were characterised by two local pits under low bulging magnitudes and by a single local pit under large bulging magnitudes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Craven, R.; Graham, D.; Dalzel-Job, J. Conceptual Design of a Composite Pressure Hull. Ocean Eng. 2016, 128, 153–162. [Google Scholar] [CrossRef]
- Carlisle, T.F. Ross Pressure Vessels External Pressure Technology, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Błachut, J.; Smith, P. Buckling of Multi-Segment Underwater Pressure Hull. Ocean Eng. 2008, 35, 247–260. [Google Scholar] [CrossRef]
- Błachut, J. Buckling of Externally Pressurised Barrelled Shells: A Comparison of Experiment and Theory. Int. J. Press. Vessel. Pip. 2002, 79, 507–517. [Google Scholar] [CrossRef]
- Błachut, J. Experimental Perspective on the Buckling of Pressure Vessel Components. Appl. Mech. Rev. 2014, 66, 30–33. [Google Scholar] [CrossRef]
- Bałchut, J.; Wang, P. Buckling of Barreled Shells Subjected to External Hydrostatic Pressure. J. Press. Vessel Technol. Trans. ASME 2001, 123, 232–239. [Google Scholar] [CrossRef]
- Błachut, J. Combined axial and pressure buckling of shells having optimal positive Gaussian curvature. Comput. Struct. 1987, 26, 513–519. [Google Scholar] [CrossRef]
- Błachut, J.; Smith, P. Tabu Search Optimization of Externally Pressurized Barrels and Domes. Eng. Optim. 2007, 39, 899–918. [Google Scholar] [CrossRef]
- Błachut, J. Optimal Barreling of Steel Shells via Simulated Annealing Algorithm. Comput. Struct. 2003, 81, 1941–1956. [Google Scholar] [CrossRef]
- Jam, J.E.; Kiani, Y. Buckling of Pressurized Functionally Graded Carbon Nanotube Reinforced Conical Shells. Compos. Struct. 2015, 125, 586–595. [Google Scholar] [CrossRef]
- Babaei, M.; Kiarasi, F.; Hossaeini Marashi, S.M.; Ebadati, M.; Masoumi, F.; Asemi, K. Stress Wave Propagation and Natural Frequency Analysis of Functionally Graded Graphene Platelet-Reinforced Porous Joined Conical–Cylindrical–Conical Shell. Waves Random Complex Media 2021, 1–33. [Google Scholar] [CrossRef]
- Mollaei, S.; Babaei, M.; Asemi, K. Torsional Buckling of Functionally Graded Graphene Reinforced Composite Laminated Cylindrical Panel. Arch. Appl. Mech. 2023, 93, 427–435. [Google Scholar] [CrossRef]
- Jasion, P.; Magnucki, K. Elastic Buckling of Barrelled Shell under External Pressure. Thin-Walled Struct. 2007, 45, 393–399. [Google Scholar] [CrossRef]
- Magnucki, K.; Jasion, P. Analytical Description of Pre-Buckling and Buckling States of Barrelled Shells under Radial Pressure. Ocean Eng. 2013, 58, 217–223. [Google Scholar] [CrossRef]
- Jasion, P.; Magnucki, K. Elastic Buckling of Horizontal Barrelled Shells Filled with Liquid—Numerical Analysis. Thin-Walled Struct. 2012, 52, 117–125. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, W.; Tang, W.; Wang, M. Experimental Study on the Geometrical and Mechanical Properties of Goose Eggshells. Rev. Bras. Cienc. Avic. 2017, 19, 455–464. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, M.; Wang, W.; Tang, W.; Zhu, Y. Investigation on Egg-Shaped Pressure Hulls. Mar. Struct. 2017, 52, 50–66. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, M.; Wang, W.; Tang, W. Buckling of Egg-Shaped Shells Subjected to External Pressure. Thin-Walled Struct. 2017, 113, 122–128. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, B.; Wang, F.; Tang, W.; Wang, W.; Zhang, M. Buckling of Prolate Egg-Shaped Domes under Hydrostatic External Pressure. Thin-Walled Struct. 2017, 119, 296–303. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, M.; Cui, W.; Wang, F.; Hua, Z.; Tang, W. Effect of Thickness on the Buckling Strength of Egg-Shaped Pressure Hulls. Ships Offshore Struct. 2018, 13, 375–384. [Google Scholar] [CrossRef]
- Liu, J.; Yu, B.; Zhou, Y.; Zhang, Y.; Duan, M. The Buckling of Spherical-Cylindrical Composite Shells by External Pressure. Compos. Struct. 2021, 265. [Google Scholar] [CrossRef]
- Zhang, M.; Tang, W.; Wang, F.; Zhang, J.; Cui, W.; Chen, Y. Buckling of Bi-Segment Spherical Shells under Hydrostatic External Pressure. Thin-Walled Struct. 2017, 120, 1–8. [Google Scholar] [CrossRef]
- Zhang, J.; Di, C.; Wang, F.; Tang, W. Buckling of Segmented Toroids under External Pressure. Ocean Eng. 2021, 239, 109921. [Google Scholar] [CrossRef]
- Di, C.; Zhang, J.; Wang, W.; Tang, W. Experimental and Numerical Study on the Buckling Performances of Segmented Toroidal Pressure Hulls. China Mech. Eng. 2021, 32, 2989–2994. [Google Scholar]
- Yuan, S.; Fan, X. Developments and Perspectives on the Precision Forming Processes for Ultra-Large Size Integrated Components. Int. J. Extrem. Manuf. 2019, 1, 022002. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, W.W.; Yuan, S.J. Research on Hydro-Forming of Spherical Shells with Different Preform Types. Int. J. Adv. Manuf. Technol. 2017, 92, 2631–2638. [Google Scholar] [CrossRef]
- Zhang, W.W.; Yuan, S.J. Reverse Geometric Modeling for Pre-Form Shape of Prolate Ellipsoid before Hydro-Forming. Int. J. Adv. Manuf. Technol. 2017, 88, 1903–1909. [Google Scholar] [CrossRef]
- Yuan, S.; Teng, B.; Wang, Z.R. A New Hydroforming Process for Large Elbow Pipes. J. Mater. Process. Technol. 2001, 117, 28–31. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, F.; Wang, F.; Tang, W.; Zhao, X. Free Bulging of Thin-Walled Cylinders Closed by Two Heavy Plates. Ocean Eng. 2021, 223, 108646. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, F.; Wang, F.; Zhao, X.; Tang, W.; Chen, F. Buckling Properties of Bulged Barrels under External Pressure. Thin-Walled Struct. 2021, 168, 108226. [Google Scholar] [CrossRef]
- Zhang, J.; Dai, M.; Wang, F.; Tang, W.; Zhao, X.; Zhu, Y. Theoretical and Experimental Study of the Free Hydroforming of Egg-Shaped Shell. Ships Offshore Struct. 2022, 17, 257–267. [Google Scholar] [CrossRef]
- Zhang, J.; Dai, M.; Wang, F.; Tang, W.; Zhao, X. Buckling Performance of Egg-Shaped Shells Fabricated through Free Hydroforming. Int. J. Press. Vessel. Pip. 2021, 193, 104435. [Google Scholar] [CrossRef]
- Gou, P.; Cui, W.C. Study of Structural Optimization Problem for Multiple Intersecting Spherical Pressure Hulls. Chuan Bo Li Xue/J. Ship Mech. 2009, 13, 269–277. [Google Scholar]
- Xiang, K. Numerical Analysis and Experimental Verification on Buckling of Multiple Intersecting Spherical Pressure Hull. Master’s Thesis, Jiangsu University of Science and Technology, Zhenjiang, China, 2018. [Google Scholar]
- Zhu, Y.; Dai, Y.; Ma, Q.; Tang, W. Buckling of Externally Pressurized Cylindrical Shell: A Comparison of Theoretical and Experimental Data. Thin-Walled Struct. 2018, 129, 309–316. [Google Scholar] [CrossRef]
- ENV 1993-1-6; Eurocode 3—Design of Steel Structures—Part 1.6: Strength and Stability of Shell Structures. CEN: Brussels, Belgium, 2007.
- China Classification Society (CCS), Rules for the Classification and Construction of Diving Systems and Submersibles; China Classification Society (CCS): Beijing, China, 2018.
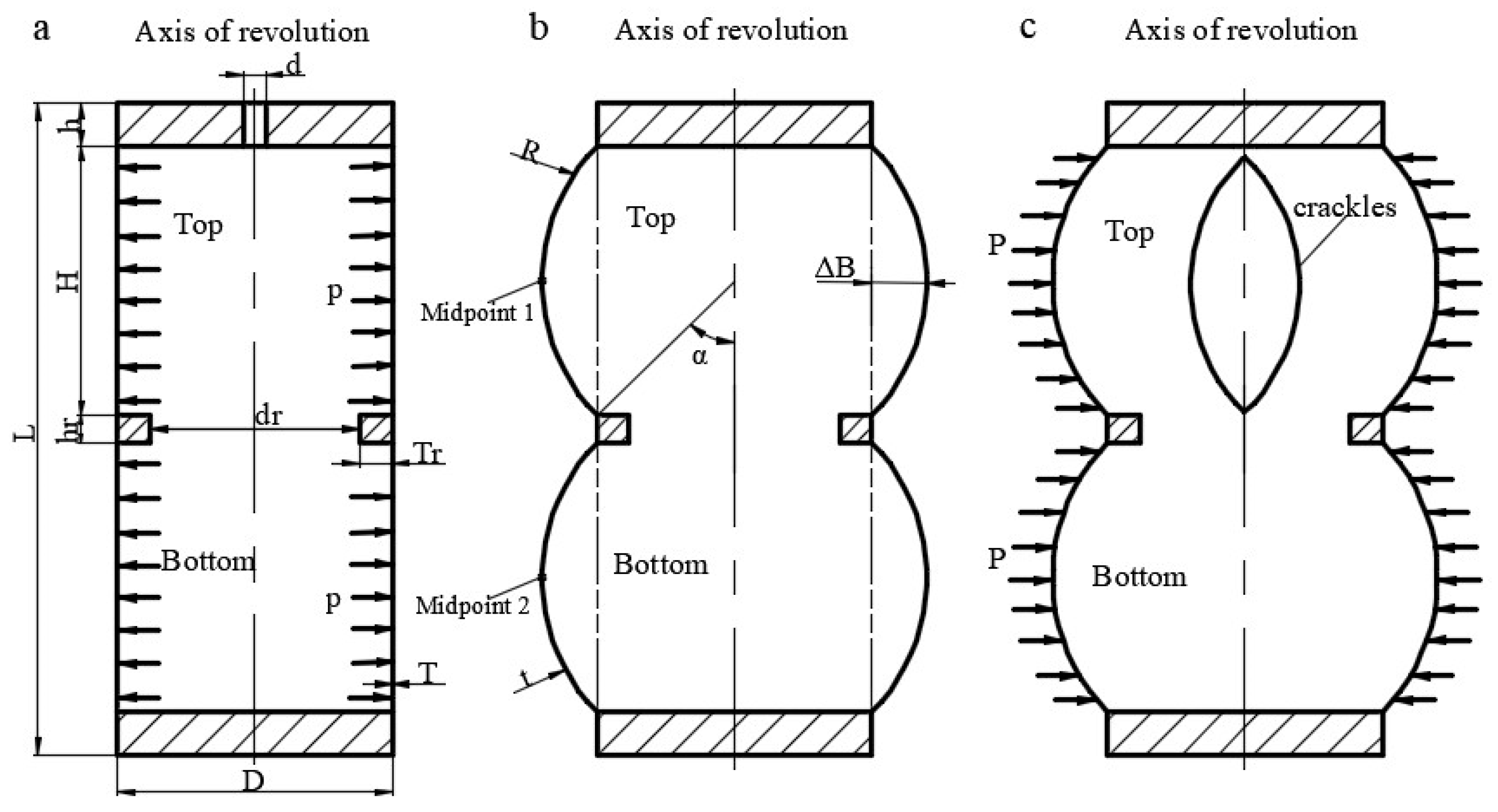
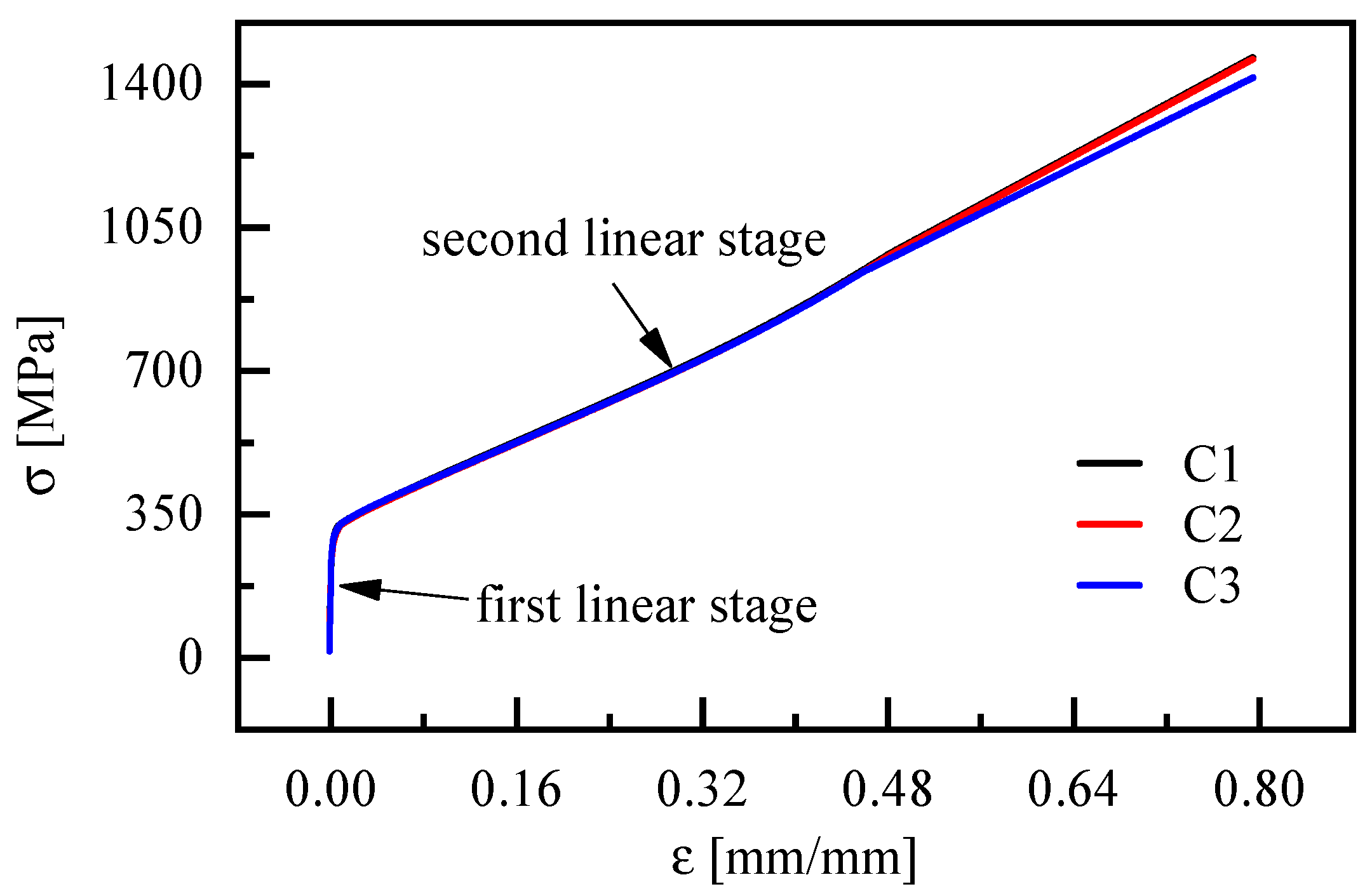






| Parameters | Values/mm |
|---|---|
| Tube Outer Diameter (D) | 102 |
| Tube Length (H) | 100 |
| Plate Diameter (D) | 102 |
| Plate Length (h) | 16 |
| Hoop Rib Inner Diameter (dr) | 78 |
| Hoop Rib Thickness (Tr) | 12 |
| Hoop Rib Length (hr) | 10 |
| Total Length (L) | 242 |
| Parameters | Values |
|---|---|
| Intersection angle (α) | 45 (°) |
| Radius of spherical shell (R) | 72.5 (mm) |
| Thickness of spherical shell (t) | 0.58 (mm) |
| Coupon | ||||
|---|---|---|---|---|
| C1 | 288.5 | 1310.6 | 214.4 | 0.27 |
| C2 | 286.2 | 1307.2 | 208.1 | 0.28 |
| C3 | 279.1 | 1298.1 | 195.5 | 0.29 |
| AVE | 284.6 | 1305.3 | 206.0 | 0.28 |
| Sample | [mm] | [mm] | [%] |
|---|---|---|---|
| 1# | 0.000 | 0.00 | 0.01 |
| 2# | 0.006 | 0.40 | −0.01 |
| 3# | 0.747 | 1.24 | −0.06 |
| 4# | 1.604 | 2.07 | −0.25 |
| 5# | 2.462 | 3.71 | −0.34 |
| 6# | 4.218 | 5.07 | −0.47 |
| Sample | 1# | 2# | 3# | 4# | 5# | 6# | |
|---|---|---|---|---|---|---|---|
| [mm] | Top | 0.972 | 0.958 | 0.938 | 0.968 | 0.952 | 0.956 |
| Bottom | 0.970 | 0.958 | 0.936 | 0.966 | 0.954 | 0.958 | |
| [mm] | Top | 0.962 | 0.952 | 0.928 | 0.956 | 0.942 | 0.948 |
| Bottom | 0.960 | 0.952 | 0.930 | 0.958 | 0.944 | 0.950 | |
| [mm] | Top | 0.968 | 0.955 | 0.933 | 0.962 | 0.948 | 0.954 |
| Bottom | 0.966 | 0.956 | 0.933 | 0.963 | 0.948 | 0.954 | |
| [mm] | Top | 0.0024 | 0.0014 | 0.0021 | 0.0021 | 0.0030 | 0.0015 |
| Bottom | 0.0028 | 0.0015 | 0.0021 | 0.0020 | 0.0029 | 0.0020 | |
| Sample | p [MPa] | [s] | [MPa/s] | P [MPa] | [s] | [MPa/s] | p/P |
|---|---|---|---|---|---|---|---|
| 1# | 0.00 | 0 | - | 3.32 | 12 | 0.28 | 0.00 |
| 2# | 7.03 | 22 | 0.32 | 3.55 | 6 | 0.59 | 1.98 |
| 3# | 8.22 | 13 | 0.63 | 3.33 | 12 | 0.28 | 2.47 |
| 4# | 9.13 | 61 | 0.15 | 3.68 | 51 | 0.07 | 2.48 |
| 5# | 9.70 | 133 | 0.07 | 3.90 | 27 | 0.14 | 2.49 |
| 6# | 11.01 | 42 | 0.26 | 4.54 | 24 | 0.19 | 2.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, Y.; Zhang, J.; Wang, F. Buckling of Bisegment Pressure Hulls Fabricated through Free Bulging. Metals 2023, 13, 576. https://doi.org/10.3390/met13030576
Teng Y, Zhang J, Wang F. Buckling of Bisegment Pressure Hulls Fabricated through Free Bulging. Metals. 2023; 13(3):576. https://doi.org/10.3390/met13030576
Chicago/Turabian StyleTeng, Yun, Jian Zhang, and Feng Wang. 2023. "Buckling of Bisegment Pressure Hulls Fabricated through Free Bulging" Metals 13, no. 3: 576. https://doi.org/10.3390/met13030576
APA StyleTeng, Y., Zhang, J., & Wang, F. (2023). Buckling of Bisegment Pressure Hulls Fabricated through Free Bulging. Metals, 13(3), 576. https://doi.org/10.3390/met13030576







