Experimental Study of Stretched Premixed Flame Stabilized in a Flat Channel near a Heated Wall

Abstract

In this work, the behavior of a lean premixed stretched flame stabilized in a flat channel near a heated wall was studied. Dependences of the flame front position on the stretch rate parameter at temperatures of the heated wall of 1000 and 1200 K and the combustible mixture composition (ϕ = 0.7 and 0.6) were obtained experimentally. The reduced thermal diffusive model was used in numerical simulation for an explanation of obtained experimental results. Theoretical estimates are in qualitative agreement with the experiment. The performed qualitative analysis may be useful in estimation of the combustion product temperature and the residence time of the nanoparticles forming in combustion products before their impact with the hot wall.

1. Introduction

The recent development of new technologies, such as the synthesis of nanomaterials in a gas flame by combustion, including nanoparticles of metal oxides [1], graphene and fullerenes [2], created a strong need to understand flame characteristics under the conditions of preheated walls in the close vicinity of reaction fronts [3,4,5]. In these flame spray pyrolysis (FSP) technologies, the nanoparticles are formed in combustion products and deposited on the substrate after the gas combustion with precursors in the stagnant zone near the substrate, which often has an elevated temperature [2,6,7,8,9]. The hot wall can stabilize the combustion of low-calorie gas mixtures and helps to control the residence time of combustion products near the stagnation zone where nanoparticles are formed. This suggests the relevance of studying the features of the premixed gas combustion in divergent flow near a heated wall. In contrast to the well-studied stretched flames that stabilize in the space between two countercurrent burners [10], there is a lack of data on the stretched flame characteristics near the hot wall. Extinguishing of a stretched flame can occur both at high and low flow rates.

At a high flow rate, flame quenching is caused by a flow velocity gradient (stretching effects) [11,12]. At low flow velocities corresponding to small values of stretch rate, flame extinction is associated with radiation heat loss from the area of hot combustion products [13,14]. Experimental studies of the low stretched flames require the creation of microgravity conditions due to the significant effect of natural convection on the flame. This demands the use of expensive experimental facilities, such as “drop towers” or free-flight experiments. Microgravity experiments using premixed stretched flames stabilized near a hot wall and their theoretical analysis showed the existence of two different flame regimes [9]. It should be noted that early theoretical Reference [15] predicted the existence of stretched flames stabilized near the hot wall at low flow rates of the combustible mixture. In experiments in Reference [9], such regimes were not found, so proofing of their existence requires additional experiments.

In references [16,17], an experimental apparatus which makes it possible to eliminate influence of the natural convection and allows low stretched flames to be investigated under normal gravity conditions was proposed. The countercurrent flames in these works were stabilized inside a flat microchannel. In the current paper, we present the results of experiments on a low stretched flame near a heated wall. In order to weaken the effect of the natural convection, the flame was stabilized in a flat channel, inside which there was a heated wall.

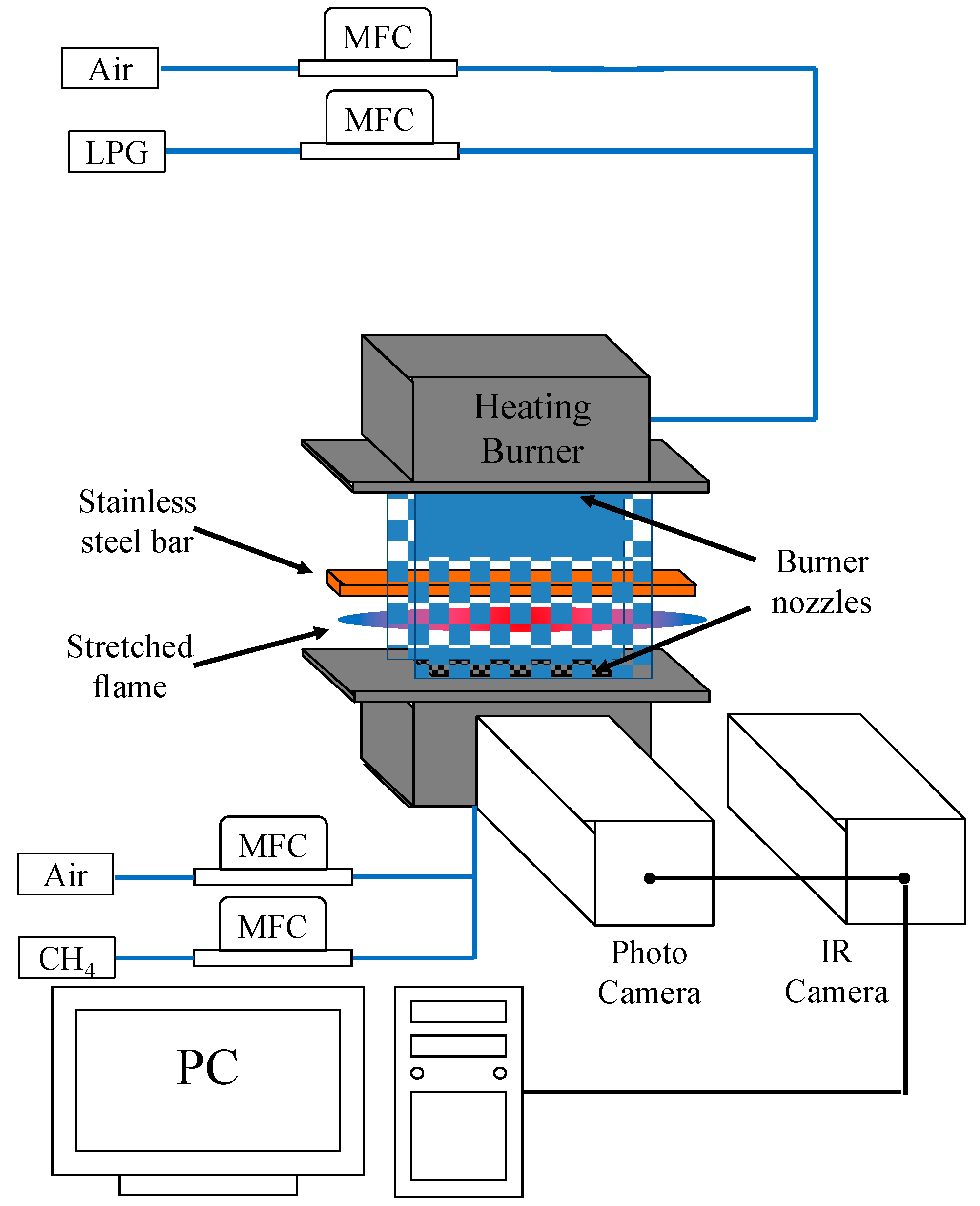
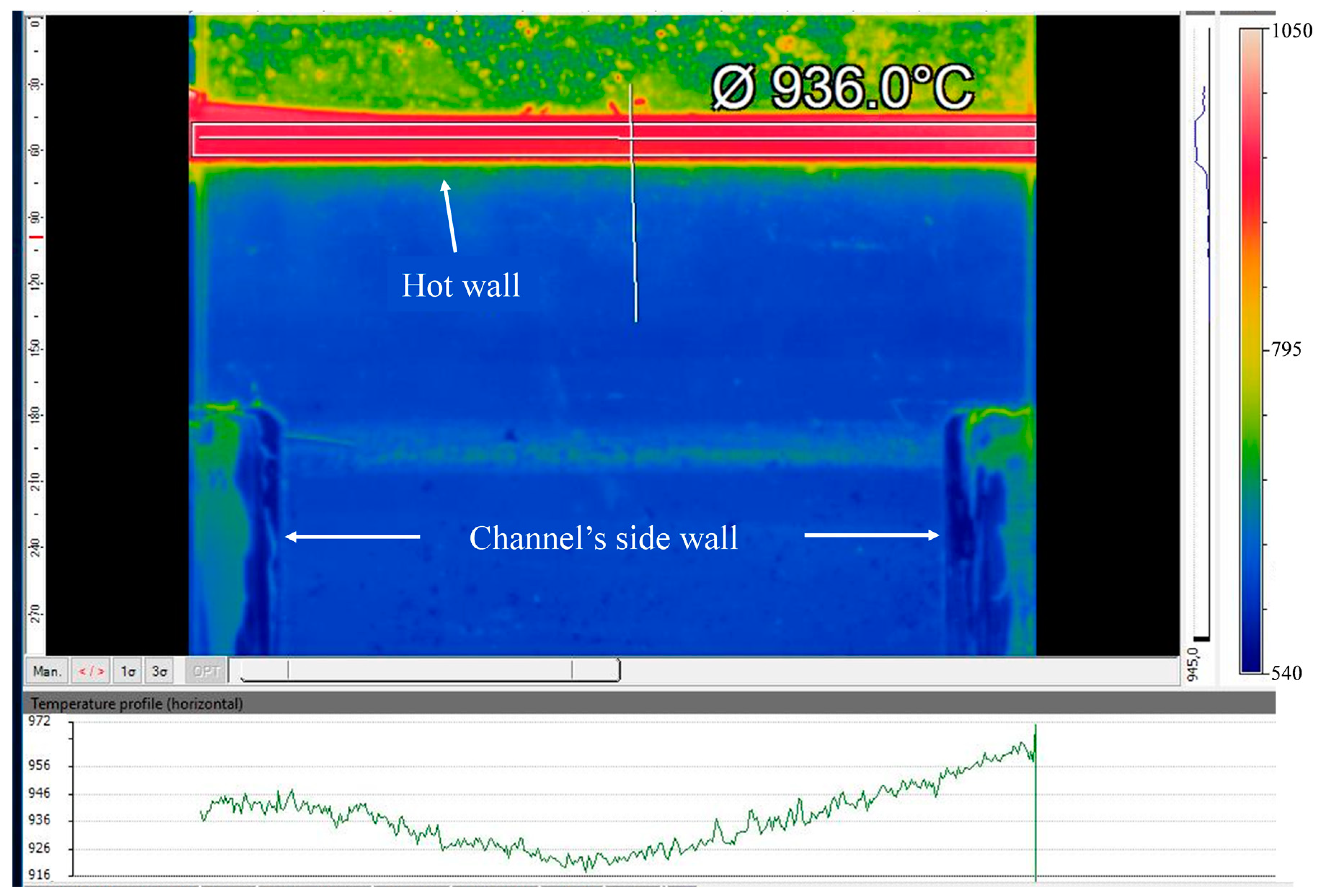
2. Experiment

A scheme of the experimental setup is shown in Figure 1. The combustible mixture was supplied from slot-jet burner into the 7 mm gap, forming two parallel 1 mm thickness quartz plates. A stainless-steel bar (SS 316, HLMMM Co., Ltd., China) with a size of 100 × 7 × 3 mm was placed at a distance of 15 mm from the burner’s nozzle. A liquid petroleum gas (LPG, Gazpromneft, Moscow, Russia)/air slot-jet burner heated the rear side of the stainless-steel bar. The hot wall temperature control was implemented by operation of the LPG/air mixture flow rate and content. The stretched flame of lean methane/air premixture was studied in the experiment. The composition and flow rate of the air/fuel mixture in the investigated burner was controlled by gas mass flow controllers connected to a computer. In order to prevent the penetration of combustion products from the burner/heater into the study area, the contact points of the steel bar and the quartz plate were sealed and side screens were installed. A digital photo camera and an infrared (IR) camera (Optris GmbH, Berlin, Germany) were used to measure the flame front position and the temperature of the heated wall, respectively. The IR camera was pre-calibrated with a K-type thermocouple (Okazaki Manufacturing Company, Kobe, Japan). The inlet temperature of the combustible mixture was measured with a K-type thermocouple maintained at the burner’s nozzle.

The flame characteristics of two methane/air mixtures with equivalence ratios ϕ = 0.6 and 0.7 were studied in the experiments. The stretch rate was defined as the ratio between the fresh mixture velocity at the burner nozzle to the distance from the burner’s nozzle to the heated wall. The distance was 15 mm. Measurements were conducted for two average temperatures of the hot wall equaling 1000 ± 20 and 1200 ± 25 K. Temperature distribution in the experimental area, obtained using an IR camera, is shown in Figure 2. As can be seen from Figure 2, the temperature profile along the surface of the heated wall was fairly uniform.

In the experiment, the position of the flame front was determined at different temperatures of the heated wall for different mixture compositions depending on the stretch rate. The flame position was determined by averaging the luminosity peaks along the flame front in the area restricted by the distance of ±1 cm from the gas flow central line. The flame front was slightly curved as shown in the momentary photo in Figure 3; therefore, to obtain one experimental point on the flame front location, we took five photos to average data and to determine the corresponding errors. The average time to establish a stationary combustion regime was about 10 min for each gas flow rate.

3. Mathematical Model

The simple model of a stretched flame near a hot wall [18] was used to estimate the flame front behavior depending on the problem parameters. Using the assumptions of constant gas density, constant transfer coefficients, potential flow and narrowness of the chemical reaction zone compared to the gas-preheating zone, the equations for temperature and fuel concentration can be written as:

$$\frac{\partial T}{\partial t}-ax\frac{\partial T}{\partial x}=\frac{{\partial }^{2}T}{\partial x^2}+\left(1-\sigma \right)W-h\left(T-\sigma \right)$$

(1)

$$\frac{\partial C}{\partial t}-ax\frac{\partial C}{\partial x}=\frac{1}{Le}\frac{{\partial }^{2}C}{\partial x^2}-W$$

(2)

here, $W=exp\left(\frac{N}{2}\left(1-\frac{1}{T_f}\right)\right)\delta \left(x-x_f\right)$ is the chemical reaction rate in the “infinitely thin reaction zone” approximation. The Arrhenius type of chemical reaction rate is expressed in term of delta function $\delta \left(x-x_f\right)$, and N is nondimensional activation energy of chemical reaction; x is the nondimensional coordinate in units of flame thickness $l_{th}=D_{th}/U_b$, where $D_{th}$ is the gas thermal diffusivity and $U_b$ is the laminar speed of the freely propagating flame. The temperature T is measured in units of adiabatic flame temperature T_b, $\sigma =T_0/T_b$ is nondimensional initial temperature, $a=V_0{D}_{th}/U_b^{2}L$ is the nondimensional stretch parameter related to the inlet gas velocity V₀ from burner and L is the distance between the burner and the hot wall. C is the nondimensional fuel concentration in units of the initial concentration of the premixture; Le is the Lewis number. H is the nondimensional parameter characterizing intensity of radiative heat loss and depending on the composition of the combustible mixture. The phenomenological formula proposed in Reference [19] allows this parameter to be estimated. Since experimental mixtures have close values of equivalence ratio, the same value of the parameter h = 10⁻⁴ is used in the calculations.

In this piecewise linear formulation, the solution of Equations (1) and (2) can be found analytically by the method proposed in Reference [18]. Application of the method to the system of Equations (1) and (2) results in algebraic equations relating flame front position x_f and flame temperature T_f with the stretch rate a and other problem parameters.

$$\sqrt{\frac{a}{2Le}}\psi \left(\sqrt{Le} \zeta \right)=exp\left(\frac{N}{2}\left(1-\frac{1}{T_f}\right)\right)$$

(3)

$$\left[T_f-\sigma -\left({\sigma }_w-\sigma \right)\frac{I^{-}\left(\zeta \right)}{I^{-}\left(0\right)}\right]\frac{d}{d\zeta } ln\left(\frac{I^{+}\left(\zeta \right)}{I^{-}\left(0\right)}-1\right)=\frac{\left(1-\sigma \right)}{\sqrt{Le}}\psi \left(\sqrt{Le} \zeta \right)$$

(4)

Here, $=x_f\sqrt{2/a}$, ${\sigma }_w=T_w/T_b$ and $T_w$ are the hot wall temperature. The functions ψ and $I^{\pm }$ have the form:

$$\psi \left(\zeta \right)=\frac{2}{\sqrt{\pi }}\frac{exp\left(-{\zeta }^2\right)}{1-erf\left(\zeta \right)},\hspace{1em}{I}^{\pm }\left(\zeta \right)=exp\left(-{\zeta }^2\right){\int }_0^{\infty }{y}^{h/a}exp\left(-\frac{y^2}{4}\pm y\zeta \right)dy$$

(5)

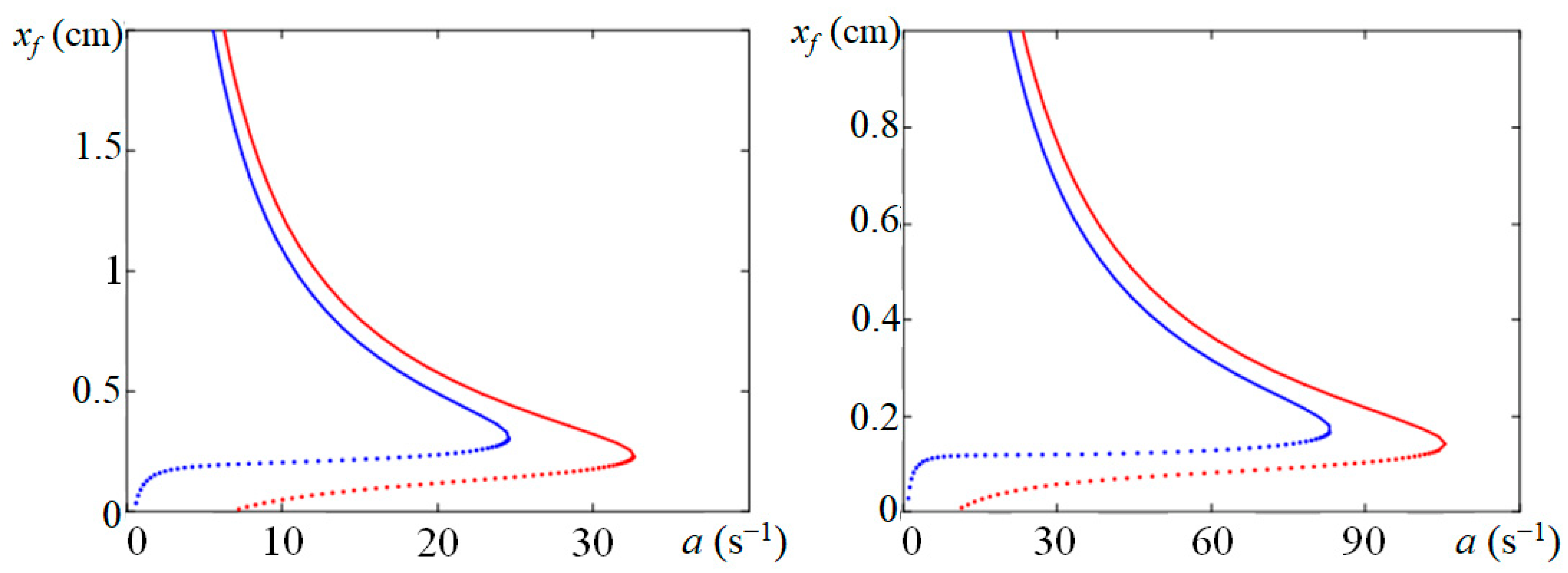
4. Results and Discussion

In the experiment, lean methane/air mixture was studied. Since the heated wall was installed inside the channel and the burner nozzle was within a sufficient distance, the fresh mixture was significantly heated due to the heat-conducting walls of the quartz channel. This led to an increase in the gas volume velocity of the fresh mixture relative to that set on the mass flow controllers. When processing the experimental data, we took into account the heating of the mixture that occurred and made an appropriate correction for the velocity of the fresh mixture and, consequently, for stretch rate. In all subsequent figures, the value of the stretching coefficient is corrected for the temperature of the fresh mixture. In addition, the increase in the temperature of the fresh mixture was taken into account in the numerical simulation. The dependency of the fresh mix temperature on the stretch ratio for equivalence ratio ϕ = 0.6 is shown in Figure 4.

As shown in Figure 4, in the case when the wall temperature was 1000 K, the temperature of the fresh mixture practically did not change and was equal to ~400 K. On the other hand, in case when the wall temperature was equal 1200 K, the temperature of the fresh mixture decreased linearly. As will be demonstrated later, this phenomenon occurred due to the fact that with an increase in the wall temperature, the flame was stabilized further from the burner nozzle, resulting in an expansion of the flammability limit. In addition, when the flame exists at higher stretch rates, and hence at higher fresh mixture velocities, the temperature of the fresh mixture decreased due to less intense heat transfer.

Dependency of the flame front position on stretch rate evaluated for equivalence ratios ϕ = 0.6 (left) and 0.7 (right) and wall temperatures 1000 (dark blue) and 1200 K (red) are shown in Figure 5. At small stretch rate values (exceeding the extreme left point), flame flashback to the burner occurred. Flame extinction at a large stretch rate (extreme right point) occurred at a finite distance from the wall that agrees with theoretical Reference [15]. At the same time, the combustion regimes near the wall, described in theoretical Reference [15], were not found. The same regimes were not observed in experiments in [9], performed under microgravity conditions.

Experimental data showed that an increase in the wall temperature shifts points to the higher stretch rate side and increases the region of flame existence. Results of the flame front position x_f depending on stretch rate a for equivalence ratios ϕ = 0.6 and 0.7 are shown in Figure 6. The following values of parameters were used in the calculations: N = 8.98, Le = 0.9, D_th = 0.7 cm²/s, U_b = 8.6 cm/s, T_b = 1670 K for ϕ = 0.6 and U_b = 16 cm/s, T_b = 1840 K for ϕ = 0.7. Since the burner was heated by the radiation from the hot wall, the measured temperatures of the fresh mixture were T₀ = 400 and T₀ = 450 K when the wall temperatures were T_w = 1000 and T_w = 1200 K, respectively. All curves in Figure 6 have an upper stable branch and unstable branches lying below turning points corresponding to the flame quenching. The conclusion on the stability of these branches follows from the linear stability analysis of the stationary solutions conducted in Reference [20]. The linear stability analysis explains why the flame was extinguished in the experiment at a certain distance from the hot wall. The increase in the wall temperature shifts the domain of existence of the stable flames towards larger values of the stretch rate. In addition, it allows the flame to be stabilized closer to the stagnation zone. The same tendency is observed with the increase in the fuel concentration in the combustion mixture. Theoretical results described above are in accordance with obtained experimental data shown in Figure 5.

5. Conclusions

Experimental data of the stretched flame location near the hot wall were obtained for different mass flow rates of lean methane/air mixtures and for two values of hot wall temperatures 1000 and 1200 K. The possibility of the simple model predicting the general tendency in estimation of the flame location with variation of the stretch rate, the lean mixture composition and the hot wall temperature was demonstrated. This qualitative analysis may be useful in estimation of the combustion product temperature and the residence time of the nanoparticles forming in combustion products before their impact with the hot wall.