Reduction Kinetics of Pre-Oxidized Ilmenite Pellets by H2-H2O Gas Mixtures
Abstract
1. Introduction
2. Materials and Methods
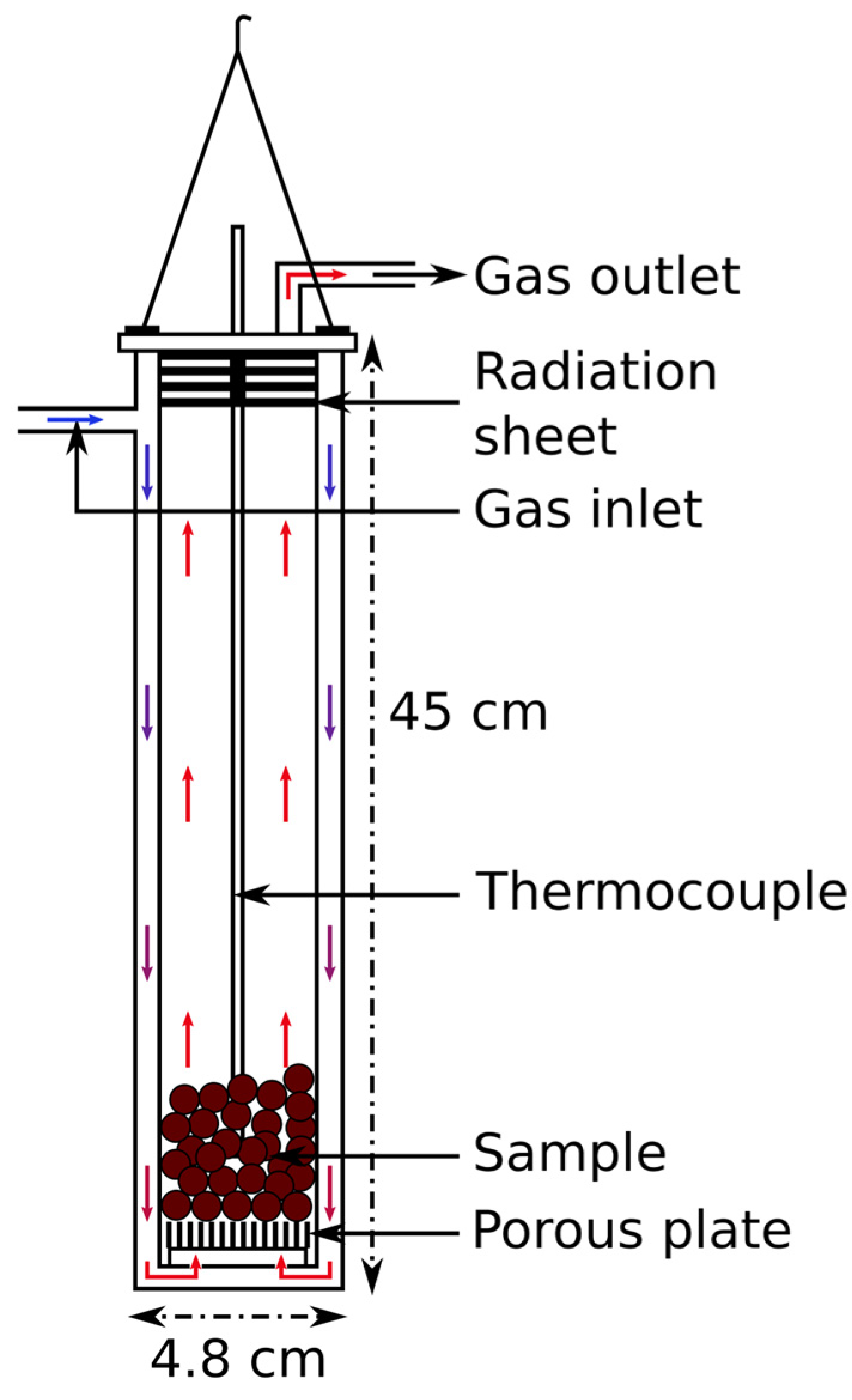
2.1. Sample Preparation and Isothermal Reduction
2.2. Sample Analysis
2.3. Reactions and Kinetic Modeling
3. Results and Discussion
3.1. Reduction Degree as a Function of Time
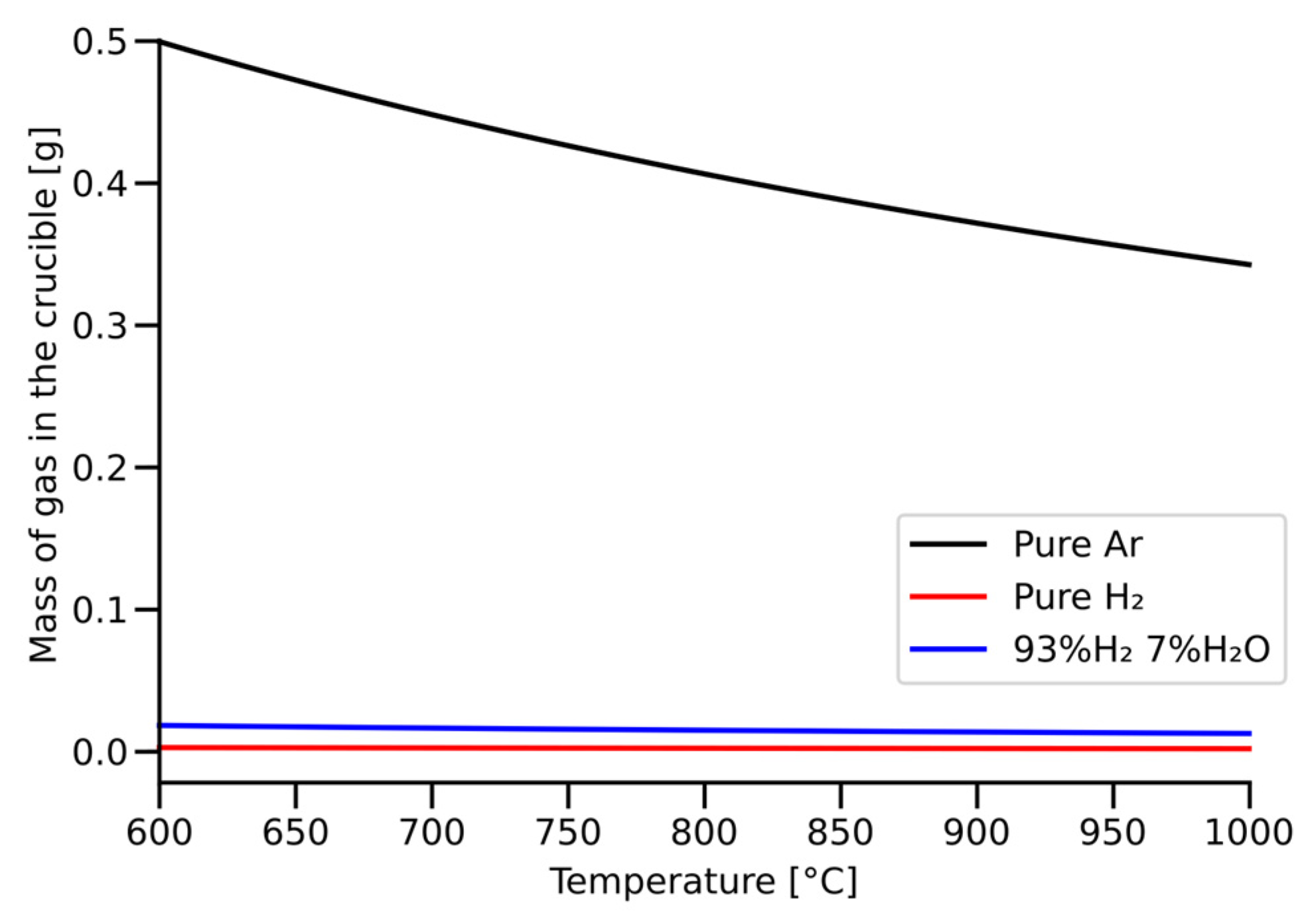
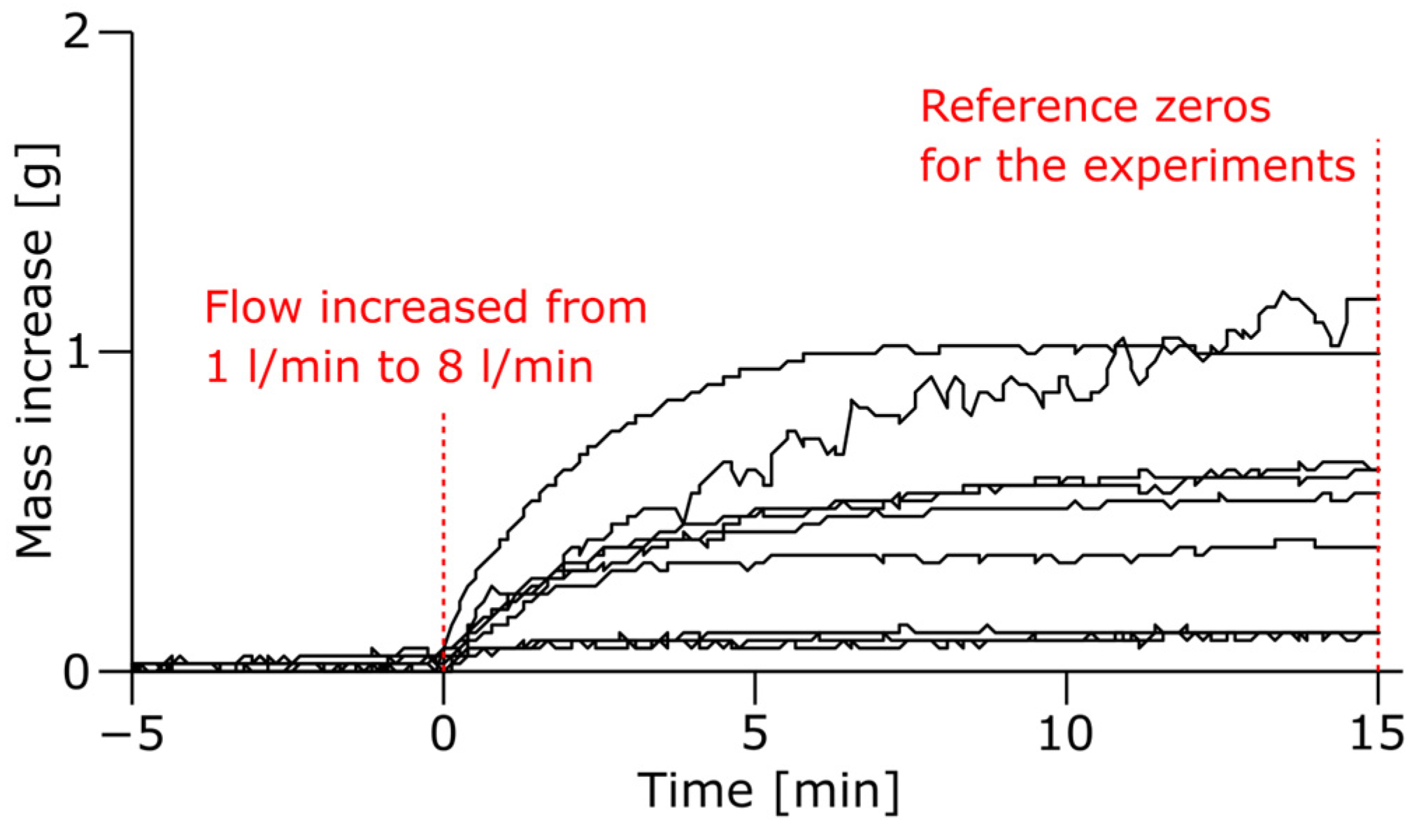
3.2. Uncertainties in the Mass Loss Measurements
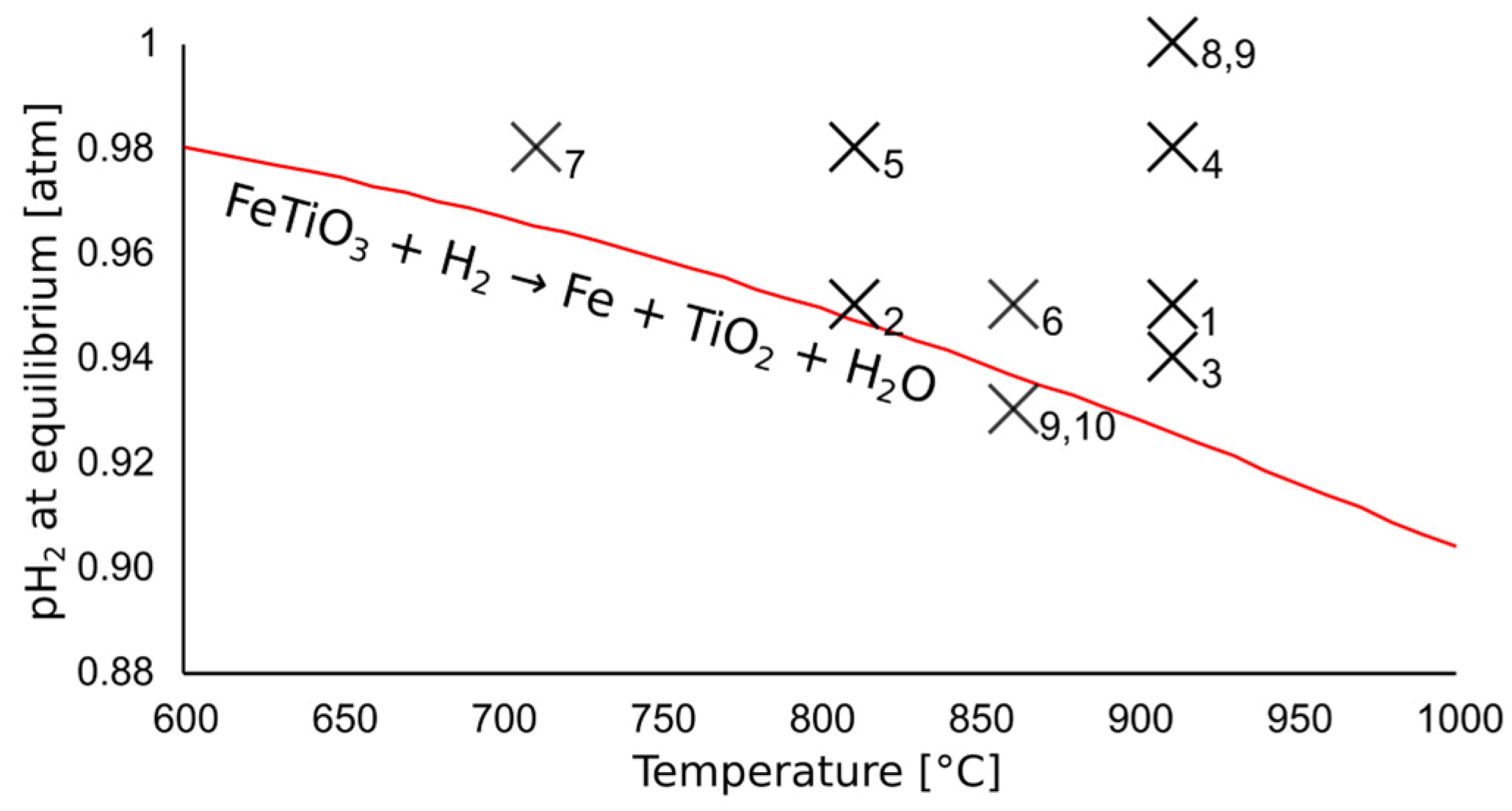
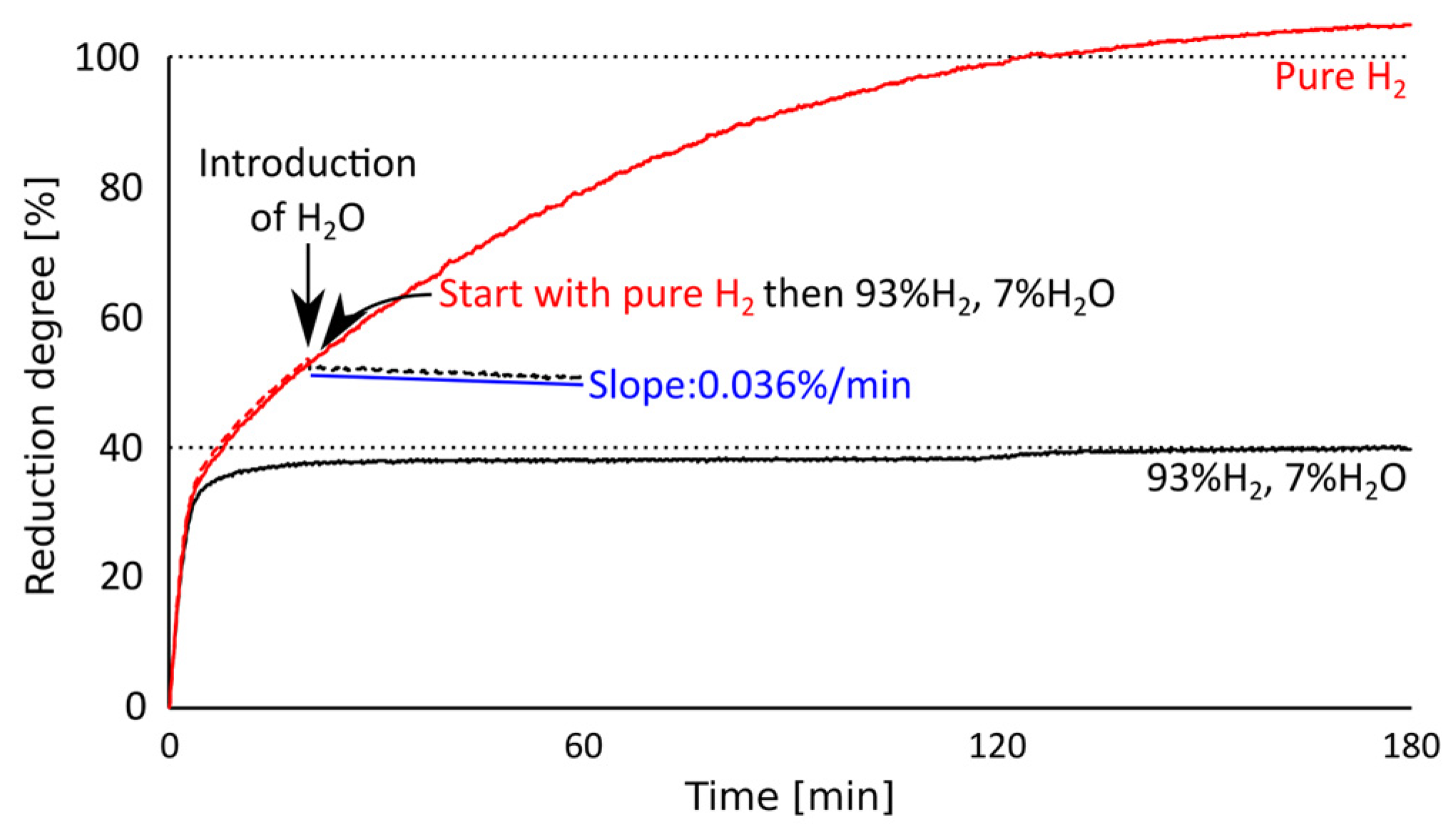
3.3. Reoxidation of Iron by Water Vapor
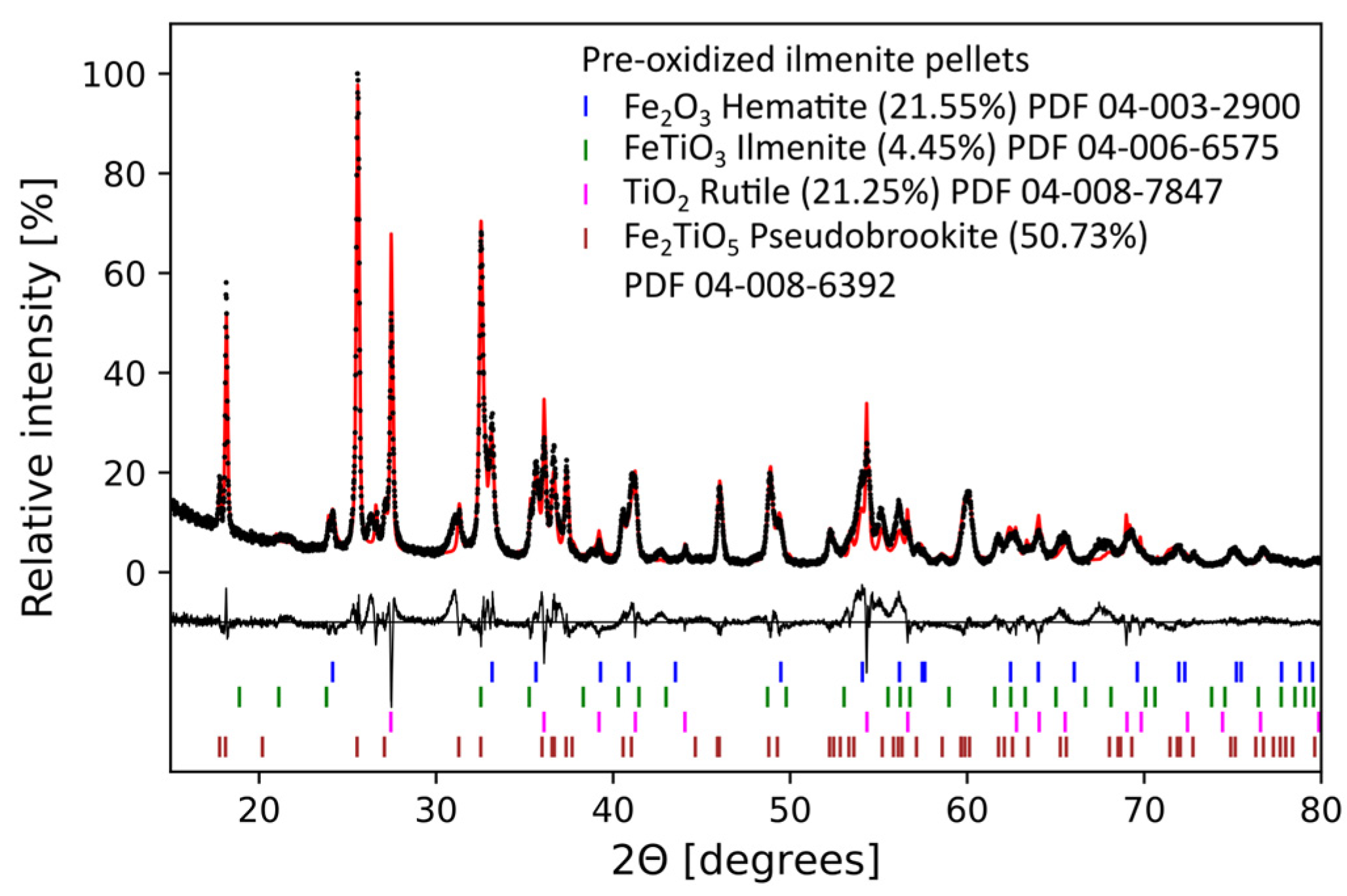
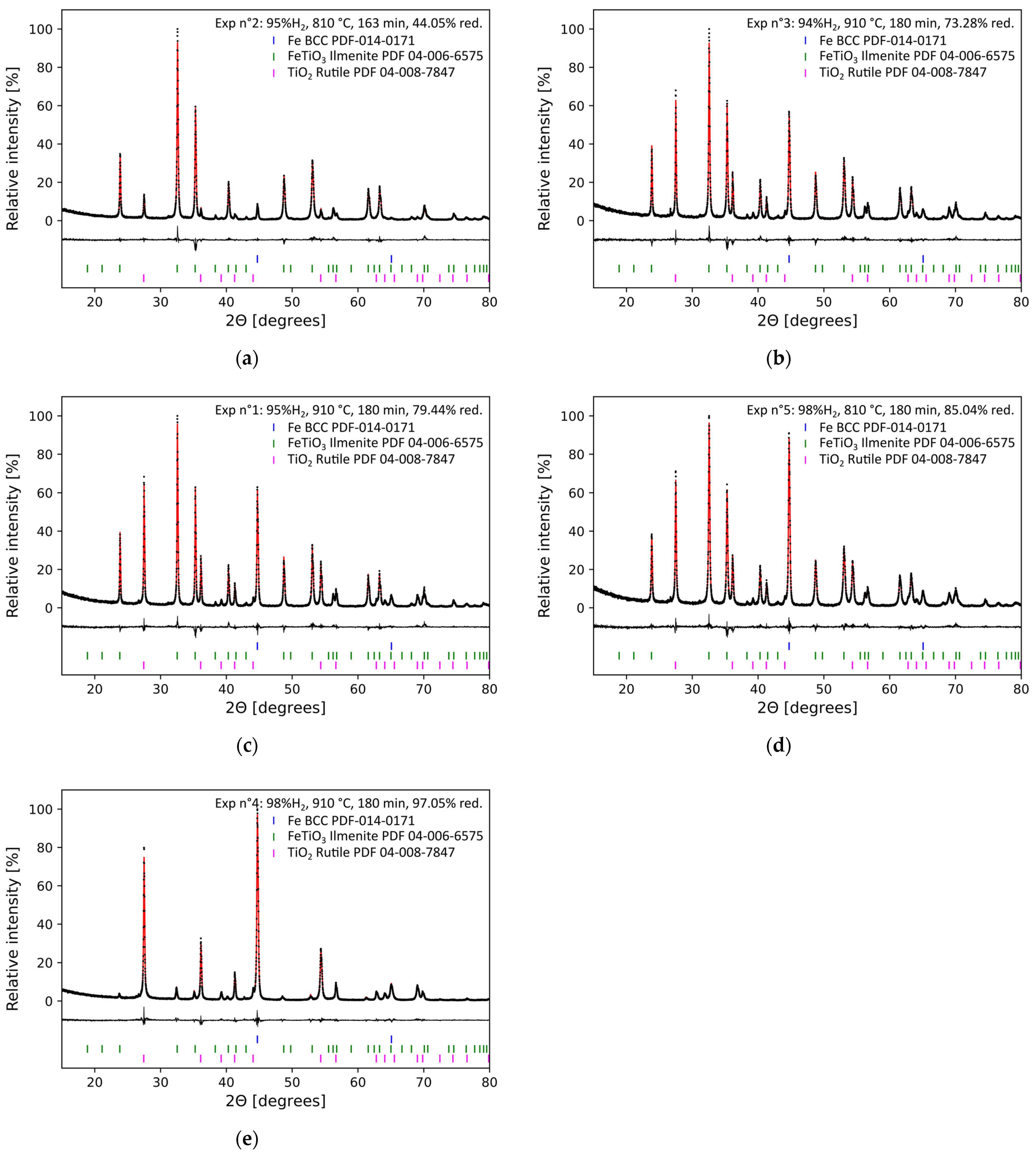
3.4. XRD Analysis
3.5. Electron Probe Microanalysis
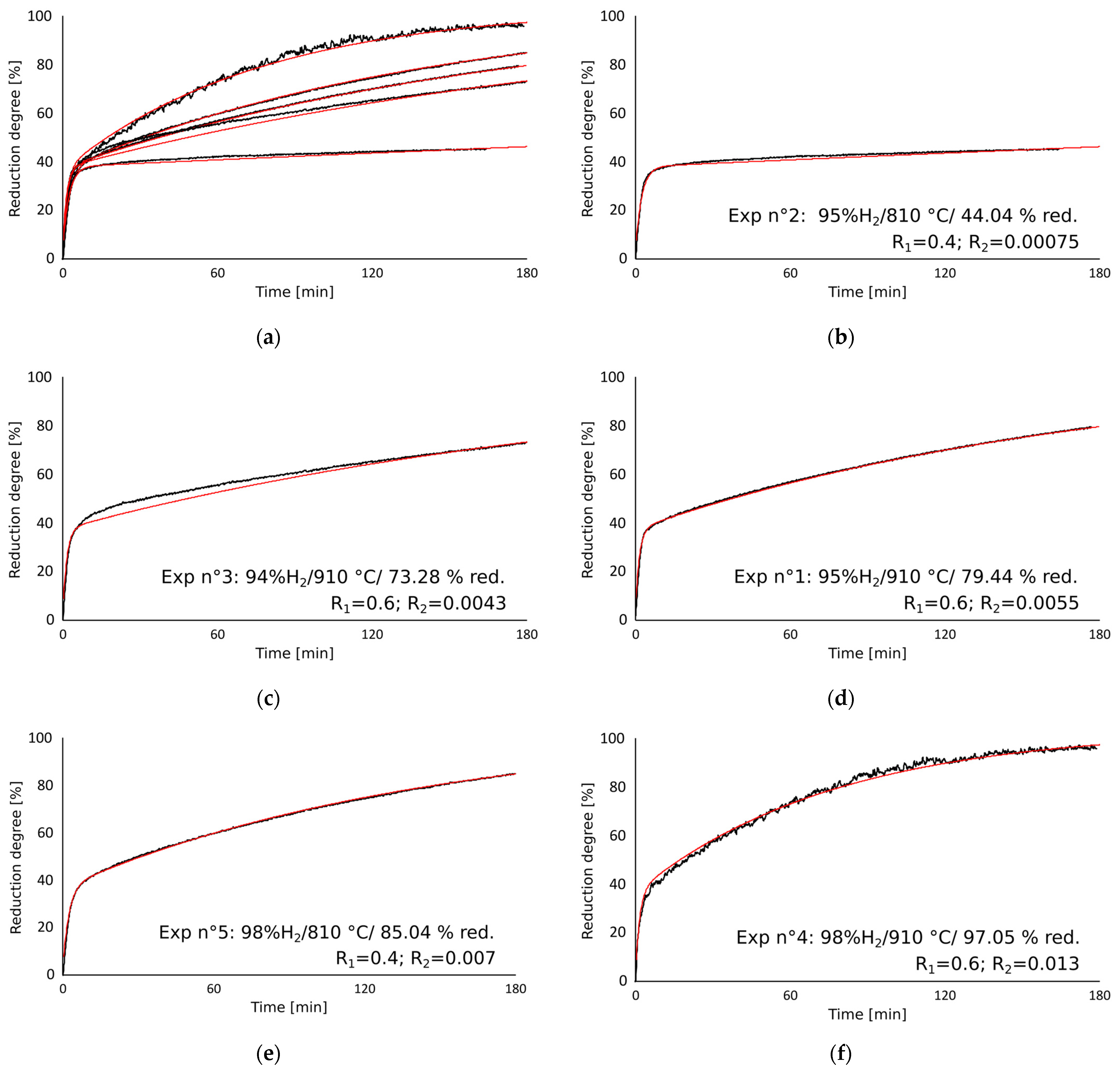
3.6. Curve Fitting of the Reduction Degree
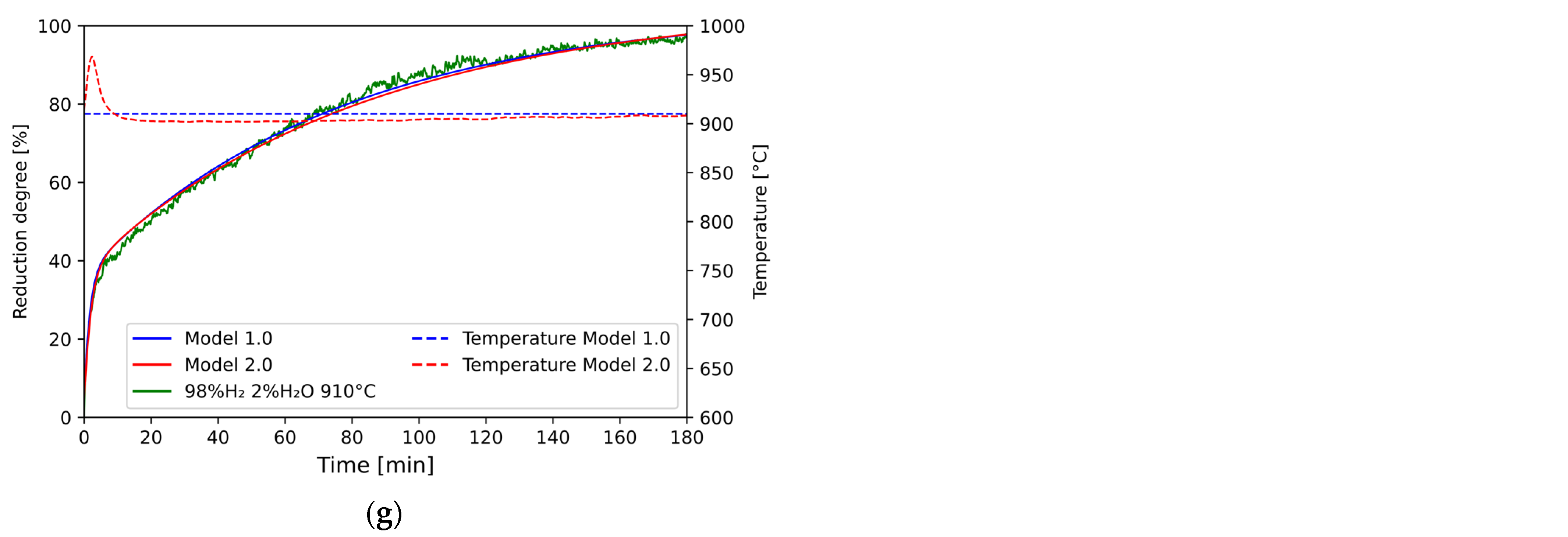
3.7. Modeling of the Reduction Process with Calculations
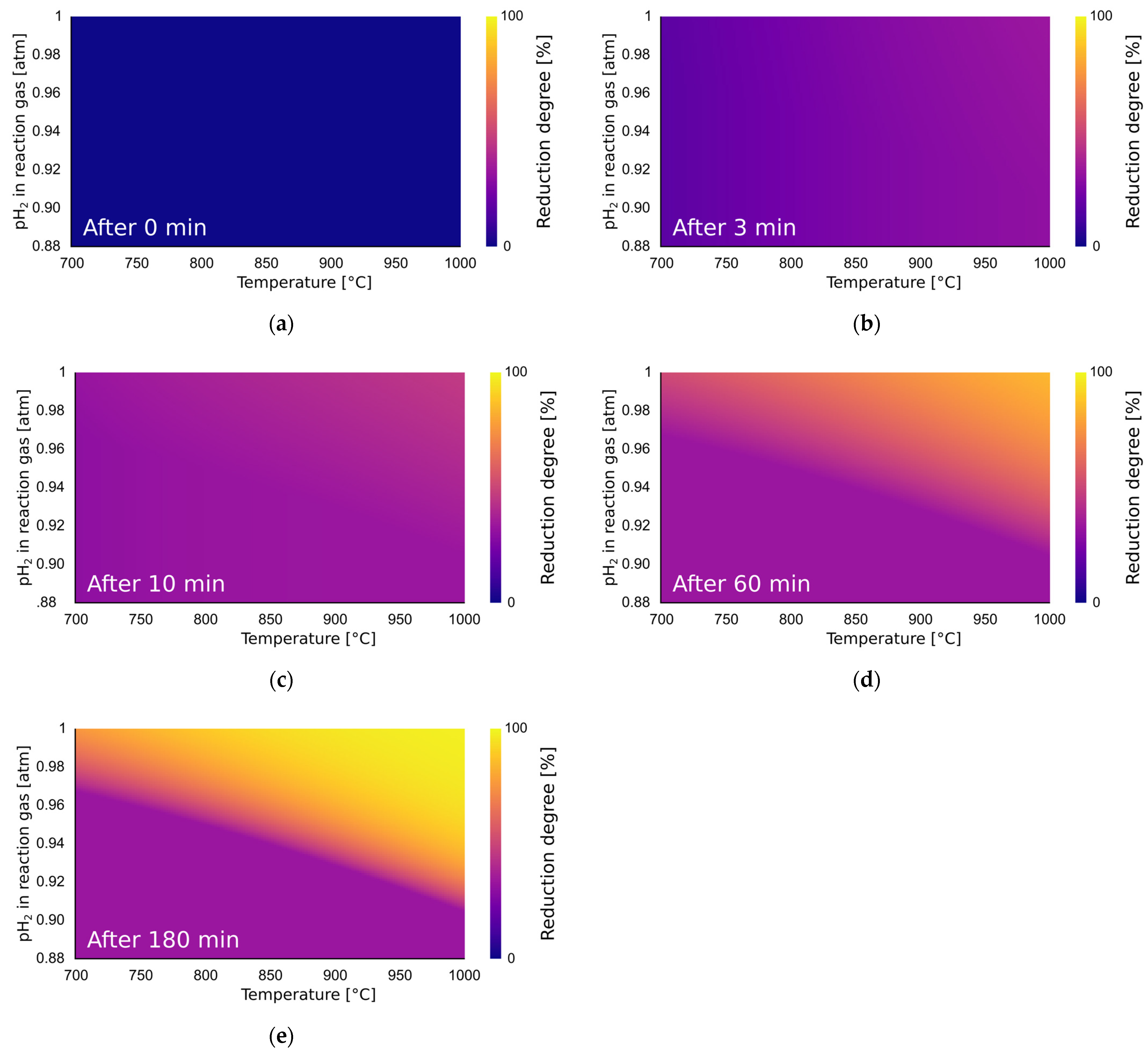
3.8. Predictive Reduction Heatmap
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Patisson, F.; Mirgaux, O. Hydrogen Ironmaking: How It Works. Metals 2020, 10, 922. [Google Scholar] [CrossRef]
- Pei, M.; Petäjäniemi, M.; Regnell, A.; Wijk, O. Toward a Fossil Free Future with HYBRIT: Development of Iron and Steelmaking Technology in Sweden and Finland. Metals 2020, 10, 972. [Google Scholar] [CrossRef]
- Wang, R.R.; Zhao, Y.Q.; Babich, A.; Senk, D.; Fan, X.Y. Hydrogen Direct Reduction (H-DR) in Steel Industry—An Overview of Challenges and Opportunities. J. Clean. Prod. 2021, 329, 129797. [Google Scholar] [CrossRef]
- Cavaliere, P.D.; Perrone, A.; Silvello, A. Water Electrolysis for the Production of Hydrogen to Be Employed in the Ironmaking and Steelmaking Industry. Metals 2021, 11, 1816. [Google Scholar] [CrossRef]
- Spreitzer, D.; Schenk, J. Iron Ore Reduction by Hydrogen Using a Laboratory Scale Fluidized Bed Reactor: Kinetic Investigation—Experimental Setup and Method for Determination. Met. Mater. Trans. B 2019, 50, 2471–2484. [Google Scholar] [CrossRef]
- Scharm, C.; Küster, F.; Laabs, M.; Huang, Q.; Volkova, O.; Reinmöller, M.; Guhl, S.; Meyer, B. Direct Reduction of Iron Ore Pellets by H2 and CO: In-Situ Investigation of the Structural Transformation and Reduction Progression Caused by Atmosphere and Temperature. Miner. Eng. 2022, 180, 107459. [Google Scholar] [CrossRef]
- Metolina, P.; Ribeiro, T.R.; Guardani, R. Hydrogen-Based Direct Reduction of Industrial Iron Ore Pellets: Statistically Designed Experiments and Computational Simulation. Int. J. Miner. Metall. Mater. 2022, 29, 1908–1921. [Google Scholar] [CrossRef]
- TiZir Titanium & Iron, a Pioneer of Metallurgy in Norway. Available online: https://www.eramet.com/en/tizir-titanium-iron-pioneer-metallurgy-norway (accessed on 8 April 2022).
- Zhao, Y.; Shadman, F. Reduction of Ilmenite with Hydrogen. Ind. Eng. Chem. Res. 1991, 30, 2080–2087. [Google Scholar] [CrossRef]
- Briggs, R.A.; Sacco, A. Hydrogen Reduction Mechanisms of Ilmenite between 823 and 1353 K. J. Mater. Res. 1991, 6, 574–584. [Google Scholar] [CrossRef]
- Vijay, P.L.; Venugopalan, R.; Sathiyamoorthy, D. Preoxidation and Hydrogen Reduction of Ilmenite in a Fluidized Bed Reactor. Met. Mater. Trans. B 1996, 27, 731. [Google Scholar] [CrossRef]
- Donnely, R.P.; Brennan, L.J.; McMulan, W.; Rouiliard, A. Reduction of Iron Oxide in Ilmenite Beach Sands. Part II-by Gaseous and by Solid Carbon Reductants as a Preliminary Step in Beneficiation by Removal of the Reduced Iron Oxide. Aust. Min. 1970, 62, 52–59. [Google Scholar]
- Jones, D.G. Kinetics of Gaseous Reduction of Ilmenite. J. Appl. Chem. Biotechnol. 1975, 25, 561–582. [Google Scholar] [CrossRef]
- Sun, K.; Takahashi, R.; Yagi, J. Reduction Kinetics of Cement-Bonded Natural Ilmenite Pellets with Hydrogen. ISIJ Int. 1992, 32, 496–504. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, Z.; Matsuura, H.; Tsukihashi, F. Reduction Extraction Kinetics of Titania and Iron from an Ilmenite by H2–Ar Gas Mixtures. ISIJ Int. 2009, 49, 164–170. [Google Scholar] [CrossRef]
- Bardi, G.; Gozzi, D.; Stranges, S. High Temperature Reduction Kinetics of Ilmenite by Hydrogen. Mater. Chem. Phys. 1987, 17, 325–341. [Google Scholar] [CrossRef]
- Lobo, S.C. Experimental Investigations and Modelling of Solid-State Ilmenite Reduction with Hydrogen and Carbon Monoxide; NTNU: Trondheim, Norway, 2015; ISBN 978-82-326-1275-8. [Google Scholar]
- Sun, K.; Akiyama, T.; Takahashi, R.; Yagi, J. Hydrogen Reduction of Natural Ilmenite in a Fluidized Bed. ISIJ Int. 1995, 35, 360–366. [Google Scholar] [CrossRef]
- Kapilashrami, A.; Arvanitidis, I.; Sichen, D. Investigation of the Kinetics of Reduction of Iron Titanate (FeTiO3) by Hydrogen. High Temp. Mater. Process. 1996, 15, 73–82. [Google Scholar] [CrossRef]
- Zhang, G.-H.; Chou, K.-C.; Zhao, H.-L. Reduction Kinetics of FeTiO3 Powder by Hydrogen. ISIJ Int. 2012, 52, 1986–1989. [Google Scholar] [CrossRef]
- Dang, J.; Hu, X.; Zhang, G.; Hou, X.; Yang, X.; Chou, K.-C. Kinetics of Reduction of Titano-Magnetite Powder by H2. High Temp. Mater. Process. 2013, 32, 229–236. [Google Scholar] [CrossRef]
- Dang, J.; Zhang, G.; Chou, K. Kinetics and Mechanism of Hydrogen Reduction of Ilmenite Powders. J. Alloys Compd. 2015, 619, 443–451. [Google Scholar] [CrossRef]
- Lobo, S.C.; (Eramet Titanium and Iron). Personal communication, 2021.
- Hayes, P.C. Stability Criteria for Product Microstructures Formed on Gaseous Reduction of Solid Metal Oxides. Met. Mater. Trans. B 2010, 41, 19–34. [Google Scholar] [CrossRef]
- Bale, C.W.; Bélisle, E.; Chartrand, P.; Decterov, S.A.; Eriksson, G.; Gheribi, A.E.; Hack, K.; Jung, I.-H.; Kang, Y.-B.; Melançon, J.; et al. FactSage Thermochemical Software and Databases, 2010–2016. Calphad 2016, 54, 35–53. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Schanche, T.; (SINTEF, Trondheim, Norway). Personal communication, 2021.



| Al2O3 | Fe(tot) | MgO | MnO | SiO2 | TiO2 | V2O5 | FeO | Fe2O3 |
|---|---|---|---|---|---|---|---|---|
| 0.6 | 31.3 | 0.4 | 1.5 | 0.5 | 50.9 | 0.3 | 0.9 | 43.7 |
| N° | Sample Mass (g) | Control Temperature (°C) | Expected Crucible Temperature a (°C) | Holding Time (min) | Gas Composition (%H2/%H2O) | Gas Flow (L/min) |
|---|---|---|---|---|---|---|
| 1 | 201.48 | 860 | 910 | 180 | 95/5 | 8 |
| 2 | 200.24 | 760 | 810 | 163 b | 95/5 | 8 |
| 3 | 200.29 | 860 | 910 | 180 | 94/6 | 8 |
| 4 | 200.05 | 860 | 910 | 180 | 98/2 | 8 |
| 5 | 200.07 | 760 | 810 | 180 | 98/2 | 8 |
| 6 | 199.96 | 810 | 860 | 180 | 95/5 | 8 |
| 7 | 200.01 | 660 | 710 | 180 | 98/2 | 8 |
| 8 | 200.01 | 810 | 860 | 180 | 100/0 c | 7.44 c |
| 9 | 200.01 | 810 | 860 | 60 | 100/0→93/7 d | 7.44→8 d |
| 10 | 199.95 | 810 | 860 | 180 | 93/7 | 8 |
| N° | T [°C] | pH2 | pH2,eq FactSage | k2 | pH2,eq “Solver” | k2 “Solver” |
|---|---|---|---|---|---|---|
| 5 | 810 | 0.980 | 0.948 | 0.011 | 0.946 | 0.011 |
| 2 | 810 | 0.950 | 0.948 | 0.019 | 0.946 | 0.011 |
| 4 | 910 | 0.980 | 0.926 | 0.018 | 0.928 | 0.018 |
| 1 | 910 | 0.950 | 0.926 | 0.017 | 0.928 | 0.018 |
| Reaction Fe3+→Fe2+ | Reaction Fe2+→Fe | ||
|---|---|---|---|
| k0,1 [min−1] | Ea1 [kJ/mol] | k0,2 [min−1] | Ea2 [kJ/mol] |
| 48.44 | 43.2 | 3.17 | 50.8 |
| Reaction Fe3+→Fe2+ | Reaction Fe2+→Fe | ||
|---|---|---|---|
| k0,1 [min−1] | Ea1 [kJ/mol] | k0,2 [min−1] | Ea2 [kJ/mol] |
| 72 | 50 | 3.1 | 51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Canaguier, V.; Ringdalen, E. Reduction Kinetics of Pre-Oxidized Ilmenite Pellets by H2-H2O Gas Mixtures. Metals 2023, 13, 332. https://doi.org/10.3390/met13020332
Canaguier V, Ringdalen E. Reduction Kinetics of Pre-Oxidized Ilmenite Pellets by H2-H2O Gas Mixtures. Metals. 2023; 13(2):332. https://doi.org/10.3390/met13020332
Chicago/Turabian StyleCanaguier, Vincent, and Eli Ringdalen. 2023. "Reduction Kinetics of Pre-Oxidized Ilmenite Pellets by H2-H2O Gas Mixtures" Metals 13, no. 2: 332. https://doi.org/10.3390/met13020332
APA StyleCanaguier, V., & Ringdalen, E. (2023). Reduction Kinetics of Pre-Oxidized Ilmenite Pellets by H2-H2O Gas Mixtures. Metals, 13(2), 332. https://doi.org/10.3390/met13020332







